Application of Machine Learning for Aboveground Biomass Modeling in Tropical and Temperate Forests from Airborne Hyperspectral Imagery
Abstract
1. Introduction
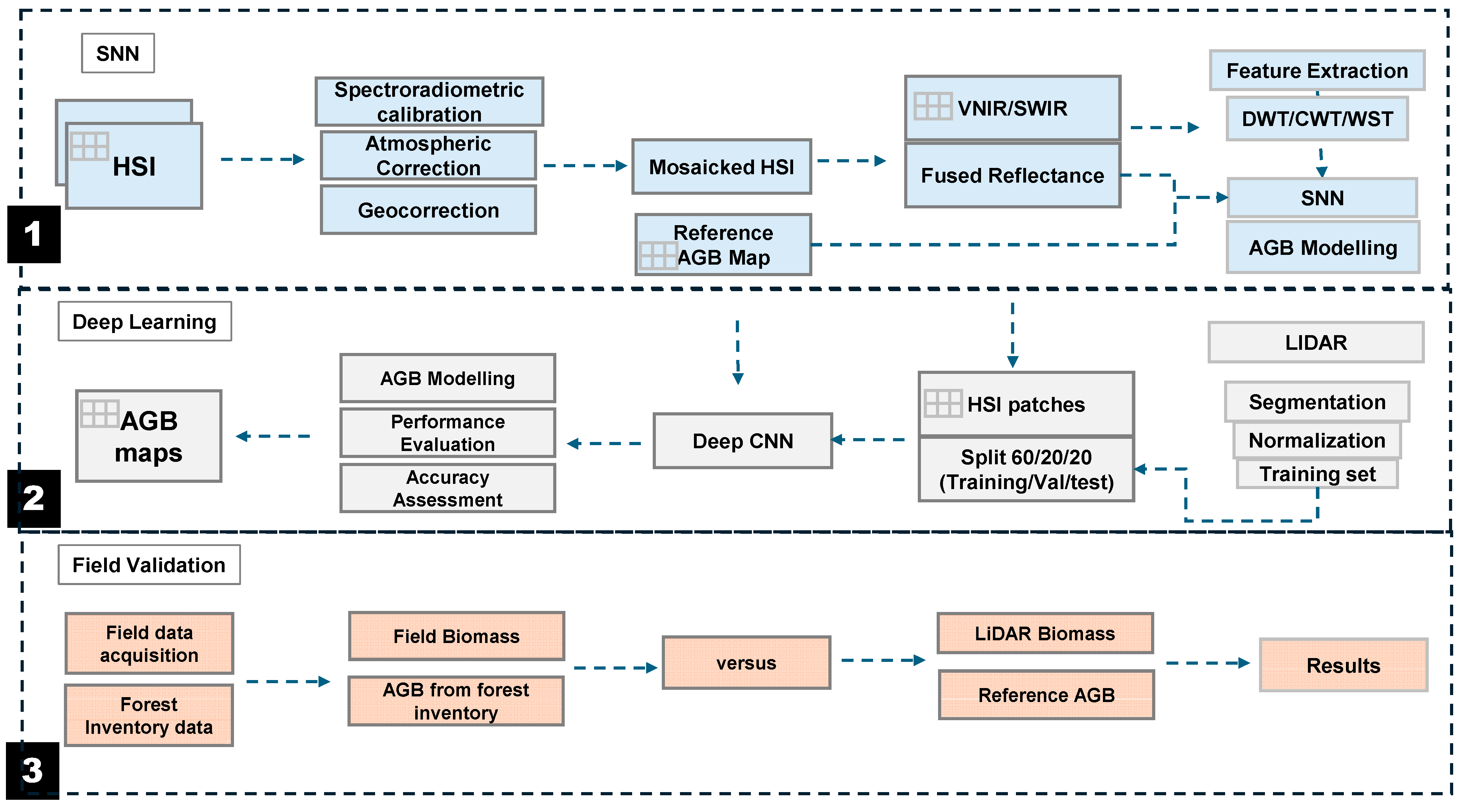
2. Materials and Methods
2.1. Study Areas
2.2. Hyperspectral Imagery
2.3. Training and Field Data
2.3.1. Global Above Ground Biomass Map (Tropical and Temperate)
2.3.2. Airborne LiDAR (Temperate Forest)
2.3.3. Field Data
2.4. Machine Learning Model Development and Evaluation
2.4.1. Wavelet Decomposition
2.4.2. Spectral Feature Selection
2.4.3. Shallow Neural Network (SNN)
2.4.4. Deep Transfer Convolutional Neural Network Framework (3D-CNN)
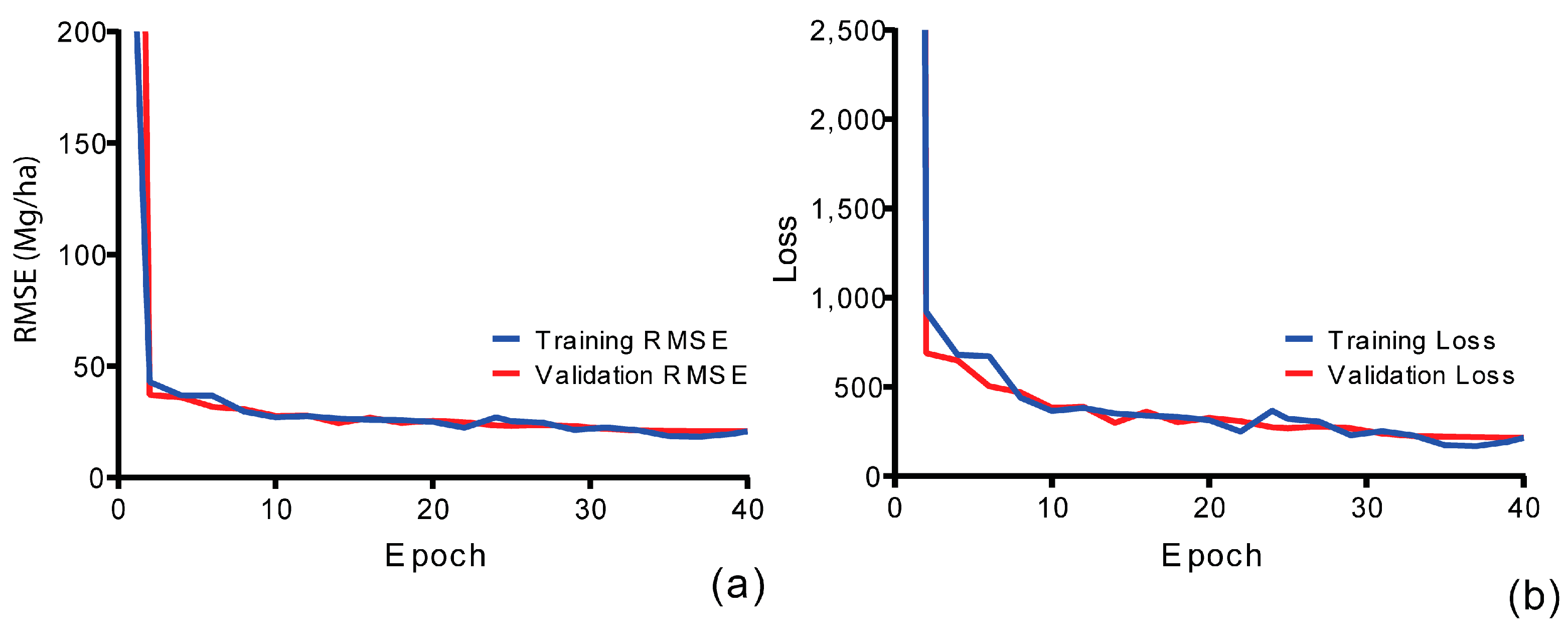
2.4.5. Hyperparameter Tuning
2.4.6. Performance Metrics for Model Evaluation
2.5. Proof-of-Concept Model Development
2.6. Aboveground Biomass Modeling in Different Forest Types
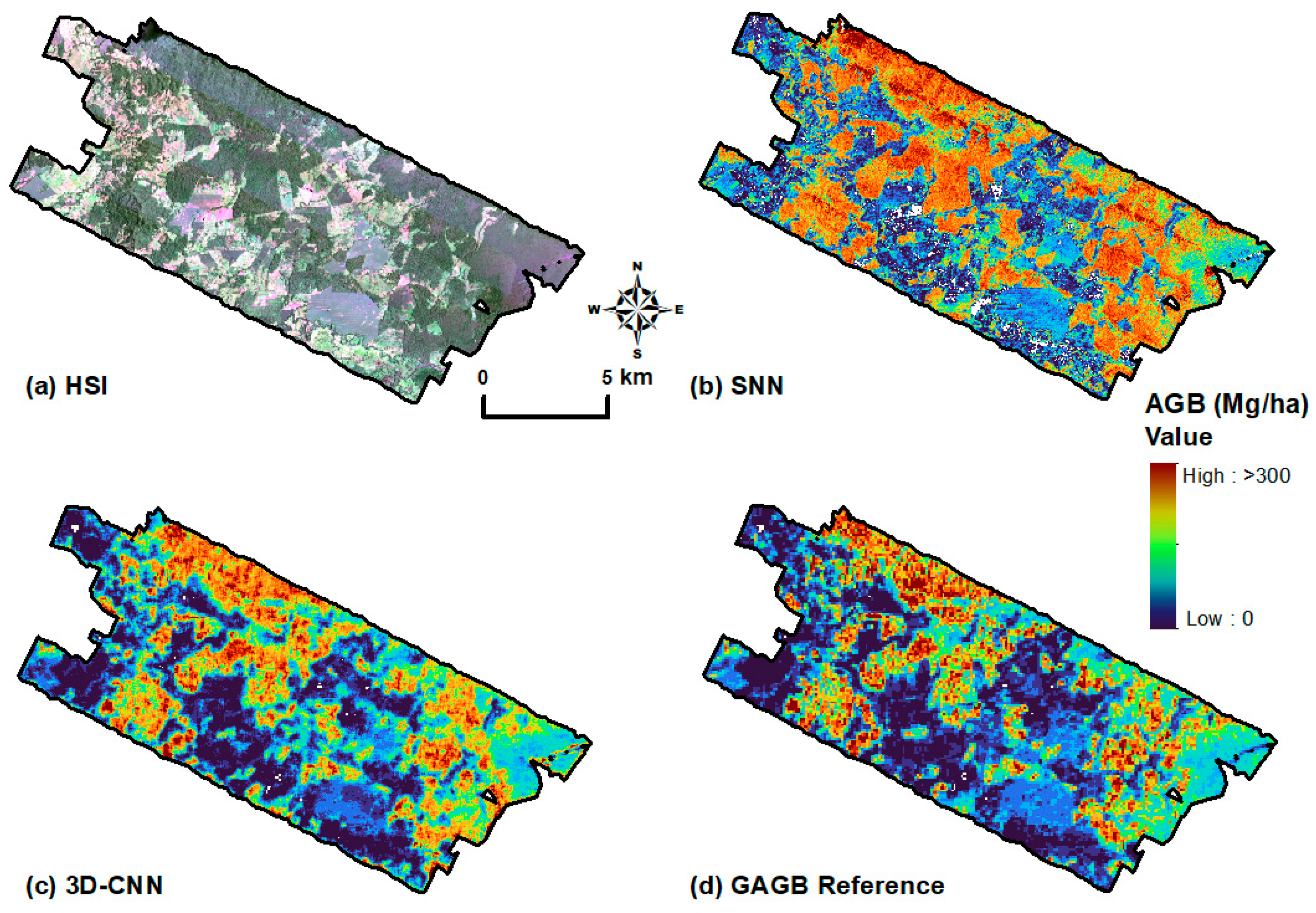
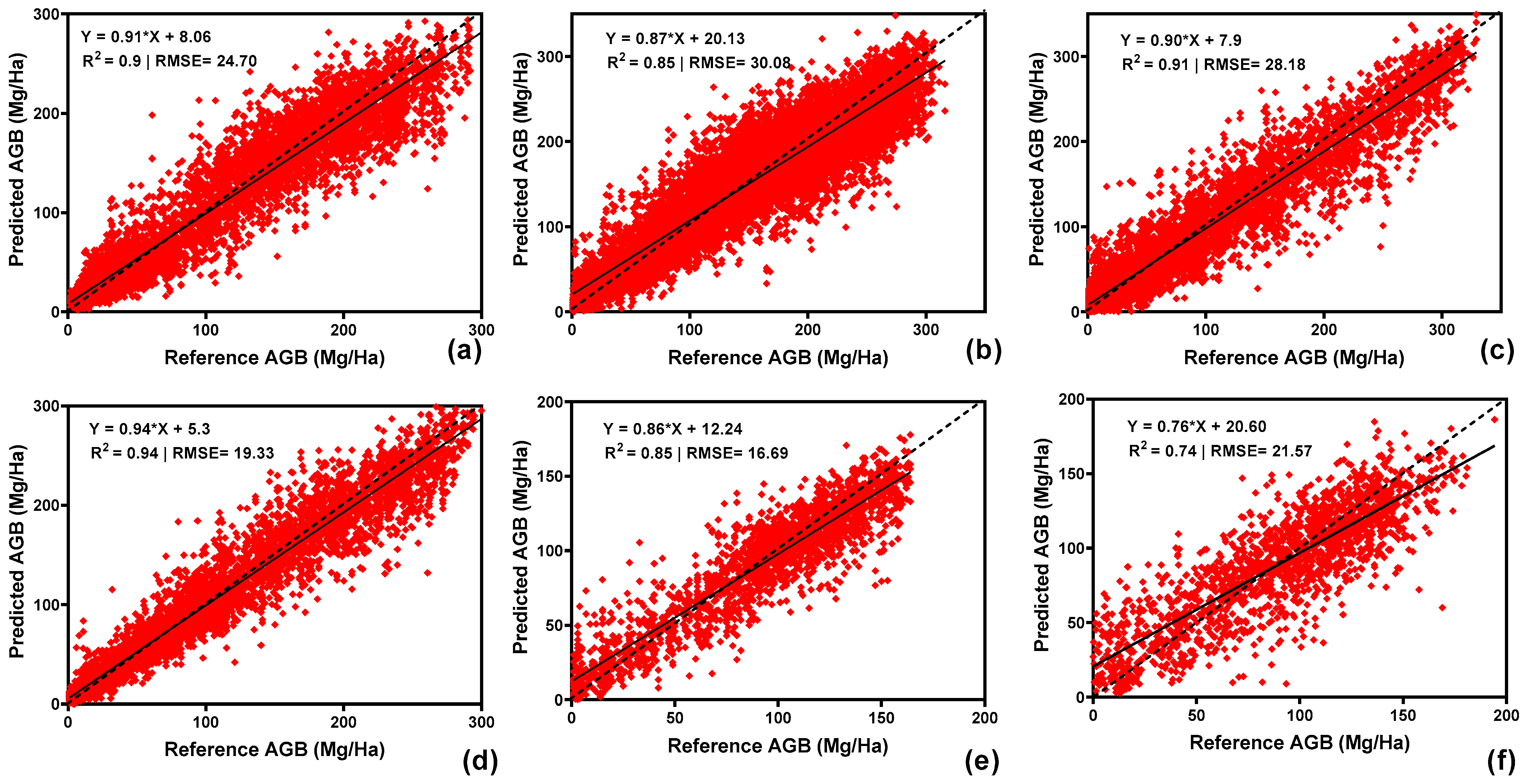
3. Results
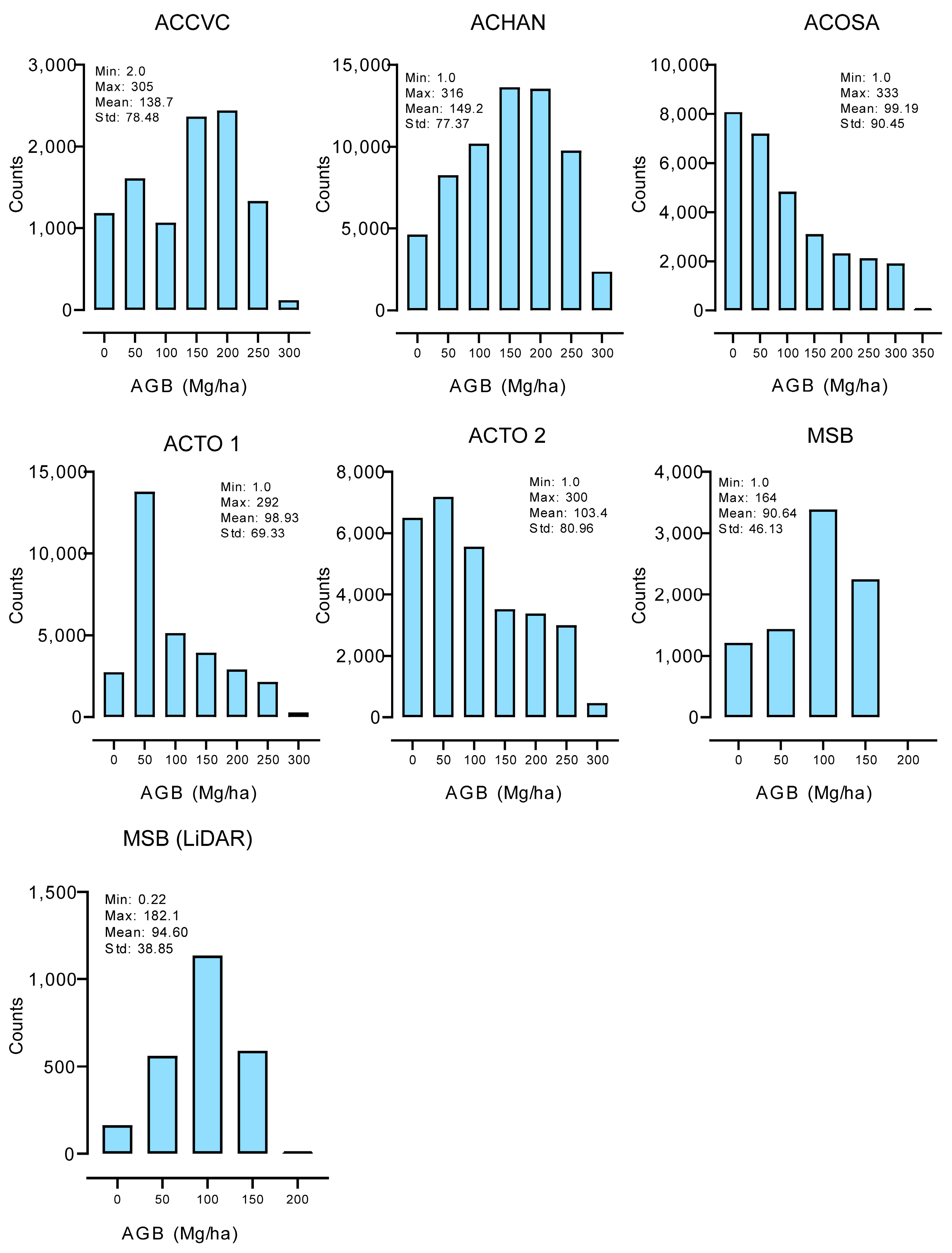
3.1. Comparison of Training Data with Field-Based AGB
3.2. Proof-of-Concept Model Comparison
3.2.1. SNN Model Comparisons
3.2.2. Spectral–Spatial Features (3D-CNN)
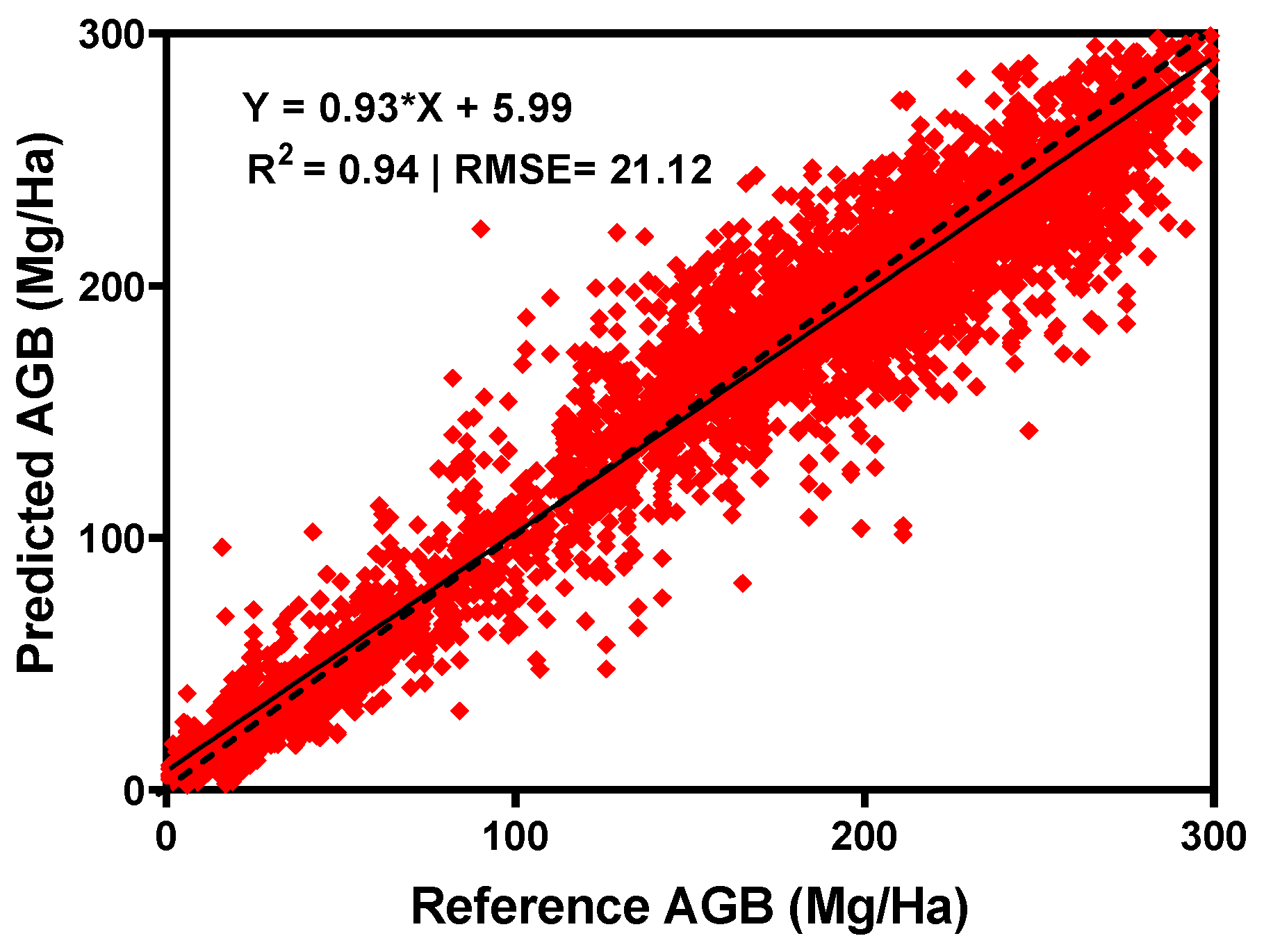
3.3. Benchmark Dataset Comparison
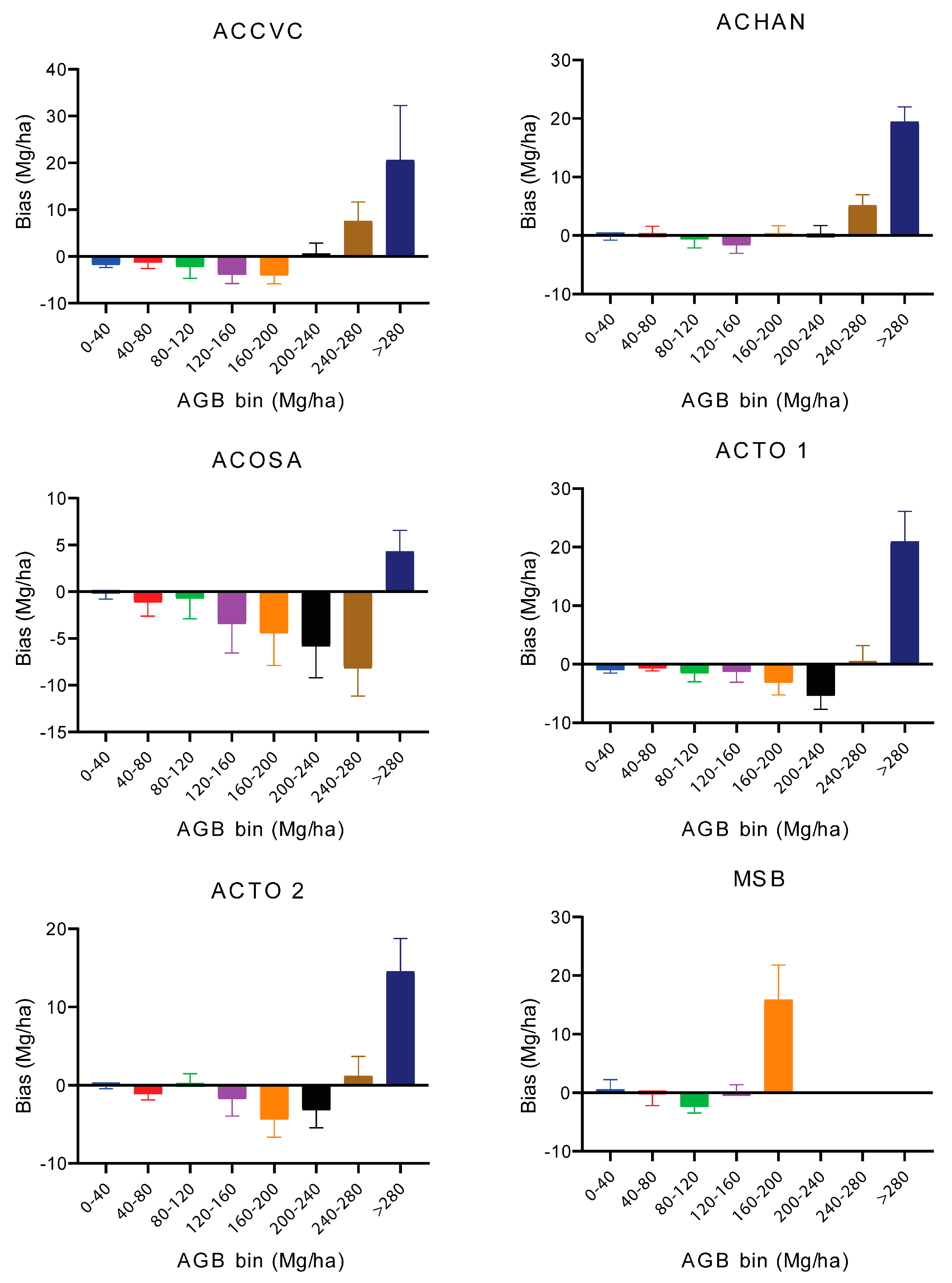
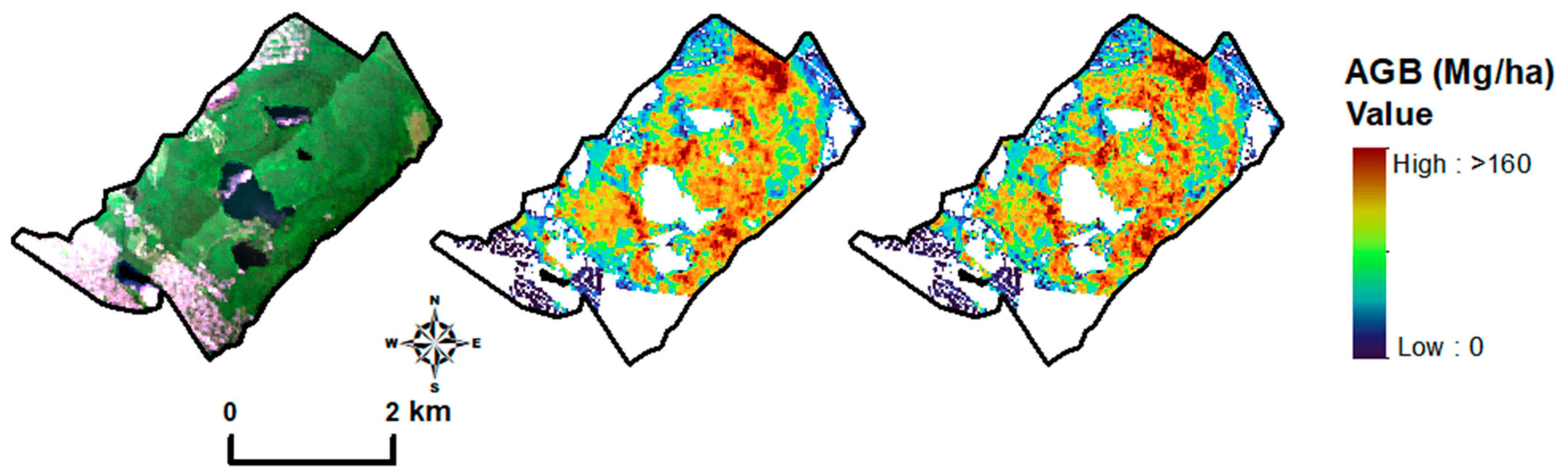
3.4. Model Performance Across Forest Types (Hyperspectral Imagery)
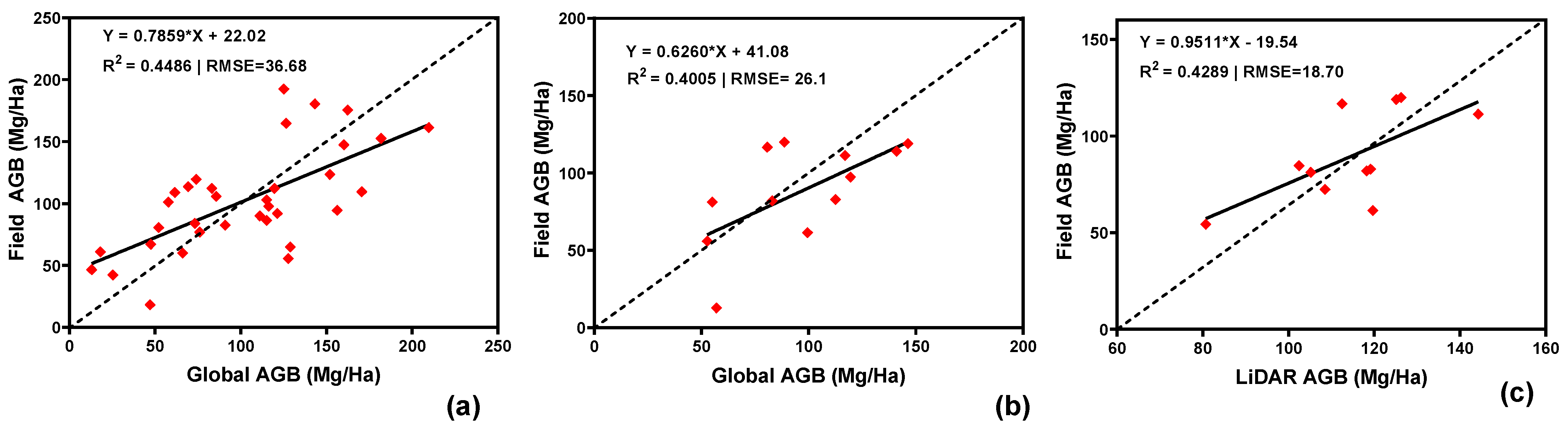
3.5. Model Performance—Airborne LiDAR
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dar, J.A.; Subashree, K.; Bhat, N.A.; Sundarapandian, S.; Xu, M.; Saikia, P.; Kumar, A.; Kumar, A.; Khare, P.K.; Khan, M.L. Role of major forest biomes in climate change mitigation: An eco-biological perspective. In Socio-Economic and Eco-Biological Dimensions in Resource Use and Conservation; Springer International Publishing: New York, NY, USA, 2020; pp. 483–526. [Google Scholar] [CrossRef]
- Sedjo, R.A. The carbon cycle and global forest ecosystem. Water Air Soil Pollut. 1993, 70, 295–307. [Google Scholar] [CrossRef]
- Birdsey, R.; Angeles-Perez, G.; Kurz, W.A.; Lister, A.; Olguin, M.; Pan, Y.; Wayson, C.; Wilson, B.; Johnson, K. Approaches to monitoring changes in carbon stocks for REDD+. Carbon Manag. 2013, 4, 519–537. [Google Scholar] [CrossRef]
- Danon, S.; Bettiati, D. Reducing Emissions from Deforestaton and Forest Degradation (REDD+)–what is behind the idea and what is the role of UN-REDD and Forest Carbon Partnership Facility (FCPF)? South-East Eur. For. 2012, 2, 95–99. [Google Scholar] [CrossRef]
- Gizachew, B.; Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O.M.; Breidenbach, J.; Zahabu, E.; Mauya, E.W. Mapping and estimating the total living biomass and carbon in low-biomass woodlands using Landsat 8 CDR data. Carbon Balance Manag. 2016, 11, 13. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; Hermosilla, T.; White, J.C.; Bater, C.W.; Hobart, G.; Bronson, S.C. Development and implementation of a stand-level satellite-based forest inventory for Canada. For. Int. J. For. Res. 2024, 97, 546–563. [Google Scholar] [CrossRef]
- Kurz, W.A.; Apps, M.J. Developing Canada’s national forest carbon monitoring, accounting and reporting system to meet the reporting requirements of the kyoto protocol. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 33–43. [Google Scholar] [CrossRef]
- Chave Jr Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Mohd Zaki, N.A.; Abd Latif, Z. Carbon sinks and tropical forest biomass estimation: A review on role of remote sensing in aboveground-biomass modelling. Geocarto Int. 2017, 32, 701–716. [Google Scholar] [CrossRef]
- Torre, L. Biomass estimation using LiDAR data. Int. J. Sustain. Energy Plan. Manag. 2018, 17, 79–90. [Google Scholar] [CrossRef]
- UNFCCC. Methodological guidance for activities relating to reducing emissions from deforestation and forest degradation and the role of conservation, sustainable management of forests and enhancement of forest carbon stocks in developing countries. In Proceedings of the Conference of the Parties, Copenhagen, Denmark, 7–19 December 2009; Decision 4/CP.15.; United Nations Framework Convention on Climate Change: Bonn, Germany, 2009; Available online: https://unfccc.int/resource/docs/2009/cop15/eng/11a01.pdf (accessed on 20 February 2023).
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef] [PubMed]
- Pizaña, J.M.G.; Hernández, J.M.N.; Romero, N.C. Remote sensing-based biomass estimation. Environ. Appl. Remote Sens. 2016, 10, 9952. [Google Scholar] [CrossRef]
- Tian, L.; Wu, X.; Tao, Y.; Li, M.; Qian, C.; Liao, L.; Fu, W. Review of remote sensing-based methods for forest aboveground biomass estimation: Progress, challenges, and prospects. Forests 2023, 14, 1086. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Liu, Y.; Wu, Y.; Tang, J.; Xu, W.; Wang, L.; Ou, G. Improving the accuracy of forest aboveground biomass using Landsat 8 OLI images by quantile regression neural network for Pinus densata forests in southwestern China. Front. For. Glob. Chang. 2023, 6, 1162291. [Google Scholar] [CrossRef]
- Bauer, L.; Huth, A.; Bogdanowski, A.; Müller, M.; Fischer, R. Edge effects in amazon forests: Integrating remote sensing and modeling to assess changes in biomass and productivity. Remote Sens. 2024, 16, 501. [Google Scholar] [CrossRef]
- Cao, L.D.; Pan, J.J.; Li, R.J.; Li, J.L.; Li, Z.F. Integrating airborne LiDAR and optical data to estimate forest aboveground biomass in arid and semi-arid regions of China. Remote Sens. 2018, 10, 532. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint LiDAR and hyperspectral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernandez, J.; Corvalan, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Shu, Q.; Xi, L.; Wang, K.; Xie, F.; Pang, Y.; Song, H. Optimization of samples for remote sensing estimation of forest aboveground biomass at the regional scale. Remote Sens. 2022, 14, 4187. [Google Scholar] [CrossRef]
- Chinembiri, T.S.; Mutanga, O.; Dube, T. A multi-source data approach to carbon stock prediction using bayesian hierarchical geostatistical models in plantation forest ecosystems. GIScience Remote Sens. 2024, 61, 2303868. [Google Scholar] [CrossRef]
- Jacon, A.D.; Galvao, L.S.; Dalagnol, R.; dos Santos, J.R. Aboveground biomass estimates over Brazilian savannas using hyperspectral metrics and machine learning models: Experiences with Hyperion/EO-1. GIScience Remote Sens. 2021, 58, 1112–1129. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Automated machine learning driven stacked ensemble modeling for forest aboveground biomass prediction using multitemporal sentinel-2 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 3442–3454. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K. Implementation of a UAV–hyperspectral pushbroom imager for ecological monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
- Huber, S.; Kneubühler, M.; Psomas, A.; Itten, K.; Zimmermann, N.E. Estimating foliar biochemistry from hyperspectral data in mixed forest canopy. For. Ecol. Manag. 2008, 256, 491–501. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Kalacska, M.; Arroyo-Mora, J.P.; Soffer, R.; Leblanc, G. Quality control assessment of the mission airborne carbon 13 (mac-13) hyperspectral imagery from Costa Rica. Can. J. Remote Sens. 2016, 42, 85–105. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L.; Liu, K.; She, G.; Ruan, H. Aboveground biomass estimation in a subtropical forest using airborne hyperspectral data. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016; IEEE: New York, NY, USA; pp. 391–394. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Beier, C.M.; Johnson, L.; Phoenix, D.B.; Mahoney, M. Decision tree-based machine learning models for above-ground biomass estimation using multi-source remote sensing data and object-based image analysis. Geocarto Int. 2022, 37, 12763–12791. [Google Scholar] [CrossRef]
- Migolet, P.; Goïta, K.; Pambo, A.F.K.; Mambimba, A.N. Estimation of the total dry aboveground biomass in the tropical forests of Congo Basin using optical, LiDAR, and radar data. GISci. Remote Sens. 2022, 59, 431–460. [Google Scholar] [CrossRef]
- Wang, L.; Ju, Y.; Ji, Y.; Marino, A.; Zhang, W.; Jing, Q. Estimation of Forest Above-Ground Biomass in the Study Area of Greater Khingan Ecological Station with Integration of Airborne LiDAR, Landsat 8 OLI, and Hyperspectral Remote Sensing Data. Forests 2024, 15, 1861. [Google Scholar] [CrossRef]
- Gao, L.; Chai, G.; Zhang, X. Above-ground biomass estimation of plantation with different tree species using airborne LiDAR and hyperspectral data. Remote Sens. 2022, 14, 2568. [Google Scholar] [CrossRef]
- Brovkina, O.; Novotny, J.; Cienciala, E.; Zemek, F.; Russ, R. Mapping forest aboveground biomass using airborne hyperspectral and LiDAR data in the mountainous conditions of Central Europe. Ecol. Eng. 2017, 100, 219–230. [Google Scholar] [CrossRef]
- Güner, Ş.T.; Diamantopoulou, M.J.; Poudel, K.P.; Çömez, A.; Özçelik, R. Employing artificial neural network for effective biomass prediction: An alternative approach. Comput. Electron. Agric. 2022, 192, 106596. [Google Scholar] [CrossRef]
- Kumari, K.; Kumar, S. Machine learning based modeling for forest aboveground biomass retrieval. In Proceedings of the 2023 International Conference on Machine Intelligence for GeoAnalytics and Remote Sensing (MIGARS), Hyderabad, India, 27–29 January 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of airborne LiDAR data and hyperspectral imagery for aboveground and belowground forest biomass estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Singh, B.; Verma, A.K.; Tiwari, K.; Joshi, R. Above ground tree biomass modeling using machine learning algorithms in western Terai Sal Forest of Nepal. Heliyon 2023, 9, e21485. [Google Scholar] [CrossRef] [PubMed]
- Thapa, B.; Lovell, S.; Wilson, J. Remote sensing and machine learning applications for aboveground biomass estimation in agroforestry systems: A review. Agroforest. Syst. 2023, 97, 1097–1111. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Prediction of Forest Aboveground Biomass Using Multitemporal Multispectral Remote Sensing Data. Remote Sens. 2021, 13, 1282. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.R.; Mohammadzadeh, A. Biomass estimation of a temperate deciduous forest using wavelet analysis. IEEE Trans. Geosci. Remote Sens. 2012, 51, 765–776. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Ranjan, P.; Girdhar, A. A comprehensive systematic review of deep learning methods for hyperspectral images classification. Int. J. Remote Sens. 2022, 43, 6221–6306. [Google Scholar] [CrossRef]
- Li, Q.; Wen, Y.; Zheng, J.; Zhang, Y.; Fu, H. HyUniDA: Breaking Label Set Constraints for Universal Domain Adaptation in Cross-Scene Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5518415. [Google Scholar] [CrossRef]
- Yin, J.; Qi, C.; Chen, Q.; Qu, J. Spatial-spectral network for hyperspectral image classification: A 3-D CNN and Bi-LSTM framework. Remote Sens. 2021, 13, 2353. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; Volume 25, Available online: https://proceedings.neurips.cc/paper_files/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf (accessed on 11 February 2023).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Tappayuthpijarn, K.; Vindevogel, B.S. High-accuracy machine learning models to estimate above ground biomass over tropical closed evergreen forest areas from satellite data. IOP Conf. Ser. Earth Environ. Sci. 2022, 1006, 012001. [Google Scholar] [CrossRef]
- Holdridge, L.R. Life Zone Ecology; Tropical Science Center: San Jose, Costa Rica, 1967. [Google Scholar]
- Svob, S.; Arroyo-Mora, J.P.; Kalacska, M. A wood density and aboveground biomass variability assessment using pre-felling inventory data in Costa Rica. Carbon Balance Manag. 2014, 9, 9. [Google Scholar] [CrossRef]
- Wallis, C.I.B.; Crofts, A.L.; Inamdar, D.; Arroyo-Mora, J.P.; Kalacska, M.; Laliberte, E.; Vellend, M. Remotely sensed carbon content: The role of tree composition and tree diversity. Remote Sens. Environ. 2023, 284, 113333. [Google Scholar] [CrossRef]
- Inamdar, D.; Kalacska, M.; Arroyo-Mora, J.P.; Leblanc, G. The directly-georeferenced hyperspectral point cloud: Preserving the integrity of hyperspectral imaging data. Front. Remote Sens. 2021, 2, 675323. [Google Scholar] [CrossRef]
- Soffer, R.J.; Ifimov, G.; Arroyo-Mora, J.P.; Kalacska, M. Validation of airborne hyperspectral imagery from laboratory panel characterization to image quality assessment: Implications for an arctic peatland surrogate simulation site. Can. J. Remote Sens. 2019, 45, 476–508. [Google Scholar] [CrossRef]
- Osei Darko, P.; Kalacska, M.; Arroyo-Mora, J.P.; Fagan, M.E. Spectral complexity of hyperspectral images: A new approach for mangrove classification. Remote Sens. 2021, 13, 2604. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Feingersh, T. Operational BRDF effects correction for wide-field-of-view optical scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2014, 53, 1855–1864. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R. Evaluation of brefcor BRDF effects correction for HYSPEX, CASI, and APEX imaging spectroscopy data. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Inamdar, D.; Kalacska, M.; Darko, P.O.; Arroyo-Mora, J.P.; Leblanc, G. Spatial response resampling (SR2): Accounting for the spatial point spread function in hyperspectral image resampling. MethodsX 2023, 10, 101998. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.; Avitabile, V.; Araza, A.; De Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P. The global forest above-ground biomass pool for 2010 estimated from high-resolution satellite observations. Earth Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Quegan, S.; Rauste, Y.; Bouvet, A.; Carreiras, J.; Cartus, O.; Carvalhais, N.; LeToan, T.; Mermoz, S.; Santoro, M. D6–Global Biomass Map: Algorithm Theoretical Basis Document. 2017. Available online: https://globbiomass.org/wp-content/uploads/DOC/Deliverables/D6_D7/GlobBiomass_D6_7_Global_ATBD_v3.pdf (accessed on 1 February 2023).
- Rozendaal, D.M.A.; Santoro, M.; Schepaschenko, D.; Avitabile, V.; Herold, M. DUE GlobBiomass (D17) Validation Report. In D17 Validation Report. 2017. Available online: https://www.dropbox.com/home?checklist=close&preview=GlobBiomass_D_17_Validation_Report_V06.pdf (accessed on 1 February 2023).
- GéoMont Acquisition of the 2008 MTQ LiDAR Survey in Montérégie. 2008. Available online: https://www.geomont.qc.ca/projets/fiche/?id_projet=70 (accessed on 1 January 2024).
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Svob, S.; Arroyo-Mora, J.P.; Kalacska, M. The development of a forestry geodatabase for natural forest management plans in Costa Rica. For. Ecol. Manag. 2014, 327, 240–250. [Google Scholar] [CrossRef]
- Brown, S.; Estimating Biomass and Biomass Change of Tropical Forests: A Primer. Food Agriculture Org. 1997. Available online: https://www.fao.org/docrep/w4095e/w4095e00.HTM (accessed on 1 February 2023).
- Crofts, A.L.; St-Jean, S.; Vellend, M. Canadian Airborne Biodiversity Observatory’s Forest Inventory Field Survey Protocol v.2. Protocols.io. 2022. Available online: https://doi.org/10.17504/protocols.io.q26g7rn23vwz/v2 (accessed on 10 February 2023).
- Ung, C.-H.; Bernier, P.; Guo, X.-J. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Paré, D.; Bernier, P.; Lafleur, B.; Titus, B.D.; Thiffault, E.; Maynard, D.G.; Guo, X. Estimating stand-scale biomass, nutrient contents, and associated uncertainties for tree species of Canadian forests. Can. J. For. Res. 2013, 43, 599–608. [Google Scholar] [CrossRef]
- Rioul, O.; Vetterli, M. Wavelets and signal processing. IEEE Signal Process. Mag. 1991, 8, 14–38. [Google Scholar] [CrossRef]
- Hubbard, B.B. The World According to Wavelets: The Story of a Mathematical Technique in the Making, Second Edition, 2nd ed.; A K Peters/CRC Press: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Bruce, L.M.; Koger, C.H.; Jiang, L. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Sun, J.; Cao, Y.; Yao, K.; Xu, M. A deep learning method for predicting lead content in oilseed rape leaves using fluorescence hyperspectral imaging. Food Chem. 2022, 409, 135251. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A.G.; Féret, J.-B.; Jacquemoud, S.; Ustin, S.L. Deriving Leaf Mass per Area (LMA) from foliar reflectance across a variety of plant species using continuous wavelet analysis. ISPRS J. Photogramm. Remote Sens. 2014, 87, 28–38. [Google Scholar] [CrossRef]
- Fu, Y.; Jia, X.; Huang, W.; Wang, J. A comparative analysis of mutual information-based feature selection for hyperspectral image classification. In Proceedings of the IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 148–152. [Google Scholar] [CrossRef]
- Schreiber, L.V.; Atkinson Amorim, J.G.; Guimarães, L.; Motta Matos, D.; Maciel da Costa, C.; Parraga, A. Above-ground biomass wheat estimation: Deep learning with UAV-based RGB images. Appl. Artif. Intell. 2022, 36, 2055392. [Google Scholar] [CrossRef]
- MATLAB. Classify Hyperspectral Images Using Deep Learning. 2023. Available online: https://www.mathworks.com/help/images/hyperspectral-image-classification-using-deep-learning.html (accessed on 10 February 2023).
- Araza, A.; De Bruin, S.; Herold, M.; Quegan, S.; Labriere, N.; Rodriguez-Veiga, P.; Avitabile, V.; Santoro, M.; Mitchard, E.T.; Ryan, C.M. A comprehensive framework for assessing the accuracy and uncertainty of global above-ground biomass maps. Remote Sens. Environ. 2022, 272, 112917. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of variable selection and forest type on forest aboveground biomass estimation using machine learning algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Dong, J.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 10. [Google Scholar] [CrossRef]
- Wheeler, C.E.; Mitchard, E.T.A.; Nalasco Reyes, H.E.; Iñiguez Herrera, G.; Marquez Rubio, J.I.; Carstairs, H.; Williams, M. A new field protocol for monitoring forest degradation. Front. For. Glob. Chang. 2021, 4, 655280. [Google Scholar] [CrossRef]
- Anand, R.; Veni, S.; Aravinth, J. Robust classification technique for hyperspectral images based on 3d-discrete wavelet transform. Remote Sens. 2021, 13, 1255. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P. Wavelet transform applied to EO-1 hyperspectral data for forest LAI and crown closure mapping. Remote Sens. Environ. 2004, 91, 212–224. [Google Scholar] [CrossRef]
- Yao, X.; Si, H.; Cheng, T.; Jia, M.; Chen, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Chen, C.; Cai, J.; et al. Hyperspectral estimation of canopy leaf biomass phenotype per ground area using a continuous wavelet analysis in wheat. Front. Plant Sci. 2018, 9, 1360. [Google Scholar] [CrossRef] [PubMed]
- de Almeida, C.T.; Galvão, L.S.; Aragão, L.E.d.O.C.e.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.d.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.d.A.; Silva, C.V.d.J.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modelling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Laurin, G.V.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with LiDAR and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J. Estimating forest aboveground biomass using temporal features extracted from multiple satellite data products and ensemble machine learning algorithm. Geocarto Int. 2023, 38, 2153930. [Google Scholar] [CrossRef]
- Mascaro, J.; Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Martin, R.E.; Anderson, C.; Higgins, M.; Chadwick, K.D. A tale of two “forests”: Random forest machine learning aids tropical forest carbon mapping. PLoS ONE 2014, 9, e85993. [Google Scholar] [CrossRef]
- Kattenborn, T.; Schiefer, F.; Frey, J.; Feilhauer, H.; Mahecha, M.D.; Dormann, C.F. Spatially autocorrelated training and validation samples inflate performance assessment of convolutional neural networks. ISPRS Open J. Photogramm. Remote Sens. 2022, 5, 100018. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the sampling strategy for evaluation of spectral-spatial methods in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 862–880. [Google Scholar] [CrossRef]
- Shi, Y.; Yin, Y.; Song, X.; Cui, H.; Zhu, D.; Song, H. A nonoverlapping sampling approach with peak data utilization for hyperspectral classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5502805. [Google Scholar] [CrossRef]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–spatial exploration for hyperspectral image classification via the fusion of fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; Cárdenas Domínguez, J.L.; Corral-Rivas, J.J.; Jiménez, E.; López-Sánchez, C.A.; Vega-Nieva, D.J. Modeling of aboveground biomass with Landsat 8 OLI and machine learning in temperate forests. Forests 2020, 11, 11. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral saturation in the remote sensing of high-density vegetation traits: A systematic review of progress, challenges, and prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar] [CrossRef]
- Kalácska, M.; Sánchez-Azofeifa, G.A.; Rivard, B.; Calvo-Alvarado, J.C.; Journet, A.R.P.; Arroyo-Mora, J.P.; Ortiz-Ortiz, D. Leaf area index measurements in a tropical moist forest: A case study from Costa Rica. Remote Sens. Environ. 2004, 91, 134–152. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; White, L.J.T.; Abernethy, K.A.; Jeffery, K.J.; Lewis, S.L.; Collins, M.; Lefsky, M.A.; Leal, M.E.; Woodhouse, I.H.; et al. Mapping tropical forest biomass with radar and spaceborne LiDAR in Lopé National Park, Gabon: Overcoming problems of high biomass and persistent cloud. Biogeosciences 2012, 9, 179–191. [Google Scholar] [CrossRef]
- Steininger, M.K. Satellite estimation of tropical secondary forest above-ground biomass: Data from Brazil and Bolivia. Int. J. Remote Sens. 2000, 21, 1139–1157. [Google Scholar] [CrossRef]
- Liao, Z.; Liu, X.; van Dijk, A.; Yue, C.; He, B. Continuous woody vegetation biomass estimation based on temporal modeling of Landsat data. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102811. [Google Scholar] [CrossRef]
- Wu, Y.; Ou, G.; Lu, T.; Huang, T.; Zhang, X.; Liu, Z.; Yu, Z.; Guo, B.; Wang, E.; Feng, Z.; et al. Improving aboveground biomass estimation in lowland tropical forests across aspect and age stratification: A case study in Xishuangbanna. Remote Sens. 2024, 16, 1276. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Chazdon, R.L.; Letcher, S.G.; Van Breugel, M.; Martínez-Ramos, M.; Bongers, F.; Finegan, B. Rates of change in tree communities of secondary Neotropical forests following major disturbances. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 273–289. [Google Scholar] [CrossRef] [PubMed]

| Region of Interest | Conservation Area | Forest Type | Precipitation (mm/Year)/Elevation (m) | Total Area (ha) | Total Flight Lines |
|---|---|---|---|---|---|
| ACCVC | Area de Conservacion Cordillera Volcanica Central | Tropical wet | 4000–8000/206 ± 182 | 50,251 | 32 |
| ACHAN | Area de Conservacion Huetar Norte | Premontane wet | 4000–8000/117 ± 44 | 11,989 | 5 |
| ACOSA | Area de Conservacion Osa | Tropical wet | 4000–8000/100 ± 119 | 67,959 | 16 |
| ACTO | Area de Conservacion Tortuguero | Tropical wet | 4000–8000/41 ± 39 | 45,177 | 15 |
| MSB | Mont Saint Bruno National Park | Temperate | 50–1300/12 ± 9 | 990 | 2 |
| Total | 176,336 | 74 |
| Sensor Characteristics | CASI-1500 | SASI-644 | SASI-600 |
|---|---|---|---|
| Field of view (°) | 39.9 | 39.7 | 39.7 |
| No. of across-track pixels | 1493 | 640 | 600 |
| No. of spectral channels | 288 (max) (programmable) | 160 (non-programmable) | 100 (non-programmable) |
| Spectral range (nm) | 375–1050 | 883–2523 | 957–2442 |
| Spectral resolution (nm) | 3.2 nm | 16 nm at 883 nm and 12 nm at 2523 | 15 nm |
| Epochs | Minibatch Size | Optimizer | Learning Rate | Loss Function | |
|---|---|---|---|---|---|
| SNN | 1000 | - | Levenberg M | 0.1 | MSE |
| CNN-3D | 40 | 256 | Adam | 0.001 | RMSE |
| Input Variable | # Extracted Features | Performance | MSE | MAE | R | R2 | RMSE |
|---|---|---|---|---|---|---|---|
| DWT-db6 | 225 | Best Model | 2032.36 | 34.97 | 0.85 | 0.72 | 45.08 |
| Average | 2132.71 | 35.88 | 0.85 | 0.72 | 46.17 | ||
| WST-N3 | 199 | Best Model | 2039.68 | 34.66 | 0.85 | 0.72 | 45.16 |
| Average | 2159.49 | 35.92 | 0.84 | 0.71 | 46.46 | ||
| WST-N2 | 210 | Best Model | 2050.8 | 35.09 | 0.85 | 0.72 | 45.29 |
| Average | 2241.14 | 36.73 | 0.84 | 0.71 | 47.33 | ||
| WST-N1 | 135 | Best Model | 2071.35 | 35.06 | 0.85 | 0.72 | 45.51 |
| Average | 2266.27 | 36.9 | 0.84 | 0.71 | 47.6 | ||
| DWT–sym7 | 203 | Best Model | 2123.02 | 35.55 | 0.85 | 0.72 | 46.08 |
| Average | 2266.12 | 36.86 | 0.83 | 0.69 | 47.58 | ||
| DWT–db5 | 213 | Best Model | 2158.07 | 36.01 | 0.84 | 0.71 | 46.46 |
| Average | 2274.16 | 37.04 | 0.83 | 0.69 | 47.68 | ||
| CWT–bump | 35 | Best Model | 3308.62 | 44.35 | 0.75 | 0.56 | 57.52 |
| Average | 3503.86 | 45.7 | 0.73 | 0.53 | 59.19 | ||
| CWT–amor | 119 | Best Model | 3530.41 | 45.95 | 0.73 | 0.53 | 59.42 |
| Average | 3688.4 | 47 | 0.71 | 0.5 | 60.73 | ||
| CWT–morse | 79 | Best Model | 3531.01 | 46.07 | 0.73 | 0.53 | 59.42 |
| Average | 3823.43 | 47.04 | 0.70 | 0.49 | 61.7 |
| PCA | MNF | t-SNE | |
|---|---|---|---|
| R square | 0.94 | 0.92 | 0.83 |
| RMSE (Mg/ha) | 21.1 | 24.15 | 35.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osei Darko, P.; Metari, S.; Arroyo-Mora, J.P.; Fagan, M.E.; Kalacska, M. Application of Machine Learning for Aboveground Biomass Modeling in Tropical and Temperate Forests from Airborne Hyperspectral Imagery. Forests 2025, 16, 477. https://doi.org/10.3390/f16030477
Osei Darko P, Metari S, Arroyo-Mora JP, Fagan ME, Kalacska M. Application of Machine Learning for Aboveground Biomass Modeling in Tropical and Temperate Forests from Airborne Hyperspectral Imagery. Forests. 2025; 16(3):477. https://doi.org/10.3390/f16030477
Chicago/Turabian StyleOsei Darko, Patrick, Samy Metari, J. Pablo Arroyo-Mora, Matthew E. Fagan, and Margaret Kalacska. 2025. "Application of Machine Learning for Aboveground Biomass Modeling in Tropical and Temperate Forests from Airborne Hyperspectral Imagery" Forests 16, no. 3: 477. https://doi.org/10.3390/f16030477
APA StyleOsei Darko, P., Metari, S., Arroyo-Mora, J. P., Fagan, M. E., & Kalacska, M. (2025). Application of Machine Learning for Aboveground Biomass Modeling in Tropical and Temperate Forests from Airborne Hyperspectral Imagery. Forests, 16(3), 477. https://doi.org/10.3390/f16030477







