Biomass Allometries for Urban Trees: A Case Study in Athens, Greece
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.1.1. Morphology and Topology
2.1.2. Climate
2.1.3. Tree-Level Data
2.2. Statistical Approaches
2.2.1. Solids of Revolution (Linear Approach)
2.2.2. Log-Linear Regression (Log Approach)
2.2.3. Generalized Nonlinear Least Squares (NLR Approach)
2.2.4. Nonlinear Seemingly Unrelated Regressions (NSUR)
MB = f2(X, β) + ε2
MT = f3(X, β) + ε3
2.2.5. Variance of the Predicted Values
2.2.6. Goodness-of-Fit Criteria
3. Results
3.1. Dendrometric Characteristics
3.2. Linear Regressions
3.3. Log-Linear Regressions
3.4. Nonlinear Regressions
3.5. NSUR Approach
3.6. Implementing NSUR Approach
3.7. Comparison to i–Tree Predictions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| M | Tree biomass |
| MT | Total aboveground dry biomass (MS + MB) in kg |
| MS | Stem dry biomass in kg |
| MB | Branches’ dry biomass in kg |
| H | Tree height (m) |
| HS | Stem height (m) |
| HC | Crown height (m) |
| CL | Crown length in centimeters (cm) |
| D0.30 | Tree diameter at a height of 0.30 above the ground in centimeters (cm) |
| D1.30 | Diameter at breast height, at a height of 1.30 above the ground in centimeters (cm) |
| DC | Diameter at the base of the crown in centimeters (cm) |
| B0.3 | Basal area at 0.3 meters aboveground (m2) |
| B1.3 | Basal area at 1.3 meters aboveground (m2) |
| BC | Basal area at the base of the crown (m2) |
Appendix A
Appendix B
References
- McPherson, E.G.; Simpson, J.R. Carbon Dioxide Reduction Through Urban Forestry: Guidelines for Professional and Volunteer Tree Planters; U.S. Department of Agriculture, Forest Service, Pacific Southwest Research Station: Albany, CA, USA, 1999. [CrossRef]
- Pataki, D.E.; Alig, R.J.; Fung, A.S.; Golubiewski, N.E.; Kennedy, C.A.; Mcpherson, E.G.; Nowak, D.J.; Pouyat, R.V.; Romero Lankao, P. Urban ecosystems and the North American carbon cycle. Glob. Change Biol. 2006, 12, 2092–2102. [Google Scholar] [CrossRef]
- McPherson, E.G.; van Doorn, N.S.; Peper, P.J. United States Department of Agriculture Urban Tree Database and Allometric Equations; General Technical Report; PSW-GTR-235; U.S. Department of Agriculture: Albany, CA, USA, 2016. [CrossRef]
- Pretzsch, H.; Forrester, D.I.; Rötzer, T. Representation of species mixing in forest growth models: A review and perspective. Ecol. Model. 2015, 313, 276–292. [Google Scholar] [CrossRef]
- Song, X.P.; Lai, H.R.; Wijedasa, L.S.; Tan, P.Y.; Edwards, P.J.; Richards, D.R. Height-diameter allometry for the management of city trees in the tropics. Environ. Res. Lett. 2020, 15, 114017. [Google Scholar] [CrossRef]
- Nowak, D.J. Understanding i-Tree; U.S. Department of Agriculture, Forest Service, Northern Research Station: Madison, WI, USA, 2021. [CrossRef]
- i-Tree Tools. Available online: https://www.itreetools.org/ (accessed on 23 June 2024).
- Lin, J.; Kroll, C.N.; Nowak, D.J.; Greenfield, E.J. A review of urban forest modeling: Implications for management and future research. Urban For. Urban Green. 2019, 43, 126366. [Google Scholar] [CrossRef]
- Pinkard, E.A.; Beadle, C.L. Aboveground biomass partitioning and crown architecture of Eucalyptus nitens following green pruning. Can. J. For. Res. 1998, 28, 1419–1428. [Google Scholar] [CrossRef]
- Bandara, G.D.; Whitehead, D.; Mead, D.J.; Moot, D.J. Effects of pruning and understorey vegetation on crown development, biomass increment and above-ground carbon partitioning in Pinus radiata D. Don trees growing at a dryland agroforestry site. For. Ecol. Manag. 1999, 124, 241–254. [Google Scholar] [CrossRef]
- Kramer, P.J.; Kozlowski, T.T. Physiology of Woody Plants; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Rhoades, R.W.; Stipes, R.J. Growth of trees on the Virginia Tech campus in response to various factors. Arboric. Urban For. 1999, 25, 211–217. [Google Scholar] [CrossRef]
- McHale, M.R.; Burke, I.C.; Lefsky, M.A.; Peper, P.J.; McPherson, E.G. Urban forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosyst. 2009, 12, 95–113. [Google Scholar] [CrossRef]
- Yoon, T.K.; Park, C.-W.; Lee, S.J.; Ko, S.; Kim, K.N.; Son, Y.; Lee, K.H.; Oh, S.; Lee, W.-K.; Son, Y. Allometric equations for estimating the aboveground volume of five common urban street tree species in Daegu, Korea. Urban For. Urban Green. 2013, 12, 344–349. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, X.; Liu, Z.; Li, P.; Tang, J.; Xie, B.; Peng, C. A Review of General Methods for Quantifying and Estimating Urban Trees and Biomass. Forests 2022, 13, 616. [Google Scholar] [CrossRef]
- Pillsbury, N.H.; Reimer, J.L. Tree Volume Equations for 10 Urban Species in California 1; U.S. Department of Agriculture, Forest Service: Albany, CA, USA, 1997.
- Huxley, J.S. Problems of Relative Growth; Methuen Publishing: London, UK, 1932. [Google Scholar]
- Broad, L.R. AIIometry and Growth. For. Sci. 1998, 44, 458–464. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-Scale Biomass Estimators for United States Tree Species. For. Sci. 2003, 49, 12–35. [Google Scholar] [CrossRef]
- Návar, J. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. For. Ecol. Manag. 2009, 257, 427–434. [Google Scholar] [CrossRef]
- Pilli, R.; Anfodillo, T.; Carrer, M. Towards a functional and simplified allometry for estimating forest biomass. For. Ecol. Manag. 2006, 237, 583–593. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Zianis, D. Predicting mean aboveground forest biomass and its associated variance. For. Ecol. Manag. 2008, 256, 1400–1407. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe. Silva Fennica Monographs 4; Finnish Society of Forest Science, Finnish Forest Research Institute: Helsinki-Uusimaa, Finland, 2005. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. Aboveground net primary productivity of a beech (Fagus moesiaca) forest: A case study of Naousa forest, northern Greece. Tree Physiol. 2005, 25, 713–722. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. Aboveground biomass relationships for beech (Fagus moesiaca Cz.) trees in Vermio Mountain, Northern Greece, and generalised equations for Fagus sp. Ann. For. Sci. 2003, 60, 439–448. [Google Scholar] [CrossRef]
- Payandeh, B. Choosing Regression Models for Biomass Prediction Equations. For. Chron. 1981, 57, 229–232. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing Tree and Stand Biomass: A Review with Examples and Critical Comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar] [CrossRef]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Sanquetta, C.R.; Netto, S.P.; Corte, A.P.D.; Rodrigues, A.L.; Behling, A.; Sanquetta, M.N.I. Quantifying biomass and carbon stocks in oil palm (Elaeis guineensis Jacq.) in Northeastern Brazil. Afr. J. Agric. Res. 2015, 10, 4067–4075. [Google Scholar] [CrossRef]
- Kozak, A. Methods for Ensuring Additivity of Biomass Components by Regression Analysis. For. Chron. 1970, 46, 402–404. [Google Scholar] [CrossRef]
- Reed, D.D.; Green, E.J. A method of forcing additivity of biomass tables when using nonlinear models. Can. J. For. Res. 1985, 15, 1184–1187. [Google Scholar] [CrossRef]
- Zellner, A. An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias. J. Am. Stat. Assoc. 1962, 57, 348–368. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Parresol, B.R. Modeling Multiplicative Error Variance: An Example Predicting Tree Diameter from Stump Dimensions in Baldcypress. For. Sci. 1993, 39, 676–679. [Google Scholar] [CrossRef]
- Hellenic Statistical Authority. Census 2021 GR. 2021. Available online: https://www.statistics.gr/2011-census-pop-hous (accessed on 25 June 2024).
- Municipality of Athens. Part I of the Climate Action Plan. 2022. Available online: https://www.cityofathens.gr/wp-content/uploads/2022/08/schedio-gia-tin-klimatiki-allagi-9-6-2022.pdf (accessed on 25 June 2024).
- World Meteorological Organization’s World Weather and Climate Extremes Archive. Available online: https://wmo.asu.edu/content/wmo-region-vi-europe-continent-only-highest-temperature (accessed on 25 June 2024).
- Hellenic National Meteorological Service. Available online: https://www.emy.gr/ (accessed on 15 January 2025).
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Baskerville, G.L. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Serv. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Beauchamp, J.J.; Olson, J.S. Corrections for Bias in Regression Estimates After Logarithmic Transformation. Ecology 1973, 54, 1403–1407. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for Bias in Log-Transformed Allometric Equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Yandle, D.O.; Wiant, H.V. Estimation of plant biomass based on the allometric equation. Can. J. For. Res. 1981, 11, 833–834. [Google Scholar] [CrossRef]
- Wiant, H.V.J.; Harner, E.J. Percent bias and standard error in logarithmic regression. For. Sci. 1979, 25, 167–168. [Google Scholar]
- JanMarvin/nlsur: Estimating Nonlinear Least Squares for Equation Systems Version 0.8 from GitHub. Available online: https://rdrr.io/github/JanMarvin/nlsur/ (accessed on 1 December 2024).
- Mehtätalo, L.; Lappi, J. Forest Biometrics with Examples in R Contents; CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. Bioscience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Thomopoulos, N.T.; Johnson, A.C. Tables And Characteristics of the Standardized Lognormal Distribution. Proc. Decis. Sci. Inst. 2003, 103, 1031–1036. [Google Scholar]
- Ezekiel, M.; Fox, K.A. Methods of Correlation and Regression Analysis: Linear and Curvilinear; John Wiley and Sons Inc.: Taipei, Taiwan, 1959. [Google Scholar]
- Furnival, G. An index for comparing equations used in constructing volume tables. For. Sci. 1961, 7, 337–341. [Google Scholar]
- Schreuder, H.T.; Swank, W.T. A comparison of several statistical models in forest biomass and surface area estimation. In Forest Biomass Studies, IUFRO, Section 25: Yield and Growth. Life Sci. and Agric. Exp. Stn., Univ. Maine. Orono, ME, USA; Young, H.E., Ed.; Springer: Berlin/Heidelberg, Germany, 1971; pp. 125–138. [Google Scholar]
- Albini, F.A.; Brown, J.K. Predicting Slash Depth for Fire Modeling; Reserch Paper; INT-RP-206; USDA Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1978.
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 1 October 2024).
- MyTree Tool. Available online: https://mytree.itreetools.org/#/ (accessed on 11 November 2024).
- Nowak, D.J. Understanding the Structure of Urban Forests. J. For. 1994, 92, 42–46. [Google Scholar] [CrossRef]
- Dutcă, I.; Zianis, D.; Petrițan, I.C.; Bragă, C.I.; Ștefan, G.; Yuste, J.C.; Petrițan, A.M. Allometric biomass models for european beech and silver fir: Testing approaches to minimize the demand for site-specific biomass observations. Forests 2020, 11, 1136. [Google Scholar] [CrossRef]
- Zapata-Cuartas, M.; Sierra, C.A.; Alleman, L. Probability distribution of allometric coefficients and Bayesian estimation of aboveground tree biomass. For. Ecol. Manag. 2012, 277, 173–179. [Google Scholar] [CrossRef]
- Zianis, D.; Spyroglou, G.; Tiakas, E.; Radoglou, K.M. Bayesian and classical models to predict aboveground tree biomass allometry. For. Sci. 2016, 62, 247–259. [Google Scholar] [CrossRef]
- Zianis, D.; Pantera, A.; Papadopoulos, A.; Losada, M.R.M. Bayesian and classical biomass allometries for open grown valonian oaks (Q. ithaburensis subs. macrolepis L.) in a silvopastoral system. Agrofor. Syst. 2017, 93, 241–253. [Google Scholar] [CrossRef]
- Aguaron, E.; McPherson, E.G. Comparison of methods for estimating carbondioxide storage by sacramento’s urban forest. In Carbon Sequestration in Urban Ecosystems; Springer: Dordrecht, The Netherlands, 2012; pp. 44–71. [Google Scholar] [CrossRef]
- Genet, A.; Wernsdörfer, H.; Jonard, M.; Pretzsch, H.; Rauch, M.; Ponette, Q.; Nys, C.; Legout, A.; Ranger, J.; Vallet, P.; et al. Ontogeny partly explains the apparent heterogeneity of published biomass equations for Fagus sylvatica in central Europe. For. Ecol. Manag. 2011, 261, 1188–1202. [Google Scholar] [CrossRef]
- Gourlet-Fleury, S.; Rossi, V.; Rejou-Mechain, M.; Freycon, V.; Fayolle, A.; Saint-André, L.; Cornu, G.; Gérard, J.; Sarrailh, J.-M.; Flores, O.; et al. Environmental filtering of dense-wooded species controls above-ground biomass stored in African moist forests. J. Ecol. 2011, 99, 981–990. [Google Scholar] [CrossRef]
- Lin, J.; Kroll, C.N.; Nowak, D.J. An uncertainty framework for i-Tree eco: A comparative study of 15 cities across the United States. Urban For. Urban Green. 2021, 60, 127062. [Google Scholar] [CrossRef]

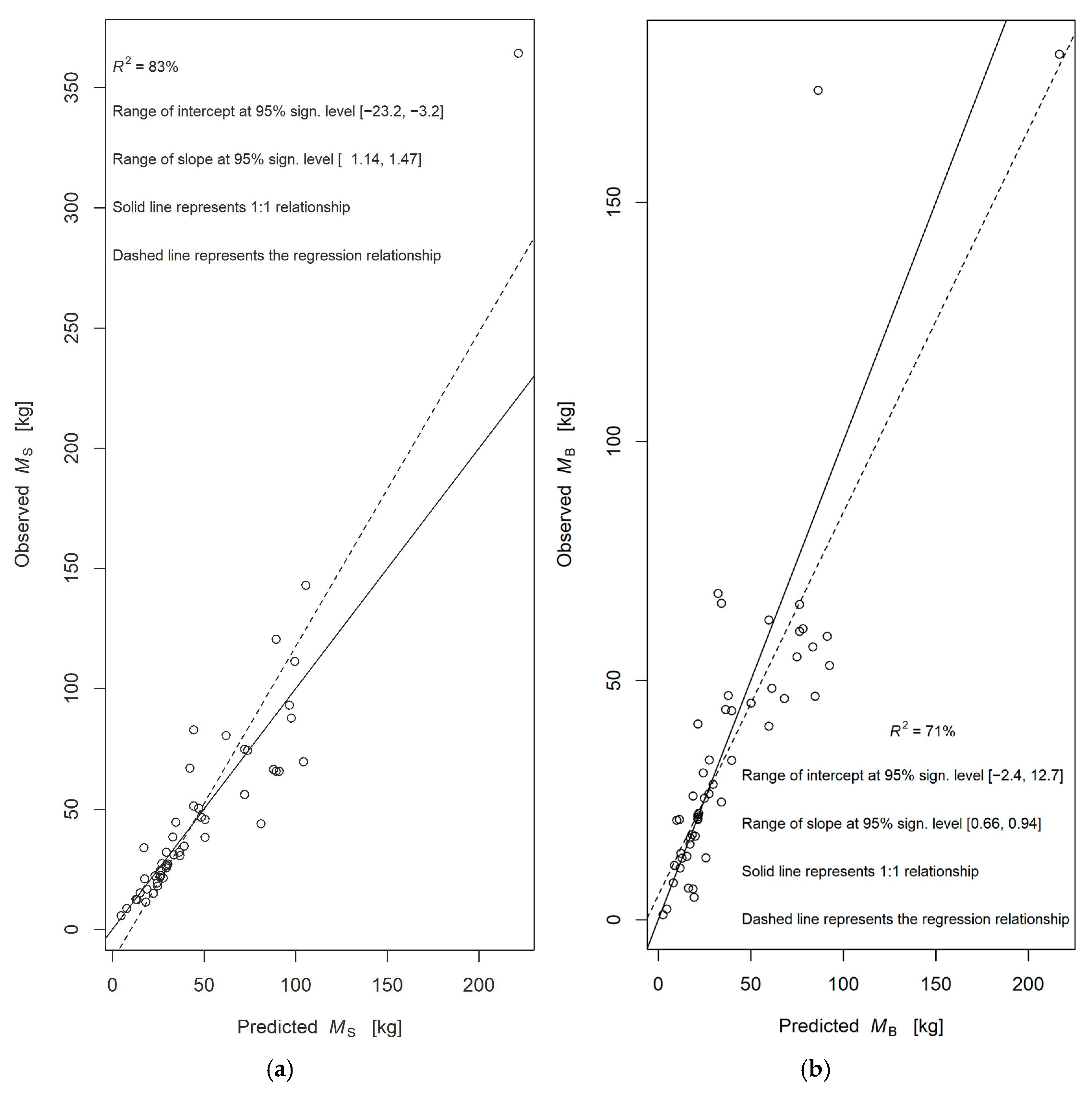
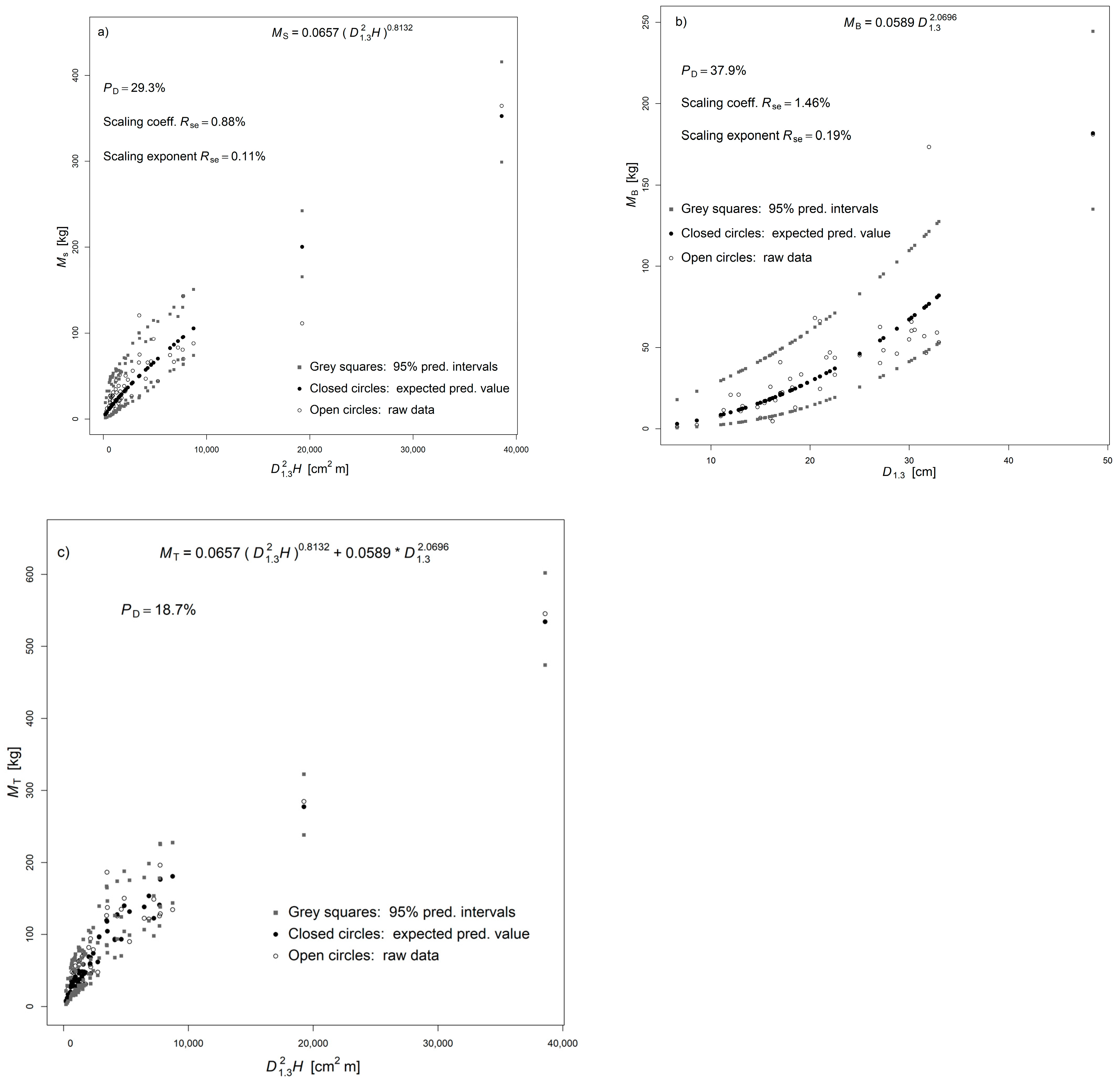
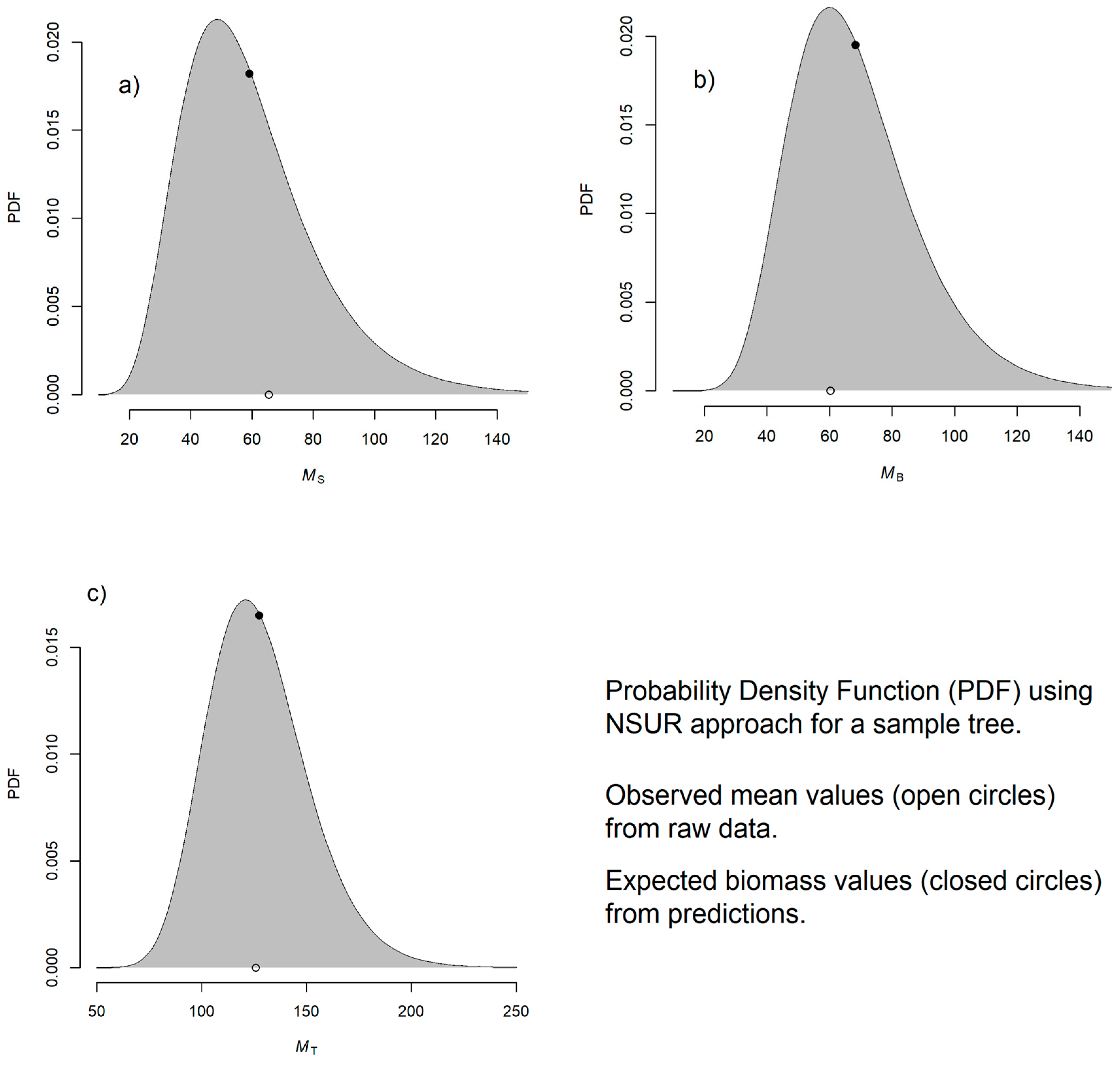
| Component | Eq. | a | b | s.e. (a) | s.e. (b) | Rse (a) % | Rse (b) % | PD (%) | AIC | BIC | R2 | RMSE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stem | A1 | 18.2608 | 93.0122 | 3.0094 | 4.7123 | 16.48 | 5.07 | 38.5 | 445.4522 | 451.1882 | 0.89 | 17.98 |
| A2 | 18.6670 | 249.9268 | 2.7520 | 11.5400 | 14.74 | 4.62 | 43.8 | 435.1883 | 440.9243 | 0.90 | 16.55 | |
| A3 | 18.7013 | 103.1666 | 3.0865 | 5.3963 | 16.50 | 5.23 | 37.7 | 448.0563 | 453.7924 | 0.88 | 18.49 | |
| A4 | 18.5975 | 285.6634 | 2.4889 | 11.8405 | 13.38 | 4.14 | 40.3 | 425.0899 | 430.8259 | 0.92 | 15.00 | |
| Branch | A5 | 18.9120 | 52.2961 | 3.1345 | 4.9082 | 16.57 | 9.39 | 103.8 | 449.5247 | 455.2607 | 0.69 | 18.73 |
| A6 | 21.3903 | 122.5919 | 3.8254 | 16.0413 | 17.88 | 13.09 | 123.7 | 468.1231 | 473.8592 | 0.54 | 23.00 | |
| A7 | 18.2353 | 61.0493 | 2.7500 | 4.8079 | 15.08 | 7.88 | 98.6 | 436.5118 | 442.2478 | 0.76 | 16.48 | |
| A8 | 20.9650 | 143.6769 | 3.6551 | 17.3884 | 17.43 | 12.1 | 119.9 | 463.5180 | 469.2540 | 0.58 | 22.02 | |
| Total | A9 | 37.1729 | 145.3086 | 4.9814 | 7.8001 | 13.4 | 5.37 | 47.6 | 495.8484 | 501.5845 | 0.81 | 36.44 |
| A10 | 40.0575 | 372.5185 | 6.0597 | 25.4104 | 15.13 | 6.82 | 56.6 | 514.1221 | 519.8582 | 0.90 | 26.44 | |
| A11 | 36.9366 | 164.2164 | 4.4118 | 7.7135 | 11.94 | 4.7 | 45.5 | 483.7824 | 489.5185 | 0.84 | 33.49 | |
| A12 | 39.5627 | 429.3403 | 5.5579 | 26.4410 | 14.05 | 6.16 | 53.6 | 505.4290 | 511.1650 | 0.87 | 29.76 |
| Y | X | lna | b | s.e. (a) | s.e. (b) | Rse (a) % | Rse (b) % | SEE | CF | % bias | % s.e. | SSE | S |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lnMS | lnD1.3 | −2.0995 | 1.9231 | 0.2919 | 0.0978 | 13.90 | 5.09 | 0.2658 | 1.03 | 3.46 | 18.95 | 31,039 | 0.79 |
| lnMB | lnD1.3 | −3.3009 | 2.2094 | 0.5007 | 0.1679 | 15.17 | 7.60 | 0.4559 | 1.10 | 9.87 | 33.09 | 19,706.17 | 0.67 |
| lnMT | lnD1.3 | −1.7598 | 1.9968 | 0.2833 | 0.095 | 16.10 | 4.76 | 0.258 | 1.03 | 3.27 | 18.39 | 55,240.98 | 0.85 |
| Y | X | PD (%) | AIC | BIC | R2 | RMSE | |||||||
| lnMS | lnD1.3 | 21.06 | 387.20 | 391.52 | 0.89 | 24.43161 | |||||||
| lnMB | lnD1.3 | 40.9 | 406.48 | 413.25 | 0.78 | 19.46702 | |||||||
| lnMT | lnD1.3 | 19.93 | 442.13 | 450.2 | 0.9 | 32.59336 |
| Component | Eq. | a | b | c | Rse (a) % | Rse (b) % | Rse (c) % | PD (%) | AIC | BIC |
|---|---|---|---|---|---|---|---|---|---|---|
| Stem | A13 | 0.0102 | 2.6833 | - | 42.64 | 4.41 | - | 29.8 | 450.5351 | 456.3888 |
| A14 | 0.1148 | 0.7518 | - | 37.24 | 5.17 | - | 27.7 | 467.9970 | 473.8508 | |
| A15 | 0.0279 | 2.2099 | 0.3007 | 40.43 | 6.49 | 26.23 | 23.3 | 440.5869 | 448.3919 | |
| A16 | 0.2397 | 0.7598 | - | 18.05 | 2.76 | - | 23.2 | 415.7359 | 421.5897 | |
| A17 | 0.2235 | 0.7655 | - | 19.66 | 2.97 | - | 21.7 | 424.1670 | 430.0208 | |
| Branch | A18 | 0.0819 | 1.9719 | - | 58.38 | 8.54 | - | 40.8 | 453.9460 | 459.7997 |
| A19 | 0.2351 | 0.6354 | - | 31.83 | 5.38 | - | 56.5 | 422.3186 | 428.1724 | |
| A20 | 0.2277 | 1.2911 | 0.6189 | 38.39 | 10.33 | 13.91 | 55.7 | 424.2816 | 432.0866 | |
| A21 | 0.1644 | 0.7052 | - | 28.53 | 4.53 | - | 49.0 | 404.3647 | 410.2184 | |
| A22 | 0.2030 | 1.2930 | 0.8048 | 33.03 | 8.33 | 9.11 | 52.2 | 404.3980 | 412.2030 | |
| Total | A23 | 0.0514 | 2.3688 | - | 41.03 | 4.89 | - | 21.0 | 505.2491 | 511.1028 |
| A24 | 0.3159 | 0.6999 | - | 25.43 | 3.84 | - | 28.8 | 487.1642 | 493.0180 | |
| A25 | 0.1626 | 1.7616 | 0.4459 | 28.20 | 5.63 | 13.17 | 19.6 | 471.6368 | 479.4417 | |
| A26 | 0.2699 | 1.7524 | 0.4285 | 36.65 | 7.02 | 17.81 | 20.8 | 482.3682 | 490.1731 | |
| A27 | 0.1235 | 1.8596 | 0.5034 | 27.21 | 4.86 | 12.11 | 19.2 | 466.5848 | 474.3897 |
| Coefficient | Estimate | s.e. | z-Value | p-Value |
|---|---|---|---|---|
| a1 | 0.0657246 | 0.0005797 | 113.39 | *** |
| b1 | 0.8131515 | 0.0008683 | 936.52 | *** |
| a2 | 0.0589474 | 0.0008623 | 68.36 | *** |
| b2 | 2.0696203 | 0.0039958 | 517.95 | *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dapsopoulou, M.; Zianis, D. Biomass Allometries for Urban Trees: A Case Study in Athens, Greece. Forests 2025, 16, 466. https://doi.org/10.3390/f16030466
Dapsopoulou M, Zianis D. Biomass Allometries for Urban Trees: A Case Study in Athens, Greece. Forests. 2025; 16(3):466. https://doi.org/10.3390/f16030466
Chicago/Turabian StyleDapsopoulou, Magdalini, and Dimitris Zianis. 2025. "Biomass Allometries for Urban Trees: A Case Study in Athens, Greece" Forests 16, no. 3: 466. https://doi.org/10.3390/f16030466
APA StyleDapsopoulou, M., & Zianis, D. (2025). Biomass Allometries for Urban Trees: A Case Study in Athens, Greece. Forests, 16(3), 466. https://doi.org/10.3390/f16030466










