Design of Rubber Tapping Mechanical Test Bench and Optimization of Rubber Tapping Machine Parameters
Abstract
1. Introduction
2. Materials and Methods
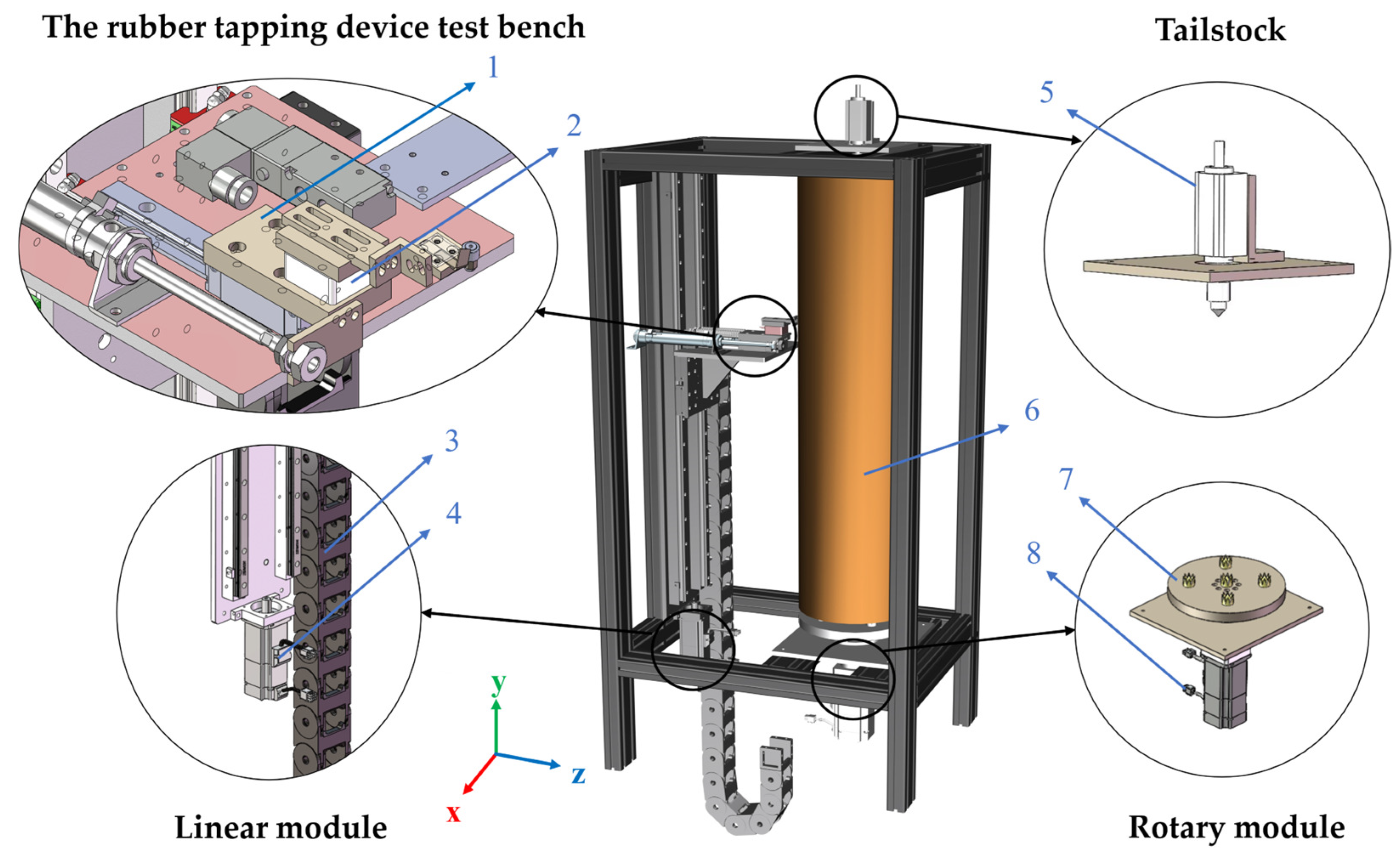
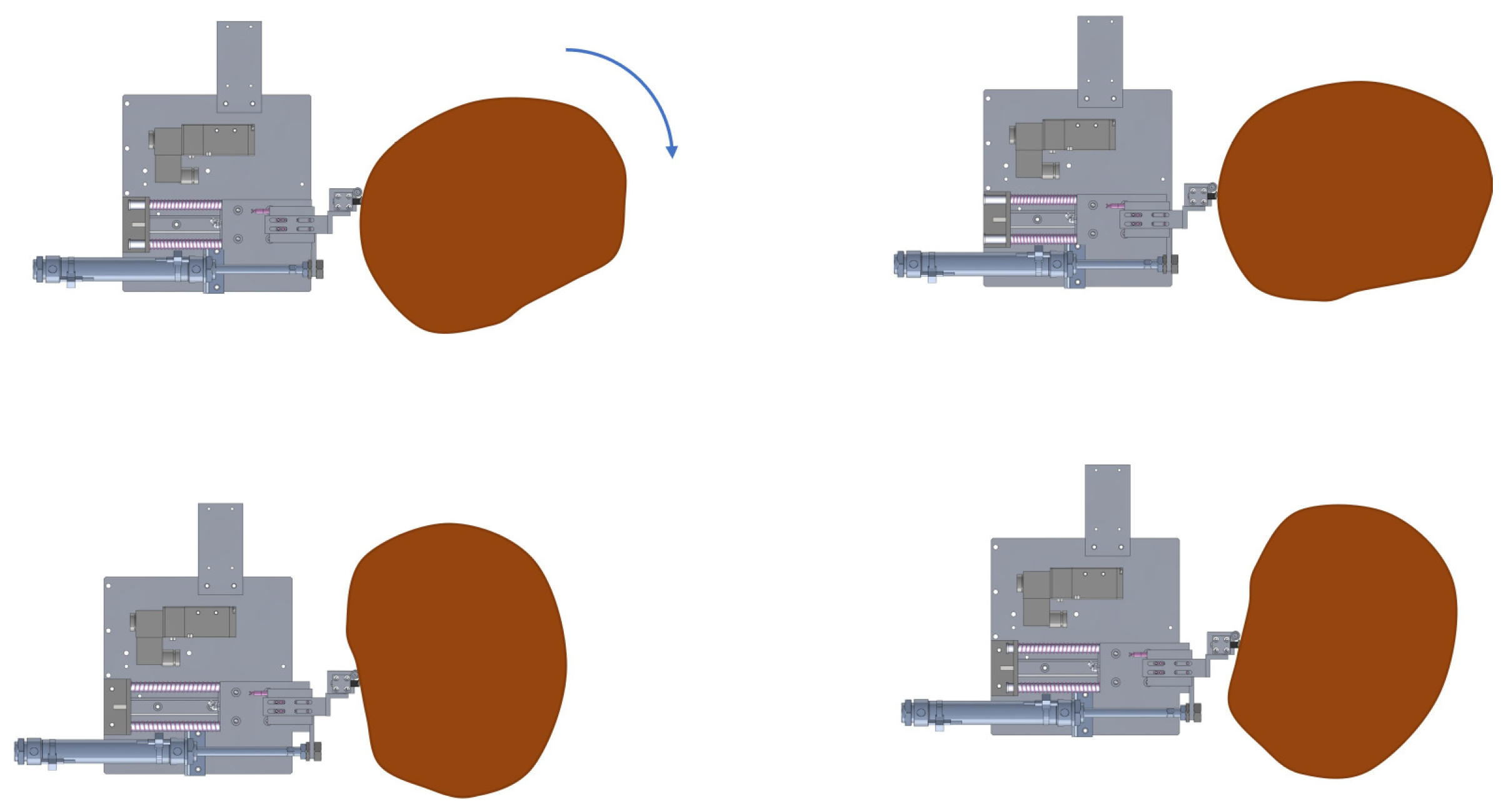
2.1. Overall Structure and Working Principle
2.2. Design of Key Components
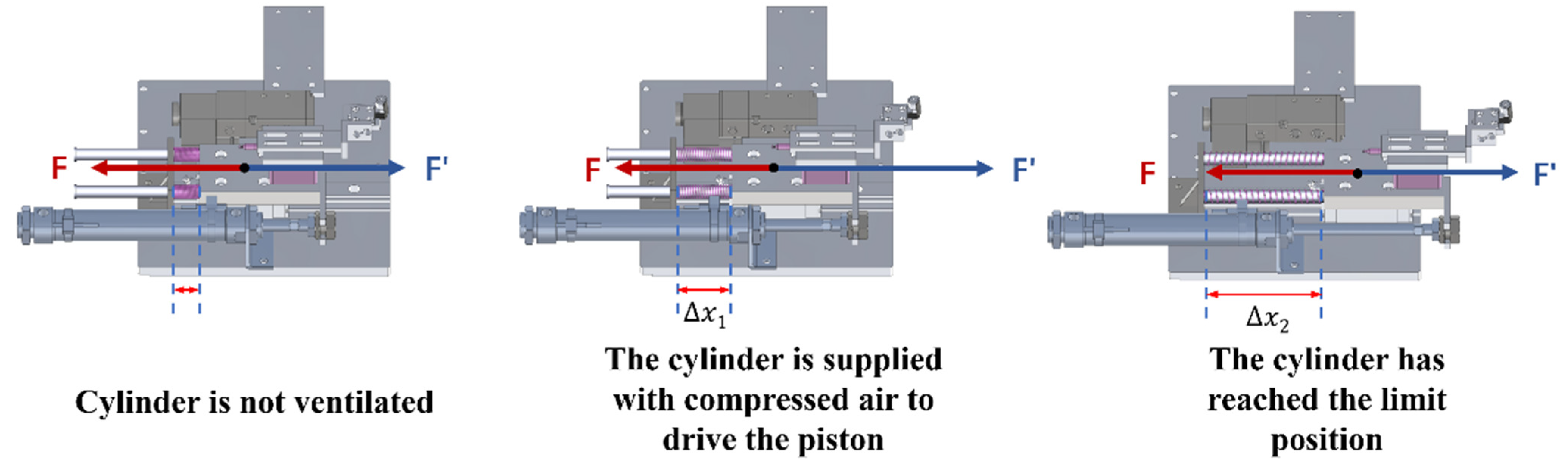
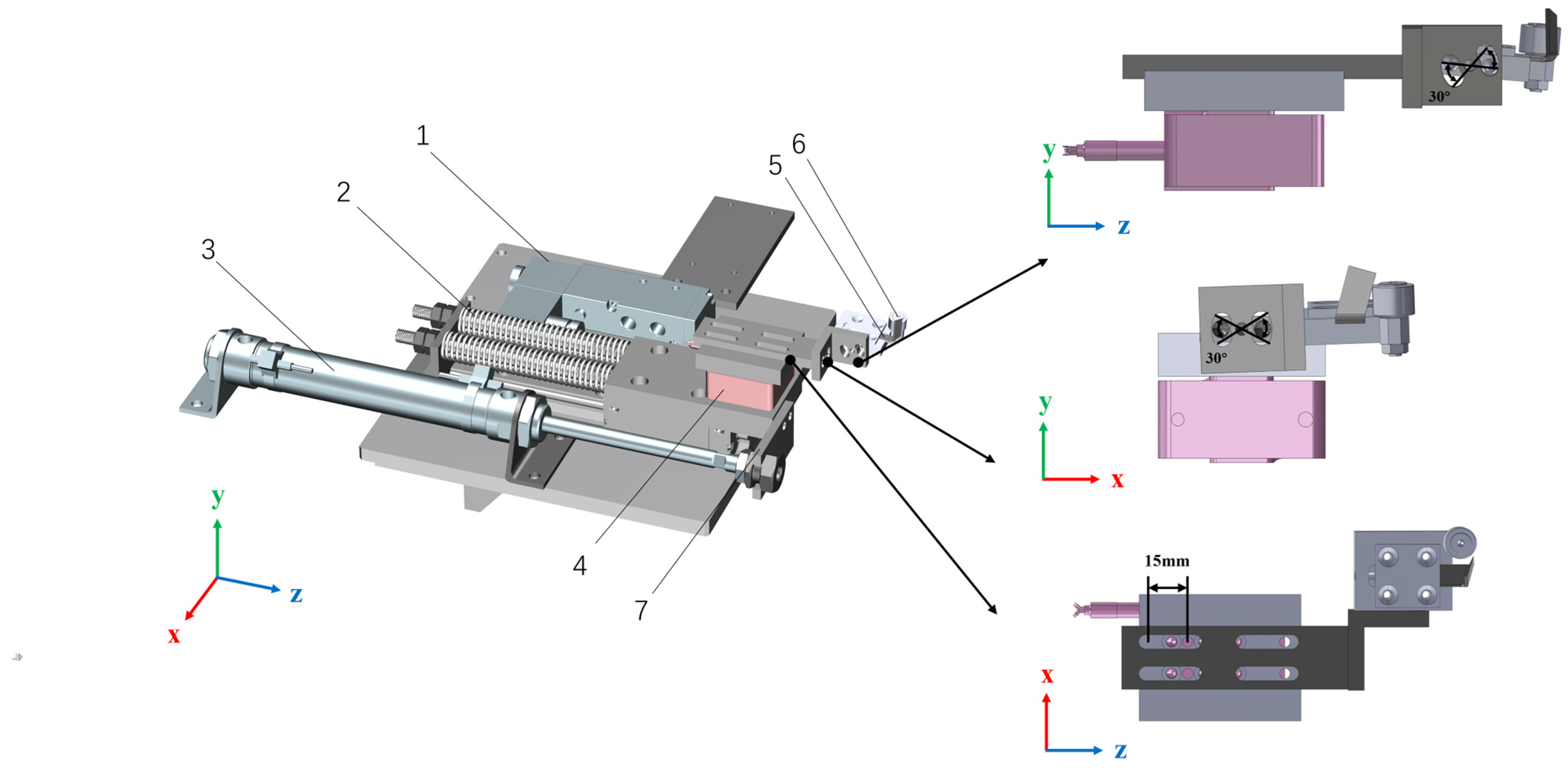
2.2.1. End Effector Design for Rubber Tapping Machines
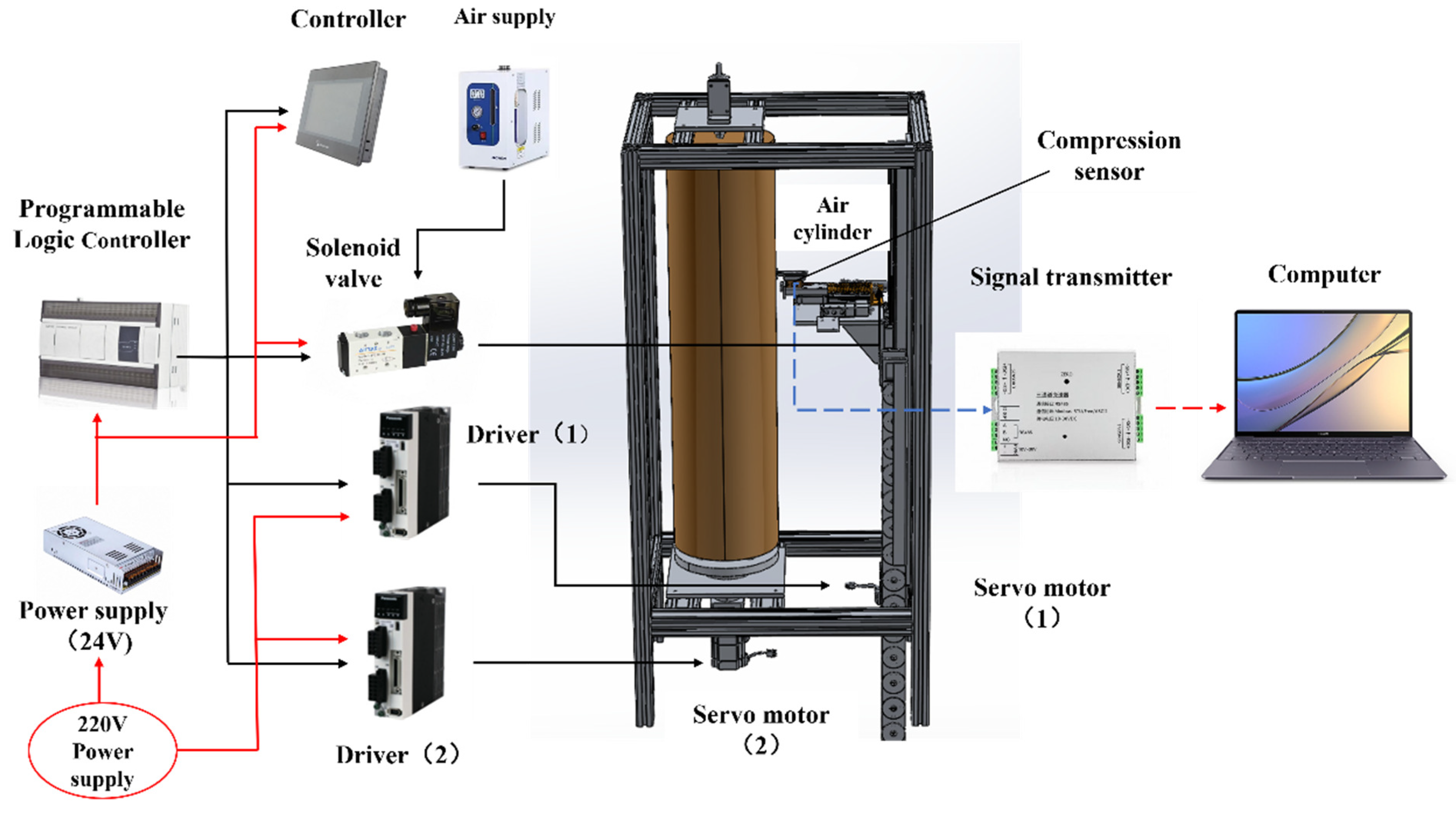
2.2.2. Design of the Control System
2.3. Single-Factor Mechanical Tests
2.3.1. Test Objects
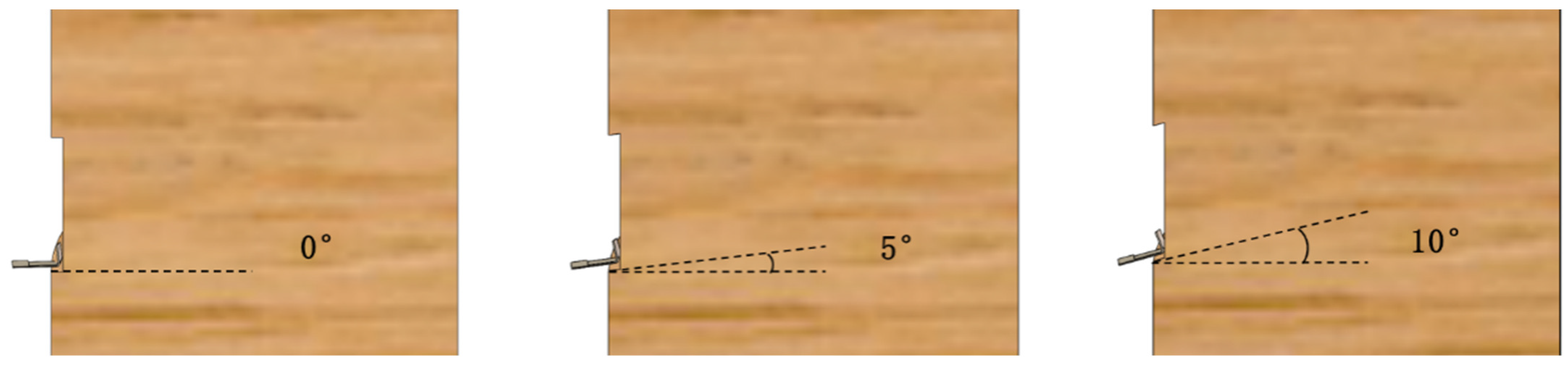
2.3.2. Test Plan
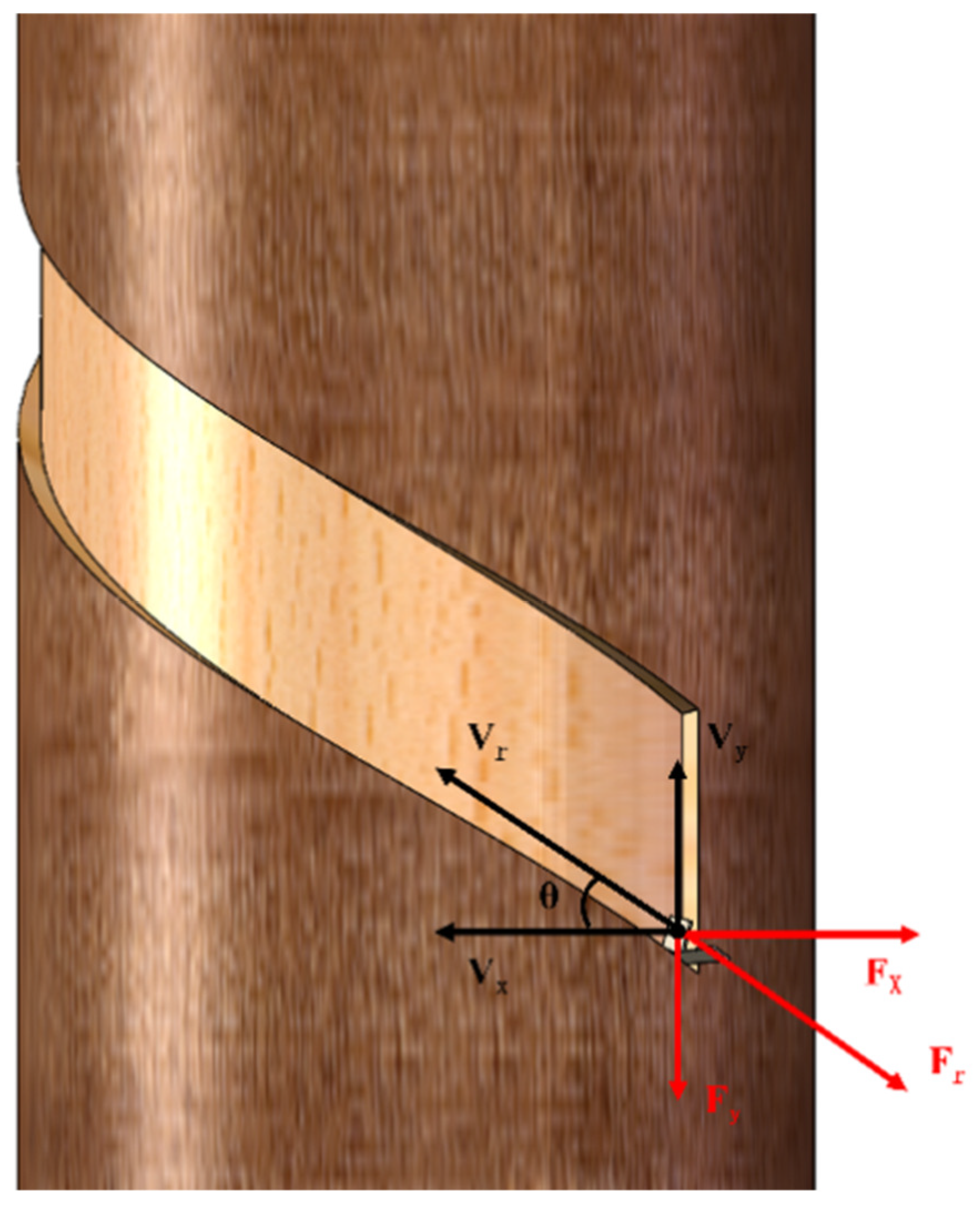
2.4. Orthogonal Experiment
Experimental Scheme
3. Experimental Results
3.1. Results of Single-Factor Mechanical Tests
3.1.1. Experimental Results of Single-Factor Test on Cutting Blade Bending Angle Key Adjustment & Explanation
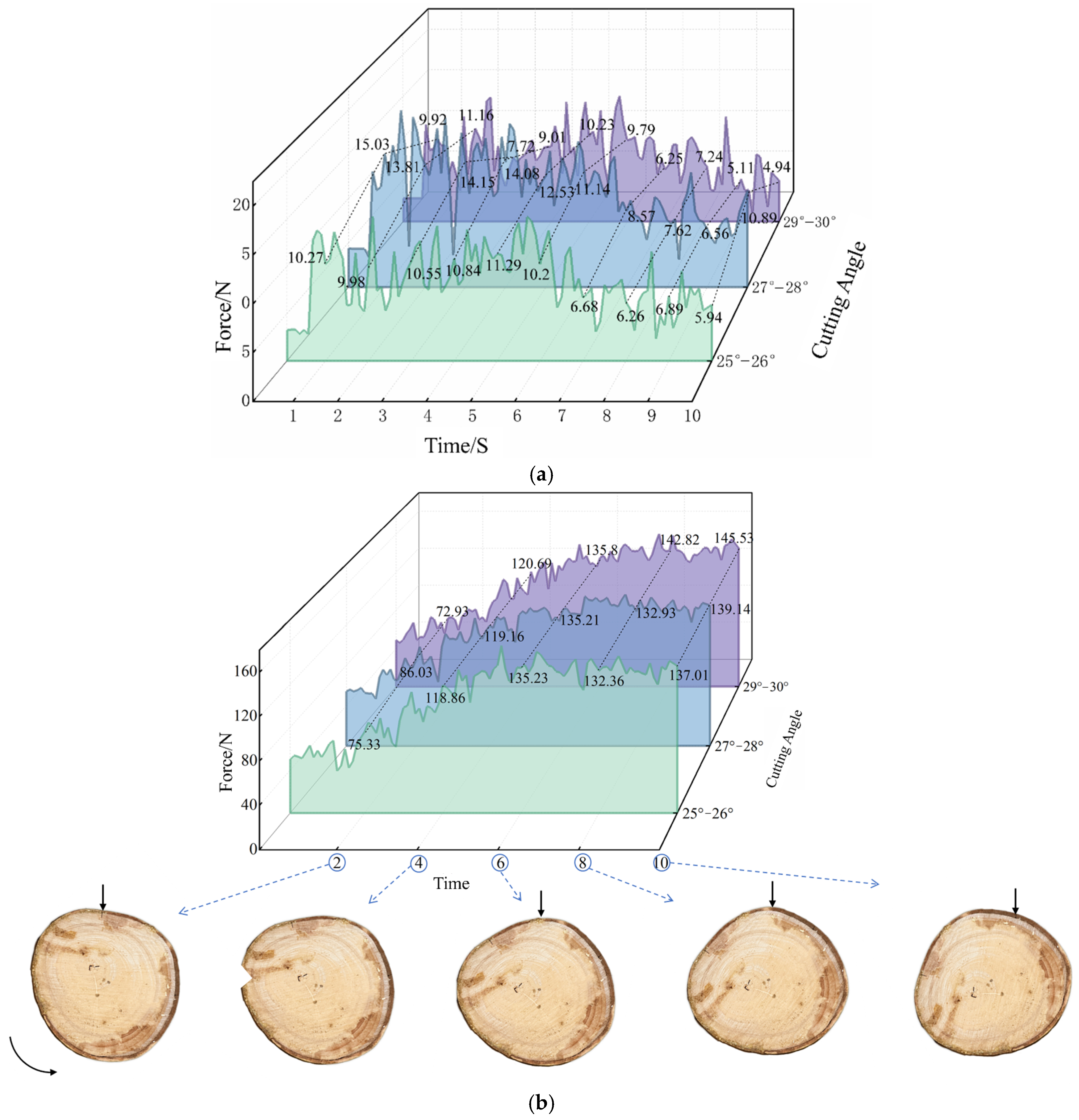
3.1.2. Experimental Results of Single-Factor Test on Cutting Angle
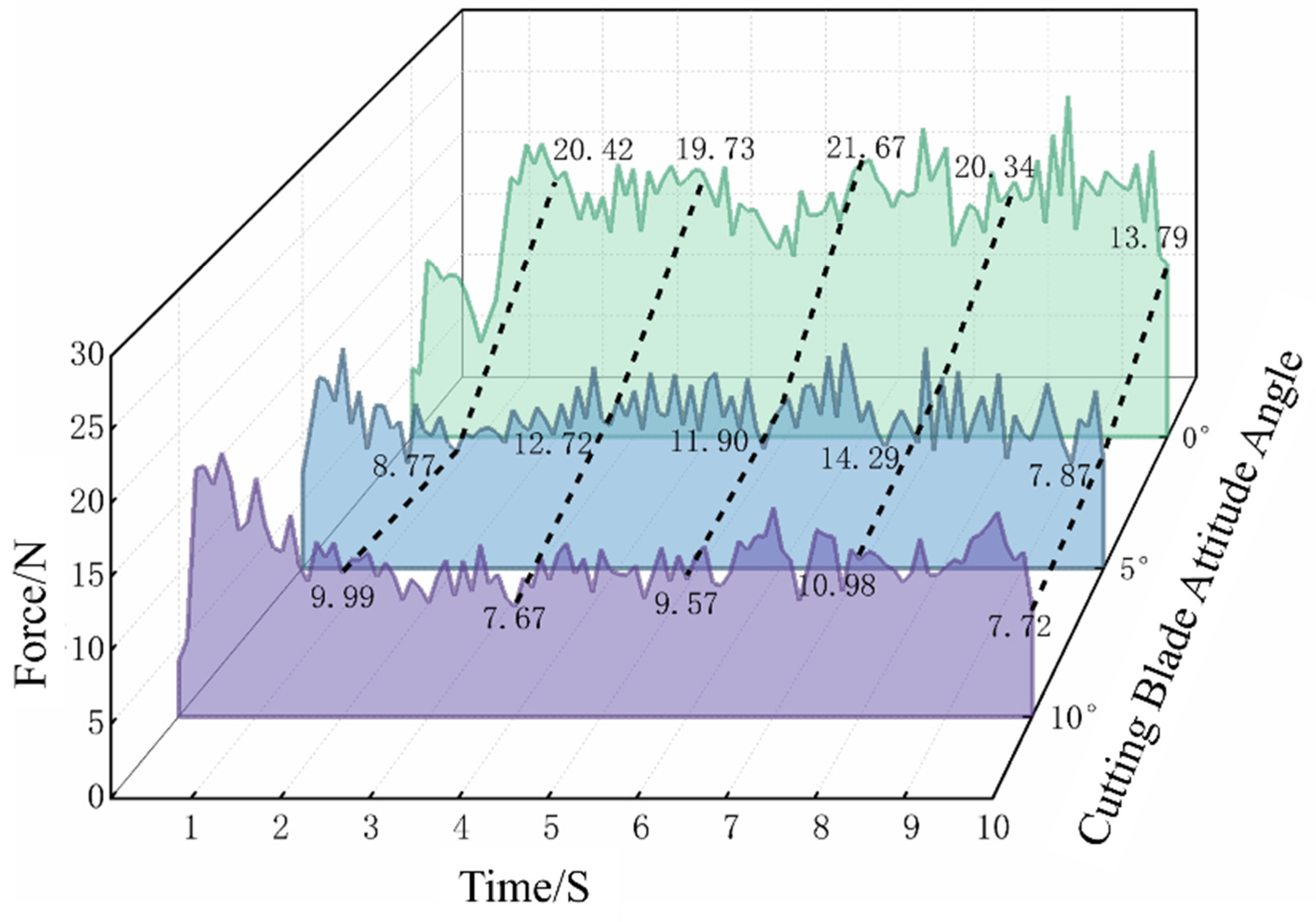
3.1.3. Experimental Results of Single-Factor Test on Cutting Blade Attitude Angle
3.2. Result Analysis
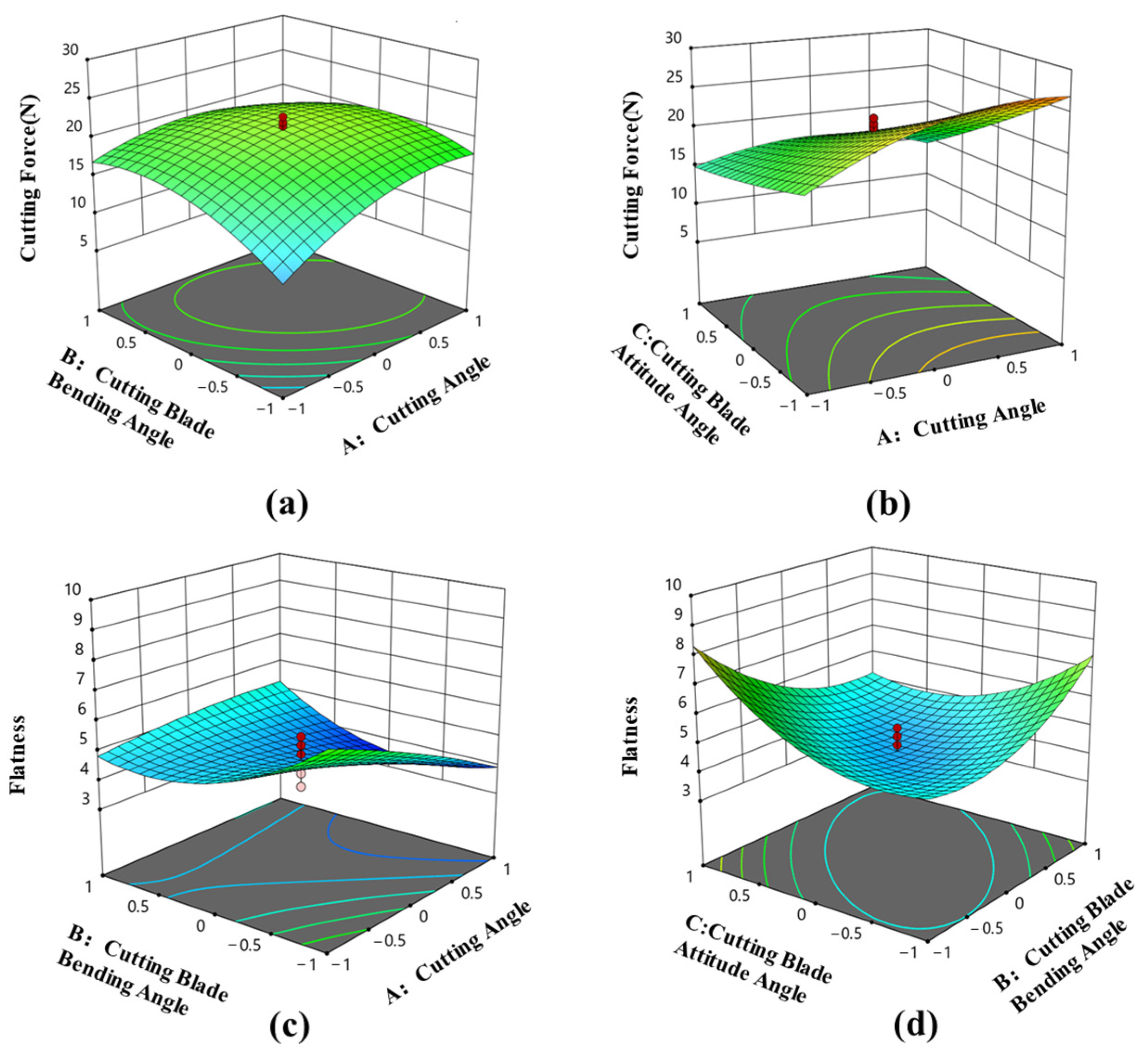
3.2.1. Analysis of Experimental Results
3.2.2. Analysis of Model Interaction Terms
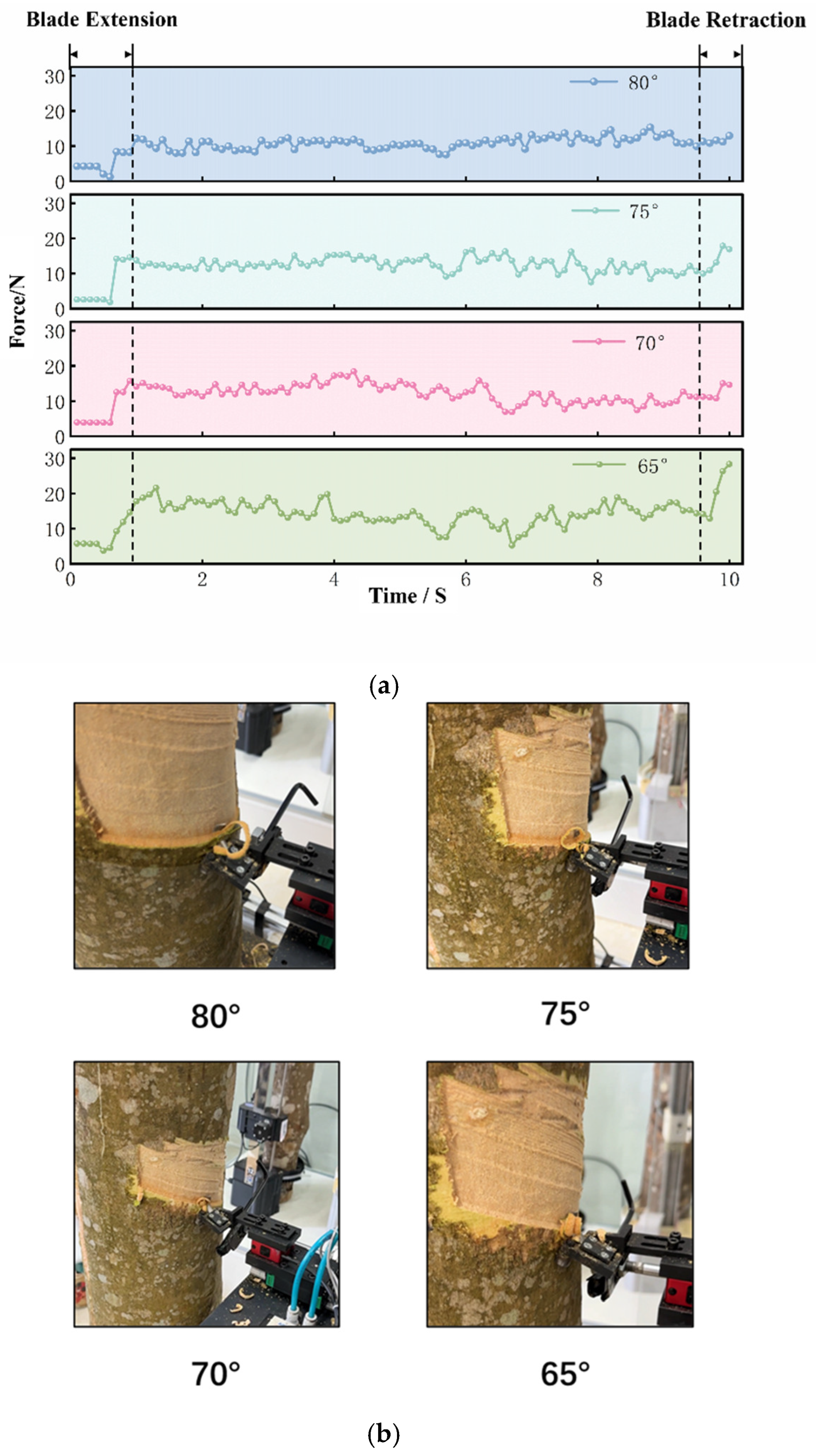
3.2.3. Comparative Analysis of Rubber Tapping Chip Morphology Under Optimal Tapping Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, L.; Guoxiong, Z.; Xiangjun, W.; Huaiqing, Z. Fine segmentation and structural parameter extraction of rubber tree point cloud based on LiDAR using the TMGH method. Comput. Electron. Agric. 2025, 239, 110950. [Google Scholar] [CrossRef]
- Baudoin, M.; Liengprayoon, S.; Khaeduang, T.; Paboeuf, G.; Musigamart, N.; Jantarasunthorn, S.; Lerksamran, T.; Chantuma, P.; Char, C.; Geniez, M.; et al. Impact of size and biochemical composition of rubber particles on their interfacial behavior using two Hevea brasiliensis genotypes. Surf. Interfaces 2025, 67, 106622. [Google Scholar] [CrossRef]
- Zhang, H.L.; Li, W.X.; He, J.J.; Luo, P. Development status and prospects of understory planting-breeding models in rubber plantations of China. J. Trop. Biol. 2022, 13, 88–94. [Google Scholar] [CrossRef]
- Liu, H.; Tan, S.; Yuan, B.; Fang, F.; He, M.; Wang, M.; Wan, R.; Chen, J.; Hui, S.; Wang, X. Differential accumulation of coronatine-induced protein correlates with secondary laticifer proliferation in vascular cambia of phloem tissues in the Hevea rubber tree. Ind. Crops Prod. 2025, 235, 121742. [Google Scholar] [CrossRef]
- Wan, J.; Fan, R.; Yang, W.; Wei, F.; Gao, H.; Wei, H.; Qiu, J. New insights into ethylene-induced latex flow in a dose-dependent manner in rubber tree. Ind. Crops Prod. 2024, 222, 120012. [Google Scholar] [CrossRef]
- Nunes, F.M.; Silva, A.L.E.; May, J.; Szarblewski, M.d.S.; Flemming, L.; Assmann, E.E.; Moraes, J.A.R.; Machado, Ê.L. Environmental impacts associated with the life cycle of natural rubbers: A review and scientometric analysis. Ind. Crops Prod. 2025, 224, 120350. [Google Scholar] [CrossRef]
- Hayichelaeh, C.; Boonkerd, K. Enhancing the tire performances of truck tire tread based on rubber compounds containing biobased processing oil by adjusting sulfur contents. Ind. Crops Prod. 2024, 224, 120451. [Google Scholar] [CrossRef]
- Zhang, C.; Sheng, X.; Zhang, S.; Gao, J.; Yuan, T.; Zhang, J.; Li, W. Experimental study on influencing factors of cutting power consumption for mechanized natural rubber tapping. Trans. Chin. Soc. Agric. Eng. 2018, 34, 32–37. [Google Scholar] [CrossRef]
- Gao, J.; Cheng, H. Rubber trees changing the world: 150 years. Sci. China Life Sci. 2024, 67, 1744–1751. [Google Scholar] [CrossRef]
- Kum-Ourm, H.; Liengprayoon, S.; Onozuka, N.; Vaysse, L.; Tarachiwin, L.; Lacote, R.; Chaiyut, J.; Jantarasunthorn, S.; Lerksamram, T.; Cakpo, C.B.; et al. Reduction of tapping frequency associated with stimulation of two Hevea brasiliensis clones in Thai non-traditional rubber area. 1. Effect on production, biochemical composition and particle size of latex. Ind. Crops Prod. 2025, 224, 121758. [Google Scholar] [CrossRef]
- Li, Y.; Pan, Y.; Luo, P.; Li, F.; Huang, M.; Yuan, K.; Yang, J.; Yuan, Z.; Xie, L. Preliminary report on daytime tapping of rubber trees [Shiyan chubao]. Chin. J. Trop. Crops. 2023, 44, 937–945. [Google Scholar] [CrossRef]
- Zhao, L.; Zeng, R.; Ding, L.; Xing, P.; Xin, Z.; Qiu, J.; Gui, H. Practices of six-day tapping system for enhanced natural rubber yield and quality in China. Ind. Crops Prod. 2025, 224, 120343. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Liu, J.; Zhang, Z.; Zhang, X. Tapped area detection and new tapping line location for natural rubber trees based on improved Mask Region Convolutional Neural Network. Front. Plant Sci. 2023, 13, 1038000. [Google Scholar] [CrossRef]
- Zhang, X.R.; Wen, Z.T.; Zhang, Z.F. Design and experiment of spiral motion automatic rubber tapping device. Trans. Chin. Soc. Agric. Mach. 2023, 54, 169–179. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, H.; Zhang, Z.; Liu, J.; Zhang, X. An Improved YOLOv5-Based Tapping Trajectory Detection Method for Natural Rubber Trees. Agriculture 2022, 12, 1309. [Google Scholar] [CrossRef]
- Wang, L.; Huang, C.; Li, T.; Cao, J.; Zheng, Y.; Huang, J. An Optimization Study on a Novel Mechanical Rubber Tree Tapping Mechanism and Technology. Forests 2023, 14, 2421. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Y.; Zhang, X.; Zhang, L.; Sun, H. Design and experiment of laser ranging controlled-depth rubber tapping machine. Trans. Chin. Soc. Agric. Mach. 2025, 56, 284–292. [Google Scholar] [CrossRef]
- Pramchoo, W.; Geater, A.F.; Harris-Adamson, C.; Tangtrakulwanich, B. Ergonomic rubber tapping knife relieves symptoms of carpal tunnel syndrome among rubber tappers. Int. J. Ind. Ergon. 2018, 68, 65–72. [Google Scholar] [CrossRef]
- Susanto, H.; Ali, S. The design of flexible rubber tapping tool with settings the depth and thickness control. IOP Conf. Ser. Mater. Sci. Eng. 2019, 506, 12002. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Zhang, Z.; Liu, J.; Zhou, J.; Dong, X.; Fu, S. Design and experiment of a three-axis automatic rubber tapping device based on laser profiling. Trans. Chin. Soc. Agric. Mach. 2025, 56, 254–266. [Google Scholar] [CrossRef]
- Wen, X.; Hong, Y.; Xiong, J.; Yu, Y.; Tan, J.; Meng, X. Design and experiment of fixed natural rubber automatic tapping machine. Trans. Chin. Soc. Agric. Mach. 2023, 54 (Suppl. 2), 128–135. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, J.; Zhang, F.; Zhang, J.; Wang, S.; Zhang, C.; Li, W. Evaluation of Cutting Stability of a Natural-Rubber-Tapping Robot. Agriculture 2023, 13, 583. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Z.; Liu, J.; Zhang, Z.; Zhang, X. The Development of Rubber Tapping Machines in Intelligent Agriculture: A Review. Appl. Sci. 2022, 12, 9304. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Li, Y.; Zhang, L. Parameter Optimization Study of Adaptive Spiral Profiling Automatic Rubber Cutter for Natural Rubber Trees. Forests 2025, 16, 414. [Google Scholar] [CrossRef]
- Zeng, S.; Wu, Y.J.; Zeng, F.Y. Design and Experiment of a Fixed Rubber Automatic Tapping Machine. J. Southwest Univ. (Nat. Sci. Ed.) 2024, 46, 92–102. [Google Scholar] [CrossRef]
- NY/T 1088-2006; Ministry of Agriculture of the People’s Republic of China—Rubber Tree Tapping Technical Regulations. Ministry of Agriculture of the People’s Republic of China: Beijing, China, 2006. (In Chinese)


| Key Components | Parameters/mm |
|---|---|
| Frame | 750 × 520 × 1500 |
| Rubber tree stump length | 700–1000 |
| Rubber tree stump Dimension | 600–900 |
| Lead screw length | 1000 |
| Cylinder stroke | 100 |
| Code | A: Cutting Angle (°) | B: Cutting Blade Bending Angle (°) | C: Cutting Blade Attitude Angle (°) |
|---|---|---|---|
| −1.6817928 | 23.29 | 66.59 | −3.41 |
| −1 | 25 | 70 | 0 |
| 0 | 27.5 | 75 | 5 |
| 1 | 30 | 80 | 10 |
| 1.6817928 | 31.7 | 83.41 | 13.41 |
| Test Number | A: Cutting Angle/° | B: Cutting Blade Bending Angle/° | C: Cutting Blade Attitude Angle/° | Cutting Force/N | Variance of Forces/N2 |
|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | 13.3 | 6.59 |
| 2 | 1 | −1 | −1 | 25.25 | 3.97 |
| 3 | −1 | 1 | −1 | 17.5 | 7.29 |
| 4 | 1 | 1 | −1 | 22.85 | 9.2 |
| 5 | −1 | −1 | 1 | 7.46 | 9.56 |
| 6 | 1 | −1 | 1 | 12.1 | 4.97 |
| 7 | −1 | 1 | 1 | 12.8 | 5.95 |
| 8 | 1 | 1 | 1 | 9.44 | 3.87 |
| 9 | −1.681792831 | 0 | 0 | 13.37 | 4.5 |
| 10 | 1.681792831 | 0 | 0 | 16.75 | 3.45 |
| 11 | 0 | −1.681792831 | 0 | 10.19 | 8.46 |
| 12 | 0 | 1.681792831 | 0 | 17.57 | 5.96 |
| 13 | 0 | 0 | −1.681792831 | 29.35 | 6.12 |
| 14 | 0 | 0 | 1.681792831 | 17.01 | 9.34 |
| 15 | 0 | 0 | 0 | 18.96 | 4.64 |
| 16 | 0 | 0 | 0 | 20.99 | 3.97 |
| 17 | 0 | 0 | 0 | 21.56 | 4.95 |
| 18 | 0 | 0 | 0 | 19.76 | 3.51 |
| 19 | 0 | 0 | 0 | 22.05 | 4.25 |
| 20 | 0 | 0 | 0 | 22.76 | 5.25 |
| Response 1: Cutting Force | Response 2: Flatness | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | ||
| Model | 577.5 | 9 | 64.17 | 15.36 | <0.0001 | significant | Model | 64.60 | 9 | 718 | 5.96 | 0.0050 | significant |
| A | 43.11 | 1 | 43.11 | 10.32 | 0.0093 | A | 6.12 | 1 | 612 | 5.09 | 0.0477 | ||
| B | 20.89 | 1 | 20.89 | 5 | 0.0493 | B | 0.65 | 1 | 065 | 0.54 | 0.4786 | ||
| C | 245.08 | 1 | 245.08 | 58.65 | <0.0001 | C | 0.54 | 1 | 054 | 0.45 | 0.5182 | ||
| AB | 26.64 | 1 | 26.64 | 6.38 | 0.0301 | AB | 6.20 | 1 | 620 | 5.15 | 0.0467 | ||
| AC | 32.08 | 1 | 32.08 | 7.68 | 0.0198 | AC | 4.44 | 1 | 4.44 | 3.60 | 0.0837 | ||
| BC | 0.0968 | 1 | 0.10 | 0.0232 | 0.8821 | BC | 14.15 | 1 | 14.15 | 11.76 | 0.0065 | ||
| A2 | 93.02 | 1 | 93.02 | 22.26 | 0.0008 | A2 | 0.35 | 1 | 036 | 0.30 | 0.5943 | ||
| B2 | 126.08 | 1 | 126.08 | 30.17 | 0.0003 | B2 | 13.98 | 1 | 13.98 | 1161 | 0.0067 | ||
| C2 | 1.57 | 1 | 1.57 | 0.3762 | 0.5534 | C2 | 19.68 | 1 | 19.68 | 16.35 | 0.0023 | ||
| Residual | 41.79 | 10 | 4.18 | Residual | 12.04 | 10 | 1.20 | ||||||
| Lack of Fit | 31.58 | 5 | 632 | 3.09 | 0.1205 | not significant | Lack of Fit | 9.95 | 5 | 199 | 4.79 | 0.0552 | not significant |
| Pure Error | 10.21 | 5 | 2.04 | Pure Error | 2.08 | 5 | 0.42 | ||||||
| Cor Total | 619.28 | Cor Total | 76.64 | 19 | |||||||||
| R2 | 0.93 | 19 | R2 | 0.84 | |||||||||
| Adjusted R2 | 0.87 | 19 | Adjusted R2 | 0.70 | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Li, Y.; Wu, X.; Liu, J.; Zhang, X. Design of Rubber Tapping Mechanical Test Bench and Optimization of Rubber Tapping Machine Parameters. Forests 2025, 16, 1764. https://doi.org/10.3390/f16121764
Huang Q, Li Y, Wu X, Liu J, Zhang X. Design of Rubber Tapping Mechanical Test Bench and Optimization of Rubber Tapping Machine Parameters. Forests. 2025; 16(12):1764. https://doi.org/10.3390/f16121764
Chicago/Turabian StyleHuang, Qirun, Yue Li, Xian Wu, Junxiao Liu, and Xirui Zhang. 2025. "Design of Rubber Tapping Mechanical Test Bench and Optimization of Rubber Tapping Machine Parameters" Forests 16, no. 12: 1764. https://doi.org/10.3390/f16121764
APA StyleHuang, Q., Li, Y., Wu, X., Liu, J., & Zhang, X. (2025). Design of Rubber Tapping Mechanical Test Bench and Optimization of Rubber Tapping Machine Parameters. Forests, 16(12), 1764. https://doi.org/10.3390/f16121764






