Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning
Abstract
1. Introduction
2. Materials and Methods
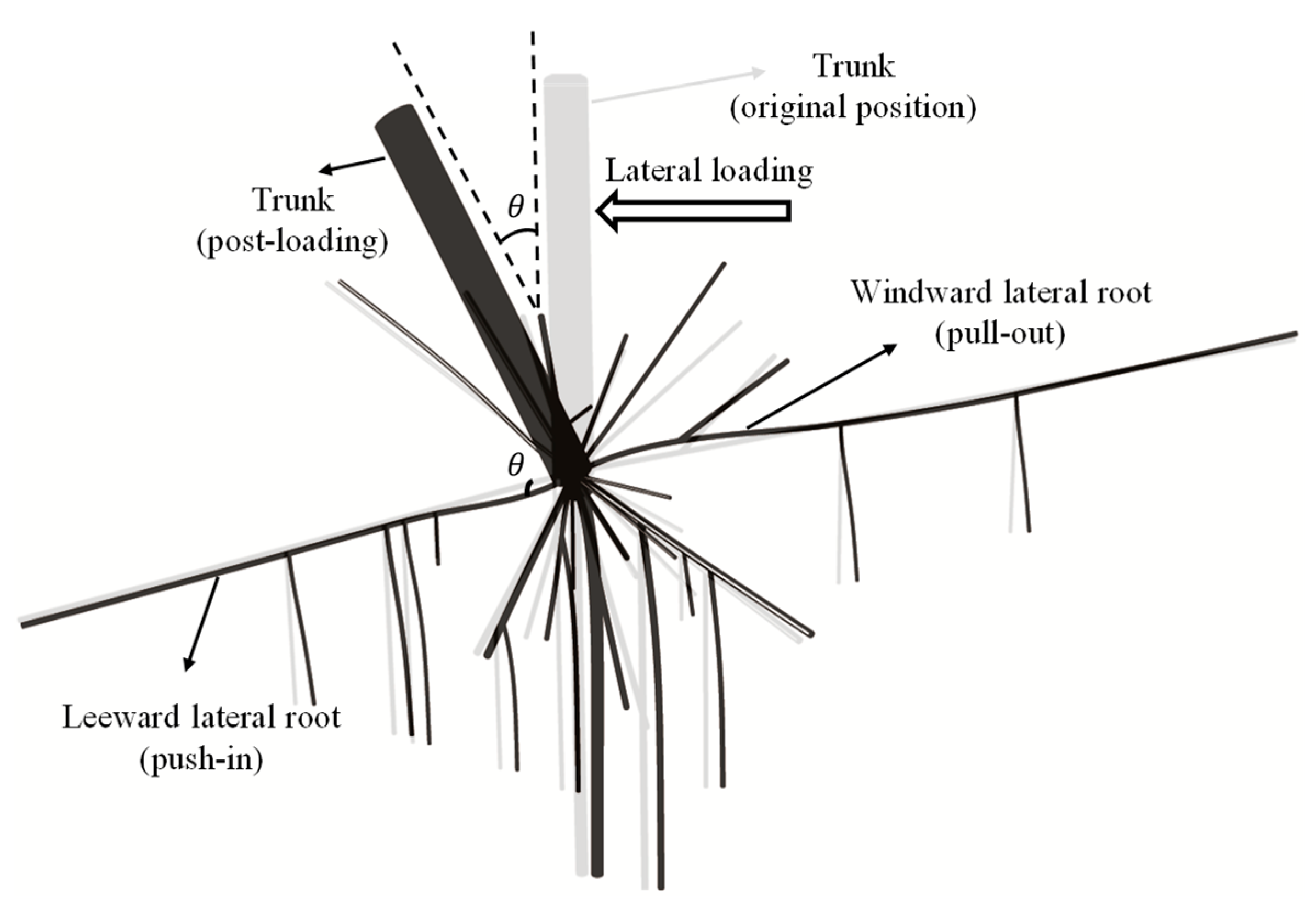
2.1. General Description of Modelling Methodology
2.2. Model Set-Up
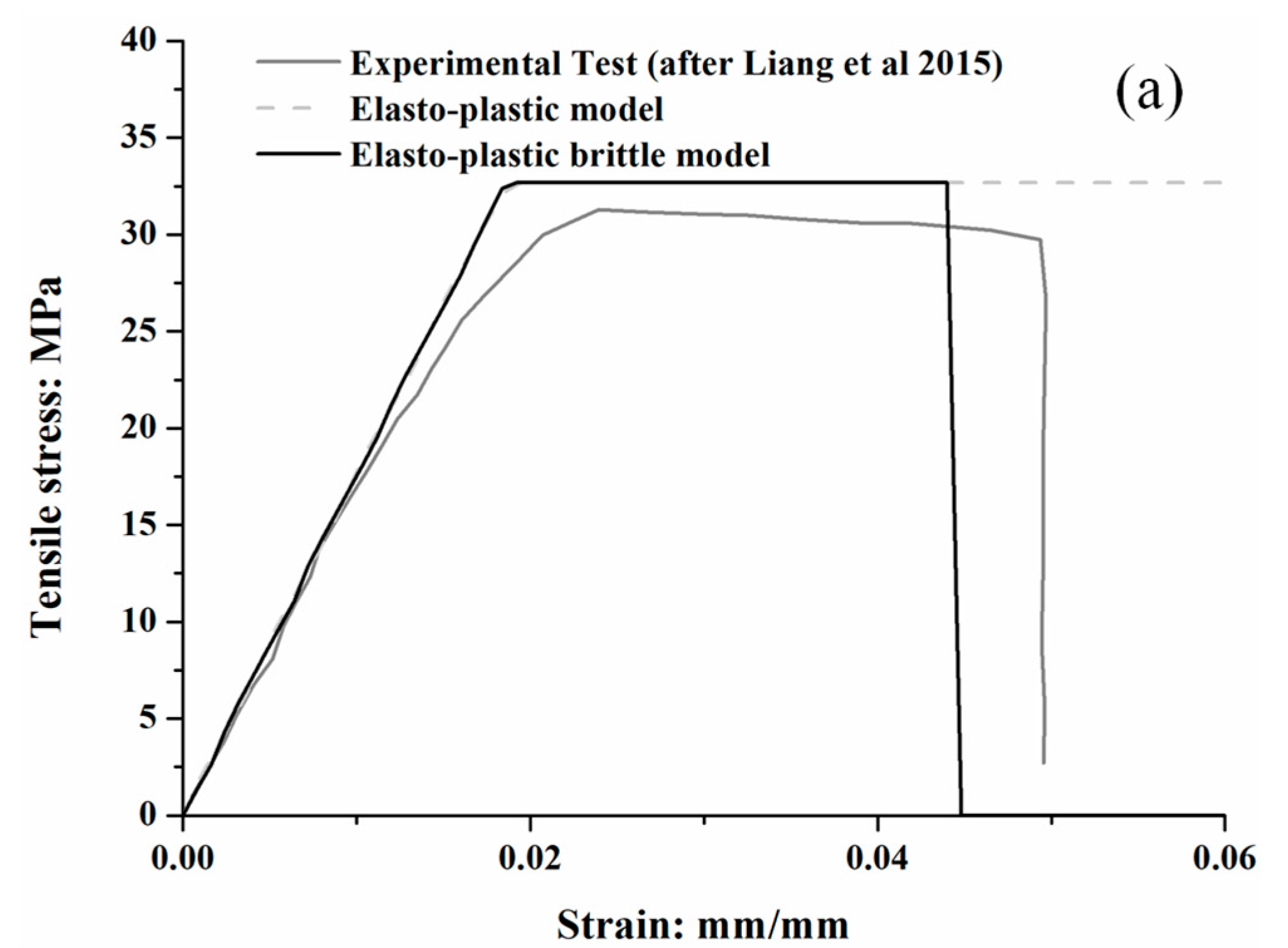
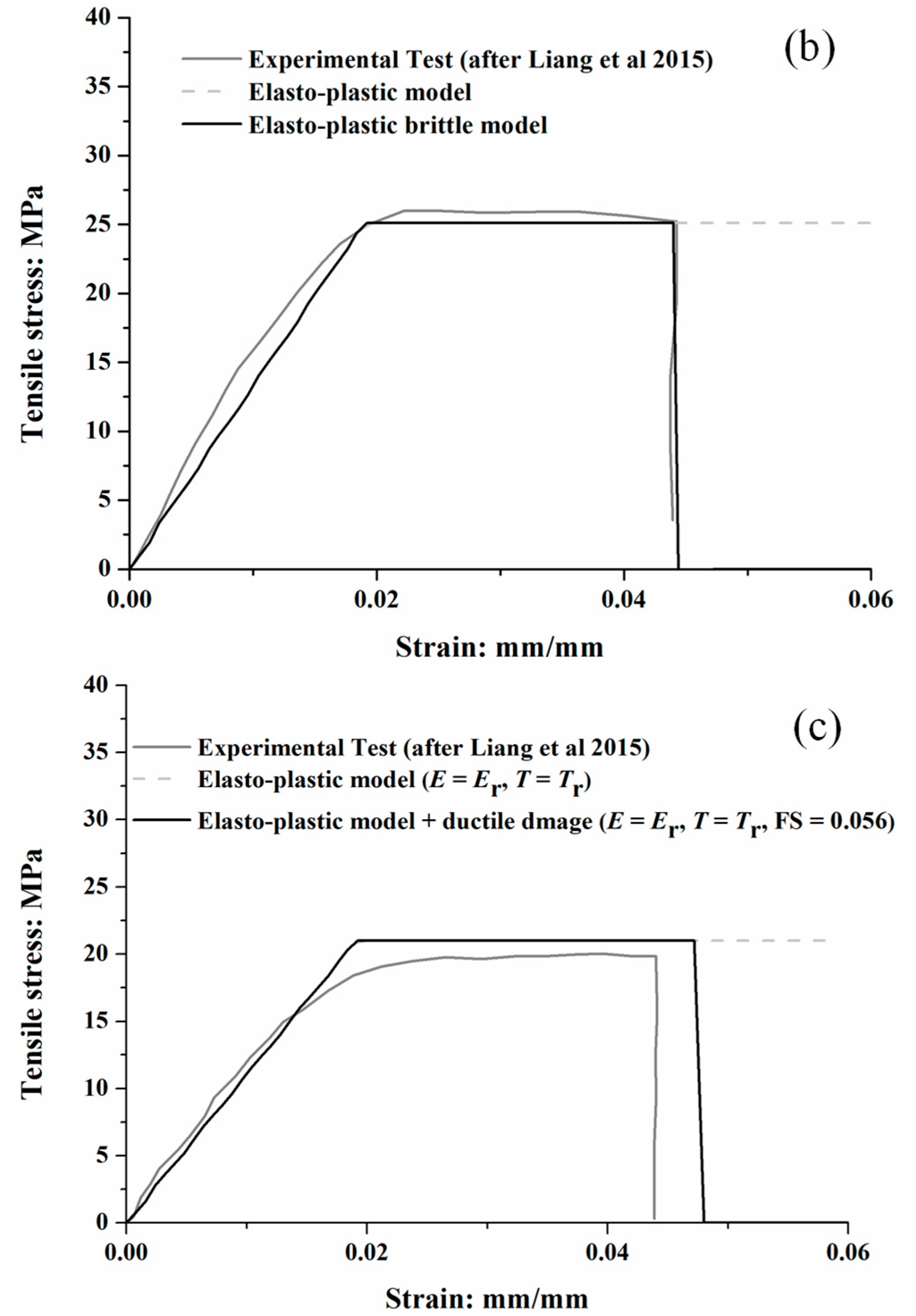
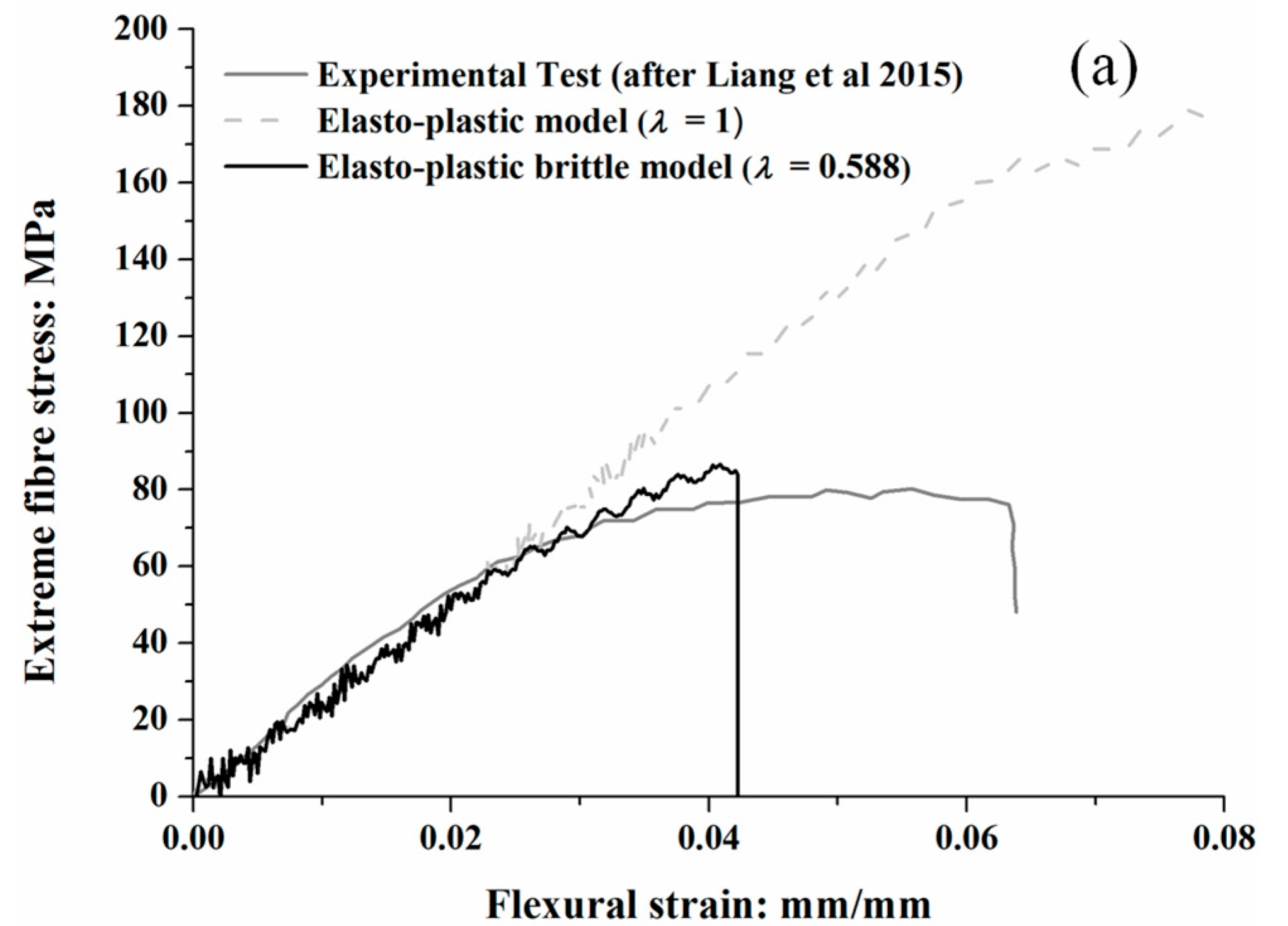
2.3. Non-Linear Properties of p-y Connectors
2.4. Non-Linear Properties of t-z Connectors
3. Results
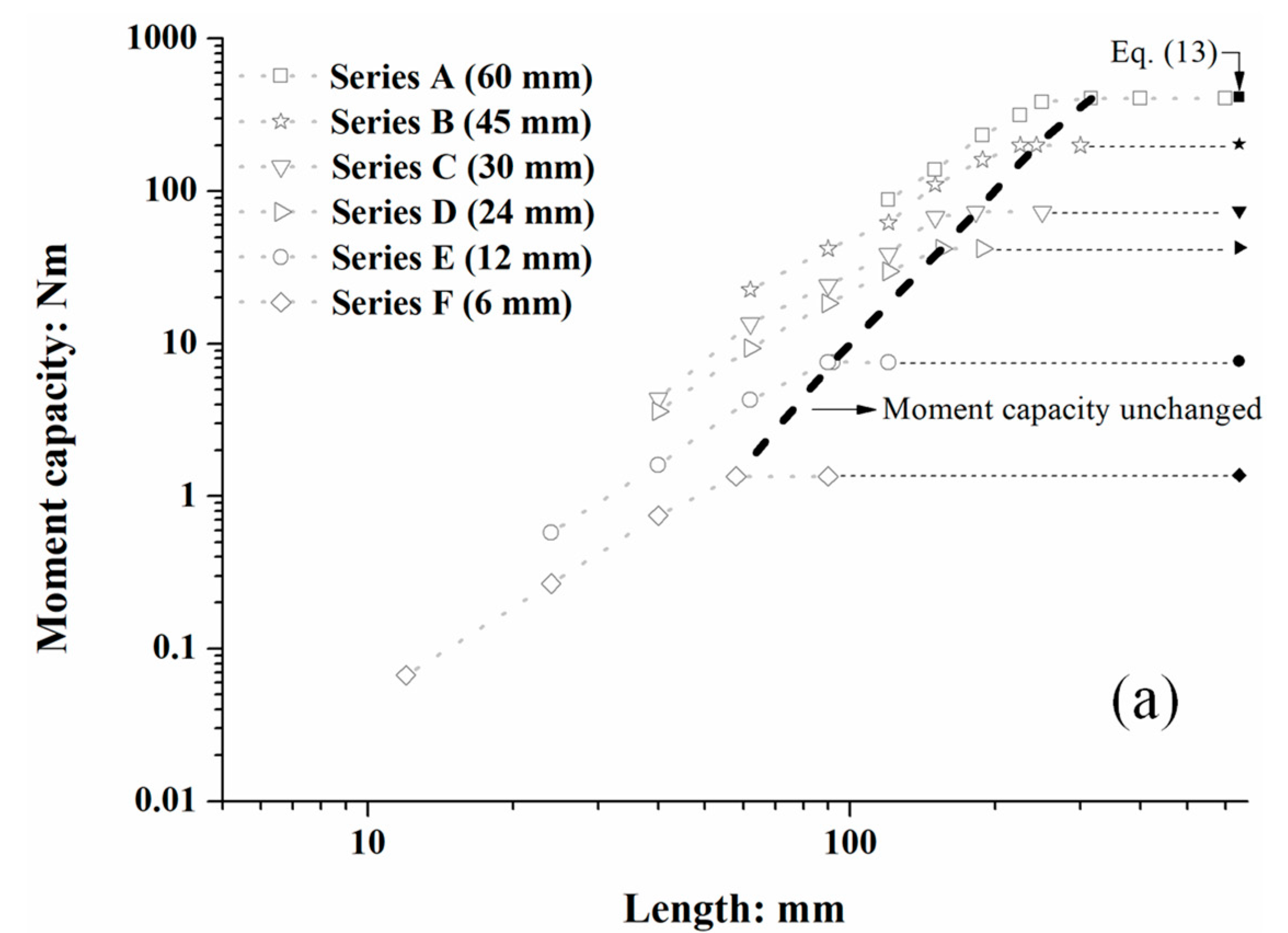
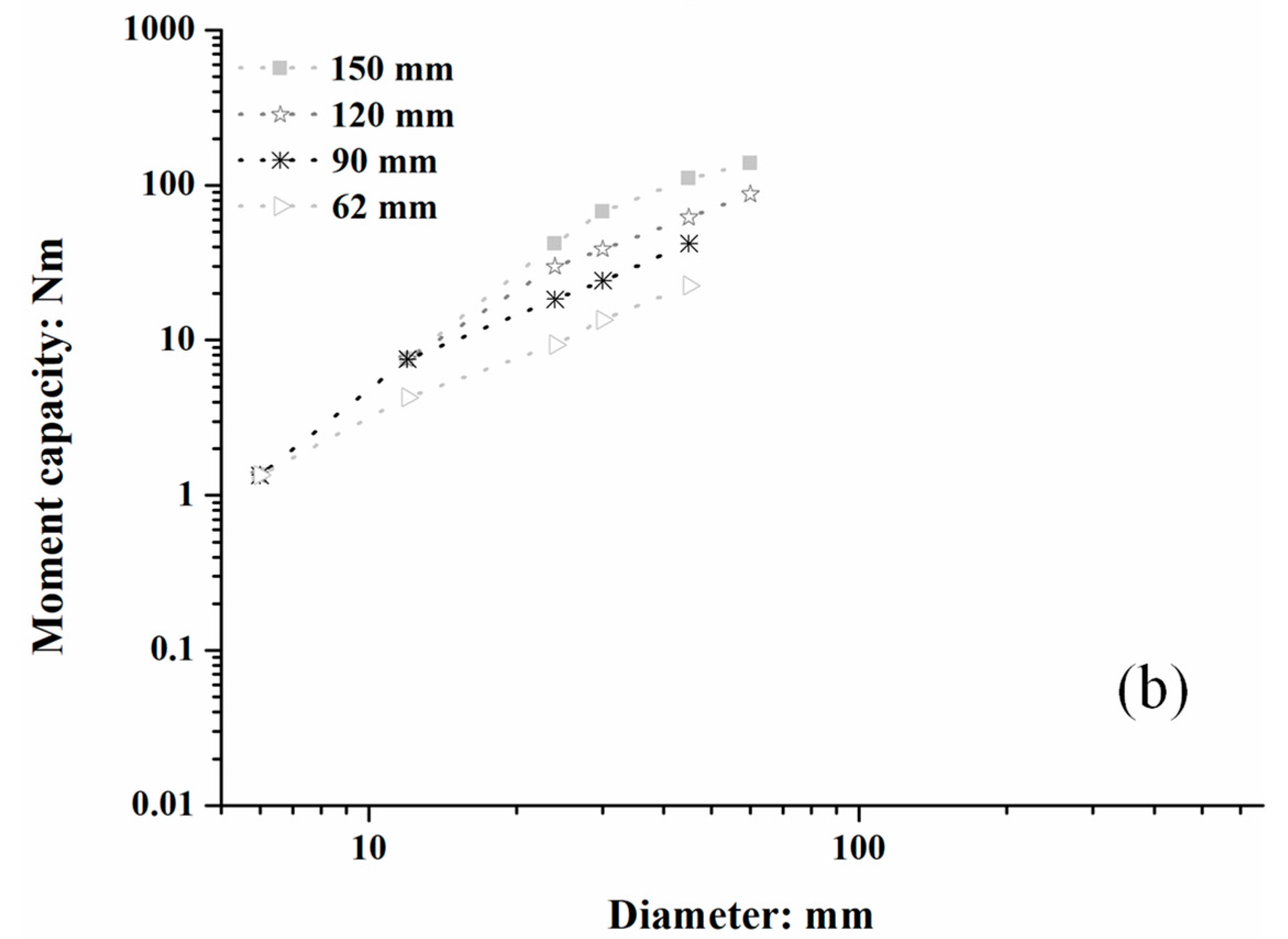
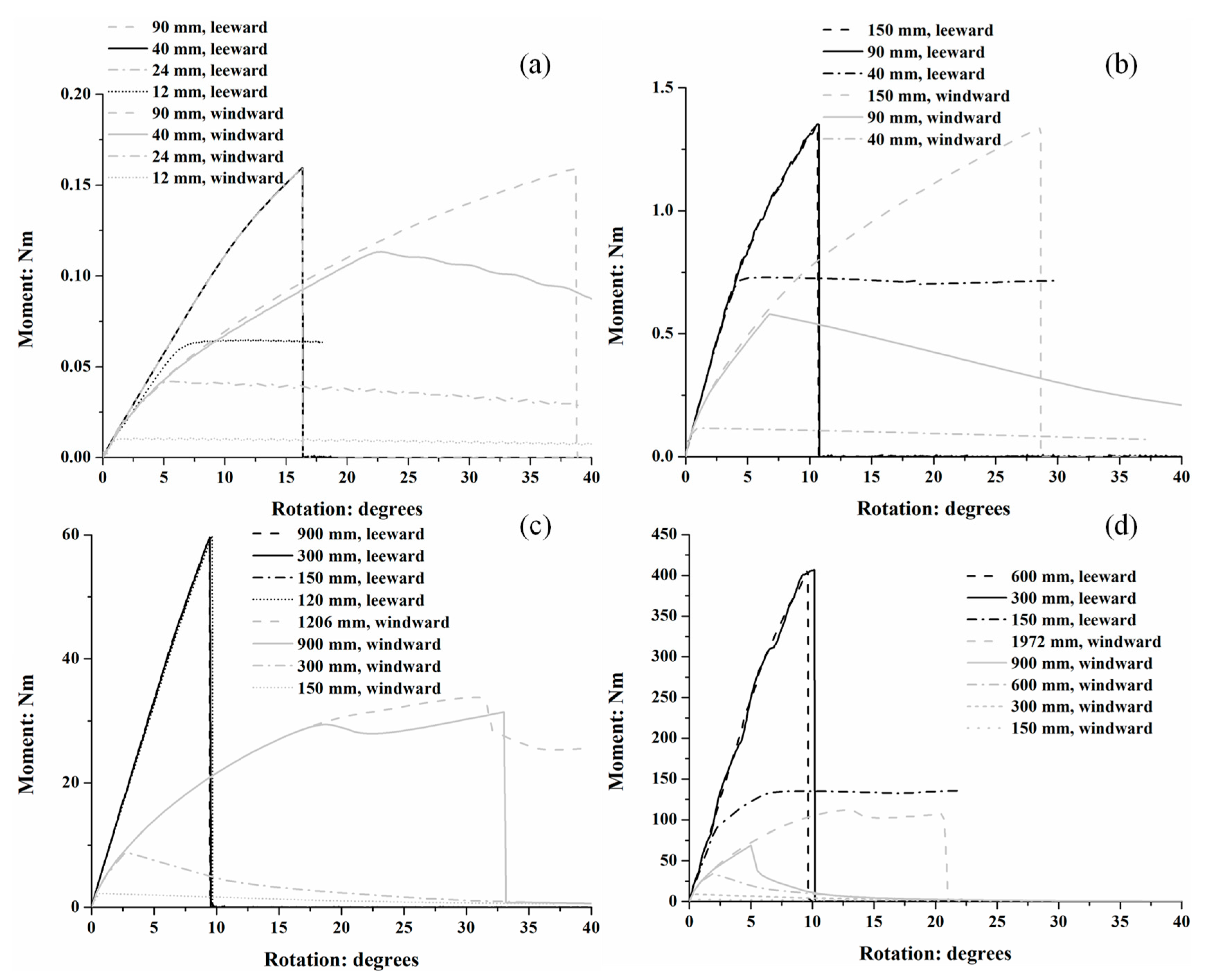
3.1. Moment–Rotation Curves of Roots of Different Sizes
3.2. Moment Capacities of Roots
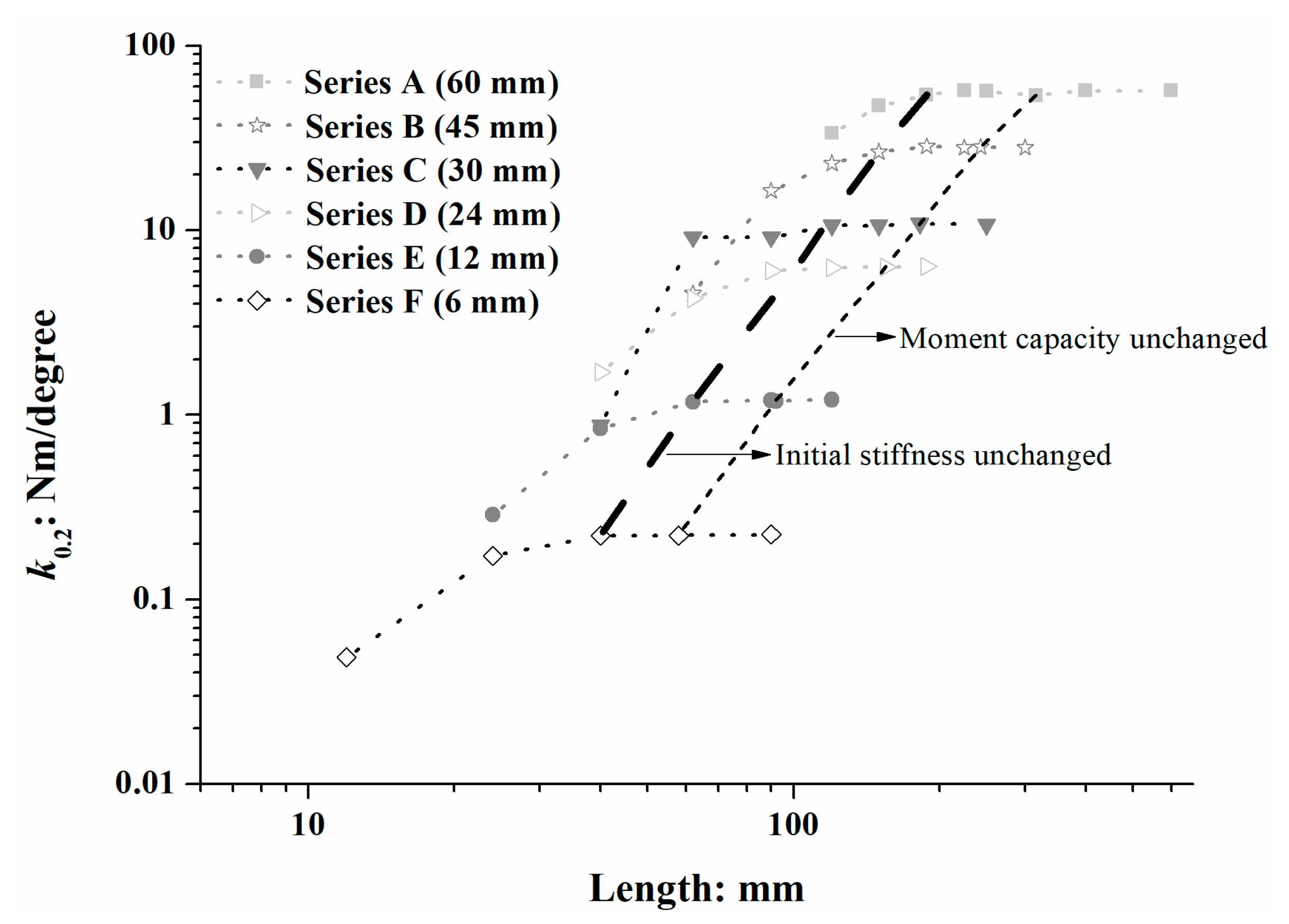
3.3. Rotational Stiffness of Roots of Different Sizes
4. Discussion
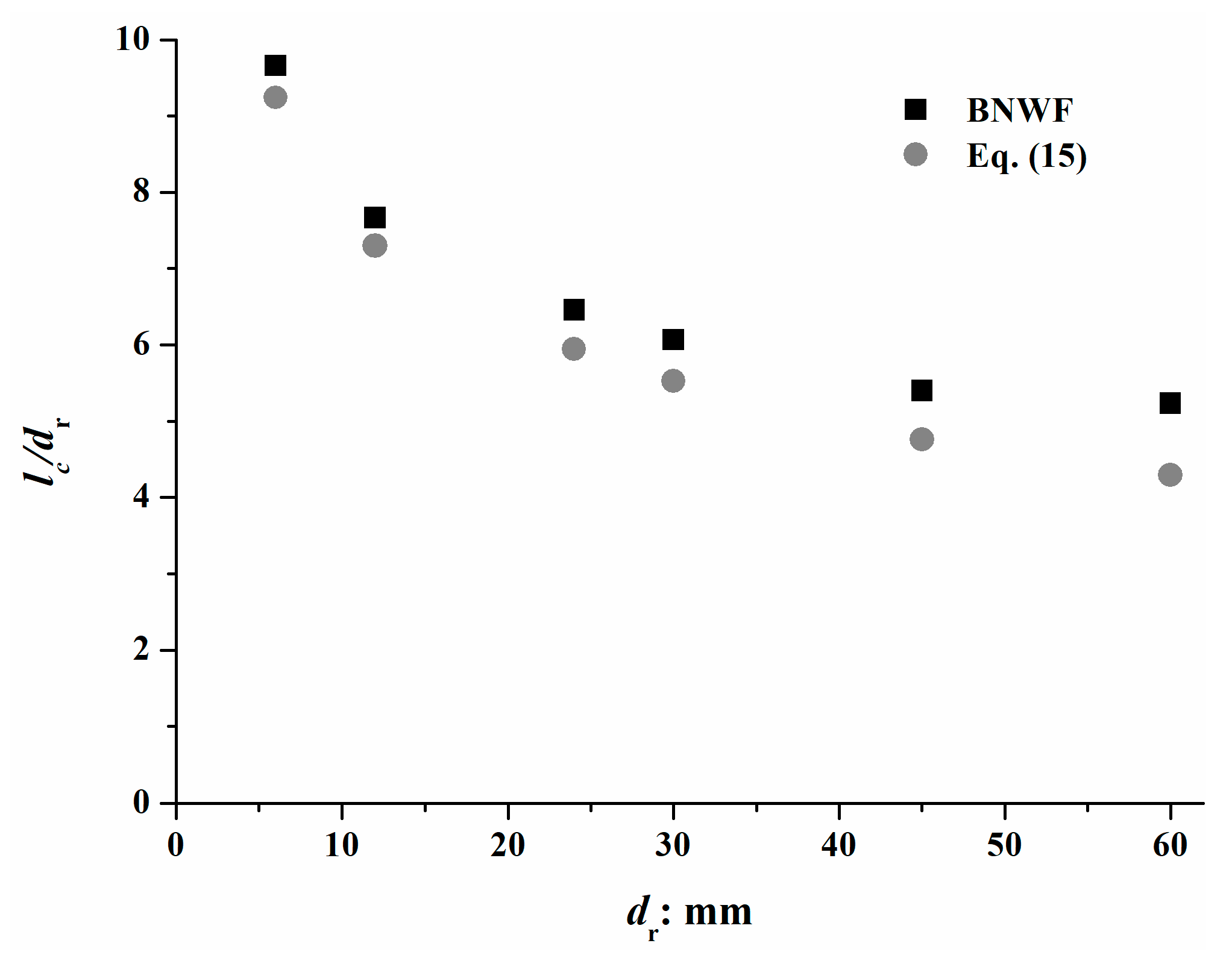
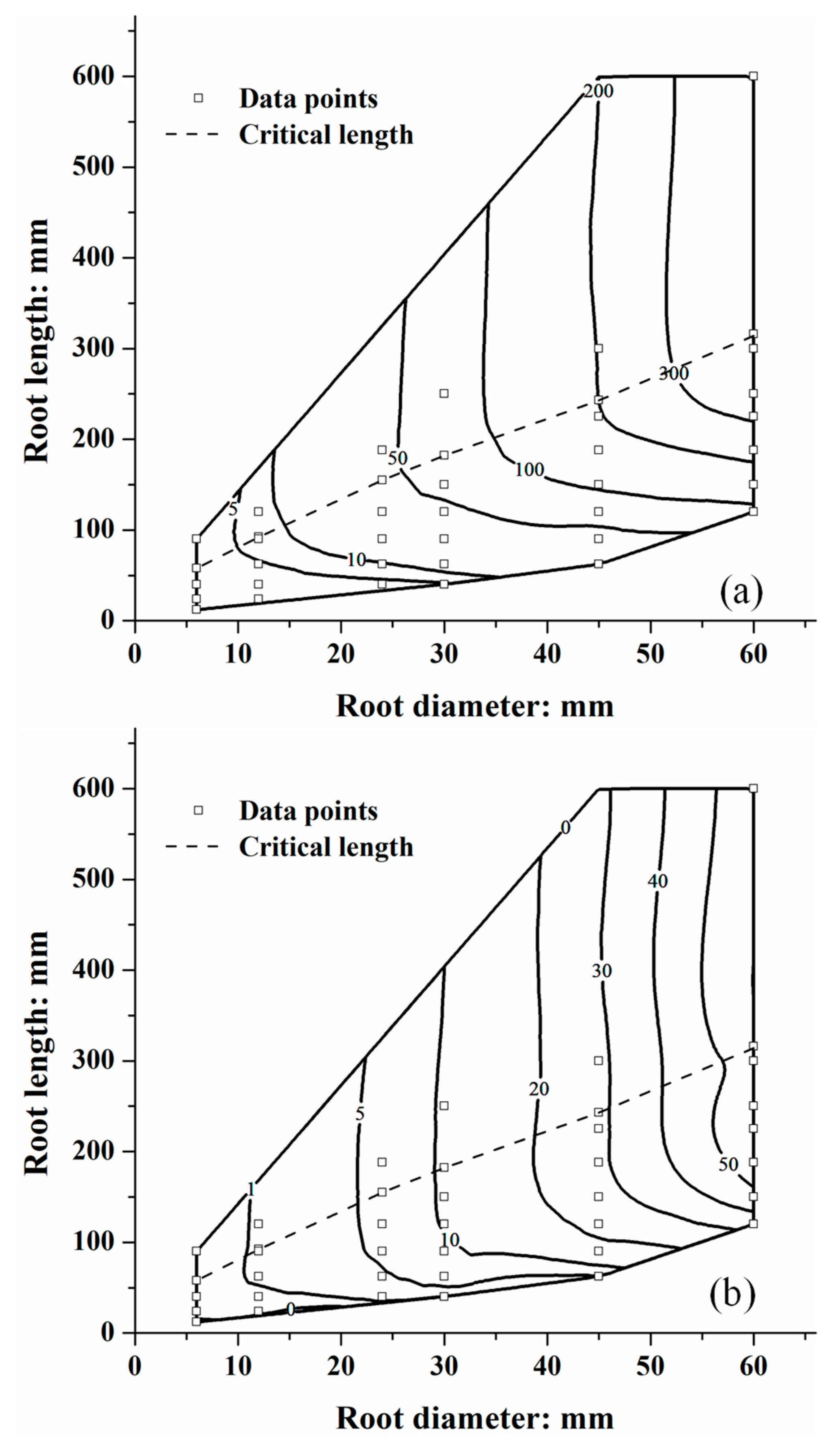
4.1. Critical Length of Roots
4.2. Implications for Tree Windthrow Resistance and Tree Winching Tests
4.3. Comparison with Windward Lateral Roots Across Different Root Properties
4.4. Consideration of Natural Variability and Model Applicability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mickovski, S.B.; Stokes, A.; van Beek, R.; Ghestem, M.; Fourcaud, T. Simulation of Direct Shear Tests on Rooted and Non-Rooted Soil Using Finite Element Analysis. Ecol. Eng. 2011, 37, 1523–1532. [Google Scholar] [CrossRef]
- Meijer, G.; Bengough, G.; Knappett, J.; Loades, K.; Nicoll, B. Measuring the Strength of Root-Reinforced Soil on Steep Natural Slopes Using the Corkscrew Extraction Method. Forests 2019, 10, 1135. [Google Scholar] [CrossRef]
- Smethurst, J.A.; Clarke, D.; Powrie, W. Factors Controlling the Seasonal Variation in Soil Water Content and Pore Water Pressures within a Lightly Vegetated Clay Slope. Géotechnique 2012, 62, 429–446. [Google Scholar] [CrossRef]
- Grimaldi, S.; Orellana, F.; Daly, E. Modelling the Effects of Soil Type and Root Distribution on Shallow Groundwater Resources. Hydrol. Process. 2015, 29, 4457–4469. [Google Scholar] [CrossRef]
- McCarthy, J.K.; Hood, I.A.; Brockerhoff, E.G.; Carlson, C.A.; Pawson, S.M.; Forward, M.; Walbert, K.; Gardner, J.F. Predicting Sapstain and Degrade in Fallen Trees Following Storm Damage in a Pinus Radiata Forest. For. Ecol. Manag. 2010, 260, 1456–1466. [Google Scholar] [CrossRef]
- Romagnoli, F.; Cadei, A.; Costa, M.; Marangon, D.; Pellegrini, G.; Nardi, D.; Masiero, M.; Secco, L.; Grigolato, S.; Lingua, E.; et al. Windstorm Impacts on European Forest-Related Systems: An Interdisciplinary Perspective. For. Ecol. Manag. 2023, 541, 121048. [Google Scholar] [CrossRef]
- Triviño, M.; Potterf, M.; Tijerín, J.; Ruiz-Benito, P.; Burgas, D.; Eyvindson, K.; Blattert, C.; Mönkkönen, M.; Duflot, R. Enhancing Resilience of Boreal Forests Through Management Under Global Change: A Review. Curr. Landsc. Ecol. Rep. 2023, 8, 103–118. [Google Scholar] [CrossRef]
- Jakob, M.; Lambert, S. Climate Change Effects on Landslides along the Southwest Coast of British Columbia. Geomorphology 2009, 107, 275–284. [Google Scholar] [CrossRef]
- Brang, P.; Schönenberger, W.; Ott, E.; Gardner, B. Forests as Protection from Natural Hazards. In The Forests Handbook, Volume 2: Applying Forest Science for Sustainable Management; Evans, J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 53–81. ISBN 9780632048236. [Google Scholar]
- Zhang, Q.; Zhang, W.; Chen, Y.D.; Jiang, T. Flood, Drought and Typhoon Disasters During the Last Half-Century in the Guangdong Province, China. Nat. Hazards 2011, 57, 267–278. [Google Scholar] [CrossRef]
- Coutts, M.P. Root Architecture and Tree Stability. Plant Soil 1983, 71, 171–188. [Google Scholar] [CrossRef]
- Nicoll, B.C.; Gardiner, B.A.; Peace, A.J. Improvements in Anchorage Provided by the Acclimation of Forest Trees to Wind Stress. Forestry 2008, 81, 389–398. [Google Scholar] [CrossRef]
- Marchi, L.; Grigolato, S.; Mologni, O.; Scotta, R.; Cavalli, R.; Montecchio, L. State of the Art on the Use of Trees as Supports and Anchors in Forest Operations. Forests 2018, 9, 467. [Google Scholar] [CrossRef]
- Danjon, F.; Barker, D.H.; Drexhage, M.; Stokes, A. Using Three-Dimensional Plant Root Architecture in Models of Shallow-Slope Stability. Ann. Bot. 2008, 101, 1281–1293. [Google Scholar] [CrossRef]
- Smith, A.; Astrup, R.; Raumonen, P.; Liski, J.; Krooks, A.; Kaasalainen, S.; Åkerblom, M.; Kaasalainen, M. Tree Root System Characterization and Volume Estimation by Terrestrial Laser Scanning and Quantitative Structure Modeling. Forests 2014, 5, 3274–3294. [Google Scholar] [CrossRef]
- Harnas, F.R.; Rahardjo, H.; Leong, E.C.; Tan, P.Y.; Ow, L.F. Stability of Containerized Urban Street Trees. Landsc. Ecol. Eng. 2016, 12, 13–24. [Google Scholar] [CrossRef]
- Zhang, X.; Knappett, J.A.; Leung, A.K.; Ciantia, M.O.; Liang, T.; Danjon, F. Small-Scale Modelling of Root-Soil Interaction of Trees Under Lateral Loads. Plant Soil 2020, 456, 289–305. [Google Scholar] [CrossRef]
- Zhang, X.; Knappett, J.A.; Leung, A.K.; Liang, T. Physical Modelling of Soil-Structure Interaction of Tree Root Systems under Lateral Loads. In Proceedings of the 9th International Conference on Physical Modelling in Geoetchnics, London, UK, 16–19 July 2018; pp. 481–486. [Google Scholar]
- Zhang, X.; Knappett, J.A.; Leung, A.K.; Ciantia, M.O.; Liang, T.; Nicoll, B.C. Centrifuge Modelling of Root-Soil Interaction of Laterally Loaded Trees Under Different Loading Conditions. Géotechnique 2023, 73, 766–780. [Google Scholar] [CrossRef]
- Dupuy, L.X.; Fourcaud, T.; Lac, P.; Stokes, A. A Generic 3D Finite Element Model of Tree Anchorage Integrating Soil Mechanics and Real Root System Architecture. Am. J. Bot. 2007, 94, 1506–1514. [Google Scholar] [CrossRef]
- Yang, M.; Défossez, P.; Danjon, F.; Fourcaud, T. Analyzing Key Factors of Roots and Soil Contributing to Tree Anchorage of Pinus Species. Trees Struct. Funct. 2018, 32, 703–712. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, Y.; Leung, A.K.; Zhu, J. Large Deformation Simulation of Uprooting of Trees with Complex Root System Architectures Using Material Point Method with Embedded Truss Elements. Plant Soil 2024, 511, 1355–1384. [Google Scholar] [CrossRef]
- Chiatante, D.; Scippa, S.G.; Di Iorio, A.; Sarnataro, M. The Influence of Steep Slopes on Root System Development. J. Plant Growth Regul. 2002, 21, 247–260. [Google Scholar] [CrossRef]
- Giadrossich, F.; Schwarz, M.; Cohen, D.; Cislaghi, A.; Vergani, C.; Hubble, T.; Phillips, C.; Stokes, A. Methods to Measure the Mechanical Behaviour of Tree Roots: A Review. Ecol. Eng. 2017, 109, 256–271. [Google Scholar] [CrossRef]
- Masi, E.B.; Segoni, S.; Tofani, V. Root Reinforcement in Slope Stability Models: A Review. Geosciences 2021, 11, 212. [Google Scholar] [CrossRef]
- Mickovski, S.B.; van Beek, L.P.H. Root Morphology and Effects on Soil Reinforcement and Slope Stability of Young Vetiver (Vetiveria zizanioides) Plants Grown in Semi-Arid Climate. Plant Soil 2009, 324, 43–56. [Google Scholar] [CrossRef]
- Karimzadeh, A.A.; Leung, A.K.; Gao, Z. Shear Strength Anisotropy of Rooted Soils. Geotechnique 2022, 74, 1033–1046. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-Soil Mechanical Interactions during Pullout and Failure of Root Bundles. J. Geophys. Res. Earth Surf. 2010, 115, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Ciantia, M.O.; Knappett, J.A.; Leung, A.K.; Liang, T. Particle Size Effects on the Axial Pull-out and Push-in Behaviour of Roots. Acta Geotech. 2024, 19, 1461–1476. [Google Scholar] [CrossRef]
- Wu, J.; Kouretzis, G.; Suwal, L. Bearing Capacity Mechanisms for Pipes Buried in Sand. Can. Geotech. J. 2021, 58, 834–847. [Google Scholar] [CrossRef]
- Reese, L.C.; Van Impe, W.F. Single Piles and Pile Groups under Lateral Loading, 2nd ed.; CRC: Leiden, The Netherlands, 2011. [Google Scholar]
- Meijer, G.J.; Wood, D.M.; Knappett, J.A.; Bengough, G.A. Analysis of Coupled Axial and Lateral Deformation of Roots in Soil. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 684–707. [Google Scholar] [CrossRef]
- Danjon, F.; Caplan, J.S.; Fortin, M.; Meredieu, C. Descendant Root Volume Varies as a Function of Root Type: Estimation of Root Biomass Lost During Uprooting in Pinus pinaster. Front. Plant Sci. 2013, 4, 402. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying Lateral Root Reinforcement in Steep Slopes—From a Bundle of Roots to Tree Stands. Earth Surf. Process. Landf. 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Mao, Z.; Saint-André, L.; Genet, M.; Mine, F.X.; Jourdan, C.; Rey, H.; Courbaud, B.; Stokes, A. Engineering Ecological Protection Against Landslides in Diverse Mountain Forests: Choosing Cohesion Models. Ecol. Eng. 2012, 45, 55–69. [Google Scholar] [CrossRef]
- Liang, T.; Knappett, J.A.; Duckett, N. Modelling the Seismic Performance of Rooted Slopes from Individual Root–Soil Interaction to Global Slope Behaviour. Géotechnique 2015, 65, 995–1009. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of Crack Formation and Crack Growth in Concrete by Means of Fracture Mechanics and Finite Elements; American Concrete Institute (ACI): Farmington Hills, MI, USA, 2008; Volume SP-249, pp. 225–237. [Google Scholar]
- Al-Defae, A.H.; Caucis, K.; Knappett, J.A. Aftershocks and the Whole-Life Seismic Performance of Granular Slopes. Géotechnique 2013, 63, 1230–1244. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Knappett, J.; Brown, M.J.; Davidson, C.; Sharif, Y. Optimised Design of Screw Anchors in Tension in Sand for Renewable Energy Applications. Ocean Eng. 2020, 217, 108010. [Google Scholar] [CrossRef]
- Zhang, X.; Knappett, J.A.; Ciantia, M.O.; Leung, A.K.; Wang, H.; Liang, T. Root Size Effects on Transverse Root-Soil Interactions. Comput. Geotech. 2024, 165, 105860. [Google Scholar] [CrossRef]
- Bolton, M.D. The Strength and Dilatancy of Sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Chakraborty, T.; Salgado, R. Dilatancy and Shear Strength of Sand at Low Confining Pressures. J. Geotech. Geoenviron. Eng. 2010, 136, 527–532. [Google Scholar] [CrossRef]
- Jaky, J. The Coefficient of Earth Pressure at Rest. J. Soc. Hung. Archit. Eng. 1944, 78, 355–358. [Google Scholar]
- Galli, A.; Sala, C.; Castellanza, R.; Marsiglia, A.; Ciantia, M.O. Lesson Learnt from Static Pulling Tests on Trees: An Experimental Study on Toppling Behaviour of Complex Foundations. Acta Geotech. 2024, 19, 1477–1494. [Google Scholar] [CrossRef]
- Schwarz, M.; Rist, A.; Cohen, D.; Giadrossich, F.; Egorov, P.; Büttner, D.; Stolz, M.; Thormann, J.J. Root Reinforcement of Soils Under Compression. J. Geophys. Res. Earth Surf. 2015, 120, 2103–2120. [Google Scholar] [CrossRef]
- Coutts, M.P. Components of Tree Stability in Sitka Spruce on Peaty Gley Soil. Forestry 1986, 59, 173–197. [Google Scholar] [CrossRef]
- Crook, M.J.; Ennos, A.R. The Mechanics of Root Lodging in Winter Wheat, Triticum aestivum L. J. Exp. Bot. 1993, 44, 1219–1224. [Google Scholar] [CrossRef]
- Ji, J.; Kokutse, N.; Genet, M.; Fourcaud, T.; Zhang, Z. Effect of Spatial Variation of Tree Root Characteristics on Slope Stability. A Case Study on Black Locust (Robinia pseudoacacia) and Arborvitae (Platycladus orientalis) Stands on the Loess Plateau, China. Catena 2012, 92, 139–154. [Google Scholar] [CrossRef]
- Crook, M.J.; Ennos, A.R. The Anchorage Mechanics of Deep Rooted Larch, Larix europea × L. japonica. J. Exp. Bot. 1996, 47, 1509–1517. [Google Scholar] [CrossRef]
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Ganga, A.; Marrosu, R.; Pirastru, M.; Capra, G.F. Large Roots Dominate the Contribution of Trees to Slope Stability. Earth Surf. Process. Landf. 2019, 44, 1602–1609. [Google Scholar] [CrossRef]

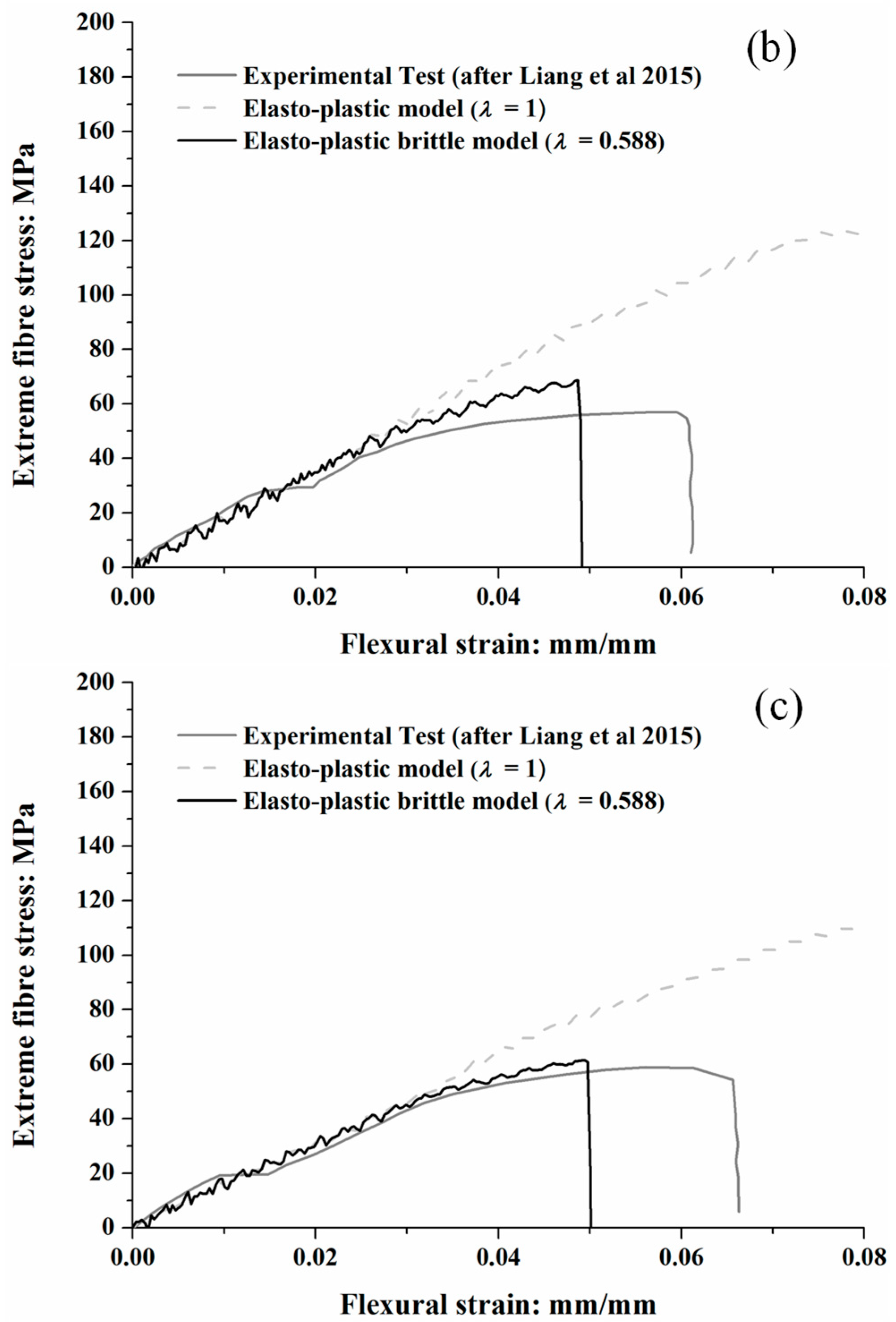
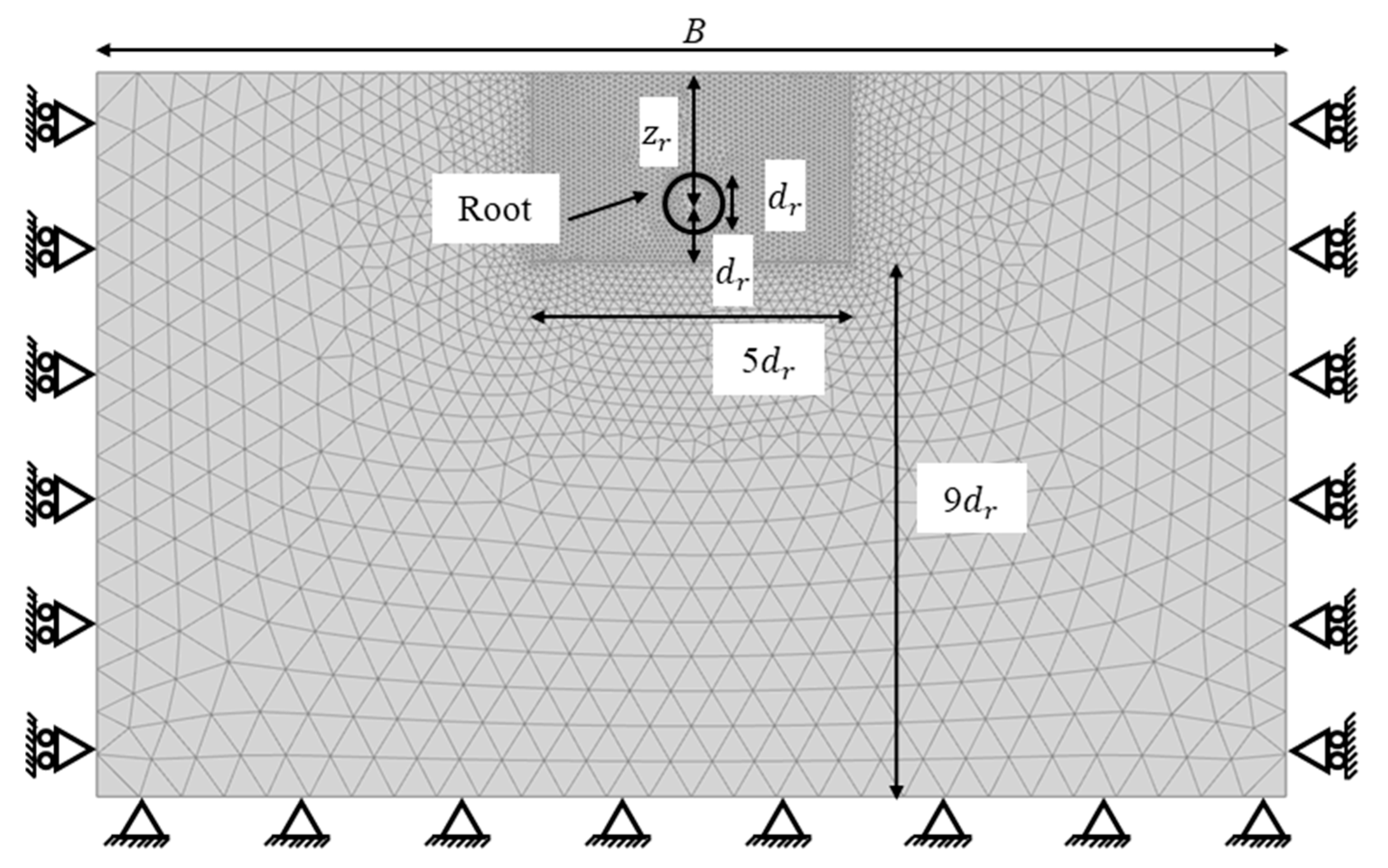
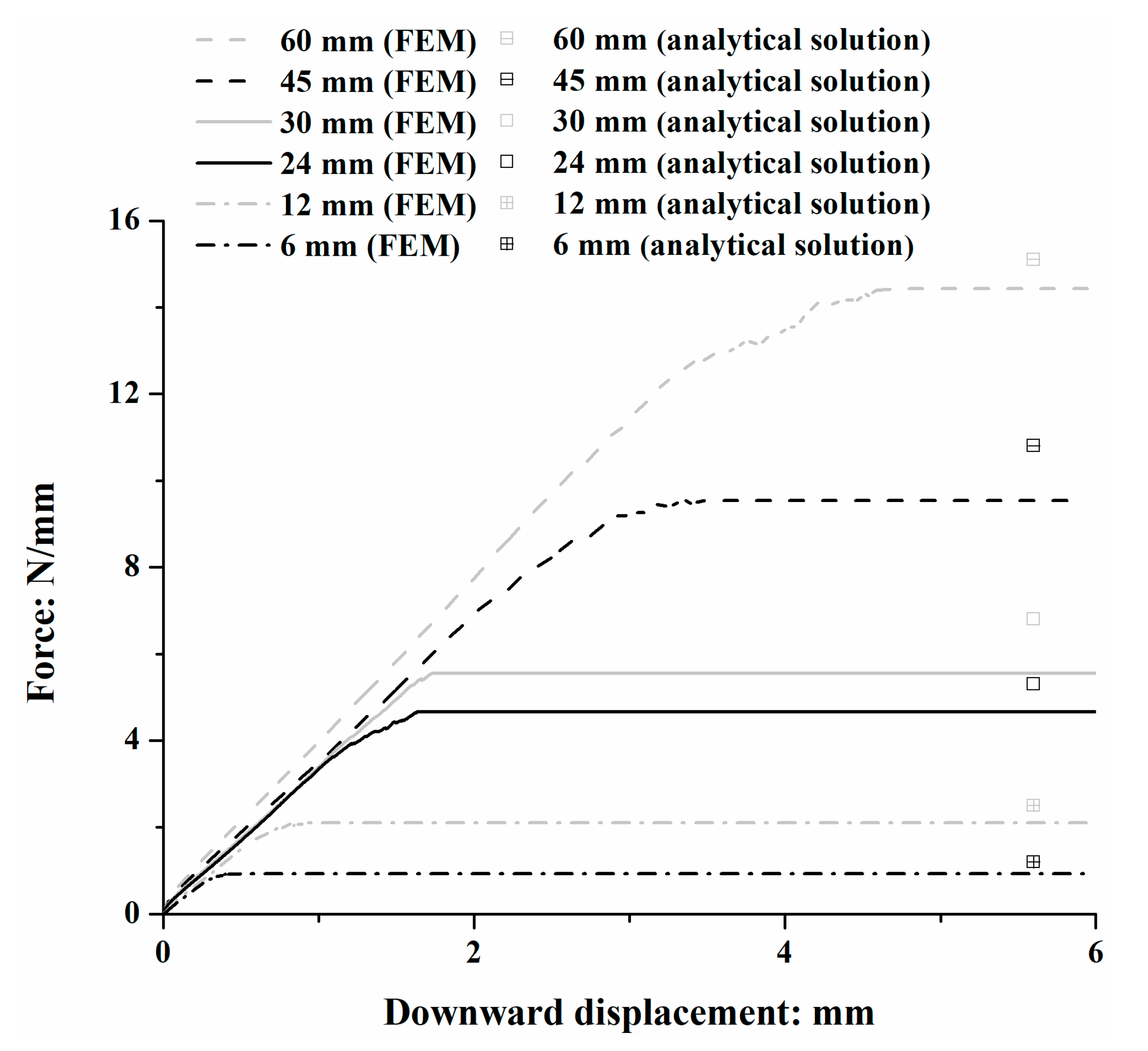

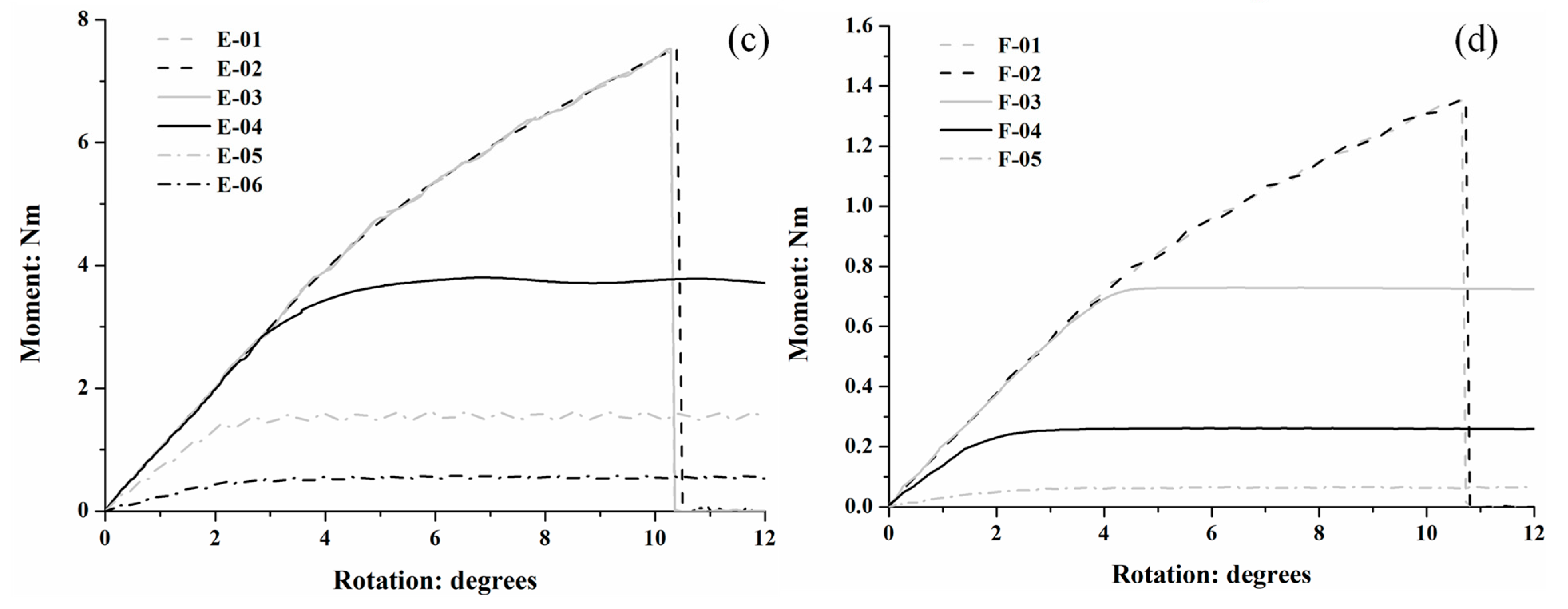
| ID | dr: mm | lr: mm | ID | dr: mm | lr: mm |
|---|---|---|---|---|---|
| A-01 | 60 | 900 | C-05 | 30 | 90 |
| A-02 | 60 | 314 | C-06 | 30 | 62 |
| A-03 | 60 | 300 | C-07 | 30 | 40 |
| A-04 | 60 | 250 | D-01 | 24 | 188 |
| A-05 | 60 | 225 | D-02 | 24 | 155 |
| A-06 | 60 | 188 | D-03 | 24 | 120 |
| A-07 | 60 | 150 | D-04 | 24 | 90 |
| A-08 | 60 | 120 | D-05 | 24 | 62 |
| B-01 | 45 | 600 | D-06 | 24 | 40 |
| B-02 | 45 | 243 | E-01 | 12 | 120 |
| B-03 | 45 | 225 | E-02 | 12 | 92 |
| B-04 | 45 | 188 | E-03 | 12 | 90 |
| B-05 | 45 | 150 | E-04 | 12 | 62 |
| B-06 | 45 | 120 | E-05 | 12 | 40 |
| B-07 | 45 | 90 | E-06 | 12 | 24 |
| B-08 | 45 | 62 | F-01 | 6 | 90 |
| C-01 | 30 | 250 | F-02 | 6 | 58 |
| C-02 | 30 | 182 | F-03 | 6 | 40 |
| C-03 | 30 | 150 | F-04 | 6 | 24 |
| C-04 | 30 | 120 | F-05 | 6 | 12 |
| Soil Index Properties | Value |
|---|---|
| : mm : mm | 0.14 0.21 |
| Minimum void ratio | 0.467 |
| Maximum void ratio | 0.769 |
| FEM parameters (corresponding to 60% relative density) | Value |
| : ° | 46 |
| : ° | 18 |
| : MPa | 35.2 |
| : MPa | 44 |
| : MPa | 105.7 |
| Reference * low strain shear modulus (): MPa | 118.8 |
| : % | 0.0169 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Knappett, J.; Zhang, T.; Zheng, Z.; Liang, T.; Ke, S.; Ciantia, M.; Leung, A. Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning. Forests 2025, 16, 1692. https://doi.org/10.3390/f16111692
Zhang X, Knappett J, Zhang T, Zheng Z, Liang T, Ke S, Ciantia M, Leung A. Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning. Forests. 2025; 16(11):1692. https://doi.org/10.3390/f16111692
Chicago/Turabian StyleZhang, Xingyu, Jonathan Knappett, Tian Zhang, Zhiwen Zheng, Teng Liang, Shitang Ke, Matteo Ciantia, and Anthony Leung. 2025. "Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning" Forests 16, no. 11: 1692. https://doi.org/10.3390/f16111692
APA StyleZhang, X., Knappett, J., Zhang, T., Zheng, Z., Liang, T., Ke, S., Ciantia, M., & Leung, A. (2025). Mechanical Behaviour of Leeward Lateral Roots During Tree Overturning. Forests, 16(11), 1692. https://doi.org/10.3390/f16111692






