A Spatiotemporal Wildfire Risk Prediction Framework Integrating Density-Based Clustering and GTWR-RFR
Abstract
1. Introduction
2. Study Area and Data Preparation
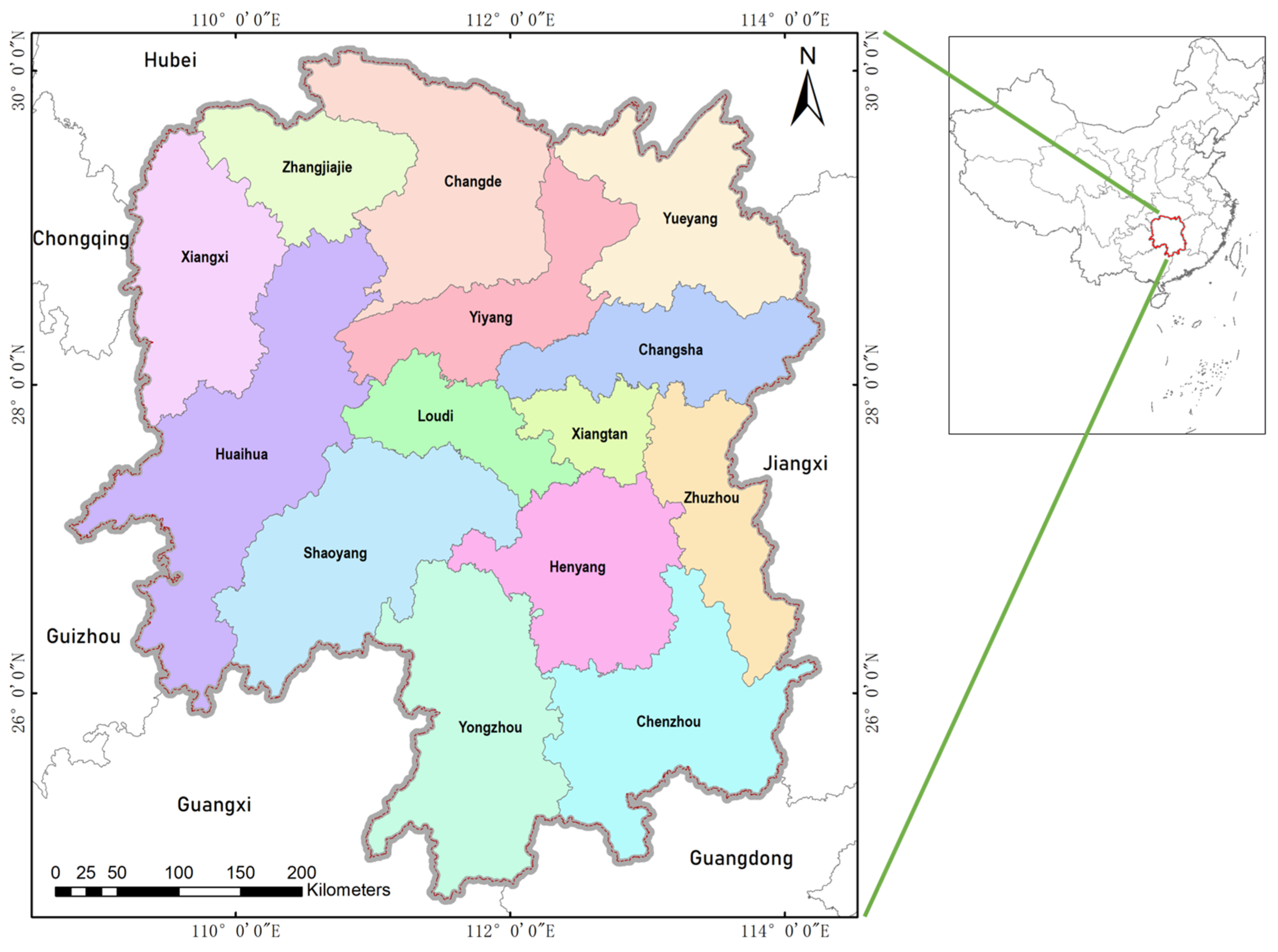
2.1. Study Area
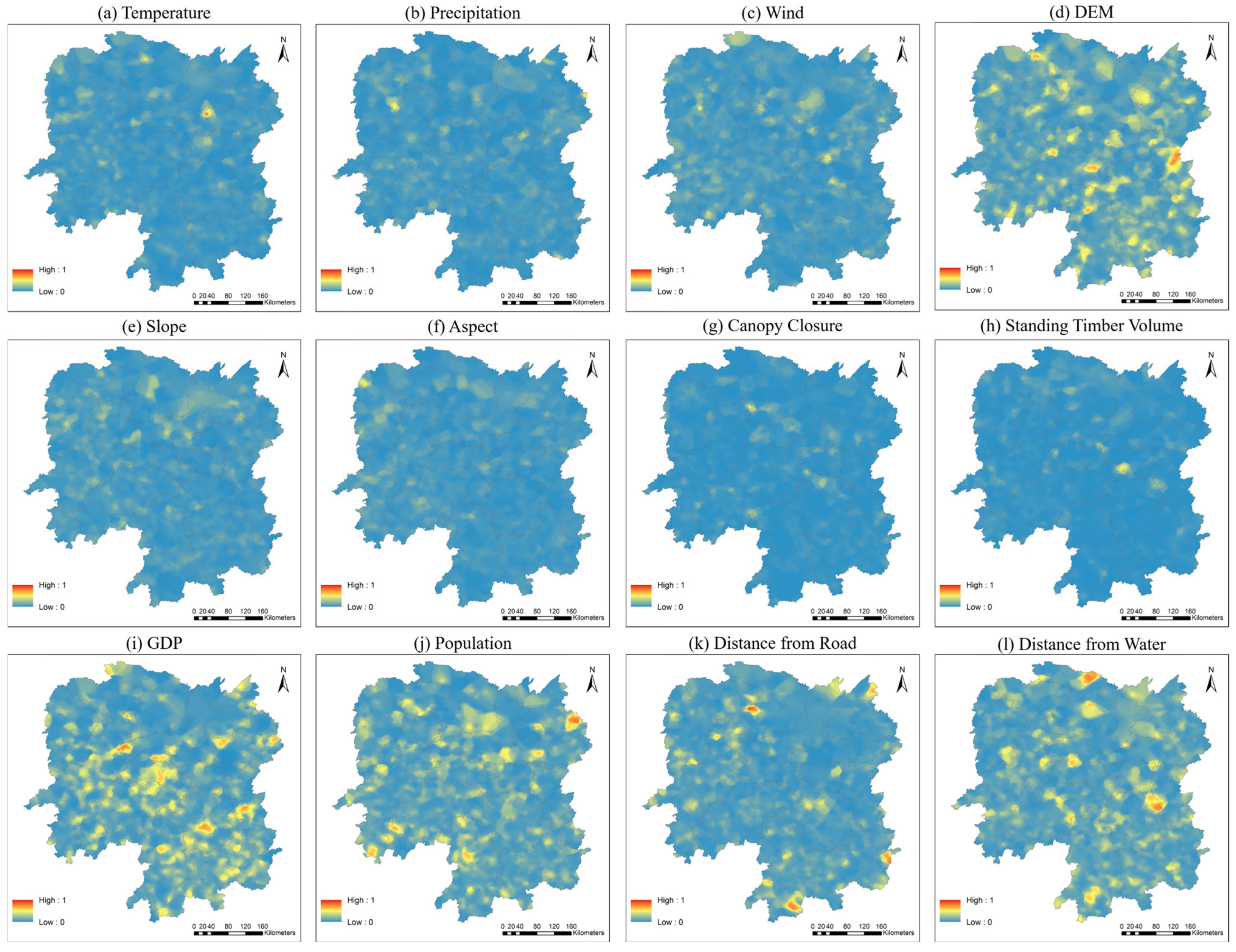
2.2. Data Collection and Preprocessing
3. Methodology
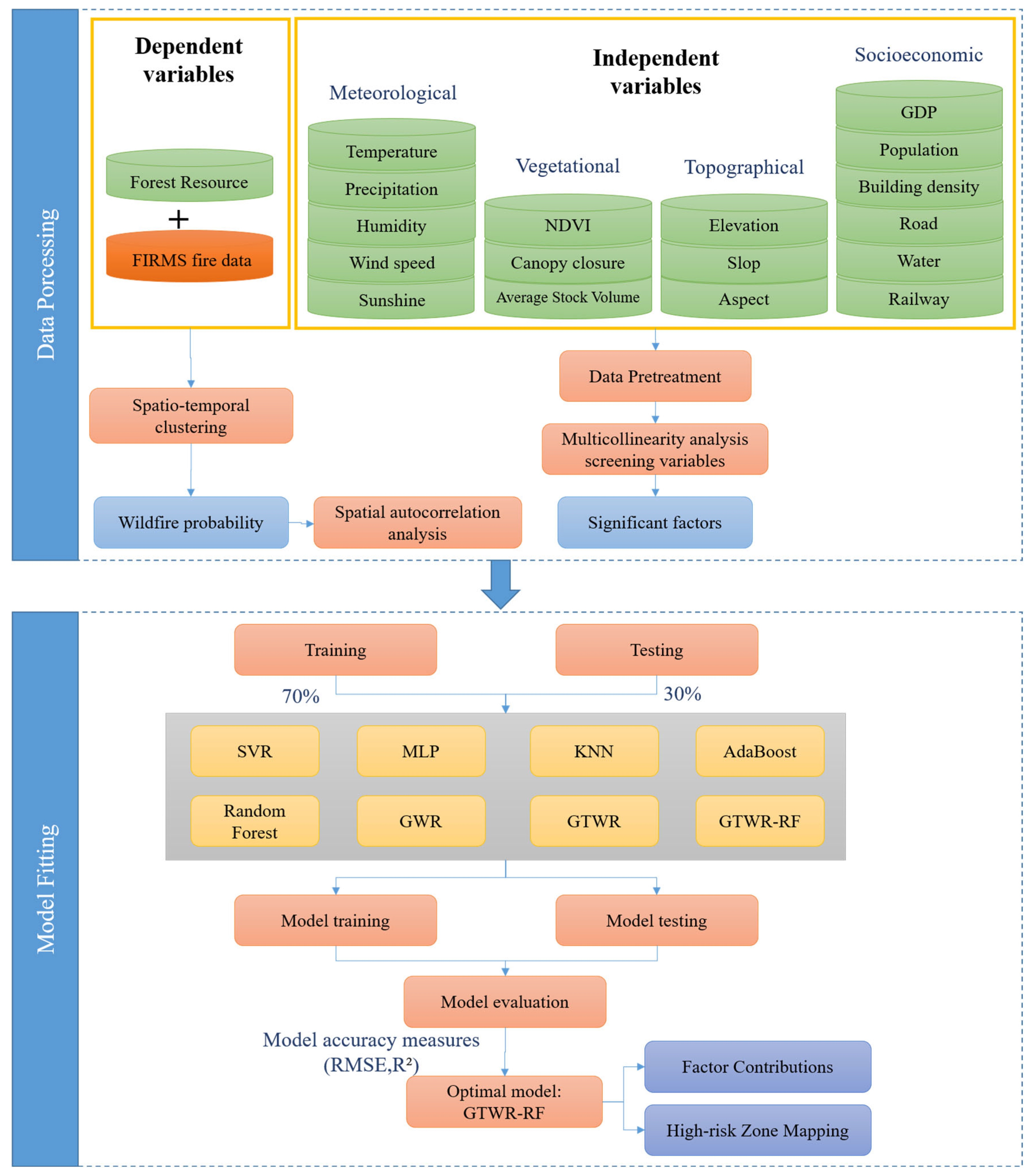
3.1. Research Process
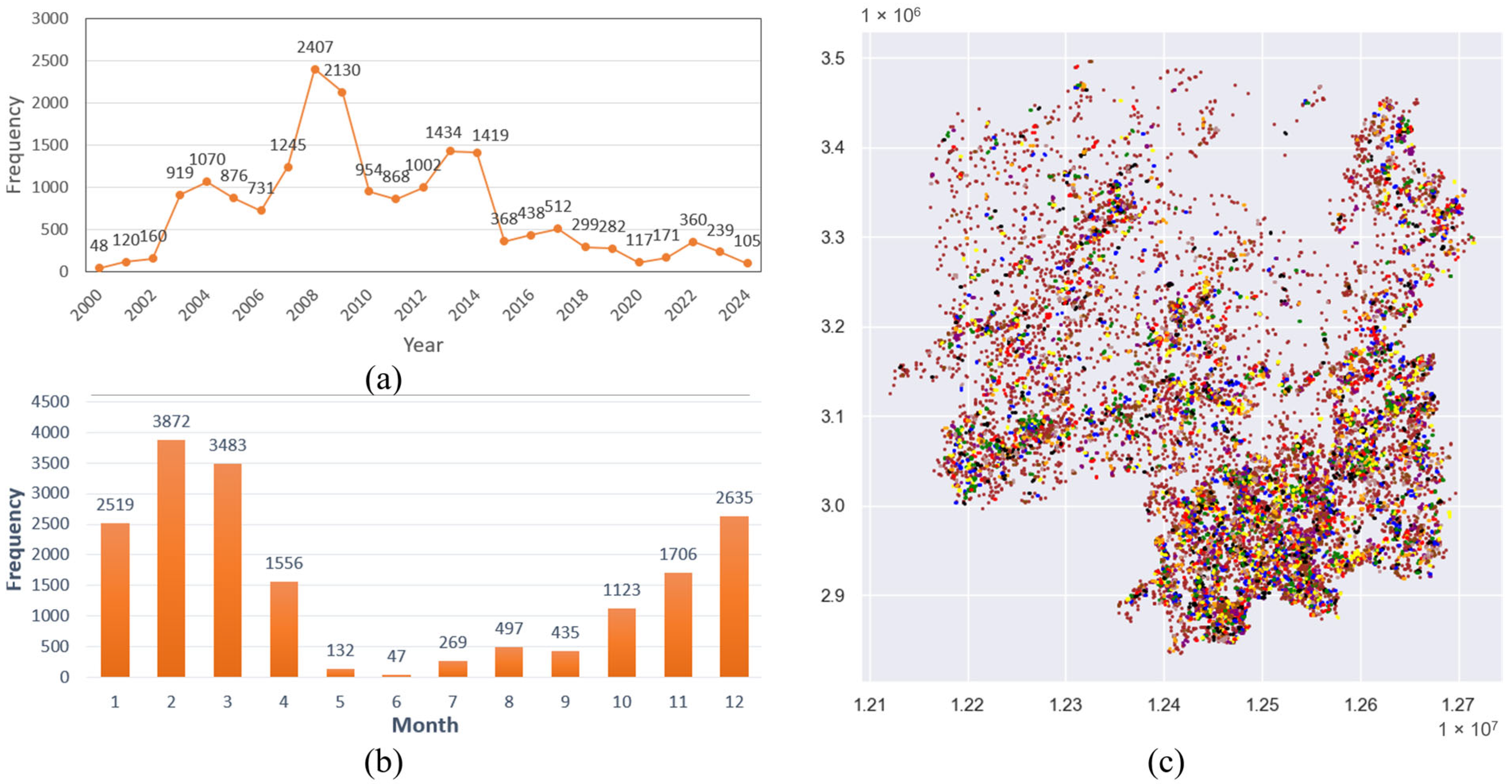
3.2. Estimating Wildfire Probability via Spatiotemporal Clustering
3.3. Geographically and Temporally Weighted Random Forest Regression and Evaluation Metrics
4. Results
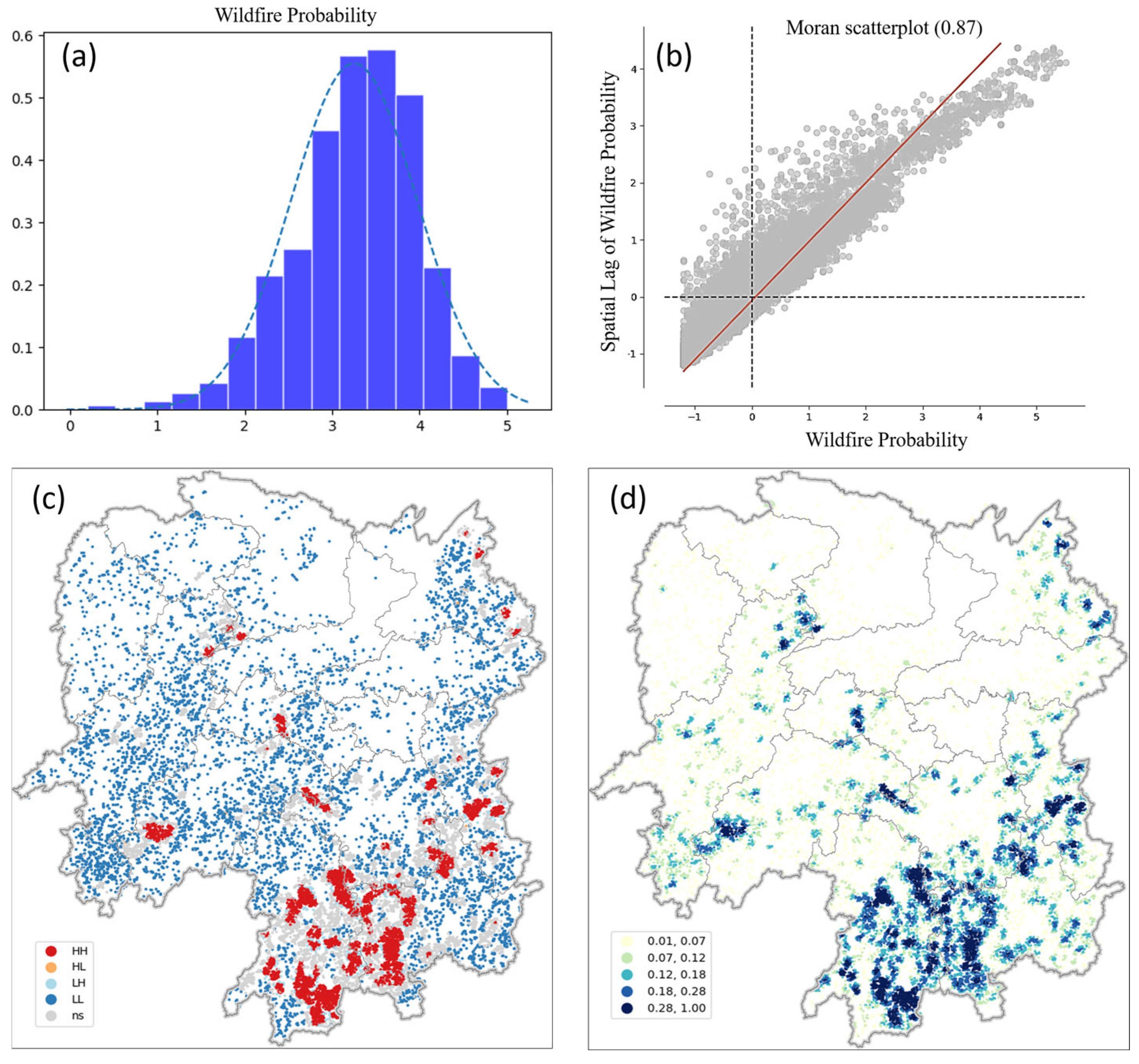
4.1. Spatial Characteristics and Feature Selection
4.2. Model Performance Evaluation
4.3. Spatial Patterns of Coefficient Estimates
4.4. Risk Classification and Spatial Distribution
5. Discussion
5.1. Advantages of Probability-Based Wildfire Modeling via ST-DBSCAN
5.2. Strengths of the GTWR-RFR Hybrid Regression
5.3. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walker, X.J.; Baltzer, J.L.; Cumming, S.G.; Day, N.J.; Ebert, C.; Goetz, S.; Johnstone, J.F.; Potter, S.; Rogers, B.M.; Schuur, E.A.G.; et al. Increasing wildfires threaten historic carbon sink of boreal forest soils. Nature 2019, 572, 520–523. [Google Scholar] [CrossRef] [PubMed]
- Modugno, S.; Balzter, H.; Cole, B.; Borrelli, P. Mapping regional patterns of large forest fires in Wildland-Urban Interface areas in Europe. J. Environ. Manag. 2016, 172, 112–126. [Google Scholar] [CrossRef]
- Guo, H.F.; Yu, W. Study weather grade prediction model of forest-fire risk in Hunan province. J. Cent. South Univ. For. Technol. 2016, 36, 44–47. [Google Scholar]
- Su, Z.; Zheng, L.; Luo, S.; Tigabu, M.; Guo, F. Modeling wildfire drivers in Chinese tropical forest ecosystems using global logistic regression and geographically weighted logistic regression. Nat. Hazards 2021, 108, 1317–1345. [Google Scholar] [CrossRef]
- Ma, W.; Feng, Z.; Cheng, Z.; Chen, S.; Wang, F. Identifying Forest Fire Driving Factors and Related Impacts in China Using Random Forest Algorithm. Forests 2020, 11, 507. [Google Scholar] [CrossRef]
- Gigović, L.; Pourghasemi, H.R.; Drobnjak, S.; Bai, S. Testing a New Ensemble Model Based on SVM and Random Forest in Forest Fire Susceptibility Assessment and Its Mapping in Serbia’s Tara National Park. Forests 2019, 10, 408. [Google Scholar] [CrossRef]
- Chen, F.; Du, Y.; Niu, S.; Zhao, J. Modeling Forest Lightning Fire Occurrence in the Daxinganling Mountains of Northeastern China with MAXENT. Forests 2015, 6, 1422–1438. [Google Scholar] [CrossRef]
- Liang, H; Wang, W.; Guo, F.; Lin, F.; Lin, X. Comparing the application of logistic and geographically weighted logistic regression models for Fujian forest fire forecasting. Acta Ecol. Sin. 2017, 37, 399–406. [Google Scholar] [CrossRef]
- Zhang, X.; Lan, M.; Ming, J.; Zhu, J.; Lo, S. Spatiotemporal Heterogeneity of Forest Fire Occurrence Based on Remote Sensing Data: An Analysis in Anhui, China. Remote Sens. 2023, 15, 598. [Google Scholar] [CrossRef]
- Pahlavani, P.; Raei, A.; Bigdeli, B.; Ghorbanzadeh, O. Identifying Influential Spatial Drivers of Forest Fires through Geographically and Temporally Weighted Regression Coupled with a Continuous Invasive Weed Optimization Algorithm. Fire 2024, 7, 33. [Google Scholar] [CrossRef]
- Santos, F.; Graw, V.; Bonilla, S. A geographically weighted random forest approach for evaluate forest change drivers in the Northern Ecuadorian Amazon. PLoS ONE 2019, 14, e0226224. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Ni, L.; Li, Z.-L.; Duan, S.-B.; Wu, H. Evaluation of Machine Learning Algorithms in Spatial Downscaling of MODIS Land Surface Temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
- Yin, Z.; Ding, J.; Liu, Y.; Wang, R.; Wang, Y.; Chen, Y.; Qi, J.; Wu, S.; Du, Z. GNNWR: An open-source package of spatiotemporal intelligent regression methods for modeling spatial and temporal nonstationarity. Geosci. Model Dev. 2024, 17, 8455–8468. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2019, 36, 121–136. [Google Scholar] [CrossRef]
- Du, Z.; Wang, Z.; Wu, S.; Zhang, F.; Liu, R. Geographically neural network weighted regression for the accurate estimation of spatial non-stationarity. Int. J. Geogr. Inf. Sci. 2020, 34, 1353–1377. [Google Scholar] [CrossRef]
- Khan, S.N.; Li, D.; Maimaitijiang, M. A Geographically Weighted Random Forest Approach to Predict Corn Yield in the US Corn Belt. Remote Sens. 2022, 14, 2843. [Google Scholar] [CrossRef]
- Fayaz, J.; Galasso, C. Interpretability and spatial efficacy of a deep-learning-based on-site early warning framework using explainable artificial intelligence and geographically weighted random forests. Geosci. Front. 2024, 15, 101839. [Google Scholar] [CrossRef]
- Birant, D.; Kut, A. ST-DBSCAN: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Su, H.; Ma, X.; Li, M. An improved spatio-temporal clustering method for extracting fire footprints based on MCD64A1 in the Daxing’anling Area of north-eastern China. Int. J. Wildland Fire 2023, 32, 679–693. [Google Scholar] [CrossRef]
- Son, M.-W.; Kim, C.-G.; Kim, B.-S. Development of an Algorithm for Assessing the Scope of Large Forest Fire Using VIIRS-Based Data and Machine Learning. Remote Sens. 2024, 16, 2667. [Google Scholar] [CrossRef]
- Ahajjam, A.; Allgaier, M.; Chance, R.; Chukwuemeka, E.; Putkonen, J.; Pasch, T. Enhancing prediction of wildfire occurrence and behavior in Alaska using spatio-temporal clustering and ensemble machine learning. Ecol. Inform. 2025, 85, 102963. [Google Scholar] [CrossRef]
- Ram, A.; Jalal, S.; Jalal, A.S.; Kumar, M. A Density Based Algorithm for Discovering Density Varied Clusters in Large Spatial Databases. Int. J. Comput. Appl. 2010, 3, 1–4. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Schmidt, A.F.; Finan, C. Linear regression and the normality assumption. J. Clin. Epidemiol. 2018, 98, 146–151. [Google Scholar] [CrossRef]
- Diniz-Filho, J.A.; Soares, T.N.; de Campos Telles, M.P. Geographically weighted regression as a generalized Wombling to detect barriers to gene flow. Genetica 2016, 144, 425–433. [Google Scholar] [CrossRef] [PubMed]
- O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Idrees, M.O.; Janizadeh, S.; Ahmadi, K.; Shabani, F. Forest Fire Susceptibility Prediction Based on Machine Learning Models with Resampling Algorithms on Remote Sensing Data. Remote Sens. 2020, 12, 3682. [Google Scholar] [CrossRef]
- Barreto, J.S.; Armenteras, D. Open Data and Machine Learning to Model the Occurrence of Fire in the Ecoregion of “Llanos Colombo–Venezolanos”. Remote Sens. 2020, 12, 3921. [Google Scholar] [CrossRef]
- Weber, R.; Schek, H.-J.; Blott, S. A Quantitative Analysis and Performance Study for Similarity-Search Methods in High-Dimensional Spaces. In Proceedings of the 24rd International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 194–205. [Google Scholar]
- DeCastro, A.L.; Juliano, T.W.; Kosović, B.; Ebrahimian, H.; Balch, J.K. A Computationally Efficient Method for Updating Fuel Inputs for Wildfire Behavior Models Using Sentinel Imagery and Random Forest Classification. Remote Sens. 2022, 14, 1447. [Google Scholar] [CrossRef]
- Van Wyk, J.; du Preez, J.; Versfeld, J. Temporal separation of whale vocalizations from background oceanic noise using a power calculation. Ecol. Inform. 2022, 69, 101627. [Google Scholar] [CrossRef]
- Liu, X.; Kounadi, O.; Zurita-Milla, R. Incorporating Spatial Autocorrelation in Machine Learning Models Using Spatial Lag and Eigenvector Spatial Filtering Features. ISPRS Int. J. Geo-Inf. 2022, 11, 242. [Google Scholar] [CrossRef]
- Arganaraz, J.P.; Radeloff, V.C.; Bar-Massada, A.; Gavier-Pizarro, G.I.; Scavuzzo, C.M.; Bellis, L.M. Assessing wildfire exposure in the Wildland-Urban Interface area of the mountains of central Argentina. J. Environ. Manag. 2017, 196, 499–510. [Google Scholar] [CrossRef]
- Shao, Y.; Feng, Z.; Sun, L.; Yang, X.; Li, Y.; Xu, B.; Chen, Y. Mapping China’s Forest Fire Risks with Machine Learning. Forests 2022, 13, 856. [Google Scholar] [CrossRef]
- Koutsias, N.; Martínez-Fernández, J.; Allgöwer, B. Do Factors Causing Wildfires Vary in Space? Evidence from Geographically Weighted Regression. GISci. Remote Sens. 2013, 47, 221–240. [Google Scholar] [CrossRef]
- Guo, F.; Wang, G.; Su, Z.; Liang, H.; Wang, W.; Lin, F.; Liu, A. What drives forest fire in Fujian, China? Evidence from logistic regression and Random Forests. Int. J. Wildland Fire 2016, 25, 505–519. [Google Scholar] [CrossRef]
- Armenteras, D.; González, T.M.; Retana, J. Forest fragmentation and edge influence on fire occurrence and intensity under different management types in Amazon forests. Biol. Conserv. 2013, 159, 73–79. [Google Scholar] [CrossRef]
- Chuvieco, E.; Aguado, I.; Yebra, M.; Nieto, H.; Salas, J.; Martín, M.P.; Vilar, L.; Martínez, J.; Martín, S.; Ibarra, P.; et al. Development of a framework for fire risk assessment using remote sensing and geographic information system technologies. Ecol. Model. 2010, 221, 46–58. [Google Scholar] [CrossRef]
- Massetti, A.; Rüdiger, C.; Yebra, M.; Hilton, J. The Vegetation Structure Perpendicular Index (VSPI): A forest condition index for wildfire predictions. Remote Sens. Environ. 2019, 224, 167–181. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, G.; Tan, S.Q.; Wang, P.; Wu, X. Assessment of forest fire risk in Hunan province based on spatial logistic model Technol. J. Cent. South Univ. For. Technol. 2020, 40, 88–95. [Google Scholar]
- Tan, C.; Feng, Z. Mapping Forest Fire Risk Zones Using Machine Learning Algorithms in Hunan Province, China. Sustainable 2023, 15, 6292. [Google Scholar] [CrossRef]
- Li, W.; Xu, Q.; Yi, J.; Liu, J. Predictive model of spatial scale of forest fire driving factors: A case study of Yunnan Province, China. Sci. Rep. 2022, 12, 19029. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Wu, Z.; Cui, S.; Hong, W.; Wang, B.; Li, M. Assessing wildfire susceptibility and spatial patterns in diverse forest ecosystems across China: An integrated geospatial analysis. J. Clean. Prod. 2025, 490, 144800. [Google Scholar] [CrossRef]
- Yang, X.; Jin, X.; Zhou, Y. Wildfire Risk Assessment and Zoning by Integrating Maxent and GIS in Hunan Province, China. Forests 2021, 12, 1299. [Google Scholar] [CrossRef]
- Wu, Z.; He, H.S.; Yang, J.; Liu, Z.; Liang, Y. Relative effects of climatic and local factors on fire occurrence in boreal forest landscapes of northeastern China. Sci. Total Environ. 2014, 493, 472–480. [Google Scholar] [CrossRef]
- Guo, F.; Su, Z.; Wang, G.; Sun, L.; Tigabu, M.; Yang, X.; Hu, H. Understanding fire drivers and relative impacts in different Chinese forest ecosystems. Sci. Total Environ. 2017, 605–606, 411–425. [Google Scholar] [CrossRef]
- Parisien, M.-A.; Snetsinger, S.; Greenberg, J.A.; Nelson, C.R.; Schoennagel, T.; Dobrowski, S.Z.; Moritz, M.A. Spatial variability in wildfire probability across the western United States. Int. J. Wildland Fire 2012, 21, 313–327. [Google Scholar] [CrossRef]
- Zhu, A.; Lv, G.; Zhou, C.; Qin, C. Geographic Similarity: Third Law of Geography? J. Geo-Inf. Sci. 2020, 22, 673–679. [Google Scholar]
- Zhu, A.X.; Turner, M. How is the Third Law of Geography different? Ann. GIS 2022, 28, 57–67. [Google Scholar] [CrossRef]
- Anwar, M.; Hadikurniawati, W.; Winarno, E.; Supriyanto, A. Wildfire Risk Map Based on DBSCAN Clustering and Cluster Density Evaluation. Adv. Sustain. Sci. Eng. Technol. 2019, 1, 4876. [Google Scholar] [CrossRef]
- Shirazi, Z.; Wang, L.; Bondur, V.G. Modeling Conditions Appropriate for Wildfire in South East China—A Machine Learning Approach. Front. Earth Sci. 2021, 9, 622307. [Google Scholar] [CrossRef]
- Li, W.; Dodwell, E.; Cook, D. A Clustering Algorithm to Organize Satellite Hotspot Data for the Purpose of Tracking Bushfires Remotely. R J. 2023, 15, 17–33. [Google Scholar] [CrossRef]
- Mabdeh, A.N.; Al-Fugara, A.k.; Khedher, K.M.; Mabdeh, M.; Al-Shabeeb, A.R.; Al-Adamat, R. Forest Fire Susceptibility Assessment and Mapping Using Support Vector Regression and Adaptive Neuro-Fuzzy Inference System-Based Evolutionary Algorithms. Sustainable 2022, 14, 9446. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, L.; Duan, W.; Zhen, Z. Global and Geographically and Temporally Weighted Regression Models for Modeling PM2.5 in Heilongjiang, China from 2015 to 2018. Int. J. Environ. Res. Public Health 2019, 16, 5107. [Google Scholar] [CrossRef]
- Ngoc Thach, N.; Bao-Toan Ngo, D.; Xuan-Canh, P.; Hong-Thi, N.; Hang Thi, B.; Nhat-Duc, H.; Dieu, T.B. Spatial pattern assessment of tropical forest fire danger at Thuan Chau area (Vietnam) using GIS-based advanced machine learning algorithms: A comparative study. Ecol. Inform. 2018, 46, 74–85. [Google Scholar] [CrossRef]


| Factors | Variable | Source | Classes | Spatial Resolution/ Units |
|---|---|---|---|---|
| Wildfire point | Historical Wildfires | NASA Fire Information Resource Management System (FIRMS) https://firms.modaps.eosdis.nasa.gov/ (accessed on 21 October 2025) | Continuous | |
| Meteorological factors | Temperature Pressure Humidity Wind speed Precipitation Sunshine | High-resolution gridded datasets https://crudata.uea.ac.uk/cru/data/hrg/ (accessed on 21 October 2025) China Geospatial Data Cloud http://data.cma.cn/ (accessed on 21 October 2025) | Continuous | 0.1 °C 0.1 hPa 1% 0.1 m/s 0.1 mm 0.1 h |
| Terrain factors | DEM Slope Aspect | Geospatial Data Cloud https://www.gscloud.cn/ (accessed on 21 October 2025) | Continuous | 1000 m |
| Vegetation factors | Vegetation type | Geospatial Information Authority of Japan (GSI) https://globalmaps.github.io/glcnmo.html (accessed on 21 October 2025) | Categorical | 1000 m |
| NDVI | MODIS Vegetation Index Products https://modis.gsfc.nasa.gov/data/dataprod/mod13.php (accessed on 21 October 2025) | Categorical | ||
| Canopy closure timber volume | National Smart Forest Resources Management Platform https://www.stgz.org.cn/ldbggzpt/ (accessed on 21 October 2025) | Continuous | ||
| Anthropogenic factors | Road Water Railway | Openstreetmap https://www.openstreetmap.org/ (accessed on 21 October 2025) | Continuous | 1000 m |
| Socioeconomic factors | GDP | Resource and Environmental Science and Data Center, https://www.resdc.cn/ (accessed on 21 October 2025) | Continuous | 1000 m |
| Population | WorldPop https://hub.worldpop.org/ (accessed on 21 October 2025) | Continuous |
| Model Variable | Variable Code | VIF | TOL |
|---|---|---|---|
| Canopy Closure | CC | 0.171556 | 5.829003 |
| Daily mean temperature | DMT | 0.171699 | 5.824144 |
| DEM | DEM | 0.173677 | 5.75782 |
| Daily mean wind speed | DMWS | 0.203361 | 4.917362 |
| Slope | Slope | 0.211842 | 4.72051 |
| Aspect | Aspect | 0.25988 | 3.847925 |
| Distance from water | NDW | 0.269735 | 3.707344 |
| 24 h precipitation | HP | 0.287977 | 3.472499 |
| Distance from road | NDR | 0.314261 | 3.18207 |
| Population density | PD | 0.382188 | 2.616512 |
| Standing timber volume | AVST | 0.390855 | 2.558495 |
| GDP | GDP | 0.420837 | 2.376215 |
| KNN | MLP | SVR | AdaBoost | RFR | GWR | GTWR | GTWR-RFR | |
|---|---|---|---|---|---|---|---|---|
| R2 | 0.376 | 0.532 | 0.478 | 0.657 | 0.802 | 0.848 | 0.885 | 0.969 |
| Explained Variance Score | 0.271 | 0.3697 | 0.3396 | 0.5209 | 0.5709 | 0.8481 | 0.8854 | 0.9696 |
| Mean Absolute Error | 0.6647 | 0.6084 | 0.619 | 0.5439 | 0.5035 | 0.2663 | 0.2255 | 0.1256 |
| Mean Squared Error | 0.7457 | 0.6408 | 0.6705 | 0.49 | 0.4368 | 0.1521 | 0.1147 | 0.0304 |
| Root Mean Squared Error | 0.8635 | 0.8005 | 0.8188 | 0.71 | 0.6609 | 0.3899 | 0.3387 | 0.1743 |
| Explained sum of squares | 1061.9 | 1671.5 | 1249.6 | 1765.9 | 1813.7 | 14,640.2 | 15,486.2 | 15,661.7 |
| Total sum of squares | 3813.5 | 3813.5 | 3813.5 | 3813.5 | 3813.8 | 18,783 | 18,783 | 18,783.0 |
| Residual sum of squares | 2801.5 | 20,606.9 | 19,022.1 | 20,961.9 | 21,141.3 | 2856.1 | 2154.8 | 570.8 |
| Model | Moran’s I | Z-Score | p-Value |
|---|---|---|---|
| AdaBoost | 0.6050 | 213.2841 | 0 |
| SVR | 0.6370 | 224.5765 | 0 |
| MLP | 0.5692 | 200.6862 | 0 |
| KNR | 0.6618 | 233.3181 | 0 |
| RFR | 0.5781 | 203.8316 | 0 |
| GWR | 0.3459 | 121.9581 | 0 |
| GTWR | 0.2959 | 104.3545 | 0 |
| GTWR-RFR | 0.2462 | 86.8203 | 0 |
| Model Variable | Code | Mean | STD | Min | Median | Max | Moran’s I | z-Score | p-Value |
|---|---|---|---|---|---|---|---|---|---|
| Daily mean temperature | DMT | 0.044 | 0.028 | 0.003 | 0.038 | 0.529 | 0.8002 | 282.2 | 0 |
| 24 h precipitation | HP | 0.046 | 0.031 | 0.003 | 0.04 | 0.544 | 0.8471 | 298.88 | 0 |
| Daily mean wind speed | DMWS | 0.056 | 0.037 | 0.003 | 0.049 | 0.682 | 0.8127 | 286.6 | 0 |
| Slope | Slope | 0.054 | 0.032 | 0.003 | 0.048 | 0.365 | 0.8525 | 300.6 | 0 |
| Altitude | DEM | 0.128 | 0.097 | 0.004 | 0.097 | 0.764 | 0.8454 | 298.1 | 0 |
| Aspect | Aspect | 0.047 | 0.027 | 0.002 | 0.043 | 0.484 | 0.8598 | 303.3 | 0 |
| Canopy Closure | CC | 0.026 | 0.021 | 0.001 | 0.022 | 0.51 | 0.8087 | 285.6 | 0 |
| Standing timber volume | AVST | 0.022 | 0.021 | 0 | 0.017 | 0.445 | 0.8535 | 301.3 | 0 |
| GDP | GDP | 0.152 | 0.117 | 0 | 0.117 | 0.795 | 0.8382 | 295.5 | 0 |
| Population density | PD | 0.129 | 0.103 | 0.007 | 0.095 | 0.821 | 0.8685 | 306.2 | 0 |
| Distance from road | NDR | 0.11 | 0.105 | 0.005 | 0.078 | 0.85 | 0.8961 | 316.0 | 0 |
| Distance from water | NDW | 0.14 | 0.111 | 0.006 | 0.102 | 0.784 | 0.8998 | 317.2 | 0 |
| Risk Classification | Fire Probability | Pixels Count | Percent (%) | Recommended Measures |
|---|---|---|---|---|
| Non-fire risk | <0.2 | 3,050,513 | 45.01% | negligible |
| Low-fire risk | 0.2~0.4 | 2,293,834 | 33.85% | routine prevention and monitoring |
| Moderate-fire risk | 0.4~0.6 | 884,769 | 13.06% | proactive assessments |
| High-fire risk | 0.6> | 547,788 | 8.08% | Intensive monitoring and targeted prevention strategies |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Xiao, H.; Zhang, G.; Xu, H. A Spatiotemporal Wildfire Risk Prediction Framework Integrating Density-Based Clustering and GTWR-RFR. Forests 2025, 16, 1632. https://doi.org/10.3390/f16111632
Xie S, Xiao H, Zhang G, Xu H. A Spatiotemporal Wildfire Risk Prediction Framework Integrating Density-Based Clustering and GTWR-RFR. Forests. 2025; 16(11):1632. https://doi.org/10.3390/f16111632
Chicago/Turabian StyleXie, Shaofeng, Huashun Xiao, Gui Zhang, and Haizhou Xu. 2025. "A Spatiotemporal Wildfire Risk Prediction Framework Integrating Density-Based Clustering and GTWR-RFR" Forests 16, no. 11: 1632. https://doi.org/10.3390/f16111632
APA StyleXie, S., Xiao, H., Zhang, G., & Xu, H. (2025). A Spatiotemporal Wildfire Risk Prediction Framework Integrating Density-Based Clustering and GTWR-RFR. Forests, 16(11), 1632. https://doi.org/10.3390/f16111632






