CO2 Estimation of Tree Biomass in Forest Stands: A Simple and IPCC-Compliant Approach
Abstract
1. Introduction
The land use sector encompasses the management of cropland, grassland, wetlands, forests, settlements, as well as changes in land use including afforestation (i.e., planting trees), deforestation, or draining of peatlands. LULUCF reporting categories comprise various types of carbon pools of living biomass (above and below ground), dead organic matter (CWD and litter), and organic soil carbon. Land-use changes are also reported, for example: deforestation, afforestation, or changes from grassland to arable land or settlements” [2].
- How can the proposed single-tree biomass functions by Riedel and Kändler 2017 [18] be effectively integrated within yield tables to develop yield tables that address the existing gap of a low-threshold estimation of the potential stock in forest stands?
- What are the differences in estimation results when using single-tree biomass functions compared to those derived from stand expansion factors?
- To what extent does the incorporation of realistic height-diameter (h-d) ratios into single-tree estimations enhance the accuracy of forest stand accounting—particularly under varying stocking densities—and support broader applicability of the method?
2. Materials and Methods
2.1. Materials
2.1.1. Input Data: A New Generation of Yield Tables
2.1.2. Foundational Models and Indices
Biomass Equations
Biomass Expansion Factors
Total Volume Production and Mean Annual Increment
h/d-Ratios
Stand Density Index
Carbon and Conversion Factors
2.2. Methods
2.2.1. Stand Calculation
Via Equations
Via Expansion
Conversion to
Extrapolation for Younger Stands
2.2.2. Development of an Online Application (Dashboard)
3. Results
3.1. CO2 Estimates for Forest Stands
3.1.1. Based on Equations
3.1.2. Based on Expansion
3.1.3. Comparison of Equation-Based Stock vs. Expansion Factor Stock
3.2. Interactive Online Application
4. Discussion
4.1. Discussion of Materials and Methods
- Stand Structure: Even in a forest of a single species, the arrangement and size variation of trees matter. Maximum density and yield are often highest in stands with moderate structural diversity, not in those that are perfectly uniform or overly heterogeneous [69].
- Site and Climate: The self-thinning relationship changes based on local conditions. Factors like site quality, solar radiation, temperature, and precipitation all alter a stand’s carrying capacity [70,71]. Therefore, management models based on self-thinning must be adapted for different latitudes and climates [71].
4.2. Discussion of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. CO2 Yield Tables
- Age: Stand age in years.
- SI: Site index, a measure of stand quality.
- N: Number of trees per hectare.
- H: Mean height in metres (m).
- H100: Top height in metres (m). The top height, defined as the height of the basal area mean stem of the 100 thickest trees per hectare at a given age, is a widely used measure of growth performance in pure, even-aged stands [76].
- BA: Basal area in .
- dbh: Diameter at breast height (1.3 m) in centimetres (cm). In our analysis, we use ‘d’ to denote diameter more generally, as our calculations include trees smaller than the standard breast height threshold.
- dbh100: Diameter corresponding to the top-height (H100); i.e., the diameter of the basal area mean stem of the 100 thickest trees per hectare.
- S: Standing stock (volume) in .
- N_YFT: Number of trees removed during thinning (YFT = yield from thinning).
- BA_YFT: Basal area of trees removed during thinning, in .
- dbh_YFT: Diameter of trees removed during thinning, in cm.
- S_YFT: Stock (volume) removed during thinning, in .
- CAI Current annual increment of the standing stock, in ; a measure of the stand’s current productivity.
- MAI: Mean annual increment of the standing stock, in ; the average yearly volume increase from establishment to the current age.
- ABV_CO2_SINGLE: Above-ground potentially stock in a single tree, in tonnes (t).
- ABV_CO2_YFT_SINGLE: Above-ground potentially stock for a single tree removed during thinning, in tonnes (t).
- ROOT_CO2_SINGLE: Belowground potentially stock in a single tree’s root system, in tonnes (t).
- ROOT_CO2_YFT_SINGLE: Belowground potentially stock from a single thinned tree’s root system, in tonnes (t). Note: We assume that the root biomass initially remains in the soil post-harvest and decomposes over time.
- FULL_TREE_CO2: Sum of ABV_CO2_SINGLE and ROOT_CO2_SINGLE.
- STAND_CO2: Product of FULL_TREE_CO2 and N, in t .
- FULL_TREE_CO2_YFT: Sum of ABV_CO2_YFT_SINGLE and ROOT_CO2_YFT_SINGLE.
- STAND_CO2_YFT: Product of FULL_TREE_CO2_YFT and N_YFT, in t .
- TVP_CO2: Total production of the stand over its lifetime, in t .
- MAI_CO2: Mean annual increment of potentially sequestered , in t .
- CAI_CO2: Current annual increment of potentially sequestered , in t .
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | − 1 | − | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | − 1 | − | 2 | 2 | 2 | 1 | 2 | 12 | 560 | 2 | 1 | 6 | 2 | 24 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 12 | 20 | 1 | 5 |
| 10 | − | 3 | 5 | 5 | 2 | 5 | 23 | 1120 | 4 | 3 | 13 | 5 | 48 | 2 | 0 | 0 | 0 | 0 | 0 | 39 | 0 | 25 | 39 | 2 | 10 | |
| 15 | −1 | − | 5 | 7 | 7 | 4 | 7 | 35 | 1681 | 5 | 4 | 19 | 8 | 72 | 3 | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 37 | 59 | 2 | 14 |
| 20 | −1 | − | 7 | 10 | 9 | 5 | 9 | 46 | 2241 | 7 | 5 | 26 | 10 | 96 | 4 | 0 | 0 | 0 | 0 | 0 | 79 | 0 | 49 | 79 | 3 | 19 |
| 25 | −1 | 4046 | 8 | 12 | 12 | 6 | 12 | 58 | 2801 | 9 | 6 | 32 | 12 | 120 | 5 | 0 | 0 | 0 | 0 | 0 | 99 | 0 | 61 | 99 | 4 | 24 |
| 30 | −1 | 2561 | 12 | 16 | 14 | 8 | 16 | 94 | 1485 | 7 | 8 | 40 | 15 | 197 | 7 | 0 | 0 | 0 | 0 | 0 | 127 | 0 | 54 | 242 | 8 | 29 |
| 35 | −1 | 1761 | 15 | 19 | 16 | 11 | 20 | 133 | 800 | 6 | 10 | 47 | 17 | 283 | 8 | 0 | 0 | 0 | 0 | 0 | 194 | 0 | 66 | 375 | 11 | 27 |
| 40 | −1 | 1214 | 18 | 22 | 18 | 14 | 24 | 174 | 548 | 6 | 12 | 51 | 18 | 375 | 9 | 0 | 0 | 0 | 0 | 0 | 247 | 0 | 68 | 495 | 12 | 24 |
| 45 | −1 | 895 | 21 | 24 | 20 | 17 | 29 | 215 | 319 | 5 | 14 | 55 | 19 | 471 | 10 | 0 | 0 | 0 | 0 | 0 | 302 | 0 | 69 | 620 | 14 | 25 |
| 50 | −1 | 697 | 23 | 26 | 22 | 20 | 33 | 255 | 198 | 5 | 18 | 57 | 20 | 568 | 11 | 0 | 0 | 0 | 0 | 1 | 355 | 0 | 71 | 744 | 15 | 25 |
| 55 | −1 | 565 | 25 | 28 | 23 | 23 | 37 | 295 | 132 | 5 | 21 | 59 | 20 | 666 | 12 | 1 | 1 | 0 | 0 | 1 | 410 | 1 | 72 | 871 | 16 | 25 |
| 60 | −1 | 470 | 27 | 30 | 24 | 26 | 41 | 334 | 94 | 4 | 24 | 60 | 20 | 765 | 13 | 1 | 1 | 0 | 0 | 1 | 462 | 1 | 73 | 996 | 17 | 25 |
| 65 | −1 | 399 | 29 | 32 | 25 | 28 | 46 | 371 | 71 | 4 | 27 | 60 | 20 | 863 | 13 | 1 | 1 | 0 | 0 | 1 | 515 | 1 | 72 | 1121 | 17 | 25 |
| 70 | −1 | 342 | 31 | 33 | 26 | 31 | 50 | 408 | 57 | 4 | 29 | 61 | 19 | 960 | 14 | 1 | 1 | 0 | 0 | 2 | 562 | 1 | 74 | 1243 | 18 | 24 |
| 75 | −1 | 296 | 32 | 35 | 27 | 34 | 54 | 443 | 46 | 4 | 32 | 61 | 19 | 1055 | 14 | 2 | 2 | 0 | 0 | 2 | 609 | 2 | 72 | 1362 | 18 | 24 |
| 80 | −1 | 257 | 34 | 36 | 28 | 37 | 57 | 477 | 39 | 4 | 34 | 60 | 19 | 1149 | 14 | 2 | 2 | 0 | 0 | 3 | 655 | 2 | 73 | 1481 | 19 | 24 |
| 85 | −1 | 224 | 35 | 37 | 28 | 40 | 61 | 509 | 33 | 3 | 36 | 60 | 18 | 1242 | 15 | 3 | 2 | 0 | 0 | 3 | 700 | 2 | 72 | 1598 | 19 | 23 |
| 90 | −1 | 196 | 36 | 38 | 29 | 44 | 65 | 541 | 28 | 3 | 38 | 59 | 18 | 1333 | 15 | 3 | 3 | 0 | 0 | 4 | 746 | 3 | 71 | 1716 | 19 | 24 |
| 95 | −1 | 172 | 37 | 40 | 30 | 47 | 68 | 572 | 24 | 3 | 40 | 59 | 18 | 1422 | 15 | 4 | 3 | 0 | 0 | 5 | 787 | 3 | 71 | 1827 | 19 | 22 |
| 100 | −1 | 152 | 38 | 40 | 31 | 51 | 72 | 601 | 21 | 3 | 42 | 58 | 18 | 1510 | 15 | 5 | 3 | 0 | 0 | 6 | 840 | 3 | 72 | 1952 | 20 | 25 |
| 105 | −1 | 134 | 40 | 41 | 31 | 54 | 76 | 629 | 18 | 3 | 45 | 57 | 17 | 1596 | 15 | 6 | 4 | 0 | 0 | 7 | 879 | 4 | 66 | 2057 | 20 | 21 |
| 110 | −1 | 118 | 40 | 42 | 32 | 58 | 79 | 657 | 16 | 3 | 47 | 57 | 17 | 1680 | 15 | 7 | 4 | 0 | 0 | 8 | 914 | 4 | 66 | 2157 | 20 | 20 |
| 115 | −1 | 105 | 41 | 43 | 32 | 63 | 82 | 684 | 14 | 3 | 50 | 56 | 16 | 1763 | 15 | 8 | 5 | 0 | 0 | 8 | 873 | 5 | 65 | 2182 | 19 | 5 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | − | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | − | 2 | 2 | 2 | 1 | 2 | 10 | 327 | 1 | 1 | 5 | 2 | 20 | 1 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 8 | 18 | 1 | 4 |
| 10 | 0 | − | 3 | 4 | 4 | 2 | 4 | 19 | 654 | 2 | 2 | 10 | 4 | 40 | 1 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 16 | 35 | 1 | 7 |
| 15 | 0 | − | 5 | 6 | 6 | 3 | 6 | 28 | 980 | 4 | 3 | 14 | 6 | 60 | 2 | 0 | 0 | 0 | 0 | 0 | 53 | 0 | 25 | 53 | 2 | 11 |
| 20 | 0 | − | 6 | 9 | 8 | 5 | 8 | 38 | 1307 | 5 | 5 | 19 | 7 | 81 | 3 | 0 | 0 | 0 | 0 | 0 | 71 | 0 | 33 | 71 | 2 | 14 |
| 25 | 0 | − | 8 | 11 | 10 | 6 | 10 | 48 | 1634 | 6 | 6 | 24 | 9 | 101 | 3 | 0 | 0 | 0 | 0 | 0 | 88 | 0 | 41 | 88 | 3 | 18 |
| 30 | 0 | 3333 | 9 | 13 | 12 | 7 | 12 | 57 | 1961 | 7 | 7 | 29 | 11 | 121 | 4 | 0 | 0 | 0 | 0 | 0 | 106 | 0 | 49 | 106 | 4 | 21 |
| 35 | 0 | 2200 | 12 | 16 | 15 | 9 | 15 | 88 | 1134 | 6 | 8 | 35 | 13 | 188 | 5 | 0 | 0 | 0 | 0 | 0 | 136 | 0 | 45 | 230 | 7 | 25 |
| 40 | 0 | 1535 | 15 | 18 | 17 | 12 | 19 | 123 | 665 | 5 | 10 | 39 | 15 | 261 | 6 | 0 | 0 | 0 | 0 | 0 | 197 | 0 | 56 | 347 | 9 | 23 |
| 45 | 0 | 1111 | 18 | 21 | 18 | 15 | 23 | 158 | 424 | 5 | 12 | 43 | 16 | 339 | 8 | 0 | 0 | 0 | 0 | 0 | 246 | 0 | 57 | 453 | 10 | 21 |
| 50 | 0 | 850 | 20 | 23 | 20 | 17 | 26 | 194 | 261 | 5 | 15 | 45 | 16 | 421 | 8 | 0 | 0 | 0 | 0 | 0 | 293 | 0 | 59 | 558 | 11 | 21 |
| 55 | 0 | 679 | 22 | 25 | 21 | 20 | 30 | 230 | 171 | 4 | 18 | 47 | 17 | 504 | 9 | 0 | 0 | 0 | 0 | 0 | 338 | 0 | 60 | 663 | 12 | 21 |
| 60 | 0 | 560 | 24 | 27 | 22 | 22 | 34 | 265 | 119 | 4 | 21 | 49 | 17 | 587 | 10 | 1 | 1 | 0 | 0 | 1 | 383 | 1 | 60 | 769 | 13 | 21 |
| 65 | 0 | 472 | 26 | 28 | 23 | 25 | 38 | 300 | 87 | 4 | 24 | 50 | 17 | 672 | 10 | 1 | 1 | 0 | 0 | 1 | 429 | 1 | 61 | 876 | 13 | 21 |
| 70 | 0 | 405 | 27 | 30 | 24 | 28 | 41 | 333 | 67 | 4 | 26 | 50 | 17 | 756 | 11 | 1 | 1 | 0 | 0 | 1 | 474 | 1 | 61 | 982 | 14 | 21 |
| 75 | 0 | 352 | 29 | 31 | 25 | 30 | 45 | 366 | 54 | 4 | 29 | 51 | 17 | 839 | 11 | 1 | 1 | 0 | 0 | 1 | 520 | 1 | 63 | 1092 | 15 | 22 |
| 80 | 0 | 307 | 30 | 32 | 26 | 33 | 48 | 398 | 44 | 3 | 31 | 51 | 16 | 922 | 12 | 2 | 1 | 0 | 0 | 2 | 557 | 1 | 62 | 1191 | 15 | 20 |
| 85 | 0 | 270 | 31 | 34 | 27 | 36 | 52 | 428 | 37 | 3 | 33 | 51 | 16 | 1004 | 12 | 2 | 2 | 0 | 0 | 2 | 598 | 2 | 62 | 1293 | 15 | 20 |
| 90 | 0 | 239 | 33 | 35 | 28 | 38 | 55 | 458 | 32 | 3 | 35 | 51 | 16 | 1084 | 12 | 2 | 2 | 0 | 0 | 3 | 642 | 2 | 63 | 1400 | 16 | 21 |
| 95 | 0 | 212 | 34 | 36 | 28 | 41 | 59 | 487 | 27 | 3 | 37 | 51 | 16 | 1164 | 12 | 3 | 2 | 0 | 0 | 3 | 680 | 2 | 62 | 1500 | 16 | 20 |
| 100 | 0 | 188 | 35 | 36 | 29 | 44 | 62 | 515 | 23 | 3 | 39 | 51 | 16 | 1242 | 12 | 3 | 3 | 0 | 0 | 4 | 716 | 3 | 61 | 1597 | 16 | 20 |
| 105 | 0 | 168 | 36 | 37 | 30 | 47 | 65 | 541 | 20 | 3 | 42 | 50 | 15 | 1319 | 13 | 4 | 3 | 0 | 0 | 4 | 754 | 3 | 61 | 1695 | 16 | 20 |
| 110 | 0 | 151 | 36 | 38 | 30 | 50 | 68 | 567 | 18 | 3 | 44 | 50 | 15 | 1395 | 13 | 5 | 3 | 0 | 0 | 5 | 785 | 3 | 62 | 1789 | 16 | 19 |
| 115 | 0 | 135 | 37 | 39 | 31 | 54 | 71 | 593 | 15 | 3 | 46 | 49 | 15 | 1469 | 13 | 5 | 4 | 0 | 0 | 6 | 819 | 4 | 59 | 1882 | 16 | 19 |
| 120 | 0 | 122 | 38 | 40 | 31 | 57 | 74 | 617 | 13 | 2 | 48 | 49 | 15 | 1542 | 13 | 6 | 5 | 0 | 0 | 7 | 857 | 5 | 59 | 1979 | 16 | 19 |
| 125 | 0 | 110 | 39 | 40 | 32 | 60 | 76 | 640 | 12 | 2 | 51 | 48 | 14 | 1614 | 13 | 7 | 5 | 0 | 0 | 8 | 886 | 5 | 61 | 2069 | 17 | 18 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | - | 1 | 2 | 2 | 1 | 2 | 8 | 217 | 1 | 1 | 3 | 1 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 5 | 16 | 0 | 2 |
| 10 | 1 | - | 3 | 4 | 4 | 2 | 3 | 15 | 434 | 2 | 2 | 7 | 3 | 32 | 1 | 0 | 0 | 0 | 0 | 0 | 33 | 0 | 11 | 33 | 1 | 5 |
| 15 | 1 | - | 4 | 6 | 6 | 3 | 5 | 23 | 651 | 2 | 3 | 10 | 4 | 48 | 1 | 0 | 0 | 0 | 0 | 0 | 49 | 0 | 16 | 49 | 1 | 7 |
| 20 | 1 | - | 6 | 7 | 8 | 4 | 6 | 31 | 867 | 3 | 4 | 14 | 5 | 63 | 2 | 0 | 0 | 0 | 0 | 0 | 65 | 0 | 22 | 65 | 2 | 10 |
| 25 | 1 | - | 7 | 9 | 9 | 5 | 8 | 39 | 1084 | 4 | 5 | 17 | 7 | 79 | 2 | 0 | 0 | 0 | 0 | 0 | 82 | 0 | 27 | 82 | 2 | 12 |
| 30 | 1 | - | 8 | 11 | 11 | 6 | 10 | 46 | 1301 | 5 | 6 | 21 | 8 | 95 | 3 | 0 | 0 | 0 | 0 | 0 | 98 | 0 | 33 | 98 | 3 | 15 |
| 35 | 1 | 3028 | 10 | 13 | 13 | 8 | 11 | 54 | 1518 | 6 | 7 | 24 | 10 | 111 | 3 | 0 | 0 | 0 | 0 | 0 | 114 | 0 | 38 | 114 | 3 | 17 |
| 40 | 1 | 2083 | 12 | 15 | 15 | 10 | 14 | 82 | 945 | 5 | 8 | 28 | 11 | 167 | 4 | 0 | 0 | 0 | 0 | 0 | 141 | 0 | 35 | 214 | 5 | 20 |
| 45 | 1 | 1487 | 15 | 18 | 17 | 12 | 18 | 112 | 596 | 4 | 10 | 31 | 12 | 228 | 5 | 0 | 0 | 0 | 0 | 0 | 192 | 0 | 34 | 299 | 7 | 17 |
| 50 | 1 | 1104 | 17 | 20 | 18 | 14 | 21 | 143 | 382 | 4 | 12 | 34 | 13 | 293 | 6 | 0 | 0 | 0 | 0 | 0 | 232 | 0 | 46 | 385 | 8 | 17 |
| 55 | 1 | 879 | 19 | 21 | 20 | 17 | 24 | 174 | 225 | 4 | 15 | 36 | 14 | 361 | 7 | 0 | 0 | 0 | 0 | 0 | 274 | 0 | 48 | 475 | 9 | 18 |
| 60 | 1 | 721 | 21 | 23 | 21 | 19 | 28 | 206 | 159 | 4 | 17 | 38 | 14 | 430 | 7 | 0 | 0 | 0 | 0 | 0 | 314 | 0 | 49 | 563 | 9 | 18 |
| 65 | 1 | 604 | 22 | 25 | 22 | 21 | 31 | 237 | 116 | 4 | 20 | 39 | 14 | 501 | 8 | 1 | 0 | 0 | 0 | 1 | 352 | 0 | 50 | 652 | 10 | 18 |
| 70 | 1 | 516 | 24 | 26 | 23 | 24 | 34 | 267 | 88 | 3 | 22 | 41 | 14 | 572 | 8 | 1 | 1 | 0 | 0 | 1 | 393 | 1 | 51 | 743 | 11 | 18 |
| 75 | 1 | 447 | 25 | 27 | 24 | 26 | 38 | 297 | 69 | 3 | 24 | 41 | 14 | 643 | 9 | 1 | 1 | 0 | 0 | 1 | 432 | 1 | 51 | 833 | 11 | 18 |
| 80 | 1 | 391 | 27 | 29 | 24 | 28 | 41 | 325 | 56 | 3 | 27 | 42 | 14 | 713 | 9 | 1 | 1 | 0 | 0 | 1 | 471 | 1 | 52 | 924 | 12 | 18 |
| 85 | 1 | 344 | 28 | 30 | 25 | 31 | 44 | 353 | 46 | 3 | 29 | 43 | 14 | 784 | 9 | 1 | 1 | 0 | 0 | 1 | 503 | 1 | 52 | 1008 | 12 | 17 |
| 90 | 1 | 305 | 29 | 31 | 26 | 33 | 47 | 380 | 39 | 3 | 31 | 43 | 14 | 854 | 10 | 2 | 1 | 0 | 0 | 2 | 539 | 1 | 53 | 1097 | 12 | 18 |
| 95 | 1 | 273 | 30 | 32 | 27 | 35 | 50 | 406 | 33 | 3 | 33 | 43 | 14 | 923 | 10 | 2 | 2 | 0 | 0 | 2 | 572 | 2 | 53 | 1183 | 12 | 17 |
| 100 | 1 | 245 | 31 | 32 | 27 | 38 | 53 | 431 | 28 | 3 | 35 | 43 | 14 | 991 | 10 | 2 | 2 | 0 | 0 | 2 | 606 | 2 | 53 | 1270 | 13 | 17 |
| 105 | 1 | 221 | 32 | 33 | 28 | 40 | 56 | 456 | 24 | 3 | 37 | 43 | 14 | 1059 | 10 | 3 | 2 | 0 | 0 | 3 | 641 | 2 | 53 | 1359 | 13 | 18 |
| 110 | 1 | 200 | 32 | 34 | 28 | 43 | 58 | 479 | 21 | 3 | 40 | 43 | 13 | 1126 | 10 | 3 | 3 | 0 | 0 | 3 | 671 | 3 | 54 | 1442 | 13 | 17 |
| 115 | 1 | 181 | 33 | 35 | 29 | 45 | 61 | 502 | 18 | 2 | 42 | 43 | 13 | 1191 | 10 | 3 | 3 | 0 | 0 | 4 | 695 | 3 | 52 | 1518 | 13 | 15 |
| 120 | 1 | 165 | 34 | 35 | 30 | 48 | 63 | 524 | 16 | 2 | 44 | 43 | 13 | 1256 | 10 | 4 | 3 | 0 | 0 | 4 | 724 | 3 | 53 | 1601 | 13 | 17 |
| 125 | 1 | 151 | 35 | 36 | 30 | 50 | 66 | 546 | 14 | 2 | 46 | 42 | 13 | 1320 | 11 | 4 | 4 | 0 | 0 | 5 | 752 | 4 | 53 | 1682 | 13 | 16 |
| 130 | 1 | 139 | 35 | 37 | 30 | 53 | 68 | 566 | 13 | 2 | 48 | 42 | 13 | 1383 | 11 | 5 | 4 | 0 | 0 | 6 | 780 | 4 | 55 | 1764 | 14 | 16 |
| 135 | 1 | 127 | 36 | 37 | 31 | 55 | 70 | 586 | 11 | 2 | 50 | 42 | 12 | 1445 | 11 | 6 | 5 | 0 | 0 | 6 | 804 | 5 | 51 | 1839 | 14 | 15 |
| 140 | 1 | 117 | 36 | 38 | 31 | 58 | 73 | 606 | 10 | 2 | 52 | 42 | 12 | 1505 | 11 | 6 | 5 | 0 | 0 | 7 | 827 | 5 | 50 | 1911 | 14 | 15 |
| 145 | 1 | 108 | 37 | 38 | 32 | 61 | 75 | 624 | 9 | 2 | 54 | 41 | 12 | 1565 | 11 | 7 | 5 | 0 | 0 | 8 | 858 | 5 | 49 | 1993 | 14 | 16 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | - | 1 | 1 | 2 | 1 | 1 | 5 | 144 | 0 | 1 | 2 | 1 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 0 | 3 | 13 | 0 | 2 |
| 10 | 2 | - | 2 | 3 | 3 | 2 | 2 | 11 | 287 | 1 | 1 | 4 | 2 | 20 | 1 | 0 | 0 | 0 | 0 | 0 | 26 | 0 | 6 | 26 | 1 | 3 |
| 15 | 2 | - | 3 | 4 | 5 | 2 | 4 | 16 | 431 | 1 | 2 | 6 | 3 | 31 | 1 | 0 | 0 | 0 | 0 | 0 | 39 | 0 | 9 | 39 | 1 | 5 |
| 20 | 2 | - | 4 | 5 | 6 | 3 | 5 | 21 | 574 | 2 | 3 | 8 | 3 | 41 | 1 | 0 | 0 | 0 | 0 | 0 | 52 | 0 | 13 | 52 | 1 | 6 |
| 25 | 2 | - | 5 | 7 | 8 | 4 | 6 | 27 | 718 | 2 | 4 | 9 | 4 | 51 | 1 | 0 | 0 | 0 | 0 | 0 | 65 | 0 | 16 | 65 | 2 | 8 |
| 30 | 2 | - | 6 | 8 | 9 | 5 | 7 | 32 | 861 | 3 | 4 | 11 | 5 | 61 | 2 | 0 | 0 | 0 | 0 | 0 | 77 | 0 | 19 | 77 | 2 | 9 |
| 35 | 2 | - | 7 | 10 | 11 | 6 | 8 | 37 | 1005 | 3 | 5 | 13 | 6 | 72 | 2 | 0 | 0 | 0 | 0 | 0 | 90 | 0 | 22 | 90 | 2 | 11 |
| 40 | 2 | - | 9 | 11 | 12 | 7 | 10 | 43 | 1148 | 4 | 6 | 15 | 7 | 82 | 2 | 0 | 0 | 0 | 0 | 0 | 103 | 0 | 25 | 103 | 3 | 12 |
| 40 | 2 | 3106 | 10 | 12 | 14 | 8 | 11 | 48 | 1292 | 4 | 6 | 17 | 8 | 92 | 2 | 0 | 0 | 0 | 0 | 0 | 116 | 0 | 28 | 116 | 3 | 14 |
| 45 | 2 | 2247 | 12 | 14 | 15 | 9 | 14 | 73 | 859 | 4 | 8 | 20 | 9 | 137 | 3 | 0 | 0 | 0 | 0 | 0 | 137 | 0 | 27 | 192 | 4 | 15 |
| 50 | 2 | 1670 | 14 | 16 | 17 | 11 | 16 | 99 | 577 | 4 | 9 | 23 | 10 | 186 | 4 | 0 | 0 | 0 | 0 | 0 | 183 | 0 | 27 | 265 | 5 | 14 |
| 55 | 2 | 1278 | 16 | 18 | 18 | 13 | 20 | 126 | 393 | 3 | 10 | 26 | 10 | 239 | 4 | 0 | 0 | 0 | 0 | 0 | 216 | 0 | 36 | 334 | 6 | 14 |
| 60 | 2 | 1006 | 17 | 20 | 19 | 16 | 22 | 153 | 272 | 3 | 12 | 28 | 11 | 294 | 5 | 0 | 0 | 0 | 0 | 0 | 250 | 0 | 37 | 405 | 7 | 14 |
| 65 | 2 | 844 | 19 | 21 | 20 | 18 | 26 | 181 | 162 | 3 | 16 | 29 | 11 | 351 | 5 | 0 | 0 | 0 | 0 | 0 | 288 | 0 | 38 | 481 | 7 | 15 |
| 70 | 2 | 718 | 20 | 22 | 21 | 19 | 28 | 207 | 126 | 3 | 18 | 31 | 12 | 409 | 6 | 0 | 0 | 0 | 0 | 0 | 319 | 0 | 40 | 552 | 8 | 14 |
| 75 | 2 | 619 | 22 | 24 | 22 | 21 | 31 | 233 | 99 | 3 | 20 | 32 | 12 | 467 | 6 | 0 | 0 | 0 | 0 | 1 | 351 | 0 | 41 | 625 | 8 | 14 |
| 80 | 2 | 538 | 23 | 25 | 23 | 23 | 34 | 259 | 80 | 3 | 21 | 33 | 12 | 526 | 7 | 1 | 1 | 0 | 0 | 1 | 384 | 1 | 42 | 700 | 9 | 15 |
| 85 | 2 | 473 | 24 | 26 | 24 | 25 | 37 | 283 | 66 | 3 | 23 | 34 | 12 | 584 | 7 | 1 | 1 | 0 | 0 | 1 | 415 | 1 | 43 | 774 | 9 | 15 |
| 90 | 2 | 418 | 25 | 27 | 24 | 27 | 40 | 307 | 54 | 3 | 25 | 35 | 12 | 643 | 7 | 1 | 1 | 0 | 0 | 1 | 445 | 1 | 43 | 847 | 9 | 15 |
| 95 | 2 | 373 | 26 | 28 | 25 | 29 | 42 | 330 | 45 | 3 | 28 | 35 | 12 | 701 | 7 | 1 | 1 | 0 | 0 | 1 | 475 | 1 | 44 | 921 | 10 | 15 |
| 100 | 2 | 335 | 27 | 28 | 26 | 31 | 45 | 352 | 38 | 3 | 30 | 36 | 12 | 759 | 8 | 1 | 1 | 0 | 0 | 2 | 504 | 1 | 45 | 994 | 10 | 15 |
| 105 | 2 | 303 | 28 | 29 | 26 | 33 | 47 | 374 | 32 | 3 | 32 | 36 | 12 | 817 | 8 | 2 | 1 | 0 | 0 | 2 | 533 | 1 | 45 | 1068 | 10 | 15 |
| 110 | 2 | 276 | 28 | 30 | 27 | 35 | 50 | 395 | 28 | 2 | 34 | 36 | 11 | 874 | 8 | 2 | 2 | 0 | 0 | 2 | 562 | 2 | 46 | 1143 | 10 | 15 |
| 115 | 2 | 252 | 29 | 31 | 27 | 37 | 52 | 415 | 24 | 2 | 36 | 36 | 11 | 931 | 8 | 2 | 2 | 0 | 0 | 2 | 583 | 2 | 46 | 1210 | 11 | 13 |
| 120 | 2 | 231 | 30 | 31 | 28 | 39 | 54 | 434 | 21 | 2 | 38 | 37 | 11 | 986 | 8 | 2 | 2 | 0 | 0 | 3 | 610 | 2 | 47 | 1284 | 11 | 15 |
| 125 | 2 | 213 | 30 | 32 | 28 | 41 | 56 | 453 | 18 | 2 | 41 | 37 | 11 | 1041 | 8 | 3 | 3 | 0 | 0 | 3 | 635 | 3 | 46 | 1355 | 11 | 14 |
| 130 | 2 | 197 | 31 | 32 | 29 | 43 | 58 | 471 | 16 | 2 | 43 | 36 | 11 | 1096 | 8 | 3 | 3 | 0 | 0 | 3 | 653 | 3 | 46 | 1419 | 11 | 13 |
| 135 | 2 | 183 | 32 | 33 | 29 | 45 | 60 | 488 | 14 | 2 | 44 | 36 | 11 | 1150 | 8 | 3 | 3 | 0 | 0 | 4 | 679 | 3 | 45 | 1490 | 11 | 14 |
| 140 | 2 | 170 | 32 | 33 | 30 | 47 | 62 | 505 | 13 | 2 | 46 | 36 | 11 | 1203 | 9 | 4 | 3 | 0 | 0 | 4 | 700 | 3 | 45 | 1555 | 11 | 13 |
| 145 | 2 | 158 | 32 | 34 | 30 | 49 | 64 | 521 | 12 | 2 | 48 | 36 | 10 | 1255 | 9 | 4 | 4 | 0 | 0 | 5 | 722 | 4 | 46 | 1624 | 11 | 14 |
| 150 | 2 | 147 | 33 | 34 | 30 | 51 | 66 | 537 | 11 | 2 | 50 | 36 | 10 | 1307 | 9 | 4 | 4 | 0 | 0 | 5 | 741 | 4 | 46 | 1690 | 11 | 13 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | - | 1 | 1 | 2 | 1 | 1 | 4 | 134 | 0 | 1 | 1 | 1 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 2 | 12 | 0 | 1 |
| 10 | 3 | - | 2 | 2 | 3 | 2 | 2 | 9 | 269 | 1 | 1 | 2 | 1 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 0 | 4 | 25 | 1 | 2 |
| 15 | 3 | - | 3 | 4 | 5 | 2 | 3 | 13 | 403 | 1 | 2 | 4 | 2 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 37 | 0 | 7 | 37 | 1 | 4 |
| 20 | 3 | - | 4 | 5 | 6 | 3 | 4 | 18 | 537 | 1 | 2 | 5 | 3 | 31 | 1 | 0 | 0 | 0 | 0 | 0 | 50 | 0 | 9 | 50 | 1 | 5 |
| 25 | 3 | - | 5 | 6 | 8 | 4 | 6 | 22 | 672 | 2 | 3 | 6 | 3 | 38 | 1 | 0 | 0 | 0 | 0 | 0 | 62 | 0 | 11 | 62 | 1 | 6 |
| 30 | 3 | - | 6 | 7 | 9 | 5 | 7 | 27 | 806 | 2 | 4 | 7 | 4 | 46 | 1 | 0 | 0 | 0 | 0 | 0 | 74 | 0 | 13 | 74 | 2 | 7 |
| 35 | 3 | - | 7 | 9 | 11 | 5 | 8 | 31 | 940 | 2 | 4 | 9 | 5 | 54 | 1 | 0 | 0 | 0 | 0 | 0 | 87 | 0 | 15 | 87 | 2 | 8 |
| 40 | 3 | - | 8 | 10 | 12 | 6 | 9 | 36 | 1075 | 3 | 5 | 10 | 5 | 61 | 1 | 0 | 0 | 0 | 0 | 0 | 99 | 0 | 17 | 99 | 2 | 9 |
| 45 | 3 | 3527 | 9 | 11 | 14 | 7 | 10 | 40 | 1209 | 3 | 6 | 11 | 6 | 69 | 2 | 0 | 0 | 0 | 0 | 0 | 112 | 0 | 20 | 112 | 2 | 11 |
| 50 | 3 | 2674 | 11 | 13 | 15 | 8 | 13 | 61 | 853 | 3 | 6 | 13 | 7 | 103 | 2 | 0 | 0 | 0 | 0 | 0 | 131 | 0 | 19 | 170 | 3 | 12 |
| 55 | 3 | 2068 | 12 | 14 | 16 | 10 | 15 | 84 | 606 | 3 | 8 | 16 | 8 | 141 | 3 | 0 | 0 | 0 | 0 | 0 | 163 | 0 | 20 | 222 | 4 | 10 |
| 60 | 3 | 1634 | 14 | 16 | 18 | 12 | 18 | 107 | 434 | 3 | 9 | 18 | 8 | 182 | 3 | 0 | 0 | 0 | 0 | 0 | 192 | 0 | 20 | 271 | 5 | 10 |
| 65 | 3 | 1319 | 16 | 17 | 19 | 13 | 20 | 130 | 315 | 3 | 10 | 20 | 9 | 225 | 4 | 0 | 0 | 0 | 0 | 0 | 221 | 0 | 28 | 328 | 5 | 11 |
| 70 | 3 | 1087 | 17 | 19 | 20 | 15 | 23 | 153 | 232 | 3 | 12 | 22 | 9 | 270 | 4 | 0 | 0 | 0 | 0 | 0 | 252 | 0 | 29 | 388 | 6 | 12 |
| 75 | 3 | 936 | 18 | 20 | 20 | 17 | 26 | 176 | 152 | 3 | 15 | 23 | 9 | 316 | 4 | 0 | 0 | 0 | 0 | 0 | 279 | 0 | 31 | 446 | 6 | 12 |
| 80 | 3 | 811 | 19 | 21 | 21 | 18 | 28 | 198 | 125 | 3 | 16 | 25 | 9 | 362 | 4 | 0 | 0 | 0 | 0 | 0 | 306 | 0 | 32 | 505 | 6 | 12 |
| 85 | 3 | 709 | 20 | 22 | 22 | 20 | 31 | 219 | 103 | 2 | 18 | 26 | 9 | 409 | 5 | 0 | 0 | 0 | 0 | 0 | 331 | 0 | 33 | 563 | 7 | 12 |
| 90 | 3 | 624 | 21 | 23 | 23 | 22 | 33 | 239 | 85 | 2 | 19 | 27 | 10 | 456 | 5 | 0 | 0 | 0 | 0 | 1 | 358 | 0 | 34 | 624 | 7 | 12 |
| 95 | 3 | 554 | 22 | 24 | 24 | 23 | 36 | 259 | 70 | 2 | 21 | 28 | 10 | 504 | 5 | 1 | 0 | 0 | 0 | 1 | 385 | 0 | 35 | 686 | 7 | 12 |
| 100 | 3 | 496 | 23 | 24 | 24 | 25 | 38 | 278 | 58 | 2 | 23 | 28 | 10 | 551 | 6 | 1 | 1 | 0 | 0 | 1 | 408 | 1 | 36 | 745 | 7 | 12 |
| 105 | 3 | 447 | 24 | 25 | 25 | 26 | 40 | 297 | 49 | 2 | 25 | 29 | 9 | 598 | 6 | 1 | 1 | 0 | 0 | 1 | 431 | 1 | 36 | 804 | 8 | 12 |
| 110 | 3 | 406 | 25 | 26 | 25 | 28 | 42 | 314 | 41 | 2 | 27 | 29 | 9 | 645 | 6 | 1 | 1 | 0 | 0 | 1 | 459 | 1 | 37 | 868 | 8 | 13 |
| 115 | 3 | 371 | 25 | 26 | 26 | 30 | 44 | 331 | 35 | 2 | 29 | 30 | 9 | 692 | 6 | 1 | 1 | 0 | 0 | 1 | 479 | 1 | 37 | 926 | 8 | 12 |
| 120 | 3 | 340 | 26 | 27 | 26 | 31 | 46 | 348 | 30 | 2 | 31 | 30 | 9 | 738 | 6 | 1 | 1 | 0 | 0 | 1 | 499 | 1 | 38 | 983 | 8 | 11 |
| 125 | 3 | 314 | 26 | 28 | 27 | 33 | 48 | 363 | 26 | 2 | 33 | 30 | 9 | 784 | 6 | 1 | 1 | 0 | 0 | 2 | 521 | 1 | 38 | 1043 | 8 | 12 |
| 130 | 3 | 292 | 27 | 28 | 27 | 34 | 50 | 379 | 23 | 2 | 35 | 30 | 9 | 830 | 6 | 2 | 2 | 0 | 0 | 2 | 543 | 2 | 39 | 1104 | 8 | 12 |
| 135 | 3 | 271 | 27 | 28 | 28 | 36 | 51 | 393 | 20 | 2 | 37 | 31 | 9 | 875 | 6 | 2 | 2 | 0 | 0 | 2 | 558 | 2 | 38 | 1157 | 9 | 11 |
| 140 | 3 | 253 | 28 | 29 | 28 | 37 | 53 | 407 | 18 | 2 | 39 | 31 | 9 | 920 | 7 | 2 | 2 | 0 | 0 | 2 | 578 | 2 | 38 | 1216 | 9 | 12 |
| 145 | 3 | 237 | 28 | 29 | 28 | 39 | 54 | 421 | 16 | 2 | 41 | 31 | 9 | 964 | 7 | 2 | 2 | 0 | 0 | 3 | 598 | 2 | 38 | 1273 | 9 | 11 |
| 150 | 3 | 222 | 29 | 30 | 29 | 40 | 56 | 434 | 15 | 2 | 42 | 31 | 9 | 1008 | 7 | 2 | 3 | 0 | 0 | 3 | 616 | 3 | 40 | 1331 | 9 | 12 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | −1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | −1 | - | 3 | 3 | 5 | 4 | 4 | 36 | 284 | 1 | 2 | 8 | 5 | 49 | 2 | 0 | 0 | 0 | 0 | 0 | 41 | 0 | 8 | 41 | 2 | 6 |
| 10 | −1 | - | 6 | 7 | 11 | 7 | 9 | 72 | 568 | 3 | 4 | 16 | 10 | 98 | 5 | 0 | 0 | 0 | 0 | 0 | 82 | 0 | 16 | 82 | 4 | 12 |
| 15 | −1 | - | 10 | 10 | 16 | 11 | 13 | 108 | 853 | 4 | 6 | 25 | 15 | 146 | 7 | 0 | 0 | 0 | 0 | 0 | 123 | 0 | 24 | 123 | 6 | 18 |
| 20 | −1 | 1372 | 13 | 14 | 22 | 14 | 18 | 144 | 1137 | 6 | 8 | 33 | 19 | 195 | 10 | 0 | 0 | 0 | 0 | 0 | 164 | 0 | 32 | 164 | 8 | 23 |
| 25 | −1 | 835 | 17 | 18 | 26 | 20 | 23 | 212 | 537 | 6 | 12 | 43 | 22 | 305 | 12 | 0 | 0 | 0 | 0 | 0 | 232 | 0 | 45 | 310 | 12 | 29 |
| 30 | −1 | 629 | 20 | 21 | 31 | 25 | 28 | 280 | 206 | 5 | 18 | 48 | 23 | 422 | 14 | 0 | 0 | 0 | 0 | 1 | 315 | 0 | 46 | 438 | 15 | 26 |
| 35 | −1 | 568 | 23 | 24 | 34 | 28 | 32 | 349 | 61 | 5 | 32 | 50 | 24 | 541 | 16 | 1 | 1 | 0 | 0 | 1 | 433 | 1 | 47 | 604 | 17 | 33 |
| 40 | −1 | 524 | 26 | 27 | 38 | 30 | 36 | 417 | 44 | 4 | 36 | 51 | 24 | 660 | 16 | 1 | 1 | 0 | 0 | 1 | 520 | 1 | 47 | 737 | 18 | 27 |
| 45 | −1 | 471 | 29 | 30 | 40 | 33 | 40 | 482 | 52 | 4 | 32 | 51 | 23 | 777 | 17 | 1 | 1 | 0 | 0 | 1 | 553 | 1 | 46 | 817 | 18 | 16 |
| 50 | −1 | 423 | 31 | 32 | 43 | 36 | 44 | 546 | 48 | 4 | 32 | 51 | 23 | 891 | 18 | 1 | 1 | 0 | 0 | 1 | 606 | 1 | 45 | 914 | 18 | 20 |
| 55 | −1 | 387 | 33 | 34 | 45 | 39 | 47 | 607 | 35 | 4 | 36 | 50 | 22 | 1003 | 18 | 1 | 1 | 0 | 0 | 2 | 673 | 1 | 44 | 1025 | 19 | 22 |
| 60 | −1 | 363 | 34 | 35 | 48 | 41 | 50 | 666 | 24 | 3 | 43 | 50 | 22 | 1111 | 18 | 2 | 2 | 0 | 0 | 2 | 748 | 2 | 42 | 1142 | 19 | 23 |
| 65 | −1 | 346 | 36 | 37 | 50 | 43 | 53 | 722 | 18 | 3 | 48 | 49 | 21 | 1217 | 19 | 2 | 2 | 0 | 0 | 2 | 835 | 2 | 42 | 1270 | 20 | 26 |
| 70 | −1 | 332 | 37 | 38 | 52 | 45 | 56 | 775 | 14 | 3 | 53 | 49 | 20 | 1319 | 19 | 2 | 3 | 0 | 0 | 3 | 909 | 3 | 39 | 1383 | 20 | 23 |
| 75 | −1 | 320 | 38 | 39 | 54 | 46 | 59 | 827 | 12 | 3 | 57 | 48 | 20 | 1418 | 19 | 2 | 3 | 0 | 1 | 3 | 976 | 3 | 39 | 1489 | 20 | 21 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | - | 2 | 3 | 4 | 2 | 4 | 21 | 364 | 1 | 2 | 6 | 4 | 30 | 2 | 0 | 0 | 0 | 0 | 0 | 29 | 0 | 7 | 29 | 1 | 4 |
| 10 | 0 | - | 5 | 5 | 8 | 5 | 7 | 42 | 727 | 3 | 3 | 12 | 7 | 60 | 3 | 0 | 0 | 0 | 0 | 0 | 57 | 0 | 14 | 57 | 3 | 9 |
| 15 | 0 | - | 7 | 8 | 13 | 7 | 11 | 64 | 1090 | 4 | 5 | 19 | 11 | 91 | 5 | 0 | 0 | 0 | 0 | 0 | 86 | 0 | 22 | 86 | 4 | 13 |
| 20 | 0 | 2161 | 10 | 11 | 17 | 10 | 14 | 85 | 1454 | 6 | 7 | 25 | 14 | 121 | 6 | 0 | 0 | 0 | 0 | 0 | 115 | 0 | 29 | 115 | 6 | 18 |
| 25 | 0 | 1329 | 13 | 14 | 21 | 14 | 19 | 140 | 832 | 5 | 9 | 34 | 18 | 210 | 8 | 0 | 0 | 0 | 0 | 0 | 165 | 0 | 32 | 227 | 9 | 22 |
| 30 | 0 | 900 | 16 | 17 | 26 | 19 | 24 | 199 | 429 | 5 | 12 | 38 | 19 | 306 | 10 | 0 | 0 | 0 | 0 | 0 | 226 | 0 | 40 | 327 | 11 | 20 |
| 35 | 0 | 708 | 20 | 20 | 30 | 23 | 28 | 259 | 192 | 5 | 17 | 41 | 20 | 407 | 12 | 0 | 0 | 0 | 0 | 0 | 296 | 0 | 39 | 436 | 12 | 22 |
| 40 | 0 | 641 | 22 | 23 | 33 | 26 | 32 | 319 | 67 | 4 | 28 | 42 | 20 | 510 | 13 | 0 | 1 | 0 | 0 | 1 | 388 | 1 | 39 | 568 | 14 | 26 |
| 45 | 0 | 604 | 24 | 25 | 36 | 27 | 35 | 379 | 37 | 4 | 37 | 42 | 20 | 612 | 14 | 1 | 1 | 0 | 0 | 1 | 495 | 1 | 40 | 714 | 16 | 29 |
| 50 | 0 | 564 | 27 | 28 | 38 | 29 | 39 | 437 | 39 | 4 | 35 | 43 | 20 | 713 | 14 | 1 | 1 | 0 | 0 | 1 | 524 | 1 | 39 | 782 | 16 | 14 |
| 55 | 0 | 519 | 28 | 29 | 40 | 32 | 42 | 494 | 46 | 4 | 32 | 43 | 20 | 812 | 15 | 1 | 1 | 0 | 0 | 1 | 546 | 1 | 39 | 843 | 15 | 12 |
| 60 | 0 | 473 | 30 | 31 | 43 | 34 | 45 | 548 | 45 | 3 | 31 | 43 | 19 | 909 | 15 | 1 | 1 | 0 | 0 | 1 | 590 | 1 | 38 | 926 | 15 | 16 |
| 65 | 0 | 434 | 32 | 32 | 45 | 36 | 47 | 599 | 39 | 3 | 33 | 43 | 19 | 1004 | 15 | 1 | 1 | 0 | 0 | 1 | 644 | 1 | 38 | 1018 | 16 | 18 |
| 70 | 0 | 404 | 33 | 34 | 47 | 38 | 50 | 649 | 31 | 3 | 36 | 43 | 18 | 1096 | 16 | 1 | 1 | 0 | 0 | 2 | 699 | 1 | 38 | 1111 | 16 | 18 |
| 75 | 0 | 381 | 34 | 35 | 49 | 40 | 52 | 695 | 23 | 3 | 41 | 43 | 18 | 1186 | 16 | 2 | 2 | 0 | 0 | 2 | 761 | 2 | 37 | 1210 | 16 | 20 |
| 80 | 0 | 363 | 35 | 36 | 50 | 42 | 54 | 740 | 17 | 3 | 46 | 43 | 18 | 1274 | 16 | 2 | 2 | 0 | 0 | 2 | 822 | 2 | 36 | 1307 | 16 | 19 |
| 85 | 0 | 349 | 36 | 37 | 52 | 43 | 57 | 781 | 14 | 3 | 50 | 43 | 17 | 1359 | 16 | 2 | 3 | 0 | 0 | 3 | 879 | 3 | 35 | 1399 | 16 | 18 |
| 90 | 0 | 336 | 37 | 38 | 53 | 45 | 59 | 821 | 13 | 3 | 52 | 43 | 16 | 1441 | 16 | 2 | 3 | 0 | 0 | 3 | 912 | 3 | 35 | 1467 | 16 | 14 |
| 95 | 0 | 324 | 37 | 38 | 54 | 46 | 60 | 858 | 13 | 3 | 52 | 43 | 16 | 1522 | 16 | 2 | 3 | 0 | 0 | 3 | 934 | 3 | 36 | 1525 | 16 | 12 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | - | 2 | 2 | 3 | 2 | 3 | 16 | 230 | 1 | 2 | 5 | 3 | 26 | 1 | 0 | 0 | 0 | 0 | 0 | 23 | 0 | 6 | 23 | 1 | 4 |
| 10 | 1 | - | 4 | 4 | 7 | 4 | 6 | 32 | 459 | 2 | 3 | 10 | 5 | 52 | 2 | 0 | 0 | 0 | 0 | 0 | 45 | 0 | 12 | 45 | 2 | 7 |
| 15 | 1 | - | 6 | 7 | 10 | 6 | 9 | 48 | 689 | 3 | 5 | 15 | 8 | 78 | 3 | 0 | 0 | 0 | 0 | 0 | 68 | 0 | 18 | 68 | 3 | 11 |
| 20 | 1 | - | 8 | 9 | 13 | 8 | 12 | 64 | 918 | 4 | 6 | 20 | 10 | 104 | 4 | 0 | 0 | 0 | 0 | 0 | 91 | 0 | 24 | 91 | 4 | 15 |
| 25 | 1 | 2211 | 10 | 11 | 16 | 10 | 15 | 80 | 1148 | 6 | 8 | 25 | 13 | 130 | 5 | 0 | 0 | 0 | 0 | 0 | 113 | 0 | 31 | 113 | 5 | 18 |
| 30 | 1 | 1497 | 13 | 14 | 21 | 13 | 19 | 127 | 714 | 5 | 10 | 30 | 15 | 206 | 7 | 0 | 0 | 0 | 0 | 0 | 162 | 0 | 31 | 223 | 7 | 22 |
| 35 | 1 | 1083 | 16 | 16 | 24 | 17 | 23 | 177 | 414 | 4 | 12 | 32 | 17 | 289 | 8 | 0 | 0 | 0 | 0 | 0 | 211 | 0 | 35 | 307 | 9 | 17 |
| 40 | 1 | 863 | 18 | 19 | 28 | 20 | 27 | 230 | 220 | 4 | 15 | 34 | 17 | 375 | 9 | 0 | 0 | 0 | 0 | 0 | 265 | 0 | 33 | 394 | 10 | 18 |
| 45 | 1 | 755 | 20 | 21 | 31 | 23 | 30 | 282 | 108 | 4 | 21 | 34 | 17 | 462 | 10 | 0 | 0 | 0 | 0 | 0 | 322 | 0 | 33 | 484 | 11 | 18 |
| 50 | 1 | 705 | 22 | 23 | 33 | 24 | 33 | 334 | 49 | 4 | 30 | 35 | 17 | 550 | 11 | 0 | 1 | 0 | 0 | 1 | 407 | 1 | 33 | 601 | 12 | 23 |
| 55 | 1 | 669 | 24 | 25 | 35 | 26 | 36 | 385 | 36 | 3 | 34 | 36 | 17 | 636 | 12 | 1 | 1 | 0 | 0 | 1 | 476 | 1 | 33 | 704 | 13 | 21 |
| 60 | 1 | 631 | 26 | 27 | 38 | 28 | 39 | 434 | 39 | 3 | 33 | 36 | 17 | 721 | 12 | 1 | 1 | 0 | 0 | 1 | 505 | 1 | 34 | 767 | 13 | 13 |
| 65 | 1 | 587 | 27 | 28 | 40 | 29 | 41 | 481 | 44 | 3 | 30 | 37 | 17 | 805 | 12 | 1 | 1 | 0 | 0 | 1 | 528 | 1 | 34 | 824 | 13 | 11 |
| 70 | 1 | 542 | 28 | 30 | 42 | 31 | 44 | 525 | 45 | 3 | 30 | 38 | 16 | 887 | 13 | 1 | 1 | 0 | 0 | 1 | 565 | 1 | 34 | 895 | 13 | 14 |
| 75 | 1 | 501 | 30 | 31 | 44 | 33 | 46 | 567 | 41 | 3 | 31 | 38 | 16 | 967 | 13 | 1 | 1 | 0 | 0 | 1 | 605 | 1 | 34 | 970 | 13 | 15 |
| 80 | 1 | 466 | 31 | 32 | 45 | 35 | 48 | 606 | 35 | 3 | 33 | 39 | 16 | 1046 | 13 | 1 | 1 | 0 | 0 | 1 | 643 | 1 | 34 | 1041 | 13 | 14 |
| 85 | 1 | 435 | 32 | 33 | 47 | 37 | 50 | 644 | 30 | 3 | 35 | 39 | 15 | 1122 | 13 | 1 | 1 | 0 | 0 | 2 | 683 | 1 | 34 | 1116 | 13 | 15 |
| 90 | 1 | 409 | 32 | 34 | 48 | 39 | 52 | 678 | 27 | 3 | 37 | 40 | 15 | 1197 | 13 | 1 | 1 | 0 | 0 | 2 | 716 | 1 | 36 | 1184 | 13 | 14 |
| 95 | 1 | 385 | 33 | 34 | 49 | 40 | 53 | 711 | 24 | 3 | 39 | 40 | 15 | 1270 | 13 | 2 | 1 | 0 | 0 | 2 | 746 | 1 | 35 | 1250 | 13 | 13 |
| 100 | 1 | 363 | 34 | 35 | 50 | 42 | 55 | 742 | 22 | 3 | 41 | 40 | 14 | 1341 | 13 | 2 | 2 | 0 | 0 | 2 | 778 | 2 | 35 | 1316 | 13 | 13 |
| 105 | 1 | 344 | 35 | 36 | 51 | 44 | 56 | 771 | 20 | 3 | 42 | 41 | 14 | 1411 | 13 | 2 | 2 | 0 | 0 | 2 | 807 | 2 | 35 | 1380 | 13 | 13 |
| 110 | 1 | 325 | 35 | 36 | 52 | 45 | 58 | 798 | 19 | 3 | 43 | 41 | 14 | 1478 | 13 | 2 | 2 | 0 | 0 | 3 | 828 | 2 | 35 | 1436 | 13 | 11 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | - | 2 | 2 | 3 | 2 | 3 | 11 | 168 | 1 | 1 | 4 | 2 | 20 | 1 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 5 | 18 | 1 | 3 |
| 10 | 2 | - | 3 | 3 | 5 | 3 | 5 | 22 | 335 | 2 | 3 | 8 | 4 | 39 | 1 | 0 | 0 | 0 | 0 | 0 | 36 | 0 | 10 | 36 | 1 | 6 |
| 15 | 2 | - | 5 | 5 | 8 | 4 | 8 | 34 | 503 | 3 | 4 | 12 | 6 | 59 | 2 | 0 | 0 | 0 | 0 | 0 | 54 | 0 | 15 | 54 | 2 | 8 |
| 20 | 2 | - | 6 | 7 | 10 | 6 | 10 | 45 | 671 | 4 | 5 | 15 | 7 | 79 | 3 | 0 | 0 | 0 | 0 | 0 | 72 | 0 | 20 | 72 | 2 | 11 |
| 25 | 2 | - | 8 | 9 | 13 | 8 | 13 | 56 | 838 | 4 | 7 | 19 | 9 | 98 | 3 | 0 | 0 | 0 | 0 | 0 | 90 | 0 | 25 | 90 | 3 | 14 |
| 30 | 2 | 2496 | 10 | 10 | 16 | 9 | 15 | 67 | 1006 | 5 | 8 | 23 | 11 | 118 | 4 | 0 | 0 | 0 | 0 | 0 | 108 | 0 | 30 | 108 | 4 | 17 |
| 35 | 2 | 1816 | 12 | 13 | 20 | 12 | 19 | 106 | 680 | 5 | 9 | 25 | 13 | 183 | 5 | 0 | 0 | 0 | 0 | 0 | 147 | 0 | 28 | 205 | 6 | 19 |
| 40 | 2 | 1373 | 14 | 15 | 23 | 15 | 22 | 148 | 443 | 4 | 11 | 27 | 14 | 252 | 6 | 0 | 0 | 0 | 0 | 0 | 188 | 0 | 30 | 276 | 7 | 14 |
| 45 | 2 | 1100 | 16 | 17 | 26 | 17 | 25 | 192 | 273 | 4 | 13 | 28 | 14 | 323 | 7 | 0 | 0 | 0 | 0 | 0 | 226 | 0 | 29 | 343 | 8 | 13 |
| 50 | 2 | 940 | 18 | 19 | 28 | 20 | 28 | 237 | 160 | 3 | 16 | 28 | 15 | 396 | 8 | 0 | 0 | 0 | 0 | 0 | 269 | 0 | 28 | 414 | 8 | 14 |
| 55 | 2 | 850 | 20 | 21 | 30 | 21 | 30 | 281 | 90 | 3 | 21 | 29 | 15 | 470 | 8 | 0 | 0 | 0 | 0 | 0 | 324 | 0 | 28 | 498 | 9 | 17 |
| 60 | 2 | 791 | 22 | 22 | 33 | 23 | 33 | 324 | 59 | 3 | 26 | 30 | 15 | 543 | 9 | 0 | 0 | 0 | 0 | 0 | 380 | 0 | 29 | 582 | 10 | 17 |
| 65 | 2 | 745 | 23 | 24 | 35 | 24 | 35 | 365 | 46 | 3 | 29 | 31 | 14 | 615 | 10 | 0 | 1 | 0 | 0 | 1 | 432 | 1 | 29 | 663 | 10 | 16 |
| 70 | 2 | 703 | 24 | 25 | 37 | 26 | 37 | 404 | 41 | 3 | 31 | 32 | 14 | 686 | 10 | 1 | 1 | 0 | 0 | 1 | 471 | 1 | 30 | 732 | 10 | 14 |
| 75 | 2 | 664 | 26 | 26 | 39 | 27 | 39 | 441 | 40 | 3 | 31 | 33 | 14 | 757 | 10 | 1 | 1 | 0 | 0 | 1 | 511 | 1 | 31 | 803 | 11 | 14 |
| 80 | 2 | 624 | 27 | 28 | 40 | 29 | 41 | 476 | 40 | 3 | 31 | 34 | 14 | 826 | 10 | 1 | 1 | 0 | 0 | 1 | 534 | 1 | 32 | 857 | 11 | 11 |
| 85 | 2 | 584 | 28 | 29 | 42 | 30 | 43 | 508 | 40 | 3 | 31 | 35 | 14 | 893 | 10 | 1 | 1 | 0 | 0 | 1 | 561 | 1 | 32 | 917 | 11 | 12 |
| 90 | 2 | 544 | 28 | 30 | 43 | 32 | 44 | 538 | 40 | 3 | 31 | 36 | 13 | 959 | 11 | 1 | 1 | 0 | 0 | 1 | 576 | 1 | 32 | 964 | 11 | 9 |
| 95 | 2 | 505 | 29 | 30 | 44 | 33 | 46 | 566 | 39 | 3 | 31 | 37 | 13 | 1024 | 11 | 1 | 1 | 0 | 0 | 1 | 604 | 1 | 33 | 1024 | 11 | 12 |
| 100 | 2 | 467 | 30 | 31 | 45 | 35 | 47 | 592 | 38 | 3 | 32 | 37 | 13 | 1088 | 11 | 1 | 1 | 0 | 0 | 1 | 631 | 1 | 34 | 1085 | 11 | 12 |
| 105 | 2 | 431 | 31 | 32 | 46 | 37 | 48 | 616 | 36 | 3 | 32 | 38 | 12 | 1150 | 11 | 1 | 1 | 0 | 0 | 2 | 652 | 1 | 34 | 1140 | 11 | 11 |
| 110 | 2 | 398 | 31 | 32 | 47 | 39 | 50 | 639 | 34 | 3 | 33 | 38 | 12 | 1210 | 11 | 1 | 1 | 0 | 0 | 2 | 675 | 1 | 34 | 1198 | 11 | 11 |
| 115 | 2 | 366 | 32 | 33 | 48 | 41 | 51 | 660 | 32 | 3 | 34 | 39 | 12 | 1270 | 11 | 2 | 1 | 0 | 0 | 2 | 699 | 1 | 34 | 1256 | 11 | 12 |
| 120 | 2 | 335 | 32 | 33 | 50 | 43 | 52 | 679 | 30 | 3 | 35 | 39 | 12 | 1328 | 11 | 2 | 1 | 0 | 0 | 2 | 718 | 1 | 33 | 1308 | 11 | 10 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | - | 1 | 1 | 2 | 1 | 2 | 10 | 86 | 1 | 1 | 3 | 1 | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 3 | 17 | 0 | 2 |
| 10 | 3 | - | 3 | 3 | 4 | 3 | 4 | 20 | 172 | 1 | 2 | 5 | 3 | 36 | 1 | 0 | 0 | 0 | 0 | 0 | 34 | 0 | 7 | 34 | 1 | 3 |
| 15 | 3 | - | 4 | 4 | 7 | 4 | 6 | 29 | 258 | 2 | 3 | 8 | 4 | 55 | 1 | 0 | 0 | 0 | 0 | 0 | 51 | 0 | 10 | 51 | 1 | 5 |
| 20 | 3 | - | 5 | 6 | 9 | 5 | 8 | 39 | 344 | 2 | 5 | 10 | 5 | 73 | 2 | 0 | 0 | 0 | 0 | 0 | 68 | 0 | 13 | 68 | 2 | 7 |
| 25 | 3 | - | 7 | 7 | 11 | 6 | 11 | 49 | 430 | 3 | 6 | 13 | 6 | 91 | 2 | 0 | 0 | 0 | 0 | 0 | 85 | 0 | 17 | 85 | 2 | 9 |
| 30 | 3 | - | 8 | 8 | 13 | 8 | 13 | 58 | 516 | 3 | 7 | 16 | 8 | 110 | 3 | 0 | 0 | 0 | 0 | 0 | 102 | 0 | 20 | 102 | 3 | 10 |
| 35 | 3 | - | 9 | 10 | 16 | 9 | 15 | 68 | 602 | 4 | 8 | 18 | 9 | 128 | 3 | 0 | 0 | 0 | 0 | 0 | 119 | 0 | 23 | 119 | 3 | 12 |
| 40 | 3 | 2261 | 10 | 11 | 18 | 10 | 17 | 78 | 688 | 4 | 9 | 21 | 10 | 146 | 4 | 0 | 0 | 0 | 0 | 0 | 136 | 0 | 27 | 136 | 3 | 14 |
| 45 | 3 | 1770 | 12 | 13 | 21 | 12 | 20 | 112 | 491 | 4 | 10 | 22 | 11 | 202 | 4 | 0 | 0 | 0 | 0 | 0 | 158 | 0 | 28 | 213 | 5 | 15 |
| 50 | 3 | 1428 | 14 | 15 | 23 | 14 | 22 | 147 | 342 | 4 | 11 | 23 | 12 | 260 | 5 | 0 | 0 | 0 | 0 | 0 | 191 | 0 | 26 | 272 | 5 | 12 |
| 55 | 3 | 1198 | 16 | 17 | 26 | 16 | 25 | 184 | 230 | 3 | 13 | 24 | 12 | 320 | 6 | 0 | 0 | 0 | 0 | 0 | 224 | 0 | 25 | 329 | 6 | 12 |
| 60 | 3 | 1049 | 17 | 18 | 28 | 18 | 27 | 219 | 150 | 3 | 16 | 24 | 12 | 380 | 6 | 0 | 0 | 0 | 0 | 0 | 262 | 0 | 25 | 392 | 7 | 13 |
| 65 | 3 | 953 | 19 | 20 | 30 | 20 | 29 | 254 | 95 | 3 | 20 | 26 | 12 | 441 | 7 | 0 | 0 | 0 | 0 | 0 | 305 | 0 | 25 | 459 | 7 | 14 |
| 70 | 3 | 893 | 20 | 21 | 32 | 21 | 31 | 287 | 60 | 3 | 25 | 27 | 12 | 501 | 7 | 0 | 0 | 0 | 0 | 0 | 359 | 0 | 26 | 539 | 8 | 16 |
| 75 | 3 | 832 | 21 | 22 | 34 | 23 | 33 | 319 | 61 | 3 | 25 | 28 | 12 | 560 | 8 | 0 | 0 | 0 | 0 | 0 | 384 | 0 | 26 | 590 | 8 | 10 |
| 80 | 3 | 784 | 22 | 23 | 36 | 24 | 34 | 348 | 48 | 3 | 28 | 30 | 12 | 619 | 8 | 0 | 1 | 0 | 0 | 1 | 425 | 1 | 27 | 658 | 8 | 14 |
| 85 | 3 | 741 | 24 | 24 | 37 | 25 | 36 | 375 | 43 | 3 | 30 | 31 | 12 | 677 | 8 | 0 | 1 | 0 | 0 | 1 | 462 | 1 | 29 | 725 | 9 | 13 |
| 90 | 3 | 699 | 24 | 25 | 38 | 26 | 37 | 401 | 43 | 3 | 30 | 32 | 11 | 735 | 8 | 1 | 1 | 0 | 0 | 1 | 479 | 1 | 30 | 771 | 9 | 9 |
| 95 | 3 | 655 | 25 | 26 | 39 | 28 | 38 | 424 | 44 | 3 | 29 | 33 | 11 | 791 | 8 | 1 | 1 | 0 | 0 | 1 | 496 | 1 | 30 | 819 | 9 | 9 |
| 100 | 3 | 609 | 26 | 27 | 40 | 29 | 40 | 445 | 45 | 3 | 29 | 34 | 11 | 846 | 8 | 1 | 1 | 0 | 0 | 1 | 518 | 1 | 31 | 871 | 9 | 11 |
| 105 | 3 | 564 | 27 | 28 | 42 | 31 | 41 | 465 | 46 | 3 | 29 | 34 | 11 | 900 | 9 | 1 | 1 | 0 | 0 | 1 | 535 | 1 | 32 | 920 | 9 | 10 |
| 110 | 3 | 518 | 27 | 28 | 42 | 32 | 42 | 483 | 46 | 3 | 29 | 35 | 11 | 953 | 9 | 1 | 1 | 0 | 0 | 1 | 552 | 1 | 32 | 968 | 9 | 10 |
| 115 | 3 | 472 | 28 | 29 | 44 | 34 | 43 | 500 | 46 | 3 | 29 | 35 | 10 | 1005 | 9 | 1 | 1 | 0 | 0 | 1 | 573 | 1 | 32 | 1021 | 9 | 11 |
| 120 | 3 | 426 | 28 | 30 | 45 | 36 | 44 | 515 | 46 | 3 | 29 | 36 | 10 | 1057 | 9 | 1 | 1 | 0 | 0 | 1 | 592 | 1 | 32 | 1072 | 9 | 10 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | −1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | −1 | - | 3 | 3 | 5 | 3 | 3 | 28 | 446 | 4 | 3 | 22 | 7 | 50 | 3 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 20 | 35 | 2 | 7 |
| 10 | −1 | - | 6 | 7 | 11 | 5 | 7 | 56 | 892 | 7 | 5 | 44 | 13 | 101 | 5 | 0 | 0 | 0 | 0 | 0 | 70 | 0 | 39 | 70 | 4 | 14 |
| 15 | −1 | - | 9 | 10 | 16 | 8 | 10 | 85 | 1338 | 11 | 8 | 67 | 20 | 152 | 8 | 0 | 0 | 0 | 0 | 0 | 106 | 0 | 59 | 106 | 5 | 21 |
| 20 | −1 | 2424 | 12 | 13 | 21 | 10 | 14 | 113 | 1784 | 15 | 10 | 89 | 27 | 202 | 10 | 0 | 0 | 0 | 0 | 0 | 141 | 0 | 78 | 141 | 7 | 28 |
| 25 | −1 | 1509 | 15 | 16 | 24 | 14 | 17 | 155 | 914 | 11 | 13 | 81 | 24 | 325 | 13 | 0 | 0 | 0 | 0 | 0 | 173 | 0 | 66 | 318 | 13 | 35 |
| 30 | −1 | 1045 | 17 | 18 | 27 | 18 | 21 | 195 | 464 | 9 | 16 | 72 | 22 | 436 | 14 | 0 | 0 | 0 | 0 | 0 | 216 | 0 | 57 | 417 | 14 | 20 |
| 35 | −1 | 742 | 20 | 21 | 29 | 22 | 24 | 232 | 303 | 7 | 17 | 64 | 20 | 538 | 15 | 0 | 0 | 0 | 0 | 0 | 260 | 0 | 50 | 512 | 15 | 19 |
| 40 | −1 | 576 | 22 | 23 | 31 | 25 | 28 | 268 | 166 | 6 | 21 | 57 | 19 | 631 | 16 | 0 | 0 | 0 | 0 | 1 | 310 | 0 | 47 | 609 | 15 | 19 |
| 45 | −1 | 479 | 24 | 25 | 32 | 28 | 31 | 302 | 97 | 5 | 26 | 52 | 17 | 716 | 16 | 1 | 0 | 0 | 0 | 1 | 358 | 0 | 44 | 701 | 16 | 18 |
| 50 | −1 | 417 | 25 | 26 | 33 | 31 | 34 | 334 | 62 | 4 | 30 | 47 | 16 | 795 | 16 | 1 | 1 | 0 | 0 | 1 | 405 | 1 | 41 | 789 | 16 | 18 |
| 55 | −1 | 373 | 27 | 28 | 34 | 33 | 38 | 364 | 44 | 4 | 33 | 43 | 15 | 868 | 16 | 1 | 1 | 0 | 0 | 1 | 445 | 1 | 38 | 867 | 16 | 16 |
| 60 | −1 | 340 | 28 | 30 | 35 | 35 | 41 | 393 | 33 | 3 | 35 | 40 | 14 | 937 | 16 | 1 | 1 | 0 | 0 | 1 | 482 | 1 | 35 | 938 | 16 | 14 |
| 65 | −1 | 313 | 30 | 31 | 36 | 37 | 44 | 420 | 27 | 3 | 37 | 37 | 13 | 1001 | 15 | 1 | 1 | 0 | 0 | 2 | 514 | 1 | 33 | 1003 | 15 | 13 |
| 70 | −1 | 291 | 31 | 32 | 36 | 39 | 47 | 447 | 22 | 3 | 39 | 34 | 12 | 1061 | 15 | 1 | 1 | 0 | 0 | 2 | 541 | 1 | 30 | 1060 | 15 | 11 |
| 75 | −1 | 272 | 32 | 33 | 36 | 41 | 50 | 471 | 18 | 2 | 41 | 32 | 11 | 1118 | 15 | 2 | 2 | 0 | 0 | 2 | 569 | 2 | 27 | 1115 | 15 | 11 |
| 80 | −1 | 257 | 33 | 34 | 37 | 42 | 52 | 495 | 15 | 2 | 43 | 30 | 11 | 1172 | 15 | 2 | 2 | 0 | 0 | 2 | 598 | 2 | 26 | 1169 | 15 | 11 |
| 85 | −1 | 245 | 34 | 35 | 37 | 44 | 55 | 517 | 13 | 2 | 45 | 29 | 10 | 1223 | 14 | 2 | 2 | 0 | 0 | 3 | 625 | 2 | 26 | 1222 | 14 | 11 |
| 90 | −1 | 234 | 34 | 36 | 37 | 45 | 58 | 539 | 11 | 2 | 48 | 27 | 10 | 1272 | 14 | 2 | 2 | 0 | 0 | 3 | 648 | 2 | 24 | 1269 | 14 | 9 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | - | 3 | 3 | 5 | 2 | 3 | 24 | 541 | 3 | 2 | 17 | 5 | 40 | 2 | 0 | 0 | 0 | 0 | 0 | 28 | 0 | 13 | 28 | 1 | 6 |
| 10 | 0 | - | 5 | 6 | 9 | 4 | 7 | 48 | 1082 | 6 | 4 | 34 | 11 | 81 | 4 | 0 | 0 | 0 | 0 | 0 | 56 | 0 | 27 | 56 | 3 | 12 |
| 15 | 0 | - | 8 | 9 | 14 | 6 | 10 | 72 | 1622 | 9 | 6 | 50 | 16 | 122 | 6 | 0 | 0 | 0 | 0 | 0 | 83 | 0 | 40 | 83 | 4 | 18 |
| 20 | 0 | 3404 | 10 | 11 | 18 | 8 | 13 | 96 | 2163 | 12 | 8 | 67 | 21 | 162 | 8 | 0 | 0 | 0 | 0 | 0 | 111 | 0 | 54 | 111 | 6 | 24 |
| 25 | 0 | 2196 | 13 | 14 | 22 | 11 | 16 | 133 | 1207 | 10 | 10 | 65 | 20 | 264 | 11 | 0 | 0 | 0 | 0 | 0 | 151 | 0 | 58 | 263 | 11 | 30 |
| 30 | 0 | 1515 | 15 | 16 | 24 | 14 | 20 | 167 | 682 | 8 | 12 | 60 | 19 | 359 | 12 | 0 | 0 | 0 | 0 | 0 | 175 | 0 | 49 | 335 | 11 | 14 |
| 35 | 0 | 1132 | 17 | 18 | 27 | 17 | 23 | 200 | 383 | 7 | 15 | 55 | 18 | 447 | 13 | 0 | 0 | 0 | 0 | 0 | 211 | 0 | 44 | 416 | 12 | 16 |
| 40 | 0 | 850 | 19 | 20 | 28 | 20 | 26 | 230 | 282 | 6 | 16 | 51 | 16 | 529 | 13 | 0 | 0 | 0 | 0 | 0 | 245 | 0 | 40 | 489 | 12 | 15 |
| 45 | 0 | 680 | 20 | 22 | 30 | 23 | 29 | 259 | 170 | 5 | 20 | 47 | 15 | 605 | 13 | 0 | 0 | 0 | 0 | 0 | 287 | 0 | 38 | 569 | 13 | 16 |
| 50 | 0 | 574 | 22 | 23 | 31 | 26 | 32 | 287 | 107 | 4 | 23 | 43 | 14 | 675 | 14 | 0 | 0 | 0 | 0 | 1 | 330 | 0 | 36 | 648 | 13 | 16 |
| 55 | 0 | 503 | 24 | 25 | 32 | 28 | 35 | 313 | 71 | 4 | 26 | 40 | 13 | 742 | 14 | 1 | 0 | 0 | 0 | 1 | 369 | 0 | 34 | 721 | 13 | 15 |
| 60 | 0 | 451 | 25 | 26 | 33 | 30 | 37 | 338 | 51 | 4 | 29 | 37 | 12 | 804 | 13 | 1 | 1 | 0 | 0 | 1 | 403 | 1 | 33 | 788 | 13 | 13 |
| 65 | 0 | 412 | 26 | 27 | 34 | 31 | 40 | 361 | 39 | 3 | 32 | 35 | 12 | 863 | 13 | 1 | 1 | 0 | 0 | 1 | 434 | 1 | 31 | 849 | 13 | 12 |
| 70 | 0 | 380 | 27 | 28 | 34 | 33 | 42 | 384 | 32 | 3 | 34 | 33 | 11 | 918 | 13 | 1 | 1 | 0 | 0 | 1 | 465 | 1 | 29 | 910 | 13 | 12 |
| 75 | 0 | 354 | 28 | 29 | 35 | 35 | 45 | 405 | 26 | 3 | 36 | 31 | 10 | 971 | 13 | 1 | 1 | 0 | 0 | 1 | 493 | 1 | 28 | 966 | 13 | 11 |
| 80 | 0 | 332 | 29 | 30 | 35 | 36 | 47 | 426 | 22 | 2 | 38 | 30 | 10 | 1021 | 13 | 1 | 1 | 0 | 0 | 2 | 520 | 1 | 27 | 1019 | 13 | 11 |
| 85 | 0 | 315 | 30 | 31 | 36 | 38 | 50 | 445 | 18 | 2 | 40 | 28 | 10 | 1069 | 13 | 1 | 1 | 0 | 0 | 2 | 548 | 1 | 26 | 1073 | 13 | 11 |
| 90 | 0 | 299 | 30 | 32 | 36 | 39 | 52 | 464 | 15 | 2 | 42 | 27 | 9 | 1114 | 12 | 1 | 2 | 0 | 0 | 2 | 571 | 2 | 24 | 1120 | 12 | 9 |
| 95 | 0 | 286 | 31 | 32 | 36 | 40 | 54 | 481 | 13 | 2 | 44 | 26 | 9 | 1158 | 12 | 1 | 2 | 0 | 0 | 2 | 590 | 2 | 23 | 1162 | 12 | 9 |
| 100 | 0 | 275 | 32 | 33 | 36 | 41 | 56 | 498 | 11 | 2 | 45 | 25 | 8 | 1199 | 12 | 2 | 2 | 0 | 0 | 2 | 609 | 2 | 21 | 1202 | 12 | 8 |
| 105 | 0 | 265 | 32 | 34 | 36 | 42 | 58 | 514 | 10 | 2 | 47 | 24 | 8 | 1239 | 12 | 2 | 2 | 0 | 0 | 2 | 627 | 2 | 21 | 1241 | 12 | 8 |
| 110 | 0 | 256 | 33 | 34 | 36 | 43 | 60 | 530 | 9 | 2 | 49 | 23 | 8 | 1278 | 12 | 2 | 2 | 0 | 0 | 3 | 645 | 2 | 20 | 1280 | 12 | 8 |
| 115 | 0 | 248 | 33 | 34 | 36 | 44 | 62 | 544 | 8 | 2 | 50 | 22 | 7 | 1315 | 11 | 2 | 2 | 0 | 0 | 3 | 658 | 2 | 19 | 1312 | 11 | 6 |
| 120 | 0 | 240 | 34 | 35 | 36 | 44 | 64 | 558 | 8 | 2 | 50 | 22 | 7 | 1350 | 11 | 2 | 2 | 0 | 1 | 3 | 668 | 2 | 20 | 1342 | 11 | 6 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | - | 2 | 2 | 4 | 2 | 3 | 21 | 309 | 2 | 2 | 10 | 3 | 31 | 1 | 0 | 0 | 0 | 0 | 0 | 23 | 0 | 8 | 23 | 1 | 4 |
| 10 | 1 | - | 4 | 5 | 7 | 4 | 6 | 43 | 617 | 4 | 3 | 20 | 7 | 62 | 2 | 0 | 0 | 0 | 0 | 0 | 45 | 0 | 15 | 45 | 2 | 8 |
| 15 | 1 | - | 6 | 7 | 11 | 5 | 9 | 64 | 926 | 5 | 5 | 29 | 10 | 94 | 4 | 0 | 0 | 0 | 0 | 0 | 68 | 0 | 23 | 68 | 3 | 12 |
| 20 | 1 | - | 8 | 9 | 15 | 7 | 12 | 86 | 1234 | 7 | 7 | 39 | 13 | 125 | 5 | 0 | 0 | 0 | 0 | 0 | 91 | 0 | 31 | 91 | 4 | 16 |
| 25 | 1 | 3141 | 10 | 12 | 19 | 9 | 15 | 107 | 1543 | 9 | 8 | 49 | 16 | 156 | 6 | 0 | 0 | 0 | 0 | 0 | 113 | 0 | 38 | 113 | 5 | 20 |
| 30 | 1 | 2195 | 12 | 14 | 21 | 11 | 18 | 137 | 947 | 8 | 10 | 49 | 16 | 234 | 8 | 0 | 0 | 0 | 0 | 0 | 150 | 0 | 44 | 232 | 8 | 24 |
| 35 | 1 | 1609 | 14 | 16 | 24 | 14 | 21 | 165 | 586 | 7 | 12 | 46 | 15 | 309 | 9 | 0 | 0 | 0 | 0 | 0 | 170 | 0 | 38 | 291 | 8 | 12 |
| 40 | 1 | 1245 | 16 | 17 | 26 | 16 | 24 | 191 | 364 | 6 | 14 | 44 | 14 | 379 | 10 | 0 | 0 | 0 | 0 | 0 | 201 | 0 | 35 | 356 | 9 | 13 |
| 45 | 1 | 1018 | 18 | 19 | 27 | 18 | 26 | 216 | 227 | 5 | 17 | 41 | 13 | 445 | 10 | 0 | 0 | 0 | 0 | 0 | 233 | 0 | 33 | 421 | 9 | 13 |
| 50 | 1 | 829 | 19 | 20 | 28 | 20 | 29 | 239 | 188 | 4 | 17 | 39 | 12 | 507 | 10 | 0 | 0 | 0 | 0 | 0 | 259 | 0 | 31 | 478 | 10 | 11 |
| 55 | 1 | 703 | 20 | 22 | 30 | 23 | 31 | 261 | 126 | 4 | 20 | 37 | 12 | 566 | 10 | 0 | 0 | 0 | 0 | 0 | 292 | 0 | 30 | 542 | 10 | 13 |
| 60 | 1 | 615 | 22 | 23 | 30 | 25 | 34 | 282 | 88 | 4 | 23 | 35 | 11 | 622 | 10 | 0 | 0 | 0 | 0 | 1 | 325 | 0 | 29 | 604 | 10 | 12 |
| 65 | 1 | 550 | 23 | 24 | 31 | 26 | 36 | 302 | 65 | 3 | 25 | 33 | 11 | 674 | 10 | 0 | 0 | 0 | 0 | 1 | 358 | 0 | 28 | 664 | 10 | 12 |
| 70 | 1 | 500 | 24 | 25 | 32 | 28 | 38 | 321 | 50 | 3 | 28 | 31 | 10 | 725 | 10 | 1 | 1 | 0 | 0 | 1 | 384 | 1 | 28 | 718 | 10 | 11 |
| 75 | 1 | 461 | 24 | 26 | 33 | 30 | 40 | 340 | 39 | 3 | 30 | 30 | 10 | 773 | 10 | 1 | 1 | 0 | 0 | 1 | 413 | 1 | 26 | 774 | 10 | 11 |
| 80 | 1 | 430 | 25 | 26 | 33 | 31 | 42 | 357 | 31 | 3 | 32 | 28 | 9 | 818 | 10 | 1 | 1 | 0 | 0 | 1 | 441 | 1 | 25 | 826 | 10 | 11 |
| 85 | 1 | 405 | 26 | 27 | 34 | 32 | 44 | 374 | 25 | 2 | 35 | 27 | 9 | 862 | 10 | 1 | 1 | 0 | 0 | 1 | 469 | 1 | 24 | 879 | 10 | 11 |
| 90 | 1 | 383 | 27 | 28 | 34 | 33 | 46 | 389 | 21 | 2 | 37 | 26 | 8 | 904 | 10 | 1 | 1 | 0 | 0 | 1 | 491 | 1 | 24 | 925 | 10 | 9 |
| 95 | 1 | 365 | 27 | 28 | 34 | 34 | 48 | 405 | 18 | 2 | 39 | 25 | 8 | 945 | 10 | 1 | 1 | 0 | 0 | 1 | 511 | 1 | 23 | 967 | 10 | 9 |
| 100 | 1 | 349 | 28 | 29 | 34 | 35 | 50 | 419 | 16 | 2 | 40 | 24 | 8 | 983 | 10 | 1 | 1 | 0 | 0 | 2 | 531 | 1 | 23 | 1010 | 10 | 9 |
| 105 | 1 | 335 | 28 | 30 | 35 | 36 | 51 | 433 | 14 | 2 | 42 | 23 | 8 | 1021 | 10 | 1 | 2 | 0 | 0 | 2 | 548 | 2 | 22 | 1049 | 10 | 8 |
| 110 | 1 | 323 | 29 | 30 | 35 | 37 | 53 | 446 | 12 | 2 | 44 | 23 | 7 | 1057 | 10 | 1 | 2 | 0 | 0 | 2 | 568 | 2 | 20 | 1090 | 10 | 8 |
| 115 | 1 | 312 | 29 | 30 | 35 | 38 | 55 | 459 | 11 | 2 | 45 | 22 | 7 | 1092 | 10 | 1 | 2 | 0 | 0 | 2 | 581 | 2 | 20 | 1122 | 10 | 7 |
| 120 | 1 | 301 | 30 | 31 | 35 | 39 | 56 | 471 | 10 | 2 | 46 | 21 | 7 | 1125 | 9 | 1 | 2 | 0 | 0 | 2 | 592 | 2 | 19 | 1153 | 10 | 6 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | - | 2 | 2 | 3 | 1 | 3 | 18 | 210 | 1 | 1 | 6 | 2 | 23 | 1 | 0 | 0 | 0 | 0 | 0 | 19 | 0 | 5 | 19 | 1 | 2 |
| 10 | 2 | - | 3 | 4 | 6 | 3 | 5 | 35 | 420 | 2 | 3 | 12 | 4 | 47 | 2 | 0 | 0 | 0 | 0 | 0 | 37 | 0 | 9 | 37 | 1 | 5 |
| 15 | 2 | - | 5 | 6 | 9 | 4 | 8 | 52 | 630 | 3 | 4 | 18 | 6 | 70 | 2 | 0 | 0 | 0 | 0 | 0 | 56 | 0 | 14 | 56 | 2 | 7 |
| 20 | 2 | - | 7 | 8 | 12 | 6 | 11 | 70 | 839 | 4 | 5 | 23 | 8 | 93 | 3 | 0 | 0 | 0 | 0 | 0 | 75 | 0 | 19 | 75 | 2 | 10 |
| 25 | 2 | - | 8 | 10 | 15 | 7 | 14 | 88 | 1049 | 5 | 7 | 29 | 10 | 117 | 4 | 0 | 0 | 0 | 0 | 0 | 93 | 0 | 23 | 93 | 3 | 12 |
| 30 | 2 | 3310 | 10 | 12 | 18 | 9 | 16 | 105 | 1259 | 6 | 8 | 35 | 12 | 140 | 5 | 0 | 0 | 0 | 0 | 0 | 112 | 0 | 28 | 112 | 4 | 15 |
| 35 | 2 | 2471 | 12 | 13 | 20 | 11 | 19 | 129 | 839 | 6 | 10 | 36 | 12 | 200 | 6 | 0 | 0 | 0 | 0 | 0 | 143 | 0 | 27 | 198 | 6 | 17 |
| 40 | 2 | 1904 | 13 | 15 | 22 | 12 | 21 | 151 | 566 | 5 | 11 | 36 | 12 | 258 | 6 | 0 | 0 | 0 | 0 | 0 | 161 | 0 | 30 | 246 | 6 | 10 |
| 45 | 2 | 1520 | 15 | 16 | 24 | 14 | 23 | 172 | 385 | 5 | 13 | 35 | 11 | 314 | 7 | 0 | 0 | 0 | 0 | 0 | 183 | 0 | 28 | 296 | 7 | 10 |
| 50 | 2 | 1257 | 16 | 17 | 25 | 16 | 26 | 192 | 263 | 4 | 15 | 33 | 11 | 367 | 7 | 0 | 0 | 0 | 0 | 0 | 206 | 0 | 27 | 346 | 7 | 10 |
| 55 | 2 | 1075 | 17 | 18 | 26 | 18 | 28 | 210 | 181 | 4 | 17 | 32 | 10 | 418 | 8 | 0 | 0 | 0 | 0 | 0 | 234 | 0 | 26 | 400 | 7 | 11 |
| 60 | 2 | 914 | 18 | 19 | 28 | 20 | 30 | 228 | 161 | 4 | 17 | 31 | 10 | 466 | 8 | 0 | 0 | 0 | 0 | 0 | 251 | 0 | 24 | 441 | 7 | 8 |
| 65 | 2 | 795 | 19 | 20 | 28 | 21 | 31 | 244 | 119 | 3 | 19 | 30 | 9 | 513 | 8 | 0 | 0 | 0 | 0 | 0 | 279 | 0 | 24 | 493 | 8 | 10 |
| 70 | 2 | 705 | 20 | 21 | 29 | 23 | 33 | 260 | 90 | 3 | 21 | 28 | 9 | 557 | 8 | 0 | 0 | 0 | 0 | 0 | 304 | 0 | 24 | 542 | 8 | 10 |
| 75 | 2 | 636 | 21 | 22 | 30 | 24 | 35 | 275 | 69 | 3 | 23 | 27 | 8 | 600 | 8 | 0 | 0 | 0 | 0 | 1 | 329 | 0 | 23 | 591 | 8 | 10 |
| 80 | 2 | 582 | 22 | 23 | 31 | 26 | 37 | 290 | 54 | 3 | 26 | 26 | 8 | 640 | 8 | 0 | 0 | 0 | 0 | 1 | 354 | 0 | 23 | 639 | 8 | 10 |
| 85 | 2 | 540 | 22 | 23 | 31 | 27 | 38 | 304 | 42 | 3 | 28 | 25 | 8 | 680 | 8 | 1 | 1 | 0 | 0 | 1 | 380 | 1 | 23 | 687 | 8 | 10 |
| 90 | 2 | 506 | 23 | 24 | 32 | 28 | 40 | 317 | 34 | 2 | 30 | 25 | 8 | 718 | 8 | 1 | 1 | 0 | 0 | 1 | 403 | 1 | 22 | 733 | 8 | 9 |
| 95 | 2 | 477 | 23 | 24 | 32 | 29 | 41 | 330 | 28 | 2 | 32 | 24 | 7 | 754 | 8 | 1 | 1 | 0 | 0 | 1 | 424 | 1 | 22 | 775 | 8 | 9 |
| 100 | 2 | 453 | 24 | 25 | 32 | 30 | 43 | 342 | 24 | 2 | 34 | 23 | 7 | 790 | 8 | 1 | 1 | 0 | 0 | 1 | 446 | 1 | 22 | 819 | 8 | 9 |
| 105 | 2 | 432 | 24 | 25 | 33 | 31 | 44 | 354 | 21 | 2 | 36 | 22 | 7 | 824 | 8 | 1 | 1 | 0 | 0 | 1 | 465 | 1 | 22 | 860 | 8 | 8 |
| 110 | 2 | 414 | 25 | 26 | 33 | 32 | 46 | 365 | 18 | 2 | 38 | 22 | 7 | 857 | 8 | 1 | 1 | 0 | 0 | 1 | 482 | 1 | 21 | 898 | 8 | 8 |
| 115 | 2 | 398 | 25 | 26 | 33 | 33 | 47 | 376 | 16 | 2 | 39 | 21 | 6 | 889 | 8 | 1 | 1 | 0 | 0 | 1 | 498 | 1 | 20 | 934 | 8 | 7 |
| 120 | 2 | 383 | 25 | 26 | 33 | 34 | 48 | 386 | 15 | 2 | 40 | 21 | 6 | 920 | 8 | 1 | 1 | 0 | 0 | 1 | 509 | 1 | 20 | 965 | 8 | 6 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | - | 1 | 1 | 2 | 1 | 2 | 14 | 102 | 1 | 1 | 3 | 1 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 3 | 16 | 0 | 1 |
| 10 | 3 | - | 3 | 3 | 5 | 2 | 5 | 28 | 205 | 1 | 2 | 6 | 2 | 34 | 1 | 0 | 0 | 0 | 0 | 0 | 31 | 0 | 5 | 31 | 1 | 3 |
| 15 | 3 | - | 4 | 4 | 7 | 4 | 7 | 42 | 308 | 2 | 3 | 10 | 3 | 52 | 1 | 0 | 0 | 0 | 0 | 0 | 47 | 0 | 8 | 47 | 1 | 4 |
| 20 | 3 | - | 5 | 6 | 9 | 5 | 9 | 56 | 410 | 2 | 4 | 13 | 5 | 69 | 2 | 0 | 0 | 0 | 0 | 0 | 63 | 0 | 10 | 63 | 2 | 6 |
| 25 | 3 | - | 7 | 7 | 11 | 6 | 11 | 70 | 512 | 3 | 5 | 16 | 6 | 86 | 2 | 0 | 0 | 0 | 0 | 0 | 79 | 0 | 13 | 79 | 2 | 7 |
| 30 | 3 | - | 8 | 9 | 14 | 7 | 14 | 84 | 615 | 4 | 6 | 20 | 7 | 104 | 3 | 0 | 0 | 0 | 0 | 0 | 94 | 0 | 15 | 94 | 2 | 9 |
| 35 | 3 | - | 9 | 10 | 16 | 8 | 16 | 98 | 718 | 4 | 7 | 23 | 8 | 121 | 3 | 0 | 0 | 0 | 0 | 0 | 110 | 0 | 18 | 110 | 3 | 10 |
| 40 | 3 | 3023 | 11 | 12 | 18 | 10 | 18 | 112 | 820 | 5 | 8 | 26 | 9 | 138 | 3 | 0 | 0 | 0 | 0 | 0 | 126 | 0 | 20 | 126 | 3 | 11 |
| 45 | 3 | 2428 | 12 | 13 | 20 | 11 | 20 | 129 | 596 | 4 | 10 | 27 | 9 | 182 | 4 | 0 | 0 | 0 | 0 | 0 | 149 | 0 | 21 | 190 | 4 | 13 |
| 50 | 3 | 1991 | 13 | 14 | 21 | 12 | 22 | 145 | 437 | 4 | 11 | 27 | 9 | 225 | 4 | 0 | 0 | 0 | 0 | 0 | 167 | 0 | 23 | 231 | 5 | 8 |
| 55 | 3 | 1668 | 14 | 15 | 23 | 14 | 24 | 161 | 323 | 4 | 12 | 27 | 8 | 267 | 5 | 0 | 0 | 0 | 0 | 0 | 181 | 0 | 22 | 267 | 5 | 7 |
| 60 | 3 | 1428 | 15 | 16 | 24 | 15 | 25 | 175 | 240 | 4 | 14 | 26 | 8 | 308 | 5 | 0 | 0 | 0 | 0 | 0 | 198 | 0 | 21 | 305 | 5 | 8 |
| 65 | 3 | 1247 | 16 | 17 | 25 | 16 | 27 | 189 | 181 | 3 | 16 | 25 | 8 | 347 | 5 | 0 | 0 | 0 | 0 | 0 | 217 | 0 | 20 | 345 | 5 | 8 |
| 70 | 3 | 1110 | 16 | 18 | 26 | 18 | 28 | 202 | 137 | 3 | 17 | 25 | 8 | 384 | 6 | 0 | 0 | 0 | 0 | 0 | 238 | 0 | 20 | 385 | 6 | 8 |
| 75 | 3 | 1005 | 17 | 18 | 26 | 19 | 30 | 214 | 105 | 3 | 19 | 24 | 7 | 421 | 6 | 0 | 0 | 0 | 0 | 0 | 259 | 0 | 20 | 426 | 6 | 8 |
| 80 | 3 | 902 | 18 | 19 | 27 | 20 | 31 | 226 | 104 | 3 | 19 | 23 | 7 | 456 | 6 | 0 | 0 | 0 | 0 | 0 | 269 | 0 | 19 | 456 | 6 | 6 |
| 85 | 3 | 819 | 18 | 20 | 28 | 21 | 32 | 237 | 82 | 3 | 20 | 23 | 7 | 490 | 6 | 0 | 0 | 0 | 0 | 0 | 288 | 0 | 19 | 494 | 6 | 8 |
| 90 | 3 | 753 | 19 | 20 | 28 | 22 | 34 | 248 | 66 | 3 | 22 | 22 | 7 | 523 | 6 | 0 | 0 | 0 | 0 | 0 | 308 | 0 | 19 | 533 | 6 | 8 |
| 95 | 3 | 699 | 19 | 21 | 29 | 24 | 35 | 258 | 54 | 2 | 24 | 22 | 6 | 555 | 6 | 0 | 0 | 0 | 0 | 0 | 329 | 0 | 19 | 573 | 6 | 8 |
| 100 | 3 | 653 | 20 | 21 | 29 | 24 | 36 | 268 | 45 | 2 | 26 | 21 | 6 | 586 | 6 | 0 | 0 | 0 | 0 | 1 | 344 | 0 | 19 | 607 | 6 | 7 |
| 105 | 3 | 615 | 20 | 21 | 30 | 25 | 37 | 277 | 38 | 2 | 27 | 21 | 6 | 616 | 6 | 0 | 0 | 0 | 0 | 1 | 360 | 0 | 19 | 642 | 6 | 7 |
| 110 | 3 | 582 | 20 | 22 | 30 | 26 | 38 | 287 | 33 | 2 | 29 | 20 | 6 | 645 | 6 | 0 | 1 | 0 | 0 | 1 | 377 | 1 | 19 | 677 | 6 | 7 |
| 115 | 3 | 554 | 21 | 22 | 31 | 27 | 39 | 295 | 28 | 2 | 31 | 20 | 6 | 674 | 6 | 0 | 1 | 0 | 0 | 1 | 392 | 1 | 18 | 711 | 6 | 7 |
| 120 | 3 | 529 | 21 | 22 | 31 | 28 | 40 | 304 | 25 | 2 | 32 | 19 | 6 | 701 | 6 | 1 | 1 | 0 | 0 | 1 | 408 | 1 | 18 | 745 | 6 | 7 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | −1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | −1 | - | 4 | 5 | 7 | 4 | 4 | 26 | 0 | 0 | 0 | 0 | 6 | 33 | 2 | 0 | 0 | 0 | 0 | 0 | 38 | 0 | 0 | 38 | 3 | 3 |
| 10 | −1 | - | 8 | 9 | 13 | 9 | 9 | 53 | 1 | 0 | 0 | 0 | 11 | 65 | 4 | 0 | 0 | 0 | 0 | 0 | 76 | 0 | 0 | 76 | 5 | 6 |
| 15 | −1 | 1091 | 12 | 14 | 20 | 14 | 13 | 79 | 1 | 0 | 0 | 0 | 17 | 98 | 7 | 0 | 0 | 0 | 0 | 0 | 115 | 0 | 0 | 115 | 8 | 9 |
| 20 | −1 | 524 | 17 | 19 | 27 | 21 | 20 | 188 | 567 | 3 | 8 | 20 | 26 | 230 | 12 | 0 | 0 | 0 | 0 | 0 | 162 | 0 | 12 | 174 | 9 | 12 |
| 25 | −1 | 275 | 22 | 24 | 33 | 30 | 27 | 306 | 249 | 4 | 13 | 40 | 31 | 386 | 16 | 1 | 0 | 0 | 0 | 1 | 192 | 0 | 38 | 242 | 10 | 14 |
| 30 | −1 | 266 | 26 | 28 | 38 | 36 | 33 | 417 | 7 | 5 | 27 | 57 | 34 | 554 | 18 | 1 | 1 | 0 | 0 | 1 | 311 | 1 | 4 | 366 | 12 | 25 |
| 35 | −1 | 269 | 29 | 31 | 43 | 40 | 40 | 517 | 1 | 6 | 41 | 71 | 35 | 727 | 21 | 1 | 1 | 0 | 0 | 2 | 451 | 1 | 1 | 508 | 15 | 28 |
| 40 | −1 | 272 | 32 | 34 | 47 | 43 | 46 | 610 | 1 | 6 | 57 | 83 | 35 | 903 | 23 | 2 | 3 | 0 | 0 | 2 | 618 | 3 | 3 | 677 | 17 | 34 |
| 45 | −1 | 262 | 35 | 37 | 50 | 46 | 52 | 692 | 10 | 6 | 63 | 89 | 34 | 1075 | 24 | 2 | 4 | 0 | 1 | 3 | 728 | 4 | 39 | 827 | 18 | 30 |
| 50 | −1 | 241 | 37 | 40 | 52 | 49 | 58 | 768 | 23 | 6 | 58 | 93 | 34 | 1245 | 25 | 2 | 3 | 0 | 0 | 3 | 759 | 3 | 77 | 934 | 19 | 22 |
| 55 | −1 | 210 | 39 | 42 | 55 | 53 | 64 | 835 | 28 | 6 | 52 | 96 | 33 | 1409 | 26 | 3 | 3 | 0 | 0 | 4 | 761 | 3 | 79 | 1016 | 18 | 16 |
| 60 | −1 | 181 | 41 | 44 | 57 | 57 | 69 | 897 | 29 | 6 | 51 | 97 | 32 | 1567 | 26 | 4 | 3 | 0 | 0 | 4 | 787 | 3 | 83 | 1125 | 19 | 22 |
| 65 | −1 | 155 | 43 | 46 | 58 | 62 | 75 | 955 | 26 | 6 | 54 | 98 | 31 | 1723 | 26 | 4 | 3 | 0 | 0 | 5 | 817 | 3 | 86 | 1241 | 19 | 23 |
| 70 | −1 | 135 | 45 | 47 | 60 | 66 | 80 | 1006 | 21 | 6 | 58 | 98 | 30 | 1872 | 27 | 5 | 4 | 1 | 0 | 6 | 856 | 4 | 85 | 1366 | 20 | 25 |
| 75 | −1 | 118 | 46 | 49 | 61 | 70 | 85 | 1053 | 16 | 5 | 62 | 96 | 29 | 2016 | 27 | 6 | 5 | 1 | 0 | 7 | 880 | 5 | 79 | 1468 | 20 | 20 |
| 80 | −1 | 106 | 48 | 50 | 62 | 74 | 90 | 1098 | 12 | 5 | 67 | 95 | 28 | 2154 | 27 | 7 | 6 | 1 | 1 | 9 | 916 | 6 | 70 | 1574 | 20 | 21 |
| 85 | −1 | 96 | 49 | 52 | 63 | 78 | 95 | 1137 | 10 | 5 | 71 | 94 | 27 | 2289 | 27 | 8 | 7 | 1 | 1 | 10 | 954 | 7 | 69 | 1681 | 20 | 21 |
| 90 | −1 | 85 | 50 | 53 | 63 | 82 | 99 | 1175 | 8 | 5 | 74 | 93 | 26 | 2419 | 27 | 10 | 8 | 1 | 1 | 11 | 960 | 8 | 61 | 1748 | 19 | 13 |
| 95 | −1 | 78 | 51 | 54 | 64 | 86 | 104 | 1211 | 9 | 4 | 74 | 90 | 25 | 2545 | 27 | 11 | 8 | 1 | 1 | 13 | 998 | 8 | 70 | 1856 | 20 | 22 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | - | 3 | 4 | 5 | 4 | 4 | 18 | 0 | 0 | 0 | 0 | 4 | 22 | 2 | 0 | 0 | 0 | 0 | 0 | 34 | 0 | 0 | 34 | 2 | 5 |
| 10 | 0 | - | 6 | 7 | 11 | 7 | 8 | 37 | 1 | 0 | 0 | 0 | 8 | 45 | 3 | 0 | 0 | 0 | 0 | 0 | 67 | 0 | 0 | 67 | 4 | 10 |
| 15 | 0 | 1815 | 9 | 11 | 16 | 11 | 12 | 55 | 1 | 0 | 0 | 0 | 12 | 67 | 4 | 0 | 0 | 0 | 0 | 0 | 101 | 0 | 0 | 101 | 7 | 15 |
| 20 | 0 | 1069 | 14 | 16 | 23 | 16 | 18 | 143 | 746 | 2 | 6 | 15 | 21 | 172 | 9 | 0 | 0 | 0 | 0 | 0 | 187 | 0 | 11 | 198 | 10 | 19 |
| 25 | 0 | 674 | 18 | 20 | 29 | 23 | 24 | 242 | 395 | 4 | 11 | 32 | 26 | 302 | 12 | 0 | 0 | 0 | 0 | 0 | 272 | 0 | 39 | 322 | 13 | 25 |
| 30 | 0 | 517 | 22 | 24 | 34 | 29 | 30 | 338 | 156 | 5 | 20 | 48 | 29 | 446 | 15 | 1 | 0 | 0 | 0 | 1 | 367 | 0 | 50 | 468 | 16 | 29 |
| 35 | 0 | 442 | 25 | 28 | 39 | 33 | 36 | 427 | 75 | 6 | 31 | 61 | 30 | 597 | 17 | 1 | 1 | 0 | 0 | 1 | 471 | 1 | 56 | 627 | 18 | 32 |
| 40 | 0 | 401 | 28 | 30 | 42 | 37 | 41 | 510 | 41 | 6 | 43 | 71 | 31 | 751 | 19 | 1 | 1 | 0 | 0 | 1 | 586 | 1 | 61 | 803 | 20 | 35 |
| 45 | 0 | 371 | 31 | 33 | 46 | 40 | 47 | 585 | 30 | 6 | 51 | 77 | 30 | 903 | 20 | 1 | 2 | 0 | 0 | 2 | 689 | 2 | 65 | 971 | 22 | 34 |
| 50 | 0 | 343 | 33 | 36 | 48 | 42 | 52 | 654 | 29 | 6 | 52 | 81 | 30 | 1054 | 21 | 2 | 2 | 0 | 0 | 2 | 751 | 2 | 70 | 1104 | 22 | 26 |
| 55 | 0 | 313 | 35 | 38 | 50 | 45 | 58 | 717 | 29 | 6 | 50 | 84 | 29 | 1201 | 22 | 2 | 2 | 0 | 0 | 3 | 793 | 2 | 71 | 1216 | 22 | 23 |
| 60 | 0 | 284 | 37 | 40 | 52 | 48 | 63 | 775 | 29 | 6 | 50 | 85 | 29 | 1344 | 22 | 2 | 3 | 0 | 0 | 3 | 836 | 3 | 73 | 1333 | 22 | 23 |
| 65 | 0 | 257 | 39 | 41 | 54 | 52 | 68 | 829 | 27 | 6 | 51 | 86 | 28 | 1484 | 23 | 3 | 3 | 0 | 0 | 3 | 889 | 3 | 74 | 1460 | 22 | 25 |
| 70 | 0 | 233 | 40 | 43 | 56 | 55 | 72 | 878 | 24 | 5 | 53 | 86 | 27 | 1619 | 23 | 3 | 3 | 0 | 0 | 4 | 938 | 3 | 74 | 1583 | 23 | 25 |
| 75 | 0 | 212 | 42 | 44 | 57 | 58 | 77 | 923 | 21 | 5 | 56 | 85 | 26 | 1750 | 23 | 4 | 4 | 0 | 0 | 5 | 996 | 4 | 75 | 1715 | 23 | 26 |
| 80 | 0 | 194 | 43 | 46 | 58 | 62 | 82 | 966 | 18 | 5 | 59 | 84 | 25 | 1876 | 24 | 4 | 4 | 0 | 0 | 5 | 1045 | 4 | 73 | 1837 | 23 | 24 |
| 85 | 0 | 178 | 44 | 47 | 58 | 65 | 87 | 1005 | 16 | 5 | 62 | 83 | 24 | 1999 | 24 | 5 | 5 | 1 | 0 | 6 | 1089 | 5 | 74 | 1955 | 23 | 24 |
| 90 | 0 | 163 | 45 | 48 | 59 | 68 | 91 | 1042 | 14 | 5 | 64 | 82 | 24 | 2118 | 24 | 6 | 5 | 1 | 1 | 7 | 1127 | 5 | 71 | 2064 | 23 | 22 |
| 95 | 0 | 150 | 46 | 49 | 60 | 71 | 95 | 1077 | 14 | 4 | 64 | 80 | 23 | 2233 | 24 | 7 | 5 | 1 | 1 | 8 | 1173 | 5 | 73 | 2183 | 23 | 24 |
| 100 | 0 | 137 | 47 | 50 | 60 | 75 | 100 | 1112 | 14 | 4 | 64 | 78 | 22 | 2348 | 24 | 7 | 5 | 1 | 1 | 9 | 1201 | 5 | 75 | 2286 | 23 | 21 |
| 105 | 0 | 124 | 48 | 51 | 61 | 78 | 104 | 1147 | 14 | 4 | 65 | 76 | 22 | 2463 | 24 | 8 | 5 | 1 | 1 | 10 | 1221 | 5 | 77 | 2382 | 23 | 19 |
| 110 | 0 | 111 | 49 | 52 | 62 | 82 | 109 | 1182 | 14 | 4 | 65 | 74 | 21 | 2578 | 24 | 10 | 6 | 1 | 1 | 11 | 1225 | 6 | 78 | 2464 | 22 | 16 |
| 115 | 0 | 98 | 50 | 53 | 63 | 85 | 113 | 1217 | 14 | 4 | 65 | 72 | 20 | 2693 | 24 | 11 | 6 | 1 | 1 | 12 | 1199 | 6 | 80 | 2519 | 22 | 11 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | - | 3 | 3 | 5 | 3 | 4 | 24 | 231 | 0 | 1 | 2 | 4 | 28 | 1 | 0 | 0 | 0 | 0 | 0 | 33 | 0 | 2 | 33 | 2 | 4 |
| 10 | 1 | - | 6 | 6 | 9 | 6 | 8 | 49 | 462 | 1 | 2 | 5 | 8 | 57 | 3 | 0 | 0 | 0 | 0 | 0 | 67 | 0 | 4 | 67 | 3 | 9 |
| 15 | 1 | - | 8 | 10 | 14 | 9 | 12 | 74 | 694 | 1 | 4 | 8 | 12 | 86 | 4 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 7 | 100 | 5 | 13 |
| 20 | 1 | 1614 | 11 | 13 | 19 | 12 | 16 | 98 | 925 | 2 | 5 | 10 | 16 | 114 | 6 | 0 | 0 | 0 | 0 | 0 | 134 | 0 | 9 | 134 | 7 | 17 |
| 25 | 1 | 1073 | 15 | 17 | 25 | 17 | 21 | 178 | 541 | 3 | 9 | 24 | 21 | 218 | 9 | 0 | 0 | 0 | 0 | 0 | 218 | 0 | 16 | 242 | 10 | 22 |
| 30 | 1 | 768 | 19 | 21 | 30 | 22 | 27 | 259 | 305 | 5 | 14 | 39 | 24 | 338 | 11 | 0 | 0 | 0 | 0 | 0 | 296 | 0 | 44 | 365 | 12 | 24 |
| 35 | 1 | 615 | 22 | 24 | 35 | 27 | 32 | 337 | 154 | 5 | 21 | 51 | 26 | 467 | 13 | 1 | 0 | 0 | 0 | 1 | 382 | 0 | 52 | 502 | 14 | 28 |
| 40 | 1 | 530 | 25 | 27 | 38 | 30 | 37 | 410 | 85 | 6 | 29 | 59 | 26 | 599 | 15 | 1 | 1 | 0 | 0 | 1 | 468 | 1 | 56 | 644 | 16 | 28 |
| 45 | 1 | 480 | 27 | 29 | 42 | 33 | 42 | 478 | 50 | 6 | 38 | 65 | 27 | 731 | 16 | 1 | 1 | 0 | 0 | 1 | 562 | 1 | 57 | 795 | 18 | 30 |
| 50 | 1 | 445 | 29 | 32 | 44 | 36 | 46 | 540 | 35 | 6 | 46 | 69 | 26 | 863 | 17 | 1 | 2 | 0 | 0 | 1 | 646 | 2 | 59 | 939 | 19 | 29 |
| 55 | 1 | 416 | 31 | 34 | 46 | 38 | 51 | 599 | 30 | 6 | 49 | 72 | 26 | 993 | 18 | 1 | 2 | 0 | 0 | 2 | 713 | 2 | 62 | 1067 | 19 | 26 |
| 60 | 1 | 387 | 33 | 35 | 48 | 40 | 56 | 653 | 29 | 5 | 49 | 73 | 26 | 1121 | 19 | 1 | 2 | 0 | 0 | 2 | 754 | 2 | 63 | 1172 | 20 | 21 |
| 65 | 1 | 359 | 35 | 37 | 50 | 42 | 61 | 703 | 28 | 5 | 49 | 74 | 25 | 1245 | 19 | 2 | 2 | 0 | 0 | 2 | 790 | 2 | 63 | 1271 | 20 | 20 |
| 70 | 1 | 331 | 36 | 38 | 51 | 44 | 65 | 750 | 27 | 5 | 49 | 74 | 24 | 1366 | 20 | 2 | 2 | 0 | 0 | 2 | 818 | 2 | 63 | 1362 | 19 | 18 |
| 75 | 1 | 306 | 37 | 40 | 53 | 47 | 70 | 793 | 26 | 5 | 49 | 74 | 24 | 1484 | 20 | 2 | 2 | 0 | 0 | 3 | 850 | 2 | 64 | 1458 | 19 | 19 |
| 80 | 1 | 282 | 38 | 41 | 54 | 49 | 74 | 834 | 24 | 5 | 50 | 73 | 23 | 1598 | 20 | 3 | 3 | 0 | 0 | 3 | 883 | 3 | 64 | 1556 | 19 | 20 |
| 85 | 1 | 260 | 40 | 42 | 54 | 52 | 78 | 873 | 22 | 5 | 52 | 72 | 22 | 1709 | 20 | 3 | 3 | 0 | 0 | 3 | 910 | 3 | 64 | 1646 | 19 | 18 |
| 90 | 1 | 241 | 41 | 43 | 55 | 54 | 83 | 909 | 20 | 4 | 53 | 71 | 22 | 1817 | 20 | 3 | 3 | 0 | 0 | 4 | 941 | 3 | 63 | 1740 | 19 | 19 |
| 95 | 1 | 222 | 42 | 44 | 56 | 56 | 87 | 943 | 19 | 4 | 54 | 70 | 21 | 1921 | 20 | 4 | 3 | 0 | 0 | 4 | 967 | 3 | 62 | 1828 | 19 | 18 |
| 100 | 1 | 204 | 42 | 45 | 57 | 60 | 91 | 975 | 18 | 4 | 54 | 69 | 20 | 2023 | 20 | 4 | 3 | 0 | 0 | 5 | 994 | 3 | 59 | 1915 | 19 | 17 |
| 105 | 1 | 187 | 43 | 46 | 58 | 63 | 95 | 1006 | 17 | 4 | 54 | 68 | 20 | 2121 | 20 | 5 | 3 | 1 | 0 | 6 | 1036 | 3 | 58 | 2014 | 19 | 20 |
| 110 | 1 | 171 | 44 | 47 | 59 | 66 | 99 | 1035 | 16 | 4 | 55 | 67 | 19 | 2217 | 20 | 5 | 4 | 1 | 0 | 6 | 1084 | 4 | 58 | 2120 | 19 | 21 |
| 115 | 1 | 156 | 45 | 47 | 60 | 70 | 103 | 1062 | 15 | 4 | 56 | 65 | 19 | 2309 | 20 | 6 | 4 | 1 | 0 | 7 | 1136 | 4 | 58 | 2230 | 19 | 22 |
| 120 | 1 | 141 | 45 | 48 | 62 | 74 | 107 | 1089 | 14 | 4 | 57 | 63 | 18 | 2401 | 20 | 7 | 4 | 1 | 0 | 8 | 1169 | 4 | 56 | 2319 | 19 | 18 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | - | 2 | 3 | 4 | 2 | 4 | 15 | 268 | 0 | 1 | 1 | 3 | 16 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 1 | 20 | 1 | 4 |
| 10 | 2 | - | 4 | 5 | 7 | 5 | 7 | 30 | 536 | 0 | 2 | 2 | 5 | 33 | 2 | 0 | 0 | 0 | 0 | 0 | 40 | 0 | 3 | 40 | 2 | 8 |
| 15 | 2 | - | 6 | 8 | 11 | 7 | 11 | 44 | 804 | 1 | 3 | 4 | 8 | 50 | 2 | 0 | 0 | 0 | 0 | 0 | 60 | 0 | 4 | 60 | 3 | 12 |
| 20 | 2 | 2207 | 8 | 10 | 14 | 9 | 14 | 59 | 1072 | 1 | 3 | 5 | 10 | 66 | 3 | 0 | 0 | 0 | 0 | 0 | 80 | 0 | 5 | 80 | 4 | 16 |
| 25 | 2 | 1524 | 12 | 14 | 21 | 13 | 19 | 122 | 683 | 3 | 7 | 16 | 16 | 145 | 6 | 0 | 0 | 0 | 0 | 0 | 162 | 0 | 13 | 180 | 7 | 20 |
| 30 | 2 | 1103 | 16 | 17 | 26 | 17 | 24 | 188 | 420 | 4 | 11 | 29 | 19 | 241 | 8 | 0 | 0 | 0 | 0 | 0 | 234 | 0 | 35 | 288 | 10 | 22 |
| 35 | 2 | 850 | 19 | 20 | 30 | 21 | 28 | 254 | 253 | 5 | 16 | 40 | 21 | 346 | 10 | 0 | 0 | 0 | 0 | 0 | 307 | 0 | 44 | 404 | 12 | 23 |
| 40 | 2 | 700 | 21 | 23 | 34 | 25 | 32 | 317 | 150 | 5 | 21 | 48 | 22 | 457 | 11 | 0 | 0 | 0 | 0 | 1 | 375 | 0 | 49 | 521 | 13 | 23 |
| 45 | 2 | 609 | 24 | 26 | 37 | 28 | 37 | 376 | 91 | 5 | 27 | 54 | 23 | 570 | 13 | 1 | 1 | 0 | 0 | 1 | 448 | 1 | 52 | 646 | 14 | 25 |
| 50 | 2 | 553 | 26 | 28 | 40 | 30 | 41 | 432 | 57 | 5 | 34 | 58 | 23 | 684 | 14 | 1 | 1 | 0 | 0 | 1 | 526 | 1 | 52 | 776 | 16 | 26 |
| 55 | 2 | 513 | 27 | 30 | 42 | 32 | 45 | 485 | 39 | 5 | 41 | 60 | 22 | 797 | 14 | 1 | 1 | 0 | 0 | 1 | 598 | 1 | 52 | 900 | 16 | 25 |
| 60 | 2 | 482 | 29 | 31 | 44 | 34 | 50 | 534 | 31 | 5 | 46 | 62 | 22 | 908 | 15 | 1 | 2 | 0 | 0 | 1 | 662 | 2 | 53 | 1016 | 17 | 23 |
| 65 | 2 | 456 | 30 | 33 | 46 | 36 | 54 | 581 | 27 | 5 | 49 | 63 | 22 | 1017 | 16 | 1 | 2 | 0 | 0 | 2 | 706 | 2 | 53 | 1114 | 17 | 19 |
| 70 | 2 | 431 | 32 | 34 | 47 | 37 | 58 | 624 | 25 | 5 | 50 | 63 | 21 | 1123 | 16 | 1 | 2 | 0 | 0 | 2 | 746 | 2 | 54 | 1207 | 17 | 19 |
| 75 | 2 | 407 | 33 | 35 | 48 | 39 | 62 | 666 | 24 | 5 | 50 | 63 | 21 | 1228 | 16 | 1 | 2 | 0 | 0 | 2 | 766 | 2 | 54 | 1281 | 17 | 15 |
| 80 | 2 | 384 | 34 | 36 | 50 | 40 | 66 | 705 | 23 | 4 | 50 | 62 | 20 | 1329 | 17 | 2 | 2 | 0 | 0 | 2 | 787 | 2 | 53 | 1356 | 17 | 15 |
| 85 | 2 | 362 | 35 | 37 | 50 | 42 | 70 | 742 | 22 | 4 | 50 | 62 | 20 | 1428 | 17 | 2 | 2 | 0 | 0 | 2 | 806 | 2 | 53 | 1428 | 17 | 14 |
| 90 | 2 | 341 | 36 | 38 | 51 | 44 | 74 | 776 | 21 | 4 | 50 | 61 | 19 | 1524 | 17 | 2 | 2 | 0 | 0 | 2 | 818 | 2 | 52 | 1492 | 17 | 13 |
| 95 | 2 | 320 | 37 | 39 | 52 | 45 | 78 | 810 | 21 | 4 | 49 | 60 | 19 | 1618 | 17 | 2 | 2 | 0 | 0 | 3 | 836 | 2 | 52 | 1562 | 16 | 14 |
| 100 | 2 | 299 | 38 | 40 | 52 | 47 | 82 | 841 | 21 | 4 | 49 | 59 | 18 | 1709 | 17 | 2 | 2 | 0 | 0 | 3 | 852 | 2 | 51 | 1629 | 16 | 13 |
| 105 | 2 | 278 | 38 | 41 | 54 | 50 | 86 | 871 | 21 | 4 | 48 | 58 | 18 | 1797 | 17 | 3 | 2 | 0 | 0 | 3 | 871 | 2 | 51 | 1698 | 16 | 14 |
| 110 | 2 | 259 | 39 | 41 | 55 | 52 | 90 | 900 | 20 | 4 | 49 | 57 | 17 | 1883 | 17 | 3 | 3 | 0 | 0 | 3 | 898 | 3 | 51 | 1777 | 16 | 16 |
| 115 | 2 | 240 | 40 | 42 | 56 | 55 | 94 | 928 | 18 | 4 | 50 | 56 | 17 | 1967 | 17 | 3 | 3 | 0 | 0 | 4 | 927 | 3 | 48 | 1853 | 16 | 15 |
| 120 | 2 | 223 | 40 | 43 | 58 | 57 | 98 | 954 | 17 | 3 | 50 | 55 | 16 | 2048 | 17 | 4 | 3 | 0 | 0 | 4 | 961 | 3 | 47 | 1934 | 16 | 16 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | - | 2 | 2 | 3 | 2 | 3 | 7 | 288 | 0 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 0 | 0 | 14 | 1 | 3 |
| 10 | 3 | - | 3 | 4 | 5 | 3 | 6 | 14 | 576 | 0 | 0 | 0 | 3 | 14 | 1 | 0 | 0 | 0 | 0 | 0 | 29 | 0 | 1 | 29 | 1 | 5 |
| 15 | 3 | - | 5 | 6 | 8 | 5 | 9 | 22 | 865 | 0 | 1 | 0 | 4 | 21 | 1 | 0 | 0 | 0 | 0 | 0 | 43 | 0 | 1 | 43 | 2 | 8 |
| 20 | 3 | 2836 | 6 | 8 | 10 | 7 | 13 | 29 | 1153 | 0 | 1 | 0 | 5 | 28 | 1 | 0 | 0 | 0 | 0 | 0 | 57 | 0 | 1 | 57 | 3 | 10 |
| 25 | 3 | 2032 | 10 | 11 | 17 | 10 | 17 | 74 | 804 | 2 | 5 | 8 | 11 | 82 | 3 | 0 | 0 | 0 | 0 | 0 | 111 | 0 | 8 | 120 | 5 | 13 |
| 30 | 3 | 1503 | 13 | 14 | 22 | 14 | 21 | 127 | 529 | 3 | 9 | 20 | 14 | 154 | 5 | 0 | 0 | 0 | 0 | 0 | 176 | 0 | 15 | 200 | 7 | 16 |
| 35 | 3 | 1160 | 16 | 17 | 26 | 17 | 25 | 180 | 343 | 4 | 12 | 30 | 17 | 238 | 7 | 0 | 0 | 0 | 0 | 0 | 241 | 0 | 35 | 299 | 9 | 20 |
| 40 | 3 | 938 | 18 | 20 | 30 | 20 | 28 | 233 | 222 | 5 | 16 | 37 | 18 | 328 | 8 | 0 | 0 | 0 | 0 | 0 | 300 | 0 | 40 | 398 | 10 | 20 |
| 45 | 3 | 794 | 20 | 22 | 33 | 23 | 32 | 284 | 144 | 5 | 21 | 43 | 19 | 422 | 9 | 0 | 0 | 0 | 0 | 0 | 359 | 0 | 44 | 501 | 11 | 21 |
| 50 | 3 | 699 | 22 | 24 | 36 | 26 | 36 | 332 | 95 | 5 | 26 | 47 | 19 | 517 | 10 | 0 | 0 | 0 | 0 | 1 | 417 | 0 | 45 | 605 | 12 | 21 |
| 55 | 3 | 634 | 24 | 26 | 38 | 28 | 40 | 378 | 65 | 5 | 31 | 49 | 19 | 612 | 11 | 1 | 1 | 0 | 0 | 1 | 478 | 1 | 46 | 711 | 13 | 21 |
| 60 | 3 | 588 | 25 | 27 | 40 | 30 | 43 | 422 | 46 | 5 | 36 | 51 | 19 | 707 | 12 | 1 | 1 | 0 | 0 | 1 | 533 | 1 | 45 | 810 | 14 | 20 |
| 65 | 3 | 553 | 26 | 28 | 42 | 31 | 47 | 464 | 35 | 5 | 41 | 52 | 19 | 800 | 12 | 1 | 1 | 0 | 0 | 1 | 588 | 1 | 45 | 910 | 14 | 20 |
| 70 | 3 | 526 | 28 | 30 | 43 | 32 | 51 | 504 | 28 | 4 | 46 | 52 | 18 | 892 | 13 | 1 | 2 | 0 | 0 | 1 | 642 | 2 | 45 | 1009 | 14 | 20 |
| 75 | 3 | 502 | 29 | 31 | 44 | 34 | 54 | 542 | 23 | 4 | 49 | 52 | 18 | 982 | 13 | 1 | 2 | 0 | 0 | 1 | 681 | 2 | 43 | 1092 | 15 | 17 |
| 80 | 3 | 482 | 30 | 32 | 45 | 35 | 58 | 578 | 21 | 4 | 51 | 52 | 18 | 1070 | 13 | 1 | 2 | 0 | 0 | 1 | 715 | 2 | 45 | 1171 | 15 | 16 |
| 85 | 3 | 463 | 30 | 33 | 46 | 36 | 62 | 613 | 19 | 4 | 52 | 52 | 17 | 1157 | 14 | 1 | 2 | 0 | 0 | 2 | 741 | 2 | 44 | 1240 | 15 | 14 |
| 90 | 3 | 445 | 31 | 34 | 47 | 37 | 66 | 646 | 18 | 4 | 53 | 51 | 17 | 1241 | 14 | 1 | 2 | 0 | 0 | 2 | 753 | 2 | 43 | 1295 | 14 | 11 |
| 95 | 3 | 426 | 32 | 34 | 47 | 38 | 69 | 677 | 19 | 4 | 51 | 50 | 16 | 1323 | 14 | 1 | 2 | 0 | 0 | 2 | 752 | 2 | 44 | 1338 | 14 | 9 |
| 100 | 3 | 407 | 33 | 35 | 48 | 39 | 73 | 708 | 19 | 4 | 49 | 50 | 16 | 1403 | 14 | 1 | 2 | 0 | 0 | 2 | 759 | 2 | 42 | 1387 | 14 | 10 |
| 105 | 3 | 387 | 33 | 36 | 50 | 40 | 77 | 737 | 20 | 4 | 48 | 49 | 16 | 1481 | 14 | 2 | 2 | 0 | 0 | 2 | 770 | 2 | 43 | 1440 | 14 | 11 |
| 110 | 3 | 368 | 34 | 36 | 51 | 42 | 81 | 764 | 19 | 4 | 48 | 48 | 15 | 1557 | 14 | 2 | 2 | 0 | 0 | 2 | 789 | 2 | 41 | 1500 | 14 | 12 |
| 115 | 3 | 349 | 34 | 37 | 52 | 44 | 84 | 791 | 19 | 3 | 48 | 47 | 15 | 1631 | 14 | 2 | 2 | 0 | 0 | 2 | 808 | 2 | 42 | 1561 | 14 | 12 |
| 120 | 3 | 331 | 35 | 37 | 53 | 45 | 88 | 817 | 18 | 3 | 48 | 46 | 14 | 1703 | 14 | 2 | 2 | 0 | 0 | 2 | 826 | 2 | 40 | 1620 | 13 | 12 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | −1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | −1 | - | 3 | 4 | 4 | 2 | 4 | 12 | 0 | 0 | 0 | 0 | 3 | 20 | 1 | 0 | 0 | 0 | 0 | 0 | 26 | 0 | 0 | 26 | 2 | 3 |
| 10 | −1 | - | 6 | 7 | 7 | 4 | 7 | 24 | 1 | 0 | 0 | 0 | 7 | 40 | 3 | 0 | 0 | 0 | 0 | 0 | 52 | 0 | 0 | 52 | 3 | 7 |
| 15 | −1 | 3126 | 8 | 11 | 11 | 7 | 11 | 36 | 1 | 0 | 0 | 0 | 10 | 60 | 4 | 0 | 0 | 0 | 0 | 0 | 79 | 0 | 0 | 79 | 5 | 10 |
| 20 | −1 | 1923 | 12 | 14 | 13 | 9 | 14 | 72 | 1203 | 5 | 7 | 29 | 13 | 126 | 6 | 0 | 0 | 0 | 0 | 0 | 118 | 0 | 29 | 147 | 7 | 14 |
| 25 | −1 | 1375 | 14 | 16 | 14 | 12 | 18 | 109 | 549 | 5 | 11 | 35 | 14 | 197 | 8 | 0 | 0 | 0 | 0 | 0 | 167 | 0 | 40 | 237 | 9 | 18 |
| 30 | −1 | 1063 | 16 | 18 | 16 | 14 | 21 | 144 | 312 | 5 | 14 | 39 | 15 | 271 | 9 | 0 | 0 | 0 | 0 | 0 | 216 | 0 | 43 | 329 | 11 | 18 |
| 35 | −1 | 860 | 18 | 20 | 18 | 16 | 24 | 178 | 203 | 4 | 16 | 41 | 15 | 346 | 10 | 0 | 0 | 0 | 0 | 0 | 267 | 0 | 45 | 425 | 12 | 19 |
| 40 | −1 | 715 | 20 | 22 | 19 | 18 | 27 | 209 | 145 | 4 | 19 | 42 | 15 | 419 | 10 | 0 | 0 | 0 | 0 | 0 | 312 | 0 | 47 | 517 | 13 | 18 |
| 45 | −1 | 605 | 22 | 23 | 20 | 21 | 30 | 238 | 110 | 4 | 21 | 43 | 14 | 490 | 11 | 0 | 0 | 0 | 0 | 1 | 355 | 0 | 48 | 608 | 14 | 18 |
| 50 | −1 | 519 | 23 | 25 | 21 | 23 | 33 | 264 | 86 | 4 | 23 | 43 | 14 | 560 | 11 | 1 | 1 | 0 | 0 | 1 | 392 | 1 | 47 | 692 | 14 | 17 |
| 55 | −1 | 450 | 24 | 26 | 22 | 25 | 35 | 289 | 69 | 3 | 25 | 43 | 14 | 628 | 11 | 1 | 1 | 0 | 0 | 1 | 425 | 1 | 47 | 772 | 14 | 16 |
| 60 | −1 | 395 | 26 | 27 | 23 | 27 | 38 | 312 | 56 | 3 | 27 | 43 | 13 | 694 | 12 | 1 | 1 | 0 | 0 | 1 | 456 | 1 | 47 | 849 | 14 | 16 |
| 65 | −1 | 350 | 27 | 28 | 23 | 29 | 41 | 333 | 45 | 3 | 29 | 43 | 13 | 757 | 12 | 1 | 1 | 0 | 0 | 1 | 485 | 1 | 46 | 925 | 14 | 15 |
| 70 | −1 | 313 | 28 | 29 | 24 | 31 | 43 | 352 | 37 | 3 | 32 | 43 | 12 | 819 | 12 | 1 | 1 | 0 | 0 | 2 | 513 | 1 | 46 | 999 | 14 | 15 |
| 75 | −1 | 283 | 28 | 30 | 24 | 33 | 46 | 370 | 30 | 3 | 34 | 42 | 12 | 879 | 12 | 1 | 1 | 0 | 0 | 2 | 544 | 1 | 44 | 1074 | 14 | 15 |
| 80 | −1 | 257 | 29 | 30 | 25 | 35 | 49 | 386 | 25 | 3 | 37 | 42 | 12 | 938 | 12 | 2 | 2 | 0 | 0 | 2 | 572 | 2 | 43 | 1145 | 14 | 14 |
| 85 | −1 | 235 | 30 | 31 | 26 | 37 | 51 | 402 | 22 | 3 | 39 | 41 | 11 | 994 | 12 | 2 | 2 | 0 | 0 | 3 | 598 | 2 | 44 | 1216 | 14 | 14 |
| 90 | −1 | 217 | 31 | 32 | 26 | 39 | 54 | 416 | 19 | 2 | 41 | 41 | 11 | 1049 | 12 | 2 | 2 | 0 | 0 | 3 | 624 | 2 | 43 | 1284 | 14 | 14 |
| 95 | −1 | 200 | 31 | 32 | 27 | 41 | 56 | 429 | 16 | 2 | 43 | 40 | 11 | 1103 | 12 | 2 | 3 | 0 | 1 | 3 | 645 | 3 | 41 | 1347 | 14 | 12 |
| 100 | −1 | 186 | 32 | 33 | 27 | 43 | 58 | 441 | 15 | 2 | 45 | 40 | 10 | 1155 | 12 | 3 | 3 | 0 | 1 | 4 | 670 | 3 | 42 | 1414 | 14 | 13 |
| 105 | −1 | 173 | 33 | 34 | 28 | 45 | 61 | 453 | 13 | 2 | 47 | 39 | 10 | 1205 | 12 | 3 | 3 | 1 | 1 | 4 | 691 | 3 | 41 | 1475 | 14 | 12 |
| 110 | −1 | 161 | 33 | 34 | 28 | 47 | 63 | 464 | 12 | 2 | 49 | 39 | 10 | 1255 | 11 | 3 | 3 | 1 | 1 | 4 | 707 | 3 | 41 | 1532 | 14 | 11 |
| 115 | −1 | 151 | 34 | 34 | 28 | 49 | 66 | 474 | 10 | 2 | 51 | 38 | 10 | 1303 | 11 | 3 | 4 | 1 | 1 | 5 | 728 | 4 | 37 | 1590 | 14 | 12 |
| 120 | −1 | 141 | 34 | 35 | 29 | 51 | 68 | 483 | 9 | 2 | 53 | 37 | 9 | 1349 | 11 | 4 | 4 | 1 | 1 | 5 | 741 | 4 | 36 | 1639 | 14 | 10 |
| 125 | −1 | 133 | 34 | 35 | 29 | 53 | 70 | 492 | 9 | 2 | 55 | 37 | 9 | 1395 | 11 | 4 | 4 | 1 | 1 | 6 | 761 | 4 | 39 | 1699 | 14 | 12 |
| 130 | −1 | 125 | 35 | 36 | 29 | 54 | 73 | 500 | 8 | 2 | 56 | 36 | 9 | 1439 | 11 | 4 | 5 | 1 | 1 | 6 | 776 | 5 | 37 | 1751 | 13 | 10 |
| 135 | −1 | 118 | 35 | 36 | 29 | 56 | 75 | 508 | 7 | 2 | 58 | 36 | 9 | 1483 | 11 | 5 | 5 | 1 | 1 | 7 | 789 | 5 | 35 | 1799 | 13 | 10 |
| 140 | −1 | 112 | 36 | 37 | 30 | 58 | 77 | 515 | 7 | 2 | 60 | 35 | 8 | 1525 | 11 | 5 | 5 | 1 | 1 | 7 | 810 | 5 | 38 | 1858 | 13 | 12 |
| 145 | −1 | 106 | 36 | 37 | 30 | 60 | 79 | 522 | 6 | 2 | 62 | 34 | 8 | 1566 | 11 | 5 | 6 | 1 | 1 | 8 | 822 | 6 | 35 | 1905 | 13 | 9 |
| 150 | −1 | 100 | 36 | 37 | 30 | 62 | 82 | 529 | 5 | 2 | 64 | 34 | 8 | 1607 | 11 | 6 | 6 | 1 | 1 | 8 | 837 | 6 | 31 | 1951 | 13 | 9 |
| 155 | −1 | 95 | 37 | 38 | 30 | 64 | 84 | 535 | 5 | 2 | 66 | 33 | 8 | 1646 | 11 | 6 | 7 | 1 | 1 | 9 | 849 | 7 | 34 | 1998 | 13 | 9 |
| 160 | −1 | 91 | 37 | 38 | 30 | 66 | 86 | 541 | 5 | 2 | 68 | 33 | 8 | 1685 | 10 | 7 | 7 | 1 | 2 | 10 | 867 | 7 | 36 | 2050 | 13 | 11 |
| 165 | −1 | 86 | 37 | 38 | 31 | 67 | 88 | 546 | 4 | 2 | 69 | 32 | 8 | 1723 | 10 | 7 | 7 | 1 | 2 | 10 | 870 | 7 | 30 | 2084 | 13 | 7 |
| 170 | −1 | 82 | 38 | 38 | 31 | 69 | 90 | 551 | 4 | 2 | 70 | 32 | 7 | 1760 | 10 | 8 | 8 | 2 | 2 | 11 | 880 | 8 | 31 | 2124 | 12 | 8 |
| 175 | −1 | 78 | 38 | 39 | 31 | 71 | 93 | 556 | 4 | 2 | 71 | 31 | 7 | 1796 | 10 | 8 | 8 | 2 | 2 | 11 | 884 | 8 | 32 | 2161 | 12 | 7 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | - | 2 | 3 | 3 | 2 | 3 | 10 | 410 | 1 | 1 | 4 | 2 | 18 | 1 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 5 | 24 | 1 | 3 |
| 10 | 0 | - | 5 | 6 | 6 | 4 | 6 | 21 | 819 | 2 | 3 | 8 | 4 | 36 | 2 | 0 | 0 | 0 | 0 | 0 | 47 | 0 | 10 | 47 | 2 | 6 |
| 15 | 0 | - | 7 | 8 | 8 | 6 | 9 | 32 | 1228 | 3 | 4 | 13 | 7 | 53 | 3 | 0 | 0 | 0 | 0 | 0 | 71 | 0 | 15 | 71 | 4 | 10 |
| 20 | 0 | 2320 | 9 | 11 | 11 | 8 | 12 | 42 | 1638 | 4 | 5 | 17 | 9 | 71 | 4 | 0 | 0 | 0 | 0 | 0 | 94 | 0 | 19 | 94 | 5 | 13 |
| 25 | 0 | 1619 | 12 | 14 | 13 | 10 | 14 | 72 | 701 | 4 | 8 | 23 | 10 | 123 | 5 | 0 | 0 | 0 | 0 | 0 | 131 | 0 | 24 | 175 | 7 | 16 |
| 30 | 0 | 1235 | 14 | 16 | 15 | 12 | 17 | 102 | 385 | 4 | 11 | 26 | 11 | 180 | 6 | 0 | 0 | 0 | 0 | 0 | 170 | 0 | 31 | 244 | 8 | 14 |
| 35 | 0 | 989 | 16 | 17 | 16 | 14 | 20 | 131 | 246 | 4 | 14 | 28 | 12 | 238 | 7 | 0 | 0 | 0 | 0 | 0 | 219 | 0 | 32 | 325 | 9 | 16 |
| 40 | 0 | 815 | 18 | 19 | 18 | 17 | 23 | 160 | 173 | 3 | 16 | 30 | 12 | 296 | 7 | 0 | 0 | 0 | 0 | 0 | 259 | 0 | 34 | 399 | 10 | 15 |
| 45 | 0 | 685 | 19 | 20 | 19 | 19 | 25 | 187 | 130 | 3 | 18 | 31 | 12 | 354 | 8 | 0 | 0 | 0 | 0 | 0 | 297 | 0 | 35 | 472 | 10 | 15 |
| 50 | 0 | 584 | 20 | 22 | 20 | 21 | 28 | 212 | 101 | 3 | 19 | 32 | 12 | 411 | 8 | 0 | 0 | 0 | 0 | 1 | 329 | 0 | 35 | 540 | 11 | 13 |
| 55 | 0 | 504 | 22 | 23 | 20 | 23 | 30 | 236 | 80 | 3 | 21 | 33 | 11 | 468 | 8 | 1 | 0 | 0 | 0 | 1 | 361 | 0 | 37 | 608 | 11 | 14 |
| 60 | 0 | 439 | 23 | 24 | 21 | 25 | 33 | 258 | 64 | 3 | 23 | 33 | 11 | 523 | 9 | 1 | 1 | 0 | 0 | 1 | 390 | 1 | 37 | 673 | 11 | 13 |
| 65 | 0 | 388 | 24 | 25 | 22 | 27 | 35 | 279 | 52 | 3 | 26 | 33 | 11 | 577 | 9 | 1 | 1 | 0 | 0 | 1 | 419 | 1 | 37 | 740 | 11 | 13 |
| 70 | 0 | 346 | 25 | 26 | 22 | 29 | 38 | 298 | 42 | 3 | 28 | 34 | 11 | 630 | 9 | 1 | 1 | 0 | 0 | 1 | 448 | 1 | 37 | 806 | 12 | 13 |
| 75 | 0 | 311 | 26 | 27 | 23 | 31 | 40 | 317 | 35 | 2 | 30 | 34 | 10 | 682 | 9 | 1 | 1 | 0 | 0 | 2 | 474 | 1 | 38 | 870 | 12 | 13 |
| 80 | 0 | 282 | 26 | 27 | 24 | 33 | 42 | 333 | 29 | 2 | 33 | 34 | 10 | 732 | 9 | 1 | 1 | 0 | 0 | 2 | 502 | 1 | 37 | 935 | 12 | 13 |
| 85 | 0 | 258 | 27 | 28 | 24 | 34 | 45 | 349 | 24 | 2 | 35 | 34 | 10 | 782 | 9 | 1 | 2 | 0 | 0 | 2 | 528 | 2 | 36 | 998 | 12 | 12 |
| 90 | 0 | 237 | 28 | 29 | 25 | 36 | 47 | 364 | 21 | 2 | 37 | 34 | 10 | 830 | 9 | 2 | 2 | 0 | 0 | 2 | 554 | 2 | 36 | 1060 | 12 | 12 |
| 95 | 0 | 218 | 28 | 29 | 25 | 38 | 50 | 378 | 18 | 2 | 39 | 34 | 9 | 877 | 9 | 2 | 2 | 0 | 0 | 3 | 576 | 2 | 35 | 1117 | 12 | 11 |
| 100 | 0 | 202 | 29 | 30 | 26 | 40 | 52 | 390 | 16 | 2 | 41 | 33 | 9 | 924 | 9 | 2 | 2 | 0 | 0 | 3 | 598 | 2 | 35 | 1175 | 12 | 12 |
| 105 | 0 | 187 | 30 | 30 | 26 | 42 | 54 | 402 | 14 | 2 | 43 | 33 | 9 | 969 | 9 | 2 | 2 | 0 | 0 | 3 | 614 | 2 | 34 | 1225 | 12 | 10 |
| 110 | 0 | 175 | 30 | 31 | 26 | 44 | 56 | 414 | 13 | 2 | 45 | 33 | 9 | 1013 | 9 | 3 | 3 | 1 | 1 | 4 | 637 | 3 | 35 | 1283 | 12 | 12 |
| 115 | 0 | 163 | 31 | 32 | 27 | 46 | 58 | 424 | 12 | 2 | 47 | 33 | 9 | 1056 | 9 | 3 | 3 | 1 | 1 | 4 | 654 | 3 | 36 | 1336 | 12 | 11 |
| 120 | 0 | 153 | 31 | 32 | 27 | 48 | 61 | 434 | 10 | 2 | 49 | 32 | 8 | 1098 | 9 | 3 | 3 | 1 | 1 | 4 | 675 | 3 | 33 | 1389 | 12 | 11 |
| 125 | 0 | 143 | 32 | 32 | 27 | 49 | 63 | 443 | 9 | 2 | 51 | 32 | 8 | 1140 | 9 | 3 | 4 | 1 | 1 | 5 | 688 | 4 | 32 | 1435 | 11 | 9 |
| 130 | 0 | 135 | 32 | 33 | 28 | 51 | 65 | 452 | 9 | 2 | 53 | 32 | 8 | 1180 | 9 | 4 | 4 | 1 | 1 | 5 | 705 | 4 | 35 | 1487 | 11 | 10 |
| 135 | 0 | 127 | 32 | 33 | 28 | 53 | 67 | 460 | 8 | 2 | 54 | 31 | 8 | 1220 | 9 | 4 | 4 | 1 | 1 | 6 | 720 | 4 | 34 | 1535 | 11 | 10 |
| 140 | 0 | 120 | 33 | 34 | 28 | 55 | 69 | 468 | 7 | 2 | 56 | 31 | 8 | 1259 | 9 | 4 | 5 | 1 | 1 | 6 | 736 | 5 | 32 | 1583 | 11 | 9 |
| 145 | 0 | 113 | 33 | 34 | 28 | 57 | 72 | 475 | 7 | 2 | 58 | 31 | 8 | 1297 | 9 | 5 | 5 | 1 | 1 | 7 | 747 | 5 | 34 | 1628 | 11 | 9 |
| 150 | 0 | 107 | 34 | 34 | 29 | 58 | 74 | 482 | 6 | 2 | 60 | 30 | 8 | 1335 | 9 | 5 | 5 | 1 | 1 | 7 | 763 | 5 | 32 | 1676 | 11 | 10 |
| 155 | 0 | 102 | 34 | 35 | 29 | 60 | 76 | 489 | 5 | 2 | 62 | 30 | 7 | 1371 | 9 | 5 | 6 | 1 | 1 | 8 | 781 | 6 | 29 | 1723 | 11 | 9 |
| 160 | 0 | 97 | 34 | 35 | 29 | 62 | 78 | 495 | 5 | 2 | 64 | 30 | 7 | 1407 | 9 | 6 | 6 | 1 | 1 | 8 | 793 | 6 | 31 | 1765 | 11 | 8 |
| 165 | 0 | 92 | 35 | 35 | 29 | 64 | 80 | 501 | 5 | 2 | 66 | 29 | 7 | 1443 | 9 | 6 | 6 | 1 | 1 | 9 | 804 | 6 | 32 | 1808 | 11 | 9 |
| 170 | 0 | 87 | 35 | 35 | 29 | 66 | 82 | 507 | 4 | 2 | 67 | 29 | 7 | 1478 | 9 | 6 | 7 | 1 | 1 | 9 | 806 | 7 | 27 | 1838 | 11 | 6 |
| 175 | 0 | 83 | 35 | 36 | 30 | 67 | 84 | 512 | 4 | 2 | 68 | 29 | 7 | 1512 | 9 | 7 | 7 | 1 | 2 | 10 | 813 | 7 | 28 | 1872 | 11 | 7 |
| 180 | 0 | 79 | 35 | 36 | 30 | 69 | 86 | 517 | 4 | 2 | 69 | 28 | 7 | 1545 | 9 | 7 | 7 | 2 | 2 | 10 | 819 | 7 | 29 | 1907 | 11 | 7 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | - | 2 | 2 | 2 | 2 | 2 | 8 | 193 | 1 | 1 | 3 | 1 | 13 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 3 | 20 | 1 | 2 |
| 10 | 1 | - | 4 | 4 | 5 | 3 | 5 | 16 | 386 | 1 | 2 | 5 | 3 | 27 | 1 | 0 | 0 | 0 | 0 | 0 | 40 | 0 | 6 | 40 | 2 | 4 |
| 15 | 1 | - | 6 | 7 | 7 | 5 | 7 | 25 | 579 | 2 | 4 | 8 | 4 | 40 | 2 | 0 | 0 | 0 | 0 | 0 | 60 | 0 | 9 | 60 | 2 | 6 |
| 20 | 1 | - | 8 | 9 | 9 | 7 | 9 | 33 | 772 | 2 | 5 | 10 | 6 | 54 | 2 | 0 | 0 | 0 | 0 | 0 | 80 | 0 | 12 | 80 | 3 | 8 |
| 25 | 1 | 1974 | 10 | 11 | 12 | 9 | 12 | 41 | 965 | 3 | 6 | 13 | 7 | 67 | 3 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 15 | 100 | 4 | 10 |
| 30 | 1 | 1472 | 12 | 13 | 13 | 11 | 14 | 65 | 502 | 3 | 8 | 16 | 8 | 108 | 4 | 0 | 0 | 0 | 0 | 0 | 129 | 0 | 17 | 161 | 5 | 12 |
| 35 | 1 | 1161 | 13 | 15 | 15 | 13 | 16 | 90 | 311 | 3 | 10 | 18 | 9 | 151 | 4 | 0 | 0 | 0 | 0 | 0 | 162 | 0 | 20 | 215 | 6 | 11 |
| 40 | 1 | 947 | 15 | 16 | 16 | 15 | 19 | 114 | 215 | 3 | 12 | 20 | 9 | 195 | 5 | 0 | 0 | 0 | 0 | 0 | 204 | 0 | 22 | 279 | 7 | 13 |
| 45 | 1 | 788 | 16 | 18 | 17 | 17 | 21 | 139 | 159 | 2 | 14 | 21 | 9 | 240 | 5 | 0 | 0 | 0 | 0 | 0 | 238 | 0 | 24 | 337 | 7 | 12 |
| 50 | 1 | 666 | 18 | 19 | 18 | 19 | 24 | 162 | 122 | 2 | 16 | 22 | 9 | 286 | 6 | 0 | 0 | 0 | 0 | 0 | 273 | 0 | 25 | 397 | 8 | 12 |
| 55 | 1 | 571 | 19 | 20 | 19 | 21 | 26 | 184 | 96 | 2 | 18 | 23 | 9 | 331 | 6 | 0 | 0 | 0 | 0 | 1 | 301 | 0 | 26 | 451 | 8 | 11 |
| 60 | 1 | 495 | 20 | 21 | 20 | 22 | 28 | 206 | 76 | 2 | 20 | 24 | 9 | 376 | 6 | 0 | 0 | 0 | 0 | 1 | 329 | 0 | 27 | 506 | 8 | 11 |
| 65 | 1 | 434 | 21 | 22 | 20 | 24 | 30 | 226 | 61 | 2 | 22 | 24 | 9 | 421 | 6 | 1 | 0 | 0 | 0 | 1 | 355 | 0 | 28 | 560 | 9 | 11 |
| 70 | 1 | 385 | 22 | 23 | 21 | 26 | 33 | 245 | 49 | 2 | 24 | 25 | 9 | 465 | 7 | 1 | 1 | 0 | 0 | 1 | 382 | 1 | 28 | 615 | 9 | 11 |
| 75 | 1 | 345 | 23 | 24 | 22 | 28 | 35 | 263 | 40 | 2 | 26 | 25 | 9 | 508 | 7 | 1 | 1 | 0 | 0 | 1 | 408 | 1 | 29 | 671 | 9 | 11 |
| 80 | 1 | 312 | 24 | 24 | 22 | 30 | 37 | 280 | 33 | 2 | 28 | 26 | 8 | 551 | 7 | 1 | 1 | 0 | 0 | 1 | 433 | 1 | 29 | 726 | 9 | 11 |
| 85 | 1 | 284 | 24 | 25 | 23 | 32 | 39 | 296 | 28 | 2 | 31 | 26 | 8 | 593 | 7 | 1 | 1 | 0 | 0 | 2 | 456 | 1 | 30 | 778 | 9 | 11 |
| 90 | 1 | 260 | 25 | 26 | 23 | 34 | 41 | 311 | 24 | 2 | 33 | 26 | 8 | 634 | 7 | 1 | 1 | 0 | 0 | 2 | 482 | 1 | 30 | 834 | 9 | 11 |
| 95 | 1 | 239 | 26 | 26 | 24 | 36 | 44 | 325 | 21 | 2 | 35 | 27 | 8 | 675 | 7 | 2 | 1 | 0 | 0 | 2 | 504 | 1 | 30 | 885 | 9 | 10 |
| 100 | 1 | 221 | 26 | 27 | 24 | 37 | 46 | 338 | 18 | 2 | 37 | 27 | 8 | 715 | 7 | 2 | 2 | 0 | 0 | 2 | 524 | 2 | 29 | 935 | 9 | 10 |
| 105 | 1 | 204 | 27 | 28 | 25 | 39 | 48 | 350 | 16 | 2 | 39 | 27 | 8 | 754 | 7 | 2 | 2 | 0 | 0 | 3 | 544 | 2 | 29 | 984 | 9 | 10 |
| 110 | 1 | 190 | 27 | 28 | 25 | 41 | 50 | 362 | 14 | 2 | 41 | 27 | 8 | 793 | 7 | 2 | 2 | 0 | 0 | 3 | 562 | 2 | 29 | 1031 | 9 | 9 |
| 115 | 1 | 177 | 28 | 28 | 25 | 43 | 52 | 373 | 13 | 2 | 43 | 27 | 8 | 831 | 7 | 2 | 2 | 0 | 0 | 3 | 582 | 2 | 30 | 1081 | 9 | 10 |
| 120 | 1 | 165 | 28 | 29 | 26 | 44 | 54 | 383 | 12 | 2 | 44 | 27 | 8 | 868 | 7 | 3 | 3 | 1 | 1 | 4 | 598 | 3 | 31 | 1127 | 9 | 9 |
| 125 | 1 | 155 | 29 | 29 | 26 | 46 | 56 | 393 | 11 | 2 | 46 | 27 | 7 | 905 | 7 | 3 | 3 | 1 | 1 | 4 | 616 | 3 | 31 | 1176 | 9 | 10 |
| 130 | 1 | 145 | 29 | 30 | 26 | 48 | 58 | 402 | 10 | 2 | 48 | 27 | 7 | 941 | 7 | 3 | 3 | 1 | 1 | 4 | 629 | 3 | 31 | 1220 | 9 | 9 |
| 135 | 1 | 137 | 30 | 30 | 26 | 50 | 60 | 411 | 9 | 2 | 50 | 27 | 7 | 977 | 7 | 3 | 3 | 1 | 1 | 5 | 646 | 3 | 30 | 1267 | 9 | 9 |
| 140 | 1 | 129 | 30 | 31 | 27 | 52 | 62 | 419 | 8 | 2 | 52 | 27 | 7 | 1012 | 7 | 4 | 4 | 1 | 1 | 5 | 661 | 4 | 29 | 1311 | 9 | 9 |
| 145 | 1 | 121 | 30 | 31 | 27 | 53 | 64 | 427 | 7 | 2 | 54 | 27 | 7 | 1046 | 7 | 4 | 4 | 1 | 1 | 6 | 670 | 4 | 28 | 1348 | 9 | 7 |
| 150 | 1 | 115 | 31 | 31 | 27 | 55 | 66 | 434 | 7 | 2 | 56 | 27 | 7 | 1080 | 7 | 4 | 4 | 1 | 1 | 6 | 691 | 4 | 30 | 1400 | 9 | 10 |
| 155 | 1 | 109 | 31 | 32 | 27 | 57 | 68 | 441 | 6 | 2 | 58 | 26 | 7 | 1113 | 7 | 4 | 5 | 1 | 1 | 6 | 705 | 5 | 28 | 1442 | 9 | 8 |
| 160 | 1 | 103 | 31 | 32 | 28 | 58 | 70 | 448 | 6 | 2 | 60 | 26 | 7 | 1146 | 7 | 5 | 5 | 1 | 1 | 7 | 713 | 5 | 30 | 1480 | 9 | 8 |
| 165 | 1 | 98 | 32 | 32 | 28 | 60 | 72 | 454 | 5 | 2 | 62 | 26 | 6 | 1179 | 7 | 5 | 5 | 1 | 1 | 7 | 727 | 5 | 27 | 1521 | 9 | 8 |
| 170 | 1 | 93 | 32 | 32 | 28 | 62 | 74 | 460 | 5 | 2 | 63 | 26 | 6 | 1210 | 7 | 5 | 6 | 1 | 1 | 8 | 734 | 6 | 28 | 1556 | 9 | 7 |
| 175 | 1 | 88 | 32 | 33 | 28 | 64 | 76 | 466 | 5 | 2 | 64 | 26 | 6 | 1242 | 7 | 6 | 6 | 1 | 1 | 8 | 735 | 6 | 29 | 1587 | 9 | 6 |
| 180 | 1 | 84 | 33 | 33 | 28 | 65 | 78 | 471 | 4 | 2 | 65 | 26 | 6 | 1273 | 7 | 6 | 6 | 1 | 1 | 9 | 746 | 6 | 24 | 1621 | 9 | 7 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | - | 2 | 2 | 2 | 2 | 2 | 6 | 120 | 0 | 1 | 2 | 1 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 2 | 17 | 1 | 1 |
| 10 | 2 | - | 3 | 4 | 4 | 3 | 4 | 11 | 240 | 1 | 2 | 3 | 2 | 18 | 1 | 0 | 0 | 0 | 0 | 0 | 35 | 0 | 3 | 35 | 1 | 2 |
| 15 | 2 | - | 5 | 5 | 6 | 5 | 6 | 17 | 360 | 1 | 3 | 4 | 3 | 27 | 1 | 0 | 0 | 0 | 0 | 0 | 52 | 0 | 5 | 52 | 2 | 3 |
| 20 | 2 | - | 6 | 7 | 8 | 6 | 8 | 23 | 481 | 1 | 4 | 6 | 3 | 36 | 1 | 0 | 0 | 0 | 0 | 0 | 70 | 0 | 7 | 70 | 2 | 4 |
| 25 | 2 | - | 8 | 9 | 10 | 8 | 9 | 28 | 601 | 2 | 5 | 8 | 4 | 45 | 2 | 0 | 0 | 0 | 0 | 0 | 87 | 0 | 8 | 87 | 3 | 5 |
| 30 | 2 | 1838 | 9 | 11 | 12 | 9 | 11 | 34 | 721 | 2 | 6 | 9 | 5 | 54 | 2 | 0 | 0 | 0 | 0 | 0 | 105 | 0 | 10 | 105 | 3 | 7 |
| 35 | 2 | 1415 | 11 | 12 | 13 | 11 | 13 | 53 | 423 | 2 | 8 | 10 | 6 | 84 | 2 | 0 | 0 | 0 | 0 | 0 | 121 | 0 | 11 | 143 | 4 | 8 |
| 40 | 2 | 1133 | 12 | 14 | 15 | 13 | 16 | 74 | 282 | 2 | 9 | 12 | 6 | 116 | 3 | 0 | 0 | 0 | 0 | 0 | 152 | 0 | 12 | 186 | 5 | 9 |
| 45 | 2 | 930 | 14 | 15 | 16 | 15 | 18 | 94 | 203 | 2 | 11 | 13 | 7 | 149 | 3 | 0 | 0 | 0 | 0 | 0 | 185 | 0 | 15 | 233 | 5 | 10 |
| 50 | 2 | 777 | 15 | 16 | 17 | 17 | 20 | 115 | 153 | 2 | 12 | 14 | 7 | 184 | 4 | 0 | 0 | 0 | 0 | 0 | 217 | 0 | 15 | 281 | 6 | 10 |
| 55 | 2 | 659 | 16 | 17 | 18 | 18 | 22 | 135 | 118 | 2 | 14 | 15 | 7 | 219 | 4 | 0 | 0 | 0 | 0 | 0 | 242 | 0 | 16 | 322 | 6 | 8 |
| 60 | 2 | 567 | 17 | 18 | 18 | 20 | 24 | 155 | 92 | 2 | 16 | 15 | 7 | 254 | 4 | 0 | 0 | 0 | 0 | 0 | 268 | 0 | 17 | 365 | 6 | 9 |
| 65 | 2 | 494 | 18 | 19 | 19 | 22 | 26 | 174 | 73 | 2 | 17 | 16 | 7 | 289 | 4 | 0 | 0 | 0 | 0 | 1 | 295 | 0 | 18 | 411 | 6 | 9 |
| 70 | 2 | 435 | 19 | 20 | 20 | 24 | 28 | 192 | 58 | 2 | 19 | 17 | 7 | 324 | 5 | 1 | 0 | 0 | 0 | 1 | 320 | 0 | 19 | 455 | 7 | 9 |
| 75 | 2 | 388 | 20 | 21 | 20 | 26 | 30 | 210 | 47 | 2 | 21 | 18 | 7 | 359 | 5 | 1 | 0 | 0 | 0 | 1 | 341 | 0 | 20 | 497 | 7 | 8 |
| 80 | 2 | 349 | 21 | 21 | 21 | 27 | 32 | 226 | 39 | 2 | 24 | 18 | 7 | 393 | 5 | 1 | 1 | 0 | 0 | 1 | 366 | 1 | 22 | 543 | 7 | 9 |
| 85 | 2 | 317 | 21 | 22 | 21 | 29 | 34 | 242 | 33 | 2 | 26 | 19 | 7 | 428 | 5 | 1 | 1 | 0 | 0 | 1 | 389 | 1 | 22 | 589 | 7 | 9 |
| 90 | 2 | 289 | 22 | 23 | 22 | 31 | 36 | 257 | 28 | 2 | 28 | 19 | 7 | 462 | 5 | 1 | 1 | 0 | 0 | 1 | 410 | 1 | 23 | 633 | 7 | 9 |
| 95 | 2 | 265 | 23 | 23 | 22 | 33 | 38 | 271 | 24 | 2 | 30 | 20 | 7 | 496 | 5 | 1 | 1 | 0 | 0 | 2 | 434 | 1 | 23 | 679 | 7 | 9 |
| 100 | 2 | 244 | 23 | 24 | 23 | 34 | 40 | 284 | 21 | 2 | 32 | 20 | 7 | 529 | 5 | 1 | 1 | 0 | 0 | 2 | 452 | 1 | 23 | 721 | 7 | 8 |
| 105 | 2 | 225 | 24 | 24 | 23 | 36 | 42 | 297 | 19 | 2 | 33 | 21 | 7 | 563 | 5 | 2 | 1 | 0 | 0 | 2 | 472 | 1 | 24 | 765 | 7 | 9 |
| 110 | 2 | 208 | 24 | 25 | 24 | 38 | 44 | 309 | 17 | 2 | 35 | 21 | 7 | 595 | 5 | 2 | 1 | 0 | 0 | 2 | 489 | 1 | 25 | 806 | 7 | 8 |
| 115 | 2 | 194 | 25 | 26 | 24 | 40 | 46 | 320 | 15 | 2 | 37 | 21 | 6 | 628 | 6 | 2 | 2 | 0 | 0 | 3 | 508 | 2 | 25 | 850 | 7 | 9 |
| 120 | 2 | 181 | 25 | 26 | 24 | 41 | 48 | 331 | 13 | 2 | 39 | 21 | 6 | 660 | 6 | 2 | 2 | 0 | 0 | 3 | 525 | 2 | 24 | 890 | 7 | 8 |
| 125 | 2 | 169 | 26 | 26 | 24 | 43 | 50 | 341 | 12 | 2 | 41 | 22 | 6 | 691 | 6 | 2 | 2 | 0 | 0 | 3 | 541 | 2 | 25 | 932 | 7 | 8 |
| 130 | 2 | 158 | 26 | 27 | 25 | 45 | 52 | 350 | 11 | 2 | 43 | 22 | 6 | 723 | 6 | 2 | 2 | 1 | 0 | 4 | 554 | 2 | 25 | 970 | 7 | 8 |
| 135 | 2 | 148 | 27 | 27 | 25 | 46 | 54 | 359 | 10 | 2 | 45 | 22 | 6 | 754 | 6 | 3 | 3 | 1 | 1 | 4 | 569 | 3 | 25 | 1010 | 7 | 8 |
| 140 | 2 | 139 | 27 | 28 | 25 | 48 | 56 | 368 | 9 | 2 | 47 | 22 | 6 | 784 | 6 | 3 | 3 | 1 | 1 | 4 | 583 | 3 | 25 | 1049 | 7 | 8 |
| 145 | 2 | 131 | 28 | 28 | 26 | 50 | 57 | 376 | 8 | 2 | 49 | 22 | 6 | 814 | 6 | 3 | 3 | 1 | 1 | 5 | 598 | 3 | 25 | 1089 | 8 | 8 |
| 150 | 2 | 124 | 28 | 28 | 26 | 52 | 59 | 384 | 7 | 2 | 51 | 22 | 6 | 844 | 6 | 3 | 3 | 1 | 1 | 5 | 614 | 3 | 24 | 1128 | 8 | 8 |
| 155 | 2 | 117 | 28 | 29 | 26 | 53 | 61 | 391 | 7 | 2 | 53 | 22 | 6 | 873 | 6 | 4 | 4 | 1 | 1 | 5 | 627 | 4 | 26 | 1166 | 8 | 8 |
| 160 | 2 | 111 | 29 | 29 | 26 | 55 | 63 | 398 | 6 | 2 | 55 | 22 | 6 | 903 | 6 | 4 | 4 | 1 | 1 | 6 | 641 | 4 | 24 | 1204 | 8 | 8 |
| 165 | 2 | 105 | 29 | 29 | 26 | 56 | 65 | 405 | 6 | 2 | 57 | 22 | 6 | 931 | 6 | 4 | 4 | 1 | 1 | 6 | 650 | 4 | 26 | 1239 | 8 | 7 |
| 170 | 2 | 100 | 29 | 30 | 26 | 58 | 67 | 411 | 5 | 1 | 58 | 22 | 6 | 960 | 6 | 5 | 5 | 1 | 1 | 7 | 661 | 5 | 23 | 1273 | 7 | 7 |
| 175 | 2 | 95 | 30 | 30 | 27 | 60 | 69 | 417 | 5 | 1 | 59 | 22 | 6 | 988 | 6 | 5 | 5 | 1 | 1 | 7 | 669 | 5 | 24 | 1305 | 7 | 6 |
| 180 | 2 | 90 | 30 | 30 | 27 | 62 | 71 | 422 | 5 | 1 | 60 | 22 | 6 | 1016 | 6 | 5 | 5 | 1 | 1 | 7 | 674 | 5 | 25 | 1335 | 7 | 6 |
| Age | SI | N | H | H100 | BA | dbh | dbh100 | S | N_YFT | BA_YFT | dbh_YFT | S_YFT | CAI | TVP | MAI | ABV_CO2_SINGLE | ABV_CO2_YFT_SINGLE | ROOT_CO2_SINGLE | ROOT_CO2_YFT_SINGLE | FULL_TREE_CO2 | STAND_CO2 | FULL_TREE_CO2_YFT | STAND_CO2_YFT | TVP_CO2 | MAI_CO2 | CAI_CO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | - | 1 | 1 | 2 | 1 | 2 | 5 | 51 | 0 | 1 | 1 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 0 | 1 | 13 | 0 | 1 |
| 10 | 3 | - | 2 | 3 | 3 | 3 | 3 | 10 | 102 | 0 | 2 | 2 | 1 | 14 | 0 | 0 | 0 | 0 | 0 | 0 | 26 | 0 | 2 | 26 | 1 | 2 |
| 15 | 3 | - | 4 | 4 | 5 | 4 | 5 | 15 | 153 | 0 | 2 | 2 | 2 | 21 | 1 | 0 | 0 | 0 | 0 | 0 | 39 | 0 | 2 | 39 | 1 | 3 |
| 20 | 3 | - | 5 | 5 | 7 | 5 | 6 | 20 | 204 | 1 | 3 | 3 | 2 | 28 | 1 | 0 | 0 | 0 | 0 | 0 | 52 | 0 | 3 | 52 | 1 | 4 |
| 25 | 3 | - | 6 | 7 | 8 | 7 | 8 | 24 | 256 | 1 | 4 | 4 | 3 | 36 | 1 | 0 | 0 | 0 | 0 | 0 | 65 | 0 | 4 | 65 | 2 | 5 |
| 30 | 3 | - | 7 | 8 | 10 | 8 | 9 | 29 | 307 | 1 | 5 | 4 | 3 | 43 | 1 | 0 | 0 | 0 | 0 | 0 | 78 | 0 | 5 | 78 | 2 | 6 |
| 35 | 3 | - | 9 | 10 | 12 | 10 | 11 | 34 | 358 | 1 | 5 | 5 | 4 | 50 | 1 | 0 | 0 | 0 | 0 | 0 | 91 | 0 | 6 | 91 | 2 | 7 |
| 40 | 3 | 1428 | 10 | 11 | 13 | 11 | 12 | 39 | 409 | 1 | 6 | 6 | 4 | 57 | 1 | 0 | 0 | 0 | 0 | 0 | 104 | 0 | 6 | 104 | 3 | 7 |
| 45 | 3 | 1146 | 11 | 12 | 14 | 13 | 14 | 55 | 282 | 1 | 7 | 6 | 4 | 80 | 2 | 0 | 0 | 0 | 0 | 0 | 132 | 0 | 7 | 146 | 3 | 8 |
| 50 | 3 | 941 | 12 | 13 | 15 | 14 | 16 | 72 | 205 | 1 | 8 | 7 | 5 | 104 | 2 | 0 | 0 | 0 | 0 | 0 | 159 | 0 | 7 | 179 | 4 | 7 |
| 55 | 3 | 786 | 13 | 14 | 16 | 16 | 18 | 89 | 155 | 1 | 10 | 8 | 5 | 129 | 2 | 0 | 0 | 0 | 0 | 0 | 189 | 0 | 8 | 217 | 4 | 8 |
| 60 | 3 | 668 | 14 | 15 | 17 | 18 | 20 | 107 | 118 | 1 | 11 | 8 | 5 | 155 | 3 | 0 | 0 | 0 | 0 | 0 | 212 | 0 | 9 | 249 | 4 | 7 |
| 65 | 3 | 576 | 15 | 16 | 17 | 20 | 22 | 124 | 92 | 1 | 13 | 9 | 5 | 181 | 3 | 0 | 0 | 0 | 0 | 0 | 235 | 0 | 10 | 282 | 4 | 7 |
| 70 | 3 | 504 | 16 | 17 | 18 | 21 | 24 | 140 | 72 | 1 | 14 | 10 | 5 | 207 | 3 | 0 | 0 | 0 | 0 | 1 | 256 | 0 | 11 | 314 | 4 | 6 |
| 75 | 3 | 446 | 17 | 18 | 19 | 23 | 26 | 157 | 58 | 1 | 16 | 10 | 5 | 234 | 3 | 0 | 0 | 0 | 0 | 1 | 279 | 0 | 12 | 350 | 5 | 7 |
| 80 | 3 | 399 | 18 | 18 | 19 | 25 | 28 | 172 | 47 | 1 | 18 | 11 | 5 | 261 | 3 | 1 | 0 | 0 | 0 | 1 | 302 | 0 | 13 | 386 | 5 | 7 |
| 85 | 3 | 360 | 18 | 19 | 20 | 26 | 29 | 187 | 39 | 1 | 20 | 12 | 5 | 288 | 3 | 1 | 0 | 0 | 0 | 1 | 324 | 0 | 14 | 422 | 5 | 7 |
| 90 | 3 | 326 | 19 | 20 | 20 | 28 | 31 | 202 | 33 | 1 | 22 | 12 | 5 | 315 | 4 | 1 | 0 | 0 | 0 | 1 | 343 | 0 | 15 | 456 | 5 | 7 |
| 95 | 3 | 298 | 20 | 20 | 21 | 30 | 33 | 216 | 29 | 1 | 24 | 13 | 5 | 341 | 4 | 1 | 1 | 0 | 0 | 1 | 364 | 1 | 16 | 492 | 5 | 7 |
| 100 | 3 | 273 | 20 | 21 | 21 | 32 | 35 | 229 | 25 | 1 | 26 | 14 | 5 | 368 | 4 | 1 | 1 | 0 | 0 | 1 | 381 | 1 | 16 | 526 | 5 | 7 |
| 105 | 3 | 251 | 21 | 22 | 22 | 33 | 37 | 241 | 22 | 1 | 27 | 14 | 5 | 395 | 4 | 1 | 1 | 0 | 0 | 2 | 401 | 1 | 17 | 563 | 5 | 7 |
| 110 | 3 | 232 | 22 | 22 | 22 | 35 | 38 | 253 | 19 | 1 | 29 | 15 | 5 | 421 | 4 | 1 | 1 | 0 | 0 | 2 | 418 | 1 | 17 | 597 | 5 | 7 |
| 115 | 3 | 215 | 22 | 23 | 22 | 36 | 40 | 265 | 17 | 1 | 31 | 15 | 5 | 448 | 4 | 1 | 1 | 0 | 0 | 2 | 436 | 1 | 18 | 633 | 6 | 7 |
| 120 | 3 | 200 | 22 | 23 | 23 | 38 | 42 | 276 | 15 | 1 | 33 | 15 | 5 | 474 | 4 | 2 | 1 | 0 | 0 | 2 | 453 | 1 | 18 | 668 | 6 | 7 |
| 125 | 3 | 186 | 23 | 24 | 23 | 40 | 44 | 286 | 14 | 1 | 35 | 16 | 5 | 500 | 4 | 2 | 1 | 0 | 0 | 3 | 468 | 1 | 19 | 702 | 6 | 7 |
| 130 | 3 | 173 | 24 | 24 | 23 | 41 | 46 | 296 | 12 | 1 | 37 | 16 | 5 | 526 | 4 | 2 | 2 | 0 | 0 | 3 | 480 | 2 | 19 | 733 | 6 | 6 |
| 135 | 3 | 162 | 24 | 24 | 24 | 43 | 48 | 305 | 11 | 1 | 39 | 16 | 5 | 552 | 4 | 2 | 2 | 0 | 0 | 3 | 494 | 2 | 19 | 766 | 6 | 7 |
| 140 | 3 | 152 | 24 | 25 | 24 | 45 | 49 | 314 | 10 | 1 | 41 | 17 | 5 | 577 | 4 | 2 | 2 | 1 | 0 | 3 | 507 | 2 | 19 | 799 | 6 | 6 |
| 145 | 3 | 143 | 25 | 25 | 24 | 46 | 51 | 322 | 9 | 1 | 43 | 17 | 5 | 603 | 4 | 3 | 2 | 1 | 0 | 4 | 522 | 2 | 19 | 832 | 6 | 7 |
| 150 | 3 | 135 | 25 | 25 | 24 | 48 | 53 | 330 | 8 | 1 | 45 | 17 | 5 | 628 | 4 | 3 | 2 | 1 | 1 | 4 | 538 | 2 | 19 | 868 | 6 | 7 |
| 155 | 3 | 127 | 25 | 26 | 25 | 50 | 55 | 338 | 8 | 1 | 47 | 17 | 5 | 653 | 4 | 3 | 3 | 1 | 1 | 4 | 548 | 3 | 21 | 900 | 6 | 6 |
| 160 | 3 | 120 | 26 | 26 | 25 | 51 | 56 | 345 | 7 | 1 | 49 | 18 | 5 | 678 | 4 | 3 | 3 | 1 | 1 | 5 | 561 | 3 | 21 | 933 | 6 | 7 |
| 165 | 3 | 114 | 26 | 26 | 25 | 53 | 58 | 352 | 6 | 1 | 50 | 18 | 5 | 702 | 4 | 3 | 3 | 1 | 1 | 5 | 574 | 3 | 19 | 965 | 6 | 6 |
| 170 | 3 | 108 | 26 | 27 | 25 | 54 | 60 | 358 | 6 | 1 | 52 | 18 | 5 | 727 | 4 | 4 | 3 | 1 | 1 | 5 | 582 | 3 | 20 | 993 | 6 | 6 |
| 175 | 3 | 102 | 27 | 27 | 25 | 56 | 62 | 365 | 6 | 1 | 53 | 18 | 5 | 751 | 4 | 4 | 4 | 1 | 1 | 6 | 592 | 4 | 22 | 1024 | 6 | 6 |
| 180 | 3 | 96 | 27 | 27 | 25 | 58 | 64 | 371 | 5 | 1 | 54 | 18 | 5 | 775 | 4 | 4 | 4 | 1 | 1 | 6 | 593 | 4 | 19 | 1044 | 6 | 4 |
Appendix B. Additional Figures
Appendix B.1. Beech
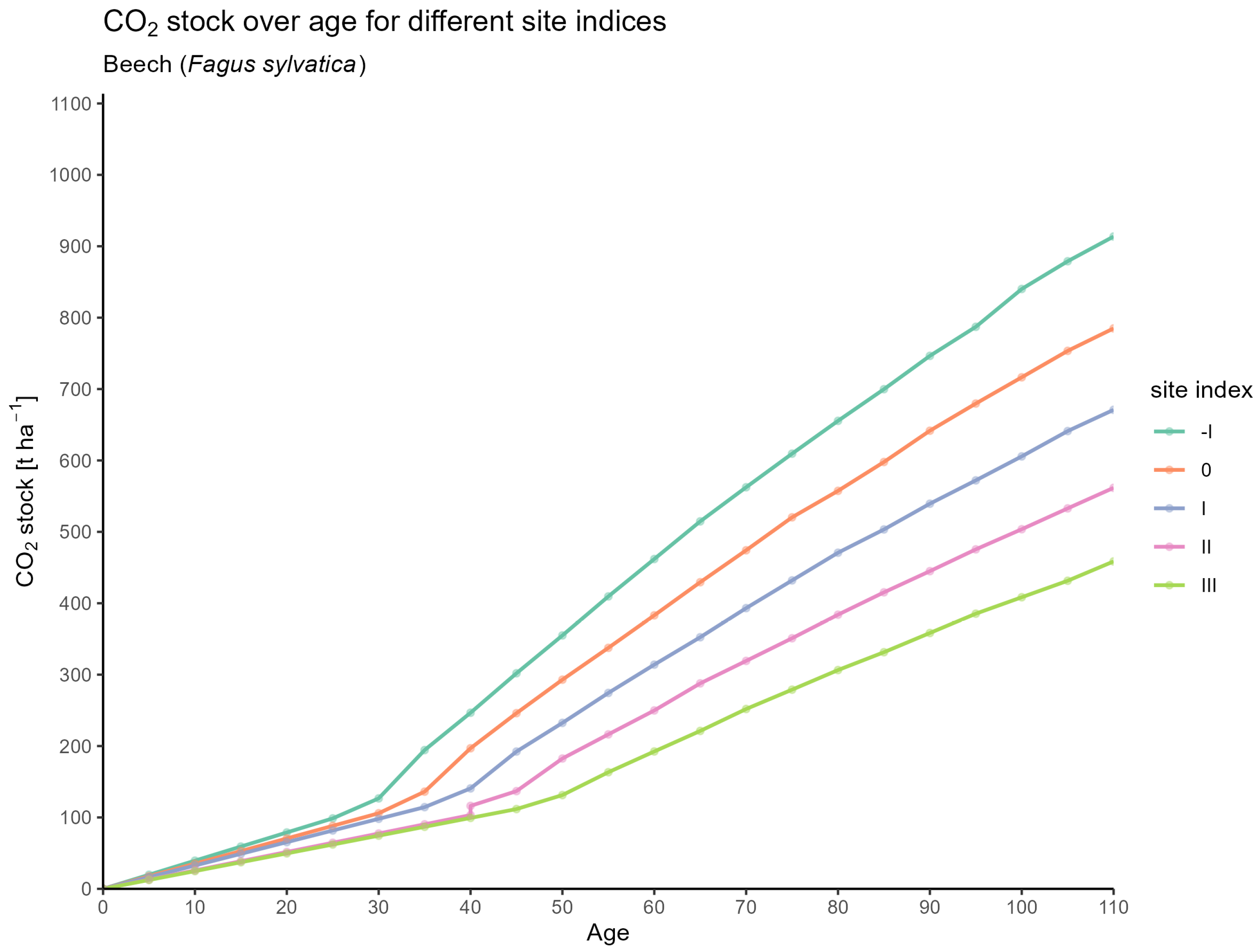

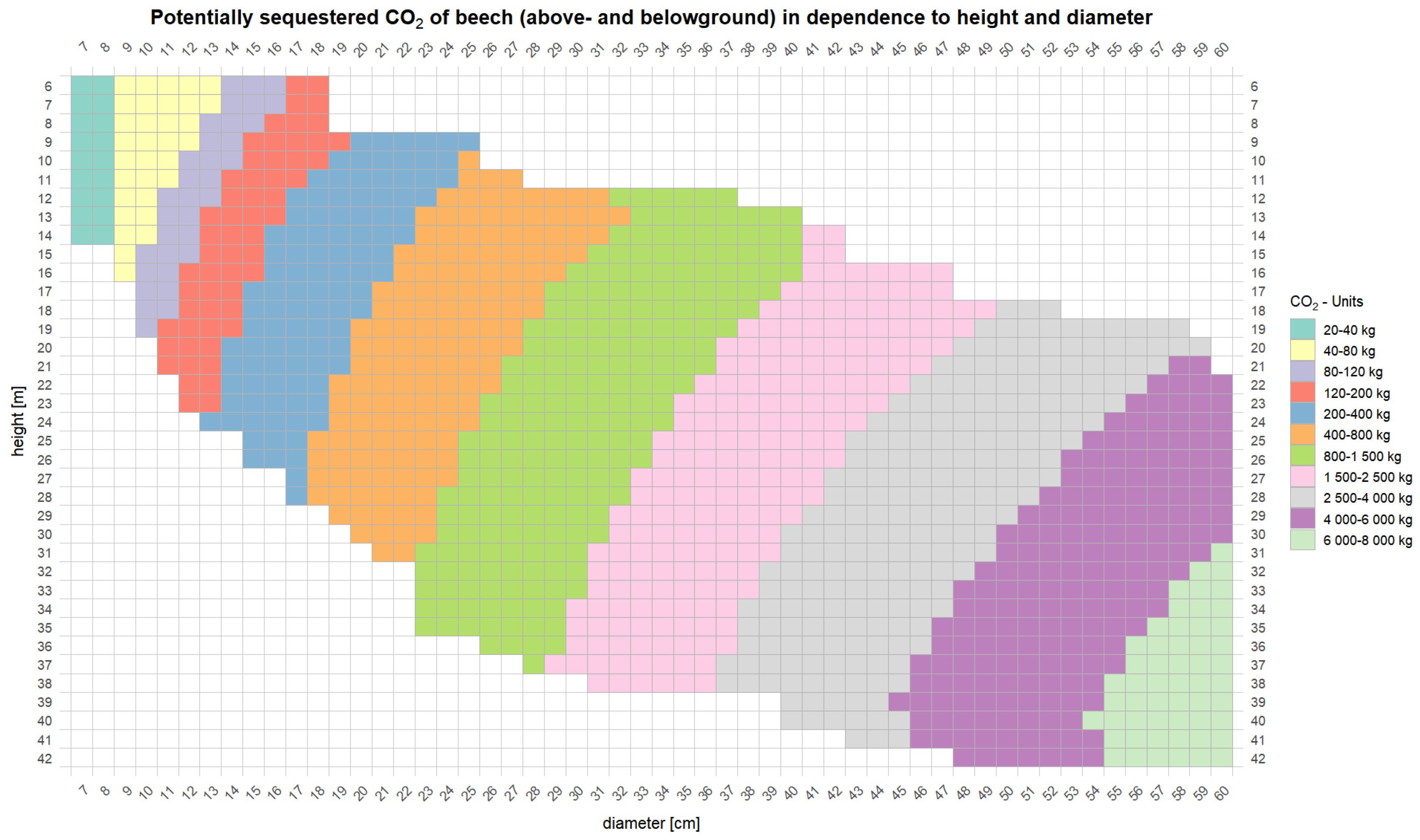
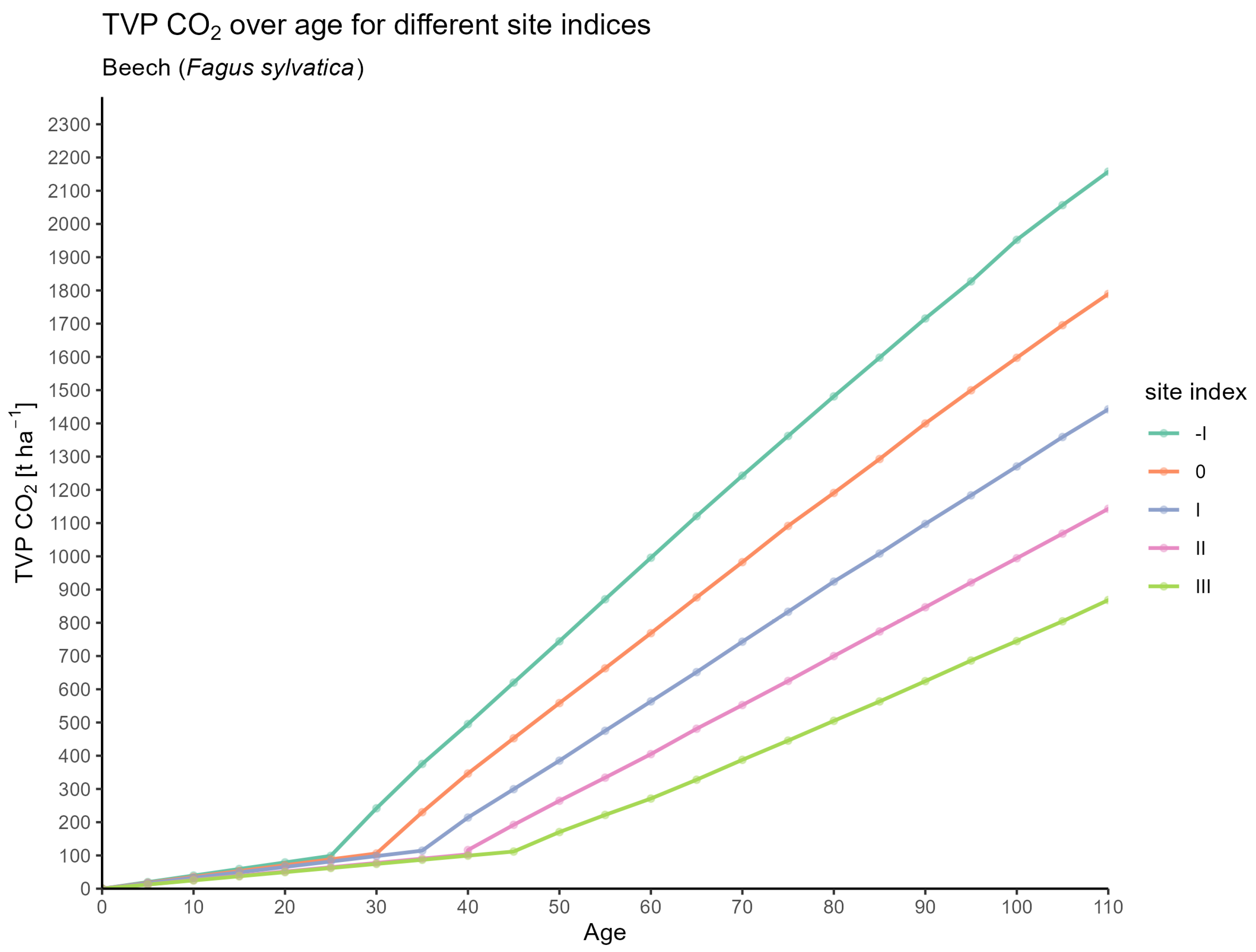
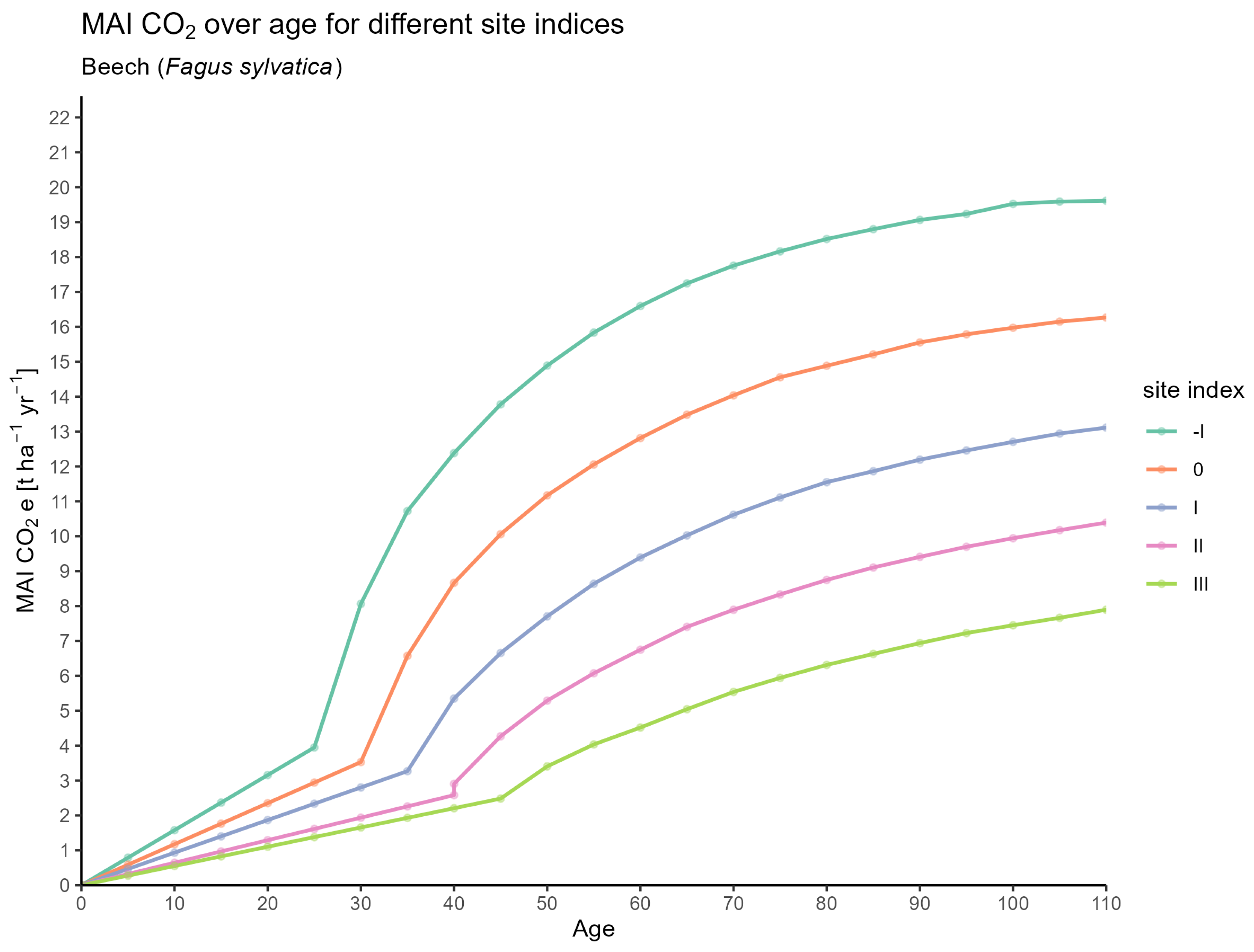
Appendix B.2. Spruce

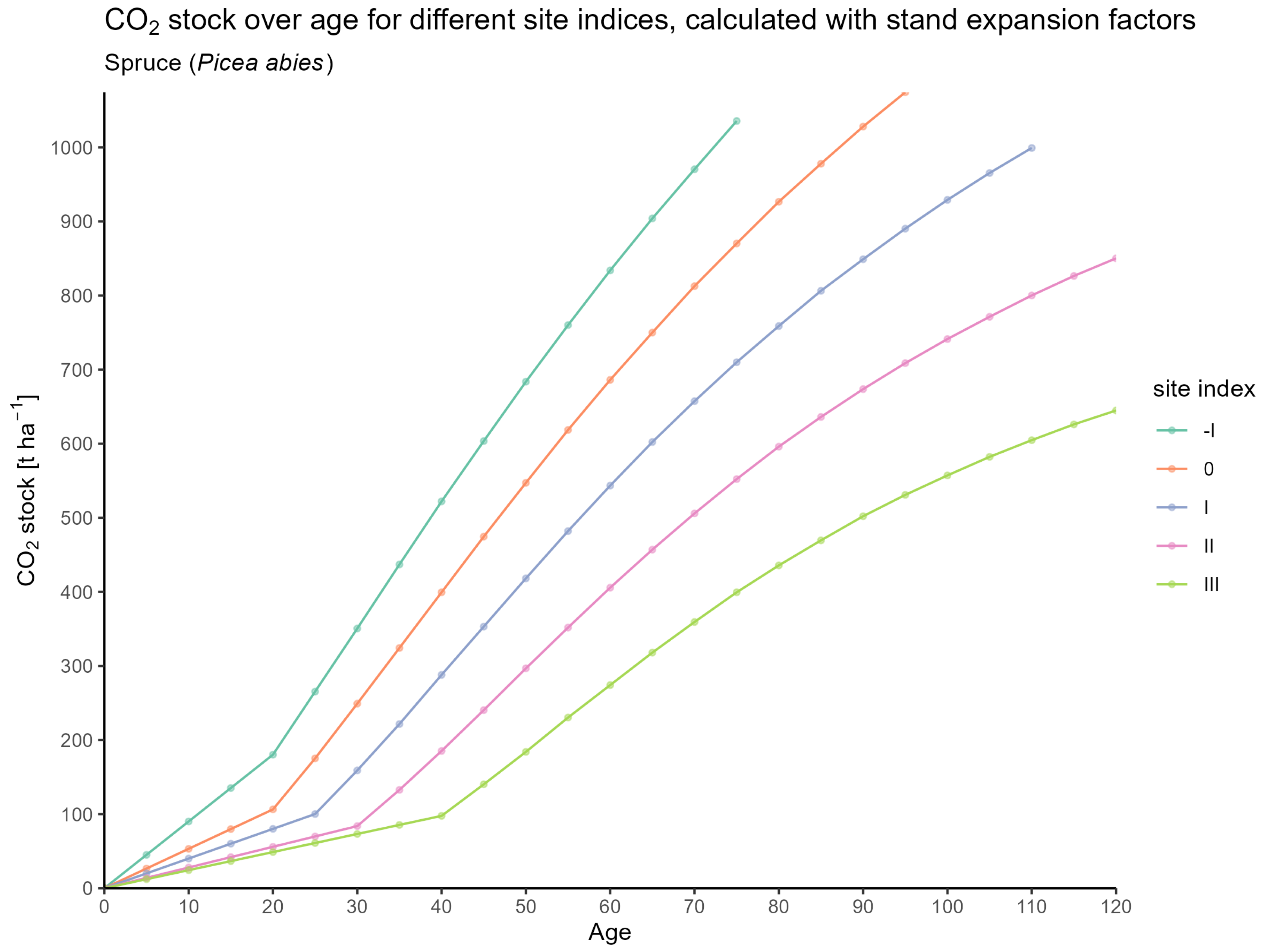
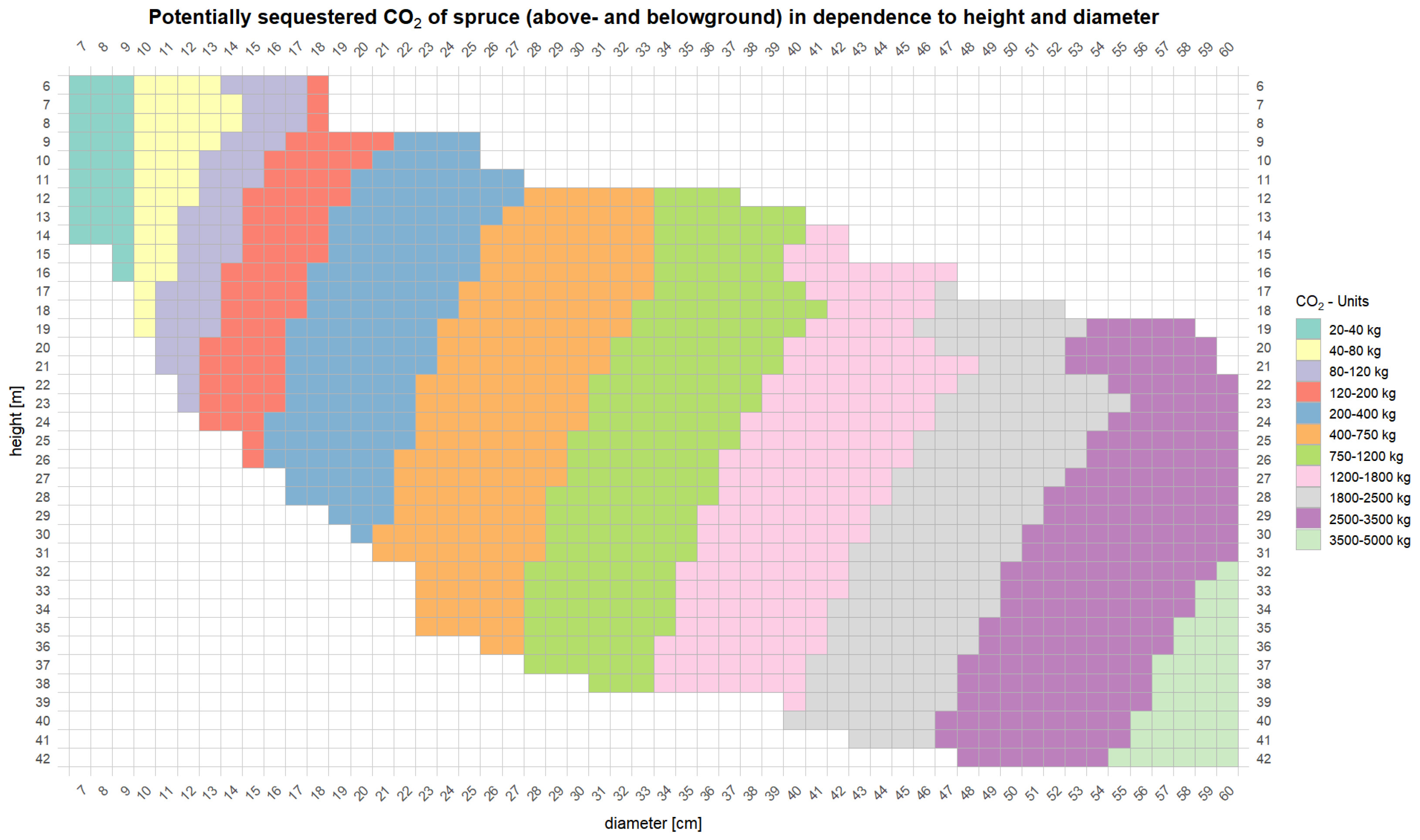
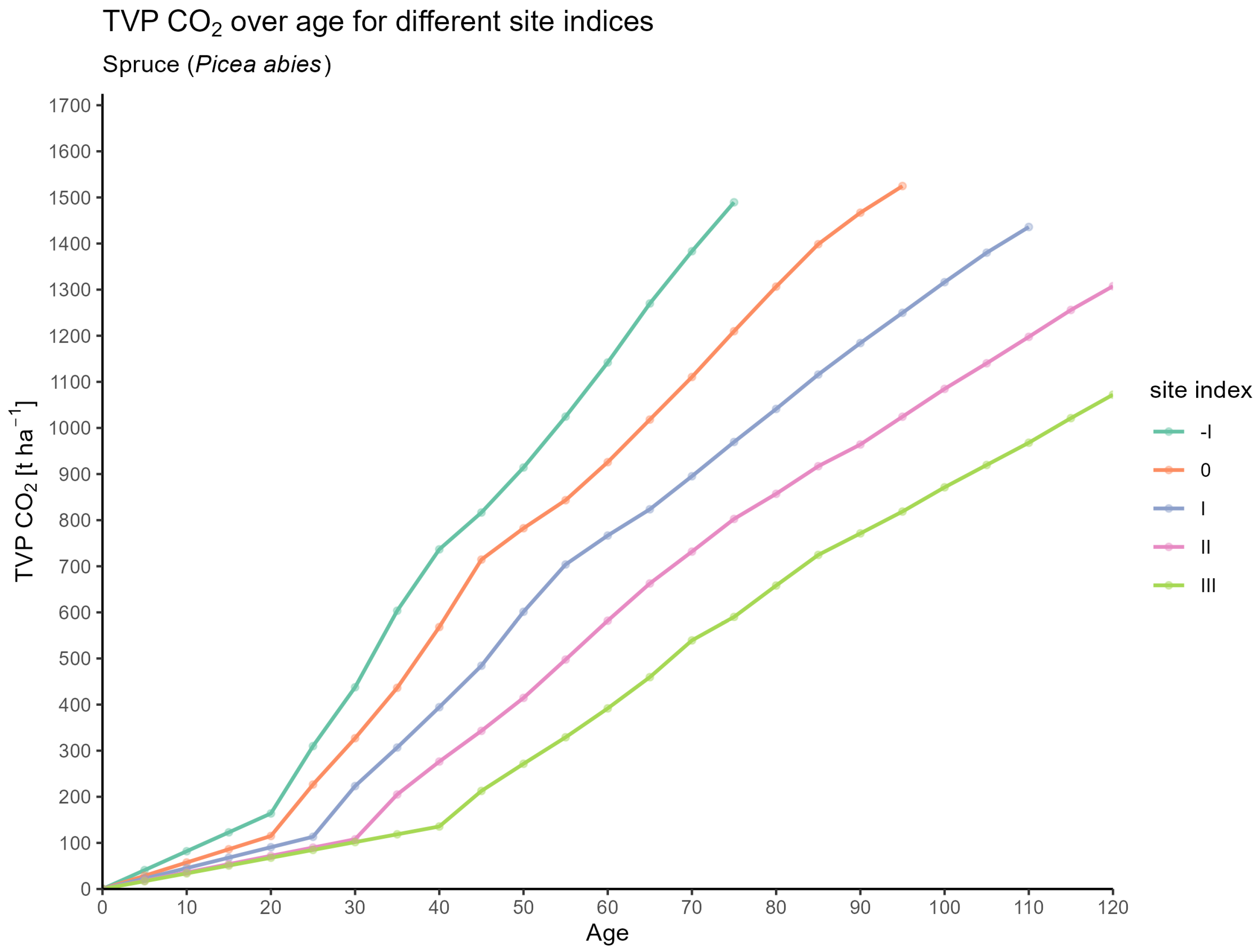
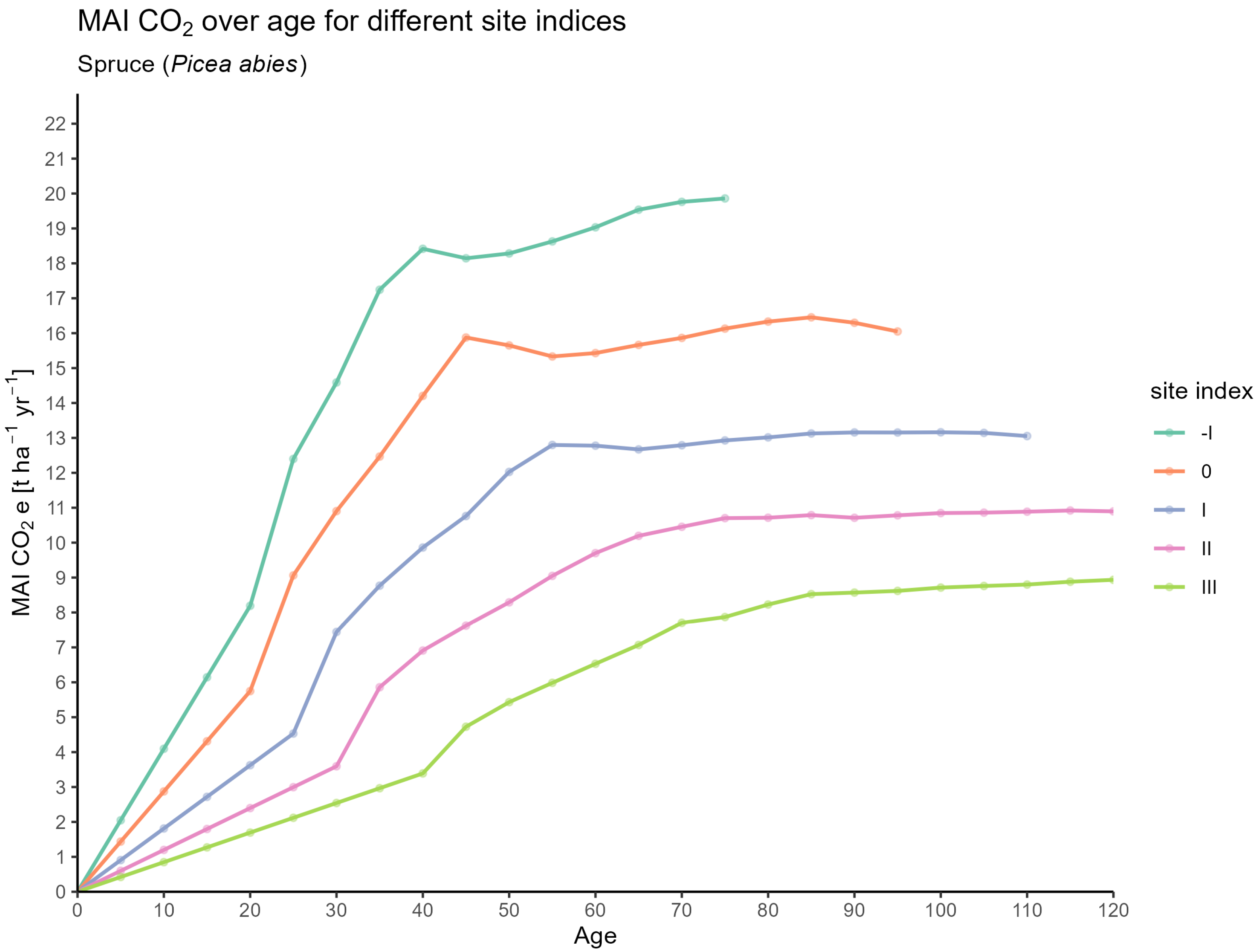
Appendix B.3. Pine

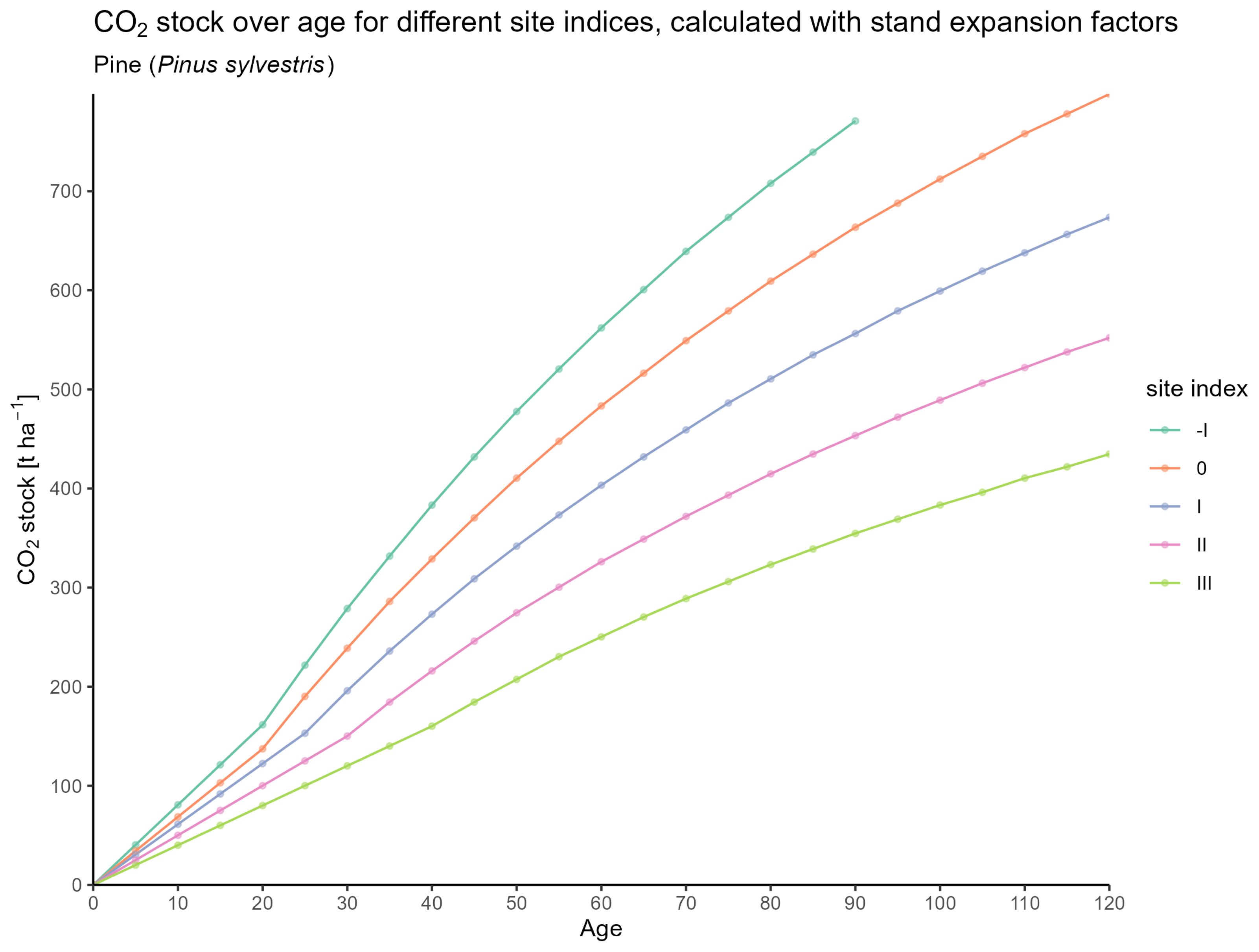
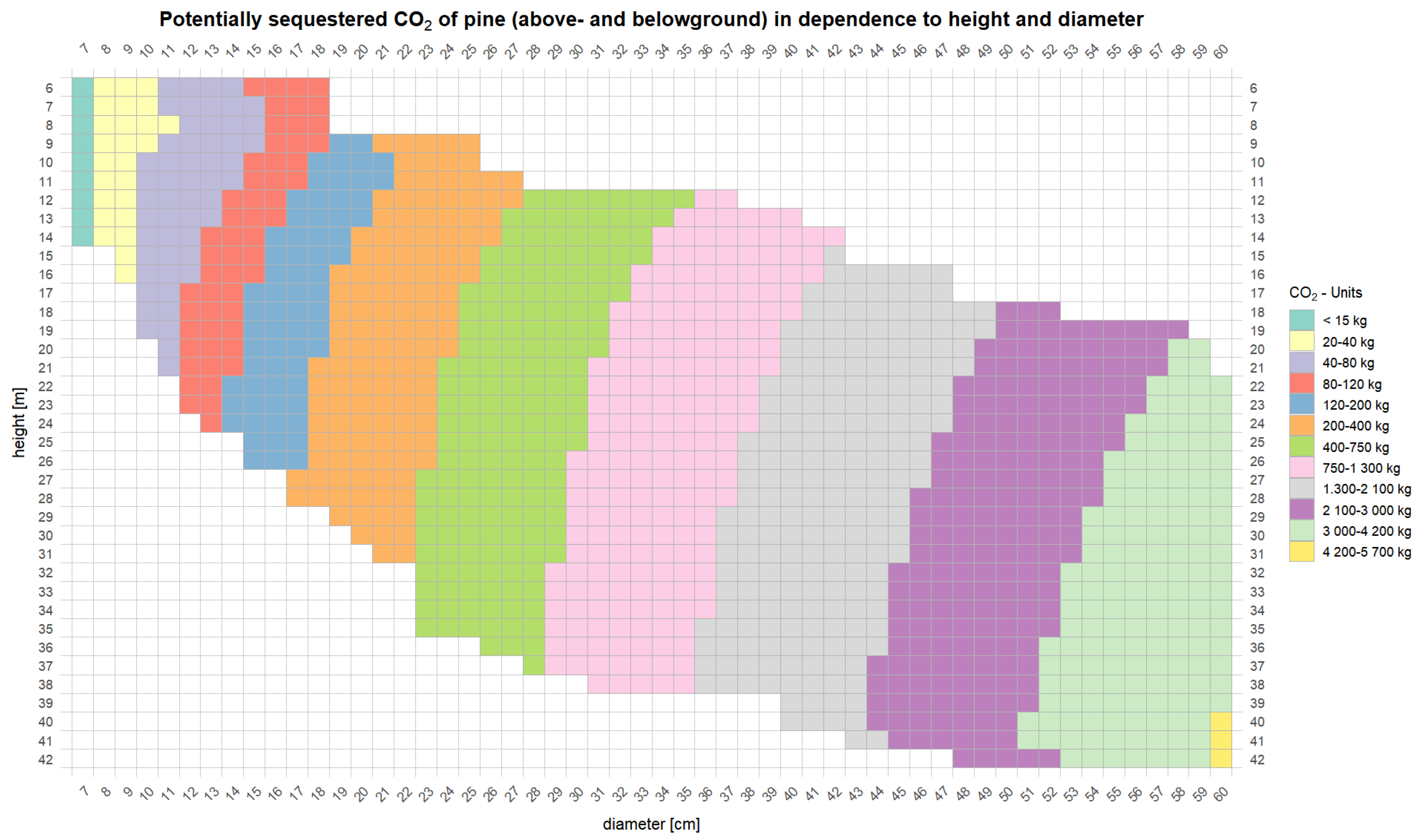
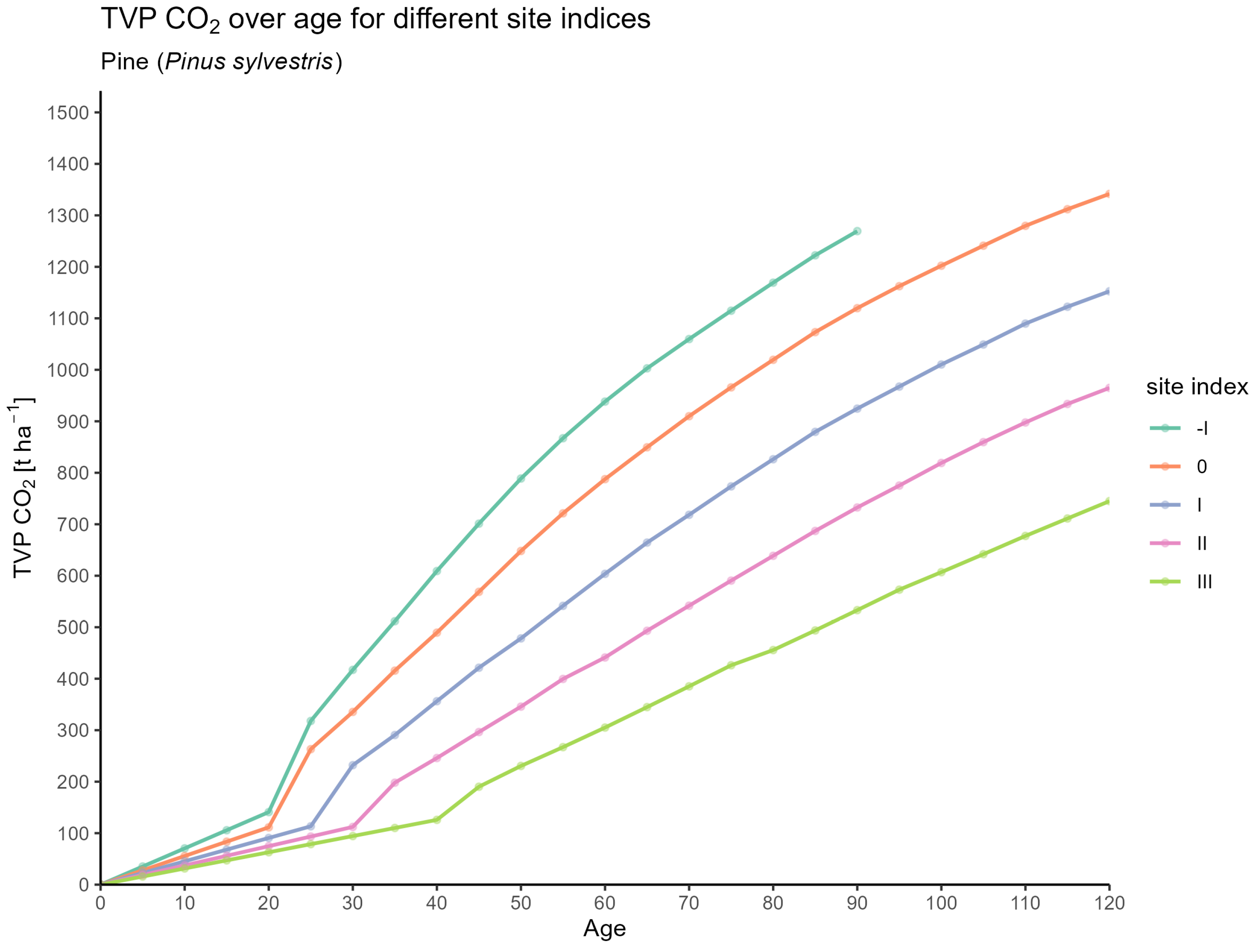
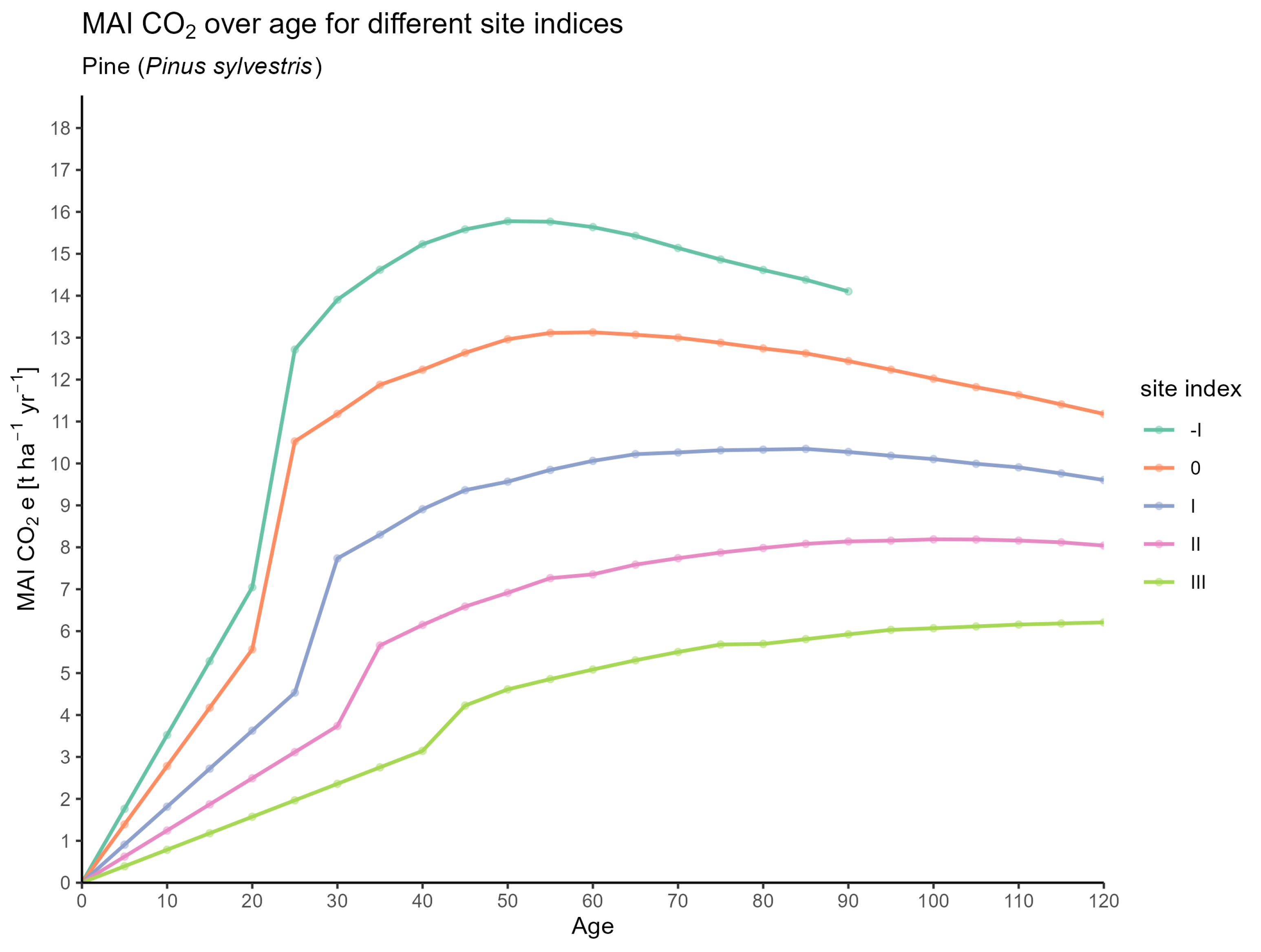
Appendix B.4. Douglas Fir

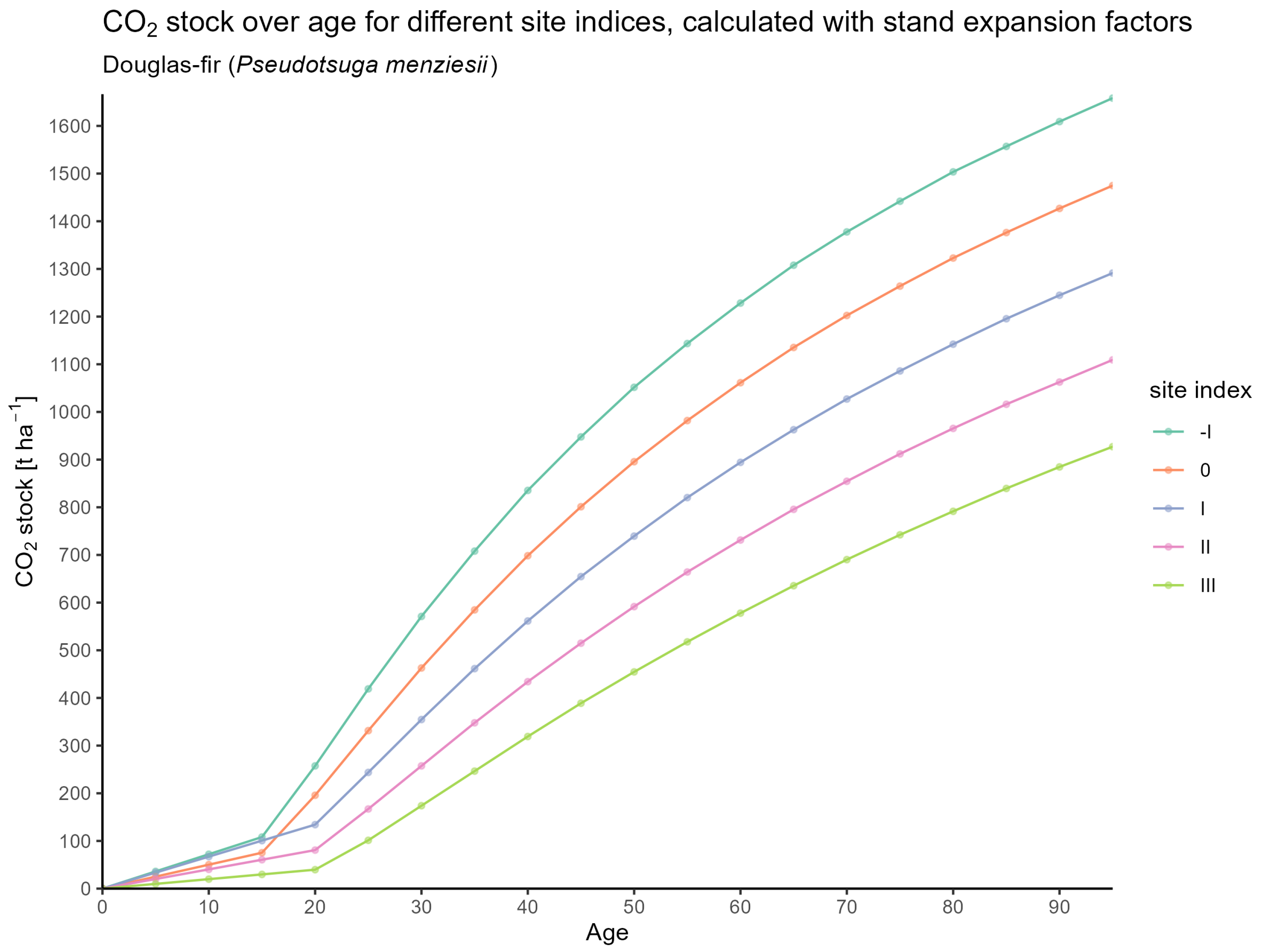
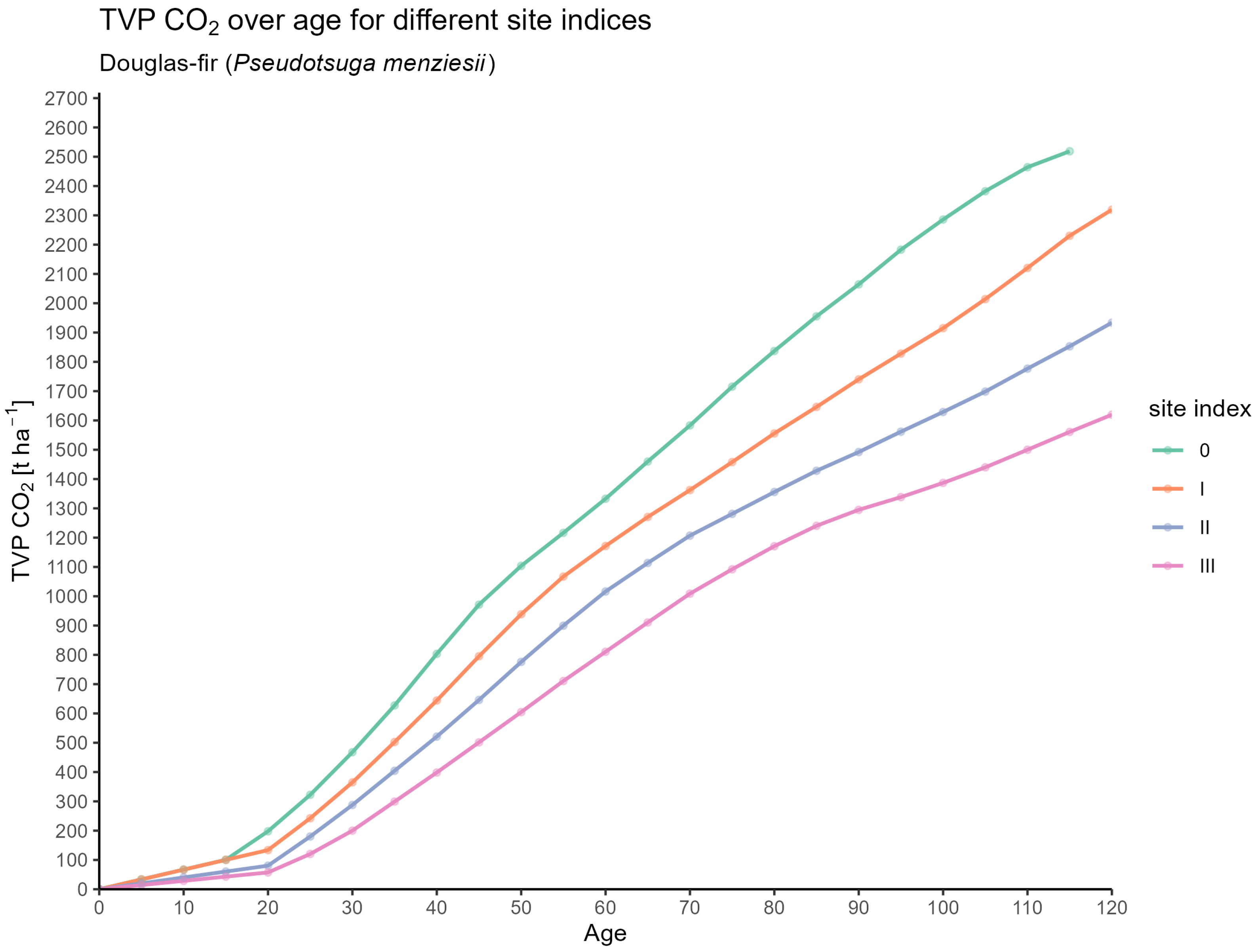
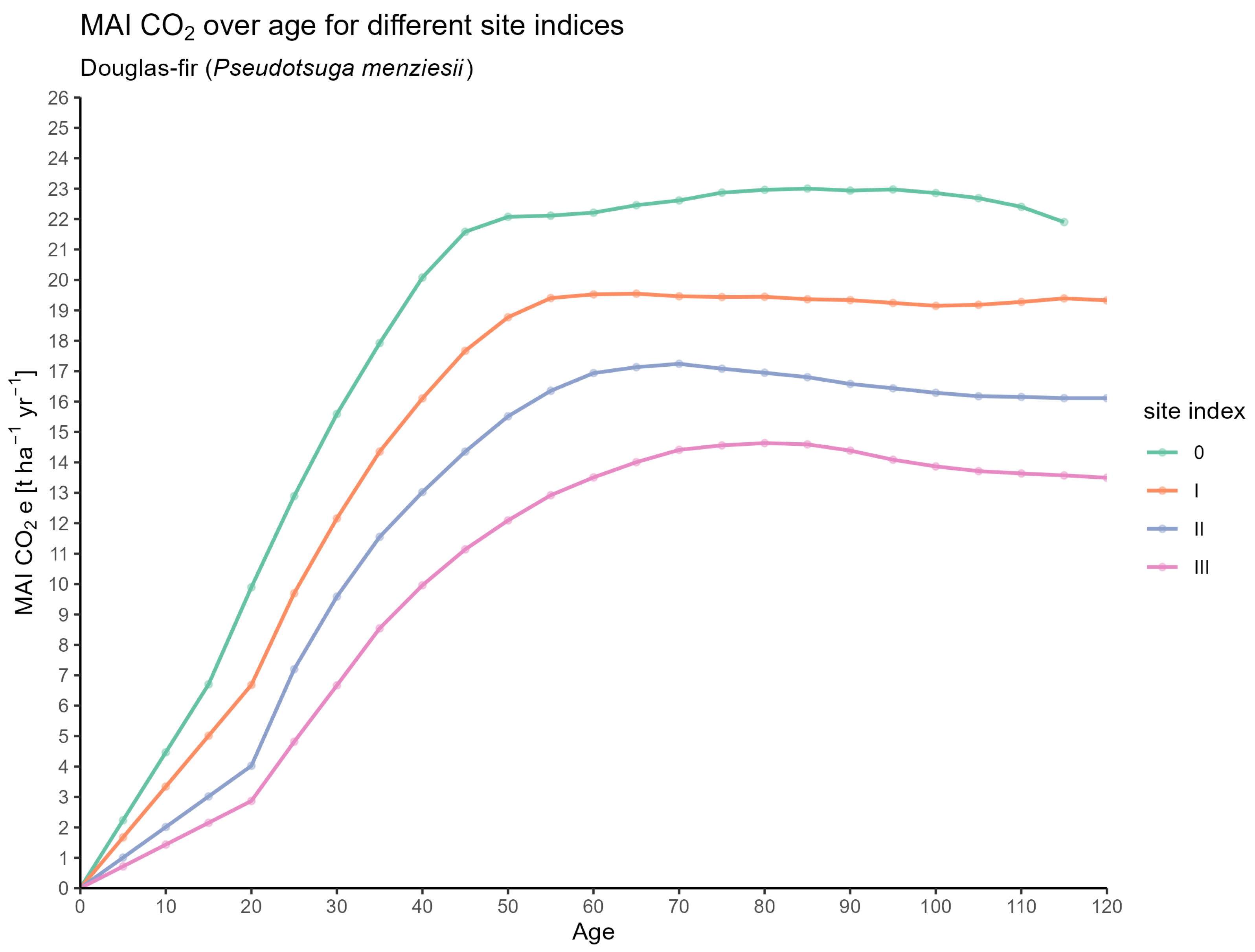
Appendix B.5. Deviation Plots for Other Tree Species
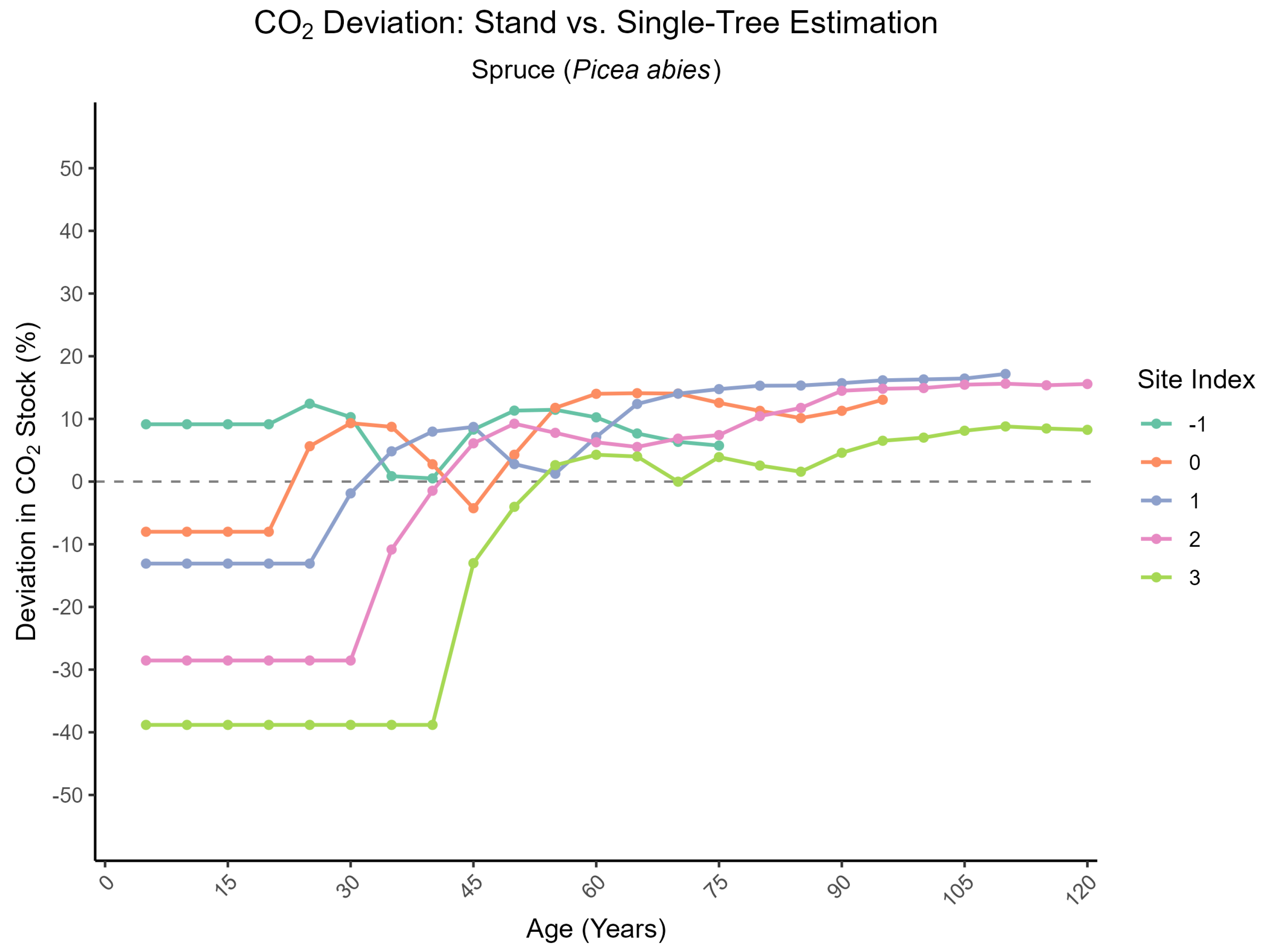
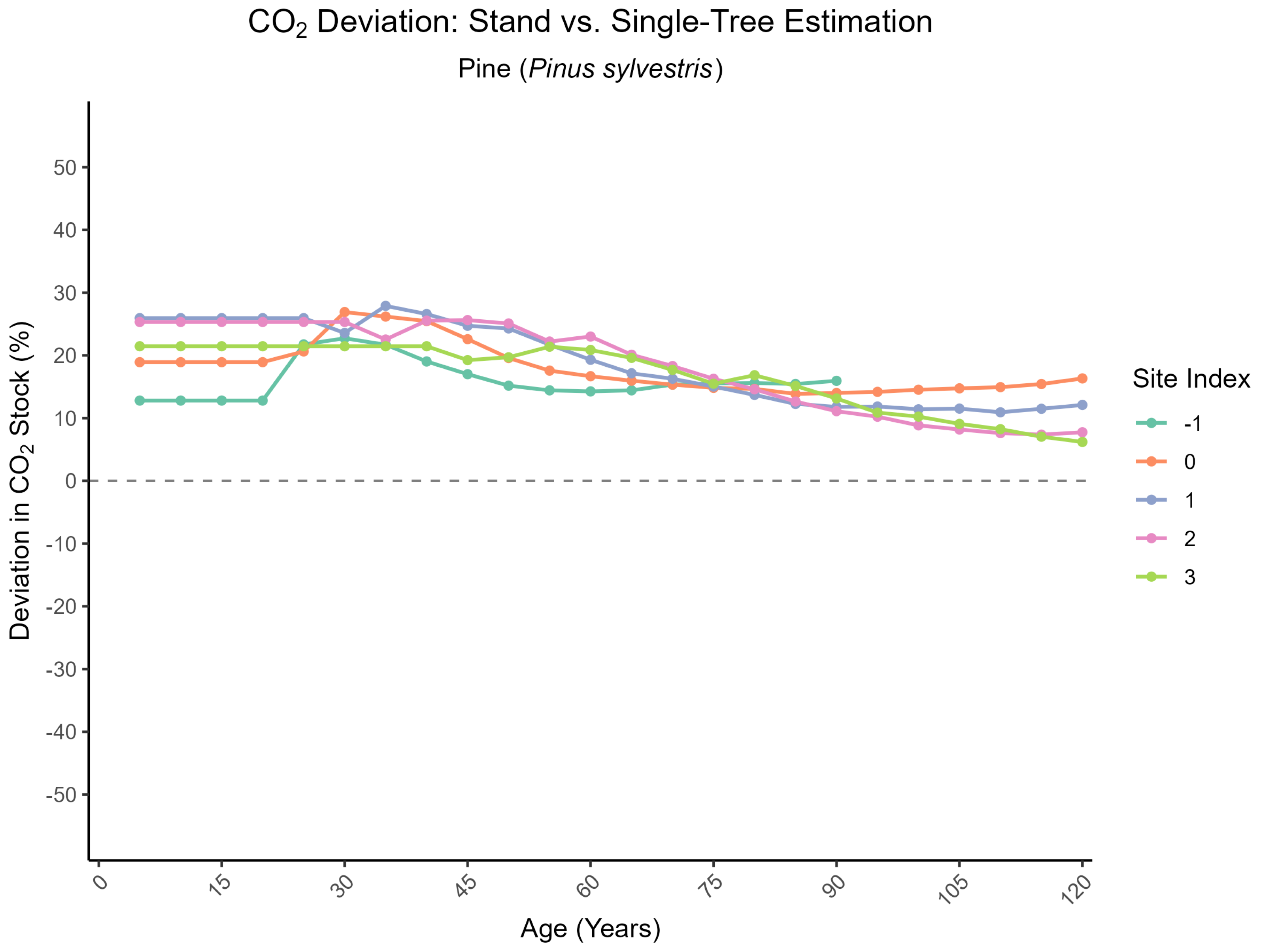
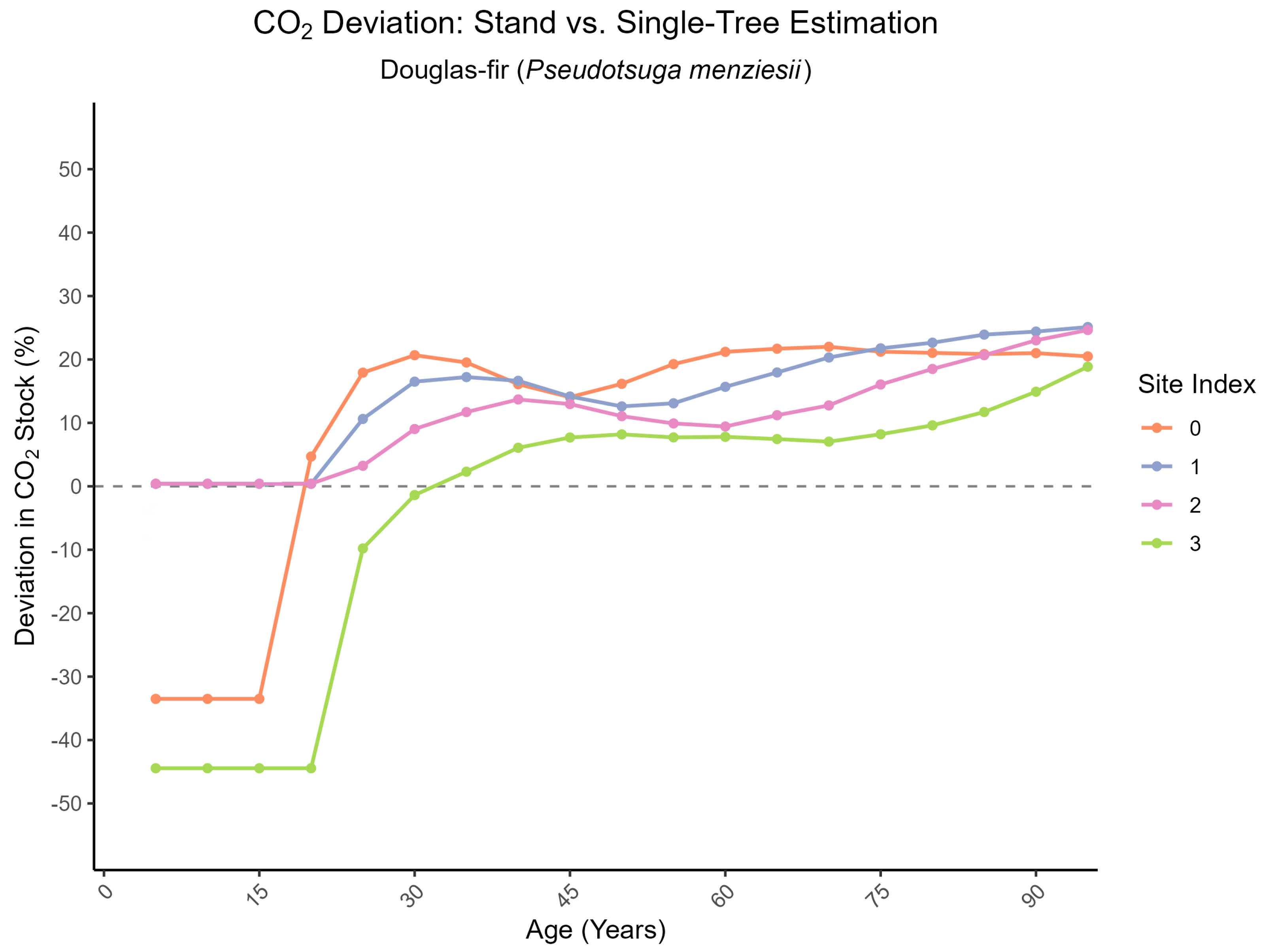
Appendix C. Code Examples
| Listing A1. R Shiny dashboard. |
 |
 |
 |
 |
References
- Eaton-Rye, J.J.; Tripathy, B.C.; Sharkey, T.D. Photosynthesis: Plastid Biology, Energy Conversion and Carbon Assimilation; Springer Science+Business Media B.V.: Berlin/Heidelberg, Germany, 2012; Volume 34. [Google Scholar] [CrossRef]
- EU Commission. Commission Implementing Regulation (EU) 2018/2066 of 19 December 2018 on the Monitoring and Reporting of Greenhouse Gas Emissions Pursuant to Directive 2003/87/EC of the European Parliament and of the Council and amending Commission Regulation (EU) No 601/2012, 2018. Legislation. Available online: https://eur-lex.europa.eu/eli/reg_impl/2018/2066/oj/eng (accessed on 2 October 2025).
- European Parliament and Council of the European Union. Regulation (EU) 2021/1119 of the European Parliament and of the Council of 30 June 2021 Establishing the Framework for Achieving Climate Neutrality and Amending Regulations (EC) No 401/2009 and (EU) 2018/1999 (‘European Climate Law’), 2021. PE/27/2021/REV/1. Available online: https://eur-lex.europa.eu/eli/reg/2021/1119/oj/eng (accessed on 2 October 2025).
- Korosuo, A.; Pilli, R.; Abad Viñas, R.; Blujdea, V.; Colditz, R.; Fiorese, G.; Rossi, S.; Vizzarri, M.; Grassi, G. The role of forests in the EU climate policy: Are we on the right track? Carbon Balance Manag. 2023, 18, 15. [Google Scholar] [CrossRef]
- Bundesministerium der Justiz und Verbraucherschutz and Bundesamt für Justiz. Bundes-Klimaschutzgesetz (KSG), 2019. Bundes-Klimaschutzgesetz vom 12. Dezember 2019 (BGBl. I S. 2513), das Zuletzt Durch Artikel 1 des Gesetzes vom 15. Juli 2024 (BGBl. 2024 I Nr. 235) GeäNdert Worden Ist. Available online: https://www.gesetze-im-internet.de/ksg/BJNR251310019.html (accessed on 2 October 2025).
- Ministry of the Environment. Climate Act. 2022. Available online: https://www.finlex.fi/api/media/statute-foreign-language-translation/687510/mainPdf/main.pdf?timestamp=2022-06-09T21%3A00%3A00.000Z (accessed on 2 October 2025).
- L’Assemblée Nationale et le Sénat. LOI n° 2019-1147 du 8 Novembre 2019 Relative à L’énergie et au Climat (1). 2019. Available online: https://www.legifrance.gouv.fr/loda/id/JORFTEXT000039355955 (accessed on 2 October 2025).
- Minister for Environment, Climate and Communications. Climate Action and Low Carbon Development (Amendment) Act 2021. 2021. Available online: https://www.irishstatutebook.ie/eli/2021/act/32/section/15/enacted/en/html (accessed on 2 October 2025).
- The Assembly of the Republic Portugal. Climate Framework Law. 2021. Available online: https://www.bportugal.pt/sites/default/files/documents/2024-07/Law%20N.98-2021_EN.pdf (accessed on 2 October 2025).
- Ledermann, T.; Braun, M.; Kindermann, G.; Jandl, R.; Ludvig, A.; Schadauer, K.; Schwarzbauer, P.; Weiss, P. Effects of Silvicultural Adaptation Measures on Carbon Stock of Austrian Forests. Forests 2022, 13, 565. [Google Scholar] [CrossRef]
- Dixon, R.K.; Solomon, A.M.; Brown, S.; Houghton, R.A.; Trexier, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Land Use, Land-Use Change and Forestry, 5.4.1.1. Identification of Carbon Pools; Technical Report; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- Hu, J.; Jåstad, E.O.; Rørstad, P.K. Exploring trade-offs in forest carbon storage: A cost-effectiveness study of Nordic forests and harvested wood products. For. Policy Econ. 2025, 179, 103619. [Google Scholar] [CrossRef]
- Howard, C.; Dymond, C.C.; Griess, V.C.; Tolkien-Spurr, D.; van Kooten, G.C. Wood product carbon substitution benefits: A critical review of assumptions. Carbon Balance Manag. 2021, 16, 9. [Google Scholar] [CrossRef]
- Leskinen, P.; Cardellini, G.; González-García, S.; Hurmekoski, E.; Sathre, R.; Seppälä, J.; Smyth, C.; Stern, T.; Verkerk, P.J. Substitution Effects of Wood-Based Products in Climate Change Mitigation; Technical Report; EFI Joensuu: Joensuu, Finland, 2018. [Google Scholar]
- Myllyviita, T.; Soimakallio, S.; Judl, J.; Seppälä, J. Wood substitution potential in greenhouse gas emission reduction–review on current state and application of displacement factors. For. Ecosyst. 2021, 8, 42. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Evaluation of Stand Biomass Estimation Methods for Major Forest Types in the Eastern Da Xing’an Mountains, Northeast China. Forests 2019, 10, 715. [Google Scholar] [CrossRef]
- Riedel, T.; Kändler, G. Nationale Treibhausgasberichterstattung: Neue Funktionen zur Schätzung der oberirdischen Biomasse am Einzelbaum. Forstarchiv 2017, 88, 31–38. [Google Scholar] [CrossRef]
- Marklund, L.G. Biomass Functions for Norway Spruce (Picea abies (L.) Karst) in Sweden. In Biomassafunktioner för Gran i Sverige; Rapport; Sveriges lantbruksuniversitet, Institutionen för Skogstaxering: Uppsala, Sweden, 1987; p. 43. [Google Scholar]
- Umweltbundesamt. Berichterstattung unter der Klimarahmenkonvention der Vereinten Nationen und dem Kyoto-Protokoll 2023: Nationaler Inventarbericht zum Deutschen Treibhausgasinventar 1990–2021; Umweltbundesamt: Berlin, Germany, 2023. [Google Scholar]
- Dieter, M.; Elsasser, P. Carbon Stocks and Carbon Stock Changes in the Tree Biomass of Germany’s Forests. Forstwiss. Cent. 2002, 121, 195–210. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth and Yield, 1. softcover print ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Sanquetta, C.R.; Corte, A.P.; da Silva, F. Biomass expansion factor and root-to-shoot ratio for Pinus in Brazil. Carbon Balance Manag. 2011, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yi, M.J.; Son, Y.; Park, P.S.; Lee, K.H.; Son, Y.M.; Kim, R.H.; Jeong, M.J. Biomass Expansion Factors of Natural Japanese Red Pine (Pinus densiflora) Forests in Korea. J. Plant Biol. 2010, 53, 381–386. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Šebeň, V. Biomass functions and expansion factors for young trees of European ash and Sycamore maple in the Inner Western Carpathians. Austrian J. For. Sci. 2015, 132, 1–26. [Google Scholar]
- Baral, S.; Lamichhane, S.; Koirala, A. Current status of improved forest management carbon offset projects in the US voluntary market. For. Policy Econ. 2025, 178, 103567. [Google Scholar] [CrossRef]
- European Parliament; Council of the European Union. Regulation (EU) 2024/3012 of the European Parliament and of the Council of 27 November 2024 Establishing a Union Certification Framework for Permanent Carbon Removals, Carbon Farming and Carbon Storage in Products. OJ L, 6 December 2024, 2024. PE/92/2024/REV/1, ELI: 32024R3012, in Force. Available online: https://eur-lex.europa.eu/eli/reg/2024/3012/oj/eng (accessed on 2 October 2025).
- Indrajaya, Y.; Weikard, H.P.; Mohren, G.; Van der Werf, E. Paying for forest carbon: Cost-effectiveness of the Verified Carbon Standard (VCS) remuneration scheme. Nat. Resour. Model. 2023, 37, e12387. [Google Scholar] [CrossRef]
- Kull, S.J.; Rampley, G.J.; Morken, S.; Metsaranta, J.M.; Neilson, E.T.; Kurz, W.A. Operational-Scale Carbon Budget Model of the Canadian Forest Sector (CBM-CFS3) Version 1.2: User’s Guide (2024) (V1.2); Technical Report; Natural Resources Canada: Ottawa, ON, Canada, 2024. [Google Scholar] [CrossRef]
- Rosenkranz, L.; Seintsch, B.; Wippel, B.; Dieter, M. Income losses due to the implementation of the Habitats Directive in forests—Conclusions from a case study in Germany. For. Policy Econ. 2014, 38, 207–218. [Google Scholar] [CrossRef]
- Rosenkranz, L.; Seintsch, B. Opportunitätskostenanalyse zur Implementierung des naturschutzorientierten Waldbehandlungskonzepts: Neue Multifunktionalität. Landbauforsch.-Appl. Agric. For. Res. 2015, 3–4, 145–160. [Google Scholar] [CrossRef]
- Rosenkranz, L. Auswirkungen der Umsetzung von Naturschutzmaßnahmen auf die Forst- und Holzwirtschaft; University of Goettingen: Goettingen, Germany, 2016. [Google Scholar] [CrossRef]
- Regelmann, C.; Rosenkranz, L.; Seintsch, B.; Dieter, M. Economic Evaluation of Different Implementation Variants and Categories of the EU Biodiversity Strategy 2030 Using Forestry in Germany as a Case Study. Forests 2023, 14, 1173. [Google Scholar] [CrossRef]
- Regelmann, C.; Brinkord, M.; Rock, J.; Seintsch, B.; Dieter, M. Unveiling the Carbon Sequestration Potential and Opportunity Costs of Beech-dominated Forest Enterprises Decommissioned from Timber Utilization. Eur. J. For. Res. 2025. [Google Scholar]
- Schober, R. Ertragstafeln Wichtiger Baumarten bei Verschiedener Durchforstung, 4. aufl. ed.; Sauerländer: Frankfurt, Germany, 1995. [Google Scholar]
- Matthews, R.W.; Jenkins, T.; Mackie, E.D.; Dick, E.C. Forest Yield: A Handbook on Forest Growth and Yield Tables for British Forestry; Forestry Commission: London, UK, 2016. [Google Scholar]
- Décourt, N. Les tables de production. leurs limites et leur utilité. Rev. For. Fr. 1964, 8–9, 640–657. [Google Scholar] [CrossRef]
- Szymkiewicz, B. Tablice Zasobności i Przyrostu Drzewostanów Ważniejszych Gatunków Drzew Leśnych/Bolesław Szymkiewicz; Państwowe Wydaw. Rolnicze i Leśne: Warszawa, Poland, 2001. [Google Scholar]
- Stage, A.R.; Renner, D.L.; Chapman, R.C. Selected Yield Tables for Plantations and Natural Stands in Inland Northwest Forests; US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1988. [CrossRef]
- Albert, M.; Nagel, J.; Schmidt, M.; Nagel, R.V.; Spellmann, H. Eine neue Generation von Ertragstafeln für die Baumarten Eiche, Buche, Fichte, Douglasie und Kiefer in Nordwestdeutschland; Beiträge aus der Nordwestdeutschen Forstlichen Versuchsanstalt; Universitätsverlag Göttingen: Göttingen, Germany, 2024; Volume 22. [Google Scholar] [CrossRef]
- Hansen, J.; Nagel, J. Waldwachstumskundliche Softwaresysteme auf Basis von TreeGrOSS—Anwendung und Theoretische Grundlagen; Beiträge aus der Nordwestdeutschen Forstlichen Versuchsanstalt; Nordwestdeutsche Forstliche Versuchsanstalt: Göttingen, Germany, 2014; Volume 11. [Google Scholar]
- FNR e.V. Waldpflege; Technical Report; Fachagentur Nachwachsende Rohstoffe e.V.: Gülzow-Prüzen, Germany, 2022. [Google Scholar]
- Kramer, H.; Gussone, H.A.; Schober, R. Waldwachstumslehre. Oekologische und Anthropogene Einfluesse auf das Wachstum des Waldes, Seine Massen-und Wertleistung und die Bestandessicherheit; Verlag Kessel: Remagen-Oberwinter, Germany, 1988; ISBN 3490056167. [Google Scholar]
- Kalkanlı Genç, Ş.; Diamantopoulou, M.J.; Özçelik, R. Tree Biomass Modeling Based on the Exploration of Regression and Artificial Neural Networks Approaches. Forests 2023, 14, 2429. [Google Scholar] [CrossRef]
- Kublin, E. Einheitliche Beschreibung der Schaftform—Methoden und Programme—BDATPro. A Uniform Description of Stem Profiles—Methods and Programs—BDATPro. Forstwiss. Cent. 2003, 122, 183–200. [Google Scholar] [CrossRef]
- Vonderach, C.; Kublin, E.; Bösch, B.; Kändler, G.; Cullmann, D. Implementation of BDAT Tree Taper Fortran Functions. 2023. Available online: https://cran.r-project.org/web/packages/rBDAT/rBDAT.pdf (accessed on 2 October 2025).
- McMinn, R. Characterization of Douglas Fir root systems. Can. J. Bot. 2011, 41, 105–122. [Google Scholar] [CrossRef]
- Bolte, A.; Hertel, D.; Ammer, C.; Schmid, I.; Nörr, R.; Kuhr, M.; Redde, N. Freilandmethoden zur Untersuchung von Baumwurzeln. Forstarchiv 2003, 74, 240–262. [Google Scholar]
- Neubauer, M.; Demant, B. Wurzeln als Kohlenstoffspeicher: Untersuchungen zur Unterirdischen Biomasse von Birke, Eiche und Kiefer; Universitätsdruckerei Freiburg, Albert-Ludwigs-Universität Freiburg: Freiburg im Breisgau, Germany, 2016. [Google Scholar]
- Drexhage, M.; Colin, F. Estimating root system biomass from breast-height diameters. Forestry 2001, 74, 491–497. [Google Scholar] [CrossRef]
- Kramer, H.; Akça, A. Leitfaden zur Waldmesslehre, 5. überarb. aufl. ed.; Sauerländer: Bad Orb, Germany, 2008. [Google Scholar]
- Reineke, L.H. Perfecting a stand-density index for even-aged forest. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Lamlom, S.H.; Savidge, R.A. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenergy 2003, 25, 381–388. [Google Scholar] [CrossRef]
- Scerri, E.R. The Periodic Table, 2nd ed.; Very Short Introductions; Oxford University Press: Oxford, UK, 2019; Volume 289. [Google Scholar]
- Paul, C.; Weber, M.; Mosandl, R. Kohlenstoffbindung junger Aufforstungsflächen; Karl Gyer Institut, Lehrstuhl fuer Waldbau der Technischen Universitaet Muenchen: Freising, Germany, 2009. [Google Scholar]
- Posit Team. RStudio: Integrated Development Environment for R; Posit Software; PBC: Boston, MA, USA, 2025. [Google Scholar]
- Nuske, R.; Staupendahl, K.; Albert, M. et.nwfva: Forest Yield Tables for Northwest Germany and their Application (0.2.0). 2025. Available online: https://cran.r-project.org/web/packages/et.nwfva/et.nwfva.pdf (accessed on 2 October 2025).
- Zhang, H.; Liu, S.; Yu, J.; Li, J.; Shangguan, Z.; Deng, L. Thinning increases forest ecosystem carbon stocks. For. Ecol. Manag. 2024, 555, 121702. [Google Scholar] [CrossRef]
- Erkan, N.; Güner, Ş.; Aydın, A. Thinning effects on stand growth, carbon stocks, and soil properties in Brutia pine plantations. Carbon Balance Manag. 2023, 18, 6. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Peltola, H.; Briceño, E.; Kellomäki, S. Changed thinning regimes may increase carbon stock under climate change: A case study from a Finnish boreal forest. Clim. Change 2007, 81, 431–454. [Google Scholar] [CrossRef]
- Pretzsch, H.; Del Río, M.; Ammer, C.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; Dirnberger, G.; Drössler, L.; et al. Growth and yield of mixed versus pure stands of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) analysed along a productivity gradient through Europe. Eur. J. For. Res. 2015, 134, 927–947. [Google Scholar] [CrossRef]
- Forrester, D.; Benneter, A.; Bouriaud, O.; Bauhus, J. Diversity and competition influence tree allometric relationships - developing functions for mixed-species forests. J. Ecol. 2016, 105, 761–774. [Google Scholar] [CrossRef]
- Rewald, B.; Leuschner, C. Belowground competition in a broad-leaved temperate mixed forest: Pattern analysis and experiments in a four-species stand. Eur. J. For. Res. 2009, 128, 387–398. [Google Scholar] [CrossRef]
- Burschel, P.; Krsten, E.; Larson, B.C.; Weber, M. Present role of German forests and forestry in the national carbon budget and options to its increase. Water Air Soil Pollut. 1993, 70, 325–340. [Google Scholar] [CrossRef]
- Wirth, C.; Schumacher, J.; Schulze, E.D. Generic biomass functions for Norway spruce in Central Europe–a meta-analysis approach toward prediction and uncertainty estimation. Tree Physiol. 2004, 24, 121–139. [Google Scholar] [CrossRef]
- Martin, A.R.; Doraisami, M.; Thomas, S.C. Global patterns in wood carbon concentration across the world’s trees and forests. Nat. Geosci. 2018, 11, 915–920. [Google Scholar] [CrossRef]
- Rivoire, M.; Le Moguedec, G. A generalized self-thinning relationship for multi-species and mixed-size forests. Ann. For. Sci. 2012, 69, 207–219. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; Condés, S.; del Río, M.; Pretzsch, H.; Ducey, M.J. Maximum stand density strongly depends on species-specific wood stability, shade and drought tolerance. For. Int. J. For. Res. 2018, 91, 459–469. [Google Scholar] [CrossRef]
- Pretzsch, H.; Hilmers, T.; del Río, M. The effect of structural diversity on the self-thinning line, yield level, and density-growth relationship in even-aged stands of Norway spruce. For. Ecol. Manag. 2024, 556, 121736. [Google Scholar]
- Forrester, D.I.; Baker, T.G.; Elms, S.R.; Hobi, M.L.; Ouyang, S.; Wiedemann, J.C.; Xiang, W.; Zell, J.; Pulkkinen, M. Self-thinning tree mortality models that account for vertical stand structure, species mixing and climate. For. Ecol. Manag. 2021, 487, 118936. [Google Scholar] [CrossRef]
- Caicoya, A.T.; Biber, P.; del Río, M.; Ruiz-Peinado, R.; Arcangeli, C.; Matthews, R.; Pretzsch, H. Self-thinning of Scots pine across Europe changes with solar radiation, precipitation and temperature but does not show trends in time. For. Ecol. Manag. 2024, 552, 121585. [Google Scholar]
- Janda, P.; Tepley, A.J.; Schurman, J.S.; Brabec, M.; Nagel, T.A.; Bače, R.; Begovič, K.; Chaskovskyy, O.; Čada, V.; Dušátko, M.; et al. Drivers of basal area variation across primary late-successional Picea abies forests of the Carpathian Mountains. For. Ecol. Manag. 2019, 435, 196–204. [Google Scholar] [CrossRef]
- Klein, D.; Schulz, C. LWF Merkblatt 27, 2023. Verantwortlich: Dr. Peter Pröbstle, Präsident der LWF. Bayerische Landesanstalt fuerWald und Forstwirtschaft. Available online: https://www.lwf.bayern.de/service/publikationen/lwf_merkblatt/022680/index.php (accessed on 2 October 2025).
- Rueter, S. Der Beitrag der Stofflichen Nutzung von Holz zum Klimaschutz. Ph.D. Thesis, Technische Universitaet Muenchen, Muenchen, Germany, 2016. [Google Scholar]
- Huynh, T.; Lee, D.J.; Applegate, G.; Lewis, T. Field methods for above and belowground biomass estimation in plantation forests. MethodsX 2021, 8, 101192. [Google Scholar] [CrossRef] [PubMed]
- Assmann, F. Waldertragskunde; Bayerischer Landwirtschaftsverlag: München, Germany, 1961; p. 490. [Google Scholar]
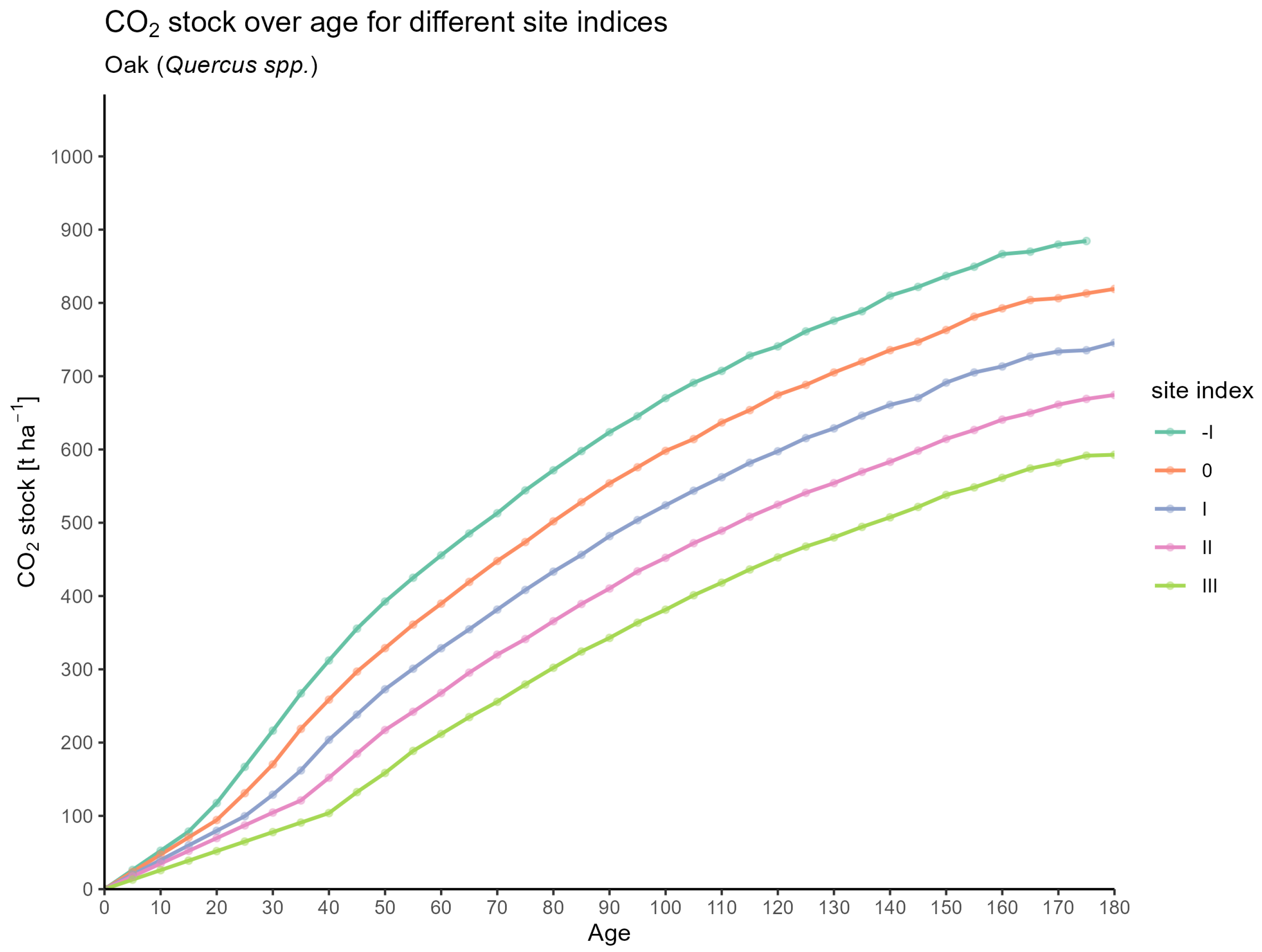
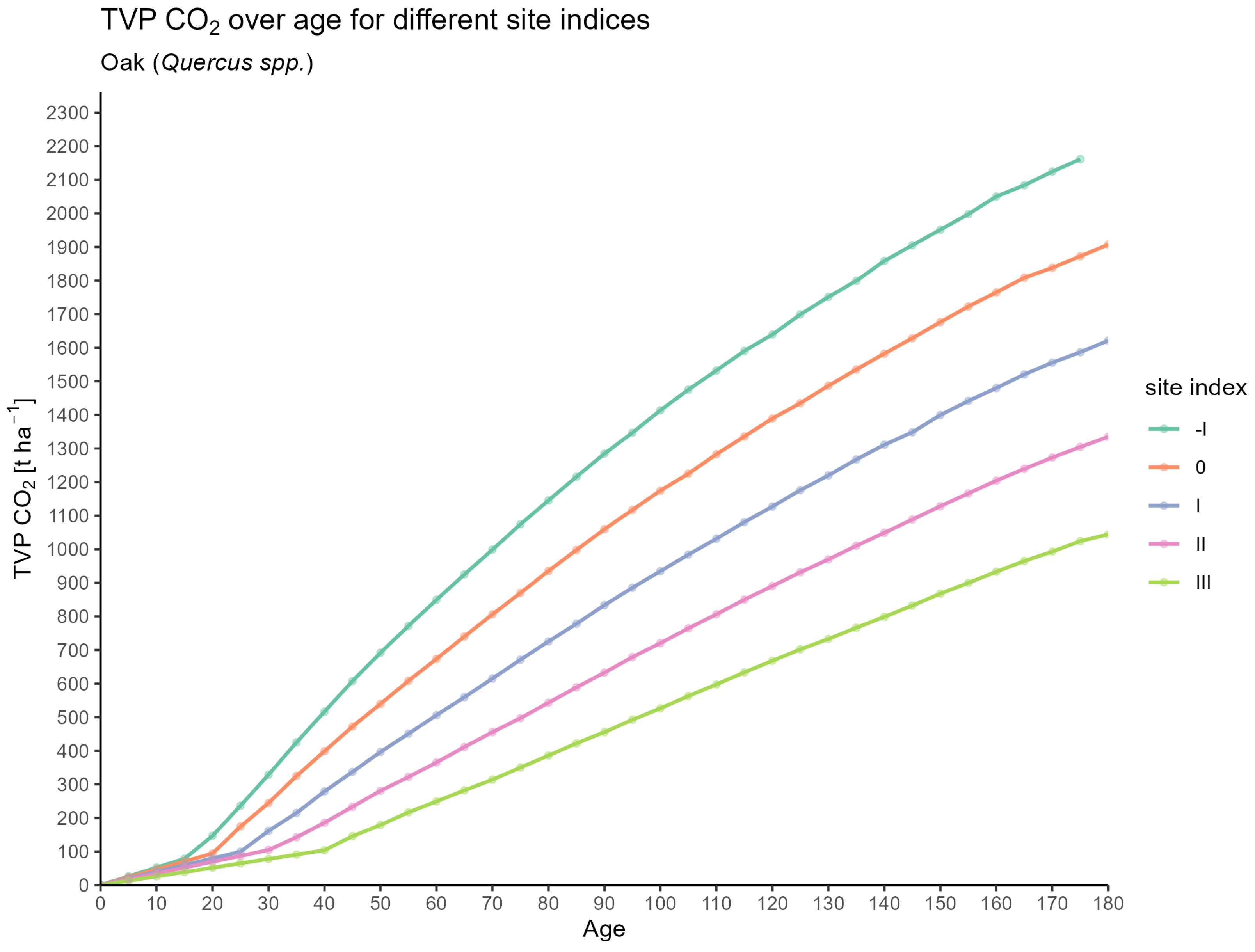
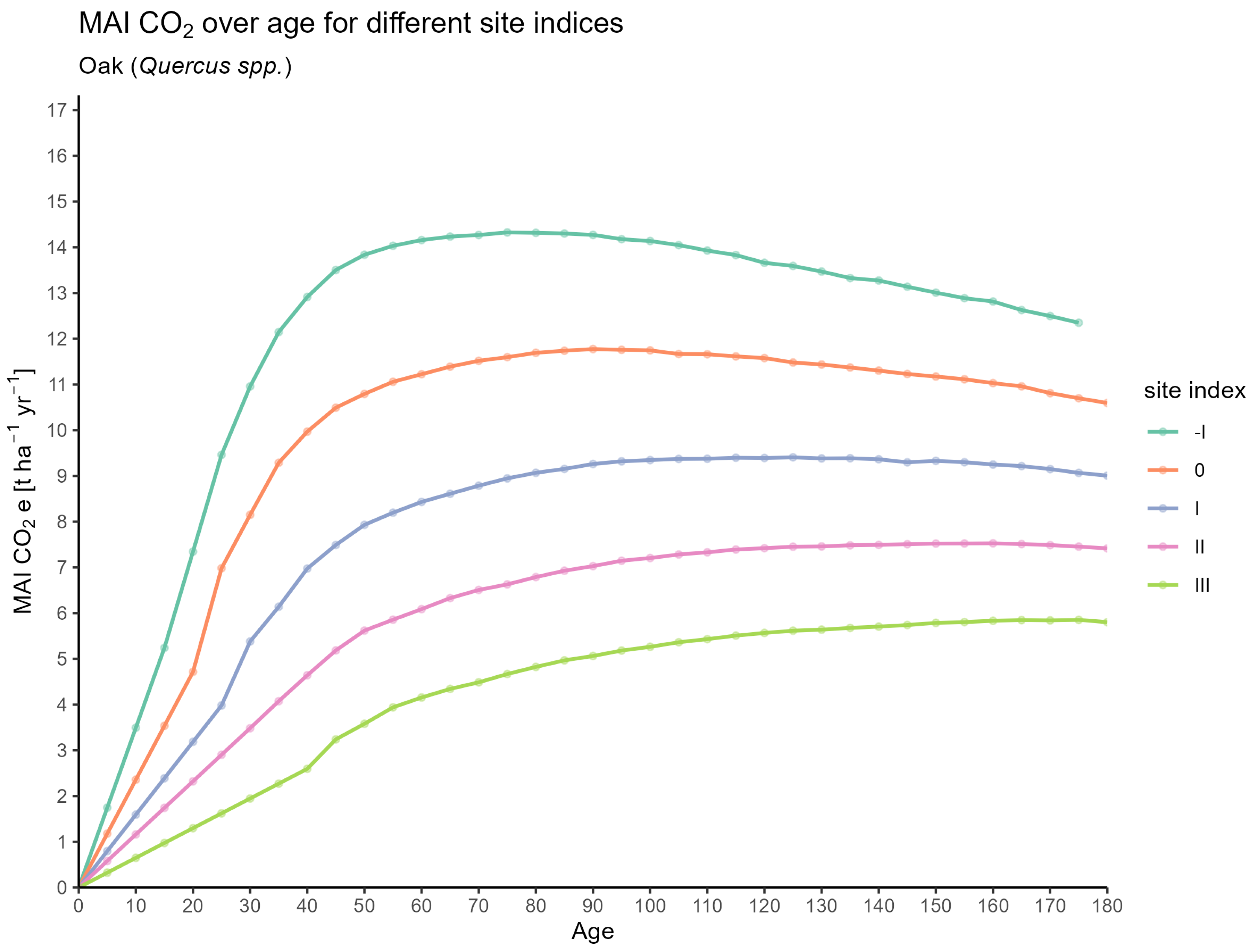
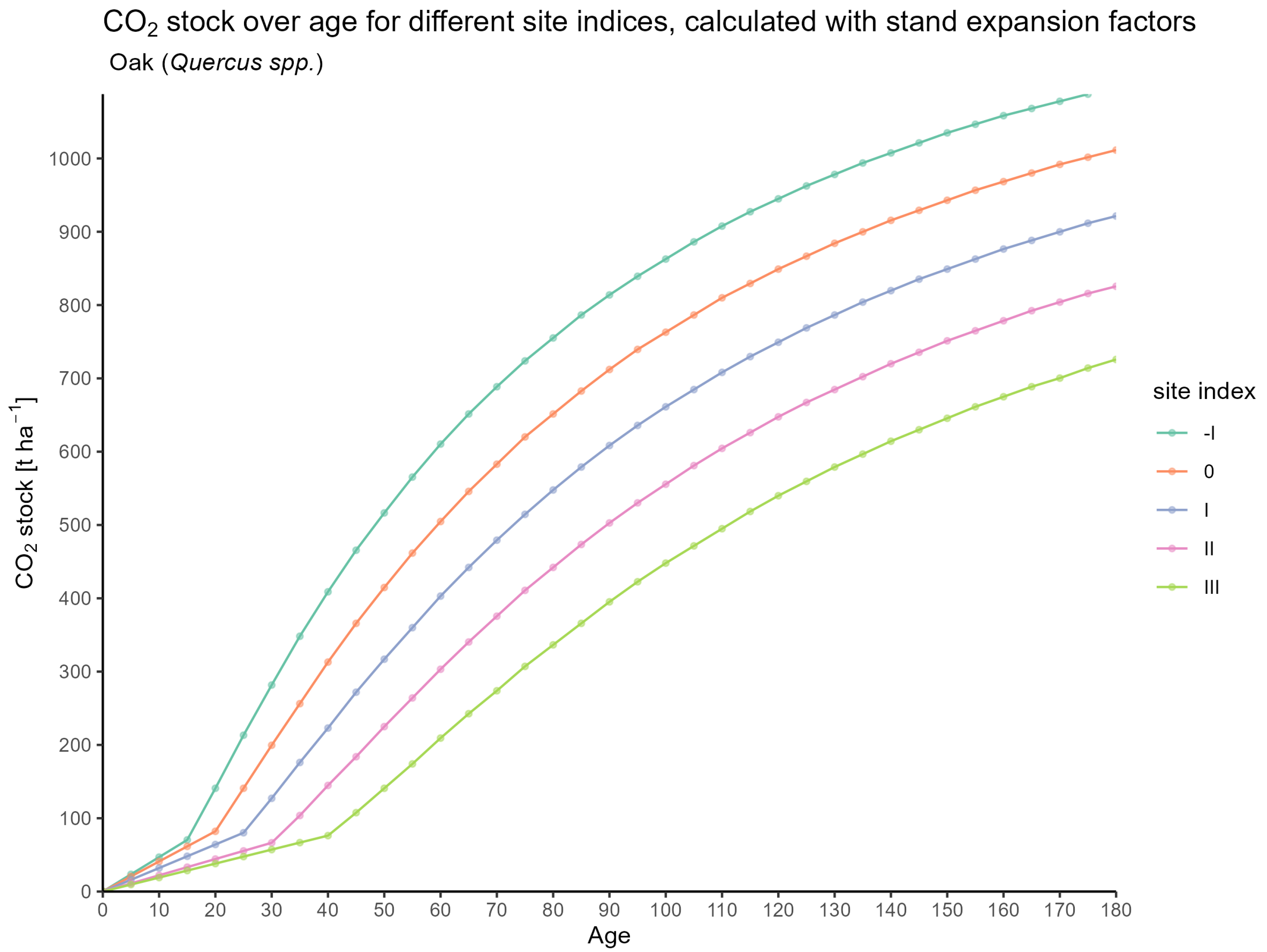
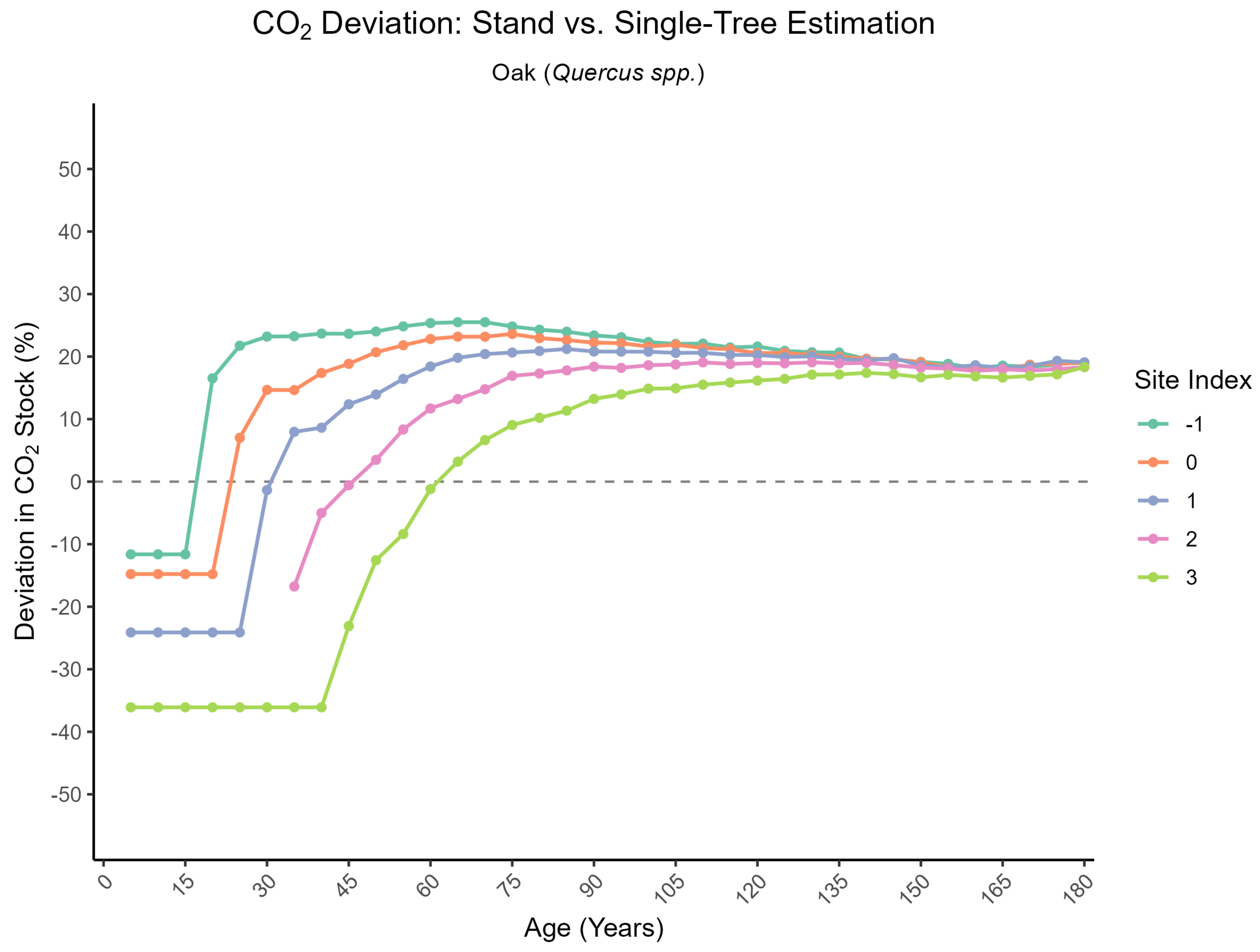
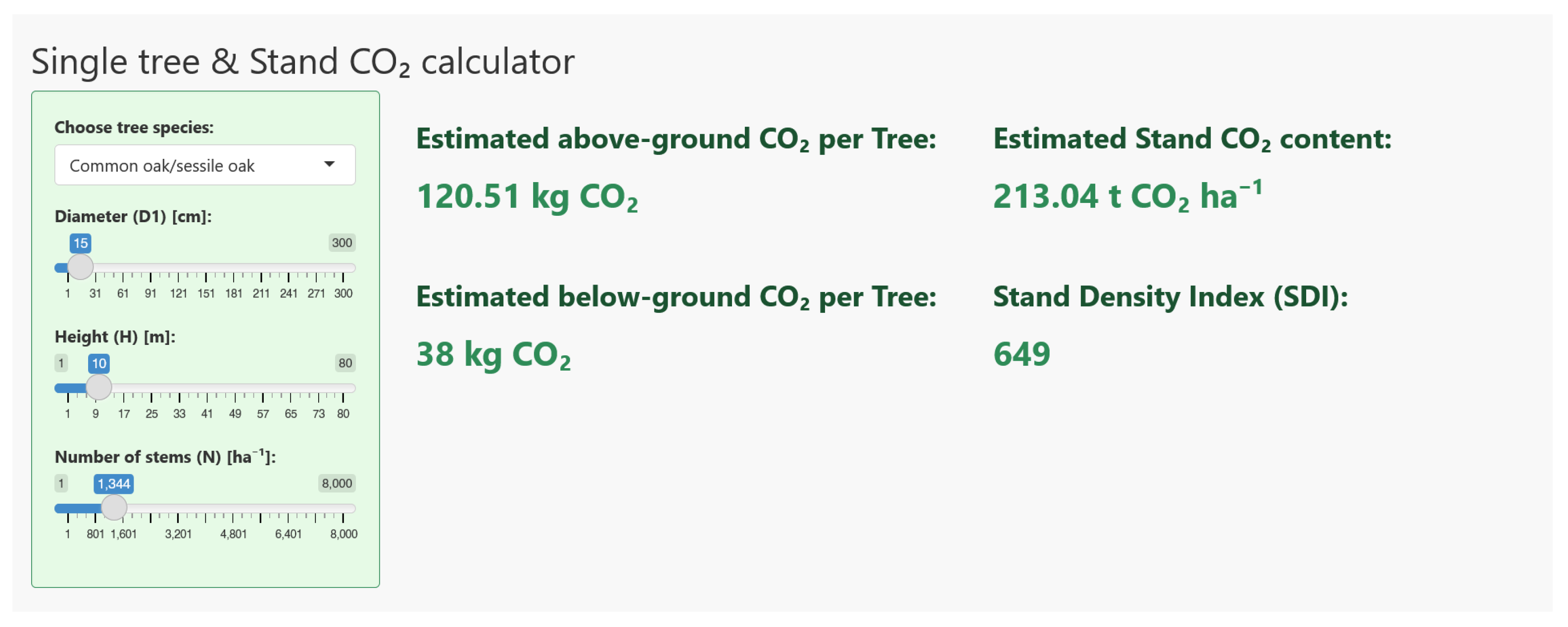
| Tree Species/Site Index | −I | 0 | I | II | III |
|---|---|---|---|---|---|
| Stand age range (years) | |||||
| Spruce (Picea abies) | 20–75 | 20–95 | 25–110 | 30–120 | 40–120 |
| Pine (Pinus sylvestris) | 20–90 | 20–120 | 25–120 | 30–120 | 40–120 |
| Douglas fir (Douglas fir) | 15–95 | 15–115 | 20–120 | 20–120 | 20–120 |
| Beech (Fagus sylvatica) | 25–115 | 30–125 | 35–145 | 40–150 | 45–150 |
| Oak (Quercus robur/petraea) | 15–175 | 20–180 | 25–180 | 30–180 | 40–180 |
| Species | ||
|---|---|---|
| Coniferous | 0.23059 | 2.20101 |
| Deciduous | 0.04940 | 2.54946 |
| Species | |||
|---|---|---|---|
| Spruce (Picea abies) | 0.4108 | 26.63122 | 0.0137 |
| Pine (Pinus sylvestris) | 0.4108 | 19.99943 | 0.00916 |
| Beech (Fagus sylvatica) | 0.09644 | 33.22328 | 0.01162 |
| Oak (Quercus robur/petraea) | 0.09644 | 28.94782 | 0.01501 |
| Species | ||||||
|---|---|---|---|---|---|---|
| Spruce (Picea abies) | 0.75285 | 2.84985 | 6.03036 | 0.62188 | 42 | 24 |
| Pine (Pinus sylvestris) | 0.33778 | 2.84055 | 6.34964 | 0.62755 | 18 | 23 |
| Beech (Fagus sylvatica) | 0.16787 | 6.25452 | 6.64752 | 0.80745 | 11 | 135 |
| Oak (Quercus robur/petraea) | 0.09428 | 10.26998 | 8.13894 | 0.55845 | 400 | 8 |
| Species | d |
|---|---|
| Spruce (Picea abies) | 69 cm |
| Pine (Pinus sylvestris) | 59 cm |
| Beech (Fagus sylvatica) | 86 cm |
| Oak (Quercus robur/petraea) | 94 cm |
| Species | Source | ||
|---|---|---|---|
| Spruce (Picea abies) | 0.003720 | 2.792465 | [48] |
| Pine (Pinus sylvestris) | 0.006089 | 2.739073 | [49] |
| Beech (Fagus sylvatica) | 0.018256 | 2.321997 | [48] |
| Oak (Quercus robur/petraea) | 0.028000 | 2.440000 | [48,50] |
| Douglas fir (Pseudotsuga menziesii) | 0.018256 | 2.321997 | [47,48] |
| Species | R (kg ) | |||
|---|---|---|---|---|
| Spruce (Picea abies) | 377.1 | 1.45 | 1.00 | 1.25 |
| Pine (Pinus sylvestris) | 430.7 | 1.45 | 1.00 | 1.25 |
| Beech (Fagus sylvatica) | 554.3 | 1.45 | 1.05 | 1.25 |
| Oak (Quercus robur/petraea) | 561.1 | 1.45 | 1.03 | 1.25 |
| Douglas Fir (Pseudotsuga menziesii) | 412.4 | 1.45 | 1.00 | 1.25 |
| Species | b |
|---|---|
| Spruce (Picea abies) | 1.664 |
| Pine (Pinus sylvestris) | 1.593 |
| Beech (Fagus sylvatica) | 1.789 |
| Oak (Quercus robur/petraea) | 1.424 |
| Douglas Fir (Pseudotsuga menziesii) | 1.664 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brinkord, M.; Seintsch, B.; Elsasser, P. CO2 Estimation of Tree Biomass in Forest Stands: A Simple and IPCC-Compliant Approach. Forests 2025, 16, 1580. https://doi.org/10.3390/f16101580
Brinkord M, Seintsch B, Elsasser P. CO2 Estimation of Tree Biomass in Forest Stands: A Simple and IPCC-Compliant Approach. Forests. 2025; 16(10):1580. https://doi.org/10.3390/f16101580
Chicago/Turabian StyleBrinkord, Marlen, Björn Seintsch, and Peter Elsasser. 2025. "CO2 Estimation of Tree Biomass in Forest Stands: A Simple and IPCC-Compliant Approach" Forests 16, no. 10: 1580. https://doi.org/10.3390/f16101580
APA StyleBrinkord, M., Seintsch, B., & Elsasser, P. (2025). CO2 Estimation of Tree Biomass in Forest Stands: A Simple and IPCC-Compliant Approach. Forests, 16(10), 1580. https://doi.org/10.3390/f16101580








