Next Article in Journal
Role of Extractable and Non-Extractable Polyphenols in the Formation of Beech (Fagus sylvatica L.) Red Heartwood Chromophores
Previous Article in Journal
Impacts of Harvesting and Prescribed Burning on Forest Soil Carbon Dynamics: A Global Meta-Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 16
Issue 10
10.3390/f16101556
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modelling Diameter Distribution in Near-Natural European Beech Forests: Are Geo-Climatic Variables Alone Sufficient?

by
Živa Bončina
1,
Christian Rosset
2 and
Matija Klopčič
1,*
1
Department of Forestry and Renewable Forest Resources, Biotechnical Faculty, University of Ljubljana, Jamnikarjeva 101, 1000 Ljubljana, Slovenia
2
School of Agricultural, Forest and Food Sciences (HAFL), Bern University of Applied Sciences, Langgässe 85, 3052 Zollikofen, Switzerland
*
Author to whom correspondence should be addressed.
Forests 2025, 16(10), 1556; https://doi.org/10.3390/f16101556
Submission received: 8 September 2025 / Revised: 2 October 2025 / Accepted: 5 October 2025 / Published: 9 October 2025
(This article belongs to the Section Forest Ecology and Management)
Browse Figures
Versions Notes

Abstract

Diameter distribution is an important indicator of stand structure and an input for many forest growth models. It is commonly modelled using theoretical functions, in which distribution parameters are expressed as a function of stand, geo-climatic and other predictors. However, modelling diameter distributions in near-natural forests remains limited, and the influence of geo-climatic factors has not been systematically assessed. Using data from 6759 sample plots, our aims were (i) to develop models of the scale (b) and shape (c) parameters of the two-parameter Weibull function for near-natural beech forests in Slovenia; (ii) to examine whether diameter distributions can be reliably modelled using only geo-climatic variables; and (iii) to determine whether separate models are required for different beech forest types. A broad set of stand, geo-climatic and forest management variables was considered in the modelling procedure. The results indicate that stand variables had the strongest influence, while geo-climatic variables were included in the best-performing models, but had negligible effects. The importance of stand-level variables over geo-climatic variables was highlighted. Models based solely on geo-climatic predictors performed poorly and are unsuitable for practical forestry applications. Model performance did not differ substantially across forest types, suggesting that separate models for forest types are unnecessary.

1. Introduction

Diameter distribution is one of the most descriptive and important stand parameters, providing valuable insights into the structure and stability of forest stands, competitive conditions for tree growth and potential timber assortments [1,2,3]. Together with stand density and the size-growth relationship, diameter distribution significantly affects forest growth [4], as many forest processes—such as light absorption, water balance and nutrient cycling—are influenced by stand structure, and vice versa [4,5]. Diameter distributions of forest stands vary spatially across forest areas due to differences in growing conditions (e.g., geo-climatic conditions and variability in resource availability) and past management interventions [4,6,7,8]. Accurate information on stand diameter distribution, i.e., the frequency distribution of trees according to their diameter at breast height (dbh), forms the basis for determining appropriate silvicultural interventions, harvesting strategies, and simulating future stand development [1,2,3,9]. For several forest growth models (e.g., Silva, SiWaWa, and Sybila), information on tree diameter (or diameter class) distribution is essential [10,11,12].
The application of theoretical distribution models is the most common method for describing stand diameter structure [13]. Among many distribution functions, the Weibull distribution function is most frequently used [14,15]. Its prominence lies in its flexibility to represent a wide range of unimodal distributions—ranging from reversed-J-shaped to right- and left-skewed, as well as exponential and normal forms [16]. The Weibull function can be parameterized in either two- or three-parameter forms, including the scale parameter b, shape parameter c, and, in the three-parameter version, the location parameter a [16]. The shape parameter c is particularly informative: when c < 1, the distribution is reversed-J-shaped; for 1 < c < 3.6, it is mound-shaped and right-skewed; and at c ≈ 3.6, it approximates a normal distribution. A special feature of this function is that its 63rd percentile corresponds to the scale parameter b in the two-parameter version or to the sum a + b in the three-parameter version [17]. In even-aged monospecific stands, this value closely approximates the quadratic mean diameter (QMD), often within an error range 2%–3% [18].
For forest management and forest growth modelling purposes, it is essential to express the (Weibull) diameter distribution function parameters as a function of various stand, geo-climatic and forest management variables [19,20,21]. A commonly employed approach to parameterize the function is the parameter prediction method (PPM), introduced by Clutter and Bennett [22]. The PPM first fits the distribution function to the empirical data to retrieve the function parameters and then models those parameters using various explanatory variables [23]. Among stand variables, quadratic mean diameter (QMD) is most frequently employed to estimate the Weibull parameters [18,24]. However, a range of additional stand parameters, such as stand basal area, minimum and maximum tree diameters, dominant stand diameter, species composition, stand volume, dominant height or the height of the largest tree, stand age and initial spacing in plantations have also been used [21,25,26,27]. Geo-climatic parameters have rarely been incorporated into these models. Some studies have considered soil properties [19,20,28] or climate-related parameters [6,29,30]. Thus, the impact of geo-climatic characteristics on diameter distribution remains largely unexplored, although soil characteristics may influence diameter distribution, as reported for larch plantations [20]. Forest management interventions, as well as natural disturbances, also influenced diameter distributions [31,32]. However, management parameters or past mortality have not been included in the parameterization of the diameter function, to our knowledge. Since obtaining stand parameters is often time-consuming and cost-intensive [33], yet many geo-climatic and forest management attributes can be easily obtained from existing GIS layers or databases, it would be valuable to develop diameter distribution models based solely on geo-climatic and/or forest management variables with sufficient predictive power.
Most studies on diameter distribution have focused on monocultures, whereas studies in near-natural forests are less frequent (however, see [18,34,35]). In our study, we focus on European beech (Fagus sylvatica L.; hereafter beech) forests. Beech is one of the most widespread and ecologically important tree species in Europe [36] and occurs in various forest types [37], from the colline to the subalpine vegetation zone [38]. It often forms homogenous forest stands, but it can also be present in mixed even-aged stands with a higher proportion of other tree species or even in multi-layered forest stands, usually accompanied by Norway spruce (Picea abies (L.) H. Karst.) or silver fir (Abies alba Mill.) [39].
Beech-dominated forests span from the colline to subalpine zones, with immense differences between vegetation belts in site and climate conditions [40]. Across the entire altitudinal gradient, beech forest types grow on both carbonate and silicate bedrock, with noticeable differences in soil conditions. Both soil and climate significantly influence beech growth [41,42], ingrowth [43,44], mortality [45,46] and structural development [47].
In beech-dominated forests, various management systems and intensities are applied [48,49], from even-aged to single-stem selection systems [50]. Forest management (system, intensity) plays a crucial role in regulating stand density and diameter distributions [2,51,52]. Natural disturbances of varying severity and frequency can have similar impacts [32,53,54]. In the context of climate change, understanding the impact of diameter distribution on tree growth in various beech forest types is increasingly important due to rising risks to beech growth and competitive ability [55,56].
Studies on tree diameter distribution in beech-dominated forests are relatively rare (however, see [18,34,35]) and are limited to some beech-dominated forest types. Comparative studies examining tree distribution in beech forests in relation to geo-climatic conditions and management regimes are lacking. The main objectives of our study were (1) to develop a general diameter distribution model for beech forests considering stand, geo-climatic and forest management variables, as well as a model without stand variables, and (2) to develop separate models for the main beech forest types to evaluate potential differences in predictive variables between forest types. We hypothesised that (H1) stand variables are the most important predictors, while geo-climatic and forest management variables are modestly important; (H2) diameter distribution models based solely on geo-climatic variables are nevertheless sufficiently reliable for forest management planning; and (H3) separate models for different beech forest types differ in predictor sets and their impacts on diameter distributions.

2. Materials and Methods

2.1. Study Area

Slovenian forests provide a suitable setting for studying the diameter distribution of beech forests. Based on potential natural vegetation, beech forests dominate approximately 70% of the forested area (1.2 million ha) [38]. Despite its relatively small surface area, Slovenia encompasses a diverse landscape, including the Alps, the Mediterranean region, the Dinaric Mountains and the Pannonian Basin. The average growing stock across all forest stands is 304 m3/ha, with a mean annual increment of 7.4 m3/ha [57]. Close-to-nature forestry has been practiced for decades, relying on natural regeneration. The most common silvicultural systems include irregular shelterwood, group selection and single-tree selection systems [58,59]. Beech is the most prevalent species in the growing stock (33.0%), followed by Norway spruce (30.0%) and silver fir (7.5%) [57].
This study focuses exclusively on beech-dominated forests, since our broader goal is to develop a growth model for beech forests in Slovenia. The study area is characterized by considerable variation in stand and geo-climatic conditions (Table 1). Climatic conditions range from Submediterranean in the southwest to temperate humid in the central region and continental in the northeast (Table 1). The most common soil types are leptosols, followed by eutric and chromic cambisols, and dystric cambisols [60]. The study also encompasses a broad spectrum of plot developmental stages, plot densities and combinations of site characteristics (Table 1).
Forests are classified according to Braun-Blanquet [62] into phytocoenological associations (syntaxa), each reflecting unique ecological conditions [63]. These associations are further classified into forest types, which primarily differ in altitude (altitudinal belts), bedrock (carbonate, mixed carbonate-silicate, silicate) and soil properties [38]. Forest types are an important tool in ecological forest management planning, allowing for site-specific planning. For this study, we identified five beech forest types. On carbonate substrates, three forest types were distinguished according to altitudinal belt, namely submontane & colline, montane, and subalpine & altimontane beech forests, with mean plot elevations of 603 m, 899 m and 1176 m, respectively. The fourth type, acidophilous beech forest, occurs on silicate bedrock with dystric soils. The elevation range of the study area spans from 150 to 1288 m, covering several altitudinal belts. The fifth type, thermophilus beech forest, is characterized by southern and southwestern exposition, shallow soils, and frequent occurrence on extreme sites, such as steep slopes and rocky terrain, on various bedrocks, although carbonate prevails (for more information see Supplementary Materials Table S1).

2.2. Data

The data originated from approximately 98,000 permanent sample plots established by the Slovenia Forest Service [57], which are systematically distributed throughout Slovenia’s forested area and remeasured every 1O years. For the study, database for the period 2004–2013 was used. On concentric circle fixed-area sample plots, trees with dbh between 10 and 29.9 cm are measured within a 200 m2 subplot (radius = 7.98 m), while those with dbh ≥ 30 cm are recorded within a larger 500 m2 subplot (radius = 12.62 m) [58]. Tree dbh measurements were rounded down to the nearest centimetre. To scale tree counts to a per-hectare basis, expansion factors of 50 (for the 200 m2 subplot) and 20 (for the 500 m2 subplot) were applied. Diameter distribution modelling was performed using data aggregated at the hectare level. The study focused exclusively on beech forest types and pure beech plots, with at least 80% of beech in the plot’s basal area (BA). Only structurally homogeneous plots were included. The Gini index, which is frequently used in forestry to assess plot structural homogeneity or heterogeneity [64,65,66], was calculated at the plot level based on the BA of trees [67]. To classify forests into homogeneous and heterogenous categories, k-means cluster analysis was performed, resulting in two clusters with a threshold of 0.33 [46], which is in accordance with the literature [64,65]. To ensure data reliability, plots with fewer than 10 trees were excluded from the analysis, e.g., [68]. The final database contained data from 6759 plots (Figure 1).

2.3. Model Procedure

2.3.1. Weibull Distribution and Parameter Prediction Method

The two-parameter Weibull distribution function [69] was used to model the diameter distribution of homogenous near-natural beech forests. Trees on plots were grouped into 5 cm diameter classes, assumed to be detailed enough for forest management planning purposes. The probability density function (PDF) of the two-parameter Weibull distribution is defined as:
f x = c b ·   x b c − 1 ·   e − x b c
where b is the scale parameter, c is the shape parameter and x is the independent variable, i.e., tree dbh. For modelling the Weibull distribution, the parameter prediction method (PPM) [22,23,70] was applied. In the PPM, the Weibull parameters b and c were predicted using regression models based on various stand characteristics [19], usually in two consecutive steps, e.g., [70]. In the first step, the Weibull function was fitted for each plot by maximizing the likelihood of the sampling distribution using the mle function from the stats4 R package (R Core Team, 2023). In the second step, parameters b and c as dependent variables were expressed with regression models composed of various stand, site, climate and other predictors [18,24].

2.3.2. Candidate Variables Included in the Modelling Procedure

The original set of potential explanatory variables included a broad selection of stand, geo-climatic and forest management parameters (Table 1). We considered variables that have been shown to significantly influence diameter distribution [21,26,30,70] or have been applied in beech diameter growth modelling studies, e.g., [41,42,71]. To avoid multicollinearity, we eliminated one variable from any pair with a Pearson correlation coefficient greater than 0.8. Correlations between categorical and numerical variables were tested using ANOVA and t tests; if ANOVA was significant, we eliminated one of the tested variables. The original set of variables was thus reduced to 11 potential explanatory variables (Table 1).
The stand variables included in the modelling procedure as potential predictors were minimum diameter (DMIN), maximum diameter (DMAX), quadratic mean diameter (QMD), basal area (BA) and proportion of beech (PBeech). BA describes stand density, DMIN and DMAX describe the variability of tree sizes, and QMD characterizes the developmental phase. PBeech was calculated based on the proportion of BA represented by beech trees. Different stand variables were included in the models for parameters b and c. Due to the known relationship between parameter b and QMD [18], QMD was included in the models for b. For models predicting parameter c, DMAX was used instead of QMD because models with DMAX exhibited better performance.
Among geo-climatic variables, three groups of variables were included in the modelling procedure. Three topographic variables were considered: elevation (ELE), slope (SLP) and aspect (ASP). ASP was transformed into a dummy variable: 1 for warmer aspects (S, SE, SW, W) and 0 for colder aspects (N, NE, NW, E), while ELE and SLP were included as continuous variables. From soil characteristics, only FAO Soil type (SoilT) was included. Soils were categorized into four groups: (i) leptosols (eutric, lithic, dystric, mollic and rendzic), (ii) eutric & chromic cambisols, (iii) dystric cambisols and (iv) other soil types (minor categories such as feric podzols, haplic luvisols, eutric fluvisols and undefined soils). The categories were formed based on soil type similarity [72] and a sufficient number of plots per category (>600). As a proxy for site productivity (SProd), a coefficient K was used, representing the volume of a tree with a reference diameter of 45 cm in a single-entry function for extracting the tree volume. Single-entry functions are often used to calculate tree volume based on its dbh [73]; in Slovenia the modified French tariffs are applied [74]. This function reflects site productivity as trees exhibit higher height and volume at more productive sites, therefore the measure is similar to the site productivity index (SPI) expressed by tree height at a given dbh [75]. K ranged from 1.20 to 2.95 m3, reflecting differences in tree heights for trees of the same dbh. Tariffs for the main tree species were determined by field measurements of trees at the compartment level [57]. All climate variables were derived using the long-term climate data for the period 1950–2018 [61]. Among climate variables, only average temperature for March, April and May (Tspr) was included due to strong correlation among climate variables. Tspr was chosen because it showed the highest correlation with the dependent variables, parameters b and c, among temperature-related predictors. Although precipitation (PCP) strongly influences forest growth [42], we used ELE instead, as precipitation is strongly linked to ELE and ELE is easier to obtain and more precise than PCP.
Among forest management variables, the basal area of removed trees (BAREM) represented the basal area of harvested and naturally dead trees over the 10-year period between consecutive plot measurements. Natural mortality and harvest were combined, as both events are rare at the plot level.

2.3.3. Model Formulation

Parameters b and c were estimated through linear regression models implemented in R 4.1.3 (R Core Team, 2023) using the lm() function from the stats R package and applying a combined forward-backward stepwise procedure in the stepAIC() function in the MASS R package [76]. Parameters b and c were modelled with different sets of variables to test whether geo-climatic variables alone could successfully predict diameter distribution. First, general models b1 and c1 were built using all listed independent variables. In the next step (models 2), most stand structural parameters (DMAX, DMIN, QMD) were excluded when modelling b2 and c2. BA and PBeech were retained because BA can be easily estimated, giving these models high practical value for forest management [18]. In the third set of models (models 3), also BA, PBeech and BAREM were excluded so that only geo-climatic variables were used to model b3 and c3. To meet the linear model assumptions, logarithm transformations were applied if necessary to both dependent and independent variables (parameter b, parameter c, DMIN, DMAX, QMD, PBeech, BAREM) (for details see Tables S2 and S3).
Multicollinearity in each model was assessed using the variance inflation factor (VIF), calculated with the vif() function in the car R package [77], with VIF = 10 adopted as the threshold for multicollinearity. We estimated the relative importance of each predictor as the relative decrease in R2 when the predictor was included versus excluded from the model, e.g., [71].
Finally, we modelled diameter distribution for each beech forest type (BType). Preliminary tests showed significant differences between the diameter distributions of all beech forest types (chi-square test, all p < 0.05), indicating the relevance of developing separate models for forest types. Consequently, six models (general and separate models for five forest types) were developed following the procedure described above, using the full set of potential predictors (Table 1).

2.3.4. Model Evaluation and Validation

The performance of models for estimating parameters b and c was evaluated using the adjusted coefficient of determination (R2), root mean square error (RMSE) and Akaike information criterion (AIC). In addition, we employed a 10-fold cross-validation approach using the trainControl function in the caret R package [42,78]. Model performance was evaluated with R2, RMSE, mean error (ME) and the standard deviation of ME (SD).

3. Results

The general models explained 99% and 72% of the variability in the Weibull function parameters b and c, respectively (Table 2). When some of the main stand variables were excluded, model performance decreased substantially (Table 2), which is also evident in the relationship between the fitted and predicted values of b and c (Figure 2). Practical examples of modelling empirical diameter distributions with all three types of models (1, 2 and 3) are provided in Figure S1 and Table S4 in Supplementary Materials.
In the general model for b, QMD was by far the strongest individual predictor; the remaining three predictors contributed less than 0.2% to the overall explained variability. Among the geo-climatic variables, only ELE had a significant impact, although it explained a very limited proportion of the variability (1.4 × 10−5%). In the general model for parameter c, a larger number of geo-climatic variables were included compared to the general model for parameter b. In model c1, stand parameters DMIN and DMAX were the most important predictors, while the combined contribution of the geo-climatic variables (ELE, SLP, Tspr and ASP) was only 0.22%.
When modelling b and c without selected stand parameters, the performance of the models b2 and c2 dropped by 81% and 93%, respectively. In model b2, the most influential predictors became BA, SProd, PBeech and BAREM. Geo-climatic predictors gained relative importance compared to model b1, with ELE, ASP and SoilT contributing 3.2% of the explained variability of b2. In model c2, the geo-climatic variables ELE, Tspr and SoilT explained 19.3% of the explained variability, with SoilT contributing the largest share.
In models b3 and c3, only geo-climatic explanatory variables were used, resulting in five predictors in b3 and four in c3. The overall explained variance dropped dramatically to 2.8% and 1.3%, respectively. In model b3, SProd was the most influential predictor, whereas in model c3, SoilT was the most important [79].
QMD reflects the mode of the distribution: higher QMD shifts the peak of the distribution to the right and widens the distribution. Similarly, larger values of DMAX increase the distribution width. In contrast, higher DMIN narrows it. A larger BA contributes little to a more peaked (narrower) distribution shape (Figure 3). The effect of other predictors is less pronounced (Figure 3 and Figure S2). The full effects of all predictors are shown in Figure S2 in Supplementary Materials.

Diameter Distribution Modelling for the Main Beech Forest Types

The models for the scale parameter b were very similar for all beech forest types (Tables S5 and S6). Differences in predictors and their effects were observed for the shape parameter c (Table 3, Table 4 and Table S7). The highest R2 (76%) was observed for thermophilus beech forest and the lowest for subalpine and acidophilous beech forest (70%) (Table 4). Stand predictors DMIN, DMAX and BA were included in all models and contributed most to the explained variability. Geo-climatic predictors ELE, Tspr, ASP were included only for montane and thermophilus beech forest types, contributing only 0.43% to the total explained variability.

4. Discussion

Our study represents one of the first attempts to model the diameter distribution of near-natural beech forests by including an extensive set of stand, geo-climatic and forest management variables. Based on 6579 plots covering a broad range of stand and site characteristics, we found stand variables to be crucial for modelling the diameter distribution of near-natural beech forests, whereas models including only geo-climatic variables exhibited low predictive power.
When interpreting the influence of the different predictors included in our models, it is important to bear in mind that these models describe the Weibull function parameters b and c, which were previously fitted to empirical distributions. Moreover, this study focuses solely on the shape of the diameter distribution and does not address other structural characteristics of forest stands, such as the number of trees directly indicating stand density.

4.1. General Diameter Distribution Model for Near-Natural Beech Forests, Developed by Including Stand, Geo-Climatic and Forest Management Variables

Our results showed that stand parameters (e.g., QMD, DMIN, DMAX, BA) were the most important predictors in the Weibull diameter distribution models. However, geo-climatic and forest management variables were also included in the general model, although their contribution to the explained variability was minor. Similar studies conducted in plantation forests, e.g., Guo et al. [20,29] reported a minor, yet slightly stronger, influence of these variables. The general model’s performance in estimating the Weibull parameters was comparable to that reported in related studies, e.g., [18,20,70].
For the scale parameter b, QMD was the most influential predictor, contributing 99.8% to the explained variability. A strong correlation between QMD and parameter b has been confirmed in several studies, e.g., [18,70]. Among the other variables, PBeech and ELE were included in the model, but contributed less than 0.2% to the total explained variability. Our results indicate lower values of parameter b in stands with a higher proportion of other tree species. Admixed tree species in beech forests (e.g., Sorbus ssp., Ostrya carpinifolia, Carpinus betulus) are often less competitive on typical beech sites due to their slower growth and smaller final dimensions (height, dbh). Therefore, their presence usually reduces the QMD of a stand. The results could differ in the case of admixture with species capable of reaching larger dimensions (e.g., Norway spruce, silver fir).
Our results also showed an increase in the value of parameter b along an elevation gradient. The amount of precipitation positively correlated with elevation, which suggests that the value of parameter b increases with higher precipitation. Precipitation has been found to positively influence the growth rate of beech trees [80,81], resulting in larger tree diameters and thus higher QMD at a given tree age.
In the model of the shape parameter c, the contribution of geo-climatic predictors to the explained variability was also minor, but slightly higher compared to that in the model for parameter b. The relatively higher impact of geo-climatic conditions on parameter c in comparison to parameter b was also observed in the study [29]. Geo-climatic variables seem to exert a slightly greater influence on the shape of the distribution (parameter c) than on its mode (parameter b). This may be due to the pronounced relationship between the scale parameter b and QMD [18], which does not apply to the relationship between QMD and parameter c. The most influential predictors for the shape parameter c were the stand variables DMIN and DMAX, which define the left and right tails of the distribution, followed by BA, together contributing more than 99.4% of the explained variability.
Other variables included in the model (PBeech, ELE, BAREM, Tspr, SLP, ASP) contributed just over 0.5% to the explained variability of parameter c, with PBeech having the highest impact among them. An increased proportion of beech in a forest stand positively influences the value of c, indicating that higher proportions of other tree species result in a less positively skewed distribution. This pattern likely arises from intra- and inter-specific competition between tree species [8,82,83], which influences tree diameter growth [84] and the dimensional differentiation of trees within a stand [7]. Beech growth is often better in mixed stands [85], which may happen due to allometric crown plasticity, spatial niche separation above and below ground, increased light-use efficiency and light absorption, hydraulic redistribution, presence of beneficial organisms (mycorrhizae or other soil microbes) or mixture with the N2-fixing species [85,86]. For example, if mixed with Pinus sylvestris, beech will enhance its growth due to beech’s crown plasticity and thus a more efficient packing of tree crowns within the canopy space, improved light interception arising from contrasting species-specific light compensation points and light-use efficiencies and complementarity in the rooting systems of both species resulting in more efficient water and nutrient uptake [85]. The boosted growth of beech in mixed stands potentially results in a higher share of large-sized trees and a more negatively skewed diameter distribution. Supporting this, studies in plantations [86] observed that mixed plantations had a higher proportion of trees in larger diameter classes compared to pure plantations, resulting in more negatively skewed diameter distributions. A negatively skewed distribution exhibits wide range of diameters with a pronounced dominance of larger trees, but also a considerable proportion of thinner trees. In near-natural forests, this may arise from several factors. Stand dynamics in near-natural forests differ significantly from those in plantations. Under close-to-nature forest management systems, such as the irregular shelterwood system [87], understorey and intermediate-layer trees are retained during tending and thinning operations. These thin trees are left in a stand to provide ecological benefits, such as shading the forest floor, protecting tree trunks or promoting self-pruning in the lower stems of crop trees [88]. In addition, beech, as a shade-tolerant species, can grow under canopy shade for several decades, even more than a century [89], and can sustain ingrowth [90]. The impact of mixing in our models might have differed if we had analysed mixed beech forests with higher admixtures of other tree species. However, our study focused primarily on “pure” beech forests, with other tree species contributing less than 20% of the total basal area.
On steeper slopes, parameter c is lower, resulting in more positively skewed diameter distributions. This implies a higher proportion of thinner trees and higher density. On steeper slopes, the stability of stands is crucial [91]. Higher stand density is important, but the dimensions of individual trees also exert significant influence [92,93]. Elevation also impacted parameter c, with higher elevations corresponding to larger c values and the diameter distributions approaching normal or negatively skewed shapes.
Several studies, e.g., [8,29] reported a significant but minor impact of temperature variables on diameter distributions, consistent with our findings. The range of climate variables was within the ecological limits of beech [94], indicating that their low influence is not related to a lack of adverse growth conditions Among climate variables, only Tspr was included in the model for parameter c, but its impact was negligible. In larch plantations in the northern China, the mean temperature of the warmest quarter was identified as a predictor, with a 2.2% improvement in model performance [29]. The impact of climatic factors on diameter distribution may be more pronounced in forest plantations than in the near-natural forests due to their lower density, more symmetrical tree arrangement, and reduced competition above and below ground. Mean annual temperature has also been shown to influence diameter distributions in near-natural silver fir-beech-spruce forests in Europe [8], although that study analyzed each tree species separately.
We also detected a significant impact of past removals on the shape of diameter distributions in beech forests. Similar findings were reported in several studies [52,53], as silvicultural practices often manipulate or maintain certain size distributions [31]. In plots with higher BAREM, diameter distributions tend to be less positively skewed, with a higher proportion of larger trees, which is consistent with close-to-nature forest management [87]. However, less positively skewed distributions could also result from severe natural disturbances [53].
Based on the analysis of general diameter distribution models, we conclude that stand variables are the primary predictors, whereas geo-climatic and forest management variables have a negligible influence in modelling diameter distributions of near-natural pure beech forests.

4.2. Models for Beech Forest Types Including Stand, Geo-Climatic and Management Variables

The models developed for beech forest types revealed some differences in the predictors, reflecting different growing conditions across forest types [38]. Differences were more pronounced in the models for the shape parameter c, while the models for the scale parameter b were almost identical to the general model, with QMD emerging as the crucial predictor. This reinforces the strong association between parameter b and QMD [18]. Models for parameter c showed only minor performance differences, with R2 highest for the thermophilus beech forest type. Contrary to expectations, diameter distribution models for individual beech forest types did not outperform the general model for all beech forests.
Across all forest-type-specific models, the combined contribution of geo-climatic and forest management variables was below 0.5%. The effects of PBeech and BAREM were observed in three forest types, whereas ELE, Tspr and ASP influenced only one beech forest type. For parameter c in the montane beech forest type, the largest number of predictors were included, encompassing PBeech, BAREM, Tspr and ASP. This model closely resembled the general model for parameter c across all sampled forests, likely due to the large number of plots representing this forest type. BAREM was included in the models for the submontane & colline, montane, and subalpine & altimontane beech forest types.
Despite these minor differences, separate diameter distribution models for individual beech forest types appear to have limited relevance for forest management and growth modelling, as their performance did not exceed that of the general model.

4.3. Diameter Distribution Models with Limited or No Stand Parameters

The importance of stand parameters in modelling the diameter distribution of near-natural beech forests is evident when comparing the performance of the general model with models excluding stand parameters (DMAX, DMIN, QMD). R2 values for the latter dropped from 99% and 72% to 19% and 5% for parameters b and c, respectively. Models using only geo-climatic predictors showed an even greater performance decline.
Models b2 and b3, in which QMD was excluded, can be interpreted as models for QMD itself. Russel et al. [6] modelled parameter b without stand parameters, and their predictors indicated that better growth conditions (represented by longitude in their study) shifted the distribution mode toward larger diameters. Despite their low overall performance, our b2 and b3 models showed a similar trend: more favourable growth conditions for beech (i.e., higher SProd, higher PBeech, more productive SoilT and colder ASP) were associated with higher values of parameter b. However, the effect of ELE was opposite to that observed in the general model.
For parameter c, the influence of ELE, SLP and Tspr increased in the models without stand parameters, but the direction of their influence remained consistent with the general model. BAREM and SLP were included in only one model, also maintaining the same effect direction.
SoilT emerged as a significant predictor in models c2 and c3, despite not being included in the general model since it was not significant. Guo et al. [20] similarly reported the significant influence of soil characteristics in larch plantations in China, improving model performance by 6%.
Overall, diameter distribution models relying solely on geo-climatic variables are not sufficiently reliable for forest management planning or forest growth simulators, and therefore H3 is rejected.

5. Conclusions

Based on the results, it can be concluded that modelling the diameter distribution of natural beech forests solely with geo-climatic variables is inappropriate. Stand parameters must be included, as the impact of geo-climatic and forest management predictors in the models was negligible.
Diameter distribution modelling can be performed for all beech forests collectively by developing a common general model for near-natural beech forests. Differences between diameter distribution models for specific beech forest types were minor and insignificant for practical applicability.
The developed general probability diameter distribution model for near-natural beech forests can be applied in forest management and planning. It can also be directly integrated into forest growth simulators, as diameter distribution is a crucial component of many forest stand growth simulators. For field forest managers, such a model could serve as a basis for decision-making. When data on required predictors are available and the number of stems is known, it is possible to derive the absolute number of trees per diameter class, which can significantly improve decision-making regarding silvicultural activities within a stand.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16101556/s1.

Author Contributions

Conceptualization, Ž.B., C.R. and M.K.; methodology, Ž.B. and M.K.; validation, Ž.B.; data curation and formal analysis, Ž.B.; writing—original draft preparation, Ž.B. and M.K.; writing—review & editing, M.K. and C.R.; visualization, Ž.B.; funding acquisition, Ž.B. and M.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was carried out within the framework of the research core funding P4-0059 “Forest, Forestry and Renewable Forest Resources” and the project “Infrastructure Center Research Forest of the Department of Forestry and Renewable Forest Resources at the Biotechnical Faculty” (part of the MRIC UL) (contract I0-0022-0481-0481-08) funded by the Slovenian Research and Innovation Agency (ARIS) and the projects V4-2014 “The Development of Forest Models for Slovenia”, V4-2211 “Managing Forest Management Risks from Climate Change”, funded by the Slovenian Research and Innovation Agency (ARIS) and Ministry of Agriculture, Forestry and Food of the Republic of Slovenia. The first author, Ž.B., received funding from the Pahernik Foundation.

Data Availability Statement

The datasets presented in this article are not readily available because they were gathered and are owned by Slovenia Forest Service. Requests to access the datasets should be directed to Slovenia Forest Service.

Acknowledgments

We thank the Slovenia Forest Service for providing measurement data from the permanent sample plots and Jan Nagel for proofreading and editing the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DMINMinimum tree diameter at breast height (cm)
QMDMean quadratic diameter (cm)
DMAXMaximum diameter (cm)
BABasal area (m2/ha)
PBeechProportion of beech in BA
ELEElevation (m)
SLPSlope (°),
ASPAspect
TsprAverage temperature for March, April and May (°C)
SProdCoefficient K (proxy of site productivity)
BAREMBA of cut and dead trees (m2/ha)
PPMParameter prediction method

References

  1. Pretzsch, H. Forest Dynamics, Growth and Yield: From Measurement to Model; Springer: Berlin/Heidelberg, Germany, 2010; p. 683. ISBN 9783540883067. [Google Scholar]
  2. Bassil, S.; Nyland, R.D.; Kern, C.C.; Kenefic, L.S. Dynamics of the Diameter Distribution after Selection Cutting in Uneven-and Even-Aged Northern Hardwood Stands: A Long-Term Evaluation. Can. J. For. Res. 2019, 49, 1525–1539. [Google Scholar] [CrossRef]
  3. Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012; p. 458. [Google Scholar] [CrossRef]
  4. Forrester, D.I. Linking Forest Growth with Stand Structure: Tree Size Inequality, Tree Growth or Resource Partitioning and the Asymmetry of Competition. Ecol. Manag. 2019, 447, 139–157. [Google Scholar] [CrossRef]
  5. Pretzsch, H.; Biber, P.; Uhl, E.; Dauber, E. Long-Term Stand Dynamics of Managed Spruce-Fir-Beech Mountain Forests in Central Europe: Structure, Productivity and Regeneration Success. Forestry 2015, 88, 407–428. [Google Scholar] [CrossRef]
  6. Russell, M.B.; Burkhart, H.E.; Amateis, R.L.; Prisley, S.P. Regional Locale and Its Influence on the Prediction of Loblolly Pine Diameter Distributions. South. J. Appl. For. 2012, 36, 198–203. [Google Scholar] [CrossRef]
  7. Forrester, D.I.; Elms, S.R.; Baker, T.G. Tree Growth-Competition Relationships in Thinned Eucalyptus Plantations Vary with Stand Structure and Site Quality. Eur. J. Res. 2013, 132, 241–252. [Google Scholar] [CrossRef]
  8. Condés, S.; del Río, M.; Forrester, D.I.; Avdagić, A.; Bielak, K.; Bončina, A.; Bosela, M.; Hilmers, T.; Ibrahimspahić, A.; Drozdowski, S.; et al. Temperature Effect on Size Distributions in Spruce-Fir-Beech Mixed Stands across Europe. Ecol. Manag. 2022, 504, 119819. [Google Scholar] [CrossRef]
  9. Gorgoso, J.J.; Rojo, A.; Camara-Obregon, A.; Dieguez-Aranda, U. A comparison of estimation methods for fitting Weibull, Johnson’s SB and beta functions to Pinus pinaster, Pinus radiata and Pinus sylvestris stands in northwest Spain. For. Syst. 2012, 21, 446–459. [Google Scholar] [CrossRef]
  10. Pretzsch, H.; Biber, P.; Ďurský, J. The Single Tree-Based Stand Simulator SILVA: Construction, Application and Evaluation. Ecol. Manag. 2002, 162, 3–21. [Google Scholar] [CrossRef]
  11. Fabrika, M.; Valent, P.; Scheer, Ľ. Thinning Trainer Based on Forest-Growth Model, Virtual Reality and Computer-Aided Virtual Environment. Environ. Model. Softw. 2018, 100, 11–23. [Google Scholar] [CrossRef]
  12. Schütz, J.P.; Rosset, C.; Dumollard, G.; Endtner, J.; Gollut, C.; Martin, V.; Sala, V.; Weber, D.; Wyss, F. SiWaWa 2.0 et Placettes Permanentes de Suivi Sylvicole (PPSS), Rapport Final (SiWaWa 2.0) and Permanent Monitoring Plots, Final Report; School of Agricultural, Forest and Food Sciences, HAFL: Zollikofen, Switzerland, 2018; p. 127. [Google Scholar]
  13. Rijal, B.; Sharma, M. Modelling Diameter at Breast Height Distribution of Jack Pine and Black Spruce Natural Stands in Eastern Canada. Can. J. For. Res. 2024, 54, 554–568. [Google Scholar] [CrossRef]
  14. Sghaier, T.; Cañellas, I.; Calama, R.; Sánchez-González, M. Modelling Diameter Distribution of Tetraclinis articulata in Tunisia Using Normal and Weibull Distributions with Parameters Depending on Stand Variables. iForest 2016, 9, 702–709. [Google Scholar] [CrossRef]
  15. Nanos, N.; de Luna, S.S. Fitting Diameter Distribution Models to Data from Forest Inventories with Concentric Plot Design. For. Syst. 2017, 26, e01S. [Google Scholar] [CrossRef]
  16. Bailey, R.L.; Dell, T.R. Quantifying Diameter Distributions with the Weibull Function. For. Sci. 1973, 19, 97–104. [Google Scholar] [CrossRef]
  17. Dubey, S.D. Some Percentile Estimators for Weibull Parameters. Technometrics 1967, 9, 119–129. [Google Scholar] [CrossRef]
  18. Schütz, J.P.; Rosset, C. Performances of Different Methods of Estimating the Diameter Distribution Based on Simple Stand Structure Variables in Monospecific Regular Temperate European Forests. Ann. Sci. 2020, 77, 47. [Google Scholar] [CrossRef]
  19. Kangas, A.; Maltamo, M. Performance of Percentile Based Diameter Distribution Prediction and Weibull Method in Independent Data Sets. Silva Fenn. 2000, 34, 381–398. [Google Scholar] [CrossRef]
  20. Guo, H.; Liu, X.; Liu, D. Soil-Sensitive Weibull Distribution Models of Larix principis-rupprechtii Plantations across Northern China. Forests 2024, 15, 1562. [Google Scholar] [CrossRef]
  21. Cao, Q.V. Predicting Future Diameter Distributions given Current Stand Attributes. Can. J. For. Res. 2022, 52, 561–567. [Google Scholar] [CrossRef]
  22. Clutter, J.L.; Bennett, F.A. Diameter Distributions in Old-Field Slash Pine Plantations; Georgia Forest Research Council: Dry Branch, GA, USA, 1965; pp. 1–9. [Google Scholar]
  23. Poudel, K.P.; Cao, Q.V. Evaluation of Methods to Predict Weibull Parameters for Characterizing Diameter Distributions. For. Sci. 2013, 59, 243–252. [Google Scholar] [CrossRef]
  24. Mehtatalo, L.; Lappi, J. Biometry for Forestry and Environmental Data with Examples in R; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9781498711487. [Google Scholar]
  25. Newton, P.F.; Lei, Y.; Zhang, S.Y. Stand-Level Diameter Distribution Yield Model for Black Spruce Plantations. Ecol. Manag. 2005, 209, 181–192. [Google Scholar] [CrossRef]
  26. Kuehne, C.; Granhus, A.; Hanssen, K.H. Analyzing Growth Characteristics and Diameter Distributions of Young Norway Spruce Plantations in Norway. New For. 2025, 56, 32. [Google Scholar] [CrossRef]
  27. Sa, Q.; Jin, X.; Pukkala, T.; Li, F. Developing Weibull-Based Diameter Distributions for the Major Coniferous Species in Heilongjiang Province, China. J. Res. 2023, 34, 1803–1815. [Google Scholar] [CrossRef]
  28. Maltamo, M. Comparing Basal Area Diameter Distributions Estimated by Tree Species and for the Entire Growing Stock in a Mixed Stand. Silva Fenn. 1997, 31, 5609. [Google Scholar] [CrossRef]
  29. Guo, H.; Lei, X.; You, L.; Zeng, W.; Lang, P.; Lei, Y. Climate-Sensitive Diameter Distribution Models of Larch Plantations in North and Northeast China. For. Ecol. Manag. 2022, 506, 119947. [Google Scholar] [CrossRef]
  30. Sanquetta, C.R.; Behling, A.; Dalla Corte, A.P.; Péllico Netto, S.; Rodrigues, A.L.; Simon, A.A. A Model Based on Environmental Factors for Diameter Distribution in Black Wattle in Brazil. PLoS ONE 2014, 9, e100093. [Google Scholar] [CrossRef] [PubMed]
  31. O’Hara, K.L.; Ramage, B.S. Silviculture in an Uncertain World: Utilizing Multi-Aged Management Systems to Integrate Disturbance. For. Int. J. For. Res. 2013, 86, 401–410. [Google Scholar] [CrossRef]
  32. Rodrigo, R.; Pettit, J.L.; Matula, R.; Kozák, D.; Bače, R.; Pavlin, J.; Janda, P.; Mikoláš, M.; Nagel, T.A.; Schurman, J.; et al. Historical Mixed-Severity Disturbances Shape Current Diameter Distributions of Primary Temperate Norway Spruce Mountain Forests in Europe. For. Ecol. Manag. 2022, 503, 119772. [Google Scholar] [CrossRef]
  33. Kuliešis, A.; Kasperavičius, A. Reliability and Efficiency of Lithuanian National Forest Inventory Sampling Design and Results. Balt. For. 2022, 10, 27–35. [Google Scholar]
  34. Mey, R.; Stadelmann, G.; Thürig, E.; Bugmann, H.; Zell, J. From Small Forest Samples to Generalised Uni- and Bimodal Stand Descriptions. Methods Ecol. Evol. 2021, 12, 634–645. [Google Scholar] [CrossRef]
  35. Mey, R.; Temperli, C.; Stillhard, J.; Nitzsche, J.; Thürig, E.; Bugmann, H.; Zell, J. Deriving Forest Stand Information from Small Sample Plots: An Evaluation of Statistical Methods. Ecol. Manag. 2023, 544, 121155. [Google Scholar] [CrossRef]
  36. Bohn, U.; Gollub, G.; Hettwer, C.; Neuhäuslová, Z.; Raus, T.; Schlüter, H.; Weber, H. Karte der Natürlichen Vegetation Europas Map of the Natural Vegetation of Europe Maßstab/Scale 1:2500000; Landwirtschaftsverlag: Münster, Germany, 2000; p. 523. [Google Scholar]
  37. Rozman, A.; Poljanec, A.; Babij, V.; Klopčič, M.; Dakskobler, I.; Kutnar, L.; Bončina, A. Gozdni rastiščni tipi Slovenije: Primerjalni pregled ekoloških, vegetacijskih, rastiščnih, sestojnih in upravljavskih značilnosti. GozdVestn 2023, 83, 1–23. [Google Scholar]
  38. Bončina, A.; Rozman, A.; Dakskobler, I.; Klopčič, M.; Babij, V.; Poljanec, A. Gozdni Rastiščni Tipi Slovenije: Vegetacijske, Sestojne, Upravljavske Značilnosti; Biotechnical Faculty, Department of Forestry and Renewable Forest Resources and Slovenia and Forest Service: Ljubljana, Slovenia, 2021; p. 575. [Google Scholar]
  39. Diaci, J.; Adamic, T.; Fidej, G.; Rozenbergar, D. Toward a Beech-Dominated Alternative Stable State in Dinaric Mixed Montane Forests: A Long-Term Study of the Pecka Old-Growth Forest. Front. For. Glob. Change 2022, 5, 937404. [Google Scholar] [CrossRef]
  40. Larsson, T.-B. European Forest Types, Categories and Types for Sustainable Forest Management Reporting and Policy; Technical Report; European Environmental Agency: Copenhagen, Denmark, 2006; p. 114. [Google Scholar]
  41. Rohner, B.; Waldner, P.; Lischke, H.; Ferretti, M.; Thürig, E. Predicting Individual-Tree Growth of Central European Tree Species as a Function of Site, Stand, Management, Nutrient, and Climate Effects. Eur. J. Res. 2018, 137, 29–44. [Google Scholar] [CrossRef]
  42. Trifković, V.; Bončina, A.; Ficko, A. Analyzing Asymmetries in the Response of European Beech to Precipitation Anomalies in Various Stand and Site Conditions Using Decadal Diameter Censuses. Agric. For. Meteorol. 2022, 327, 109195. [Google Scholar] [CrossRef]
  43. Trifković, V.; Bončina, A.; Ficko, A. Recruitment of European Beech, Norway Spruce and Silver Fir in Uneven-Aged Forests: Optimal and Critical Stand, Site and Climatic Conditions. For. Ecol. Manag. 2023, 529, 120679. [Google Scholar] [CrossRef]
  44. Lexerød, N.L. Recruitment Models for Different Tree Species in Norway. Ecol. Manag. 2005, 206, 91–108. [Google Scholar] [CrossRef]
  45. Pretzsch, H.; Heym, M.; Hilmers, T.; Bravo-Oviedo, A.; Ahmed, S.; Ammer, C.; Avdagić, A.; Bielak, K.; Bravo, F.; Brazaitis, G.; et al. Mortality Reduces Overyielding in Mixed Scots Pine and European Beech Stands along a Precipitation Gradient in Europe. For. Ecol. Manag. 2023, 539, 121008. [Google Scholar] [CrossRef]
  46. Trifković, V.; Bončina, A.; Ficko, A. Density-Dependent Mortality Models for Mono- and Multi-Species Uneven-Aged Stands: The Role of Species Mixture. For. Ecol. Manag. 2023, 545, 121260. [Google Scholar] [CrossRef]
  47. Moreno, A.; Neumann, M.; Hasenauer, H. Climate Limits on European Forest Structure across Space and Time. Glob. Planet. Change 2018, 169, 168–178. [Google Scholar] [CrossRef]
  48. Schulze, E.D.; Aas, G.; Grimm, G.W.; Gossner, M.M.; Walentowski, H.; Ammer, C.; Kühn, I.; Bouriaud, O.; von Gadow, K. A Review on Plant Diversity and Forest Management of European Beech Forests. Eur. J. Res. 2016, 135, 51–67. [Google Scholar] [CrossRef]
  49. Antonucci, S.; Santopuoli, G.; Marchetti, M.; Tognetti, R.; Chiavetta, U.; Garfì, V. What Is Known About the Management of European Beech Forests Facing Climate Change? A Review. Curr. For. Rep. 2021, 7, 321–333. [Google Scholar] [CrossRef]
  50. Schütz, J.-P. The Swiss Experience: More than One Hundred Years of Experience with a Single-Tree-Selection Management-System in Mountainous Mixed-Forests of Spruce, Fir and Beech from an Empirically Developed Utilization in Small-Scale Private Forests to an Elaborate and Original Concept of Silviculture; UFRO Interdisciplinary Uneven-Aged Management Symposium; Oregon State University: Corvallis, OR, USA, 1997. [Google Scholar]
  51. Bončina, A.; Kadunc, A.; Robič, D. Effects of Selective Thinning on Growth and Development of Beech (Fagus sylvatica L.) Forest Stands in South-Eastern Slovenia. Ann. Sci. 2007, 64, 47–57. [Google Scholar] [CrossRef]
  52. Newton, P.F. Stand Density Management Diagrams: Modelling Approaches, Variants, and Exemplification of Their Potential Utility in Crop Planning. Can. J. For. Res. 2021, 51, 236–256. [Google Scholar] [CrossRef]
  53. Rodrigo, R.M.; Pettit, J.L.; Janda, P.; Pavlin, J.; Ralhan, D.; Kozak, D.; Matula, R.; Marchand, W.; Bače, R.; Dušátko, M.; et al. Past Disturbances Shape Present Tree Size Distribution in European Temperate Primary Beech-Dominated Forests. For. Ecol. Manag. 2024, 574, 122364. [Google Scholar] [CrossRef]
  54. Merganič, J.; Sterba, H. Characterisation of Diameter Distribution Using the Weibull Function: Method of Moments. Eur. J. Res. 2006, 125, 427–439. [Google Scholar] [CrossRef]
  55. Geßler, A.; Keitel, C.; Kreuzwieser, J.; Matyssek, R.; Seiler, W.; Rennenberg, H. Potential Risks for European Beech (Fagus sylvatica L.) in a Changing Climate. Trees—Struct. Funct. 2007, 21, 1–11. [Google Scholar] [CrossRef]
  56. Martinez del Castillo, E.; Zang, C.S.; Buras, A.; Hacket-Pain, A.; Esper, J.; Serrano-Notivoli, R.; Hartl, C.; Weigel, R.; Klesse, S.; Resco de Dios, V.; et al. Climate-Change-Driven Growth Decline of European Beech Forests. Commun. Biol. 2022, 5, 163. [Google Scholar] [CrossRef]
  57. Slovenia Forest Service. Forestry Databases; Slovenia Forest Service: Ljubljana, Slovenia, 2014. [Google Scholar]
  58. Poljanec, A.; Ficko, A.; Boncina, A. Spatiotemporal Dynamic of European Beech (Fagus sylvatica L.) in Slovenia, 1970–2005. For. Ecol. Manag. 2010, 259, 2183–2190. [Google Scholar] [CrossRef]
  59. Bončina, A. History, Current Status and Future Prospects of Uneven-Aged Forest Management in the Dinaric Region: An Overview. Forestry 2011, 84, 467–478. [Google Scholar] [CrossRef]
  60. Slovenian Environment Agency. Databases; Slovenian Environment Agency: Ljubljana, Slovenia, 2021. [Google Scholar]
  61. Ministry of Agriculture, Forestry and Food. Databases; Ministry of Agriculture, Forestry and Food: Ljubljana, Slovenia, 2021. [Google Scholar]
  62. Braun-Blanquet, J. Zur Wertung Der Gesellschaftstreue in der Pflanzensoziologie. Vierteljahrsschr. Naturforschenden Ges. Zürich 1925, 70, 122–149. [Google Scholar]
  63. Kutnar, L.; Dakskobler, I.; Dakskobler, I.; Robič, D. Tipologija Gozdnih Rastišč Slovenije Na Podlagi Ekoloških in Vegetacijskih Razmer Za Potrebe Usmerjanja Razvoja Gozdov. Gozdarski Vestn. 2012, 70, 195–214. [Google Scholar]
  64. O’Hara, K.L.; Hasenauer, H.; Kindermann, G. Sustainability in Multi-Aged Stands: An Analysis of Long-Term Plenter Systems. Forestry 2007, 80, 163–181. [Google Scholar] [CrossRef]
  65. Duduman, G. A Forest Management Planning Tool to Create Highly Diverse Uneven-Aged Stands. Forestry 2011, 84, 301–314. [Google Scholar] [CrossRef]
  66. Klopčič, M.; Poljanec, A.; Dolinar, M.; Kastelec, D.; Bončina, A. Ice-Storm Damage to Trees in Mixed Central European Forests: Damage Patterns, Predictors and Susceptibility of Tree Species. Forestry 2020, 93, 430–443. [Google Scholar] [CrossRef]
  67. Dănescu, A.; Albrecht, A.T.; Bauhus, J. Structural Diversity Promotes Productivity of Mixed, Uneven-Aged Forests in Southwestern Germany. Oecologia 2016, 182, 319–333. [Google Scholar] [CrossRef]
  68. Palahí, M.; Pukkala, T.; Trasobares, A. Modelling the Diameter Distribution of Pinus sylvestris, Pinus nigra and Pinus halepensis Forest Stands in Catalonia Using the Truncated Weibull Function. Forestry 2006, 79, 553–562. [Google Scholar] [CrossRef]
  69. Weibull, W. A Statistical Theory of the Strength of Materials. Vetenskapa Acadmiend Handligar 1939, 151, 1–45. [Google Scholar]
  70. Schmidt, L.N.; Sanquetta, M.N.I.; McTague, J.P.; da Silva, G.F.; Fraga Filho, C.V.; Sanquetta, C.R.; Soares Scolforo, J.R. On the Use of the Weibull Distribution in Modeling and Describing Diameter Distributions of Clonal Eucalypt Stands. Can. J. For. Res. 2020, 50, 1050–1063. [Google Scholar] [CrossRef]
  71. Bončina, A.; Klopčič, M.; Trifković, V.; Ficko, A.; Simončič, P. Tree and Stand Growth Differ among Soil Classes in Semi-Natural Forests in Central Europe. Catena 2023, 222, 106854. [Google Scholar] [CrossRef]
  72. Jones, A.; Montanarella, L.; Jones, R. Soils Atlas of Europe; The European Soil Bureau, Joint Research Centre: Ispra, Italy, 2005; Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC32396 (accessed on 17 May 2024).
  73. Cailliez, F.; Alder, D. Forest Volume Estimation and Yield Prediction; Food and Agriculture Organization of the United Nations: Rome, Italy, 1980; ISBN 9251009236. [Google Scholar]
  74. Kušar, G.; Hočevar, M. Selection of appropriate tariff functions of adapted uniform French tariffs for stand’s growing stock computation by control sampling method. In Control Sampling Method in Slovenia—History, Characteristics and Use, Špela Planinšek; Gozdarski Inštitut Slovenije, Silva Slovenica: Ljubljana, Slovenia, 2009; pp. 69–83. [Google Scholar]
  75. Beltran, H.A.; Chauchard, L.; Velásquez, A.; Sbrancia, R.; Pastur, G.M. Índice de Sítio Diamétrico: Um Método Alternativo Para Estimar a Qualidade Do Sítio Em Florestas de Nothofagus Obliqua e N. Alpina. Cerne 2016, 22, 345–354. [Google Scholar] [CrossRef]
  76. Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. Available online: https://www.stats.ox.ac.uk/pub/MASS4/ (accessed on 13 March 2023).
  77. Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2019; Available online: https://www.john-fox.ca/Companion/ (accessed on 14 March 2023).
  78. Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
  79. Knox, R.G.; Peet, R.K.; Christensen, N.L. Population Dynamics in Loblolly Pine Stands: Changes in Skewness and Size Inequality. Ecology 1989, 70, 1153–1167. [Google Scholar] [CrossRef]
  80. Stojanović, D.B.; Levanič, T.; Matović, B.; Stjepanović, S.; Orlović, S. Growth Response of Different Tree Species (Oaks, Beech and Pine) from SE Europe to Precipitation over Time. Dendrobiology 2018, 79, 97–110. [Google Scholar] [CrossRef]
  81. Weigel, R.; Bat-Enerel, B.; Dulamsuren, C.; Muffler, L.; Weithmann, G.; Leuschner, C. Summer Drought Exposure, Stand Structure, and Soil Properties Jointly Control the Growth of European Beech along a Steep Precipitation Gradient in Northern Germany. Glob. Change Biol. 2023, 29, 763–779. [Google Scholar] [CrossRef]
  82. Binkley, D. Seven Decades of Stand Development in Mixed and Pure Stands of Conifers and Nitrogen-Fixing Red Alder. Can. J. For. Res. 2003, 33, 2274–2279. [Google Scholar] [CrossRef]
  83. Binkley, D.; Senock, R.; Bird, S.; Cole, T.G. Twenty Years of Stand Development in Pure and Mixed Stands of Eucalyptus saligna and Nitrogen-Fixing Facaltaria moluccana. Ecol. Manag. 2003, 182, 93–102. [Google Scholar] [CrossRef]
  84. Forrester, D.I.; Smith, R.G.B. Faster Growth of Eucalyptus grandis and Eucalyptus pilularis in Mixed-Species Stands than Monocultures. Ecol. Manag. 2012, 286, 81–86. [Google Scholar] [CrossRef]
  85. Pretzsch, H.; del Río, M.; Ammer, C.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; Dirnberger, G.; Drössler, L.; et al. Growth and Yield of Mixed versus Pure Stands of Scots Pine (Pinus sylvestris L.) and European Beech (Fagus sylvatica L.) Analysed along a Productivity Gradient through Europe. Eur. J. Res. 2015, 134, 927–947. [Google Scholar] [CrossRef]
  86. Forrester, D.I.; Bauhus, J.; Khanna, P.K. Growth Dynamics in a Mixed-Species Plantation of Eucalyptus globulus and Acacia mearnsii. Ecol. Manag. 2004, 193, 81–95. [Google Scholar] [CrossRef]
  87. Diaci, J. Gozdna Ekologija in Nega; Univerza v Ljubljani: Ljubljana, Slovenia, 2021; p. 434. [Google Scholar]
  88. Diaci, J. Nature-Based Silviculture in Slovenia: Origins, Development and Future Trends. In Nature-Based Forestry in Central Europe; University in Ljubljana: Ljubljana, Slovenia, 2006; pp. 119–131. [Google Scholar]
  89. Petrovska, R.; Bugmann, H.; Hobi, M.L.; Ghosh, S.; Brang, P. Survival Time and Mortality Rate of Regeneration in the Deep Shade of a Primeval Beech Forest. Eur. J. Res. 2022, 141, 43–58. [Google Scholar] [CrossRef]
  90. Heiri, C.; Wolf, A.; Rohrer, L.; Bugmann, H. Forty Years of Natural Dynamics in Swiss Beech Forests: Structure, Composition, and the Influence of Former Management. Ecol. Appl. 2009, 19, 1920–1934. [Google Scholar] [CrossRef]
  91. Fidej, G.; Mikoš, M.; Rugani, T.; Jež, J.; Kumelj, Š.; Diaci, J. Assessment of the Protective Function of Forests against Debris Flows in a Gorge of the Slovenian Alps. iForest 2014, 8, 73–81. [Google Scholar] [CrossRef]
  92. Lingua, E.; Bettella, F.; Pividori, M.; Marzano, R.; Garbarino, M.; Piras, M.; Kobal, M.; Berger, F. The Protective Role of Forests to Reduce Rockfall Risks and Impacts in the Alps Under a Climate Change Perspective. In Climate Change Management; Springer: Berlin/Heidelberg, Germany, 2020; pp. 333–347. [Google Scholar]
  93. Scheidl, C.; Heiser, M.; Vospernik, S.; Lauss, E.; Perzl, F.; Kofler, A.; Kleemayr, K.; Bettella, F.; Lingua, E.; Garbarino, M.; et al. Assessing the Protective Role of Alpine Forests against Rockfall at Regional Scale. Eur. J. Res. 2020, 139, 969–980. [Google Scholar] [CrossRef]
  94. Fang, J.; Lechowicz, M.J. Climatic Limits for the Present Distribution of Beech (Fagus L.) Species in the World. J. Biogeogr. 2006, 33, 1804–1819. [Google Scholar] [CrossRef]
Forests 16 01556 g001
Figure 1. Location of the analysed sample plots (black dots, n = 6759) in the forests of Slovenia.
Figure 1. Location of the analysed sample plots (black dots, n = 6759) in the forests of Slovenia.
Forests 16 01556 g001
Forests 16 01556 g002
Figure 2. Fitted vs. modelled values of the scale parameter b and shape parameter c across different models: b1 and c1—general models including all variables; b2 and c2—models excluding some stand parameters (QMD, DMIN, DMAX); b3 and c3—models including only geo-climatic variables.
Figure 2. Fitted vs. modelled values of the scale parameter b and shape parameter c across different models: b1 and c1—general models including all variables; b2 and c2—models excluding some stand parameters (QMD, DMIN, DMAX); b3 and c3—models including only geo-climatic variables.
Forests 16 01556 g002
Forests 16 01556 g003
Figure 3. Weibull diameter distributions under varying stand predictors: minimum diameter (DMIN), maximum diameter (DMAX), quadratic mean diameter (QMD), basal area (BA), proportion of beech (PBeech) and elevation (ELE) when all other predictors were held constant at their mean values (see Table 1); aspect (ASP) was fixed at the reference level “cold”, and soil type (SoilT) at the reference level “eutric & chromic cambisols”. For each stand predictor, the distribution is shown at the 0.10 quantile (q10), mean and 0.90 quantile (q90) of its value.
Figure 3. Weibull diameter distributions under varying stand predictors: minimum diameter (DMIN), maximum diameter (DMAX), quadratic mean diameter (QMD), basal area (BA), proportion of beech (PBeech) and elevation (ELE) when all other predictors were held constant at their mean values (see Table 1); aspect (ASP) was fixed at the reference level “cold”, and soil type (SoilT) at the reference level “eutric & chromic cambisols”. For each stand predictor, the distribution is shown at the 0.10 quantile (q10), mean and 0.90 quantile (q90) of its value.
Forests 16 01556 g003
Table 1. Description of candidate variables for model development (n = 6759). SD = standard deviation of the mean. Columns b and c indicate whether a variable was included in the modelling procedure for the scale parameter b and the shape parameter c, respectively (marked with +). Variables marked with - were excluded from the modelling to avoid multicollinearity.
Table 1. Description of candidate variables for model development (n = 6759). SD = standard deviation of the mean. Columns b and c indicate whether a variable was included in the modelling procedure for the scale parameter b and the shape parameter c, respectively (marked with +). Variables marked with - were excluded from the modelling to avoid multicollinearity.
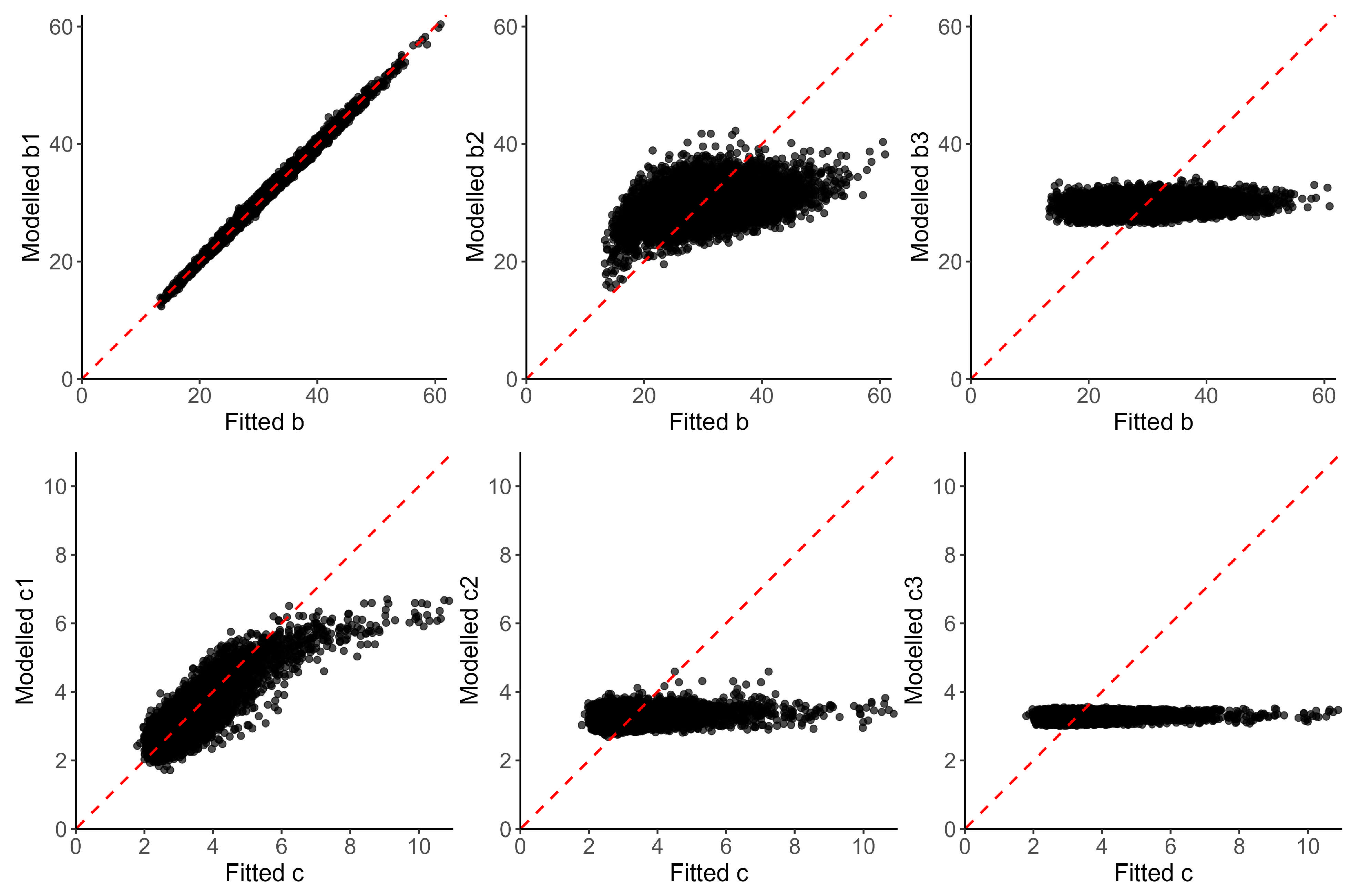
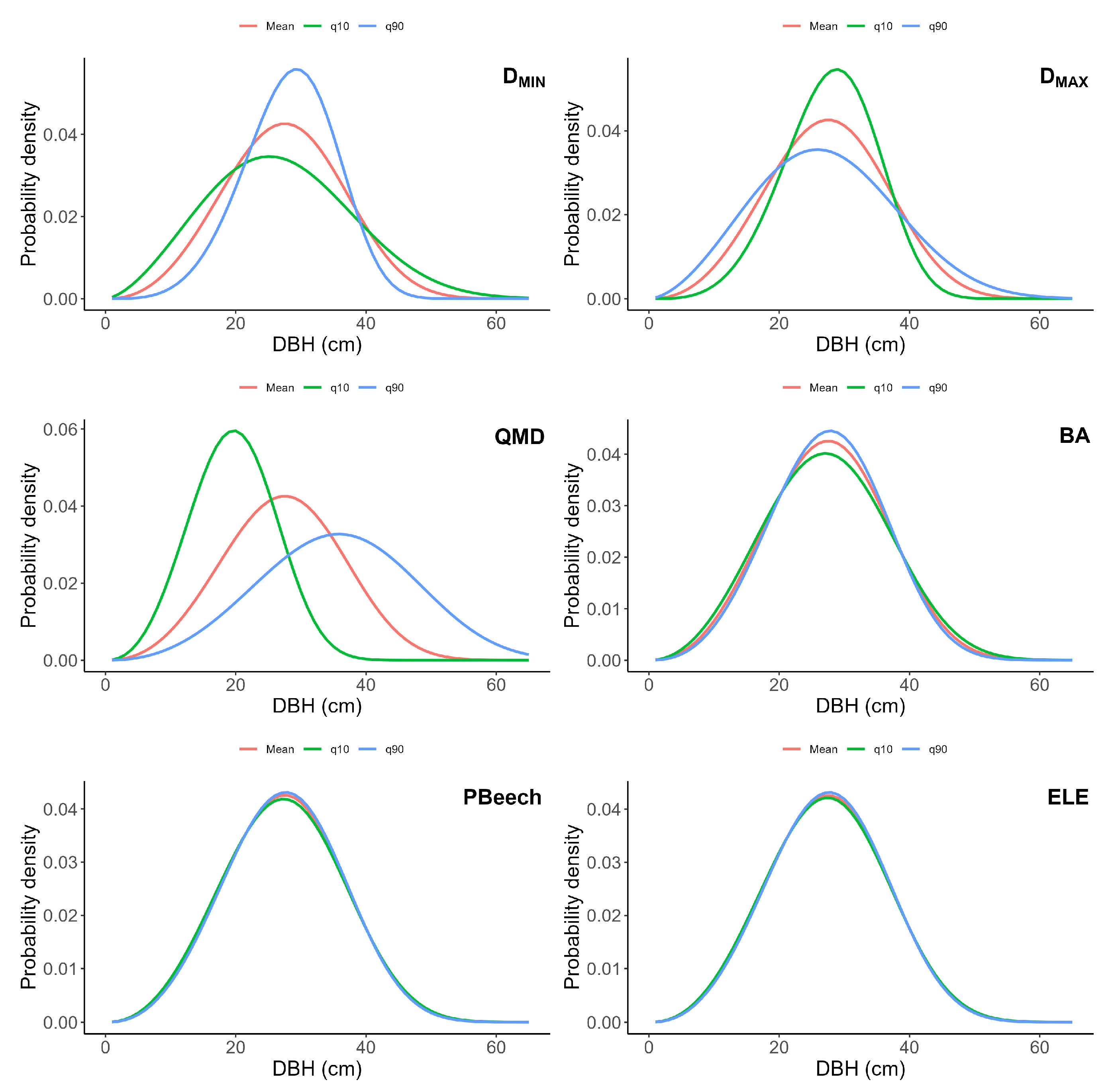
VariableDescriptionMeanSDMinMaxbc
DMINMinimum tree diameter at breast height (cm)14.05.21045++
QMDMean quadratic diameter (cm)28.56.911.057.1+-
DDOMDominant tree diameter (mean diameter of the 100 thickest trees per ha (cm))40.57.71469--
DMAXMaximum diameter (cm)47.09.71588-+
BABasal area (m2/ha)33.610.23.685.6++
NNumber of trees per hectare6053202002900--
PBeechProportion of beech in BA0.930.070.801.00++
ELEElevation (m)6773051391646++
SLPSlope (°)16.88.20.046.8++
ASPAspectDummy variable (cold, warm)++
TsprAverage temperature for March. April. May (°C)7.42.0112++
Tspr_sumSum temperature for March, April, May (°C)22.25.9336--
SOLRADSolar radiation (kJ/m2)1904.6105.915802395--
BIO1Annual mean temperature (°C)7.91.7313--
BIO2Mean diurnal range (Tmax–Tmin) (°C)9.12.3014--
BIO10Mean temperature of warmest quarter (°C)16.42.110.321.8--
BIO11Mean temperature of coldest quarter (°C)−0.61.4−4.35.7--
PCPPrecipitation (mm)1752.1480.103600--
PCP_DDays with precipitation187937--
DSoilDepth of soil (cm)58.722.70300--
DSoil_ADepth of soil (organic A horizon) (cm)13.44.9052--
pHSoil pH (average)5.181.0807.5--
pH_ASoil pH (organic A horizon)5.111.2807.5--
SoilTFAO soil class (leptosols, eutric & chromic cambisols, dystric cambisols, other soil classes) ++
SProdCoefficient K (proxy for site productivity)1.980.281.202.95++
BAREMBasal area of cut and dead trees (m2/ha) 3.24.50.041.9++
Data sources: Slovenia Forest Service database [57]; Slovenian Environment Agency database [60]; Ministry of Agriculture, Forestry and Food database [61]. Variable types: SoilT and ASP are categorical; all others are numerical.
Table 2. Impact of predictors in the models for the scale parameter b and shape parameter c of the two-parameter Weibull distribution function and model performance and validation metrics for multiple linear regression models. The relative decrease of R2 (%) when the predictor is omitted from the model is shown, together with the direction of the effect of each predictor in the model (↑ positive; ↓ negative). Parameters c and b were modelled with different sets of potential explanatory variables (1—all variables; 2—some stand variables excluded; 3—all stand variables excluded). Variables deliberately excluded from the modelling process are marked with X. Further details regarding model coefficients, significance and the transformation of dependent and independent variables are provided in Tables S2 and S3 in the Supplementary Material. R2 = coefficient of determination; RMSE = root mean square error; ME = mean error; SD = standard deviation of ME.
Table 2. Impact of predictors in the models for the scale parameter b and shape parameter c of the two-parameter Weibull distribution function and model performance and validation metrics for multiple linear regression models. The relative decrease of R2 (%) when the predictor is omitted from the model is shown, together with the direction of the effect of each predictor in the model (↑ positive; ↓ negative). Parameters c and b were modelled with different sets of potential explanatory variables (1—all variables; 2—some stand variables excluded; 3—all stand variables excluded). Variables deliberately excluded from the modelling process are marked with X. Further details regarding model coefficients, significance and the transformation of dependent and independent variables are provided in Tables S2 and S3 in the Supplementary Material. R2 = coefficient of determination; RMSE = root mean square error; ME = mean error; SD = standard deviation of ME.
b1b2b3c1c2c3
DMIN1.6 × 10−3 ↑xx59.70 ↑xx
QMD99.83 ↑ excluded due to MC
DMAXexcluded due to MC37.44 ↓
BA 80.97 ↑x2.28 ↑11.73 ↓x
PBeech4.7 × 10−5 ↑4.37 ↑x0.28 ↑62.54 ↑x
ELE1.4 × 10−5 ↑1.90 ↓5.74 ↓0.11 ↑2.71 ↑13.47 ↑
SLP 4.76 ↑0.03 ↓ 9.43 ↓
Tspr 0.06 ↓4.79 ↓23.90 ↓
ASP warm 0.46 ↓2.62 ↓0.02 ↓
SoilT D. Cambisol ↑↑ ↑↑
SoilT Leptosols 0.85 ↑7.91 ↑ 11.76 ↑53.20 ↑
SoilT Other ↑↑
SProd 8.98 ↑78.97 ↑
BAREM 2.45 ↑x0.07 ↑6.46 ↑x
Performance
evaluation
AIC−35,915−1369−154−701112781523
R2 (%)99.518.82.8 72.04.91.3
RMSE0.01700.21830.23890.14380.26560.2705
Validation
R2 (%)99.518.72.772.14.81.4
RMSE0.01690.21580.23910.14400.26570.2706
ME4.907 × 10−8−2.947 × 10−6−7.895 × 10−71.268 × 10−56.0525 × 10−51.185 × 10−5
SD1.697 × 10−22.166 × 10−12.389 × 10−11.392 × 10−12.659 × 10−12.708 × 10−1
Table 3. Impact of predictors of the shape parameter c for the main beech forest types. The relative decrease in R2 (%) when a predictor is omitted is shown, together with the direction of the effect (↑ positive, ↓ negative). Further details on model coefficients, level of statistical significance and the transformation of dependent and independent variables are provided in Table S7.
Table 3. Impact of predictors of the shape parameter c for the main beech forest types. The relative decrease in R2 (%) when a predictor is omitted is shown, together with the direction of the effect (↑ positive, ↓ negative). Further details on model coefficients, level of statistical significance and the transformation of dependent and independent variables are provided in Table S7.
Submontane & CollineMontaneSubalpine & AltimontaneAcidophilousThermophilus
DMIN61.48 ↑59.11 ↑62.12 ↑61.94 ↑59.73 ↑
DMAX35.79 ↓37.29 ↓36.25 ↓35.46 ↓38.06 ↓
BA2.36 ↑2.69 ↑1.23 ↑2.60 ↑1.36 ↑
PBeech0.28 ↑0.46 ↑ 0.64 ↑
ELE 0.21 ↑
SLP
Tspr 0.16 ↓
ASP warm 0.07 ↓
SoilT D. Cambisol
SoilT Leptosol
SoilT Other
SProd
BAREM0.08 ↑0.20 ↑0.03 ↑
Table 4. Linear regression model performance for scale parameter b and shape parameter c for the main beech forest types. N = the number of plots per beech forest type, R2 = coefficient of determination, RMSE = root mean square error.
Table 4. Linear regression model performance for scale parameter b and shape parameter c for the main beech forest types. N = the number of plots per beech forest type, R2 = coefficient of determination, RMSE = root mean square error.
Submontane & CollineMontaneSubalpine & AltimontaneAcidophilousThermophilus
N181421555951487531
bR2 (%)99.599.699.699.499.6
RMSE0.1660.01710.01690.01690.0167
cR2 (%)72.471.771.269.975.6
RMSE0.1410.1500.1510.1380.140
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bončina, Ž.; Rosset, C.; Klopčič, M. Modelling Diameter Distribution in Near-Natural European Beech Forests: Are Geo-Climatic Variables Alone Sufficient? Forests 2025, 16, 1556. https://doi.org/10.3390/f16101556

AMA Style

Bončina Ž, Rosset C, Klopčič M. Modelling Diameter Distribution in Near-Natural European Beech Forests: Are Geo-Climatic Variables Alone Sufficient? Forests. 2025; 16(10):1556. https://doi.org/10.3390/f16101556

Chicago/Turabian Style

Bončina, Živa, Christian Rosset, and Matija Klopčič. 2025. "Modelling Diameter Distribution in Near-Natural European Beech Forests: Are Geo-Climatic Variables Alone Sufficient?" Forests 16, no. 10: 1556. https://doi.org/10.3390/f16101556

APA Style

Bončina, Ž., Rosset, C., & Klopčič, M. (2025). Modelling Diameter Distribution in Near-Natural European Beech Forests: Are Geo-Climatic Variables Alone Sufficient? Forests, 16(10), 1556. https://doi.org/10.3390/f16101556

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop