Effects of Stand Age Gradient and Thinning Intervention on the Structure and Productivity of Larix gmelinii Plantations
Abstract
1. Introduction
2. Materials and Methods
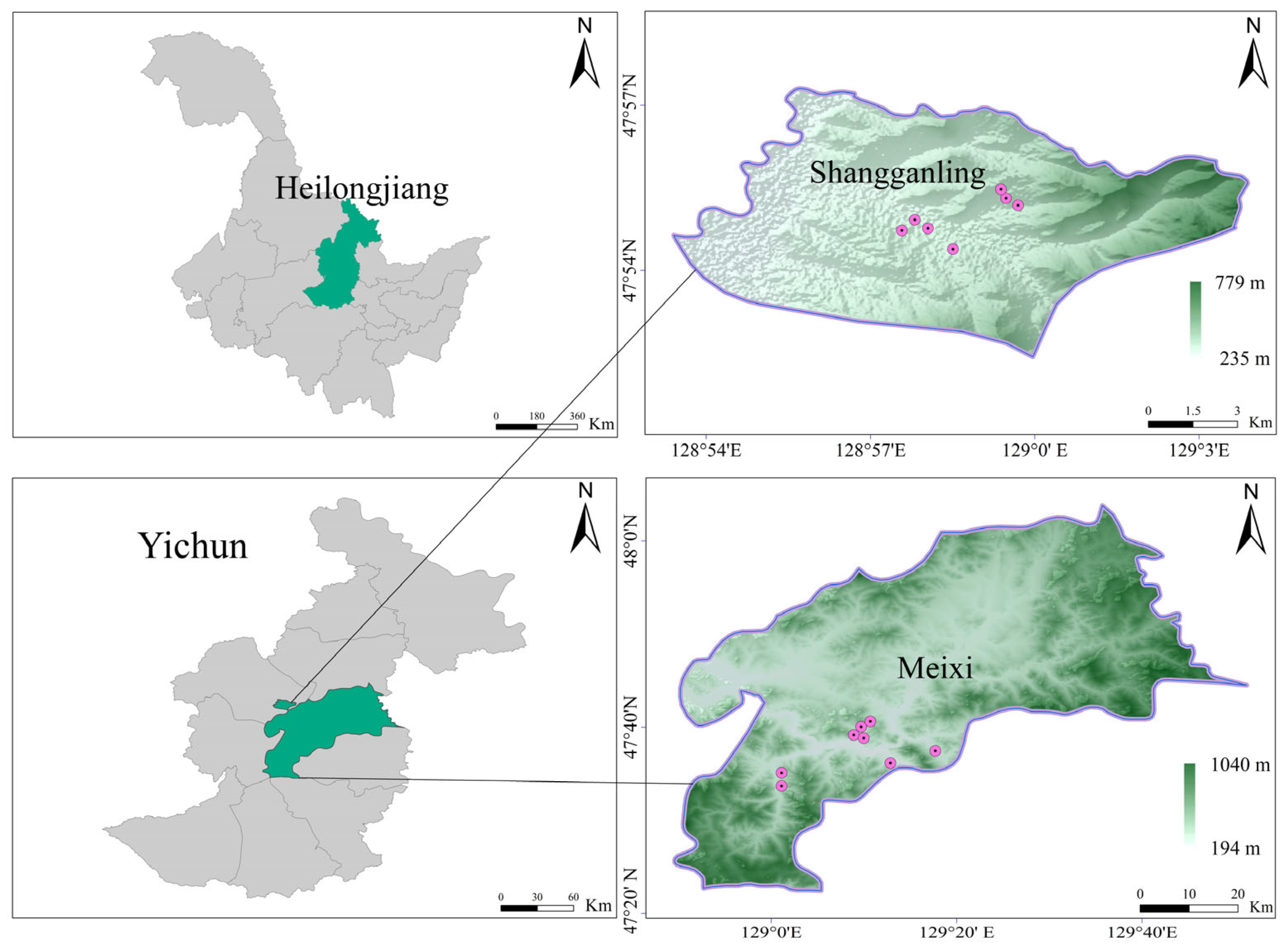
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. Monitoring Plot Layout and Data Collection
2.2.2. Data Preprocessing
2.3. Calculation of Structural and Functional Indicators
2.3.1. Calculation and Classification of Spatial Structural Parameters
2.3.2. Construction of TSSI and FSSI
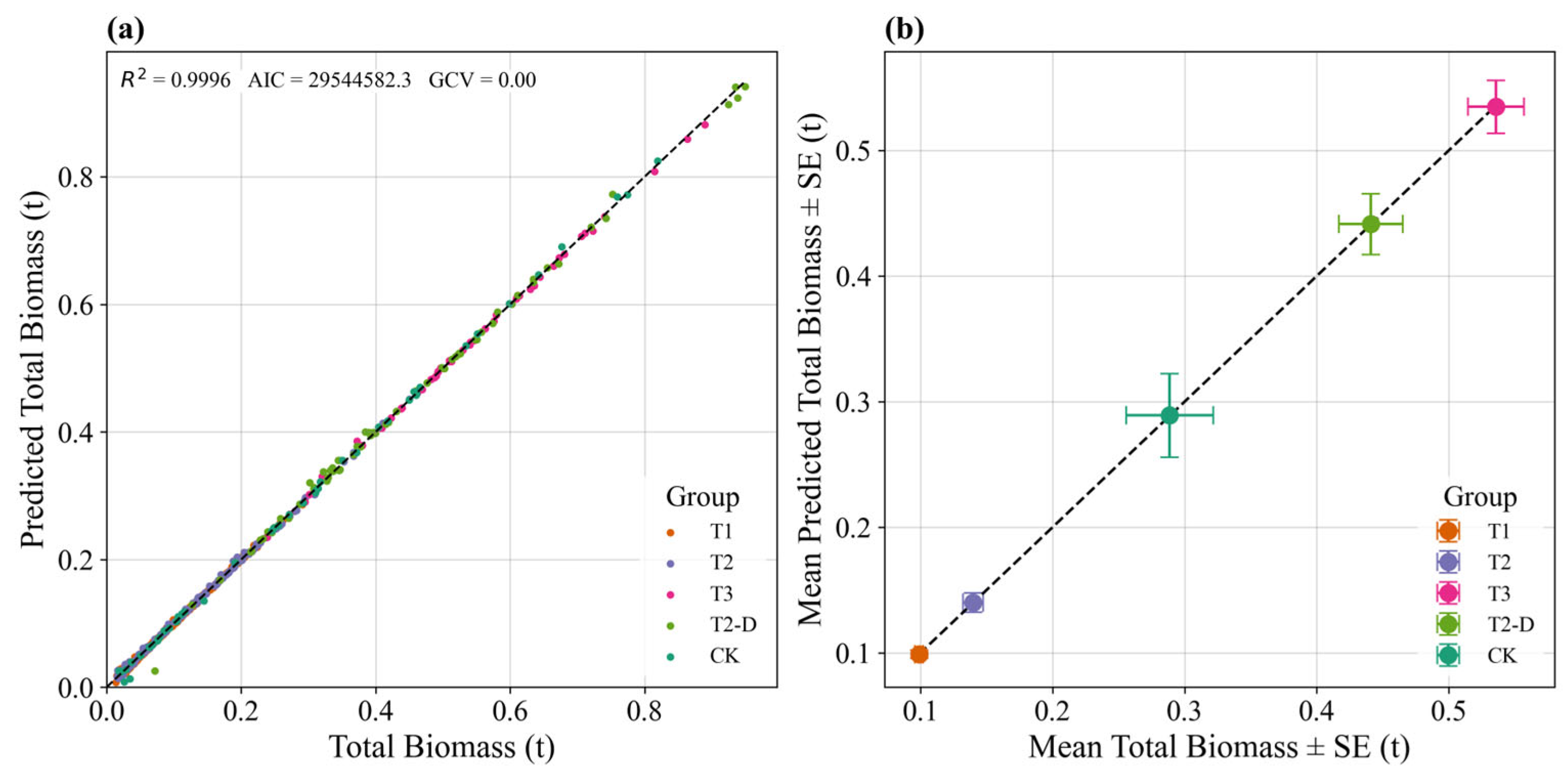
2.3.3. LBP-GAM Model Construction
2.3.4. Calculation of Stand Structural and Functional Parameters
- (1)
- HDR and MHDR
- (2)
- TB
- (3)
- SD
- (4)
- CD
2.4. Data Analysis Procedures and Statistical Methods
3. Results
3.1. Structural and Functional Parameters
3.1.1. Tree-Level Parameter Calculations
3.1.2. Stand-Level Parameter Calculations
3.2. Tree and Stand Spatial Structure Indices
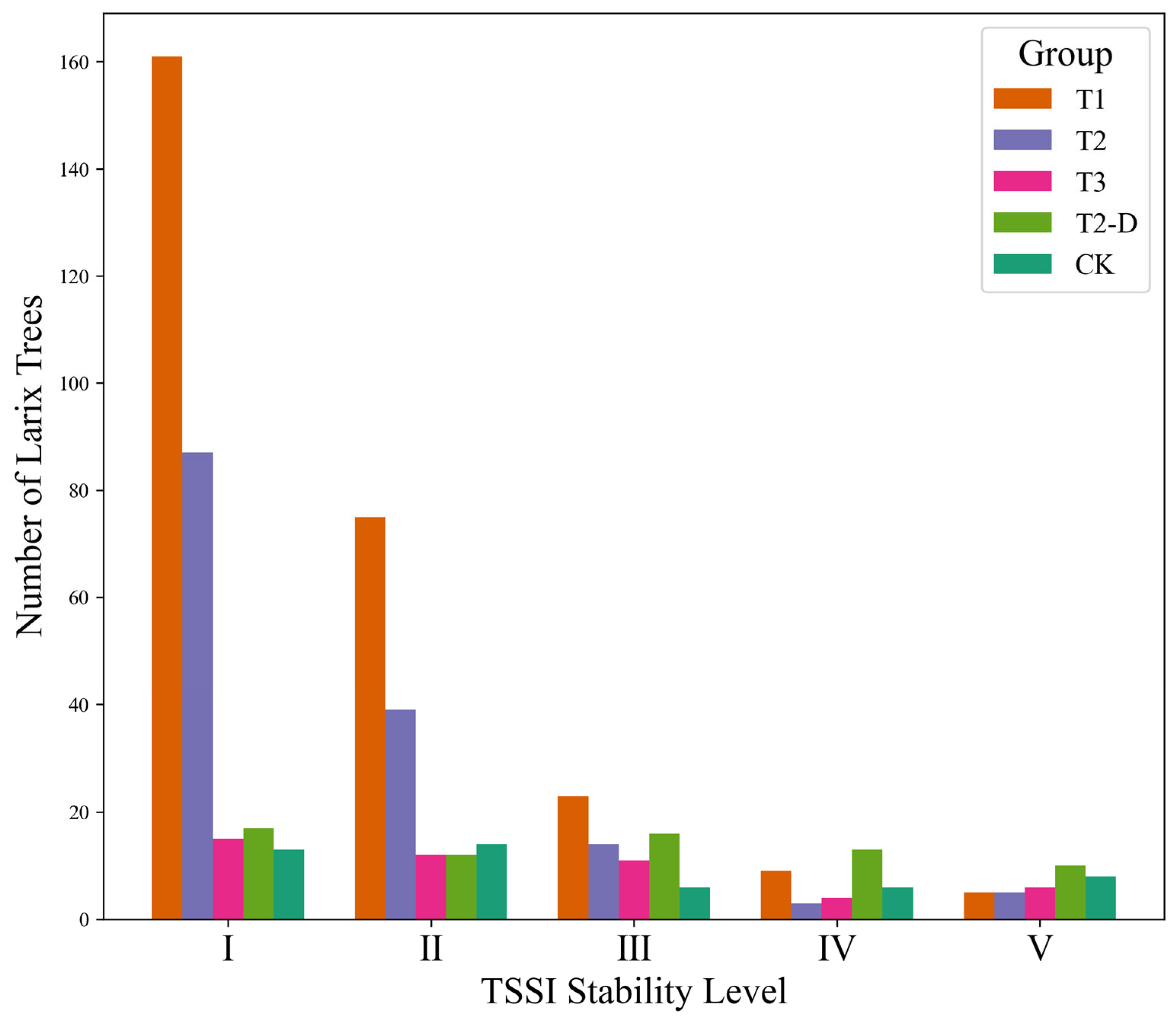
3.2.1. Tree-Level TSSI Results
3.2.2. Classification of Tree Structural Stability Levels
3.2.3. Stand-Level FSSI Results
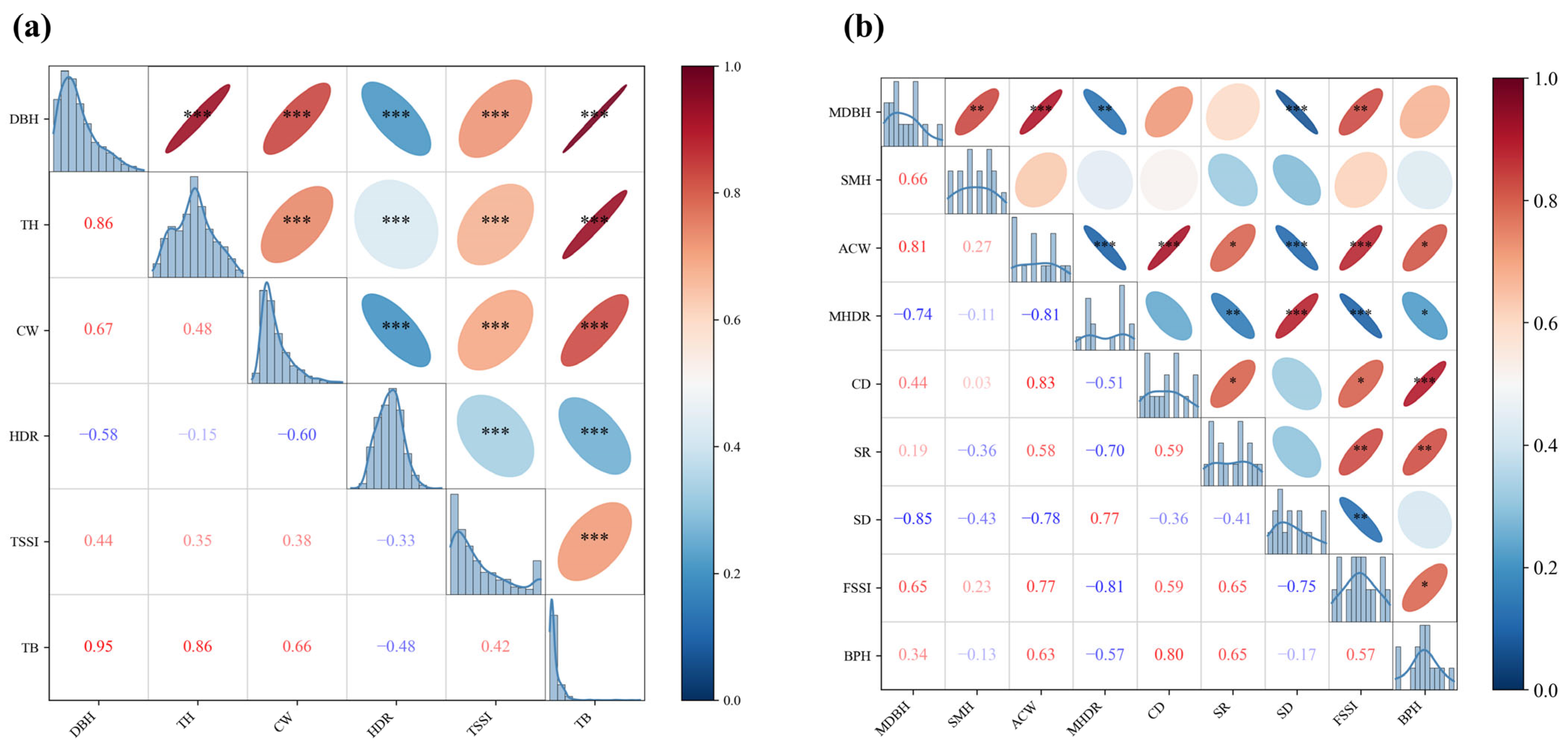
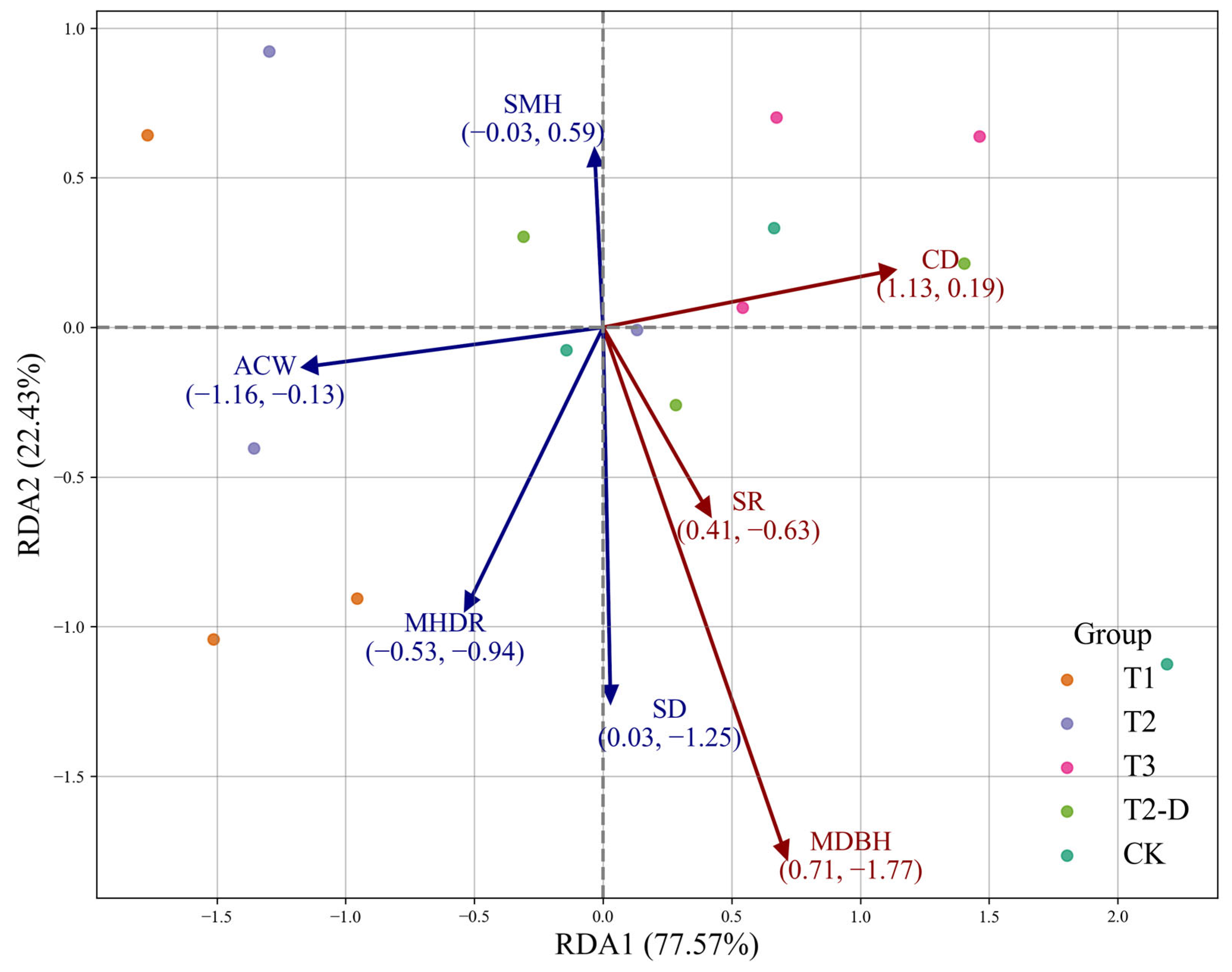
3.3. Correlation Between Stand Structural Attributes and Ecosystem Functions
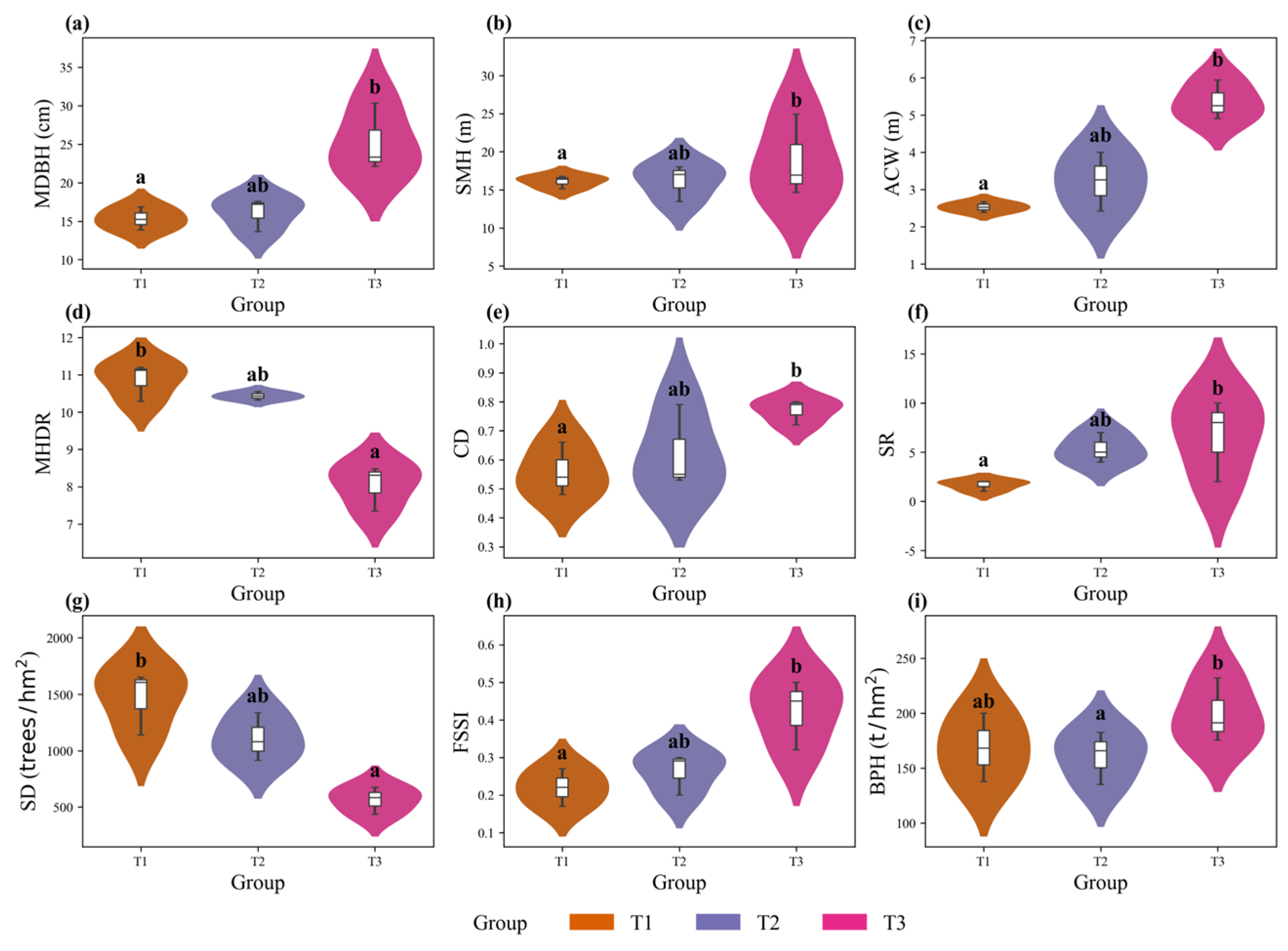
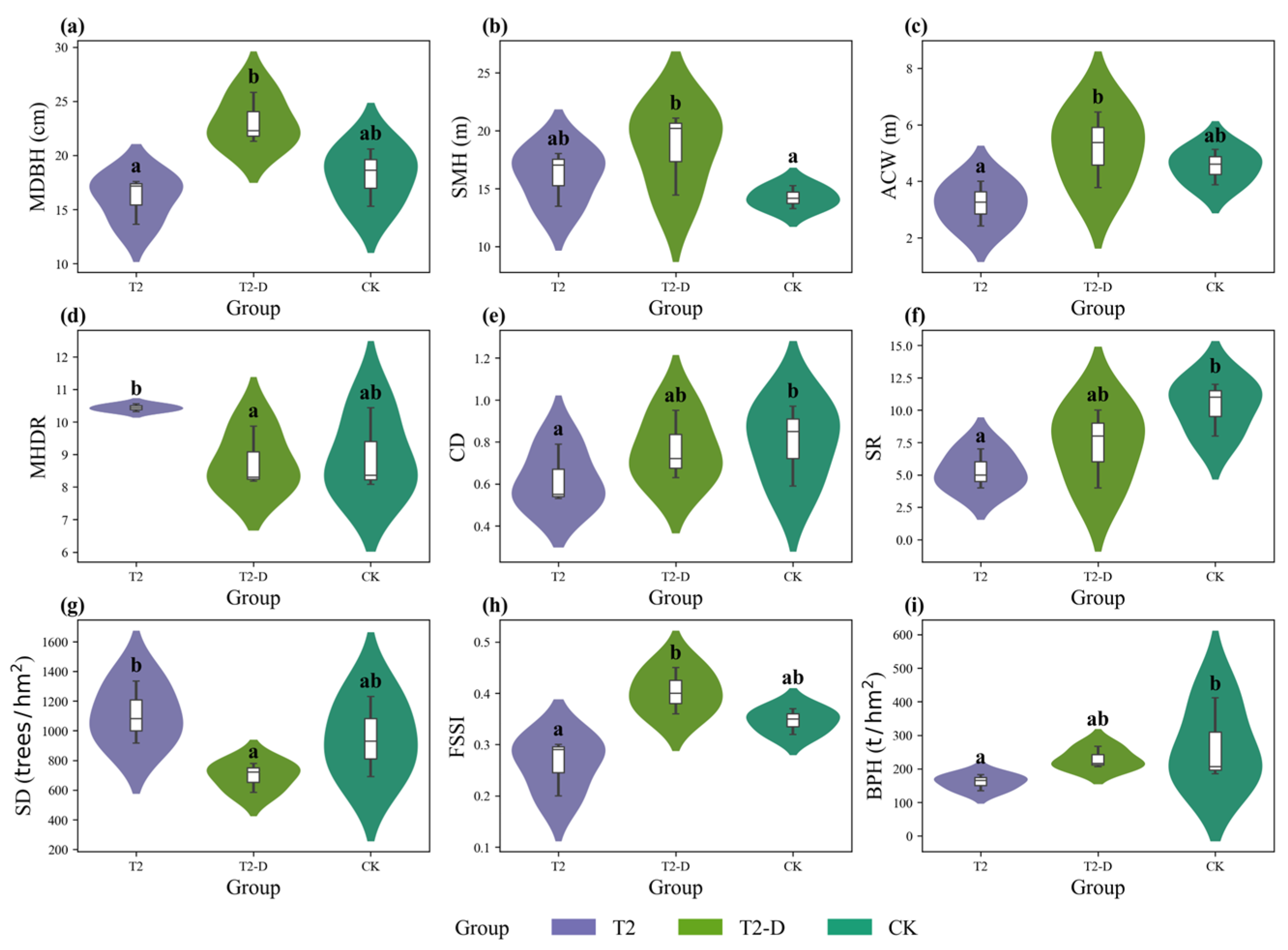
3.4. Stand Structural and Functional Comparisons Under Different Scenarios
3.4.1. Variation Along the Stand-Age Gradient
3.4.2. Variation After Thinning Intervention
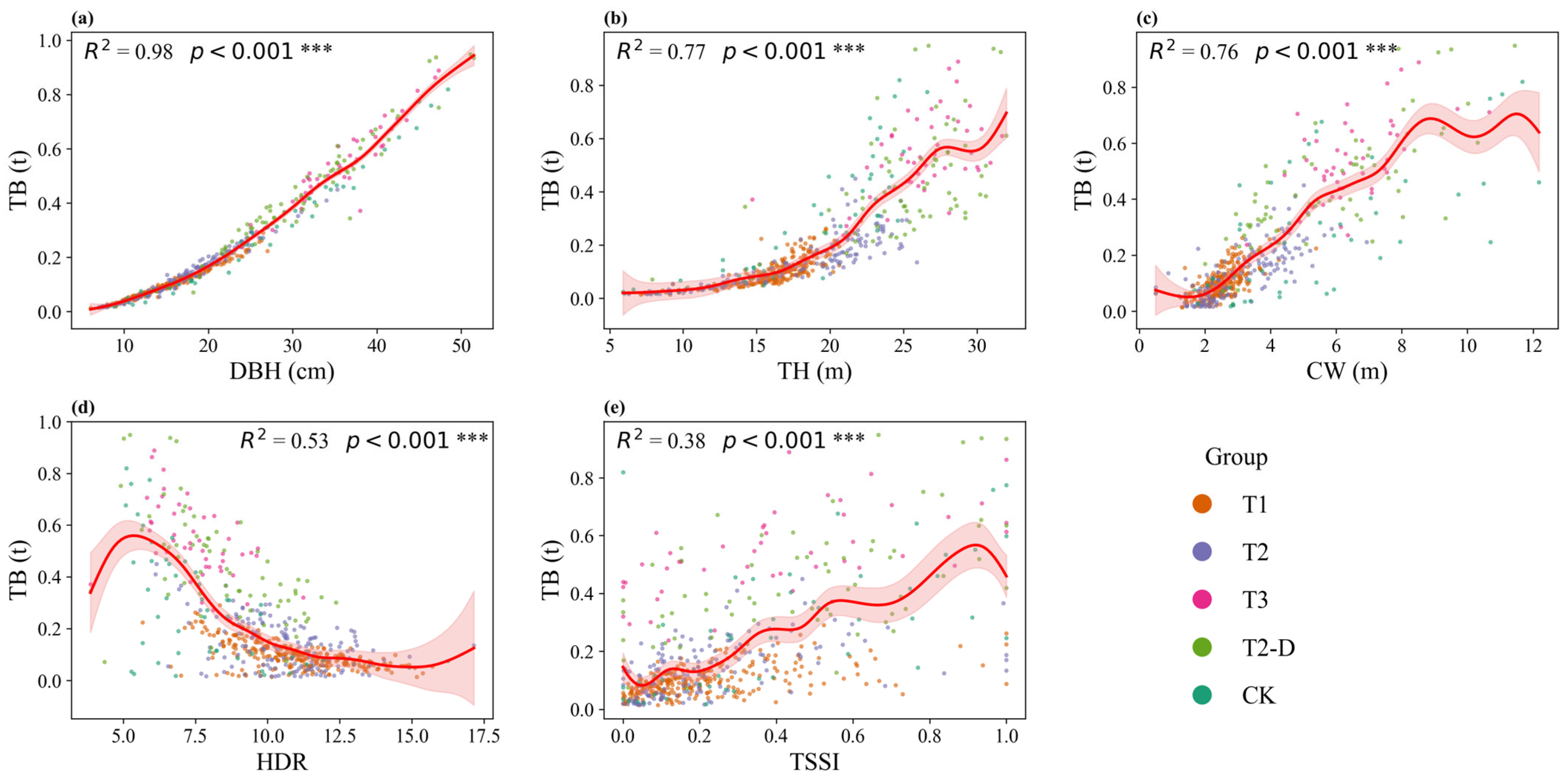
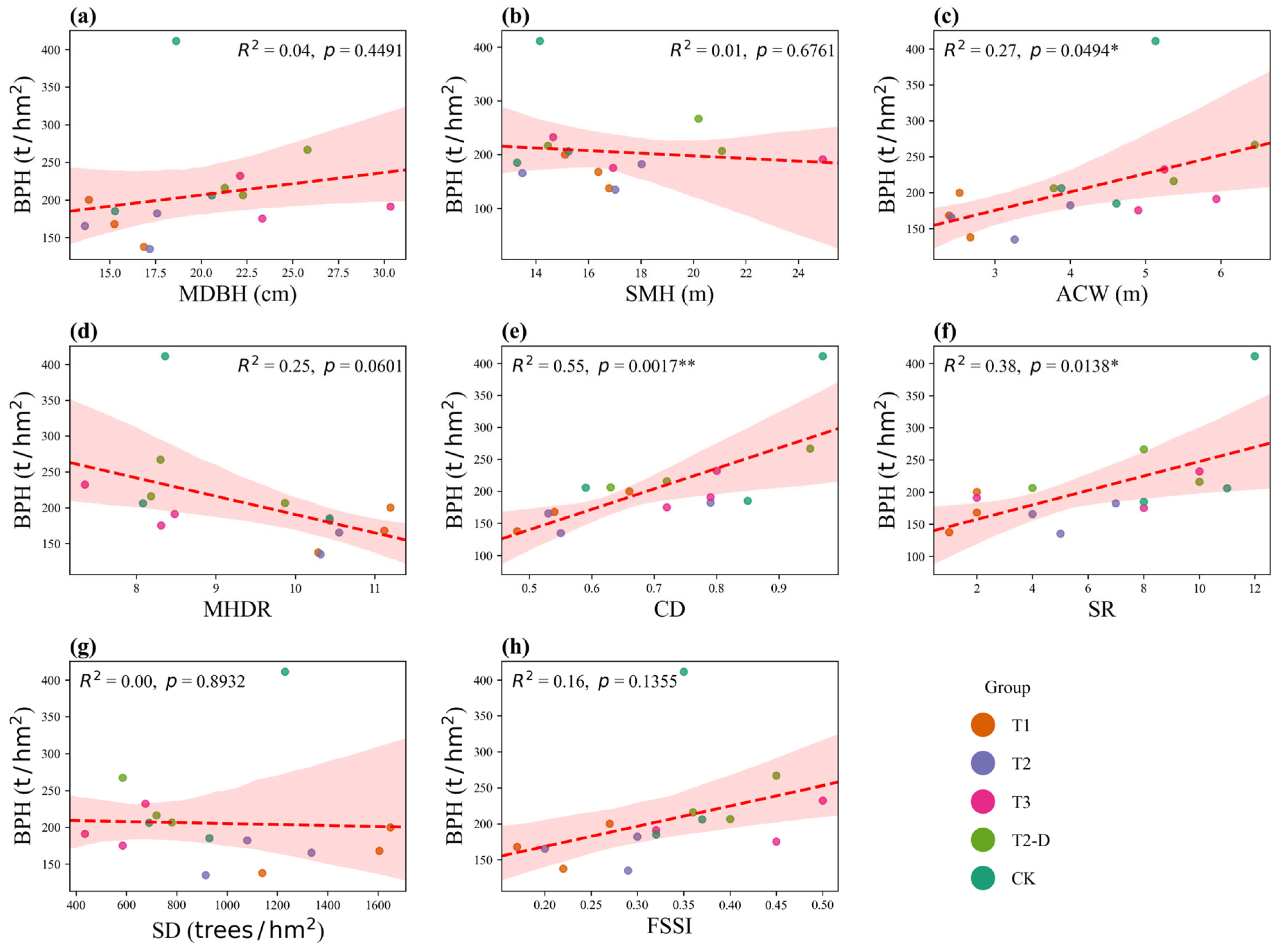
3.5. Relationships Between Structural Factors and Productivity
3.5.1. Tree-Level Factors and Biomass
3.5.2. Stand-Level Factors and Productivity
3.6. Dominant Effects of Stand-Level Factors on Stability and Productivity
4. Discussion
4.1. Structural and Functional Dynamics of L. gmelinii Plantations Under Different Scenarios
4.1.1. Responses of Structure and Productivity to Increasing Stand Age
4.1.2. Effects of Thinning Intervention on Structure and Productivity
4.2. Pathways and Mechanisms of Structural Factors in Enhancing Productivity
4.3. Management Implications for L. gmelinii Plantations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2022—Impacts, Adaptation and Vulnerability: Working Group II Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Zeng, Y.; Gou, M.; Ouyang, S.; Chen, L.; Fang, X.; Zhao, L.; Li, J.; Peng, C.; Xiang, W. The Impact of Secondary Forest Restoration on Multiple Ecosystem Services and Their Trade-Offs. Ecol. Indic. 2019, 104, 248–258. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, Y.; Ren, Y.; Chen, A.; Xiang, T.; Qi, Z.; Huang, G.; Yang, H.; Chen, Y.; Yang, Z.; et al. Natural Forest Restoration Potential to Mitigate Climate Change in China. Earth’s Future 2025, 13, e2024EF005794. [Google Scholar] [CrossRef]
- Cheng, K.; Yang, H.; Tao, S.; Su, Y.; Guan, H.; Ren, Y.; Hu, T.; Li, W.; Xu, G.; Chen, M.; et al. Carbon Storage through China’s Planted Forest Expansion. Nat. Commun. 2024, 15, 4106. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, Y.; Yang, H.; Ren, Y.; Xiang, T.; Chen, Y.; Yang, Z.; Chen, M.; Xu, J.; Huang, G.; et al. China’s Naturally Regenerated Forests Currently Have Greater Aboveground Carbon Accumulation Rates than Newly Planted Forests. Commun. Earth Environ. 2025, 6, 345. [Google Scholar] [CrossRef]
- Feng, Y.; Schmid, B.; Loreau, M.; Forrester, D.I.; Fei, S.; Zhu, J.; Tang, Z.; Zhu, J.; Hong, P.; Ji, C.; et al. Multispecies Forest Plantations Outyield Monocultures across a Broad Range of Conditions. Science 2022, 376, 865–868. [Google Scholar] [CrossRef]
- Hua, F.; Bruijnzeel, L.A.; Meli, P.; Martin, P.A.; Zhang, J.; Nakagawa, S.; Miao, X.; Wang, W.; McEvoy, C.; Peña-Arancibia, J.L.; et al. The Biodiversity and Ecosystem Service Contributions and Trade-Offs of Forest Restoration Approaches. Science 2022, 376, 839–844. [Google Scholar] [CrossRef]
- Yu, Z.; You, W.; Agathokleous, E.; Zhou, G.; Liu, S. Forest Management Required for Consistent Carbon Sink in China’s Forest Plantations. For. Ecosyst. 2021, 8, 54. [Google Scholar] [CrossRef]
- FAO (Food and Agriculture Organization of the United Nations). Global Forest Resources Assessment 2020; Food and Agricultural Organization of the United Nations: Rome, Italy, 2020. [Google Scholar]
- Zhao, X.; Hao, Y.; Wang, T.; Dong, L.; Li, F. Competition Is Critical to the Growth of Larix gmelinii and Betula platyphylla in Secondary Forests in Northeast China under Climate Change. Global Ecol. Conserv. 2024, 51, e02935. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, Y.; Jiang, Y.; Yang, Z. Estimating Biomass and Net Primary Production from Forest Inventory Data: A Case Study of China’s Larix Forests. For. Ecol. Manag. 2002, 169, 149–157. [Google Scholar] [CrossRef]
- National Forestry and Grassland Administration (NFGA). The Ninth National Forest Resources Inventory (2014–2018); NFGA: Beijing, China, 2019. [Google Scholar]
- Ma, W.; Lei, S.; Sun, Y.; Grabosky, J. Forest Succession in Post-Agricultural Larix olgensis Plantations in Northeast China. J. For. Res. 2020, 31, 2495–2505. [Google Scholar] [CrossRef]
- Gao, M.; Zhao, G.; Zhang, S.; Wang, Z.; Wen, X.; Liu, L.; Zhang, C.; Tie, N.; Sa, R. Priority Conservation Area of Larix gmelinii under Climate Change: Application of an Ensemble Modeling. Front. Plant Sci. 2023, 14, 1177307. [Google Scholar] [CrossRef] [PubMed]
- Duan, B.; Man, X.; Cai, T.; Xiao, R.; Ge, Z. Increasing Soil Organic Carbon and Nitrogen Stocks along with Secondary Forest Succession in Permafrost Region of the Daxing’an Mountains, Northeast China. Glob. Ecol. Conserv. 2020, 24, e01258. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, H.; Lu, J.; Zhang, X. Disturbances and Succession Laws of Main Natural Secondary Forests in Northeast China. For. Res. 2021, 34, 175–183. [Google Scholar] [CrossRef]
- Guariguata, M.R.; Ostertag, R. Neotropical Secondary Forest Succession: Changes in Structural and Functional Characteristics. For. Ecol. Manag. 2001, 148, 185–206. [Google Scholar] [CrossRef]
- Shorohova, E.; Kuuluvainen, T.; Kangur, A.; Jõgiste, K. Natural Stand Structures, Disturbance Regimes and Successional Dynamics in the Eurasian Boreal Forests: A Review with Special Reference to Russian Studies. Ann. For. Sci. 2009, 66, 201. [Google Scholar] [CrossRef]
- Lin, B.; Ge, J. To Harvest or Not to Harvest? Forest Management as a Trade-off between Bioenergy Production and Carbon Sink. J. Clean. Prod. 2020, 268, 122219. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; Pretzsch, H.; Del Río, M. (Eds.) Dynamics, Silviculture and Management of Mixed Forests; Managing Forest Ecosystems; Springer International Publishing: Cham, Switzerland, 2018; Volume 31, ISBN 978-3-319-91952-2. [Google Scholar]
- Forrester, D.I.; Bauhus, J. A Review of Processes Behind Diversity—Productivity Relationships in Forests. Curr. For. Rep. 2016, 2, 45–61. [Google Scholar] [CrossRef]
- Schuler, L.J.; Bugmann, H.; Snell, R.S. From Monocultures to Mixed-Species Forests: Is Tree Diversity Key for Providing Ecosystem Services at the Landscape Scale? Landsc. Ecol. 2017, 32, 1499–1516. [Google Scholar] [CrossRef]
- Tatsumi, S. Tree Diversity Effects on Forest Productivity Increase through Time Because of Spatial Partitioning. For. Ecosyst. 2020, 7, 24. [Google Scholar] [CrossRef]
- Liu, H.; Dong, X.; Qin, S.; Gao, T. Matter-Element Evaluation of Ecological Quality in Gaps of Temperate Secondary Forests. Ecol. Indic. 2025, 175, 113552. [Google Scholar] [CrossRef]
- Gandolfi, S.; Joly, C.A.; Rodrigues, R.R. Permeability—Impermeability: Canopy Trees as Biodiversity Filters. Sci. Agric. 2007, 64, 433–438. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.; Wang, S.; Sun, Q. Effect of the Close-to-Nature Transformation of Larix Gmelinii Pure Stands on Plant Diversity of Understory Vegetation in Xiaoxing’an Mountains of China. Sci. Silvae Sin. 2011, 47, 6–14. [Google Scholar]
- Pelt, R.V.; Franklin, J.F. Influence of Canopy Structure on the Understory Environment in Tall, Old-Growth, Conifer Forests. Can. J. For. Res. 2000, 30, 1231–1245. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, H.; Dong, L.; Chen, Y.; Liu, Z. Effects of Different Intermediate Cutting Intensities on the Spatial Structure of Larix gmelinii Forest. J. Northeast. For. Univ. 2018, 46, 9–14. [Google Scholar] [CrossRef]
- Blois, J.L.; Williams, J.W.; Fitzpatrick, M.C.; Jackson, S.T.; Ferrier, S. Space Can Substitute for Time in Predicting Climate-Change Effects on Biodiversity. Proc. Natl. Acad. Sci. USA 2013, 110, 9374–9379. [Google Scholar] [CrossRef]
- Ruan, F.; Yan, L.; Wang, D. Policy Effects on the Sustainable Development of Resource-Based Cities in China: A Case Study of Yichun City. Resour. Policy 2021, 72, 102145. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Chen, S.; Wu, K. Forest Management Type Identification Based on Stacking Ensemble Learning. Forests 2024, 15, 887. [Google Scholar] [CrossRef]
- Xu, L.; Yu, H.; Zhong, L. Sustainable Futures for Transformational Forestry Resource-Based City: Linking Landscape Pattern and Administrative Policy. J. Clean. Prod. 2025, 496, 145087. [Google Scholar] [CrossRef]
- Stevens, J.T.; Safford, H.D.; North, M.P.; Fried, J.S.; Gray, A.N.; Brown, P.M.; Dolanc, C.R.; Dobrowski, S.Z.; Falk, D.A.; Farris, C.A.; et al. Average Stand Age from Forest Inventory Plots Does Not Describe Historical Fire Regimes in Ponderosa Pine and Mixed-Conifer Forests of Western North America. PLoS ONE 2016, 11, e0147688. [Google Scholar] [CrossRef]
- GB/T 38590-2020; Technical Regulations for Continuous Forest Inventory. Standards Press of China: Beijing, China, 2020.
- Vargas G., G.; Marcano-Vega, H.; Ruzycki, T.; Wood, T.E.; Anderegg, W.R.L.; Powers, J.S.; Helmer, E.H. Aridity and Forest Age Mediate Landscape Scale Patterns of Tropical Forest Resistance to Cyclonic Storms. J. Ecol. 2025, 113, 53–67. [Google Scholar] [CrossRef]
- Lucas-Borja, M.E.; Hedo, J.; Cerdá, A.; Candel-Pérez, D.; Viñegla, B. Unravelling the Importance of Forest Age Stand and Forest Structure Driving Microbiological Soil Properties, Enzymatic Activities and Soil Nutrients Content in Mediterranean Spanish Black Pine (Pinus nigra Ar. ssp. Salzmannii) Forest. Sci. Total Environ. 2016, 562, 145–154. [Google Scholar] [CrossRef]
- Wen, G.; Ma, J.; Xu, W.; Wang, J.; He, W.; Wang, Y.; Wang, X.; Li, T.; Ye, M.; Chen, G.; et al. Response of Understory Plant Functional Groups to Changes in Stand Spatial Structure in Masson Pine (Pinus massoniana Lamb.) Plantations Depends on Thinning Mode and Intensity. J. Environ. Manag. 2025, 376, 124441. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Li, J.; Feng, Y.; Hu, Y.; Zhang, C.; Fang, X.; Deng, C. Analysis and Evaluation of the Stand Spatial Structure of Cunninghamia Lanceolata Ecological Forest. Sci. Silvae Sin. 2015, 51, 37–48. [Google Scholar]
- Lin, F.; Wang, W.; Men, X.; Sun, Y.; Li, G.; Liu, D. Spatial Structure Optimal of Larix gmelinii Plantation. J. Beijing For. Univ. 2021, 43, 68–76. [Google Scholar] [CrossRef]
- Qing, D.; Zhang, J.; Li, J.; Peng, J.; Liu, S. Research on the Difference of Mingling Degree under Different Selection Schemes of Adjacent Trees. For. Grassl. Resour. Res. 2021, 4, 69–78. [Google Scholar] [CrossRef]
- Hu, Y.; Hui, G. How to Describe the Crowding Degree of Trees Based on the Relationship of Neighboring Trees. J. Beijing For. Univ. 2015, 37, 1–8. [Google Scholar]
- Lai, M.; Lai, R.; Hu, R.; Ye, W. Analysis and Correlation Study on Spatial Structure Parameters of Artificial Cunninghamia Lanceolata Forest Stand. Ecol. Sci. 2021, 40, 58–63. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, J.; Wang, Q.; Sun, P.; Pu, C. Preview of Spatial Structure of Cryptomeria Fortunei Plantation after Stand Improvement. Sci. Silvae Sin. 2006, 42, 8–13. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Wen, X.; Wang, Q.; Ye, J. Spatial Structure Analysis and Comprehensive Index Evaluation of Fir Plantation Stands. J. Northwest For. Univ. 2024, 39, 10–16. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Y.; Pan, L.; Sun, Y. Hegyi Competition Index Decomposition to Improve Estimation Accuracy of Larix olgensis Crown Radius. Ecol. Indic. 2022, 143, 109322. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, S.; Tian, J.; Cheng, F.; Zhao, S.; Wang, S. Establishment of Thinning Models for Larix olgensis Plantation Based on Spatial Structure Optimization. J. Cent. South Univ. For. Technol. 2023, 43, 72–83. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, C.; Ge, Z.; Zhang, Z. Stand Spatial Structure and Productivity Based on Random Structural Unit in Larix principis-rupprechtii Forests. Ecosphere 2024, 15, e4824. [Google Scholar] [CrossRef]
- Wang, X.; Dallimer, M.; Scott, C.E.; Shi, W.; Gao, J. Tree Species Richness and Diversity Predicts the Magnitude of Urban Heat Island Mitigation Effects of Greenspaces. Sci. Total Environ. 2021, 770, 145211. [Google Scholar] [CrossRef] [PubMed]
- Yan, M.; Huang, Q.; Wang, J.; Wang, S. Research on Height to Diameter Ratio of Forest Trees: A Review. World For. Res. 2023, 36, 59–65. [Google Scholar] [CrossRef]
- Liu, Z.; Qiang, B.; Zhang, H.; Fu, L.; Guo, J. Influence of Climate and Site Grade on Biomass Estimation of Larix gmelinii Stand. J. Beijing For. Univ. 2025, 47, 22–28. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Ouyang, Z.; Lu, F.; Feng, L.; Tao, J. A Review of Biomass Equations for China’s Tree Species. Earth Syst. Sci. Data 2020, 12, 21–40. [Google Scholar] [CrossRef]
- Xu, E.; Guo, Y.; Chen, E.; Li, Z.; Zhao, L.; Liu, Q. An Estimation Model for Regional Forest Canopy Closure Combined with UAV LiDAR and High Spatial Resolution Satellite Remote Sensing Data. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1298–1308. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B.; Qin, S.; Li, S.; Huang, X. Review of Research and Application of Forest Canopy Closure and Its Measuring Methods. World For. Res. 2008, 21, 006. [Google Scholar] [CrossRef]
- He, W.; Luo, C.; Wang, Y.; Wen, X.; Wang, Y.; Li, T.; Chen, G.; Zhao, K.; Li, X.; Fan, C. Response Strategies of Root System Architecture to Soil Environment: A Case Study of Single-Species Cupressus funebris Plantations. Front. Plant Sci. 2022, 13, 822223. [Google Scholar] [CrossRef]
- Moreau, G.; Chagnon, C.; Achim, A.; Caspersen, J.; D’Orangeville, L.; Sánchez-Pinillos, M.; Thiffault, N. Opportunities and Limitations of Thinning to Increase Resistance and Resilience of Trees and Forests to Global Change. For. Int. J. For. Res. 2022, 95, 595–615. [Google Scholar] [CrossRef]
- Forrester, D.I.; Pretzsch, H. Tamm Review: On the Strength of Evidence When Comparing Ecosystem Functions of Mixtures with Monocultures. For. Ecol. Manag. 2015, 356, 41–53. [Google Scholar] [CrossRef]
- Abbasi, U.A.; Gilani, H.; Hussain, K.; Ali, A. Increasing Stand Stature Weakens the Positive Effects of Tree Richness and Structural Imbalance on Aboveground Biomass in Temperate Forests: The Stand Stature Hypothesis. For. Ecol. Manag. 2023, 539, 121040. [Google Scholar] [CrossRef]
- Alexandrov, G.A. Carbon Stock Growth in a Forest Stand: The Power of Age. Carbon Balance Manag. 2007, 2, 4. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Pukkala, T.; Jin, X.; Li, F. Optimal Management of Larch (Larix olgensis A. Henry) Plantations in Northeast China When Timber Production and Carbon Stock Are Considered. Ann. For. Sci. 2018, 75, 63. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Q.; Liu, X.; Xu, Z.; Dai, Y.; Liu, Y.; Chen, Y. Variation Patterns of Plant Composition/Diversity in Dacrydium pectinatum Communities and Their Driving Factors in a Biodiversity Hotspot on Hainan Island, China. Glob. Ecol. Conserv. 2020, 22, e01034. [Google Scholar] [CrossRef]
- Yang, S.; Tan, W.; Chen, X.; Tang, J.; Yang, Z.; Wu, Y. Study on Stand Spatial Structure of Typical Pinus massoniana Mixed Forest in Liping County of Guizhou Province. For. Grassl. Resour. Res. 2023, 3, 105–114. [Google Scholar] [CrossRef]
- Liu, F.; Tan, C.; Yang, Z.; Li, J.; Xiao, H.; Tong, Y. Regeneration and Growth of Tree Seedlings and Saplings in Created Gaps of Different Sizes in a Subtropical Secondary Forest in Southern China. For. Ecol. Manag. 2022, 511, 120143. [Google Scholar] [CrossRef]
- Chai, Z.; Wang, D.; Hao, Y.; Zhang, L.; Zhu, H.; Zhang, C. Succession Dynamics of Larix principis-rupprechtii Plantation in Intermediate Section of Qinling Mountains. Sci. Silvae Sin. 2014, 50, 14–21. [Google Scholar]
- Ren, G.; Young, S.S.; Wang, L.; Wang, W.; Long, Y.; Wu, R.; Li, J.; Zhu, J.; Yu, D.W. Effectiveness of China’s National Forest Protection Program and Nature Reserves: Deforestation and Protected Areas in China. Conserv. Biol. 2015, 29, 1368–1377. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, K.; Zhang, Q.; Zhou, C.; Su, Y.; Gao, T.; Lu, D.; Zhang, J. Research Progress on the Effects of Stand Age on Carbon Accumulation and Stability in Forest Ecosystems. Chin. J. Soil Sci. 2025, 56, 1189–1200. [Google Scholar] [CrossRef]
- Xu, C.; Wu, X.; Tian, Y.; Shi, L.; Qi, Y.; Zhang, J.; Liu, H. Short Lifespan and ‘Prime Period’ of Carbon Sequestration Call for Multi-Ages in Dryland Tree Plantations. For. Ecosyst. 2024, 11, 100224. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Marčiš, P.; Šebeň, V. Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians. Plants 2025, 14, 2992. [Google Scholar] [CrossRef]
- Lin, N.; Deng, N.; Lu, D.; Xie, H.; Feng, M.; Chen, S. Short-Term Effects of Thinning on Tree Growth and Soil Nutrients in the Middle-Aged Chinese Fir (Cunninghamia lanceolata (Lamb.) Hook.) Plantations. Forests 2022, 14, 74. [Google Scholar] [CrossRef]
- Valinger, E.; Sjögren, H.; Nord, G.; Cedergren, J. Effects on Stem Growth of Scots Pine 33 Years after Thinning and/or Fertilization in Northern Sweden. Scand. J. For. Res. 2019, 34, 33–38. [Google Scholar] [CrossRef]
- Hilt, D.E. Diameter Growth of Upland Oaks After Thinning; U.S. Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Broomall, PA, USA, 1979.
- Wang, H.; Liu, W.; Wang, W.; Zu, Y. Influence of Long-term Thinning on the Biomass Carbon and Soil Respiration in a Larch (Larix gmelinii ) Forest in Northeastern China. Sci. World J. 2013, 2013, 865645. [Google Scholar] [CrossRef]
- Ma, Y.; Cheng, X.; Kang, F.; Han, H. Effects of Thinning on Soil Aggregation, Organic Carbon and Labile Carbon Component Distribution in Larix principis-rupprechtii Plantations in North China. Ecol. Indic. 2022, 139, 108873. [Google Scholar] [CrossRef]
- Sun, C.; Li, L.; Dong, X.; Qin, F.; Yang, Z. Variations and Factors Characterizing Ecological Niches of Understory Herbaceous Species in Plantation Forests. Sustainability 2022, 14, 10719. [Google Scholar] [CrossRef]
- Feng, Y.-C.; Zheng, X.-Y.; Wang, Z.-N.; Liu, B.; Lan, S.-R. Niche Characteristics of Plant Populations in Understory Herbaceous Layer of Cunninghamia lanceolata Pure Forest and Mixed Forest. J. Ecol. Rural Environ. 2019, 35, 217–224. [Google Scholar] [CrossRef]
- Georgi, L.; Kunz, M.; Fichtner, A.; Reich, K.F.; Bienert, A.; Maas, H.-G.; Von Oheimb, G. Effects of Local Neighbourhood Diversity on Crown Structure and Productivity of Individual Trees in Mature Mixed-Species Forests. For. Ecosyst. 2021, 8, 26. [Google Scholar] [CrossRef]
- Jucker, T.; Fischer, F.J.; Chave, J.; Coomes, D.A.; Caspersen, J.; Ali, A.; Loubota Panzou, G.J.; Feldpausch, T.R.; Falster, D.; Usoltsev, V.A.; et al. The Global Spectrum of Tree Crown Architecture. Nat. Commun. 2025, 16, 4876. [Google Scholar] [CrossRef]
- Wang, X.; Huang, X.; Wang, Y.; Yu, P.; Guo, J. Impacts of Site Conditions and Stand Structure on the Biomass Allocation of Single Trees in Larch Plantations of Liupan Mountains of Northwest China. Forests 2022, 13, 177. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Z.; She, P.; Ma, J.; Jia, B.; Wang, Z. Effects of Stand Density on Understory Plant Diversity of Larix principis-rupprechtii Plantation—A Case Study in Diediegou Small Watershed in Liupan Mountain. J. Gansu Agric. Univ. 2021, 56, 114–120. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Zhang, W.; Chen, B.; Yang, L.; Li, M.; Zhu, J.; Cai, Q. The Effects of Thinning on Tree Growth and Stand Biomass in a Chronosequence of Pinus tabulaeformis Plantations in the Loess Plateau of China. Forests 2023, 14, 1620. [Google Scholar] [CrossRef]
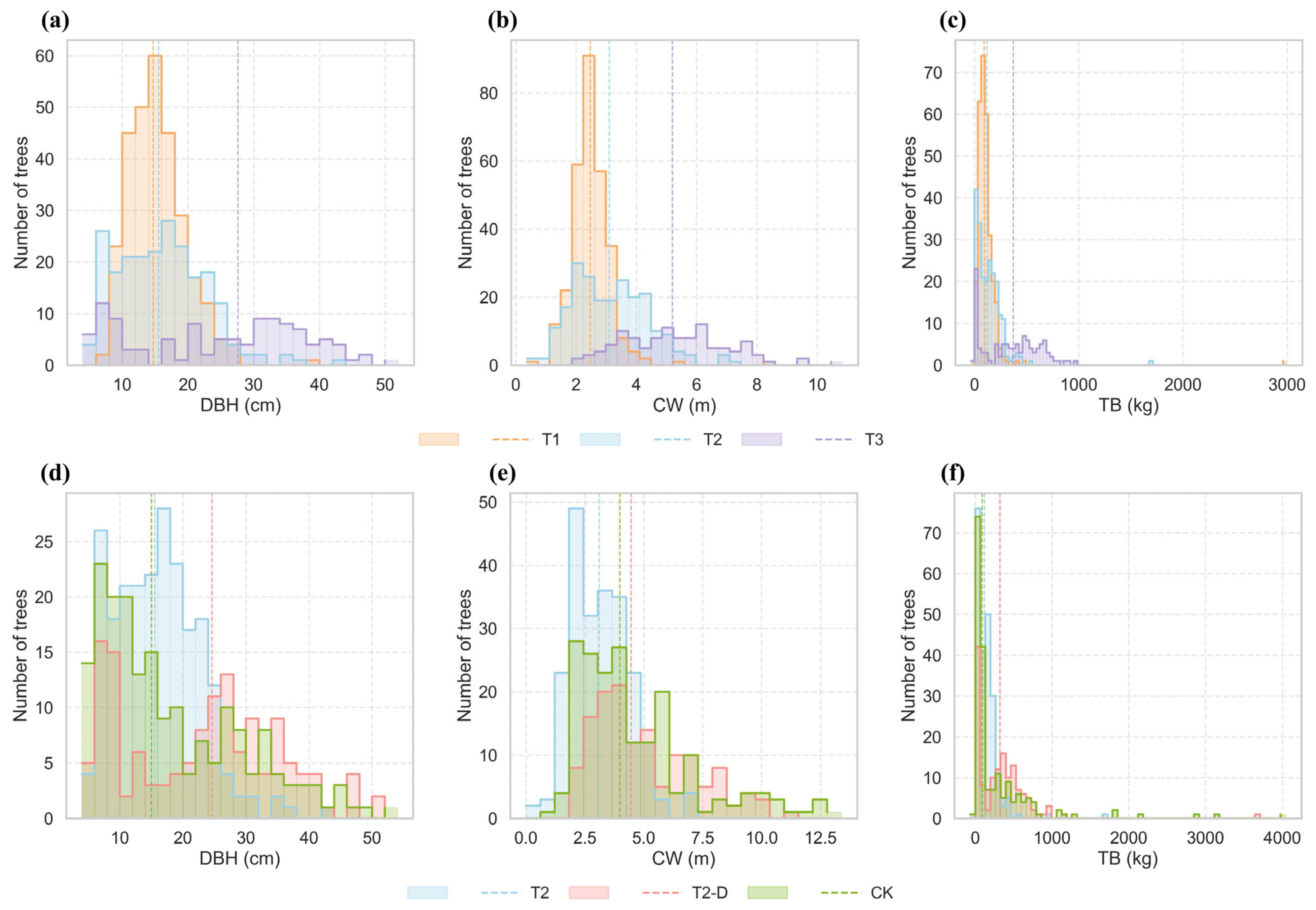
| Type | DBH (cm) | TH (m) | CW (m) | TB (kg) | HDR | MD | OD | UAI | C | NC | CI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | 6.00 | 5.90 | 0.50 | 13.92 | 3.86 | 0.00 | 0.08 | 0.00 | 0.00 | 0.00 | 0.21 |
| Max | 51.50 | 32.00 | 12.18 | 948.99 | 17.15 | 1.00 | 0.60 | 0.75 | 1.00 | 1.00 | 7.80 |
| Mean | 20.00 | 18.42 | 3.59 | 200.27 | 9.99 | 0.24 | 0.19 | 0.47 | 0.69 | 0.42 | 1.83 |
| Standard Deviation | 9.41 | 5.45 | 2.01 | 190.16 | 2.25 | 0.30 | 0.08 | 0.17 | 0.29 | 0.35 | 1.03 |
| ID | AG | AA (a) | Species Composition | MD | OD | UAI | C | NC | CI |
|---|---|---|---|---|---|---|---|---|---|
| T1-1 | 1 | 19 | Planted L. gmelinii (100%) | 0.06 | 0.14 | 0.47 | 0.62 | 0.49 | 2.22 |
| T1-2 | 1 | 19 | Planted L. gmelinii (100%) | 0 | 0.15 | 0.46 | 0.6 | 0.45 | 2.08 |
| T1-3 | 1 | 19 | Planted L. gmelinii (70%), Betula platyphylla (30%) | 0.22 | 0.15 | 0.46 | 0.66 | 0.49 | 2.27 |
| T2-1 | 2 | 26 | Planted L. gmelinii (90%), Ulmus pumila (10%) | 0.39 | 0.18 | 0.48 | 0.61 | 0.51 | 2.33 |
| T2-2 | 2 | 26 | Planted L. gmelinii (80%), Picea asperata (10%), B. platyphylla (10%) | 0.41 | 0.17 | 0.47 | 0.86 | 0.47 | 2.19 |
| T2-3 | 2 | 23 | Planted L. gmelinii (60%), B. platyphylla (30%), P. asperata (10%) | 0.45 | 0.19 | 0.48 | 0.53 | 0.49 | 2.44 |
| T3-1 | 4 | 46 | Planted L. gmelinii (100%) | 0.22 | 0.21 | 0.48 | 0.86 | 0.47 | 1.42 |
| T3-2 | 3 | 36 | Planted L. gmelinii (60%), P. asperata (30%), Pinus koraiensis (10%) | 0.71 | 0.27 | 0.46 | 0.77 | 0.46 | 2.12 |
| T3-3 | 4 | 56 | Planted L. gmelinii (70%), P. koraiensis (30%) | 0.8 | 0.33 | 0.49 | 0.91 | 0.48 | 2.77 |
| T2-D-1 | 2 | 26 | Planted L. gmelinii (100%) | 0.39 | 0.18 | 0.43 | 0.69 | 0.49 | 2.05 |
| T2-D-2 | 2 | 26 | Planted L. gmelinii (70%), B. platyphylla (10%), P. asperata (10%), Fraxinus mandshurica (10%) | 0.74 | 0.25 | 0.47 | 0.96 | 0.48 | 1.9 |
| T2-D-3 | 2 | 26 | Planted L. gmelinii (80%), P. koraiensis (20%) | 0.8 | 0.25 | 0.47 | 0.9 | 0.49 | 3.06 |
| CK-1 | 2 | 63 | L. gmelinii (50%), U. pumila (20%), F. mandshurica (10%), B. platyphylla (10%), Betula dahurica (10%) | 0.66 | 0.24 | 0.51 | 0.9 | 0.48 | 4.68 |
| CK-2 | 2 | 64 | L. gmelinii (30%), B. dahurica (30%), Quercus mongolica (20%), B. platyphylla (20%) | 0.78 | 0.23 | 0.48 | 0.93 | 0.51 | 3.05 |
| CK-3 | 2 | 66 | L. gmelinii (70%), B. platyphylla (20%), P. asperata (10%) | 0.8 | 0.32 | 0.49 | 0.62 | 0.44 | 2.02 |
| Group | MDBH (cm) | SMH (m) | ACW (m) | MHDR | CD | SR | SD (Tree·hm−2) | BPH (t·hm−2) |
|---|---|---|---|---|---|---|---|---|
| T1 | 15.32 ± 1.5 | 16.09 ± 0.87 | 2.53 ± 0.14 | 10.87 ± 0.5 | 0.56 ± 0.09 | 1.67 ± 0.58 | 1465.0 ± 282.36 | 168.68 ± 31.19 |
| T2 | 16.13 ± 2.17 | 16.17 ± 2.39 | 3.23 ± 0.79 | 10.43 ± 0.12 | 0.62 ± 0.14 | 5.33 ± 1.53 | 1110.0 ± 211.6 | 161.03 ± 24.01 |
| T3 | 25.27 ± 4.44 | 18.84 ± 5.39 | 5.36 ± 0.53 | 8.05 ± 0.61 | 0.77 ± 0.04 | 6.67 ± 4.16 | 565.0 ± 121.24 | 199.65 ± 29.34 |
| T2-D | 23.12 ± 2.38 | 18.57 ± 3.6 | 5.2 ± 1.34 | 8.78 ± 0.94 | 0.77 ± 0.17 | 7.33 ± 3.06 | 695.0 ± 99.87 | 229.87 ± 32.45 |
| CK | 18.16 ± 2.67 | 14.22 ± 0.98 | 4.54 ± 0.63 | 8.96 ± 1.28 | 0.8 ± 0.19 | 10.33 ± 2.08 | 950.0 ± 270.55 | 267.58 ± 125.01 |
| ID | Species | Count | Mean | Variance | Standard Deviation | Median |
|---|---|---|---|---|---|---|
| 1 | L. gmelinii | 584 | 0.28 | 0.06 | 0.25 | 0.20 |
| 2 | P. koraiensis | 73 | 0.39 | 0.12 | 0.35 | 0.28 |
| 3 | B. platyphylla | 73 | 0.31 | 0.10 | 0.31 | 0.22 |
| 4 | U. pumila | 56 | 0.31 | 0.11 | 0.34 | 0.21 |
| 5 | F. mandshurica | 42 | 0.42 | 0.12 | 0.35 | 0.32 |
| 6 | P. asperata | 29 | 0.38 | 0.19 | 0.44 | 0.07 |
| 7 | B. dahurica | 21 | 0.37 | 0.14 | 0.37 | 0.22 |
| 8 | Q. mongolica | 21 | 0.25 | 0.10 | 0.31 | 0.14 |
| 9 | Acer pictum Thunb. | 12 | 0.37 | 0.19 | 0.43 | 0.19 |
| 10 | Phellodendron amurense Rupr. | 9 | 0.44 | 0.26 | 0.51 | 0.03 |
| TSSI Level | DBH (cm) | TH (m) | CW (m) | HDR | TSSI | TB (kg) | Number of L. gmelinii Trees |
|---|---|---|---|---|---|---|---|
| I | 15.39 | 16.33 | 2.81 | 11.04 | 0.09 | 117.23 | 293 |
| II | 20.45 | 18.92 | 3.63 | 9.71 | 0.29 | 196.81 | 152 |
| III | 27.22 | 21.44 | 4.81 | 8.28 | 0.50 | 326.86 | 70 |
| IV | 28.36 | 22.47 | 4.73 | 8.48 | 0.68 | 365.38 | 35 |
| V | 34.24 | 23.82 | 6.50 | 7.37 | 0.94 | 500.69 | 34 |
| Average | 20.00 | 18.42 | 3.59 | 9.99 | 0.28 | 200.27 | 584 |
| ID | Count | Mean | Variance | Standard Deviation | Median |
|---|---|---|---|---|---|
| T1-1 | 107 | 0.17 | 0.03 | 0.18 | 0.12 |
| T1-2 | 76 | 0.22 | 0.04 | 0.2 | 0.16 |
| T1-3 | 110 | 0.27 | 0.04 | 0.21 | 0.22 |
| T2-1 | 61 | 0.29 | 0.07 | 0.27 | 0.22 |
| T2-2 | 72 | 0.3 | 0.09 | 0.3 | 0.21 |
| T2-3 | 89 | 0.2 | 0.05 | 0.22 | 0.13 |
| T3-1 | 29 | 0.32 | 0.08 | 0.28 | 0.26 |
| T3-2 | 39 | 0.45 | 0.12 | 0.35 | 0.45 |
| T3-3 | 45 | 0.5 | 0.15 | 0.38 | 0.52 |
| T2-D-1 | 52 | 0.4 | 0.09 | 0.3 | 0.37 |
| T2-D-2 | 39 | 0.45 | 0.14 | 0.38 | 0.38 |
| T2-D-3 | 48 | 0.36 | 0.14 | 0.37 | 0.16 |
| CK-1 | 62 | 0.32 | 0.11 | 0.34 | 0.19 |
| CK-2 | 82 | 0.35 | 0.11 | 0.34 | 0.25 |
| CK-3 | 46 | 0.37 | 0.14 | 0.37 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Huang, X.; Chen, S.; Zheng, P.; Han, D.; Liu, W. Effects of Stand Age Gradient and Thinning Intervention on the Structure and Productivity of Larix gmelinii Plantations. Forests 2025, 16, 1552. https://doi.org/10.3390/f16101552
Liu J, Huang X, Chen S, Zheng P, Han D, Liu W. Effects of Stand Age Gradient and Thinning Intervention on the Structure and Productivity of Larix gmelinii Plantations. Forests. 2025; 16(10):1552. https://doi.org/10.3390/f16101552
Chicago/Turabian StyleLiu, Jiang, Xin Huang, Shaozhi Chen, Pengfei Zheng, Dongyang Han, and Wendou Liu. 2025. "Effects of Stand Age Gradient and Thinning Intervention on the Structure and Productivity of Larix gmelinii Plantations" Forests 16, no. 10: 1552. https://doi.org/10.3390/f16101552
APA StyleLiu, J., Huang, X., Chen, S., Zheng, P., Han, D., & Liu, W. (2025). Effects of Stand Age Gradient and Thinning Intervention on the Structure and Productivity of Larix gmelinii Plantations. Forests, 16(10), 1552. https://doi.org/10.3390/f16101552






