Acoustic Resonance Characteristics of Birch Wood Loudspeaker Enclosures: Analysis of Influence of Shape and Filling
Abstract
1. Introduction
2. Materials and Methods
2.1. Production of Enclosures
2.2. Software and Measurements
- Notebook running REW V5.20.13;
- RME Fireface UC sound card;
- Microphone cable (balanced line);
- Earthworks M23 measurement microphone.
- Notebook running REW V5.20.13;
- RME Fireface UC sound card;
- Unbalanced cable;
- GHXAMP TPA3116 amplifier (considered for future use with loudspeakers);
- Speaker cable;
- Tested loudspeaker.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AVE | Average |
| BL | Force factor |
| CNC | Computer numerical control |
| Cms | Mechanical compliance of the suspension |
| ESS | Exponential sine sweep |
| Fs | Resonant frequency |
| Le | Voice coil inductance |
| MDF | Medium density fiberboard |
| Mms | Moving mass |
| Re | DC resistance |
| REW | Room EQ Wizard |
| Qes | Electrical quality factor |
| Qms | Mechanical quality factor |
| Qts | Total quality factor |
| SD | Standard deviation |
| Sd | Effective piston area |
| SPL | Sound pressure level |
| Vas | Equivalent volume |
| VC Diameter | Voice coil diameter |
| Vd | Displacement Volume |
| Xmax | Maximum excursion |
References
- Cherradi, Y.; Rosca, I.C.; Cerbu, C.; Kebir, H.; Guendouz, A.; Benyoucef, M. Acoustic properties for composite materials based on alfa and wood fibers. Appl. Acoust. 2021, 174, 107759. [Google Scholar] [CrossRef]
- Čulík, M. Drevo a Jeho Využitie vo Výrobe Hudobných Nástrojov. Vedecká Štúdia (Wood and Its Use in the Production of Musical Instruments); A Scientific Study; Technical University in Zvolen: Zvolen, Slovakia, 2013; ISBN 978-80-228-2511-5. [Google Scholar]
- Newell, P.; Holland, K. Loudspeakers for Music Recording and Reproduction; Routledge: London, UK, 2018; ISBN 9781315149202. [Google Scholar]
- Kol, H.S.; Keskin, H.; Korkut, S.; Akbulut, T. Laminated veneer lumber from Rowan (Sorbus aucuparia Lipsky). Afr. J. Agric. Res. 2009, 4, 1101–1105. [Google Scholar]
- Warmbier, K.; Wilczyński, A.; Danecki, L. Properties of one-layer experimental particleboards from willow (Salix viminalis) and industrial wood particles. Eur. J. Wood Prod. 2013, 71, 25–28. [Google Scholar] [CrossRef][Green Version]
- Balatinecz, J.; Mertens, P.; Boever, L.D.; Yukun, H.; Ju, J.; Wan, J.J.; Acker, J.V. Properties, processing and utilization. In Poplars and Willows: Trees for Society and the Environment; CABI: Wallingford, UK, 2014; pp. 527–561. [Google Scholar][Green Version]
- Van Acker, J.; Defoirdt, N.; Van den Bulcke, J. Enhanced potential of poplar and willow for engineered wood products. In Proceedings of the 2nd Conference on Engineered Wood Products Based on Poplar/Willow Wood, 8–10 September 2016; pp. 187–210. [Google Scholar][Green Version]
- Borůvka, V.; Dudík, R.; Zeidler, A.; Holeček, T. Influence of Site Conditions and Quality of Birch Wood on Its Properties and Utilization after Heat Treatment. Part I—Elastic and Strength Properties, Relationship to Water and Dimensional Stability. Forests 2019, 10, 189. [Google Scholar] [CrossRef]
- Li, N.; Bao, M.; Chen, Y.; Zhang, Y.; Bao, Y.; Yu, W. Influence of density on properties of compressed weeping willow (Salix babylonica) wood panels. For. Prod. J. 2017, 67, 44–49. [Google Scholar] [CrossRef]
- Dudík, R.; Borůvka, V.; Zeidler, A.; Holeček, T.; Riedl, M. Influence of Site Conditions and Quality of Birch Wood on Its Properties and Utilization after Heat Treatment. Part II—Surface Properties and Marketing Evaluation of the Effect of the Treatment on Final Usage of Such Wood. Forests 2020, 11, 556. [Google Scholar] [CrossRef]
- Dubois, H.; Verkasalo, E.; Claessens, H. Potential of Birch (Betula pendula Roth and B. pubescens Ehrh.) for Forestry and Forest-Based Industry Sector within the Changing Climatic and Socio-Economic Context of Western Europe. Forests 2020, 11, 336. [Google Scholar] [CrossRef]
- Horák, P.; Borůvka, V.; Novák, D.; Kozel, J. Acoustic Parameters of Birch Wood Compared to Maple Wood and Medium Density Fibreboard. In Proceedings of the 32nd International Conference on Wood Science and Technology—ICWST 2023: Unleashing the Potential of Wood-Based Materials, Zagreb, Croatia, 7–8 December 2023; pp. 75–82, ISBN 978-953-292-083-3. [Google Scholar]
- Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Štruktúra a Vlastnosti Dreva (Structure and Properties of Wood); Príroda: Bratislava, Slovakia, 1993; p. 485. ISBN 80-07-00600-1. [Google Scholar]
- Bucur, V. Acoustics of Wood; Springer: Berlin/Heidelberg, Germany, 2006; p. 394. ISBN 978-3-540-30594-1. [Google Scholar]
- Olson, H.F. Direct radiator loudspeaker enclosures. J. Audio Eng. Soc. 1969, 17, 22–29. [Google Scholar] [CrossRef]
- Crocker, M.J. Handbook of Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 978-0-471-25293-1. [Google Scholar]
- Liu, Y.; Zeng, X.; Wang, H. 3D meshless FEM-BEM model for prediction of sound fields in cabins due to external sound disturbances. J. Vibroengineering 2017, 19, 5346–5360. [Google Scholar] [CrossRef][Green Version]
- van’t Wout, E. Stable and efficient FEM-BEM coupling with OSRC regularisation for acoustic wave transmission. J. Comput. Phys. 2022, 450, 110867. [Google Scholar] [CrossRef]
- Gabrielsson, A.; Lindström, B.; Till, O. Loudspeaker frequency response and perceived sound quality. J. Acoust. Soc. Am. 1991, 90, 707–719. [Google Scholar] [CrossRef]
- Rossing, T. (Ed.) Springer Handbook of Acoustics; Springer Science & Business Media, LLC: New York, NY, USA, 2007; ISBN 978-0-387-30446-5. [Google Scholar]
- Anderson, N. Acoustic Characterization of Rooms Using Directional and Omnidirectional Sources. Ph.D. Thesis, Brigham Young University-Idaho, Rexburg, ID, USA, 2022. [Google Scholar]
- Farina, A. Advancements in impulse response measurements by sine sweeps. In Proceedings of the 122nd Convention of the Audio Engineering Society, Vienna, Austria, 5–8 May 2007; Audio Engineering Society Convention Paper. Volume 122. [Google Scholar]
- Toft, R. Digital Audio: Sampling, Dither, and Bit Depth. 2024. Available online: https://ir.lib.uwo.ca/popmusicforum_techmatters/11 (accessed on 8 August 2025).
- Horák, P.; Borůvka, V. Acoustic Parameters of Pioneer Wood Species. In Proceedings of the 11th Hardwood Conference Proceedings, Sopron, Hungary, 30–31 May 2024; pp. 219–223, ISBN 978-963-334-518-4. [Google Scholar]
- Kozel, J. Analysis of the Acoustic Parameters of Wood-Based Speaker Enclosures. Master’s Thesis, Department of Wood processing and Biomaterials, Faculty of Forestry and Wood Sciences, Czech University of Life Sciences, Prague, Czech Republic, 2021. [Google Scholar]
- Gu, J.; Shen, Y.; Feng, X. Comments on “A Diffractive Study on the Relation Between Finite Baffle and Loudspeaker Measurement”. J. Audio Eng. Soc. 2021, 69, 294–296. [Google Scholar] [CrossRef]
- D’appolito, J. Testing Loudspeakers: Which Measurements Matter, Part 1. Audioxpress. 2016. Available online: https://audioxpress.com/article/testing-loudspeakers-which-measurements-matter-part-1 (accessed on 23 May 2024).
- Cobianchi, M.; Rousseau, M. Modelling the Sound Radiation by Loudspeaker Cabinets. In Proceedings of the Comsol International Conference 2014, Cambridge, UK, 17–19 September 2014. [Google Scholar]
- Červenka, M.; Šoltés, M.; Bednařík, M. Optimal shaping of acoustic resonators for the generation of high-amplitude standing waves. J. Acoust. Soc. Am. 2014, 136, 1003–1012. [Google Scholar] [CrossRef] [PubMed]
- Kirsch, C.; Ewert, S.D. Effects of measured and simulated diffraction from a plate on sound source localization. J. Acoust. Soc. Am. 2024, 155, 3118–3131. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.R. Fundamentals of diffraction. J. Audio Eng. Soc. 1997, 45, 347–356. [Google Scholar] [CrossRef]
- Harrell, J.A.; Hixson, E.L. Constant-Beamwidth One-Octave Bandwidth End-Fire Line Array of Loudspeakers; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1995; Available online: https://aes2.org/publications/elibrary-page/?id=7936 (accessed on 25 August 2025).
- Dobrucki, A. Diffraction correction of frequency response for loudspeaker in rectangular baffle. Arch. Acoust. 2006, 31, 537–542. [Google Scholar]
- Eargle, J. Loudspeaker handbook; Springer Science & Business Media: Boston, MA, USA, 2003; ISBN 978-1-4419-5390-2. [Google Scholar]
- Walker, P.J. The loudspeaker in the home. J. Br. Inst. Radio Eng. 1953, 13, 377–380. [Google Scholar] [CrossRef]
- Bauer, B.B. Acoustic damping for loudspeakers. In Transactions of the IRE Professional Group on Audio; University of Minnesota: Minneapolis, MN, USA, 1953; Volume 3, pp. 23–34. [Google Scholar] [CrossRef]
- Backman, J. Computation of diffraction for loudspeaker enclosures. J. Audio Eng. Soc. 1989, 37, 353–362. [Google Scholar]
- Klippel, W.; Schlechter, J. Distributed mechanical parameters of loudspeakers, part 1: Measurements. J. Audio Eng. Soc. 2009, 57, 500–511. Available online: https://aes2.org/publications/elibrary-page/?id=14830 (accessed on 8 August 2025).
- Bezzola, A.; Kubota, G.S.; Devantier, A. Acoustic Mass and Resistance as Function of Drive Level for Straight, Bent, and Flared Loudspeaker Ports. In Proceedings of the 149th Convention of the Audio Engineering Society, Online, 27–30 October 2020; Audio Engineering Society Convention Paper. Volume 149. [Google Scholar]
- Ahonen, J.; Karjalainen, M.; Rauhala, J.; Tikander, M. Perception and physical behavior of loudspeaker nonlinearities at bass frequencies in closed vs. reflex enclosures. In Proceedings of the 124th Convention of the Audio Engineering Society, Amsterdam, The Netherlands, 17–20 May 2008; Audio Engineering Society Convention Paper. Volume 124. [Google Scholar]
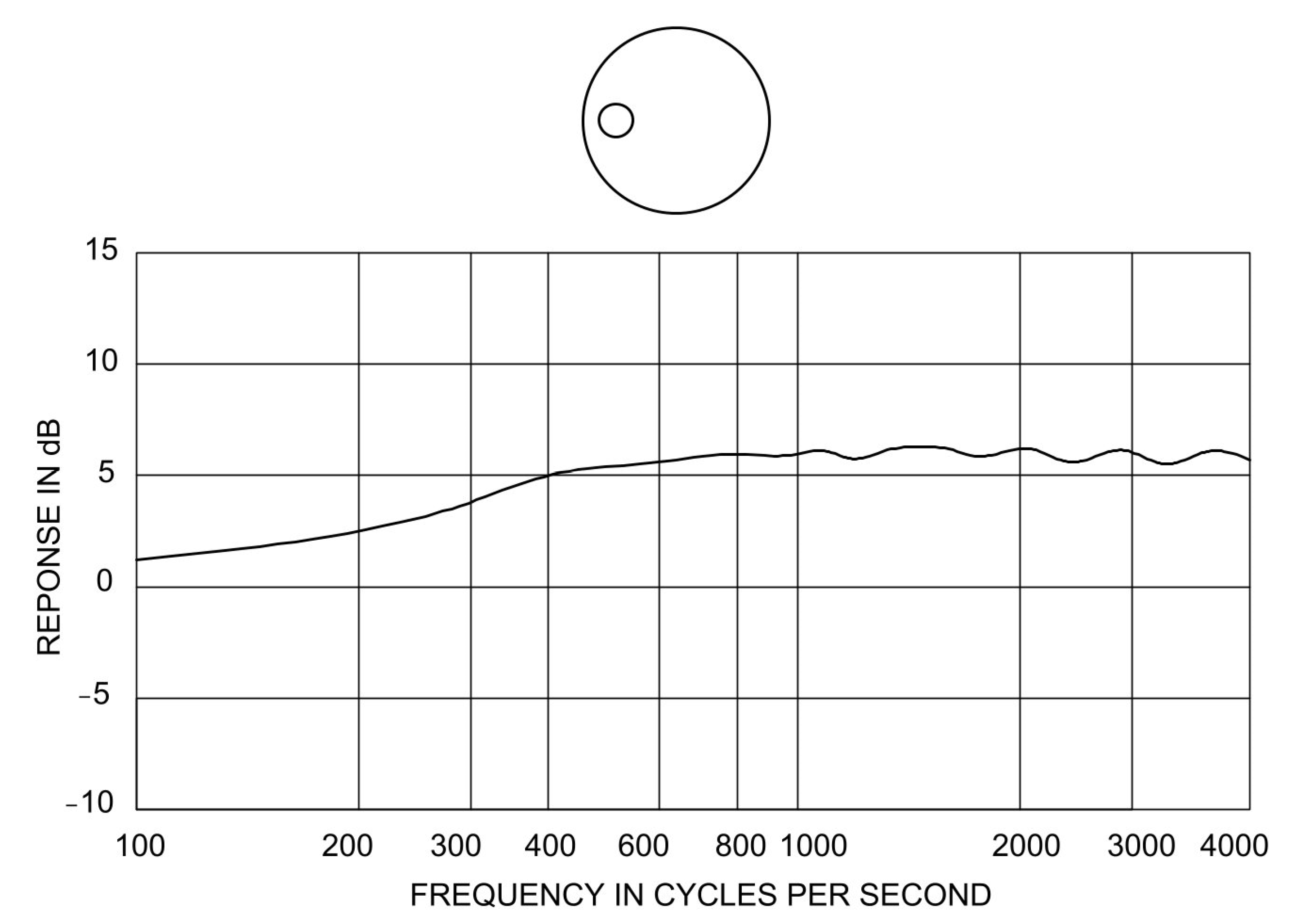
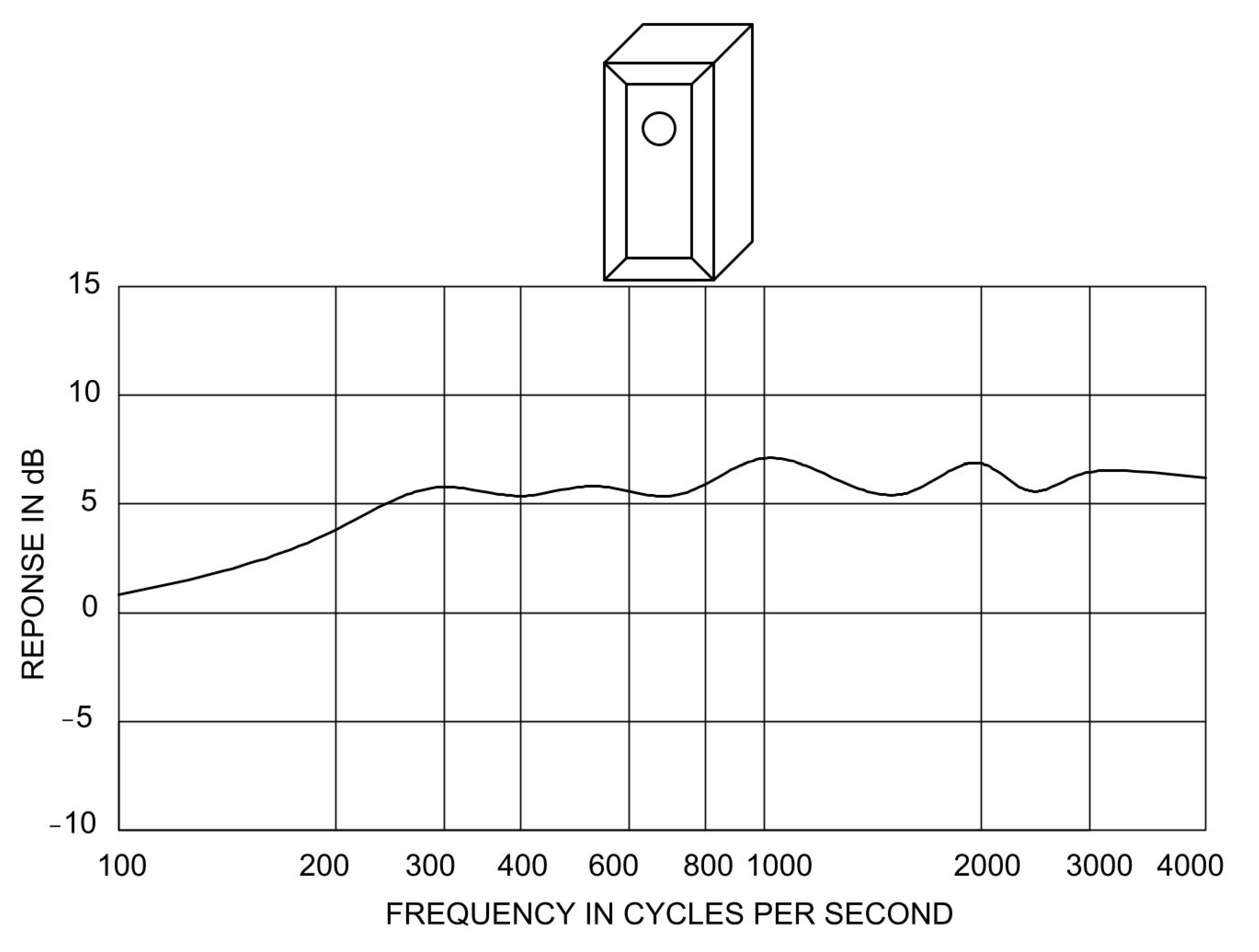


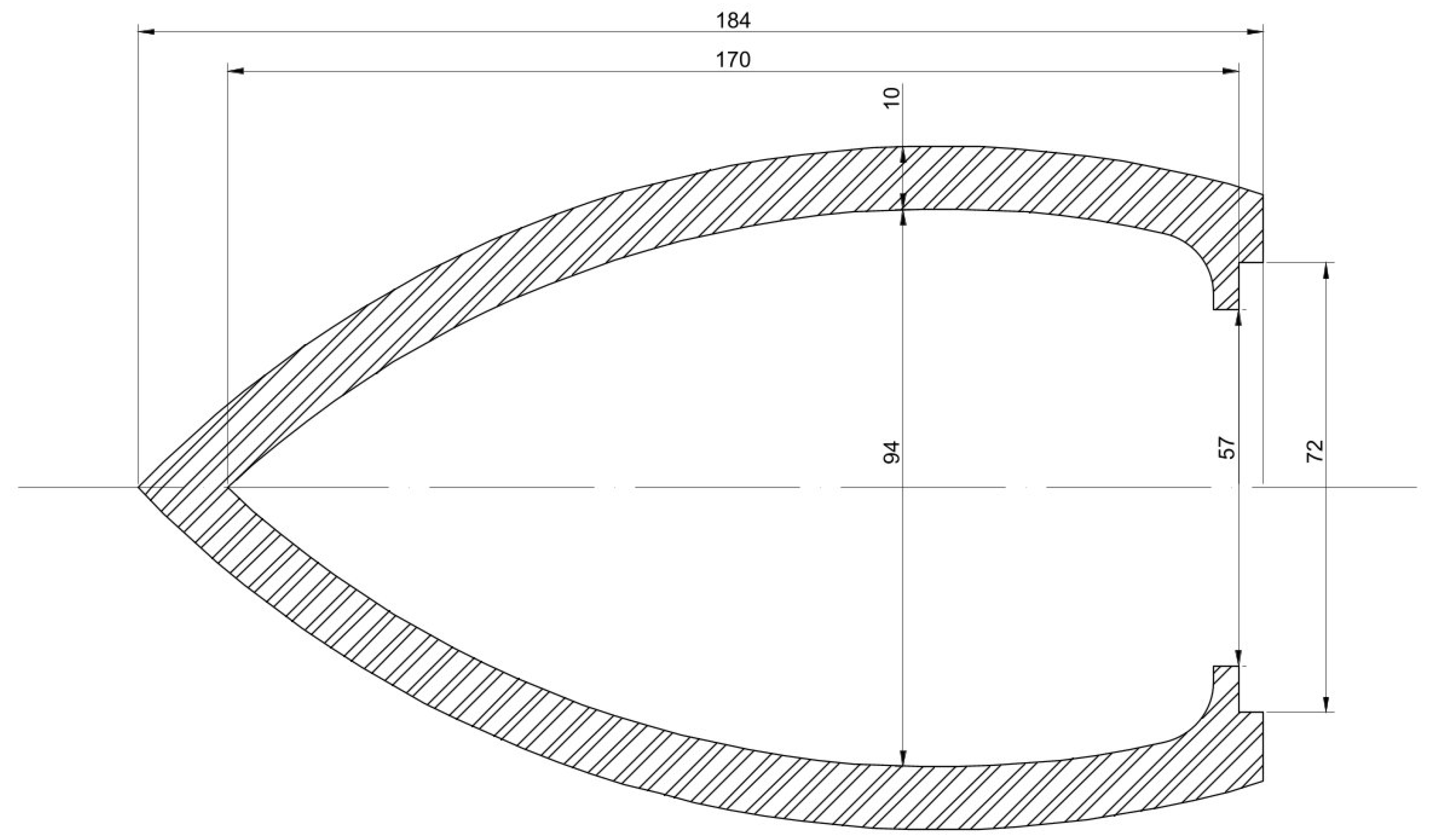
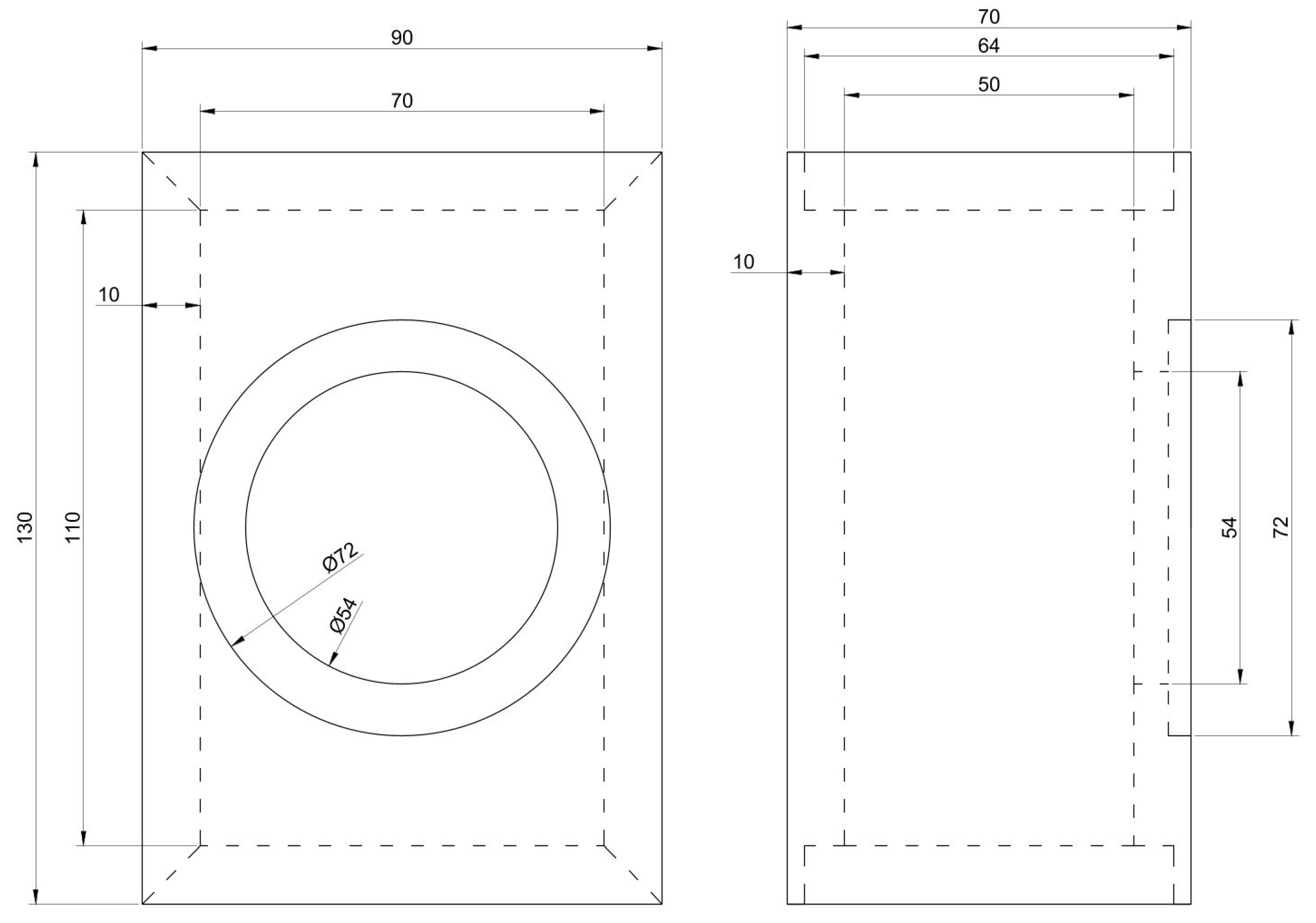
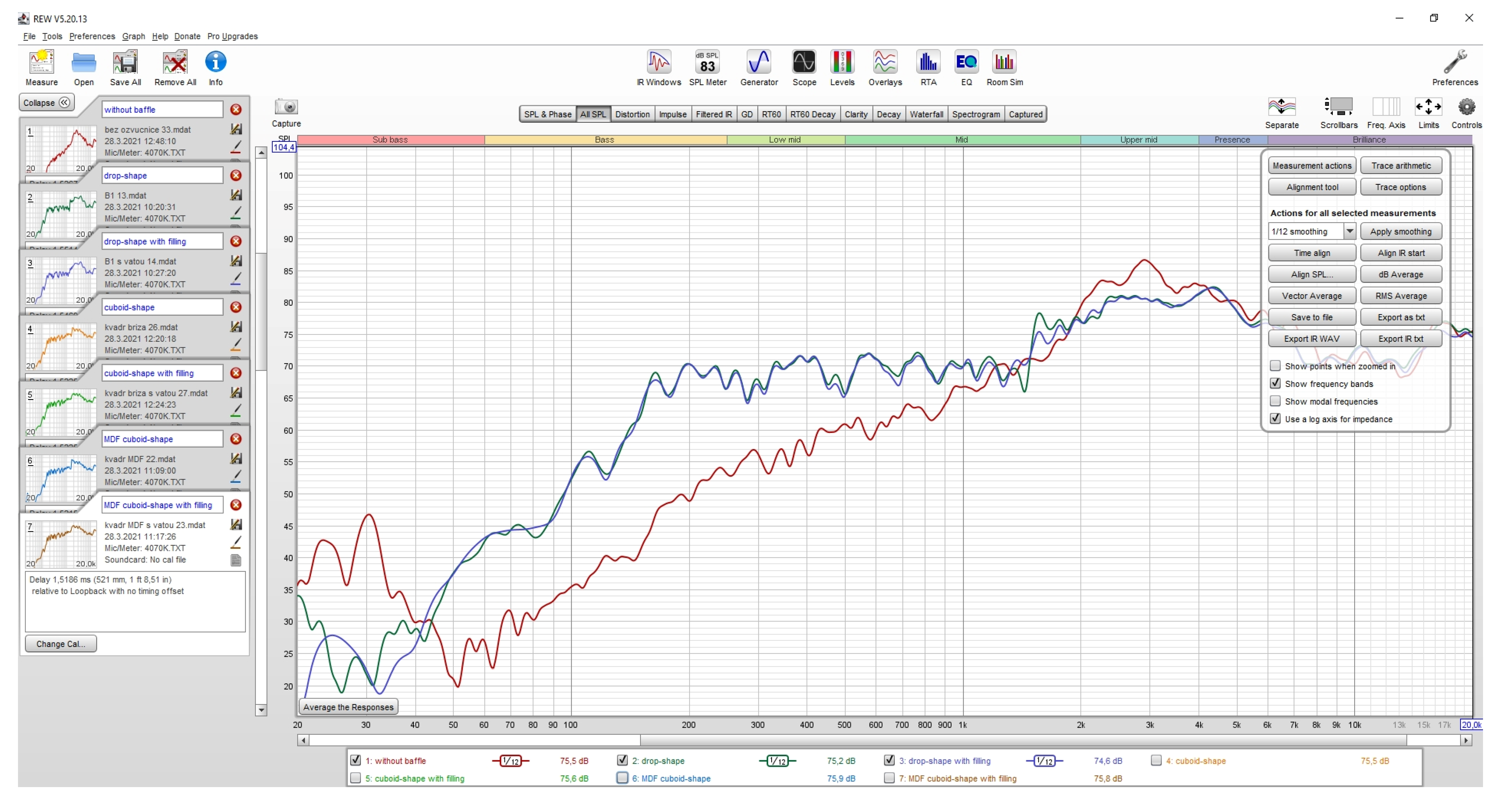
| Impedance | 4 Ω | Sd | 12 cm2 |
| Re | 3.1 Ω | Vd | 1.31 cm3 |
| Le | 0.72 mH @ 1 kHz | BL | 2.01 Tm |
| Fs | 177 Hz | Vas | 0.14 l |
| Qms | 5.76 | Xmax | 1.1 mm |
| Qes | 0.97 | VC Diameter | 16 mm |
| Qts | 0.83 | SPL | 85.2 dB |
| Mms | 1.1 g | RMS Power Handling | 15 W |
| Cms | 0.72 mm/N | Usable Frequency Range (Hz) | 170–20 000 Hz |
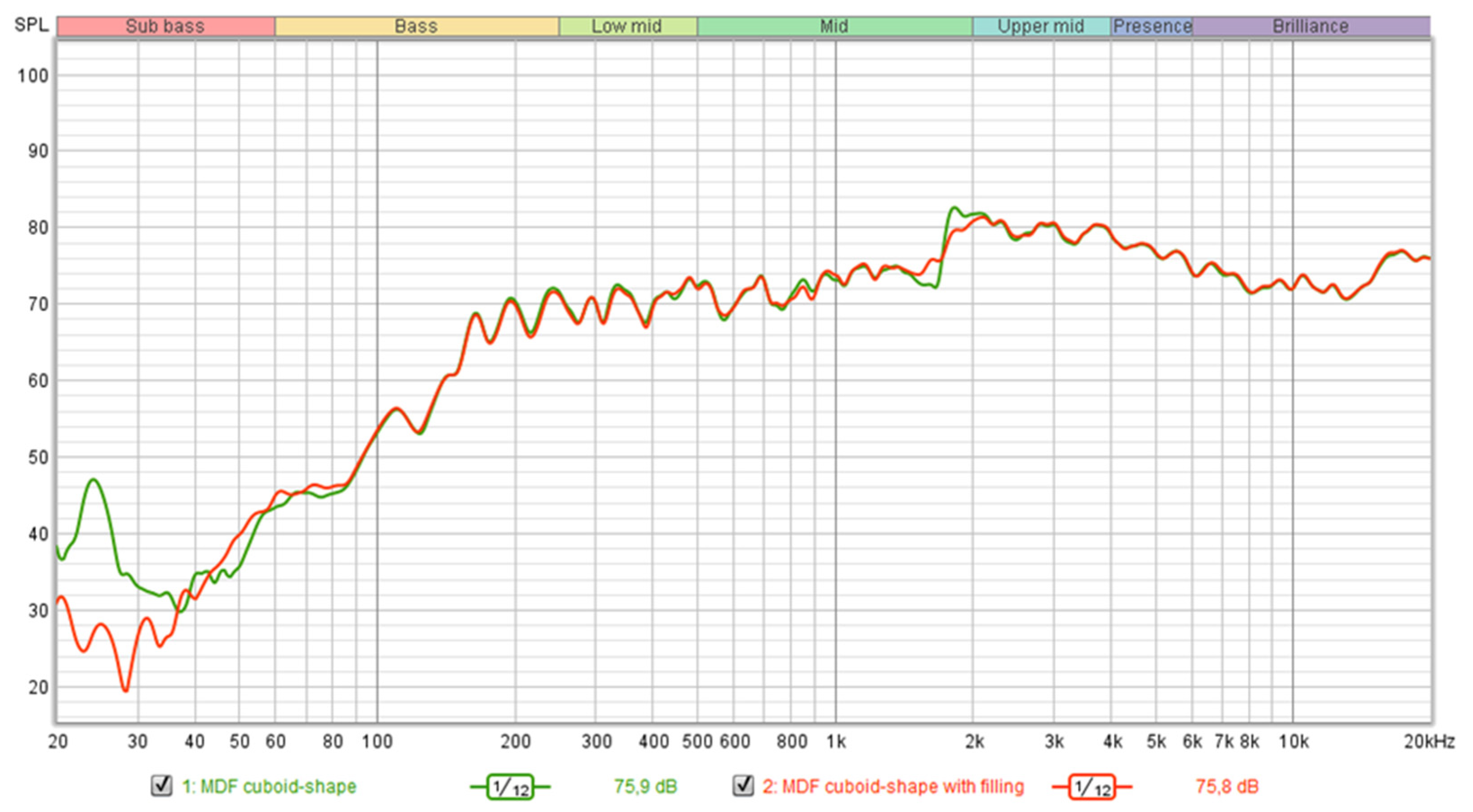
| Category | Solid Birch | MDF Cuboid-Shape | |
|---|---|---|---|
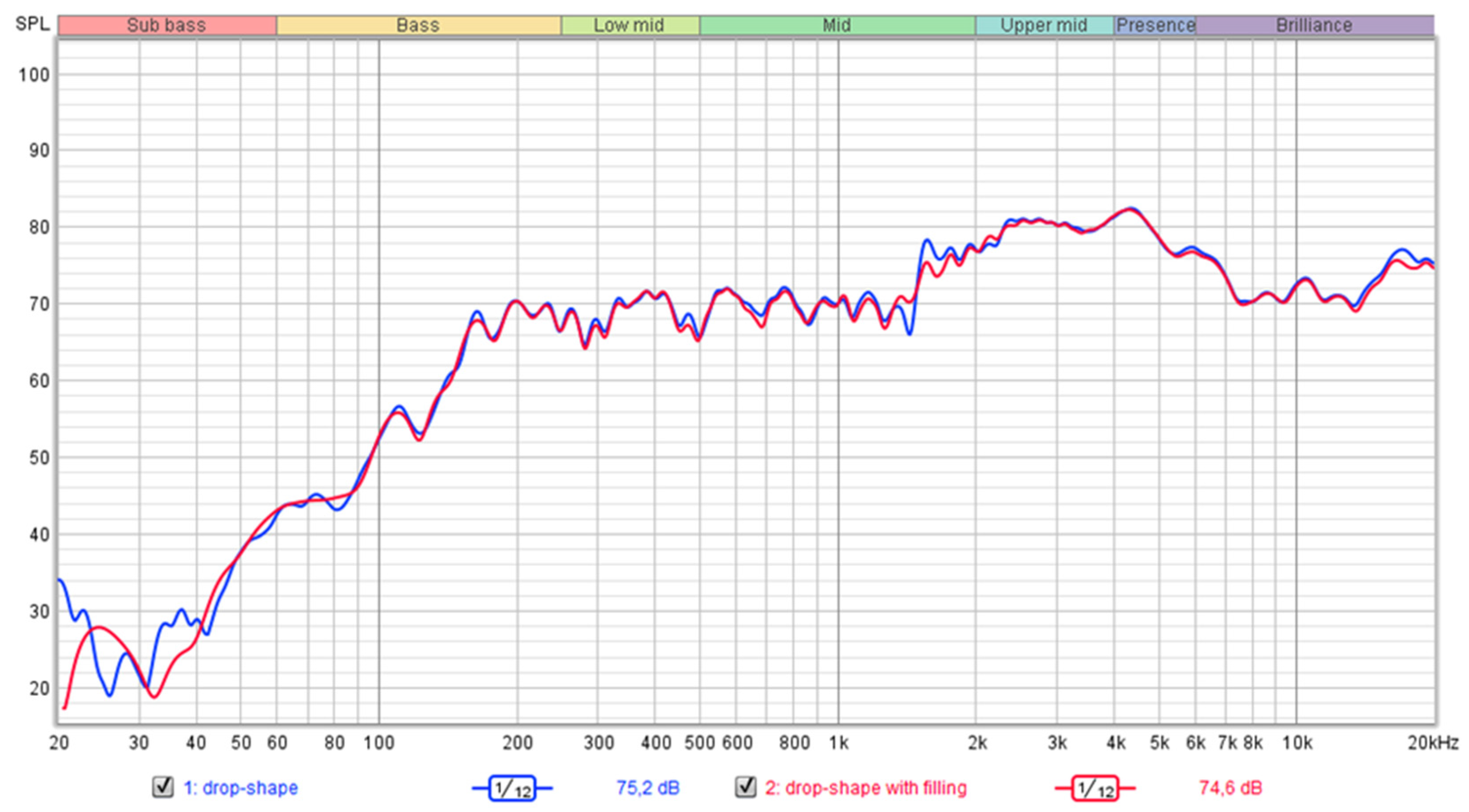
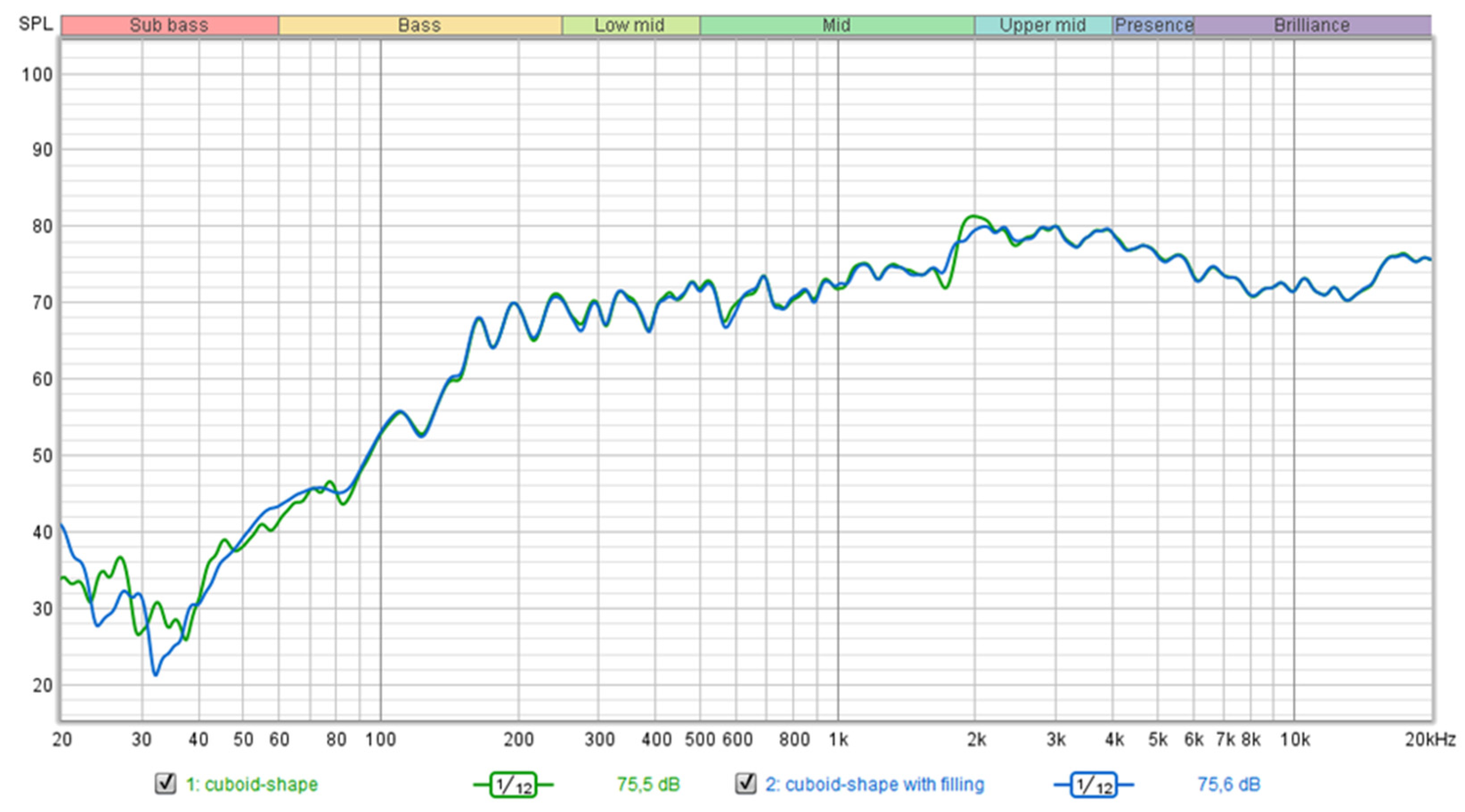
| Drop-Shape | Cuboid-Shape | ||
| Sub-bass resonance (<30 Hz) | −8 dB | −3 dB | −10 dB |
| Dip smoothing (40−50 Hz) | +2 dB | +2 dB | +4 dB |
| Effectiveness of filling | High | Moderate | Very high |
| Need for filling | Strongly recommended | Helpful but optional | Essential |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horák, P.; Borůvka, V. Acoustic Resonance Characteristics of Birch Wood Loudspeaker Enclosures: Analysis of Influence of Shape and Filling. Forests 2025, 16, 1530. https://doi.org/10.3390/f16101530
Horák P, Borůvka V. Acoustic Resonance Characteristics of Birch Wood Loudspeaker Enclosures: Analysis of Influence of Shape and Filling. Forests. 2025; 16(10):1530. https://doi.org/10.3390/f16101530
Chicago/Turabian StyleHorák, Petr, and Vlastimil Borůvka. 2025. "Acoustic Resonance Characteristics of Birch Wood Loudspeaker Enclosures: Analysis of Influence of Shape and Filling" Forests 16, no. 10: 1530. https://doi.org/10.3390/f16101530
APA StyleHorák, P., & Borůvka, V. (2025). Acoustic Resonance Characteristics of Birch Wood Loudspeaker Enclosures: Analysis of Influence of Shape and Filling. Forests, 16(10), 1530. https://doi.org/10.3390/f16101530








