Fitting and Evaluating Taper Functions to Predict Upper Stem Diameter of Planted Teak (Tectona grandis L.f.) in Eastern and Central Regions of Nepal
Abstract
:1. Introduction
2. Materials and Methods
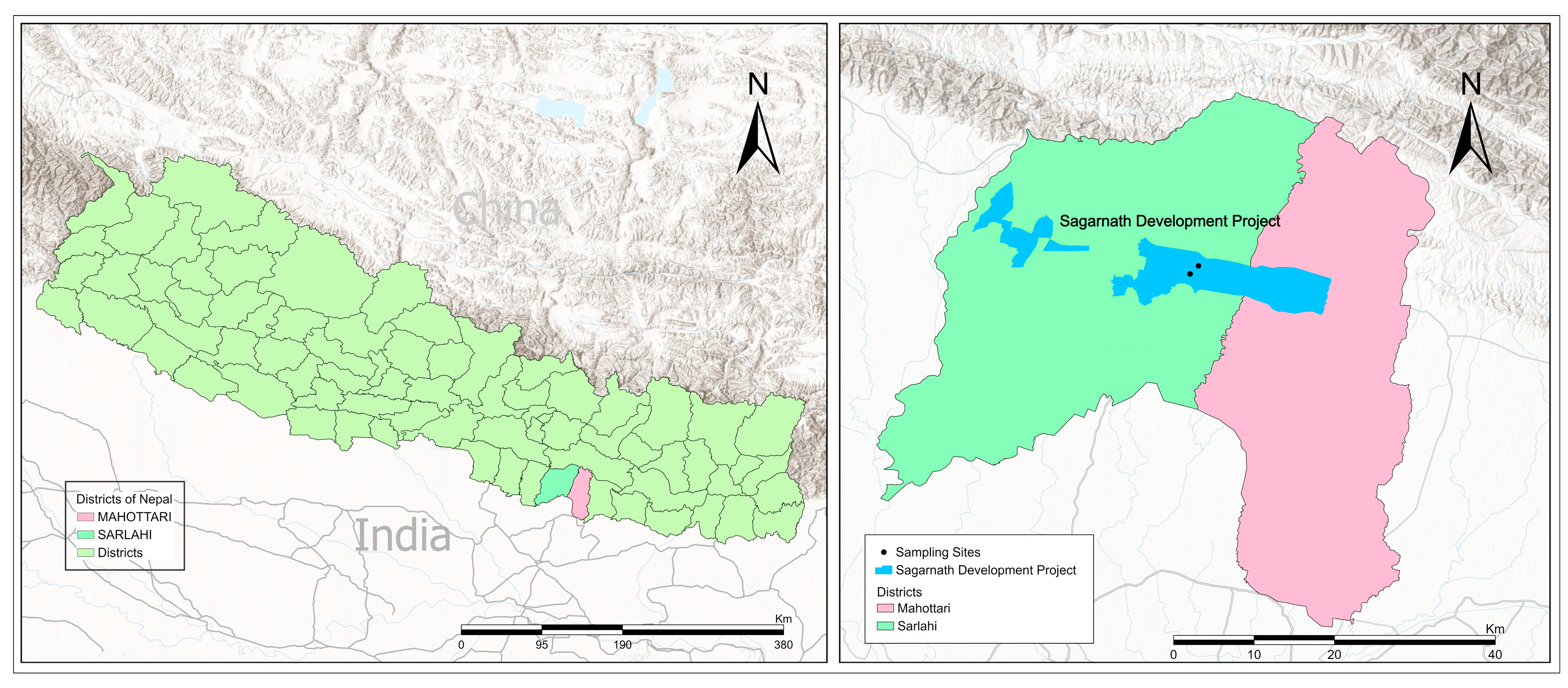
2.1. Study Area
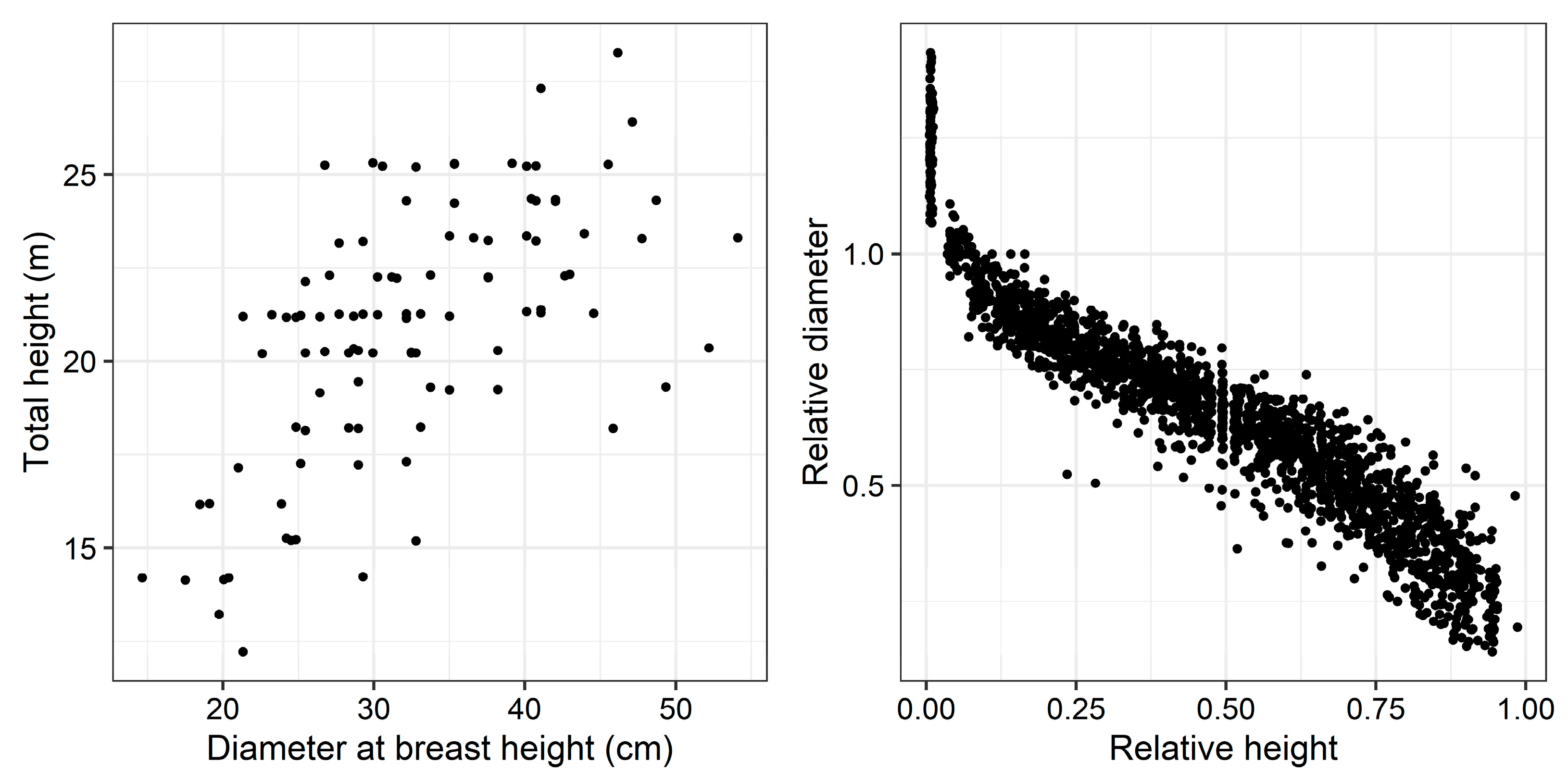
2.2. Sampling and Measurements
2.3. Taper Equations
2.4. Model Fitting and Evaluation
3. Results
3.1. Taper Equations and Performance
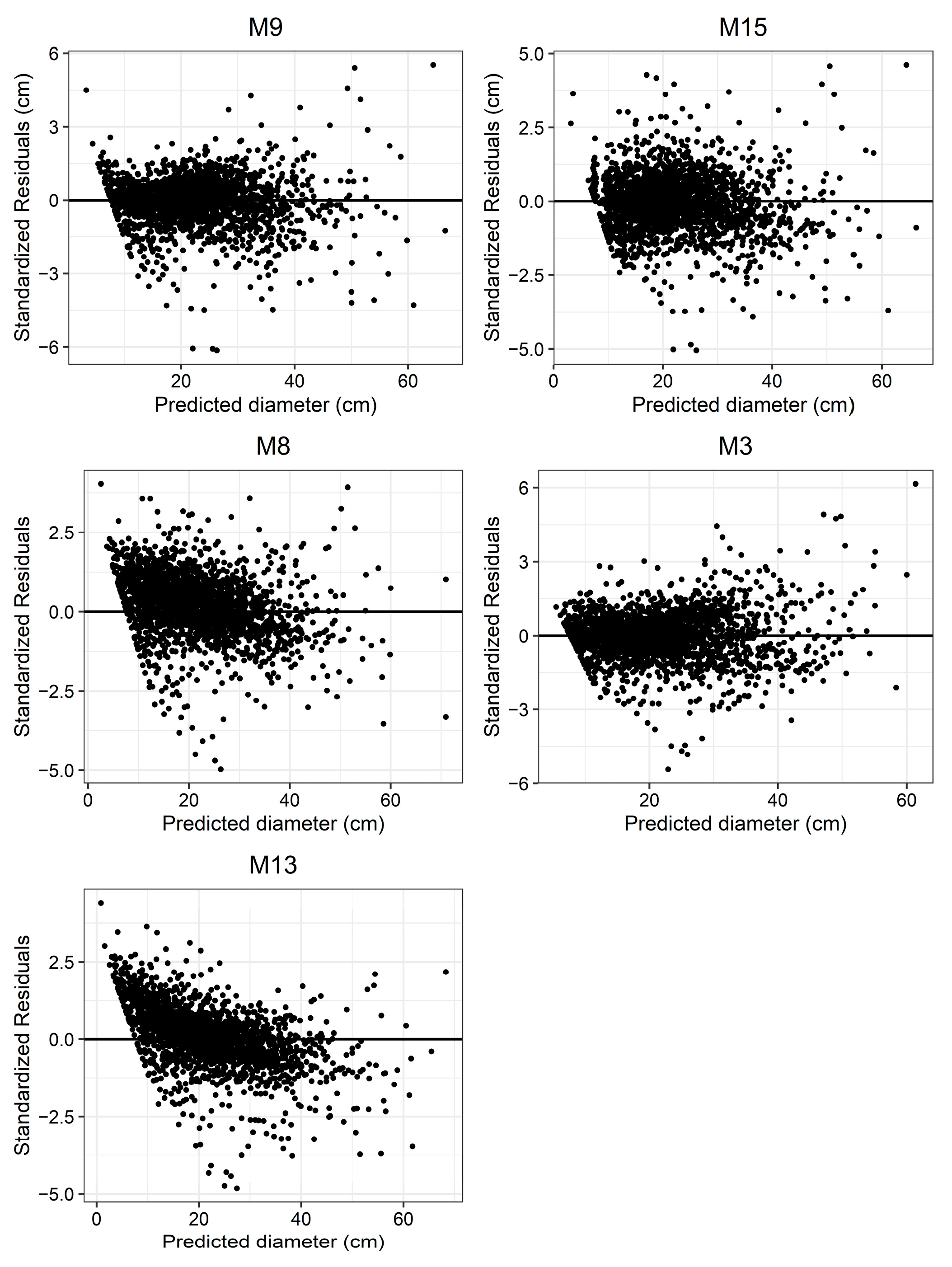
3.2. Residual Diagnostic
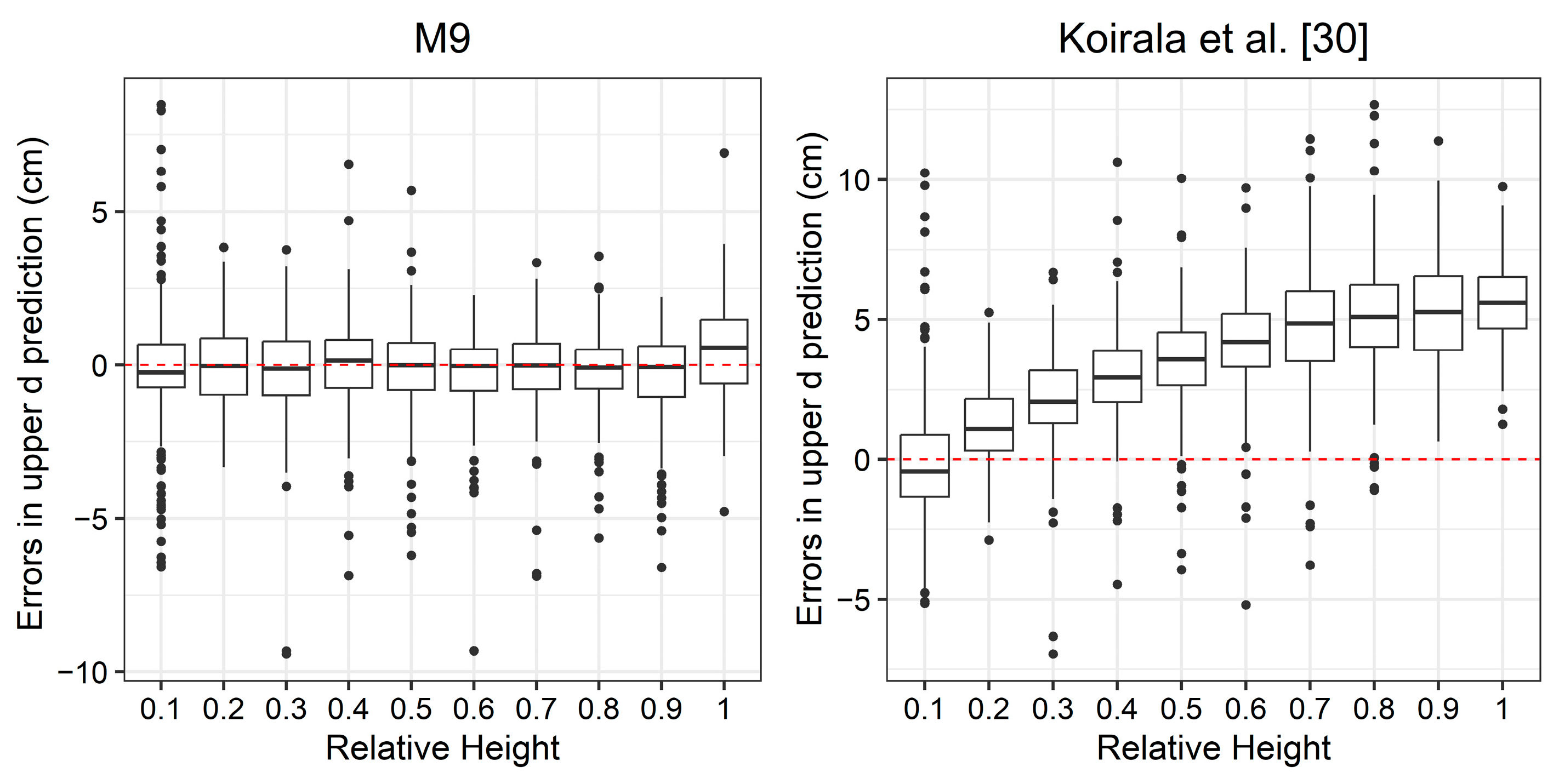
3.3. Model Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Berlin/Heidelberg, Germany, 2012; Volume 457. [Google Scholar]
- Parresol, B.R. Assessing Tree and Stand Biomass: A Review with Examples and Critical Comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar] [CrossRef]
- Westfall, J.A.; Coulston, J.W.; Gray, A.N.; Shaw, J.D.; Radtke, P.J.; Walker, D.M.; Weiskittel, A.R.; MacFarlane, D.W.; Affleck, D.L.R.; Zhao, D. A National-Scale Tree Volume, Biomass, and Carbon Modeling System for the United States; Gen. Tech. Rep. WO-104; US Department of Agriculture, Forest Service: Washington, DC, USA, 2024; Volume 104. [Google Scholar]
- Kozak, A. My Last Words on Taper Equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R. Comparison of Model Forms for Estimating Stem Taper and Volume in the Primary Conifer Species of the North American Acadian Region (Comparaison de Formules Modèles Pour Estimer La Décroissance de La Tige et Le Volume Des Principales Espèces de Conifères Dan). Ann. For. Sci. 2010, 67, 302. [Google Scholar]
- Fonweban, J.; Gardiner, B.; Macdonald, E.; Auty, D. Taper Functions for Scots Pine (Pinus sylvestris L.) and Sitka Spruce (Picea Sitchensis (Bong.) Carr.) in Northern Britain. Forestry 2011, 84, 49–60. [Google Scholar] [CrossRef]
- Dahlen, J.; Auty, D.; Eberhardt, T.L. Models for Predicting Specific Gravity and Ring Width for Loblolly Pine from Intensively Managed Plantations, and Implications for Wood Utilization. Forests 2018, 9, 292. [Google Scholar] [CrossRef]
- Rojo, A.; Perales, X.; Sánchez-Rodríguez, F.; Álvarez-González, J.G.; von Gadow, K. Stem Taper Functions for Maritime Pine (Pinus pinaster Ait.) in Galicia (Northwestern Spain). Eur. J. For. Res. 2005, 124, 177–186. [Google Scholar] [CrossRef]
- Diéguez-Aranda, U.; Castedo-Dorado, F.; Álvarez-González, J.G.; Rojo, A. Compatible Taper Function for Scots Pine Plantations in Northwestern Spain. Can. J. For. Res. 2006, 36, 1190–1205. [Google Scholar] [CrossRef]
- Ulak, S.; Ghimire, K.; Gautam, R.; Bhandari, S.K.; Poudel, K.P.; Timilsina, Y.P.; Pradhan, D.; Subedi, T. Predicting the Upper Stem Diameters and Volume of a Tropical Dominant Tree Species. J. For. Res. 2022, 33, 1725–1737. [Google Scholar] [CrossRef]
- Saud, P.; Chapagain, T.R.; Bhandari, S.K.; Moser, W.K. Taper Functions to Predict the Upper Stem Diameter of Chir Pine (Pinus roxburghii) in the Mid-Hills of Nepal. Trees For. People 2024, 17, 100627. [Google Scholar] [CrossRef]
- Tasissa, G.; Burkhart, H.E. An Application of Mixed Effects Analysis to Modeling Thinning Effects on Stem Profile of Loblolly Pine. For. Ecol. Manag. 1998, 103, 87–101. [Google Scholar] [CrossRef]
- Sabatia, C.O.; Burkhart, H.E. Segmented Taper Equation to New Trees. For. Sci. 2015, 61, 411–423. [Google Scholar]
- Max, T.; Burkhart, H.E. Segmented Polynomial Regression Applied to Taper Equations. For. Sci. 1976, 22, 283–289. [Google Scholar]
- McTague, J.P.; Weiskittel, A. Evolution, History, and Use of Stem Taper Equations: A Review of Their Development, Application, and Implementation. Can. J. For. Res. 2021, 51, 210–235. [Google Scholar] [CrossRef]
- Zapata-Cuartas, M.; Bullock, B.P.; Montes, C.R. A Taper Equation for Loblolly Pine Using Penalized Spline Regression. For. Sci. 2021, 67, 1–13. [Google Scholar] [CrossRef]
- Scolforo, H.F.; McTague, J.P.; Raimundo, M.R.; Weiskittel, A.; Carrero, O.; Scolforo, J.R.S. Comparison of Taper Functions Applied to Eucalypts of Varying Genetics in Brazil: Application and Evaluation of the Penalized Mixed Spline Approach. Can. J. For. Res. 2018, 48, 568–580. [Google Scholar] [CrossRef]
- Nunes, M.H.; Görgens, E.B. Artificial Intelligence Procedures for Tree Taper Estimation within a Complex Vegetation Mosaic in Brazil. PLoS ONE 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Yang, S.I.; Burkhart, H.E. Robustness of Parametric and Nonparametric Fitting Procedures of Tree-Stem Taper with Alternative Definitions for Validation Data. J. For. 2020, 118, 576–583. [Google Scholar] [CrossRef]
- Salekin, S.; Catalán, C.H.; Boczniewicz, D.; Phiri, D.; Morgenroth, J.; Meason, D.F.; Mason, E.G. Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters. Forests 2021, 12, 913. [Google Scholar] [CrossRef]
- Yang, S.I.; Burkhart, H.E.; Seki, M. Evaluating Semi- and Nonparametric Regression Algorithms in Quantifying Stem Taper and Volume with Alternative Test Data Selection Strategies. Forestry 2023, 96, 465–480. [Google Scholar] [CrossRef]
- Trincado, G.; Burkhart, H.E. A Generalized Approach for Modeling and Localizing Stem Profile Curves. For. Sci. 2006, 52, 670–682. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, S.; Trincado, G.; Meng, S.X. Nonlinear Mixed-Effects Modeling of Variable-Exponent Taper Equations for Lodgepole Pine in Alberta, Canada. Eur. J. For. Res. 2009, 128, 415–429. [Google Scholar] [CrossRef]
- Gómez-García, E.; Crecente-Campo, F.; Diéguez-Aranda, U. Selection of Mixed-Effects Parameters in a Variable-Exponent Taper Equation for Birch Trees in Northwestern Spain. Ann. For. Sci. 2013, 70, 707–715. [Google Scholar] [CrossRef]
- Berger, A.; Gschwantner, T.; McRoberts, R.E.; Schadauer, K. Effects of Measurement Errors on Individual Tree Stem Volume Estimates for the Austrian National Forest Inventory. For. Sci. 2014, 60, 14–24. [Google Scholar] [CrossRef]
- Zhao, D.; Lynch, T.B.; Westfall, J.; Coulston, J.; Kane, M.; Adams, D.E. Compatibility, Development, and Estimation of Taper and Volume Equation Systems. For. Sci. 2019, 65, 1–13. [Google Scholar] [CrossRef]
- He, P.; Hussain, A.; Khurram Shahzad, M.; Jiang, L.; Li, F. Evaluation of Four Regression Techniques for Stem Taper Modeling of Dahurian Larch (Larix gmelinii) in Northeastern China. For. Ecol. Manag. 2021, 494, 119336. [Google Scholar] [CrossRef]
- Noda, I.; Himmapan, W.; Furuya, N.; Hitsuma, G. Taper Equations for Evaluating Private Plantation Teak (Tectona grandis) in Thailand. Jpn. Agric. Res. Q. 2023, 57, 329–343. [Google Scholar] [CrossRef]
- Poudel, K.P.; Özçelik, R.; Yavuz, H. Differences in Stem Taper of Black Alder (Alnus Glutinosa Subsp. Barbata) by Origin. Can. J. For. Res. 2020, 50, 581–588. [Google Scholar] [CrossRef]
- Koirala, A.; Montes, C.R.; Bullock, B.P.; Wagle, B.H. Developing Taper Equations for Planted Teak (Tectona grandis L.f.) Trees of Central Lowland Nepal. Trees For. People 2021, 5, 100103. [Google Scholar] [CrossRef]
- Lumumba, V.W.; Kiprotich, D.; Makena, N.G.; Kavita, M.D.; Mpaine, M.L. Comparative Analysis of Cross-Validation Techniques: LOOCV, K-Folds Cross-Validation, and Repeated K-Folds Cross-Validation in Machine Learning Models. Am. J. Theor. Appl. Stat. 2024, 13, 127–137. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R; Spinger: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Adhikari, A.; Montes, C.R.; Peduzzi, A. A Comparison of Modeling Methods for Predicting Forest Attributes Using Lidar Metrics. Remote. Sens. 2023, 15, 1284. [Google Scholar] [CrossRef]
- Bennett, F.; Swindel, B. Taper Curves for Planted Slash Pine. USDA For. Serv. Res. Note Southeast. For. Exp. Stn. 1972, 4, ref.5. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Fitting Nonlinear Mixed-Effects Models. In Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000; pp. 337–421. [Google Scholar]
- Poudel, K.P.; Temesgen, H.; Gray, A.N. Estimating Upper Stem Diameters and Volume of Douglas-Fir and Western Hemlock Trees in the Pacific Northwest. For. Ecosyst. 2018, 5, 16. [Google Scholar] [CrossRef]
- Littell, R.; Stroup, W.; Wolfinger, R.; Schabenberger, O.; Milliken, G.A. SAS for Mixed Models, 2nd ed.; SAS Institute Inc.: Cary, NC, USA, 2006; p. 814. [Google Scholar]
- Davidian, M.; Giltinan, D.M. Nonlinear Models for Repeated Measurement Data; Routledge: New York, NY, USA, 2017; ISBN 9780203745502. [Google Scholar]
- Lindstrom, M.J.; Bates, D.M. Nonlinear Mixed Effects Models for Repeated Measures Data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Weiskittel, A.; Dick, A.R.; Kershaw, J.A.; Seymour, R.S. Regional Stem Taper Equations for Eleven Conifer Species in the Acadian Region of North America: Development and Assessment. North. J. Appl. For. 2012, 29, 5–14. [Google Scholar] [CrossRef]
- de-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating Marginal and Conditional Predictions of Taper Models in the Absence of Calibration Data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Tewari, D.N. A Monograph on Teak (Tectona grandis Linn. f.); International Book Distributors: Dehra Dun, India, 1992; Volume 479. [Google Scholar]
- Kollert, W.; Kleine, M. The Global Teak Study. Analysis, Evaluation and Future Potential of Teak Resources; International Union of Forest Research Organizations: Vienna, Austria, 2017. [Google Scholar]
- Moya, R.; Bond, B.; Quesada, H. A Review of Heartwood Properties of Tectona Grandis Trees from Fast-Growth Plantations. Wood Sci. Technol. 2014, 48, 411–433. [Google Scholar] [CrossRef]
- ADB. Project Performance Audit Report Sagarnath Forestry Development Project in Nepal; Asian Development Bank: Kathmandu, Nepal, 1987. [Google Scholar]
- Adu-Bredu, S.; Bi, A.F.T.; Bouillet, J.P.; Mé, M.K.; Kyei, S.Y.; Saint-André, L. An Explicit Stem Profile Model for Forked and Un-Forked Teak (Tectona grandis) Trees in West Africa. For. Ecol. Manag. 2008, 255, 2189–2203. [Google Scholar] [CrossRef]
- Shuaibu, R. Developing Stem Taper Equation for Tectona grandis (Teak) Plantation in Agudu Forest Reserve, Nasarawa State, Nigeria. J. Sci. Technol. 2016, 5, 199–206. [Google Scholar]
- Goodwin, A.N. A Cubic Tree Taper Model. Aust. For. 2009, 72, 87–98. [Google Scholar] [CrossRef]
- Warner, A.J.; Jamroenprucksa, M.; Puangchit, L. Development and Evaluation of Teak (Tectona grandis L.f.) Taper Equations in Northern Thailand. Agric. Nat. Resour. 2016, 50, 362–367. [Google Scholar] [CrossRef]
- Choochuen, T.; Suksavate, W.; Meunpong, P. Development of a Taper Equation for Teak (Tectona grandis l.f.) Growing in Western Thailand. Environ. Nat. Resour. J. 2021, 19, 176–185. [Google Scholar] [CrossRef]
- Kozak, A.; Munro, D.D.; Smith, J.H.G. Taper Functions and Their Application in Forest Inventory. For. Chron. 1969, 45, 278–283. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Spruce Plantations Using Dimensional Analysis. For. Sci. 2009, 55, 268–282. [Google Scholar]
- García, O. Dynamic Modelling of Tree Form. Math. Comput. For. Nat. Resour. Sci. 2015, 7, 9–15. [Google Scholar]
- FRA/DFRS. Terai Forests of Nepal (2010–2012), Forest Resource Assessment Nepal Project/Department of Forest Research and Survey; FRA/DFRS: Babarmahal, Kathmandu, Nepal, 2014. [Google Scholar]
- ADB. Re-Evaluation of the Sagarnath Forestry Development Project in Nepal; Asian Development Bank: Kathmandu, Nepal, 1993. [Google Scholar]
- Bi, H. Trigonometric Variable-Form Taper Equations for Australian Eucalypts. For. Sci. 2000, 46, 397–409. [Google Scholar] [CrossRef]
- Cervera, J.M. El Área Basimétrica Reducida, El Volumen Reducido y El Perfil. Montes 1973, 174, 415–418. [Google Scholar]
- Amidon, E.L. A General Taper Functional Form to Predict Bole Volume for Five Mixed-Conifer Species in California. For. Sci. 1984, 30, 166–171. [Google Scholar]
- Oderwald, R.G.; Rayamajhi, J.N. Biomass Inventory with Tree Taper Equations. Bioresour. Technol. 1991, 36, 235–239. [Google Scholar] [CrossRef]
- Ormerod, D.W. A Simple Bole Model. For. Chron. 1973, 49, 136–138. [Google Scholar] [CrossRef]
- Clutter, J.L. Development of Taper Functions from Variable-Top Merchantable Volume Equations. For. Sci. 1980, 26, 117–120. [Google Scholar] [CrossRef]
- Sharma, M.; Oderwald, R.G. Dimensionally Compatible Volume and Taper Equations. Can. J. For. Res. 2001, 31, 797–803. [Google Scholar] [CrossRef]
- Sharma, M.; Zhang, S.Y. Variable-Exponent Taper Equations for Jack Pine, Black Spruce, and Balsam Fir in Eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Diéguez-Aranda, U.; Puerta, F.R.; López-Sánchez, C.A.; Líbano, E.C.; Obregón, A.C.; Castedo-Dorado, F. Modelling and Localizing a Stem Taper Function for Pinus Radiata in Spain. Can. J. For. Res. 2015, 45, 647–658. [Google Scholar] [CrossRef]
- Poudel, K.P.; Cao, Q.V. Evaluation of Methods to Predict Weibull Parameters for Characterizing Diameter Distributions. For. Sci. 2013, 59, 243–252. [Google Scholar] [CrossRef]
- Subedi, M.R.; Oli, B.N.; Shrestha, S.; Chhin, S. Height-Diameter Modeling of Cinnamomum Tamala Grown in Natural Forest in Mid-Hill of Nepal. Int. J. For. Res. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Raut, S.; Dahlen, J.; Bullock, B.; Montes, C.; Dickens, D. Models to Predict Whole-Disk Specific Gravity and Moisture Content in Planted Longleaf Pine from Cutover and Old Field Sites. Can. J. For. Res. 2022, 52, 137–147. [Google Scholar] [CrossRef]
- Aryal, S.; Gaire, N.P.; Pokhrel, N.R.; Rana, P.; Sharma, B.; Kharal, D.K.; Poudel, B.S.; Dyola, N.; Fan, Z.X.; Grießinger, J.; et al. Spring Season in Western Nepal Himalaya Is Not yet Warming: A 400-Year Temperature Reconstruction Based on Tree-Ringwidths of Himalayan Hemlock (Tsuga dumosa). Atmosphere 2020, 11, 132. [Google Scholar] [CrossRef]
- Dahlen, J.; Auty, D.; Eberhardt, T.L.; Schimleck, L.; Pokhrel, N.R. Determination of Ring-Level Dynamic Modulus of Elasticity in Loblolly Pine from Measurements of Ultrasonic Velocity and Specific Gravity. Forestry 2023, 96, 588–604. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- RStudio Team. R Studio: Integrated Development for R; RStudio: Vienna, Austria, 2024. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Heisterkamp, S.; Van Willigen, B.; Maintainer, R. Package ‘Nlme’. Linear Nonlinear Mix. Eff. Models Version 2017, 3, 274. [Google Scholar]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; D’Agostino McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons, Ltd.: Milton, QLD, Australia, 2011; ISBN 0470665009. [Google Scholar]
- Mehtatalo, L.; Lappi, J. Biometry for Forestry and Environmental Data: With Examples in R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; ISBN 0429173466. [Google Scholar]
- Weiskittel, A.R.; Li, R. Development of Regional Taper and Volume Equations: Hardwood Species. In Cooperative Forestry Research Unit: 2011 Annual Report; University of Maine: Orono, ME, USA, 2012; Volume i, pp. 76–83. [Google Scholar]
- Yang, Y.; Huang, S.; Meng, S.X. Development of a Tree-Specific Stem Profile Model for White Spruce: A Nonlinear Mixed Model Approach with a Generalized Covariance Structure. Forestry 2009, 82, 541–555. [Google Scholar] [CrossRef]
- Subedi, M.R.; Zhao, D.; Dwivedi, P.; Costanzo, B.E.; Martin, J.A. Site Index Models for Loblolly Pine Forests in the Southern United States Developed with Forest Inventory and Analysis Data. For. Sci. 2023, 69, 597–609. [Google Scholar] [CrossRef]
- Wang, M.; Montes, C.R.; Bullock, B.P.; Zhao, D. An Empirical Examination of Dominant Height Projection Accuracy Using Difference Equation Models. For. Sci. 2020, 66, 267–274. [Google Scholar] [CrossRef]
- dos Santos, M.L.; Miguel, E.P.; Biali, L.J.; de Souza, H.J.; dos Santos, C.R.C.; Matricardi, E.A.T. The Effect of Age on the Evolution of the Stem Profile and Heartwood Proportion of Teak Clonal Trees in the Brazilian Amazon. Forests 2023, 14, 1962. [Google Scholar] [CrossRef]
- Garber, S.M.; Maguire, D.A. Modeling Stem Taper of Three Central Oregon Species Using Nonlinear Mixed Effects Models and Autoregressive Error Structures. For. Ecol. Manag. 2003, 179, 507–522. [Google Scholar] [CrossRef]
- Leites, L.P.; Robinson, A.P. Improving Taper Equations of Loblolly Pine with Crown Dimensions in a Mixed-Effects Modeling Framework. For. Sci. 2004, 50, 204–212. [Google Scholar] [CrossRef]
- Warner, A.J.; Jamroenprucksa, M.; Puangchit, L. Buttressing Impact on Diameter Estimation in Plantation Teak (Tectona grandis L.f.) Sample Trees in Northern Thailand. Agric. Nat. Resour. 2017, 51, 520–525. [Google Scholar] [CrossRef]

| Diameter Class | n | D (cm) | H (m) | ||||
|---|---|---|---|---|---|---|---|
| (cm) | Mean ± sd | Min | Max | Mean ± sd | Min | Max | |
| <25 | 19 | 21.84 ± 2.73 | 14.64 | 24.83 | 17.15 ± 3.01 | 12.22 | 21.25 |
| 25–30 | 25 | 27.71 ± 1.54 | 25.15 | 29.92 | 20.77 ± 2.40 | 14.23 | 25.32 |
| 30–35 | 18 | 32.14 ± 1.06 | 30.24 | 33.74 | 21.4 ± 2.44 | 15.19 | 25.23 |
| 35–40 | 13 | 36.58 ± 1.45 | 35.01 | 39.15 | 22.87 ± 2.04 | 19.24 | 25.31 |
| 40+ | 25 | 43.96 ± 3.86 | 40.11 | 54.11 | 23.58 ± 2.30 | 18.21 | 28.27 |
| Overall | 100 | 33.48 ± 8.23 | 14.64 | 54.11 | 21.43 ± 3.23 | 12.22 | 28.27 |
| Model | Equations | Authors |
|---|---|---|
| M1 | Kozak et al. (1969) [51] | |
| M2 | Bennett and Swindel (1972) [34] | |
| M3 | Cervera (1973) [57] | |
| M4 | Amidon (1984) [58] | |
| M5 | Oderwald and Rayamajhi (1991) [59] | |
| M6 | Ormerod (1973) [60] | |
| M7 | Clutter (1980) [61] | |
| M8 | Sharma and Oderwald (2001) [62] | |
| M9 | Sharma and Zhang (2004) [63] | |
| M10 | where , , | Kozak (2004) [4] |
| M11 | Sharma and Parton (2009) [52] | |
| M12 | Arias-Rodil (2015) [64] | |
| M13 | García (2015) [53] | |
| M14 | where | Max and Burkhart (1976) [14] |
| M15 | Modified Bi (2000) [56] |
| Model | Fit Statistics | Validation Statistics | Total Ranking | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MB | MAB | RMSE | Adj.R2 | Rank | MB | MAB | RMSE | Adj.R2 | Rank | ||
| M1 | 0.275 (8.5) | 2.222 (14.3) | 2.886 (12.8) | 0.908 (12.3) | 48 (12.2) | 0.005 (1.0) | 2.318 (14.1) | 2.979 (13.4) | 0.89 (13.1) | 41.6 (12.0) | 89.6 (12.2) |
| M2 | 0.170 (5.5) | 1.787 (7.7) | 2.371 (7.1) | 0.938 (6.3) | 26.6 (6.4) | −0.208 (5.0) | 1.933 (8.8) | 2.64 (9.8) | 0.913 (9.0) | 32.6 (8.8) | 59.2 (7.5) |
| M3 | −0.198 (6.3) | 1.674 (5.9) | 2.294 (6.3) | 0.942 (5.5) | 24.0 (7.0) | −0.446 (9.8) | 1.66 (5.0) | 2.203 (5.1) | 0.94 (4.3) | 24.2 (7.5) | 48.2 (5.8) |
| M4 | 0.438 (13.2) | 2.268 (15.0) | 3.083 (15.0) | 0.895 (15.0) | 58.2 (10.2) | 0.176 (4.4) | 2.382 (15.0) | 3.124 (15) | 0.879 (15) | 49.4 (7.5) | 107.6 (15) |
| M5 | −0.454 (13.6) | 2.114 (12.6) | 2.84 (12.3) | 0.911 (11.8) | 50.4 (7.1) | −0.707 (15) | 2.14 (11.7) | 2.849 (12.0) | 0.9 (11.3) | 50 (4.2) | 100.4 (13.9) |
| M6 | 0.055 (2.2) | 2.178 (13.6) | 2.939 (13.4) | 0.905 (13.0) | 42.3 (5.4) | −0.211 (5.1) | 2.243 (13.1) | 2.959 (13.2) | 0.892 (12.7) | 44.1 (7.7) | 86.4 (11.7) |
| M7 | 0.133 (4.4) | 1.989 (10.7) | 2.816 (12.1) | 0.913 (11.5) | 38.7 (1.0) | −0.096 (2.8) | 2.021 (10.0) | 2.707 (10.5) | 0.909 (9.7) | 33.1 (1.0) | 71.8 (9.5) |
| M8 | 0.459 (13.8) | 1.700 (6.3) | 2.186 (5.1) | 0.947 (4.3) | 29.5 (6.4) | 0.247 (5.8) | 1.651 (4.9) | 2.116 (4.1) | 0.945 (3.4) | 18.3 (8.8) | 47.8 (5.7) |
| M9 | −0.253 (7.9) | 1.537 (3.8) | 2.170 (4.9) | 0.948 (4.2) | 20.8 (5.7) | −0.489 (10.6) | 1.552 (3.5) | 2.122 (4.2) | 0.944 (3.5) | 21.9 (5.9) | 42.7 (5.0) |
| M10 | −0.013 (1.0) | 1.883 (9.1) | 2.514 (8.7) | 0.930 (7.9) | 26.7 (15.0) | −0.315 (7.2) | 1.933 (8.8) | 2.531 (8.6) | 0.919 (7.9) | 32.5 (14.8) | 59.2 (7.5) |
| M11 | −0.150 (4.9) | 1.833 (8.3) | 2.460 (8.1) | 0.933 (7.2) | 28.6 (12.9) | −0.405 (9.0) | 1.799 (6.9) | 2.376 (6.9) | 0.93 (6.0) | 28.9 (15.0) | 57.5 (7.2) |
| M12 | 0.501 (15.0) | 1.851 (8.6) | 2.538 (9.0) | 0.929 (8.1) | 40.7 (10.7) | 0.286 (6.6) | 1.834 (7.4) | 2.467 (7.9) | 0.925 (7.0) | 28.9 (12.9) | 69.6 (9.1) |
| M13 | 0.460 (13.8) | 1.666 (5.8) | 2.196 (5.2) | 0.947 (4.4) | 29.3 (9.7) | 0.198 (4.8) | 1.677 (5.2) | 2.208 (5.1) | 0.939 (4.4) | 19.6 (9.0) | 48.9 (5.9) |
| M14 | −0.285 (8.8) | 1.573 (4.4) | 2.199 (5.2) | 0.947 (4.5) | 22.9 (7.2) | −0.56 (12.1) | 1.704 (5.6) | 2.306 (6.2) | 0.934 (5.4) | 29.2 (3.8) | 52.1 (6.4) |
| M15 | −0.107 (3.7) | 1.352 (1.0) | 1.815 (1.0) | 0.964 (1.0) | 6.7 (4.8) | −0.326 (7.4) | 1.37 (1.0) | 1.824 (1.0) | 0.958 (1.0) | 10.4 (5.1) | 17.1 (1.0) |
| Model | Mixed Effects Parameter | Fit Statistics | Test Statistics | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MB | MAB | RMSE | Adj.R2 | MB | MAB | RMSE | Adj.R2 | ||
| M15-Fixed | - | −0.1222 | 1.3546 | 1.8144 | 0.9630 | 0.6846 | 1.3782 | 1.9475 | 0.9575 |
| M15-Mixed | β2 | −0.1652 | 1.1587 | 1.5781 | 0.9720 | 0.6888 | 1.3884 | 1.9853 | 0.9558 |
| M9-Fixed | - | −0.2678 | 1.5376 | 2.1624 | 0.9475 | 0.6045 | 1.4331 | 1.9881 | 0.9560 |
| M9-Mixed | β3 | −0.1424 | 1.0878 | 1.5466 | 0.9732 | 0.6165 | 1.4301 | 1.9867 | 0.9561 |
| M8-Fixed | - | 0.3889 | 1.6828 | 2.1686 | 0.9473 | 1.2721 | 1.8352 | 2.3853 | 0.9375 |
| M8-Mixed | β1 | 0.3423 | 1.4934 | 1.9117 | 0.9591 | 1.2027 | 1.7858 | 2.3398 | 0.9399 |
| M3-Fixed | - | −0.2116 | 1.6663 | 2.2784 | 0.9417 | 0.6368 | 1.5802 | 2.1536 | 0.9482 |
| M3-Mixed | β0 | −0.0413 | 1.3606 | 1.8605 | 0.9611 | 0.5492 | 1.6368 | 2.1463 | 0.9485 |
| M13-Fixed | - | 0.4342 | 1.6568 | 2.1767 | 0.9469 | 1.2842 | 1.8774 | 2.3614 | 0.9382 |
| M13-Mixed | β3 | 0.1430 | 1.5932 | 2.1483 | 0.9483 | 0.9780 | 1.7786 | 2.3859 | 0.9369 |
| Model | Mixed Effects Parameter | Fixed Effects Parameters | Variance–Covariance Parameters | Fit Statistics | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β1 | β2 | β3 | β4 | β5 | β6 | σβ | Φ | δ | MB | MAB | RMSE | Adj.R2 | ||
| M15-Fixed | - | 0.8631 (0.1006) | −0.5631 (0.0517) | −0.0740 (0.0100) | −0.2816 (0.0563) | 0.0646 (0.0069) | −0.0322 (0.0126) | −0.1086 | 1.3522 | 1.8291 | 0.9626 | |||
| M15-Mixed | β2 | 0.6199 (0.0711) | −0.3909 (0.036) | −0.0409 (0.0078) | −0.1629 (0.0379) | 0.0613 (0.0028) | −0.0382 (0.0053) | 0.0254 | 0.0004 | −0.1570 | −0.1469 | 1.1409 | 1.5766 | 0.9722 |
| M9-Fixed | - | 0.9565 (0.0047) | 2.1915 (0.0033) | −0.2846 (0.0339) | −0.1497 (0.0442) | - | - | −0.2606 | 1.5315 | 2.1652 | 0.9476 | |||
| M9-Mixed | β3 | 0.9555 (0.0094) | 2.1923 (0.0058) | −0.3080 (0.0362) | −0.1849 (0.0472) | - | - | 0.1815 | 0.6664 | −0.4017 | −0.1304 | 1.0705 | 1.5395 | 0.9735 |
| M8-Fixed | - | 2.1635 (0.0020) | - | - | - | - | - | 0.4684 | 1.6917 | 2.1886 | 0.9465 | |||
| M8-Mixed | β1 | 2.1564 (0.0060) | - | - | - | - | - | 0.0385 | 0.7640 | −0.3765 | 0.3901 | 1.4998 | 1.9373 | 0.9581 |
| M3-Fixed | - | 0.2498 (0.0132) | 0.1496 * (0.1402) | 3.9458 (0.4665) | −7.3717 (0.6006) | 4.0500 (0.2616) | - | −0.2045 | 1.6621 | 2.2818 | 0.9418 | |||
| M3-Mixed | β0 | 0.2276 (0.0096) | 0.2828 (0.1099) | 4.0384 (0.4095) | −8.1436 (0.561) | 4.6339 (0.2525) | - | 0.0424 | 0.7351 | −0.2895 | −0.4000 | 1.3644 | 1.8750 | 0.9607 |
| M13-Fixed | - | 0.6823 (0.1254) | 0.9335 (0.0204) | 1.0981 (0.021) | - | - | - | 0.4130 | 1.6503 | 2.1793 | 0.9469 | |||
| M13-Mixed | β3 | 1.2923 (0.1626) | 1.0132 (0.0346) | 0.7791 (0.0344) | - | - | - | 0.2102 | 0.7870 | −0.3719 | 0.1191 | 1.5654 | 2.1259 | 0.9495 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pokhrel, N.R.; Subedi, M.R.; Malego, B. Fitting and Evaluating Taper Functions to Predict Upper Stem Diameter of Planted Teak (Tectona grandis L.f.) in Eastern and Central Regions of Nepal. Forests 2025, 16, 77. https://doi.org/10.3390/f16010077
Pokhrel NR, Subedi MR, Malego B. Fitting and Evaluating Taper Functions to Predict Upper Stem Diameter of Planted Teak (Tectona grandis L.f.) in Eastern and Central Regions of Nepal. Forests. 2025; 16(1):77. https://doi.org/10.3390/f16010077
Chicago/Turabian StylePokhrel, Nawa Raj, Mukti Ram Subedi, and Bibek Malego. 2025. "Fitting and Evaluating Taper Functions to Predict Upper Stem Diameter of Planted Teak (Tectona grandis L.f.) in Eastern and Central Regions of Nepal" Forests 16, no. 1: 77. https://doi.org/10.3390/f16010077
APA StylePokhrel, N. R., Subedi, M. R., & Malego, B. (2025). Fitting and Evaluating Taper Functions to Predict Upper Stem Diameter of Planted Teak (Tectona grandis L.f.) in Eastern and Central Regions of Nepal. Forests, 16(1), 77. https://doi.org/10.3390/f16010077







