Evaluation of Height Changes in Uneven-Aged Spruce–Fir–Beech Forest with Freely Available Nationwide Lidar and Aerial Photogrammetry Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition and Preparation
2.2.1. Field Measurement of Tree Heights
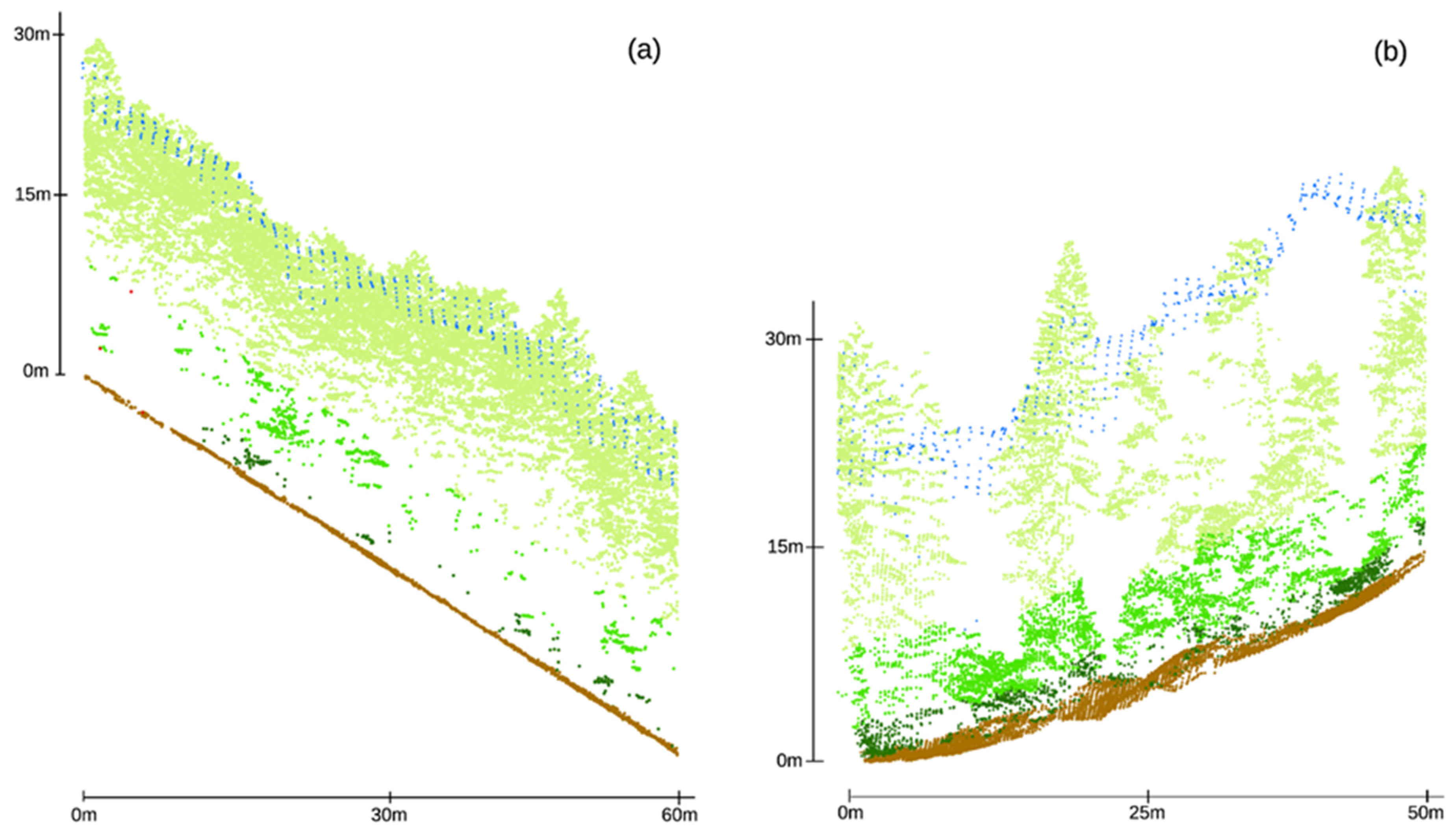
2.2.2. Remote Sensing Data
2.3. Data Analysis
2.3.1. Analysis of Field Measurements
2.3.2. Extraction of Tree Heights from National ALS and DAP Data
2.3.3. Canopy Height Diversity Analysis
2.3.4. Detection and Analysis of Changes in the Dominant Heights of Trees
3. Results
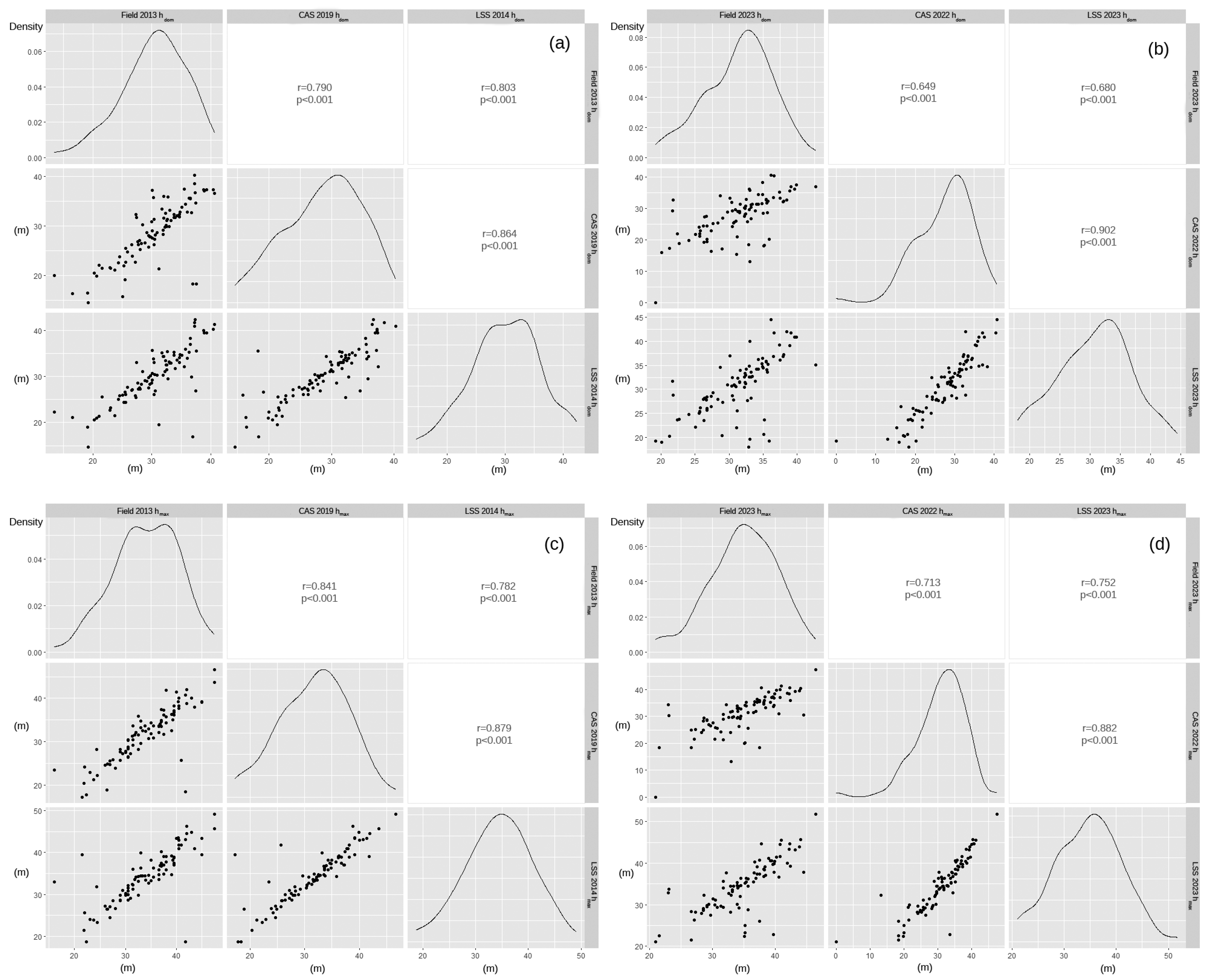
3.1. Analyses of Dominant and Maximum Tree Heights and Canopy Height Diversity Derived from Field Measurements, Lidar Data, and Cyclic Aerial Survey Data
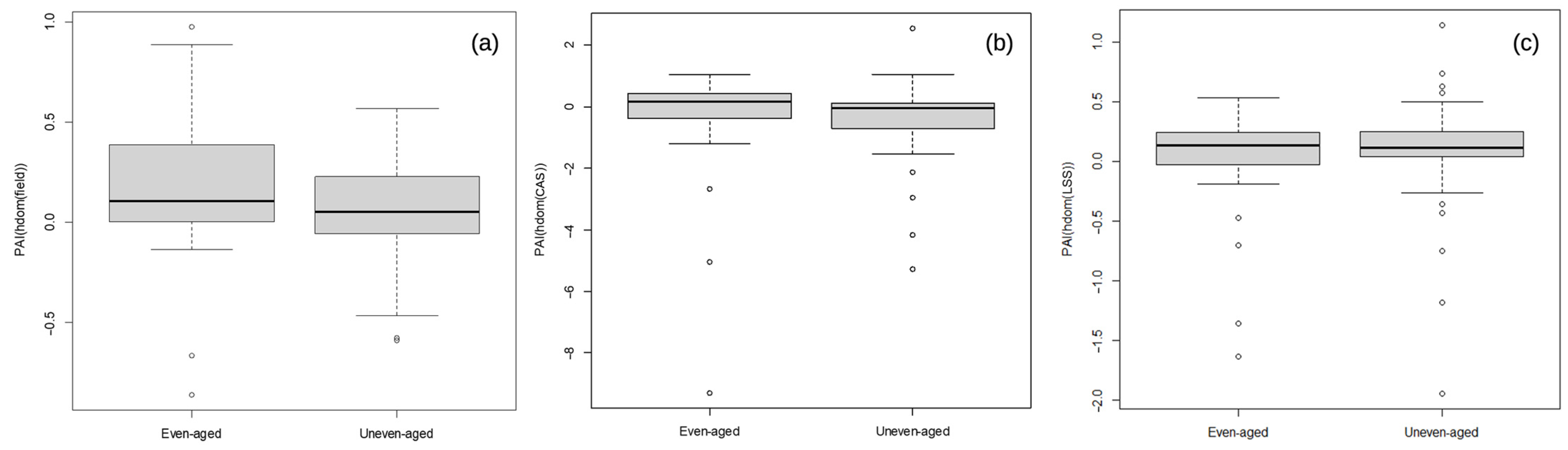
3.2. Periodic Annual Increment Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- St-Onge, B.; Jumelet, J.; Cobello, M.; Véga, C. Measuring individual tree height using a combination of stereophotogrammetry and lidar. Can. J. For. Res. 2004, 34, 2122–2130. [Google Scholar] [CrossRef]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: An example from low density, fire prone ponderosa pine forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
- Rahimizadeh, N.; Sahebi, M.R.; Babaie Kafaky, S.; Mataji, A. Estimation of trees height and vertical structure using SAR interferometry in uneven-aged and mixed forests. Environ. Monit. Assess. 2021, 193, 298. [Google Scholar] [CrossRef]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
- Bončina, A. Primerjava strukture gozdnih sestojev in sestave rastlinskih vrst v pragozdu in gospodarskem gozdu ter presoja uporabnosti izsledkov za gozdarsko načrtovanje. Zb. Gozdarstva Lesar. 2000, 63, 153–181. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. Earth Environ. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Rodríguez-Vivancos, A.; Manzanera, J.A.; Martín-Fernández, S.; García-Cimarras, A.; García-Abril, A. Analysis of structure from motion and airborne laser scanning features for the evaluation of forest structure. Eur. J. For. Res. 2022, 141, 447–465. [Google Scholar] [CrossRef]
- Stepper, C.; Straub, C.; Pretzsch, H. Assessing height changes in a highly structured forest using regularly acquired aerial image data. For. Int. J. For. Res. 2015, 88, 304–316. [Google Scholar] [CrossRef]
- Ganz, S.; Käber, Y.; Adler, P. Measuring Tree Height with Remote Sensing—A Comparison of Photogrammetric and LiDAR Data with Different Field Measurements. Forests 2019, 10, 694. [Google Scholar] [CrossRef]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparison of airborne laser scanning and digital stereo imagery for characterizing forest canopy gaps in coastal temperate rainforests. Remote Sens. Environ. 2018, 208, 1–14. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
- GURS. Daljinsko zaznavanje. 2024. Available online: https://www.e-prostor.gov.si/podrocja/drzavni-topografski-sistem/daljinsko-zaznavanje/ (accessed on 13 November 2024).
- Haala, N. The landscape image matching algorithms. In Proceedings of the 54th Photogrammetric Week, Stuttgart, Germany, 9–13 September 2013; pp. 271–284. [Google Scholar]
- Triglav Čekada, M.; Bric, V. Končan je projekt Laserskega skeniranja Slovenije. Geod. Vestn. 2015, 59, 586–592. [Google Scholar]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Achim, A.; Mulverhill, C. Framework for near real-time forest inventory using multi source remote sensing data. For. Int. J. For. Res. 2022, 96, 1–19. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing biophysical forest characteristics estimated from photogrammetric matching of aerial images and airborne laser scanning data. Scand. J. For. Res. 2015, 30, 73–86. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Digital aerial photogrammetry can efficiently support large-area forest inventories in Norway. For. Int. J. For. Res. 2017, 90, 710–718. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Mager, C.; Waser, L.T.; Kanjir, U.; Schäfer, J.; Buhvald, A.P.; Shafeian, E.; Schiefer, F.; Stančič, L.; Immitzer, M.; et al. Forest practitioners’ requirements for remote sensing-based canopy height, wood-volume, tree species, and disturbance products. For. Int. J. For. Res. 2024, cpae021, 1–20. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Mangold, D.; Schäfer, J.; Immitzer, M.; Kattenborn, T.; Koch, B.; Latifi, H. Estimating stand density, biomass and tree species from very high resolution stereo-imagery–towards an all-in-one sensor for forestry applications? For. Int. J. For. Res. 2017, 90, 613–631. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; White, J.C.; Wulder, M.A.; Næsset, E. Remote sensing in forestry: Current challenges, considerations and directions. For. Int. J. For. Res. 2023, 97, 11–37. [Google Scholar] [CrossRef]
- Pintar, A.M.; Hladnik, D. Strukturna pestrost gozdnih sestojev na Pahernikovi gozdni posesti. Acta Silvae Ligni 2018, 117, 1–16. [Google Scholar] [CrossRef]
- Pintar, A.M.; Skudnik, M. Usefulness of National Airborne Laser Scanning and Aerial Survey Data in Forest Canopy Gap Detection. Geod. Vestn. 2024, 68, 180–193. Available online: https://10.0.59.188/geodetski-vestnik.2024.02.180-193 (accessed on 1 September 2024). [CrossRef]
- Pintar, A.M.; Skudnik, M. Identifying Even- and Uneven-Aged Forest Stands Using Low-Resolution Nationwide Lidar Data. Forests 2024, 15, 1407. [Google Scholar] [CrossRef]
- ForestEurope. State of Europe’s Forests 2015 Report. In Ministerial Conference on the Protection of Forests in Europe; FOREST EUROPE Liaison Unit Madrid: Madrid, Spain, 2015; p. 312. [Google Scholar]
- Kutnar, L.; Kermavnar, J.; Pintar, A.M. Climate change and disturbances will shape future temperate forests in the transition zone between Central and SE Europe. Ann. For. Res. 2021, 64, 67–86. [Google Scholar] [CrossRef]
- Kermavnar, J.; Kutnar, L.; Pintar, A.M. Ecological factors affecting the recent Picea abies decline in Slovenia: The importance of bedrock type and forest naturalness. Iforest-Biogeosciences For. 2023, 16, 105–115. [Google Scholar] [CrossRef]
- Leiter, M.; Pucher, C.; Kessler, M.; Hönigsberger, F.; Lexer, M.J.; Vacik, H.; Hasenauer, H. Identifying suitable areas for plenter forest management. For. Ecosyst. 2024, 100267. [Google Scholar] [CrossRef]
- West, P.W. Tree and Forest Measurement, 3rd ed.; Springer: Cham, Switzerland, 2015; pp. XII, 214. [Google Scholar] [CrossRef]
- Tarmu, T.; Laarmann, D.; Kiviste, A. Mean height or dominant height–what to prefer for modelling the site index of Estonian forests? For. Stud. 2020, 72, 121–138. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012; pp. XIV, 458. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.M.; Mund, J.-P.; Greve, K. UAV-Based Photogrammetric Tree Height Measurement for Intensive Forest Monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Gyawali, A.; Aalto, M.; Peuhkurinen, J.; Villikka, M.; Ranta, T. Comparison of Individual Tree Height Estimated from LiDAR and Digital Aerial Photogrammetry in Young Forests. Sustainability 2022, 14, 3720. [Google Scholar] [CrossRef]
- SFS. Posestni načrt za Gozdove Pahernikove Ustanove 2014–2023; Slovenia Forest Service: Slovenj Gradec, Slovenia, 2015; p. 90. [Google Scholar]
- Sušek, M. Pahernikovi Gozdovi: Biografija Rodbine Pahernik; Pahernikov sklad: Radlje, Slovenia, 2005; p. 83. [Google Scholar]
- SFS. Permanent Sample Plots Data; Slovenia Forest Service: Slovenj Gradec, Slovenia, 2023. [Google Scholar]
- Pintar, A.; Ferreira, A.; Krajnc, L.; Kušar, G.; Skudnik, M. Pestrost in pojavljanje domačih in tujerodnih drevesnih in grmovnih vrst na ploskvah Nacionalne gozdne inventure v Sloveniji. Acta Silvae Ligni 2024, 134, 11–26. [Google Scholar] [CrossRef]
- SFS. Slovenia Forest Service. 2024. Available online: http://www.zgs.si/eng/homepage/index.html (accessed on 10 July 2024).
- GURS. Data from the Laser Scanning of Slovenia 2014 Project; MNRSP—Surveying and Mapping Authority of the Republic of Slovenia: Ljubljana, Slovenia, 2015. [Google Scholar]
- GURS. Data from the Cyclic Laser Scanning of Slovenia 2023 Project; MNRSP—Surveying and Mapping Authority of the Republic of Slovenia: Ljubljana, Slovenia, 2024. [Google Scholar]
- GURS. Data from the Cyclic Aerial Survey of Slovenia 2019 Project; MNRSP—Surveying and Mapping Authority of the Republic of Slovenia: Ljubljana, Slovenia, 2019. [Google Scholar]
- GURS. Data from the Cyclic Aerial Survey of Slovenia 2022 Project; MNRSP—Surveying and Mapping Authority of the Republic of Slovenia: Ljubljana, Slovenia, 2022. [Google Scholar]
- Pegan Žvokelj, B.; Bric, V.; Triglav Čekada, M.; Obreza, A.; Tršan, S.; Dejak, B.; Karničnik, I. Izvedba Lasreskega Skeniranja Slovenije: Blok 23: Tehnično Poročilo o Izdelavi Izdelkov; Geodetski inštitut Slovenije: Ljubljana, Slovenia, 2015; p. 19. [Google Scholar]
- FT. CLSS 2023—Velenje—Tehnično Poročilo ZLS; Flycom Techologies: Ljubljana, Slovenia, 2023. [Google Scholar]
- Kobler, A. Canopy height model derived from the Laser Scanning of Slovenia; Slovenian Forestry Institute: Ljubljana, Slovenia, 2015. [Google Scholar]
- GCV. Tehnično Poročilo—Digitalni Model Višin OAF 12 Velenje; Geodetski zavod Celje: Celje, Slovenia, 2022. [Google Scholar]
- Šprah, R. Ocenjevanje ekotipov v gozdnogospodarski enoti Lovrenc na Pohorju. Biotehniška fakulteta, Oddelek za gozdarstvo in obnovljive gozdne vire: Ljubljana, Slovenia, 2019. [Google Scholar]
- Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; van Con, T.; Chavanne, A.; Seifert, T.; et al. Crown size and growing space requirement of common tree species in urban centres, parks, and forests. Urban For. Urban Green. 2015, 14, 466–479. [Google Scholar] [CrossRef]
- ESRI. ArcMap 10.8; ESRI: Redlands, CA, USA, 2018. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: http://www.R-project.org (accessed on 23 September 2024).
- Fradette, M.-S.; Leboeuf, A.; Riopel, M.; Bégin, J. Method to Reduce the Bias on Digital Terrain Model and Canopy Height Model from LiDAR Data. Remote Sens. 2019, 11, 863. [Google Scholar] [CrossRef]
- Ginzler, C.; Hobi, M.L. Countrywide Stereo-Image Matching for Updating Digital Surface Models in the Framework of the Swiss National Forest Inventory. Remote Sens. 2015, 7, 4343–4370. [Google Scholar] [CrossRef]
- Sibona, E.; Vitali, A.; Meloni, F.; Caffo, L.; Dotta, A.; Lingua, E.; Motta, R.; Garbarino, M. Direct Measurement of Tree Height Provides Different Results on the Assessment of LiDAR Accuracy. Forests 2017, 8, 7. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Hladnik, D.; Kobler, A.; Pirnat, J. Evaluation of Forest Edge Structure and Stability in Peri-Urban Forests. Forests 2020, 11, 338. [Google Scholar] [CrossRef]
- Pearse, G.D.; Watt, M.S.; Dash, J.P.; Stone, C.; Caccamo, G. Comparison of models describing forest inventory attributes using standard and voxel-based lidar predictors across a range of pulse densities. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 341–351. [Google Scholar] [CrossRef]
- Jacon, A.D.; Galvão, L.S.; Martins-Neto, R.P.; Crespo-Peremarch, P.; Aragão, L.E.O.C.; Ometto, J.P.; Anderson, L.O.; Vedovato, L.B.; Silva-Junior, C.H.L.; Lopes, A.P.; et al. Characterizing Canopy Structure Variability in Amazonian Secondary Successions with Full-Waveform Airborne LiDAR. Remote Sens. 2024, 16, 2085. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Q.; Wu, X.; Hu, T.; Liu, Z.; Liu, L.; Guo, Q.; Su, Y. A novel entropy-based method to quantify forest canopy structural complexity from multiplatform lidar point clouds. Remote Sens. Environ. 2022, 282, 113280. [Google Scholar] [CrossRef]
- Ming, L.; Liu, J.; Quan, Y.; Li, M.; Wang, B.; Wei, G. Mapping tree species diversity in a typical natural secondary forest by combining multispectral and LiDAR data. Ecol. Indic. 2024, 159, 111711. [Google Scholar] [CrossRef]
- Senf, C.; Mori, A.S.; Müller, J.; Seidl, R. The response of canopy height diversity to natural disturbances in two temperate forest landscapes. Landsc. Ecol. 2020, 35, 2101–2112. [Google Scholar] [CrossRef]
- Bakx, T.R.M.; Koma, Z.; Seijmonsbergen, A.C.; Kissling, W.D. Use and categorization of Light Detection and Ranging vegetation metrics in avian diversity and species distribution research. Divers. Distrib. 2019, 25, 1045–1059. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Ramage, B.S. Silviculture in an uncertain world: Utilizing multi-aged management systems to integrate disturbance. For. Int. J. For. Res. 2013, 86, 401–410. [Google Scholar] [CrossRef]


| hdom (m) | SD1 (m) | Statistical Test and p Value (hdom) | hmax (m) | SD2 (m) | Statistical Test and p Value (hmax) | ||
|---|---|---|---|---|---|---|---|
| Field 2013 | Even-aged | 28.7 | 6.3 | Two-Sample t-test | 31.6 | 6.7 | Two-Sample t-test |
| Uneven-aged | 31.6 | 4.6 | p < 0.05 | 35.8 | 5.6 | p < 0.01 | |
| LSS 2014 | Even-aged | 28.6 | 6.0 | Two-Sample t-test | 32.5 | 5.7 | Two-Sample t-test |
| Uneven-aged | 31.4 | 5.5 | p < 0.05 | 35.8 | 6.4 | p < 0.05 | |
| CAS 2019 | Even-aged | 27.0 | 6.0 | Two-Sample t-test | 29.8 | 5.7 | Two-Sample t-test |
| Uneven-aged | 29.9 | 5.8 | p < 0.05 | 33.1 | 6.4 | p < 0.05 | |
| Field 2023 | Even-aged | 30.2 | 5.3 | Two-Sample t-test | 33.0 | 5.1 | Two-Sample t-test |
| Uneven-aged | 32.2 | 4.5 | p < 0.05 | 36.3 | 5.2 | p < 0.01 | |
| LSS 2023 | Even-aged | 29.0 | 5.4 | Two-Sample t-test | 32.8 | 5.4 | Two-Sample t-test |
| Uneven-aged | 32.0 | 6.2 | p < 0.05 | 35.9 | 6.5 | p < 0.05 | |
| CAS 2022 | Even-aged | 26.1 | 6.3 | Wilcoxon rank sum test | 28.9 | 6.2 | Wilcoxon rank sum test |
| Uneven-aged | 28.8 | 7.3 | p < 0.05 | 32.4 | 7.5 | p < 0.01 |
| Mean | SD | Statistical Test and p Value | ||
|---|---|---|---|---|
| LSS 2014 | Even-aged CHD | 1.46 | 0.23 | Two-Sample t-test |
| Uneven-aged CHD | 1.66 | 0.26 | p < 0.001 | |
| CAS 2019 | Even-aged CHD | 1.16 | 0.32 | Two-Sample t-test |
| Uneven-aged CHD | 1.30 | 0.31 | p < 0.05 | |
| LSS 2023 | Even-aged CHD | 1.47 | 0.24 | Wilcoxon rank sum test |
| Uneven-aged CHD | 1.64 | 0.25 | p < 0.01 | |
| CAS 2022 | Even-aged CHD | 1.20 | 0.28 | Wilcoxon rank sum test |
| Uneven-aged CHD | 1.38 | 0.36 | p < 0.01 |
| PAI | Mean (m/year) | Median (m/year) | Min (m/year) | Max (m/year) | SD (m/year) | Statistical Test and p Value |
|---|---|---|---|---|---|---|
| Even-aged PAI(hdom(field)) | 0.16 | 0.11 | −0.86 | 0.98 | 0.34 | Wilcoxon rank sum test |
| Uneven-aged PAI(hdom(field)) | 0.06 | 0.05 | −0.59 | 0.57 | 0.23 | p > 0.05 |
| Even-aged PAI(hdom(LSS)) | 0.04 | 0.14 | −1.64 | 0.53 | 0.45 | Wilcoxon rank sum test |
| Uneven-aged PAI(hdom(LSS)) | 0.08 | 0.11 | −1.95 | 1.15 | 0.45 | p > 0.05 |
| Even-aged PAI(hdom(CAS)) | −0.42 | 0.17 | −9.32 | 1.05 | 1.84 | Wilcoxon rank sum test |
| Uneven-aged PAI(hdom(CAS)) | −0.42 | −0.04 | −5.27 | 2.56 | 1.22 | p > 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pintar, A.M.; Skudnik, M. Evaluation of Height Changes in Uneven-Aged Spruce–Fir–Beech Forest with Freely Available Nationwide Lidar and Aerial Photogrammetry Data. Forests 2025, 16, 35. https://doi.org/10.3390/f16010035
Pintar AM, Skudnik M. Evaluation of Height Changes in Uneven-Aged Spruce–Fir–Beech Forest with Freely Available Nationwide Lidar and Aerial Photogrammetry Data. Forests. 2025; 16(1):35. https://doi.org/10.3390/f16010035
Chicago/Turabian StylePintar, Anže Martin, and Mitja Skudnik. 2025. "Evaluation of Height Changes in Uneven-Aged Spruce–Fir–Beech Forest with Freely Available Nationwide Lidar and Aerial Photogrammetry Data" Forests 16, no. 1: 35. https://doi.org/10.3390/f16010035
APA StylePintar, A. M., & Skudnik, M. (2025). Evaluation of Height Changes in Uneven-Aged Spruce–Fir–Beech Forest with Freely Available Nationwide Lidar and Aerial Photogrammetry Data. Forests, 16(1), 35. https://doi.org/10.3390/f16010035







