Incorporating Spatial Autocorrelation into GPP Estimation Using Eigenvector Spatial Filtering
Abstract
1. Introduction
2. Data and Preprocessing
2.1. Eddy Covariance Flux Tower Data
2.2. Remote Sensing Data
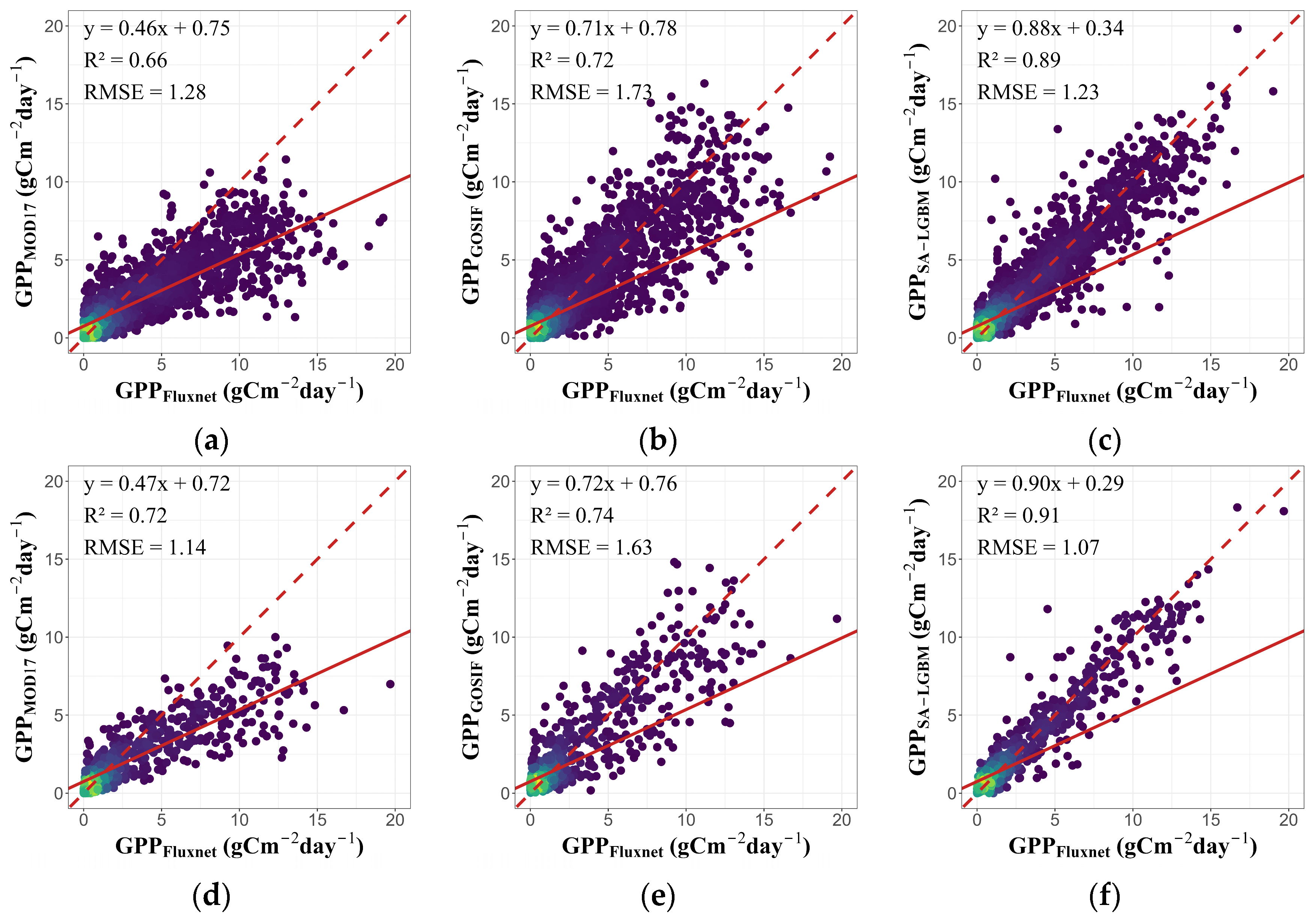
2.3. Comparative Analysis of GPP Products
3. Methodology
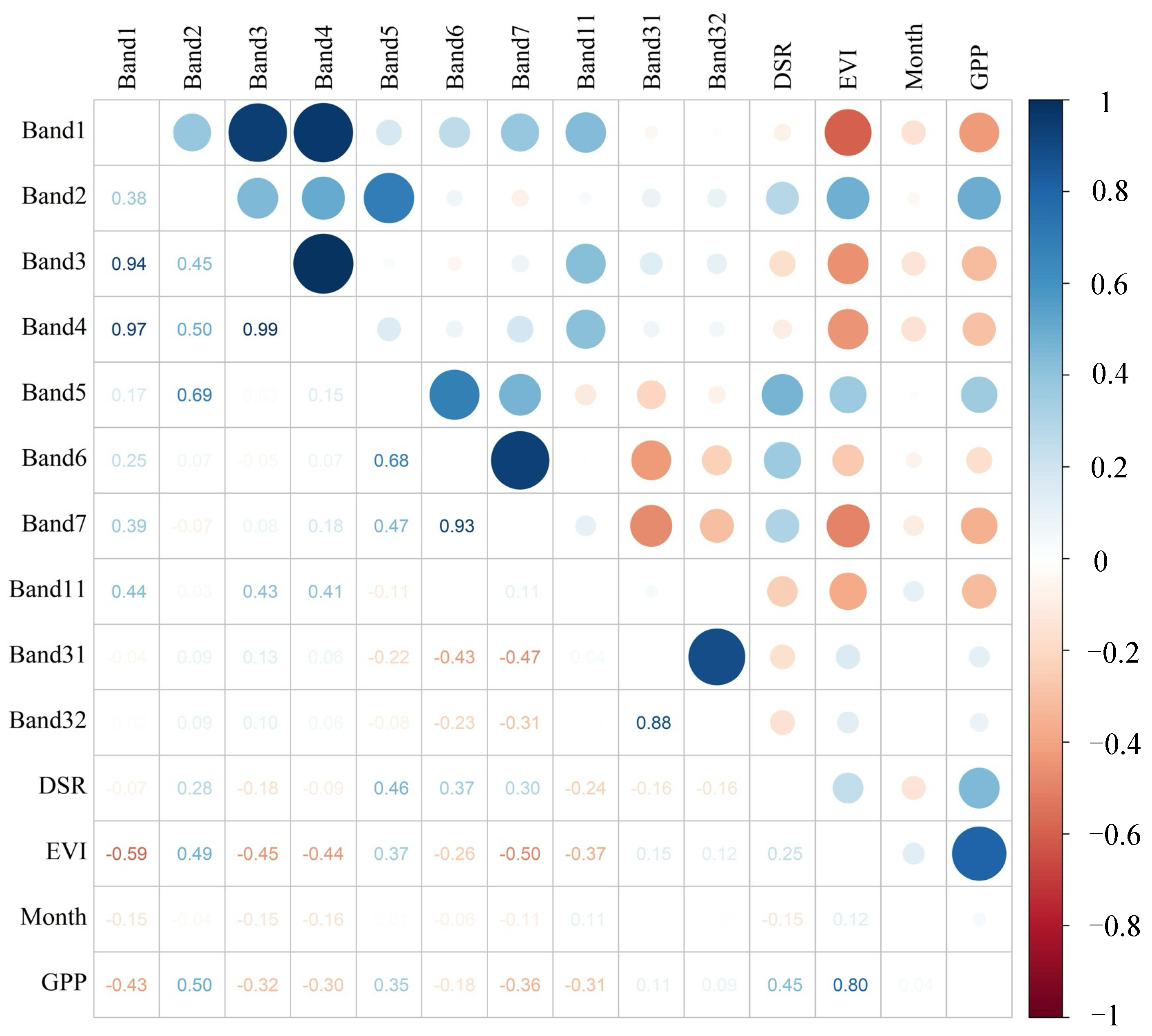
3.1. Variables Selection for GPP Estimation Model
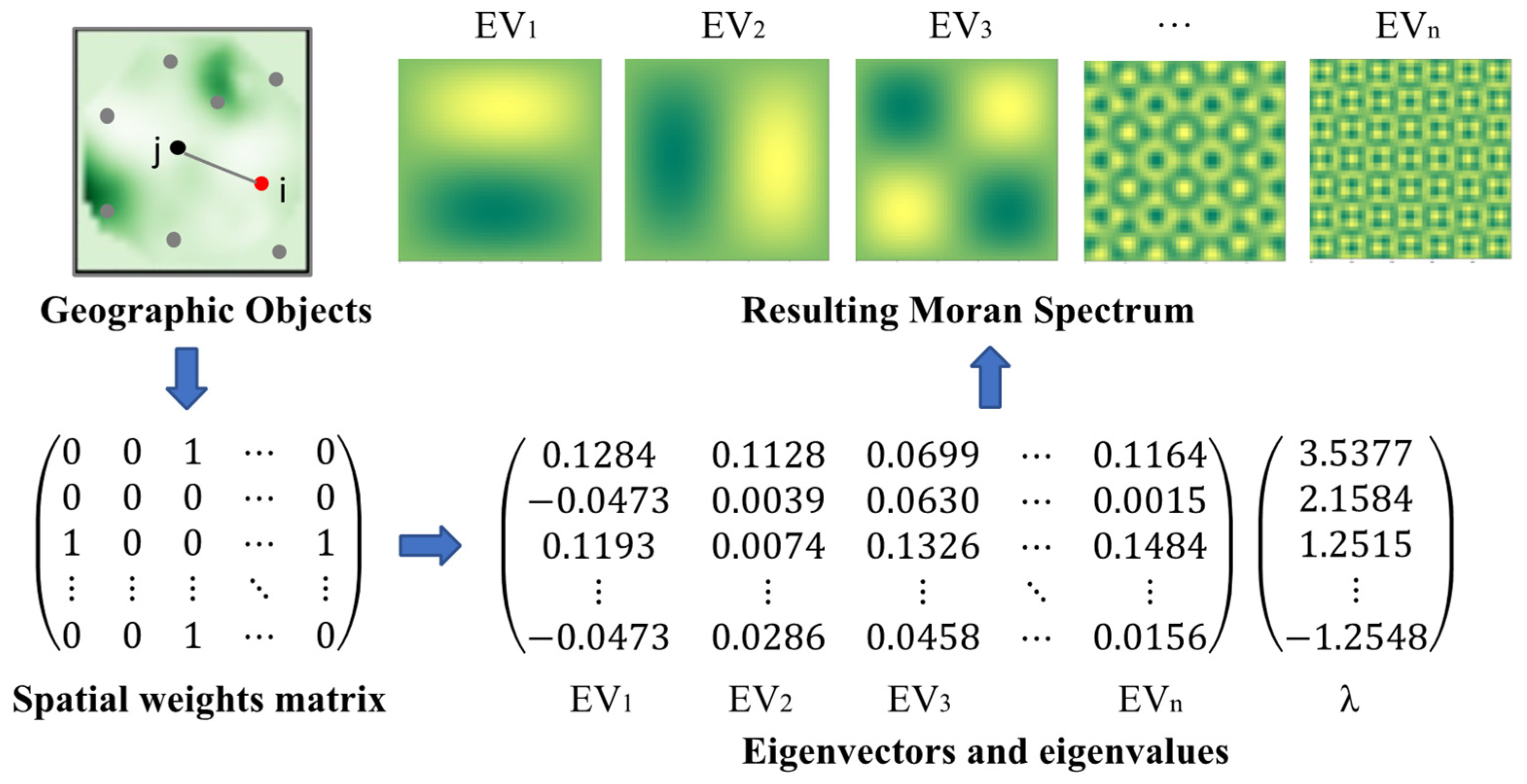
3.2. Extraction of Spatial Factors at American Flux Sites
- (1)
- Building the spatial weights matrix: The initial phase entails constructing the spatial weights matrix by leveraging the spatial connections inherent in the American flux site data. This matrix is created using the Spatial Covariance Function for the coordinates of the monitoring sites. The Gaussian model assumes that the weights decay with distance in the form of a Gaussian distribution. Equation (3) represents the Gaussian model:where and denote location points and , respectively; denotes the neighborhood weight between location points and ; and denotes the furthest distance in the smallest spanning tree across all locations.
- (2)
- Centralizing the spatial weights matrix: The spatial weights matrix is centralized employing the subsequent approach:where is an n-dimensional unit matrix, is an n × n matrix with all elements within the matrix equal to 1, and is the number of flux sites.
- (3)
- Extraction of eigenvalues and eigenvectors: We perform eigen decomposition on the centralized matrix, yielding eigenvalues and eigenvectors, while ensuring they satisfy the conditions of Equation (5):where Det represents the matrix determinant operator, λ is the eigenvalue, and I is the identity matrix. Each eigenvector obtained through this process represents a specific spatial pattern. The relationship between the spatial weights matrix and its corresponding eigenvalues and eigenvectors is illustrated in Figure 3.
- (4)
- Eigenvector screening: An initial screening of eigenvectors is carried out using a threshold of 0.25. must meet the following criteria with respect to their corresponding eigenvalues : 1. > 0; 2. The ratio of the eigenvalue to the maximum eigenvalue in the set should exceed 0.25. The screened eigenvectors can reflect varying degrees of spatial clustering, with larger eigenvalues indicating stronger clustering, which are subsequently integrated with the model as independent variables.
3.3. Construction of the GPP Estimation Model
3.4. Accuracy Assessment
3.4.1. Model Evaluation Indicators
3.4.2. Accuracy Comparison
3.4.3. Assessment of the Spatial Effects
4. Results
4.1. Variable Selection for GPP Estimation Model
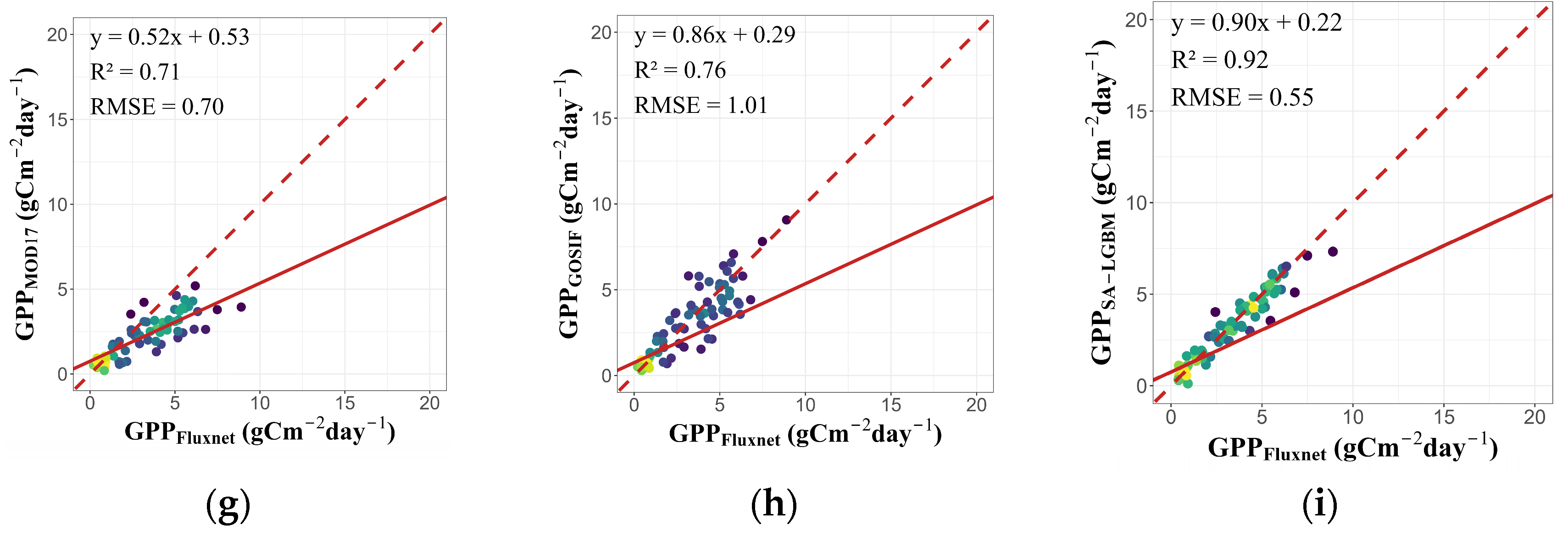
4.2. Model Fitting and Validation
4.3. Assessment of GPP at Different Temporal Scales
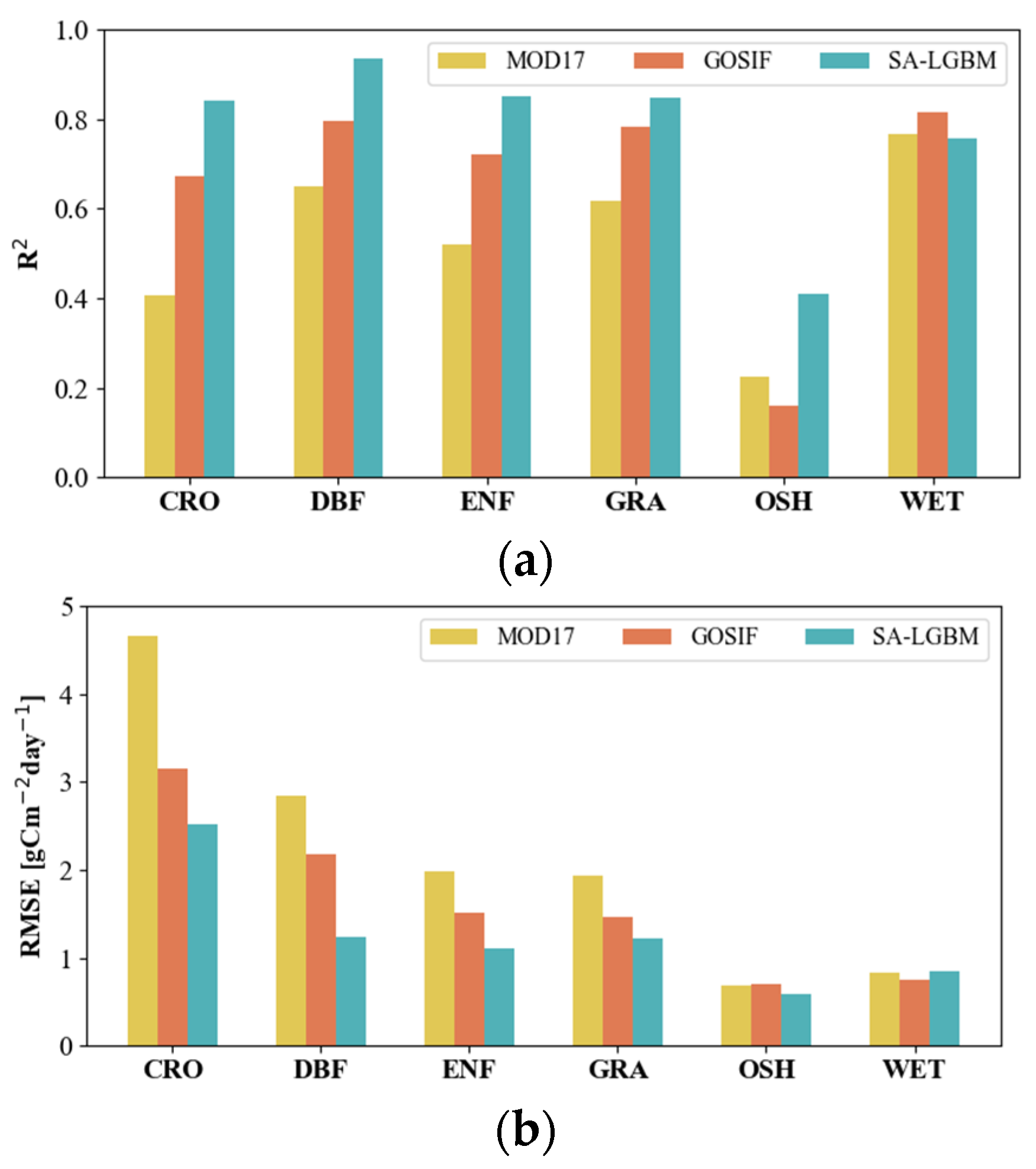
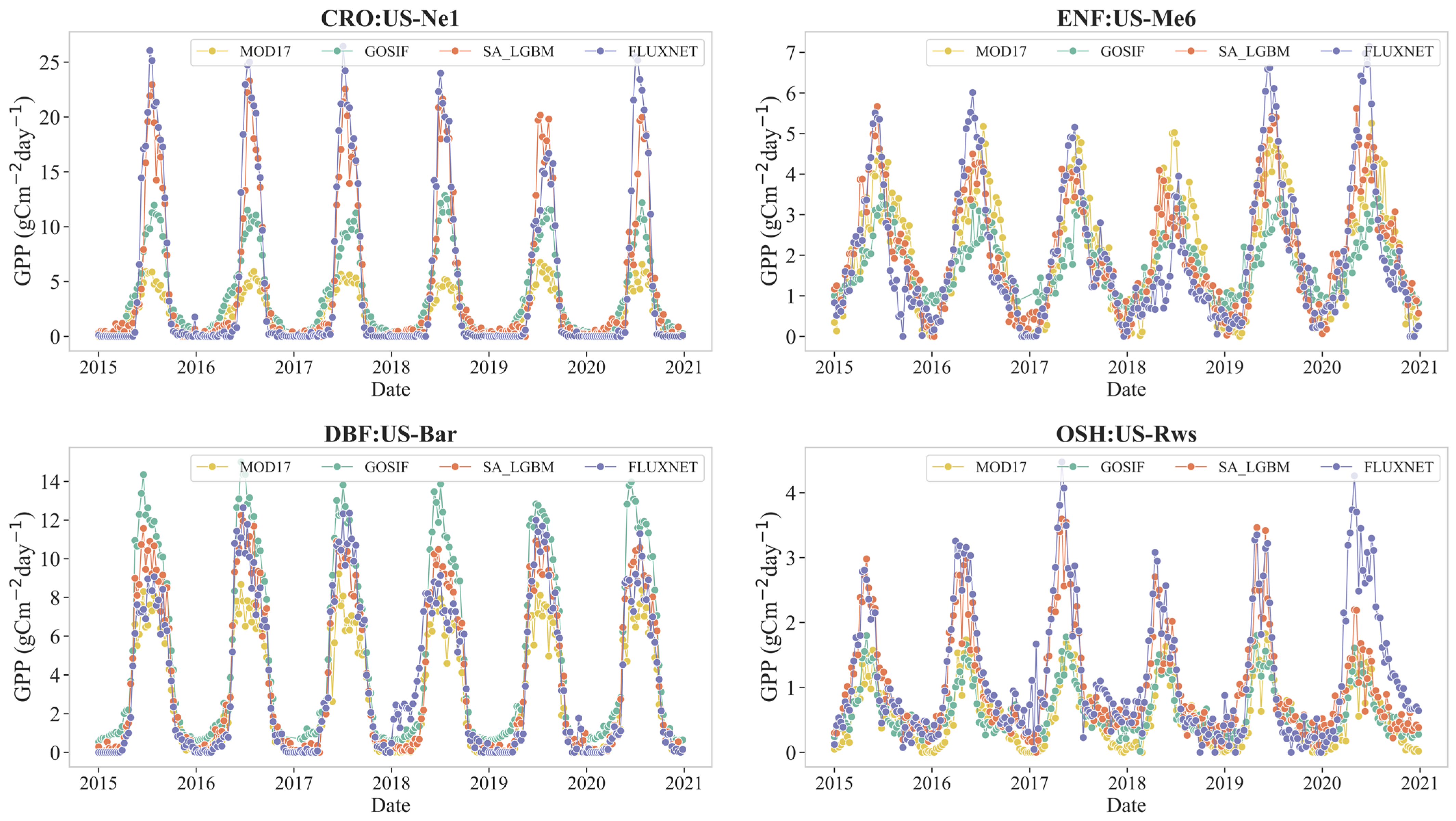
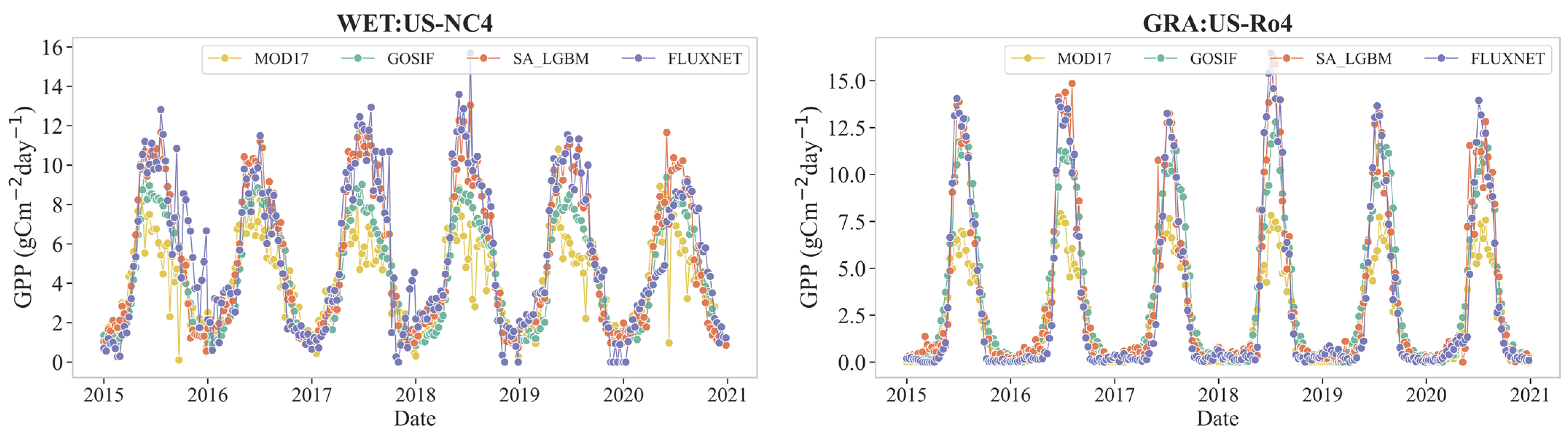
4.4. Assessment of GPP in Different Vegetation Types
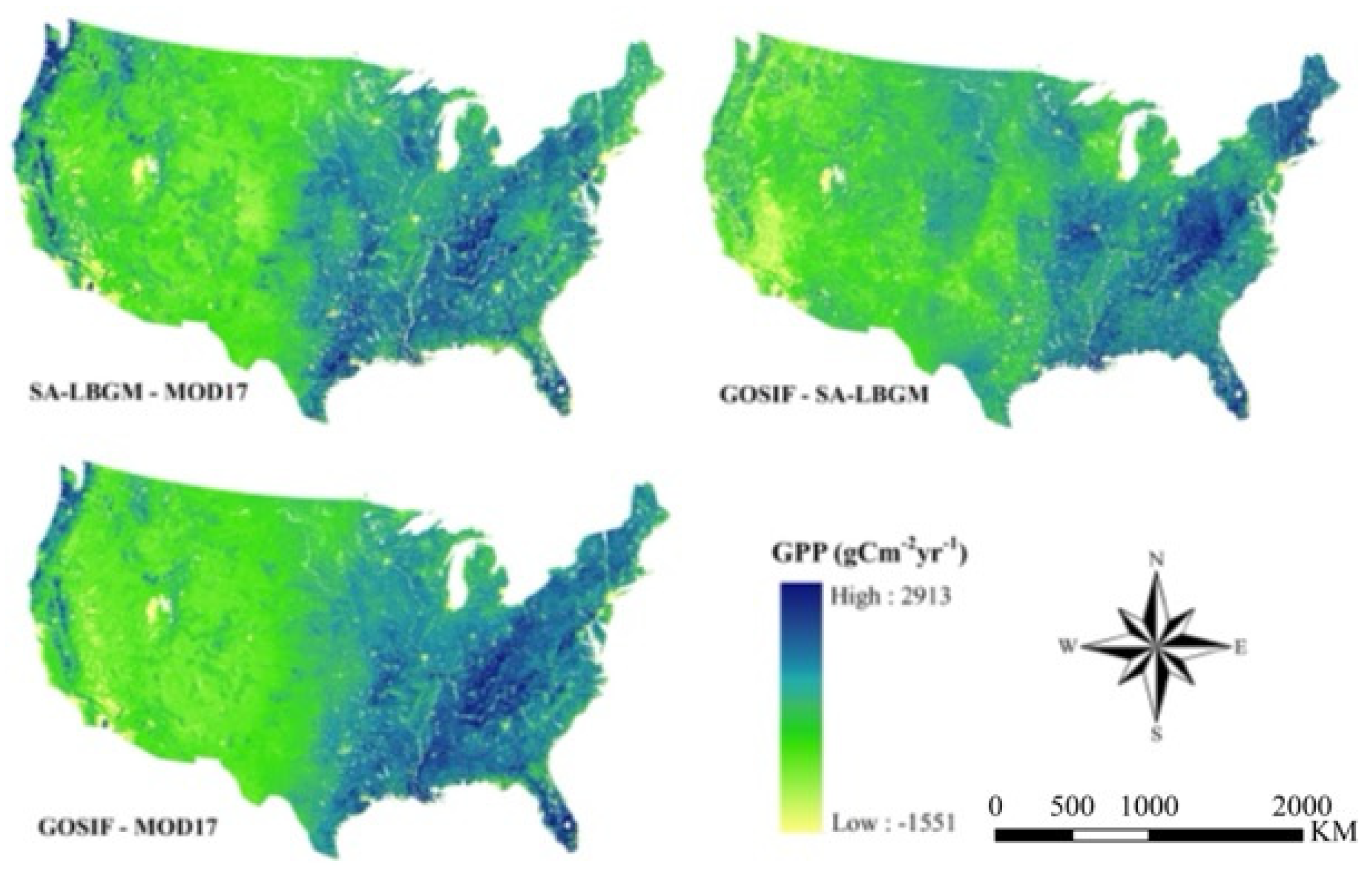
4.5. Mapping and Comparison of GPP Estimation Results
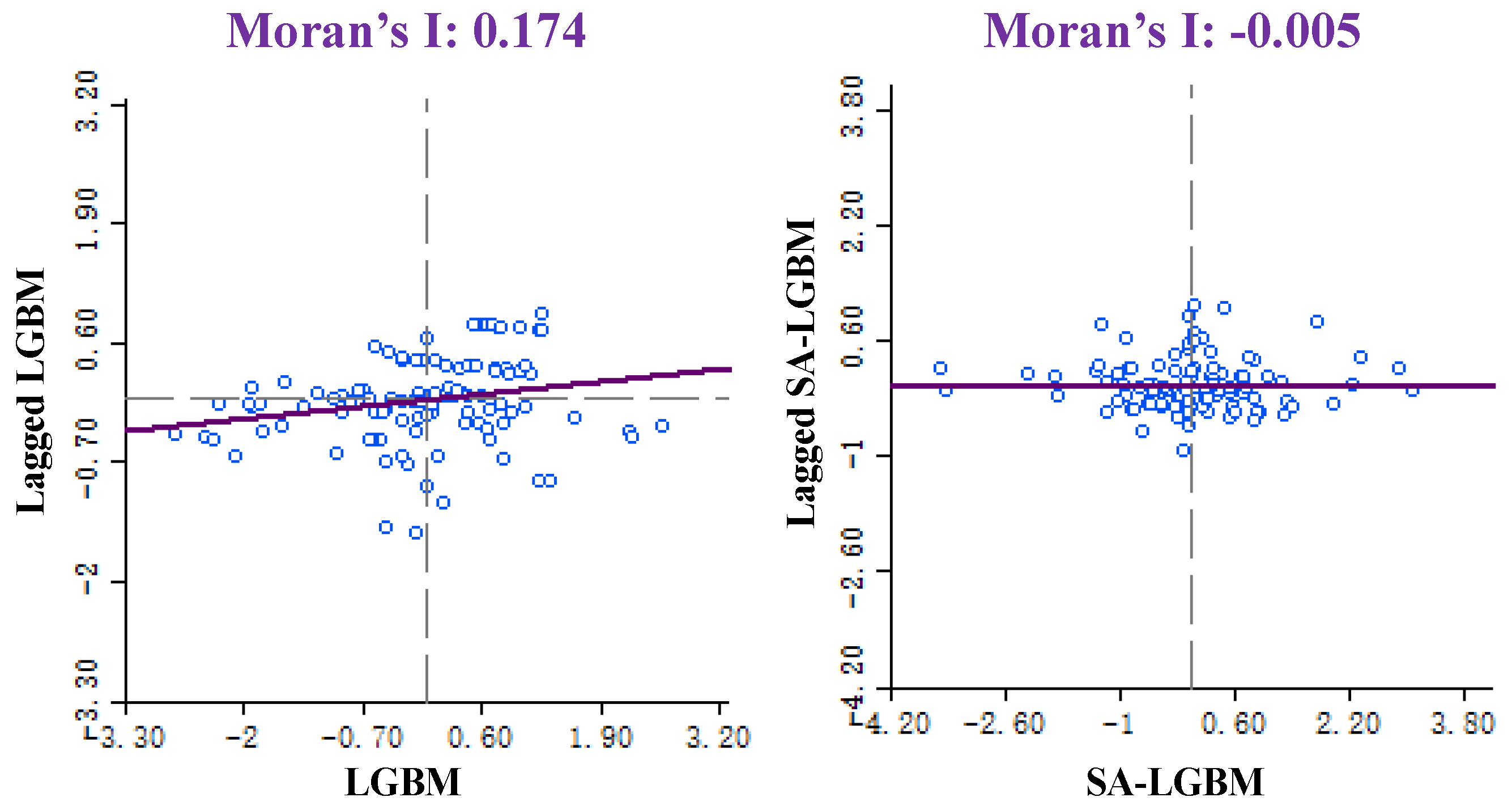
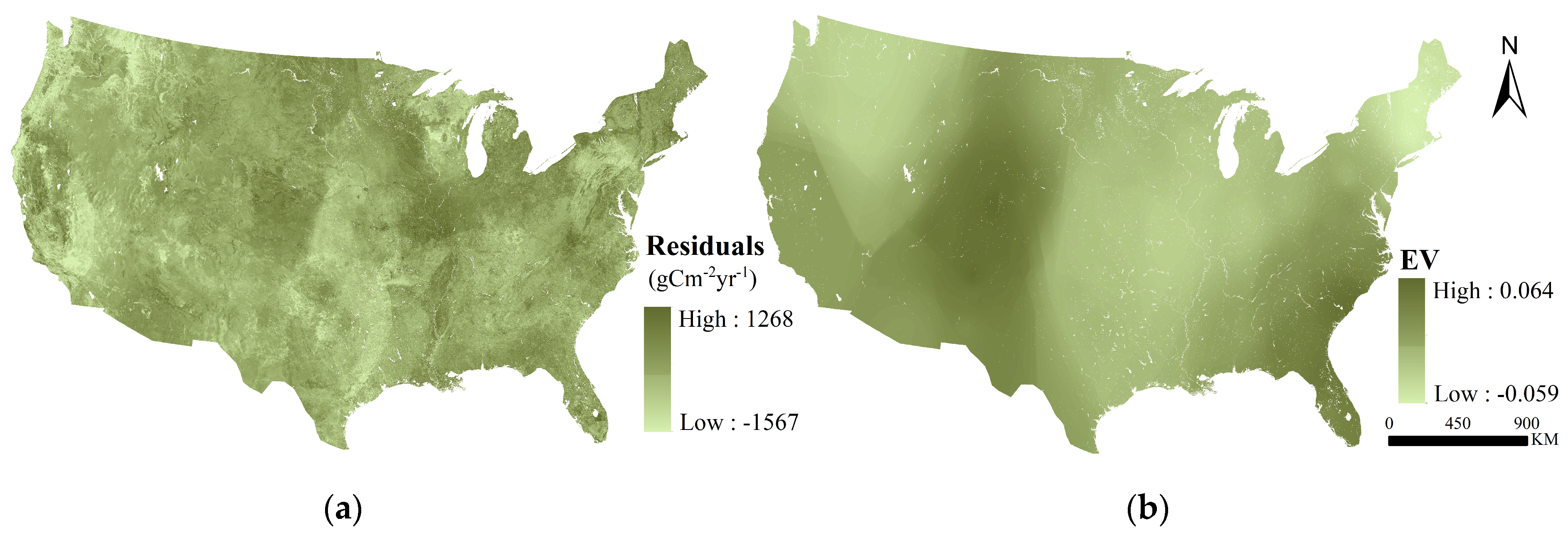
4.6. Impact Assessment of Spatial Effects
5. Discussion
5.1. Advantages of SA-LGBM
5.2. Ability of the Three GPP Products to Capture GPP Variations
5.3. Limitations and Future Enhancement
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Chen, J.M.; Chen, J.; Gough, C.M.; Martin, T.A.; Dragoni, D. Evaluating Spatial and Temporal Patterns of MODIS GPP over the Conterminous U.S. against Flux Measurements and a Process Model. Remote Sens. Environ. 2012, 124, 717–729. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Hauck, J.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; Le Quéré, C.; et al. Global Carbon Budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- Dunkl, I.; Lovenduski, N.; Collalti, A.; Arora, V.K.; Ilyina, T.; Brovkin, V. Gross Primary Productivity and the Predictability of CO2: More Uncertainty in What We Predict than How Well We Predict It. Biogeosciences 2023, 20, 3523–3538. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Ju, W.; Zhou, Y.; Cheng, X. Improved Estimation of Global Gross Primary Productivity during 1981–2020 Using the Optimized P Model. Sci. Total Environ. 2022, 838, 156172. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Zhou, B.; Zhu, J.; Jia, H.; Fei, X. A Critical Review of Methods, Principles and Progress for Estimating the Gross Primary Productivity of Terrestrial Ecosystems. Front. Environ. Sci. 2023, 11, 464. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Z.; Wang, J.; Gao, X.; Yang, C.; Yang, F.; Wu, G. Temporal Upscaling of MODIS Instantaneous FAPAR Improves Forest Gross Primary Productivity (GPP) Simulation. Int. J. Appl. Earth Obs. Geoinf. 2023, 121, 103360. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, X.; Zhang, X.; Tani, H.; Guo, E.; Yin, S.; Zhang, T. Evaluating and Comparing Remote Sensing Terrestrial GPP Models for Their Response to Climate Variability and CO2 Trends. Sci. Total Environ. 2019, 668, 696–713. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Cai, W.; Liu, D.; Dong, W. Satellite-Based Vegetation Production Models of Terrestrial Ecosystem: An Overview. Adv. Earth Sci. 2014, 29, 541. [Google Scholar] [CrossRef]
- Wen, J.; Köhler, P.; Duveiller, G.; Parazoo, N.C.; Magney, T.S.; Hooker, G.; Yu, L.; Chang, C.Y.; Sun, Y. A Framework for Harmonizing Multiple Satellite Instruments to Generate a Long-Term Global High Spatial-Resolution Solar-Induced Chlorophyll Fluorescence (SIF). Remote Sens. Environ. 2020, 239, 111644. [Google Scholar] [CrossRef]
- Running, S.W.; Hunt, E.R. 8—Generalization of a Forest Ecosystem Process Model for Other Biomes, BIOME-BGC, and an Application for Global-Scale Models. In Scaling Physiological Processes; Ehleringer, J.R., Field, C.B., Eds.; Physiological Ecology; Academic Press: San Diego, CA, USA, 1993; pp. 141–158. ISBN 978-0-12-233440-5. [Google Scholar]
- Running, S.W.; Coughlan, J.C. A General Model of Forest Ecosystem Processes for Regional Applications I. Hydrologic Balance, Canopy Gas Exchange and Primary Production Processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Lieth, H. Modeling the Primary Productivity of the World. In Primary Productivity of the Biosphere; Lieth, H., Whittaker, R.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1975; pp. 237–263. ISBN 978-3-642-80913-2. [Google Scholar]
- Lieth, H.; Whittaker, R.H. Primary Productivity of the Biosphere; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 14, ISBN 3-642-80913-8. [Google Scholar]
- Chen, Y.; Gu, H.; Wang, M.; Gu, Q.; Ding, Z.; Ma, M.; Liu, R.; Tang, X. Contrasting Performance of the Remotely-Derived GPP Products over Different Climate Zones across China. Remote Sens. 2019, 11, 1855. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global Net Primary Production: Combining Ecology and Remote Sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Lv, Y.; Chi, H.; Shi, P.; Huang, D.; Gan, J.; Li, Y.; Gao, X.; Han, Y.; Chang, C.; Wan, J.; et al. Phenology-Based Maximum Light Use Efficiency for Modeling Gross Primary Production across Typical Terrestrial Ecosystems. Remote Sens. 2023, 15, 4002. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Mooney, H.A., Howarth, R.W., Eds.; Springer: New York, NY, USA, 2000; pp. 44–57. ISBN 978-1-4612-1224-9. [Google Scholar]
- Xu, H.; Zhang, Z.; Wu, X.; Wan, J. Light Use Efficiency Models Incorporating Diffuse Radiation Impacts for Simulating Terrestrial Ecosystem Gross Primary Productivity: A Global Comparison. Agric. For. Meteorol. 2023, 332, 109376. [Google Scholar] [CrossRef]
- Zhang, Z.; Xin, Q.; Li, W. Machine Learning-Based Modeling of Vegetation Leaf Area Index and Gross Primary Productivity Across North America and Comparison with a Process-Based Model. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002802. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, Q.; Sun, R. Comparison of Machine Learning Methods to Up-Scale Gross Primary Production. Remote Sens. 2021, 13, 2448. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y. Satellite-Based Reflectances Capture Large Fraction of Variability in Global Gross Primary Production (GPP) at Weekly Time Scales. Agric. For. Meteorol. 2020, 291, 108092. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep Learning and Process Understanding for Data-Driven Earth System Science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Griffith, D.A. Important Considerations about Space-Time Data: Modeling, Scrutiny, and Ratification. Trans. GIS 2021, 25, 291–310. [Google Scholar] [CrossRef]
- Griffith, D.; Chun, Y.; Li, B. Spatial Regression Analysis Using Eigenvector Spatial Filtering; Academic Press: Cambridge, MA, USA, 2019; ISBN 978-0-12-815692-6. [Google Scholar]
- Islam, M.D.; Li, B.; Lee, C.; Wang, X. Incorporating Spatial Information in Machine Learning: The Moran Eigenvector Spatial Filter Approach. Trans. GIS 2022, 26, 902–922. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Murakami, D.; Griffith, D.A. Random Effects Specifications in Eigenvector Spatial Filtering: A Simulation Study. J. Geogr. Syst. 2015, 17, 311–331. [Google Scholar] [CrossRef]
- Liu, X.; Kounadi, O.; Zurita-Milla, R. Incorporating Spatial Autocorrelation in Machine Learning Models Using Spatial Lag and Eigenvector Spatial Filtering Features. ISPRS Int. J. Geo-Inf. 2022, 11, 242. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting Carbon Dioxide and Energy Fluxes across Global FLUXNET Sites with Regression Algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Coops, N.C.; Neinavaz, E.; Ali, A.; Schaepman, M.E.; Paganini, M.; Kissling, W.D.; Vihervaara, P.; Darvishzadeh, R.; Feilhauer, H.; et al. Priority List of Biodiversity Metrics to Observe from Space. Nat. Ecol. Evol. 2021, 5, 896–906. [Google Scholar] [CrossRef]
- Bai, Y.; Liang, S.; Yuan, W. Estimating Global Gross Primary Production from Sun-Induced Chlorophyll Fluorescence Data and Auxiliary Information Using Machine Learning Methods. Remote Sens. 2021, 13, 963. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, D.; Liu, Q.; Yao, Y.; Jia, K.; He, T.; Jiang, B.; Wei, Y.; Ma, H.; Zhao, X.; et al. An Operational Approach for Generating the Global Land Surface Downward Shortwave Radiation Product from MODIS Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4636–4650. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The Photochemical Reflectance Index (PRI) and the Remote Sensing of Leaf, Canopy and Ecosystem Radiation Use Efficiencies: A Review and Meta-Analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Xiao, X. Light Absorption by Leaf Chlorophyll and Maximum Light Use Efficiency. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1933–1935. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. BioScience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J. A Global, 0.05-Degree Product of Solar-Induced Chlorophyll Fluorescence Derived from OCO-2, MODIS, and Reanalysis Data. Remote Sens. 2019, 11, 517. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.-E.; et al. Reply to Magnani et al.: Linking Large-Scale Chlorophyll Fluorescence Observations with Cropland Gross Primary Production. Proc. Natl. Acad. Sci. USA 2014, 111, E2511. [Google Scholar] [CrossRef] [PubMed]
- Qiu, R.; Han, G.; Ma, X.; Xu, H.; Shi, T.; Zhang, M. A Comparison of OCO-2 SIF, MODIS GPP, and GOSIF Data from Gross Primary Production (GPP) Estimation and Seasonal Cycles in North America. Remote Sens. 2020, 12, 258. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A New Model of Gross Primary Productivity for North American Ecosystems Based Solely on the Enhanced Vegetation Index and Land Surface Temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of Multiple Models for Estimating Gross Primary Production Using MODIS and Eddy Covariance Data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S. A Continuous Measure of Gross Primary Production for the Conterminous United States Derived from MODIS and AmeriFlux Data. Remote Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef]
- Nightingale, J.M.; Coops, N.C.; Waring, R.H.; Hargrove, W.W. Comparison of MODIS Gross Primary Production Estimates for Forests across the U.S.A. with Those Generated by a Simple Process Model, 3-PGS. Remote Sens. Environ. 2007, 109, 500–509. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2018; Volume 31. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Rigatti, S.J. Random Forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Behrens, T.; Schmidt, K.; Viscarra Rossel, R.A.; Gries, P.; Scholten, T.; MacMillan, R.A. Spatial Modelling with Euclidean Distance Fields and Machine Learning. Eur. J. Soil Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Drineas, P.; Mahoney, M.W. Approximating a Gram Matrix for Improved Kernel-Based Learning. In Learning Theory; Auer, P., Meir, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 323–337. [Google Scholar]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter Tuning and Performance Assessment of Statistical and Machine-Learning Algorithms Using Spatial Data. Ecol. Model. 2019, 406, 109–120. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, J.; Wang, X.; Ma, M. Improving the Global MODIS GPP Model by Optimizing Parameters with FLUXNET Data. Agric. For. Meteorol. 2021, 300, 108314. [Google Scholar] [CrossRef]
- Lin, S.; Li, J.; Liu, Q.; Gioli, B.; Paul-Limoges, E.; Buchmann, N.; Gharun, M.; Hörtnagl, L.; Foltýnová, L.; Dušek, J.; et al. Improved Global Estimations of Gross Primary Productivity of Natural Vegetation Types by Incorporating Plant Functional Type. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102328. [Google Scholar] [CrossRef]
- Kim, H.-J.; Mawuntu, K.B.A.; Park, T.-W.; Kim, H.-S.; Park, J.-Y.; Jeong, Y.-S. Spatial Autocorrelation Incorporated Machine Learning Model for Geotechnical Subsurface Modeling. Appl. Sci. 2023, 13, 4497. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Wilson, J.P.; Yang, J.; Su, H.; Xu, R. A Multifactor Eigenvector Spatial Filtering-Based Method for Resolution-Enhanced Snow Water Equivalent Estimation in the Western United States. Remote Sens. 2023, 15, 3821. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, J.; He, W.; Zhou, Y.; Tu Nguyen, N.; Bi, W.; Wei, X.; Chen, H. How Well Do Light-Use Efficiency Models Capture Large-Scale Drought Impacts on Vegetation Productivity Compared with Data-Driven Estimates? Ecol. Indic. 2023, 146, 109739. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, A. Would the Obtainable Gross Primary Productivity (GPP) Products Stand up? A Critical Assessment of 45 Global GPP Products. Sci. Total Environ. 2021, 783, 146965. [Google Scholar] [CrossRef]
- Yan, X.; Feng, Y.; Tong, X.; Li, P.; Zhou, Y.; Wu, P.; Xie, H.; Jin, Y.; Chen, P.; Liu, S.; et al. Reducing Spatial Autocorrelation in the Dynamic Simulation of Urban Growth Using Eigenvector Spatial Filtering. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102434. [Google Scholar] [CrossRef]
- Park, Y.; Kim, S.H.; Kim, S.P.; Ryu, J.; Yi, J.; Kim, J.Y.; Yoon, H.-J. Spatial Autocorrelation May Bias the Risk Estimation: An Application of Eigenvector Spatial Filtering on the Risk of Air Pollutant on Asthma. Sci. Total Environ. 2022, 843, 157053. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Li, L.; Wang, Y.; Zhang, B.; Wang, Z.; Li, L. A Comparative Assessment of Geostatistical, Machine Learning, and Hybrid Approaches for Mapping Topsoil Organic Carbon Content. ISPRS Int. J. Geo-Inf. 2019, 8, 174. [Google Scholar] [CrossRef]
- Kiely, T.J.; Bastian, N.D. The Spatially Conscious Machine Learning Model. Stat. Anal. Data Min. ASA Data Sci. J. 2020, 13, 31–49. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Xu, C.-Y.; Sun, P.; Hu, P. Reconstruction of High Spatial Resolution Surface Air Temperature Data across China: A New Geo-Intelligent Multisource Data-Based Machine Learning Technique. Sci. Total Environ. 2019, 665, 300–313. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Shen, R.; Wang, Y.; Li, X.; Liu, S.; Liang, S.; Chen, J.M.; Ju, W.; Zhang, L.; Yuan, W. Improved Estimate of Global Gross Primary Production for Reproducing Its Long-Term Variation, 1982–2017. Earth Syst. Sci. Data 2020, 12, 2725–2746. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a Light Use Efficiency Model from Eddy Covariance Flux Data for Predicting Daily Gross Primary Production across Biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Jung, M.; Schwalm, C.; Migliavacca, M.; Walther, S.; Camps-Valls, G.; Koirala, S.; Anthoni, P.; Besnard, S.; Bodesheim, P.; Carvalhais, N.; et al. Scaling Carbon Fluxes from Eddy Covariance Sites to Globe: Synthesis and Evaluation of the FLUXCOM Approach. Biogeosciences 2020, 17, 1343–1365. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, C.; Xie, Z. An End-to-End Satellite-Based GPP Estimation Model Devoid of Meteorological and Land Cover Data. Agric. For. Meteorol. 2023, 331, 109337. [Google Scholar] [CrossRef]
- Chen, S.; Sui, L.; Liu, L.; Liu, X.; Li, J.; Huang, L.; Li, X.; Qian, X. NIRvP as a Remote Sensing Proxy for Measuring Gross Primary Production across Different Biomes and Climate Zones: Performance and Limitations. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103437. [Google Scholar] [CrossRef]
- Lin, S.; Hao, D.; Zheng, Y.; Zhang, H.; Wang, C.; Yuan, W. Multi-Site Assessment of the Potential of Fine Resolution Red-Edge Vegetation Indices for Estimating Gross Primary Production. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 102978. [Google Scholar] [CrossRef]
- Rogers, C.A.; Chen, J.M. Land Cover and Latitude Affect Vegetation Phenology Determined from Solar Induced Fluorescence across Ontario, Canada. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103036. [Google Scholar] [CrossRef]



| Product | Band | Temporal Resolution | Spatial Resolution | Source |
|---|---|---|---|---|
| GLASS | DSR | Daily | 0.05° | http://www.glass.umd.edu/ (accessed on 16 April 2024) |
| MCD43A4 | Band1 (620–670 nm) | Daily | 500 m | https://lpdaac.usgs.gov/products/mcd43a4v061/ (accessed on 19 April 2024) |
| Band2 (841–876 nm) | ||||
| Band3 (459–479 nm) | ||||
| Band4 (545–565 nm) | ||||
| Band5 (1230–1250 nm) | ||||
| Band6 (1628–1652 nm) | ||||
| Band7 (2105–2155 nm) | ||||
| MOD11A1 | Band31 (10.780–11.280 μm) | Daily | 1 km | https://lpdaac.usgs.gov/products/mod11a1v061/ (accessed on 19 April 2024) |
| Band32 (11.770–12.270 μm) | ||||
| MODOCGA | Band11 (526–536 nm) | Daily | 1 km | https://lpdaac.usgs.gov/products/modocgav006/ (accessed on 19 April 2024) |
| MOD13Q1 | EVI | 16 days | 250 m | https://lpdaac.usgs.gov/products/mod13q1v061/ (accessed on 19 April 2024) |
| Variables | Importance | Stddev | p-Value |
|---|---|---|---|
| Band2 | 1.52 | 0.04 | 7.45 × 10−9 |
| Band1 | 1.31 | 0.02 | 2.81 × 10−8 |
| DSR | 1.18 | 0.05 | 3.70 × 10−7 |
| EVI | 0.96 | 0.02 | 1.21 × 10−8 |
| Band7 | 0.79 | 0.01 | 4.28 × 10−8 |
| Band5 | 0.59 | 0.02 | 5.82 × 10−7 |
| Band6 | 0.31 | 0.01 | 4.75 × 10−7 |
| Band31 | 0.18 | 0.01 | 5.47 × 10−6 |
| Band11 | 0.01 | 0.00 | 0.000283 |
| Model | Test Set (Without Spatial Factors) | Test Set (With Spatial Factors) | ||
|---|---|---|---|---|
| RMSE | RMSE | |||
| PyTorch Neural Net model | 0.80 | 1.70 | 0.86 | 1.46 |
| XGBoost | 0.80 | 1.69 | 0.86 | 1.44 |
| CatBoost | 0.81 | 1.66 | 0.88 | 1.35 |
| ExtraTrees | 0.80 | 1.69 | 0.86 | 1.45 |
| Random Forest | 0.81 | 1.67 | 0.87 | 1.43 |
| LightGBM | 0.82 | 1.63 | 0.89 | 1.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Chen, Y.; Han, G.; Guo, M.; Wilson, J.P.; Min, W.; Ma, J. Incorporating Spatial Autocorrelation into GPP Estimation Using Eigenvector Spatial Filtering. Forests 2024, 15, 1198. https://doi.org/10.3390/f15071198
Xu R, Chen Y, Han G, Guo M, Wilson JP, Min W, Ma J. Incorporating Spatial Autocorrelation into GPP Estimation Using Eigenvector Spatial Filtering. Forests. 2024; 15(7):1198. https://doi.org/10.3390/f15071198
Chicago/Turabian StyleXu, Rui, Yumin Chen, Ge Han, Meiyu Guo, John P. Wilson, Wankun Min, and Jianshen Ma. 2024. "Incorporating Spatial Autocorrelation into GPP Estimation Using Eigenvector Spatial Filtering" Forests 15, no. 7: 1198. https://doi.org/10.3390/f15071198
APA StyleXu, R., Chen, Y., Han, G., Guo, M., Wilson, J. P., Min, W., & Ma, J. (2024). Incorporating Spatial Autocorrelation into GPP Estimation Using Eigenvector Spatial Filtering. Forests, 15(7), 1198. https://doi.org/10.3390/f15071198







