Optimizing Sensor Positions in the Stress Wave Tomography of Internal Defects in Hardwood
Abstract
1. Introduction
2. Materials and Methods
2.1. Review of Traditional Stress Wave Tomography and the EBSI Method
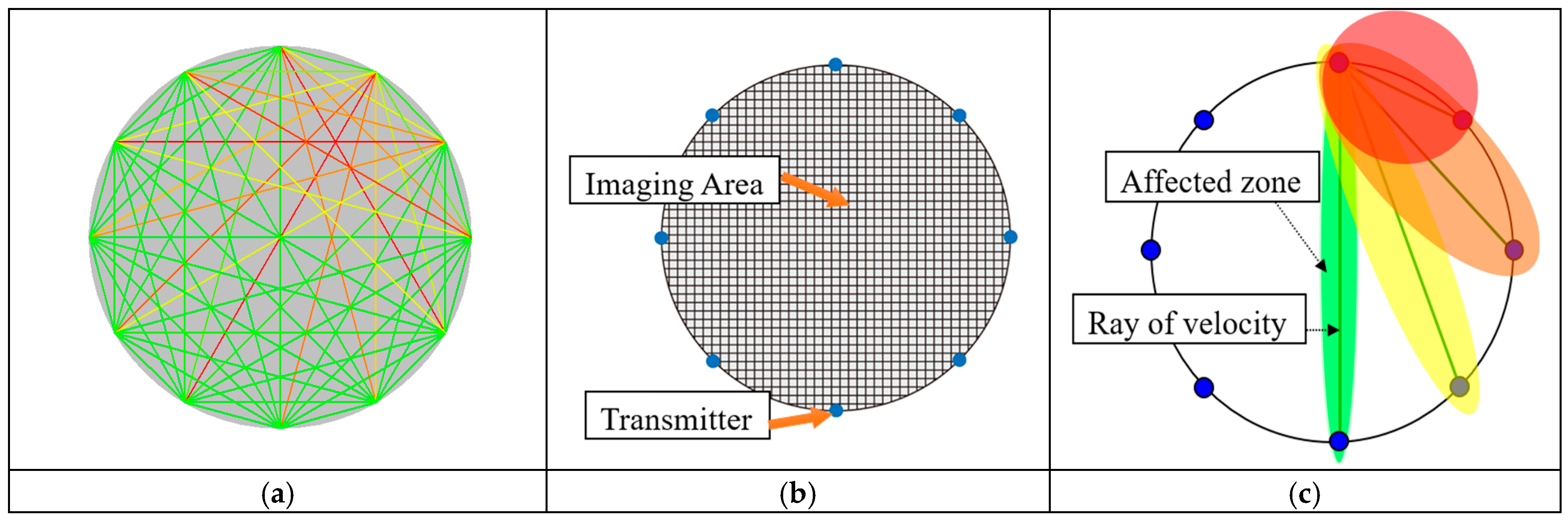
2.2. Influence of Ray Penetration Ratio and Degree of Equidistant Distribution of Sensors on Imaging
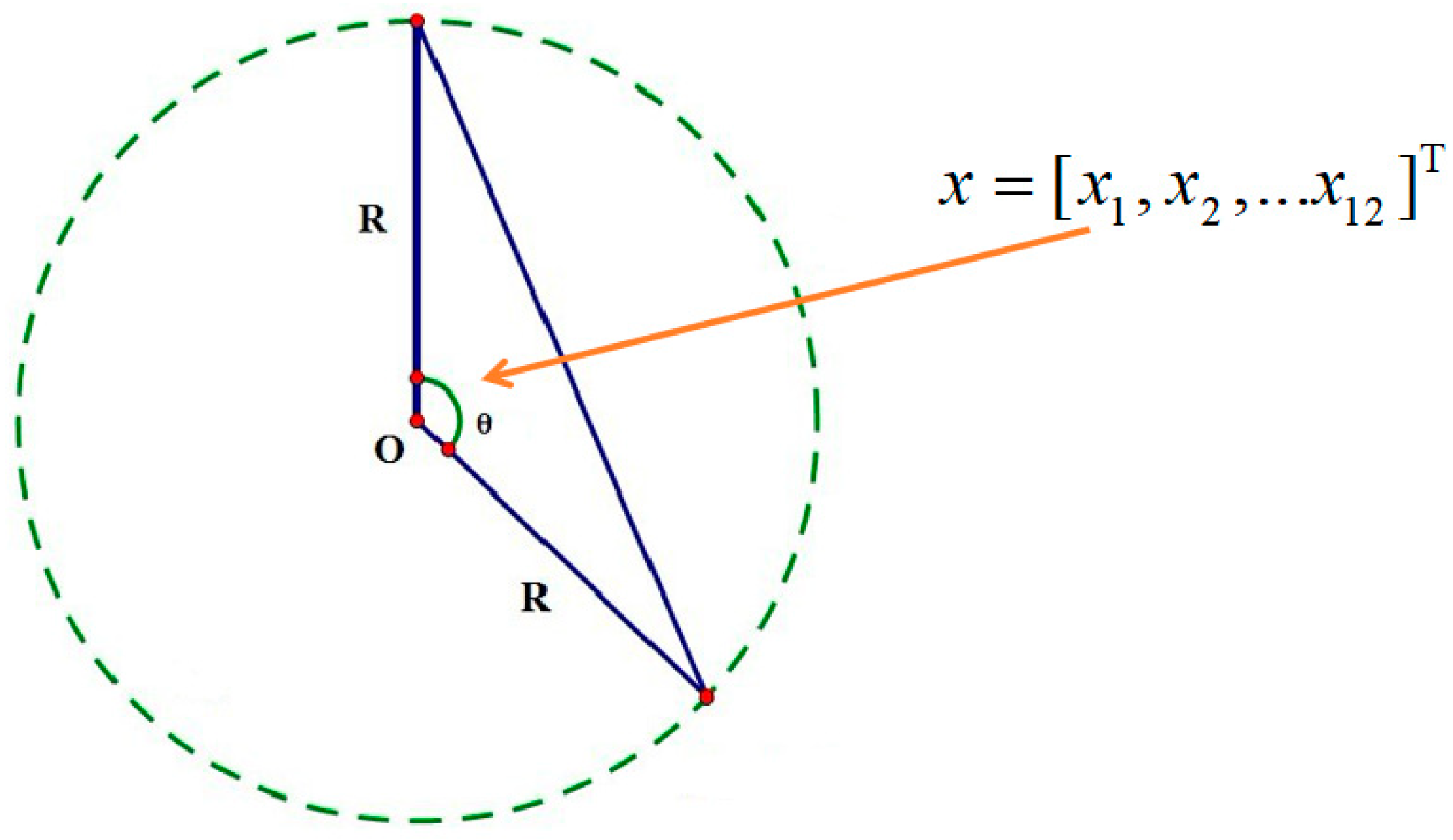
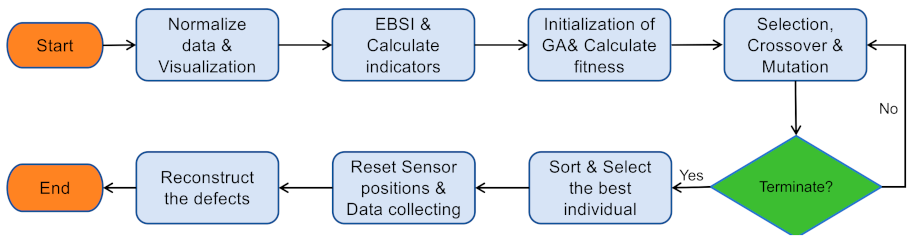
2.3. Optimizing Sensor Positions Based on Defect Distribution Perception
2.4. Signal Acquisition and Experimental Samples
3. Results and Discussion
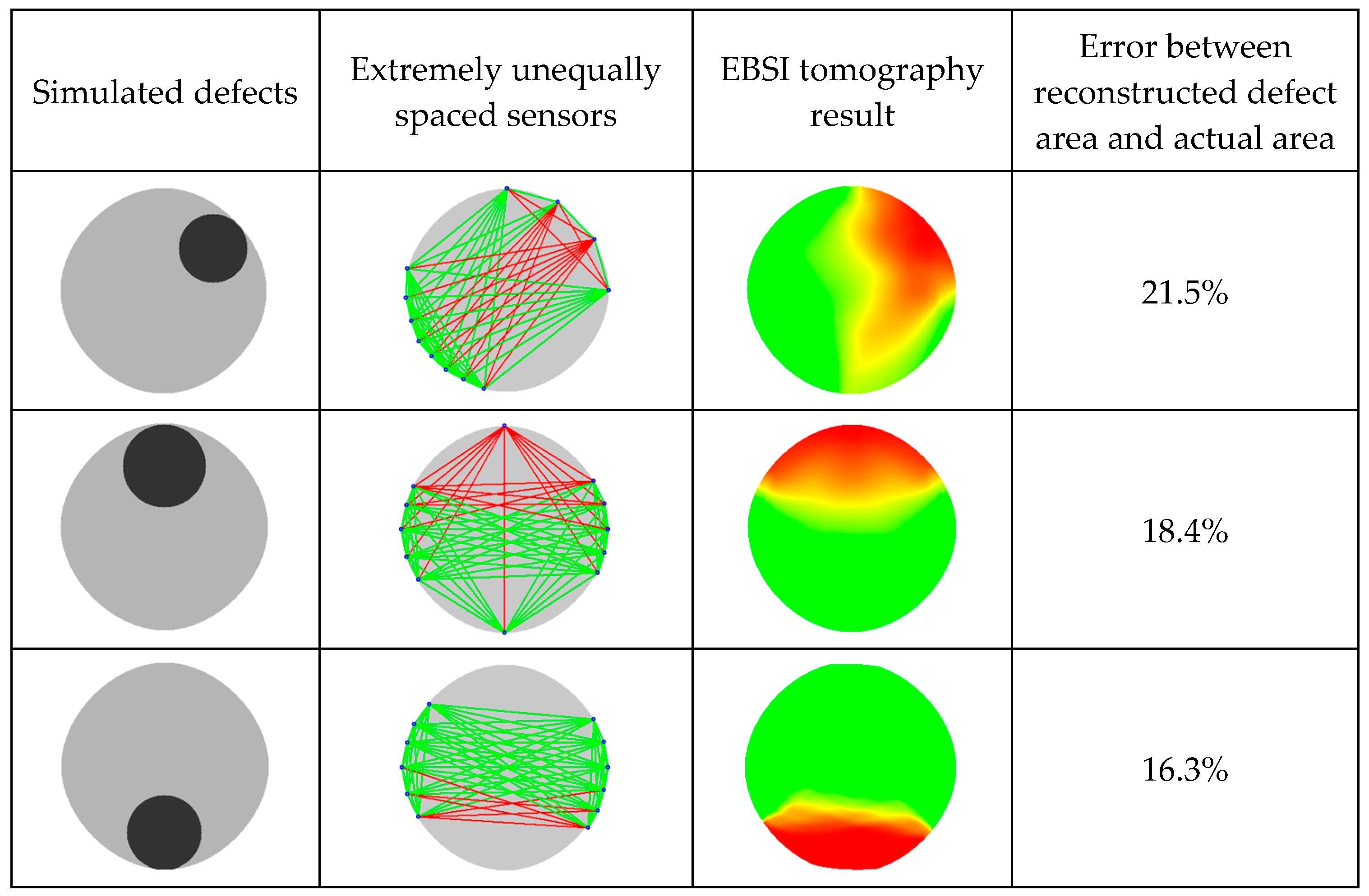
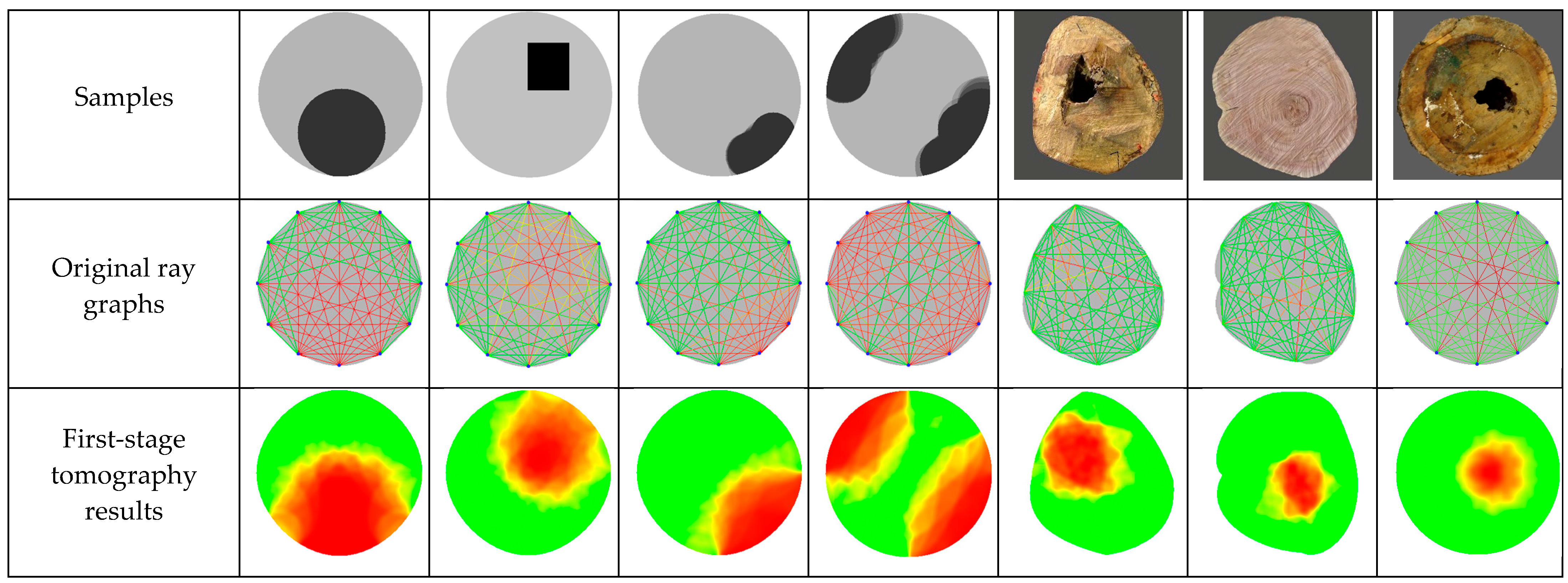
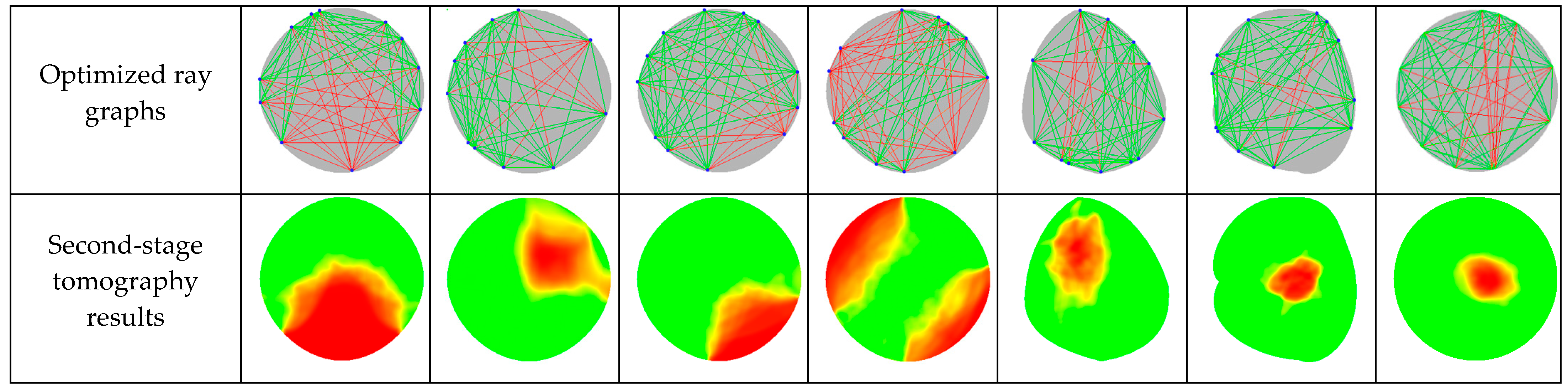
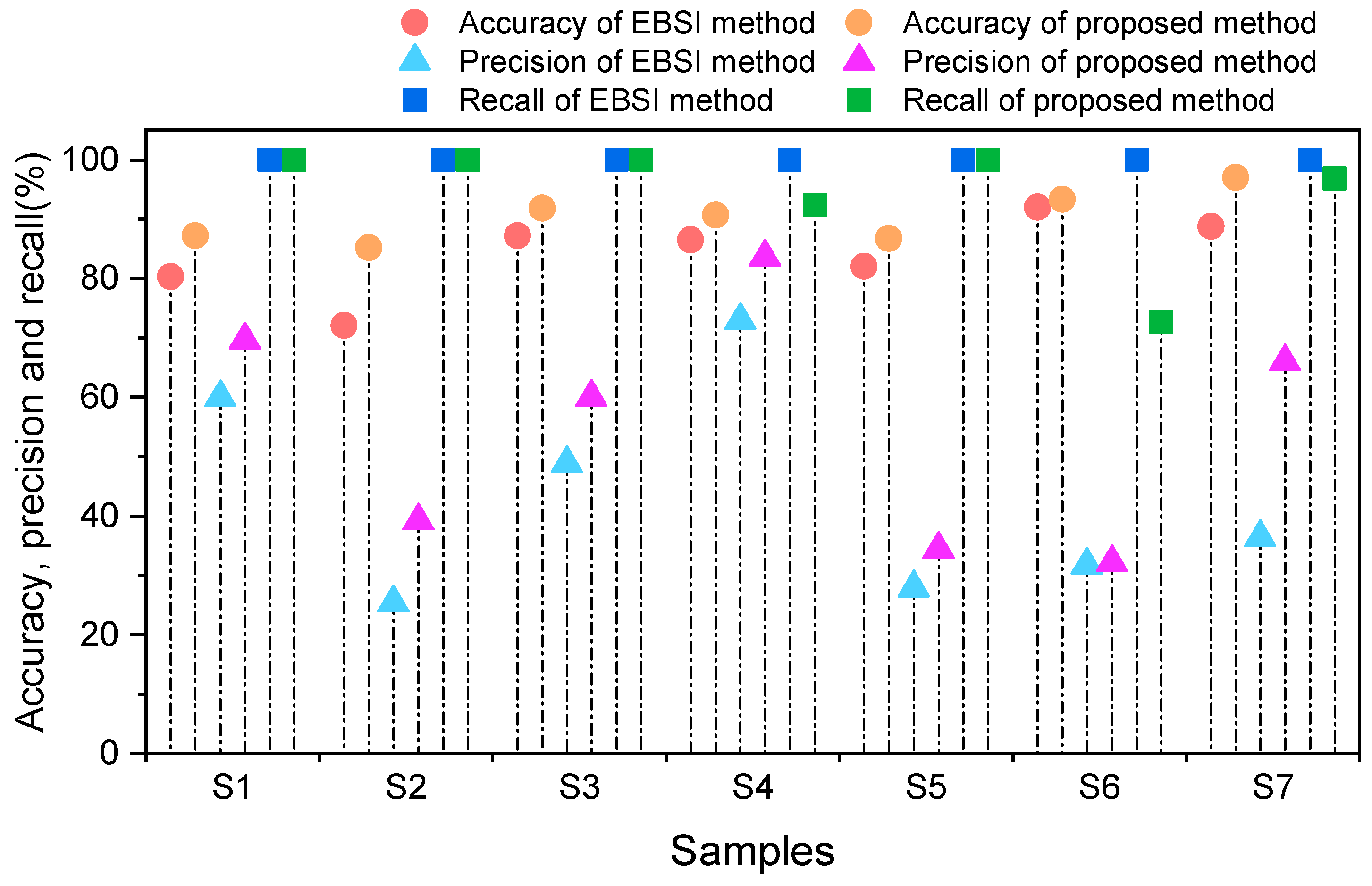
3.1. Tomography Results Based on Proposed Optimization Algorithm for Sensor Positions
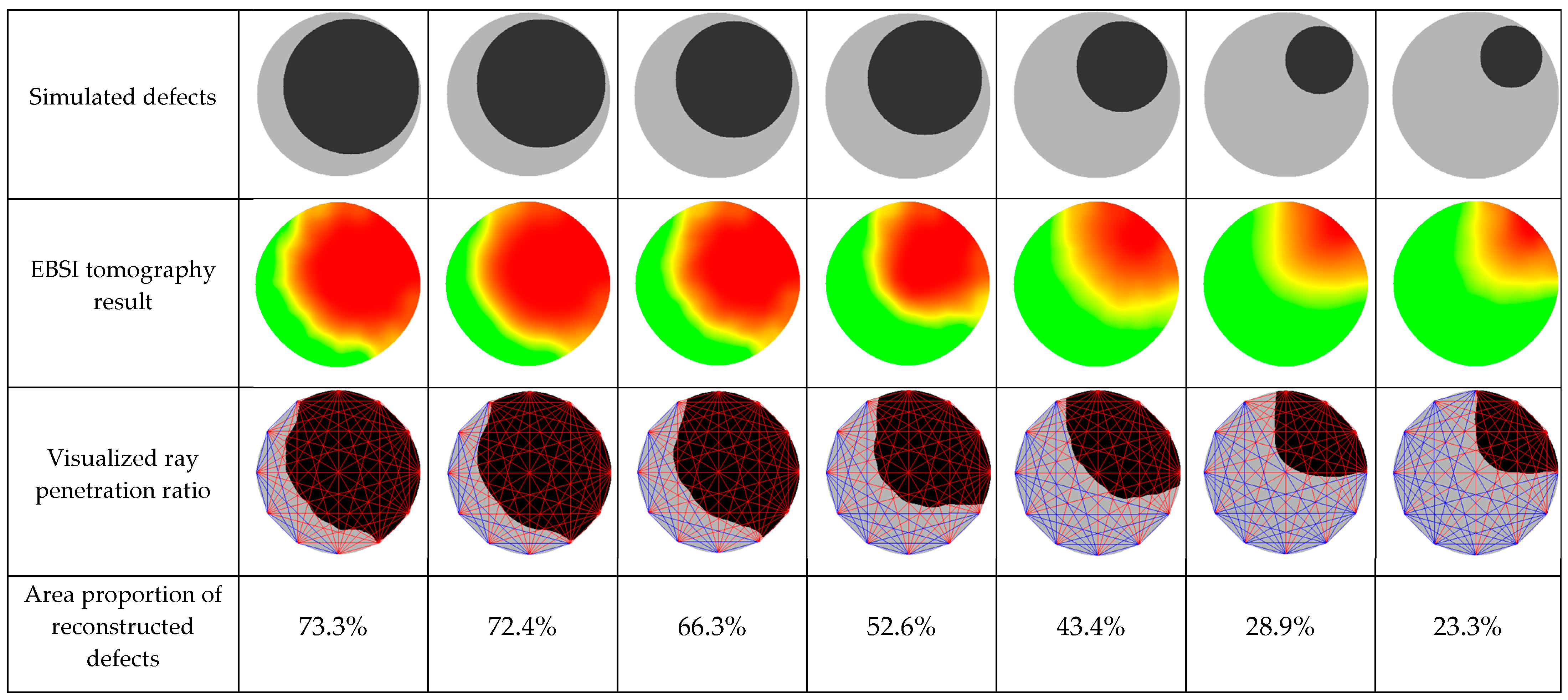
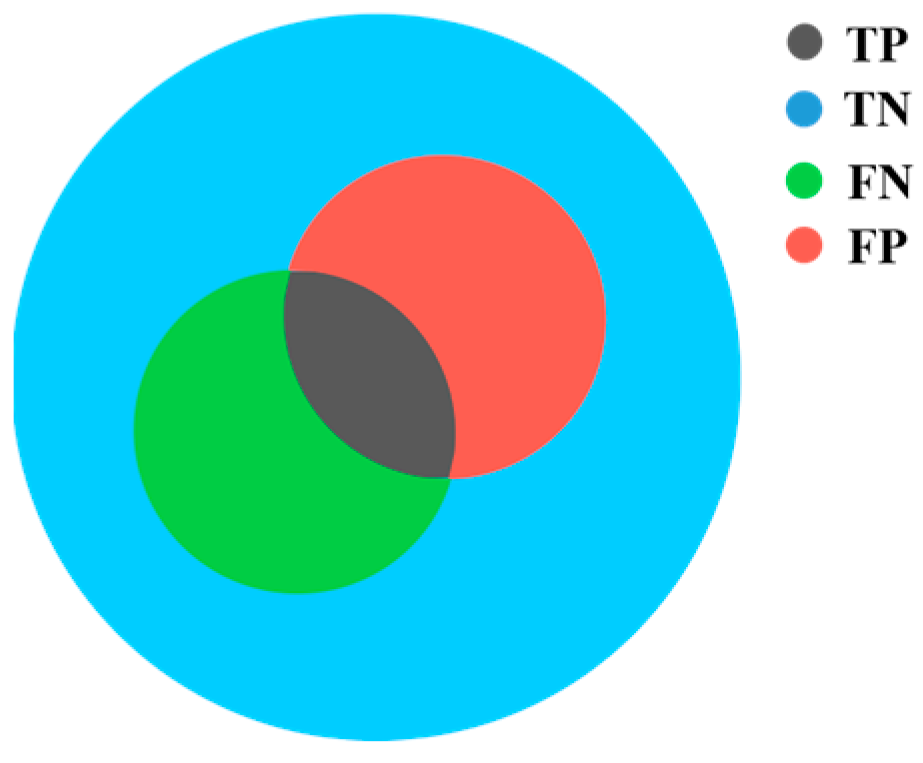
3.2. Area Analysis of Reconstructed Defects
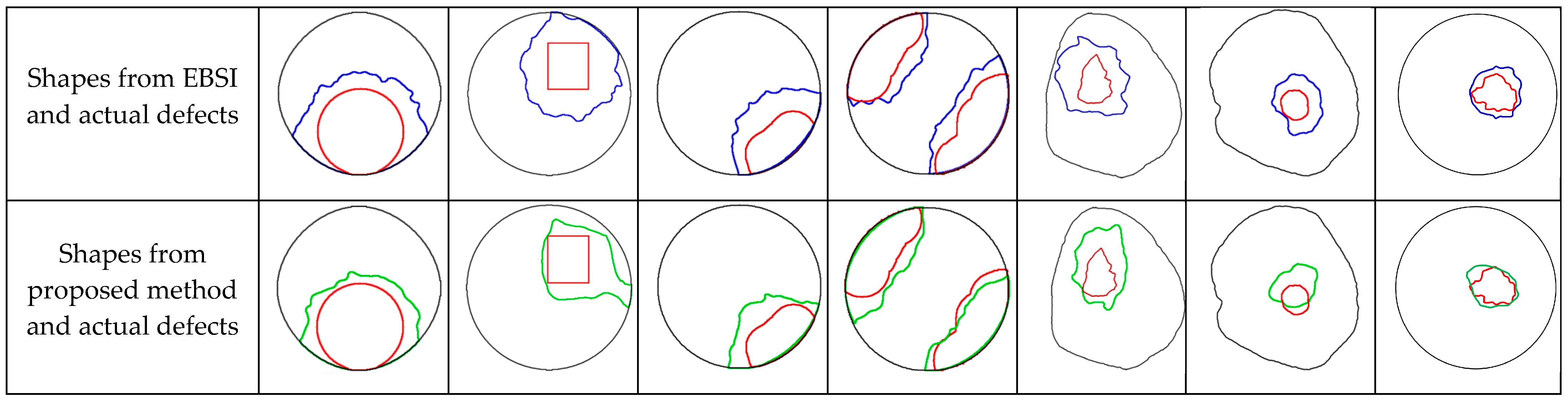
3.3. Shape Analysis of Reconstructed Defects
4. Conclusions
- (1)
- Different from traditional stress wave tomography methods that focus on designing image reconstruction algorithms to improve imaging accuracy, the optimized sensor position strategy proposed in this paper also improves imaging accuracy. After optimizing the planar distribution of sensors, the area of reconstructed defects is closer to the area of actual defects, and the contour of reconstructed defects is also closer to the contour of actual defects.
- (2)
- The proposed algorithm perceived the space distribution pattern of defects through the ray penetration ratio defined in this paper, improved the quality of the tomography algorithm input data through the optimization of sensor positions, and helped obtain better tomography results. After optimizing the planar distribution of sensors, the average accuracy of the EBSI method increased by 6.2% compared with the original EBSI method, while the average accuracy increased by 11.7%.
- (3)
- The traditional clock distribution of 12 sensors for data acquisition is a simple and usable strategy that can be used as a universal sensor layout for the stress wave tomography of internal hardwood defects. However, in situations where the ray penetration ratio is not ideal or when there is a need to achieve high-quality defect reconstruction, the sensor position’s optimization method proposed in this paper can effectively improve the quality of stress wave tomography.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kobza, M.; Ostrovsk, R.; Adamčíková, K.; Pastirčáková, K. Stability of trees infected by wood decay fungi estimated by acoustic tomography: A field survey. Trees 2021, 36, 103–112. [Google Scholar] [CrossRef]
- Madhoushi, M.; Ebrahimi, S.; Omidvar, A. Structural health assessment of a historical building by using in situ stress wave ndt: A case study in iran. Cerne 2021, 27, e-102535. [Google Scholar] [CrossRef]
- Radwan, M.; Thiel, D.; Espinosa, H. Single-sided microwave near-field scanning of pine wood lumber for defect detection. Forests 2021, 12, 1486. [Google Scholar] [CrossRef]
- Cascón, I.; Sarasua, J.; Tena, M.; Uria, A. Development of an acoustic method for wood disease assessment. Comput. Electron. Agric. 2021, 186, 106195. [Google Scholar] [CrossRef]
- Tomazello, M.; Brazolin, S.; Chagas, M.P.; Oliveira, J.T.S.; Ballarin, A.W.; Benjamin, C.A. Application of x-ray technique in nondestructive evaluation of eucalypt wood. Maderas-Cienciay Tecnol. 2008, 10, 139–150. [Google Scholar] [CrossRef]
- Ken, W.; Yukie, S.; Stavros, A.; Satoshi, S. Non-destructive measurement of moisture distribution in wood during drying using digital x-ray microscopy. Drying Technol. 2008, 26, 590–595. [Google Scholar]
- Rinn, F.; Schweingruber, F.; Schär, E. RESISTOGRAPH and X-ray Density Charts of Wood. Comparative Evaluation of Drill Resistance Profiles and X-ray Density Charts of Different Wood Species. Holzforschung 1996, 50, 303–311. [Google Scholar] [CrossRef]
- Tannert, T.; Anthony, R.; Kasal, B.; Kloiber, M.; Piazza, M.; Riggio, M.; Rinn, F.; Widmann, R. In Situ Assessment of Structural Timber Using Semi-Destructive Techniques. Mater. Struct. 2013, 47, 767–785. [Google Scholar] [CrossRef]
- Dackermann, U.; Crews, K.; Kasal, B.; Li, J.; Riggio, M.; Rinn, F.; Tannert, T. In situ assessment of structural timber using stress-wave measurements. Mater. Struct. 2014, 47, 787–803. [Google Scholar] [CrossRef]
- Yamasaki, M.; Tsuzuki, C.; Sasaki, Y.; Onishi, Y. Influence of moisture content on estimating young’s modulus of full-scale timber using stress wave velocity. J. Wood Sci. 2017, 63, 225–235. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, Z.; Hse, C.; Liu, R. Assessing the impact of wood decay fungi on the modulus of elasticity of slash pine (pinus elliottii) by stress wave non-destructive testing. Int. Biodeterior. Biodegrad. 2017, 117, 123–127. [Google Scholar] [CrossRef]
- Garcia, R.; Carvalho, A.; Matos, J.; Santos, W.; Silva, R. Nondestructive evaluation of heat-treated eucalyptus grandis, hill ex maiden wood using stress wave method. Wood Sci. Technol. 2012, 46, 41–52. [Google Scholar] [CrossRef]
- Wessels, C.; Malan, F.; Rypstra, T. A review of measurement methods used on standing trees for the prediction of some mechanical properties of timber. Eur. J. For. Res. 2011, 130, 881–893. [Google Scholar] [CrossRef]
- Legg, M.; Bradley, S. Measurement of stiffness of standing trees and felled logs using acoustics: A review. J. Acoust. Soc. Am. 2017, 139, 588–604. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Allison, R. Decay detection in red oak trees using a combination of visual inspection, acoustic testing, and resistance microdrilling. Arboric. Urban. For. 2008, 34, 1–4. [Google Scholar] [CrossRef]
- Ross, R.; Brashaw, B.; Pellerin, R. Nondestructive evaluation of wood. For. Prod. J. 1998, 48, 14–19. [Google Scholar]
- Johnstone, D.; Moore, G.; Tausz, M.; Nicolas, M. The measurement of wood decay in landscape trees. Arboric. Urban. For. 2010, 36, 121–127. [Google Scholar] [CrossRef]
- Mattheck, C.; Bethge, K. Detection of decay in trees with the Metriguard Stress Wave Timer. J. Arboric. 1993, 19, 374–378. [Google Scholar] [CrossRef]
- Rabe, C.; Ferner, D.; Fink, S.; Schwarze, F. Detection of decay in trees with stress waves and interpretation of acoustic tomograms. Arboric. Assoc. J. 2004, 28, 3–19. [Google Scholar] [CrossRef]
- Godio, A.; Sambuelli, L.; Socco, L. Application and comparison of three tomographic techniques for detection of decay in trees. J. Arboric. 2003, 28, 3–19. [Google Scholar]
- Deflorio, G.; Fink, S.; Schwarze, F. Detection of incipient decay in tree stems with sonic tomography after wounding and fungal inoculation. Wood Sci. Technol. 2008, 42, 117–132. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Wang, L.; Allison, R. Acoustic tomography in relation to 2d ultrasonic velocity and hardness mappings. Wood Sci. Technol. 2012, 46, 551–561. [Google Scholar] [CrossRef]
- Liang, S.; Fu, F. Effect of sensor number and distribution on accuracy rate of wood defect detection with stress wave tomography. Wood Res. 2014, 59, 521–531. [Google Scholar]
- Lin, C.; Chang, T.; Juan, M.; Lin, T.; Tseng, C.; Wang, Y. Stress wave tomography for the quantification of artificial hole detection in camphor trees (cinnamomum camphora). Taiwan. J. For. Sci. 2011, 26, 17–32. [Google Scholar]
- Gejdoš, M.; Michajlová, K.; Gretsch, D. The use of the acoustic tomograph and digital image analysis in the qualitative assessment of harvested timber—case study. Cent. Eur. For. J. 2023, 69, 106–111. [Google Scholar] [CrossRef]
- Qiu, Q.; Qin, R.; Lam, J.; Tang, A.; Leung, M.; Lau, D. An innovative tomographic technique integrated with acoustic-laser approach for detecting defects in tree trunk. Comput. Electron. Agric. 2019, 156, 129–137. [Google Scholar] [CrossRef]
- Arciniegas, A.; Brancheriau, L.; Lasaygues, P. Tomography in standing trees: Revisiting the determination of acoustic wave velocity. Ann. For. Sci. 2015, 72, 685–691. [Google Scholar] [CrossRef]
- Zeng, B.; Li, X.; Mao, Z. Correlation inversion detection algorithm and imaging simulation of wood defects focused by stress signal based on symlets wavelet. J. Phys. Conf. Ser. 2020, 1651, 012085. [Google Scholar] [CrossRef]
- Wei, X.; Xu, S.; Sun, L.; Tian, C.; Du, C. Propagation velocity model and two-dimensional defect imaging of stress wave in larch (larix gmelinii) wood. BioResources 2021, 4, 6799. [Google Scholar] [CrossRef]
- Zhan, H.; Jiao, Z.; Li, G. Velocity Error Correction Based Tomographic Imaging for Stress Wave Nondestructive Evaluation of Wood. Bioresources 2018, 13, 2530–2545. [Google Scholar]
- Wang, X.; Wiedenbeck, J.; Liang, S. Acoustic tomography for decay detection in black cherry trees. Wood Fiber Sci. 2009, 41, 127–137. [Google Scholar]
- Wang, X. Acoustic measurements on trees and logs: A review and analysis. Wood Fiber Sci. 2013, 47, 965–975. [Google Scholar] [CrossRef]
- Yue, X.; Wang, L.; Wacker, J. Electric resistance tomography and stress wave tomography for decay detection in trees-a comparison study. PeerJ 2019, 7, e6444. [Google Scholar] [CrossRef]
- Giryes, R.; Eldar, Y.; Bronstein, A.; Sapiro, G. Tradeoffs between convergence speed and reconstruction accuracy in inverse problems. IEEE Trans. Signal Process 2018, 66, 1676–1690. [Google Scholar] [CrossRef]
- Zeng, L.; Lin, J.; Huang, L. A modified lamb wave time-reversal method for health monitoring of composite structures. Sensors 2017, 17, 955. [Google Scholar] [CrossRef]
- Hettler, J.; Tabatabaeipour, M.; Delrue, S.; Van, D. Linear and nonlinear guided wave imaging of impact damage in cfrp using a probabilistic approach. Materials 2016, 9, 901. [Google Scholar] [CrossRef]
- Du, X.; Li, S.; Li, G.; Feng, H.; Chen, S. Stress Wave Tomography of Wood Internal Defects using Ellipse-Based Spatial Interpolation and Velocity Compensation. Bioresources 2015, 10, 3948–3962. [Google Scholar] [CrossRef]
- Qin, R.; Qiu, Q.; Lam, J.; Tang, A.; Leung, M.; Lau, D. Health assessment of tree trunk by using acoustic-laser technique and sonic tomography. Wood Sci. Technol. 2018, 52, 1113–1132. [Google Scholar] [CrossRef]
- Strobel, A.; Renato, J.; Carvalho, G.; Antonio, M.; Goncalves, R. Quantitative image analysis of acoustic tomography in woods. Eur. J. Wood Wood Prod. 2018, 76, 1379–1389. [Google Scholar] [CrossRef]
- Du, X.; Li, J.; Feng, H.; Chen, S. Image reconstruction of internal defects in wood based on segmented propagation rays of stress waves. Appl. Sci. 2018, 8, 1778. [Google Scholar] [CrossRef]
- Wang, L.; Xu, H.; Yan, Z. Effects of sensor quantity and planar distribution on testing results of log defects based on stress wave. Sci. Silvae Sin. 2008, 44, 115–121. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- He, S.; Wu, Q.; Saunders, J. Group search optimizer: An optimization algorithm inspired by animal searching behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Zheng, Y.; Feng, H. Optimizing Sensor Positions in the Stress Wave Tomography of Internal Defects in Hardwood. Forests 2024, 15, 465. https://doi.org/10.3390/f15030465
Du X, Zheng Y, Feng H. Optimizing Sensor Positions in the Stress Wave Tomography of Internal Defects in Hardwood. Forests. 2024; 15(3):465. https://doi.org/10.3390/f15030465
Chicago/Turabian StyleDu, Xiaochen, Yilei Zheng, and Hailin Feng. 2024. "Optimizing Sensor Positions in the Stress Wave Tomography of Internal Defects in Hardwood" Forests 15, no. 3: 465. https://doi.org/10.3390/f15030465
APA StyleDu, X., Zheng, Y., & Feng, H. (2024). Optimizing Sensor Positions in the Stress Wave Tomography of Internal Defects in Hardwood. Forests, 15(3), 465. https://doi.org/10.3390/f15030465




