A Comparison of Probability Density Functions Fitted by Moments and Maximum Likelihood Estimation Methods Used for Diameter Distribution Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Set
2.2. Distributions and Fitting Methods
2.2.1. The Charlier Distribution
2.2.2. The Beta Function
2.2.3. The Gamma Distribution
2.2.4. The Generalized Beta Distribution (GBD)
2.2.5. The Gumbel Function
2.2.6. The Johnson’s SB Function
2.2.7. The Weibull Function (2P and 3P)
2.2.8. Parameters’ Specifications
2.2.9. Numerical Optimization or MLE Method: ‘optim’ Function
2.3. Goodness of Fit
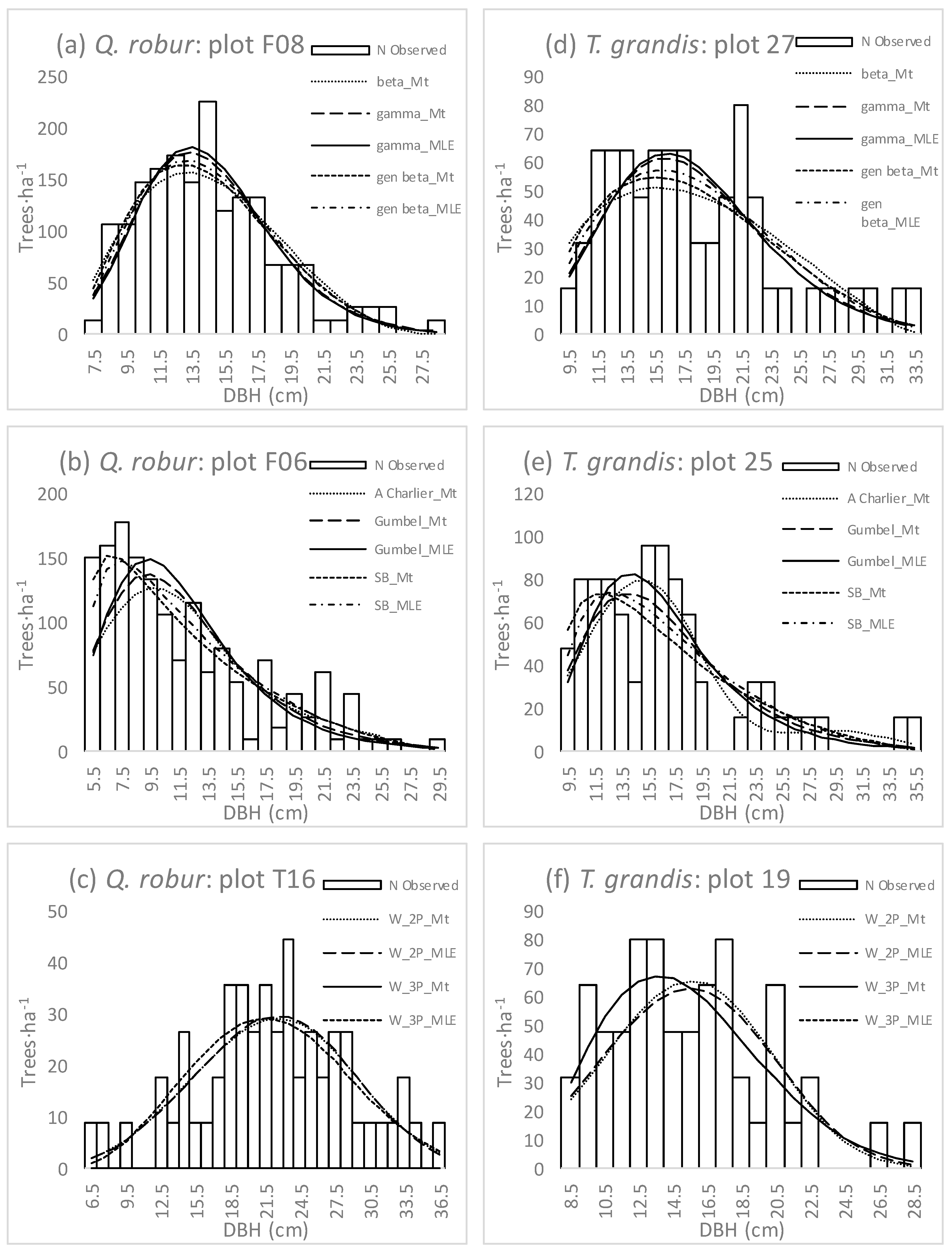
3. Results
4. Discussion
Implications for Forestry
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Function | Fit | Dn | W2 | Bias | MAE | MSE | -ΛΛ |
|---|---|---|---|---|---|---|---|
| A Charlier | Moments | 0.1088 | 0.0686 | 0.001370 | 0.018684 | 0.000610 | |
| MLE | No fit | No fit | No fit | No fit | No fit | No fit | |
| Beta | Moments | 0.1125 | 0.0705 | 0.000670 | 0.019086 | 0.000632 | |
| MLE | No fit | No fit | No fit | No fit | No fit | No fit | |
| Gamma-2P | Moments | 0.1284 | 0.0692 | 0.001240 | 0.019169 | 0.000648 | |
| MLE | 0.1275 | 0.0663 | 0.001353 | 0.019192 | 0.000649 | −189.76 | |
| Generalized beta | Moments | 0.1154 | 0.0578 | 0.000897 | 0.018852 | 0.000618 | |
| MLE | 0.1187 | 0.0584 | 0.000913 | 0.019092 | 0.000633 | −175.34 | |
| Gumbel | Moments | 0.1263 | 0.0678 | 0.001229 | 0.019739 | 0.000694 | |
| MLE | 0.1185 | 0.0667 | 0.001746 | 0.019390 | 0.000664 | −190.59 | |
| Johnson’s SB | Moments | 0.1228 | 0.0435 | 0.000641 | 0.018863 | 0.000617 | |
| MLE | 0.1239 | 0.0523 | 0.000568 | 0.019088 | 0.000627 | −187.85 | |
| Weibull-2P | Moments | 0.1121 | 0.0650 | 0.001566 | 0.019324 | 0.000659 | |
| MLE | 0.1119 | 0.0661 | 0.001555 | 0.019330 | 0.000660 | −190.50 | |
| Weibull-3P | Moments | 0.1043 | 0.0489 | 0.001012 | 0.018901 | 0.000623 | |
| MLE | 0.1073 | 0.0513 | 0.000923 | 0.018957 | 0.000627 | −188.51 |
| Function | Fit | Dn | W2 | Bias | MAE | MSE | -ΛΛ |
|---|---|---|---|---|---|---|---|
| A Charlier | Moments | 0.1273 | 0.0642 | 0.001879 | 0.022755 | 0.000902 | |
| MLE | No fit | No fit | No fit | No fit | No fit | No fit | |
| Beta | Moments | 0.1303 | 0.0809 | 0.001456 | 0.023183 | 0.000927 | |
| MLE | No fit | No fit | No fit | No fit | No fit | No fit | |
| Gamma-2P | Moments | 0.1324 | 0.0552 | 0.001797 | 0.023169 | 0.000925 | |
| MLE | 0.1324 | 0.0552 | 0.001706 | 0.023121 | 0.000925 | −142.093 | |
| Generalized beta | Moments | 0.1285 | 0.0553 | 0.001477 | 0.022736 | 0.000889 | |
| MLE | 0.1270 | 0.0490 | 0.001119 | 0.022851 | 0.000899 | −141.270 | |
| Gumbel | Moments | 0.1239 | 0.0477 | 0.001537 | 0.023632 | 0.000963 | |
| MLE | 0.1239 | 0.0477 | 0.001885 | 0.023033 | 0.000926 | −142.248 | |
| Johnson’s SB | Moments | 0.1319 | 0.0364 | 0.001100 | 0.022523 | 0.000874 | |
| MLE | 0.1294 | 0.0366 | 0.000878 | 0.022609 | 0.000881 | −140.772 | |
| Weibull-2P | Moments | 0.1333 | 0.0804 | 0.002460 | 0.024083 | 0.001011 | |
| MLE | 0.1312 | 0.0799 | 0.002793 | 0.024128 | 0.001012 | −144.362 | |
| Weibull-3P | Moments | 0.1138 | 0.0487 | 0.001575 | 0.022839 | 0.000899 | |
| MLE | 0.1170 | 0.0525 | 0.001575 | 0.022839 | 0.000899 | −141.563 |
References
- Zucchini, W.; Schmidt, M.; Gadow, K. A model for the diameter-height distribution in an uneven-aged beech forest and a method to assess the fit of such models. Silva Fenn. 2001, 35, 169–183. [Google Scholar] [CrossRef]
- Martin-Benito, D.; Molina-Valero, J.A.; Pérez-Cruzado, C.; Bigler, C.; Bugmann, H. Development and long-term dynamics of old-growth beech-fir forests in the Pyrenees: Evidence from dendroecology and dynamic vegetation modelling. For. Ecol. Manag. 2022, 524, 120541. [Google Scholar] [CrossRef]
- Gorgoso-Varela, J.J.; Rojo-Alboreca, A. Use of Gumbel and Weibull functions to model extreme values of diameter distributions in forest stands. Ann. For. Sci. 2014, 71, 741–750. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, Z.; Yun, T.; Wang, G.; Ruan, H.; She, G. Estimating tree volume distributions in subtropical forests using airborne LiDAR data. Remote Sens. 2019, 11, 97. [Google Scholar] [CrossRef]
- Loetsch, F.; Zöhrer, F.; Haller, K.E. Forest Inventory 2; BLV: Munich, Germany, 1973; 469p. [Google Scholar]
- Gorgoso-Varela, J.J.; Ogana, F.N.; Ige, P.O. A comparison between derivative and numerical optimization methods used for diameter distribution estimation. Scand. J. For. Res. 2020, 35, 156–164. [Google Scholar] [CrossRef]
- Li, F.; Zhang, L.; Davis, C.J. Modeling the joint distribution of tree diameters and heights by bivariate generalized Beta distribution. For. Sci. 2002, 48, 47–58. [Google Scholar]
- Podlaski, R. Characterization of diameter distribution data in near-natural forests using the Birnbaum–Saunders distribution. Can. J. For. Res. 2008, 38, 518–527. [Google Scholar] [CrossRef]
- Ige, P.O.; Adedapo, S.M. Modelling diameter distributions of Nauclea diderrichii (De Wild.) Merr. stands with Gamma and Weibull functions in Southwest Nigeria. World Sci. News 2021, 160, 247–262. [Google Scholar]
- Fonseca, T.F.; Marques, C.P.; Parresol, B.R. Describing maritime pine diameter distributions with Johnson’s SB distribution using a new all-parameter recovery approach. For Sci. 2009, 55, 367–373. [Google Scholar]
- de Lima, R.A.F.; Batista, J.L.F.; Prado, P.I. Modeling tree diameter distributions in natural forests: An evaluation of 10 statistical models. For. Sci. 2014, 61, 320–327. [Google Scholar] [CrossRef]
- Palahí, M.; Pukkala, T.; Blasco, E.; Trasobares, A. Comparison of beta, Johnson’s SB, Weibull and truncated Weibull functions for modelling the diameter distribution of forest stands in Catalonia (northeast of Spain). Eur. J. Forest Res. 2007, 126, 563–571. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Diéguez-Aranda, U.; Álvarez-González, J.G.; Pérez-Cruzado, C.; Castedo-Dorado, F.; González-Ferreiro, E. Modeling diameter distributions in radiata pine plantations in Spain with existing countrywide LiDAR data. Ann. For. Sci. 2018, 75, 36. [Google Scholar] [CrossRef]
- Pogoda, P.; Ochał, W.; Orzeł, S. Modeling Diameter Distribution of Black Alder (Alnus glutinosa (L.) Gaertn.) Stands in Poland. Forests 2019, 10, 412. [Google Scholar] [CrossRef]
- Schnur, G.L. Diameter distributions for old-field loblolly pine stands in Maryland. J. Agric. Res. 1934, 49, 731–743. [Google Scholar]
- Cao, Q. Predicting parameters of a Weibull function for modeling diameter distribution. For. Sci. 2004, 50, 682–685. [Google Scholar]
- Mateus, A.; Tomé, M. Modelling the diameter distribution of Eucalyptus plantations with Johnson’s probability density function: Parameters recovery from a compatible system of equations to predict stand variables. Ann. For. Sci. 2011, 68, 325–335. [Google Scholar] [CrossRef][Green Version]
- Sun, S.; Cao, Q.V.; Cao, T. Characterizing diameter distributions for uneven-aged pine-oak mixed forests in the Qinling Mountains of China. Forests 2019, 10, 596. [Google Scholar] [CrossRef]
- Mehtätalo, L.; Lappi, J. Biometry for Forestry and Environmental Data, 1st ed.; Taylor and Francis, LLC: New York, NY, USA, 2020; 426p. [Google Scholar]
- Zhang, L.; Kevin, C.P.; Chuanmin, L. A comparison of estimation methods for fitting Weibull and Johnson’s SB distributions to mixed spruce-fir stands in north-eastern North America. Can. J. For. Res. 2003, 33, 1340–1347. [Google Scholar] [CrossRef]
- Bončina, Z.; Trifković, V.; Rosset, C.; Klopčič, M. Evaluation of estimation methods for fitting the three-parameter Weibull distribution to European beech forests. iForest 2022, 15, 484. [Google Scholar] [CrossRef]
- Maltamo, M.; Puumalaine, J.; Päivinen, R. Comparison of beta and Weibull functions for modelling basal area diameter distribution in stands of Pinus sylvestris and Picea abies. Scan. J. For. Res. 1995, 10, 284–295. [Google Scholar] [CrossRef]
- Nelson, T.C. Diameter distribution and growth of loblolly pine. For. Sci. 1964, 10, 105–115. [Google Scholar]
- Gorgoso-Varela, J.J.; Alonso Ponce, R.; Rodríguez-Puerta, F. Modeling Diameter Distributions with Six Probability Density Functions in Pinus halepensis Mill. Plantations Using Low-Density Airborne Laser Scanning Data in Aragón (Northeast Spain). Remote Sens. 2021, 13, 2307. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistical Theory of Extreme Values and Some Practical Applications; Applied Mathematics Series, 33; Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1954; 60p. [Google Scholar]
- Gorgoso-Varela, J.J.; García-Villabrille, J.D.; Rojo-Alboreca, A. Modeling extreme values for height distributions in Pinus pinaster, Pinus radiata and Eucalyptus globulus stands in northwestern Spain. iForest 2015, 9, 23–29. [Google Scholar] [CrossRef]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Cosenza, D.N.; Soares, P.; Guerra-Hernández, J.; Pereira, L.; González-Ferreiro, E.; Castedo-Dorado, F.; Tomé, M. Comparing Johnson’s SB and Weibull Functions to Model the Diameter Distribution of Forest Plantations through ALS data. Remote Sens. 2019, 11, 2792. [Google Scholar] [CrossRef]
- Bailey, R.L.; Dell, T.R. Quantifying Diameter Distributions with the Weibull Function. For. Sci. 1973, 19, 97–104. [Google Scholar]
- Gerald, C.F.; Wheatley, P.O. Applied Numerical Analysis, 4th ed.; Addison-Wesley Publishing Co.: Reading, MA, USA, 1989. [Google Scholar]
- Parresol, B.R. Recovering Parameters of Johnson’s SB Distribution; Res. Paper SRS-31; US Forest Service: Asheville, NC, USA, 2003; 9p. Available online: https://www.fs.usda.gov/research/treesearch/5455 (accessed on 1 June 2023).
- SAS Institute Inc. SAS/STAT 9.1 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2004; 5136p. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 16 June 2023).
- Nelder, J.A.; Mead, R. A simplex algorithm for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Wang, M. Distributional Modelling in Forestry and Remote Sensing. Ph.D. Thesis, University of Greenwich, London, UK, 2005. [Google Scholar]
- Wang, M.; Rennolls, K. Bivariate distribution modeling with tree diameter and height data. For. Sci. 2007, 53, 16–24. [Google Scholar]
- Tewari, V.P.; Singh, B. Total wood volume equation for Tectona grandis Linn F. stands in Gujarat, India. J. For. Environ. Sci. 2018, 34, 313–320. [Google Scholar]
- Scolforo, J.R.S.; Vitti, F.C.; Grisi, R.L.; Acerbi, F.; De Assis, A.L. SB distribution’s accuracy to represent the diameter distribution of Pinus taeda, through five fitting methods. For. Ecol. Manag. 2003, 175, 489–496. [Google Scholar] [CrossRef]
- Zhou, B.; McTague, J.P. Comparison and evaluation of five methods of estimation of the Johnson System parameters. Can. J. For. Res. 1996, 26, 928–935. [Google Scholar] [CrossRef]
- Ogana, F.N.; Itam, E.S.; Osho, J.S. Modeling diameter distributions of Gmelina arborea plantation in Omo Forest Reserve, Nigeria with Johnson’s SB. J. Sustain. For. 2017, 36, 121–133. [Google Scholar] [CrossRef]
- Mayrinck, R.C.; Filho, A.C.F.; Ribeiro, A.; de Oliveira, X.M.; de Lima, R.R. A comparison of diameter distribution models for Khaya ivorensis A. Chev. plantations in Brazil. South. For. 2018, 80, 373–380. [Google Scholar] [CrossRef]
- Dubey, S.D. Some percentile estimators for Weibull parameters. Technometrics 1967, 9, 119–129. [Google Scholar] [CrossRef]
- Hafley, W.L.; Buford, M.A. A bivariate model for growth and yield prediction. For. Sci. 1985, 31, 237–247. [Google Scholar]
- Hafley, W.L.; Schreuder, H.T. Statistical distributions for fitting diameter and height data in even-aged stands. Can. J. For. Res. 1977, 7, 481–487. [Google Scholar] [CrossRef]
- Knoebel, B.R.; Burkhart, H.E. A bivariate distribution approach to modeling forest diameter distributions at two points in time. Biometrics 1991, 47, 241–253. [Google Scholar] [CrossRef]
| Variable | Mean | Max | Min | SD | |
|---|---|---|---|---|---|
| Quercus robur (N = 167 plots) | N | 854.6 | 3022.2 | 302.2 | 452.5 |
| G | 28.6 | 72.9 | 7.7 | 9.1 | |
| dg | 22.2 | 40.0 | 8.6 | 5.9 | |
| HO | 17.1 | 25.6 | 7.2 | 3.2 | |
| RS | 22.0 | 39.8 | 12.7 | 4.8 | |
| Tectona grandis (N = 59 plots) | N | 899.3 | 1744.0 | 624.0 | 181.6 |
| G | 26.9 | 50.8 | 11.5 | 8.9 | |
| dg | 19.3 | 23.5 | 14.3 | 2.3 | |
| HO | 21.9 | 28.4 | 17.7 | 2.2 | |
| RS | 15.6 | 20.1 | 9.9 | 2.4 |
| Function | Fit | Param | Mean | St Dev | Min | Max |
|---|---|---|---|---|---|---|
| A Charlier | Derivative (Moments) | μ | 21.0193 | 5.7681 | 8.3323 | 37.7631 |
| σ2 | 52.7453 | 32.9372 | 4.0278 | 196.5813 | ||
| asym | 0.3697 | 0.5164 | −0.9847 | 2.0729 | ||
| Kurt | 0.0548 | 1.017 | −1.1844 | 6.1667 | ||
| Beta | Derivative (Moments) | c | 0.0013 | 0.0030 | 6.00·Exp−11 | 0.0218 |
| L | 6.3530 | 2.5962 | 3.7500 | 19.0125 | ||
| U | 37.9093 | 9.8654 | 16.3000 | 71.6000 | ||
| α | 0.9685 | 0.6740 | −0.1582 | 3.2457 | ||
| γ | 1.3249 | 0.7836 | 0.0083 | 4.4221 | ||
| Gamma-2P | Derivative (Moments) | α | 10.7038 | 5.5632 | 2.9692 | 29.9842 |
| β | 2.3936 | 1.2093 | 0.4782 | 8.0624 | ||
| Optimization (MLE) | α | 10.1891 | 5.3742 | 2.9513 | 30.8548 | |
| β | 2.5451 | 1.3837 | 0.4421 | 10.0525 | ||
| Generalized beta | Derivative (Moments) | 170.4135 | 560.1196 | 1.9032 | 4290.0584 | |
| B1 | 6.3530 | 2.5962 | 3.7500 | 19.0125 | ||
| B2 | 37.9093 | 9.8654 | 16.3000 | 71.6000 | ||
| B3 | 1.4699 | 0.9587 | 0.0084 | 4.5858 | ||
| B4 | 2.9449 | 1.4354 | 0.7609 | 7.9256 | ||
| Optimization (MLE) | 209.6410 | 784.4000 | 3.0108 | 7154.8607 | ||
| B1 | 6.3530 | 2.5962 | 3.7500 | 19.0125 | ||
| B2 | 37.9093 | 9.8654 | 16.3000 | 71.6000 | ||
| B3 | 1.5057 | 0.91418 | 0.1710 | 4.0093 | ||
| B4 | 3.0330 | 1.5694 | 0.8589 | 8.4234 | ||
| Gumbel | Derivative (Moments) | μ | 17.8914 | 5.2504 | 7.4290 | 32.9807 |
| β | 5.4191 | 1.6476 | 1.5648 | 10.9319 | ||
| Optimization (MLE) | μ | 17.7025 | 5.1462 | 7.4249 | 32.8833 | |
| β | 6.0555 | 1.9661 | 1.5796 | 12.5816 | ||
| Johnson’s SB | Derivative (Moments) | ε | 6.3530 | 2.5962 | 3.7500 | 19.0125 |
| λ | 37.9093 | 9.8654 | 16.3000 | 71.6000 | ||
| γ | 0.6328 | 0.3998 | −0.5518 | 1.6197 | ||
| δ | 1.1268 | 0.21093 | 0.7208 | 1.6982 | ||
| Optimization (MLE) | ε | 6.3530 | 2.5962 | 3.7500 | 19.0125 | |
| λ | 37.9093 | 9.8654 | 16.3000 | 71.6000 | ||
| γ | 0.6296 | 0.3844 | −0.4715 | 1.6283 | ||
| δ | 1.1226 | 0.2021 | 0.7435 | 1.7484 | ||
| Weibull-2P | Derivative (Moments) | b | 23.3373 | 6.2908 | 9.1039 | 42.2053 |
| c | 3.4887 | 0.9731 | 1.7634 | 6.3410 | ||
| Optimization (MLE) | b | 23.3570 | 6.2746 | 9.1213 | 42.1990 | |
| c | 3.4653 | 0.9180 | 1.8427 | 6.0898 | ||
| Weibull-3P | Derivative (Moments) | a | 6.3530 | 2.5962 | 3.7500 | 19.0125 |
| b | 16.4731 | 5.1672 | 5.0848 | 34.7842 | ||
| c | 2.2804 | 0.5399 | 1.3474 | 4.3502 | ||
| Optimization (MLE) | a | 6.3530 | 2.5962 | 3.7500 | 19.01225 | |
| b | 16.4569 | 5.1075 | 5.0926 | 34.6642 | ||
| c | 2.3116 | 0.54702 | 1.3650 | 4.5155 |
| Function | Fit | Param | Mean | St Dev | Min | Max |
|---|---|---|---|---|---|---|
| A Charlier | Derivative (Moments) | μ | 18.6115 | 2.3531 | 13.5467 | 22.8062 |
| σ2 | 27.5001 | 11.2797 | 12.3188 | 65.1082 | ||
| asym | 0.57652 | 0.4351 | −0.4617 | 1.4558 | ||
| Kurt | 0.2409 | 1.1994 | −1.1160 | 5.1092 | ||
| Beta | Derivative (Moments) | c | 0.0016 | 0.0039 | 4.95·Exp−11 | 0.0227 |
| L | 7.5775 | 1.6863 | 4.3500 | 11.1750 | ||
| U | 31.7254 | 4.6026 | 21.3000 | 39.2000 | ||
| α | 1.1593 | 0.7226 | 0.1094 | 3.3500 | ||
| γ | 1.6320 | 0.9387 | 0.3156 | 5.1150 | ||
| Gamma-2P | Derivative (Moments) | α | 14.7649 | 5.6418 | 4.3942 | 28.6115 |
| β | 1.4635 | 0.6380 | 0.6929 | 3.7585 | ||
| Optimization (MLE) | α | 15.0228 | 5.6265 | 4.3999 | 26.9948 | |
| β | 1.4323 | 0.6207 | 0.7082 | 3.6163 | ||
| Generalized beta | Derivative (Moments) | 432.0867 | 1194.5728 | 1.9972 | 7589.0738 | |
| B1 | 7.5775 | 1.6863 | 4.3500 | 11.1750 | ||
| B2 | 31.7254 | 4.6026 | 21.3000 | 39.2000 | ||
| B3 | 1.8115 | 0.9587 | 0.0313 | 4.4257 | ||
| B4 | 4.2003 | 1.7369 | 1.0530 | 10.3882 | ||
| Optimization (MLE) | 562.4069 | 1590.6532 | 3.5278 | 11,607.4026 | ||
| B1 | 7.5775 | 1.6863 | 4.3500 | 11.1750 | ||
| B2 | 31.7254 | 4.6026 | 21.3000 | 39.2000 | ||
| B3 | 1.9993 | 0.8892 | 0.2448 | 4.1809 | ||
| B4 | 4.5639 | 1.8122 | 1.4330 | 10.8203 | ||
| Gumbel | Derivative (Moments) | μ | 16.2938 | 2.3630 | 11.4856 | 20.1282 |
| β | 4.0155 | 0.7772 | 2.7366 | 6.2913 | ||
| Optimization (MLE) | μ | 16.2134 | 2.3629 | 11.3835 | 20.1133 | |
| β | 4.2340 | 0.7465 | 2.7812 | 6.5603 | ||
| Johnson’s SB | Derivative (Moments) | ε | 7.5775 | 1.6863 | 4.3500 | 11.1750 |
| λ | 31.7254 | 4.6026 | 21.3000 | 39.2000 | ||
| γ | 0.9011 | 0.3319 | 0.1835 | 1.8047 | ||
| δ | 1.2655 | 0.2212 | 0.7413 | 1.7499 | ||
| Optimization (MLE) | ε | 7.5775 | 1.6863 | 4.3500 | 11.1750 | |
| λ | 31.7254 | 4.6026 | 21.3000 | 39.2000 | ||
| γ | 0.9090 | 0.3415 | 0.2055 | 1.7963 | ||
| δ | 1.2961 | 0.2090 | 0.8062 | 1.7604 | ||
| Weibull-2P | Derivative (Moments) | b | 20.4748 | 2.4730 | 15.1130 | 25.0459 |
| c | 4.2068 | 0.9295 | 2.1778 | 6.1998 | ||
| Optimization (MLE) | b | 20.5079 | 2.4735 | 15.1411 | 25.0836 | |
| c | 3.9932 | 0.8209 | 2.2678 | 6.4435 | ||
| Weibull-3P | Derivative (Moments) | a | 7.5775 | 1.6863 | 4.3500 | 11.1750 |
| b | 12.4075 | 1.7067 | 8.6744 | 16.6523 | ||
| c | 2.3337 | 0.4648 | 1.3990 | 3.6479 | ||
| Optimization (MLE) | a | 7.5775 | 1.6863 | 4.3500 | 11.1750 | |
| b | 12.4075 | 1.7067 | 8.6744 | 16.6523 | ||
| c | 2.3337 | 0.4648 | 1.3990 | 3.6479 |
| Species | Fit | Function | Dn | W2 | Bias | MAE | MSE | -ΛΛ | ΣRank |
|---|---|---|---|---|---|---|---|---|---|
| Q. robur | Moments (Derivative) | A Charlier | 2 | 6 | 7 | 1 | 1 | - | 17 |
| beta | 4 | 8 | 2 | 5 | 5 | - | 24 | ||
| Gamma-2P | 8 | 7 | 6 | 6 | 6 | - | 33 | ||
| generalized beta | 5 | 3 | 3 | 2 | 3 | - | 16 | ||
| Gumbel | 7 | 5 | 5 | 8 | 8 | - | 33 | ||
| Johnson’s SB | 6 | 1 | 1 | 3 | 2 | - | 13 | ||
| Weibull-2P | 3 | 4 | 8 | 7 | 7 | - | 29 | ||
| Weibull-3P | 1 | 2 | 4 | 4 | 4 | - | 15 | ||
| MLE (Optimization) | A Charlier | - | - | - | - | - | - | - | |
| beta | - | - | - | - | - | - | - | ||
| Gamma-2P | 6 | 4 | 4 | 4 | 4 | 3 | 25 | ||
| generalized beta | 4 | 3 | 2 | 3 | 3 | 6 | 21 | ||
| Gumbel | 3 | 6 | 6 | 6 | 6 | 1 | 28 | ||
| Johnson’s SB | 5 | 2 | 1 | 2 | 1 | 5 | 16 | ||
| Weibull-2P | 2 | 5 | 5 | 5 | 5 | 2 | 24 | ||
| Weibull-3P | 1 | 1 | 3 | 1 | 1 | 4 | 11 | ||
| T. grandis | Moments (Derivative) | A Charlier | 3 | 6 | 7 | 3 | 4 | - | 23 |
| beta | 5 | 8 | 2 | 6 | 6 | - | 27 | ||
| Gamma-2P | 7 | 4 | 6 | 5 | 5 | - | 27 | ||
| generalized beta | 4 | 5 | 3 | 2 | 2 | - | 16 | ||
| Gumbel | 2 | 2 | 4 | 7 | 7 | - | 22 | ||
| Johnson’s SB | 6 | 1 | 1 | 1 | 1 | - | 10 | ||
| Weibull-2P | 8 | 7 | 8 | 8 | 8 | - | 39 | ||
| Weibull-3P | 1 | 3 | 5 | 4 | 2 | - | 15 | ||
| MLE (Optimization) | A Charlier | - | - | - | - | - | - | - | |
| beta | - | - | - | - | - | - | - | ||
| Gamma-2P | 6 | 5 | 4 | 5 | 4 | 3 | 27 | ||
| generalized beta | 3 | 3 | 2 | 3 | 2 | 5 | 18 | ||
| Gumbel | 2 | 2 | 5 | 4 | 5 | 2 | 20 | ||
| Johnson’s SB | 4 | 1 | 1 | 1 | 1 | 6 | 14 | ||
| Weibull-2P | 5 | 6 | 6 | 6 | 6 | 1 | 30 | ||
| Weibull-3P | 1 | 4 | 3 | 2 | 2 | 4 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorgoso-Varela, J.J.; Adedapo, S.M.; Ogana, F.N. A Comparison of Probability Density Functions Fitted by Moments and Maximum Likelihood Estimation Methods Used for Diameter Distribution Estimation. Forests 2024, 15, 425. https://doi.org/10.3390/f15030425
Gorgoso-Varela JJ, Adedapo SM, Ogana FN. A Comparison of Probability Density Functions Fitted by Moments and Maximum Likelihood Estimation Methods Used for Diameter Distribution Estimation. Forests. 2024; 15(3):425. https://doi.org/10.3390/f15030425
Chicago/Turabian StyleGorgoso-Varela, Jose Javier, Segun M. Adedapo, and Friday N. Ogana. 2024. "A Comparison of Probability Density Functions Fitted by Moments and Maximum Likelihood Estimation Methods Used for Diameter Distribution Estimation" Forests 15, no. 3: 425. https://doi.org/10.3390/f15030425
APA StyleGorgoso-Varela, J. J., Adedapo, S. M., & Ogana, F. N. (2024). A Comparison of Probability Density Functions Fitted by Moments and Maximum Likelihood Estimation Methods Used for Diameter Distribution Estimation. Forests, 15(3), 425. https://doi.org/10.3390/f15030425







