ODCA-YOLO: An Omni-Dynamic Convolution Coordinate Attention-Based YOLO for Wood Defect Detection
Abstract
:1. Introduction
- Introducing ODCA, a novel attention mechanism that enhances the network’s capability to detect small targets, thus improving feature representation within the network.
- An omni-dimensional dynamic convolution coordinate attention-based YOLO model (ODCA-YOLO) for wood defects detection is proposed.
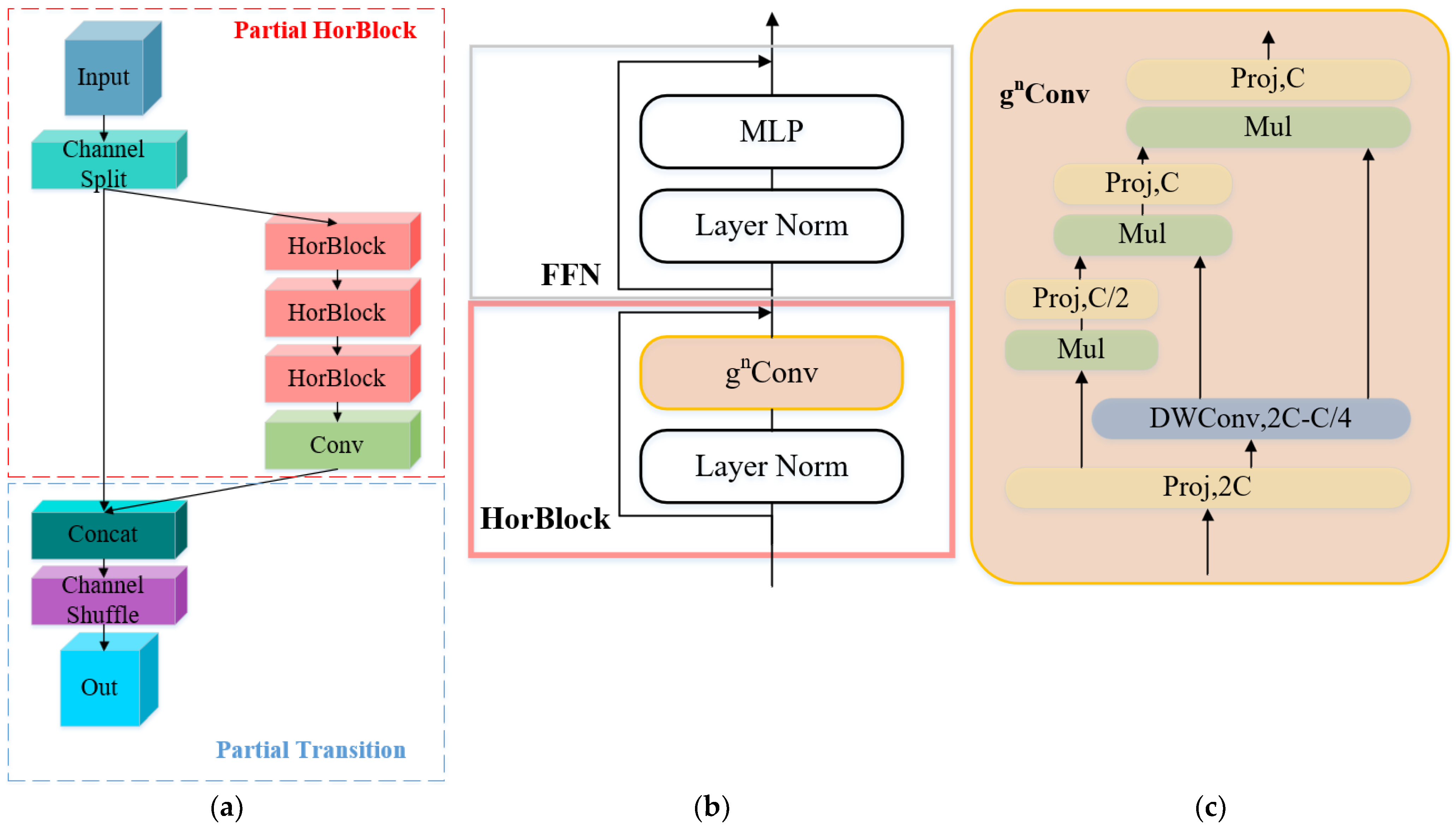
- Designing an efficient features extraction network block (S-HorBlock) specifically for ODCA-YOLO. S-HorBlock enhances the network’s learning capacity and improves its ability to extract diverse types of defective wood features.
2. Methodology
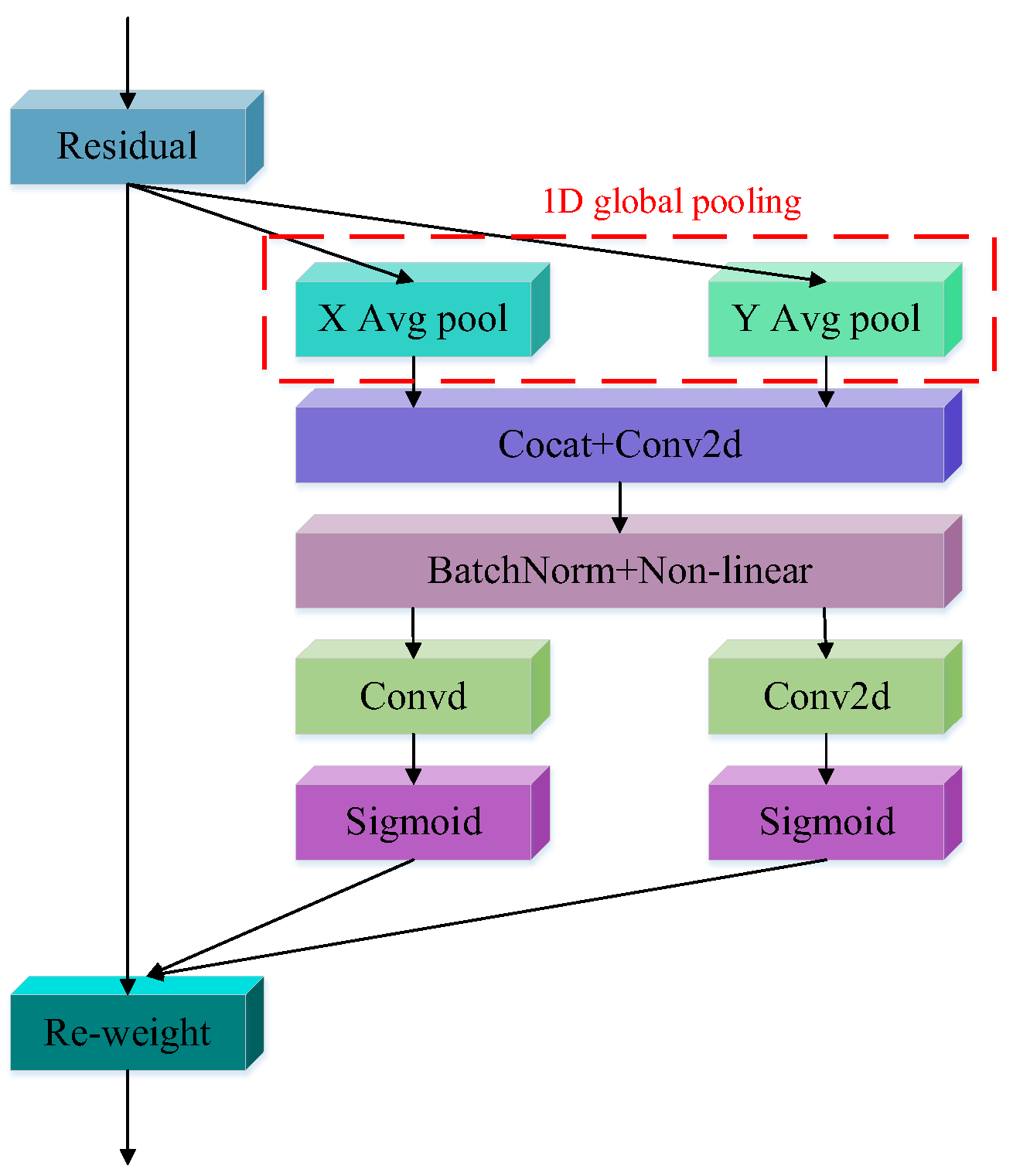
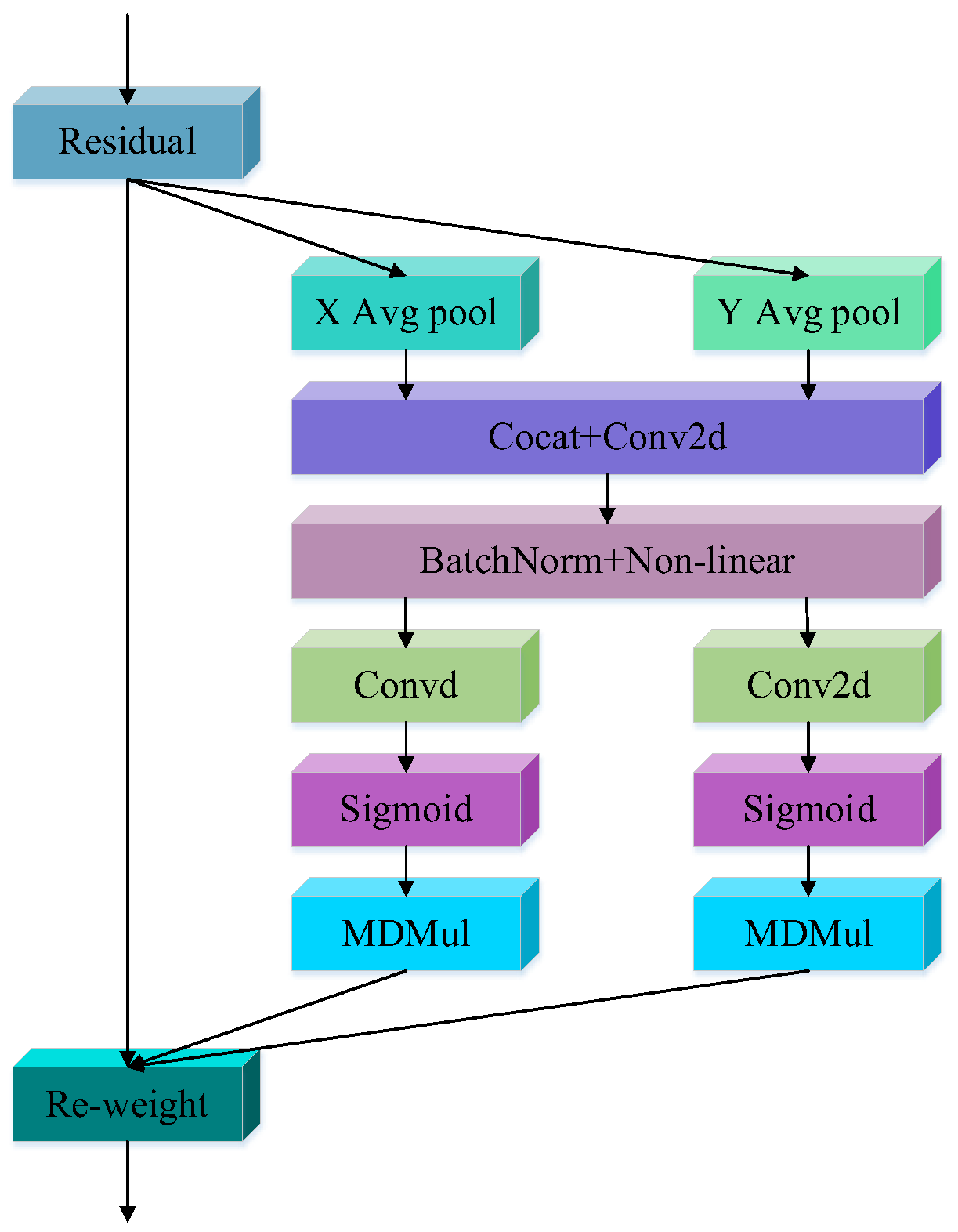
2.1. Omni-Dimensional Dynamic Coordinate Attention
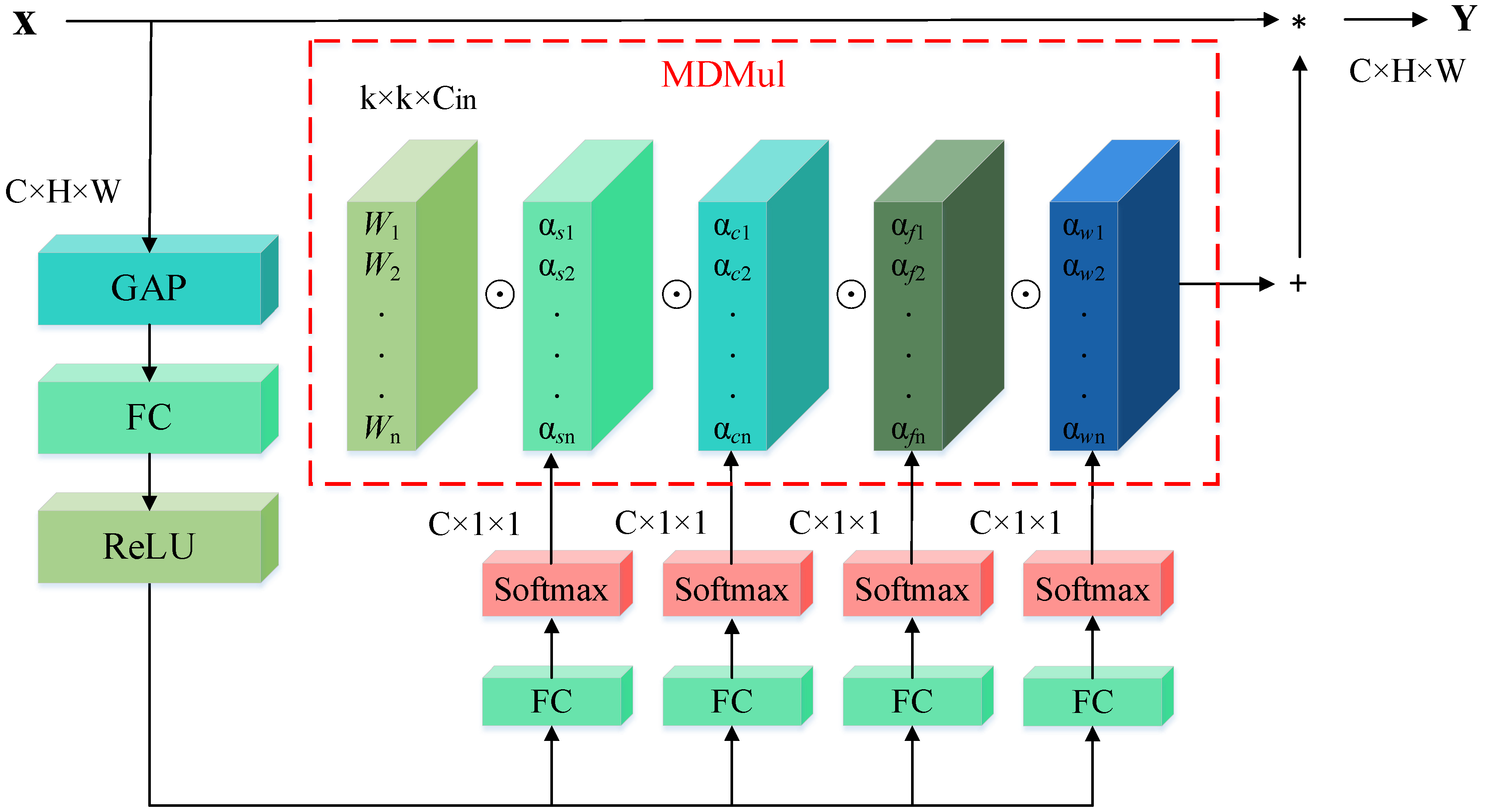
2.1.1. Review of Omni-Dimensional Dynamic Convolution
| Algorithm 1: ODConv |
| Input: Output: # Initialization Step 1: Step 2: Step 3: Step 4: Step 5: Step 6: Step 7: Step 8: |
2.1.2. Design of ODCA
| Algorithm 2: ODCA |
| Input: Output: # Initialization Step 1: Step 2: Step 3: Step 4: Step 5: Step 6: Step7: Step 8: |
2.2. S-HorBlock Module
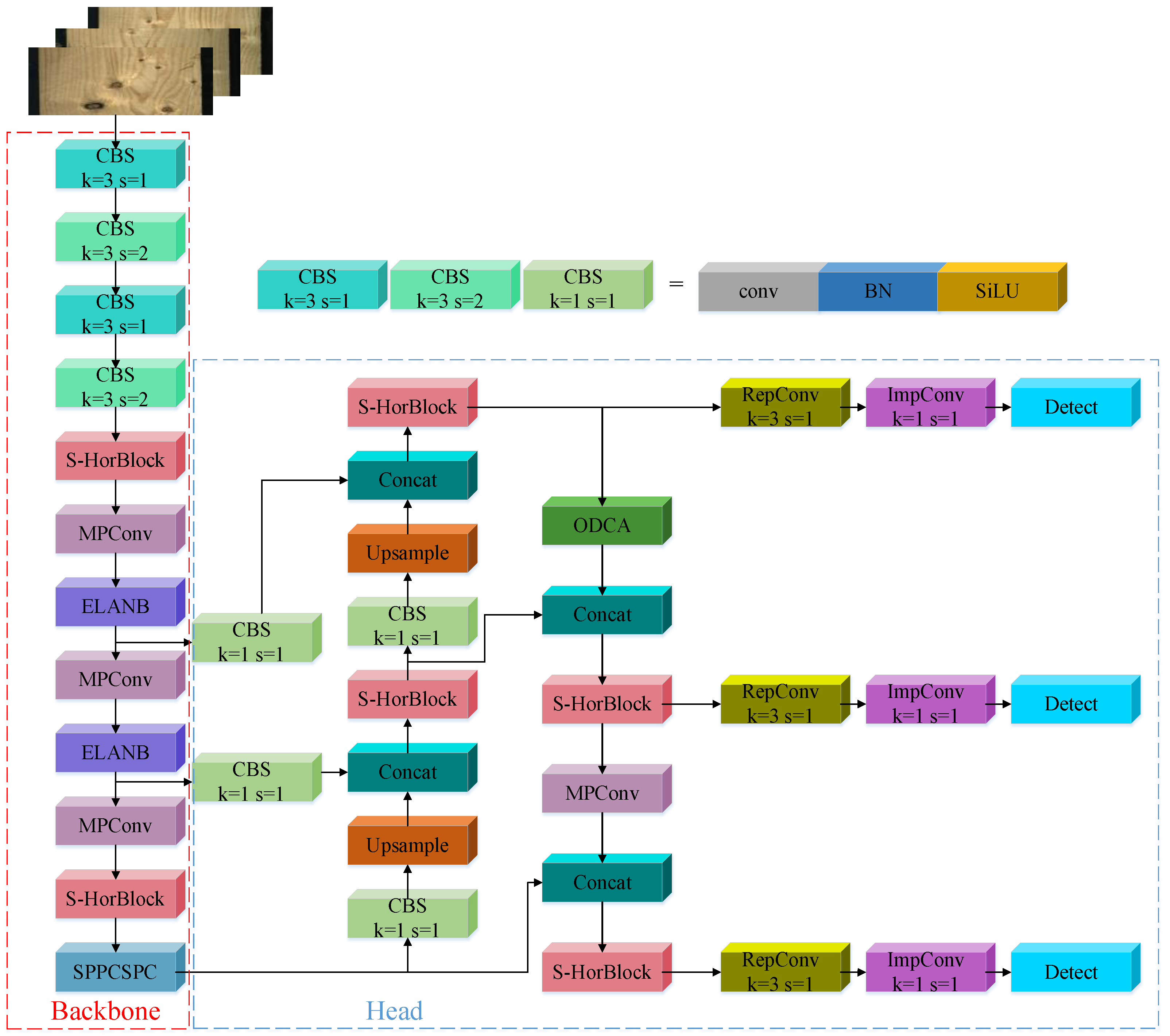
2.3. The Proposed ODCA-YOLO
3. Experiment and Results
3.1. Experimental Details and Dataset
3.2. Performance Evaluation
3.3. Ablation Experiments
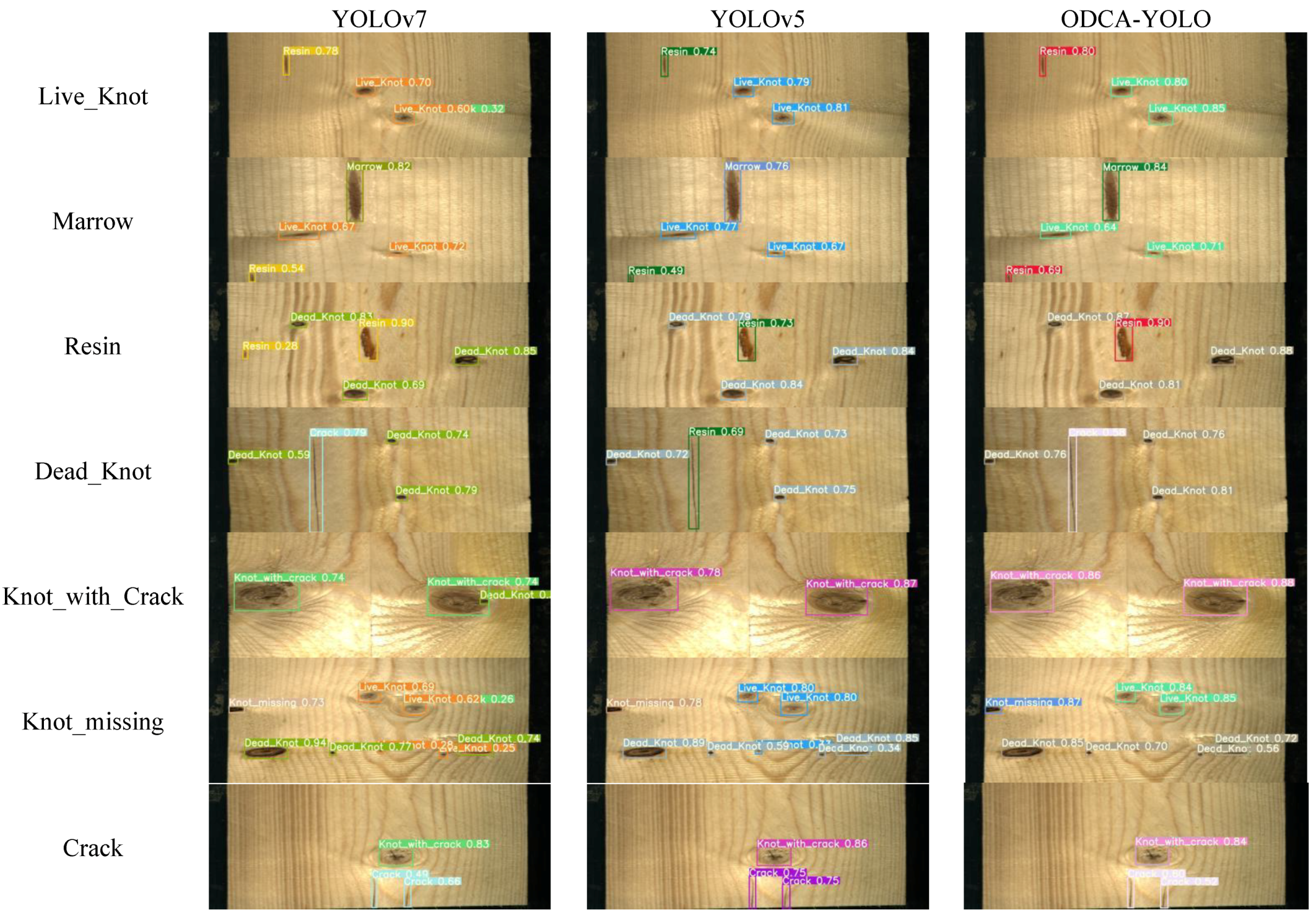
3.4. Comparisons with Other Methods and Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Longuetaud, F.; Mothe, F.; Kerautret, B.; Krähenbühl, A.; Hory, L.; Leban, J.M.; Debled-Rennesson, I. Automatic knot detection and measurements from X-ray CT images of wood: A review and validation of an improved algorithm on softwood samples. Comput. Electron. Agric. 2012, 85, 77–89. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, C.; Ren, Z.; Na, B. Review of the current state of application of wood defect recognition technology. BioResources 2022, 18, 2288–2302. [Google Scholar] [CrossRef]
- Deflorio, G.; Fink, S.; Schwarze, F.W.M.R. Detection of incipient decay in tree stems with sonic tomography after wounding and fungal inoculation. Wood Sci. Technol. 2008, 42, 117–132. [Google Scholar] [CrossRef]
- Fang, Y.; Lin, L.; Feng, H.; Lu, Z.; Emms, G.W. Review of the use of air-coupled ultrasonic technologies for nondestructive testing of wood and wood products. Comput. Electron. Agric. 2017, 137, 79–87. [Google Scholar] [CrossRef]
- Yang, H.; Yu, L. Feature extraction of wood-hole defects using wavelet-based ultrasonic testing. J. For. Res. 2017, 28, 395–402. [Google Scholar] [CrossRef]
- Li, X.; Qian, W.; Cheng, L.; Chang, L. A coupling model based on grey relational analysis and stepwise discriminant analysis for wood defect area identification by stress wave. BioResources 2020, 15, 1171–1186. [Google Scholar] [CrossRef]
- Du, X.; Li, J.; Feng, H.; Chen, S. Image Reconstruction of Internal Defects in Wood Based on Segmented Propagation Rays of Stress Waves. Appl. Sci. 2018, 8, 1778. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, X.; Yang, S. Predicting Density and Moisture Content of Populus xiangchengensis and Phyllostachys edulis using the X-Ray Computed Tomography Technique. For. Prod. J. 2020, 70, 193–199. [Google Scholar] [CrossRef]
- Qiu, Q. Thermal conductivity assessment of wood using micro computed tomography based finite element analysis (μCT-based FEA). NDT E Int. 2023, 139, 102921. [Google Scholar] [CrossRef]
- Lai, F.; Luo, T.; Ding, R.; Luo, R.; Deng, T.; Wang, W.; Li, M. Application of Image Processing Technology to Wood Surface Defect Detection. For. Mach. Woodwork Equip. 2021, 49, 16–21. [Google Scholar] [CrossRef]
- Siekański, P.; Magda, K.; Malowany, K.; Rutkiewicz, J.; Styk, A.; Krzesłowski, J.; Kowaluk, T.; Zagórski, A. On-Line Laser Triangulation Scanner for Wood Logs Surface Geometry Measurement. Sensors 2019, 19, 1074. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yue, L.; Xiao, N. Simultaneous Wood Defect and Species Detection with 3D Laser Scanning Scheme. Int. J. Opt. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Hu, C.; Tanaka, C.; Ohtani, T. Locating and identifying splits and holes on sugi by the laser displacement sensor. J. Wood Sci. 2003, 49, 492–498. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Wang, B.; Yang, C.; Deng, L. Detection method of timber defects based on target detection algorithm. Measurement 2022, 203, 111937. [Google Scholar] [CrossRef]
- Shi, J.; Li, Z.; Zhu, T.; Wang, D.; Ni, C. Defect Detection of Industry Wood Veneer Based on NAS and Multi-Channel Mask R-CNN. Sensors 2020, 20, 4398. [Google Scholar] [CrossRef]
- Han, S.; Jiang, X.; Wu, Z. An Improved YOLOv5 Algorithm for Wood Defect Detection Based on Attention. IEEE Access 2023, 11, 71800–71810. [Google Scholar] [CrossRef]
- Cui, Y.; Lu, S.; Liu, S. Real-time detection of wood defects based on SPP-improved YOLO algorithm. Multimed Tools Appl. 2023, 82, 21031–21044. [Google Scholar] [CrossRef]
- Gao, M.; Wang, F.; Song, P.; Liu, J.; Qi, D. BLNN: Multiscale Feature Fusion-Based Bilinear Fine-Grained Convolutional Neural Network for Image Classification of Wood Knot Defects. J. Sens. 2021, 2021, 1–18. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. arXiv 2022, arXiv:2207.02696. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2016, arXiv:1506.02640. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. arXiv 2016, arXiv:1612.08242. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Li, C.; Li, L.; Jiang, H.; Weng, K.; Geng, Y.; Li, L.; Ke, Z.; Li, Q.; Cheng, M.; Nie, W.; et al. YOLOv6: A Single-Stage Object Detection Framework for Industrial Applications. arXiv 2022, arXiv:2209.02976. [Google Scholar]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. YOLOX: Exceeding YOLO Series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Sirisha, U.; Praveen, S.P.; Srinivasu, P.N.; Barsocchi, P.; Bhoi, A.K. Statistical Analysis of Design Aspects of Various YOLO-Based Deep Learning Models for Object Detection. Int. J. Comput. Intell. Syst. 2023, 16, 126. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, X.; Liu, M.; Chen, D.; Yuan, L.; Liu, Z. Dynamic Convolution: Attention Over Convolution Kernels. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 11027–11036. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2019, arXiv:1709.01507. [Google Scholar]
- Li, C.; Zhou, A.; Yao, A. Omni-Dimensional Dynamic Convolution. arXiv 2022, arXiv:2209.07947. [Google Scholar]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 13708–13717. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. arXiv 2018, arXiv:1807.11164. [Google Scholar]
- Rao, Y.; Zhao, W.; Tang, Y.; Zhou, J.; Lim, S.-N.; Lu, J. HorNet: Efficient High-Order Spatial Interactions with Recursive Gated Convolutions. arXiv 2022, arXiv:2207.14284. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Kodytek, P.; Bodzas, A.; Bilik, P. A large-scale image dataset of wood surface defects for automated vision-based quality control processes. F1000Research 2022, 10, 581. [Google Scholar] [CrossRef] [PubMed]


| Defect Type | Number of Occurrences | Number of Images with the Defect | Images with the Defect in the Dataset (%) |
|---|---|---|---|
| Live_Knot | 4070 | 2256 | 62.7 |
| Marrow | 206 | 191 | 5.3 |
| Resin | 650 | 523 | 14.5 |
| Dead_Knot | 2934 | 1875 | 52.1 |
| Knot_with_crack | 542 | 398 | 11.1 |
| Knot_missing | 121 | 110 | 3.1 |
| Crack | 517 | 371 | 10.3 |
| without any defects | — | 7 | 0.2 |
| mAP | AP | |||||||
|---|---|---|---|---|---|---|---|---|
| Live_Knot | Morrow | Resin | Dead_Knot | Knot_with_Crack | Knot_Missing | Crack | ||
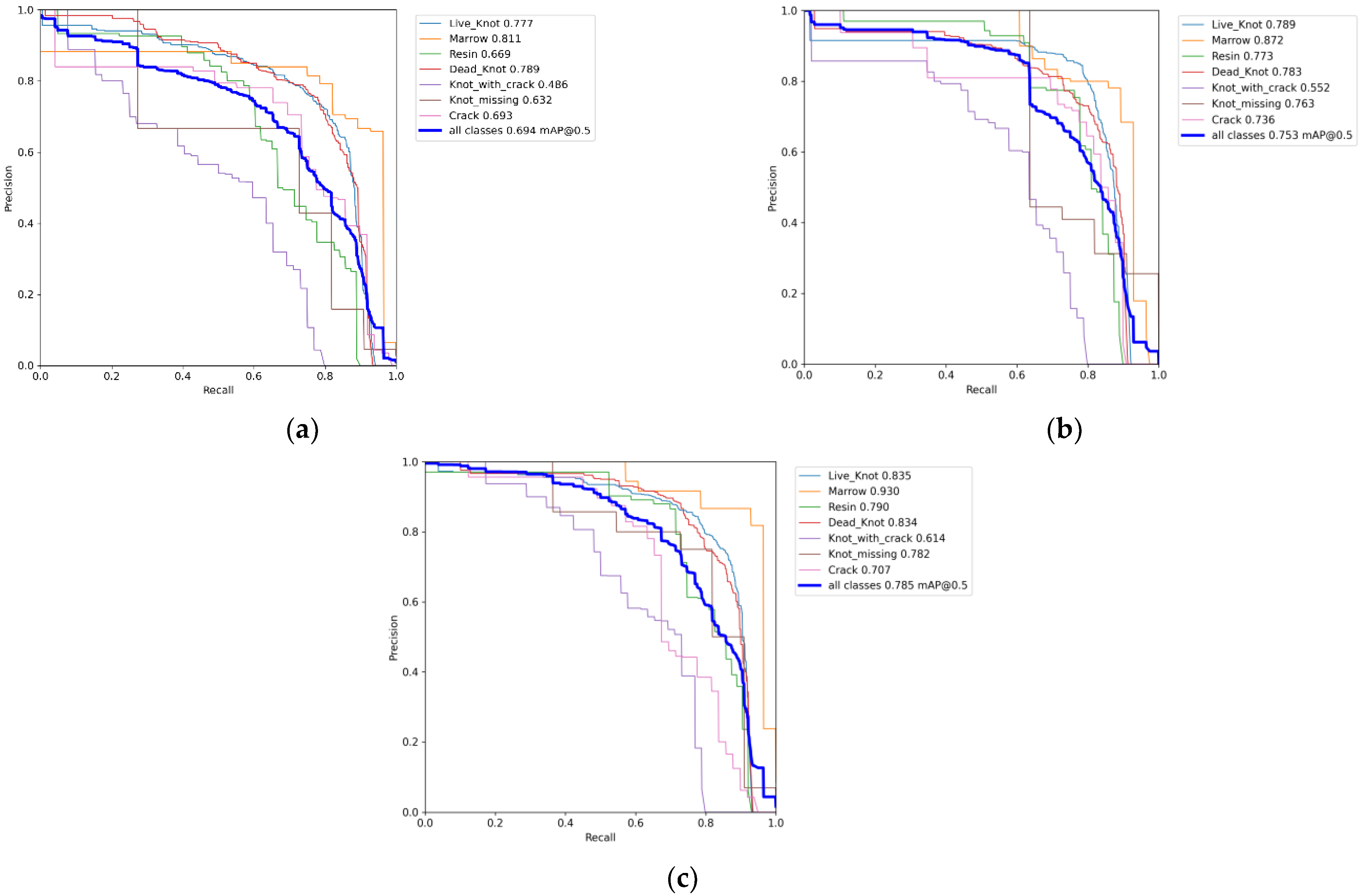
| YOLOv7 | 0.694 | 0.777 | 0.811 | 0.669 | 0.789 | 0.486 | 0.632 | 0.693 |
| YOLOv7+S-HorBlock | 0.745 | 0.830 | 0.747 | 0.698 | 0.832 | 0.543 | 0.868 | 0.694 |
| YOLOv7+ODCA | 0.753 | 0.842 | 0.807 | 0.793 | 0.836 | 0.592 | 0.736 | 0.668 |
| ODCA-YOLO | 0.785 | 0.835 | 0.930 | 0.790 | 0.834 | 0.614 | 0.782 | 0.707 |
| mAP | AP | |||||||
|---|---|---|---|---|---|---|---|---|
| Live_Knot | Morrow | Resin | Dead_Knot | Knot_with_Crack | Knot_Missing | Crack | ||
| YOLOv5 | 0.753 | 0.789 | 0.872 | 0.773 | 0.783 | 0.552 | 0.763 | 0.736 |
| YOLOv7 | 0.694 | 0.777 | 0.811 | 0.669 | 0.789 | 0.486 | 0.632 | 0.693 |
| YOLOX | 0.600 | 0.692 | 0.661 | 0.760 | 0.666 | 0.403 | 0.474 | 0.544 |
| SSD | 0.605 | 0.695 | 0.642 | 0.774 | 0.650 | 0.511 | 0.483 | 0.479 |
| RetinaNet | 0.526 | 0.684 | 0.413 | 0.735 | 0.633 | 0.541 | 0.477 | 0.196 |
| ODCA-YOLO | 0.785 | 0.835 | 0.930 | 0.790 | 0.834 | 0.614 | 0.782 | 0.707 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Liang, F.; Wang, B.; Mou, X. ODCA-YOLO: An Omni-Dynamic Convolution Coordinate Attention-Based YOLO for Wood Defect Detection. Forests 2023, 14, 1885. https://doi.org/10.3390/f14091885
Wang R, Liang F, Wang B, Mou X. ODCA-YOLO: An Omni-Dynamic Convolution Coordinate Attention-Based YOLO for Wood Defect Detection. Forests. 2023; 14(9):1885. https://doi.org/10.3390/f14091885
Chicago/Turabian StyleWang, Rijun, Fulong Liang, Bo Wang, and Xiangwei Mou. 2023. "ODCA-YOLO: An Omni-Dynamic Convolution Coordinate Attention-Based YOLO for Wood Defect Detection" Forests 14, no. 9: 1885. https://doi.org/10.3390/f14091885
APA StyleWang, R., Liang, F., Wang, B., & Mou, X. (2023). ODCA-YOLO: An Omni-Dynamic Convolution Coordinate Attention-Based YOLO for Wood Defect Detection. Forests, 14(9), 1885. https://doi.org/10.3390/f14091885







