Constructing Coupling Model of Generalized B-Spline Curve and Crown (CMGBCC) to Explore the 3D Modeling of Chinese Fir Polymorphism
Abstract
1. Introduction
2. Materials and Methods
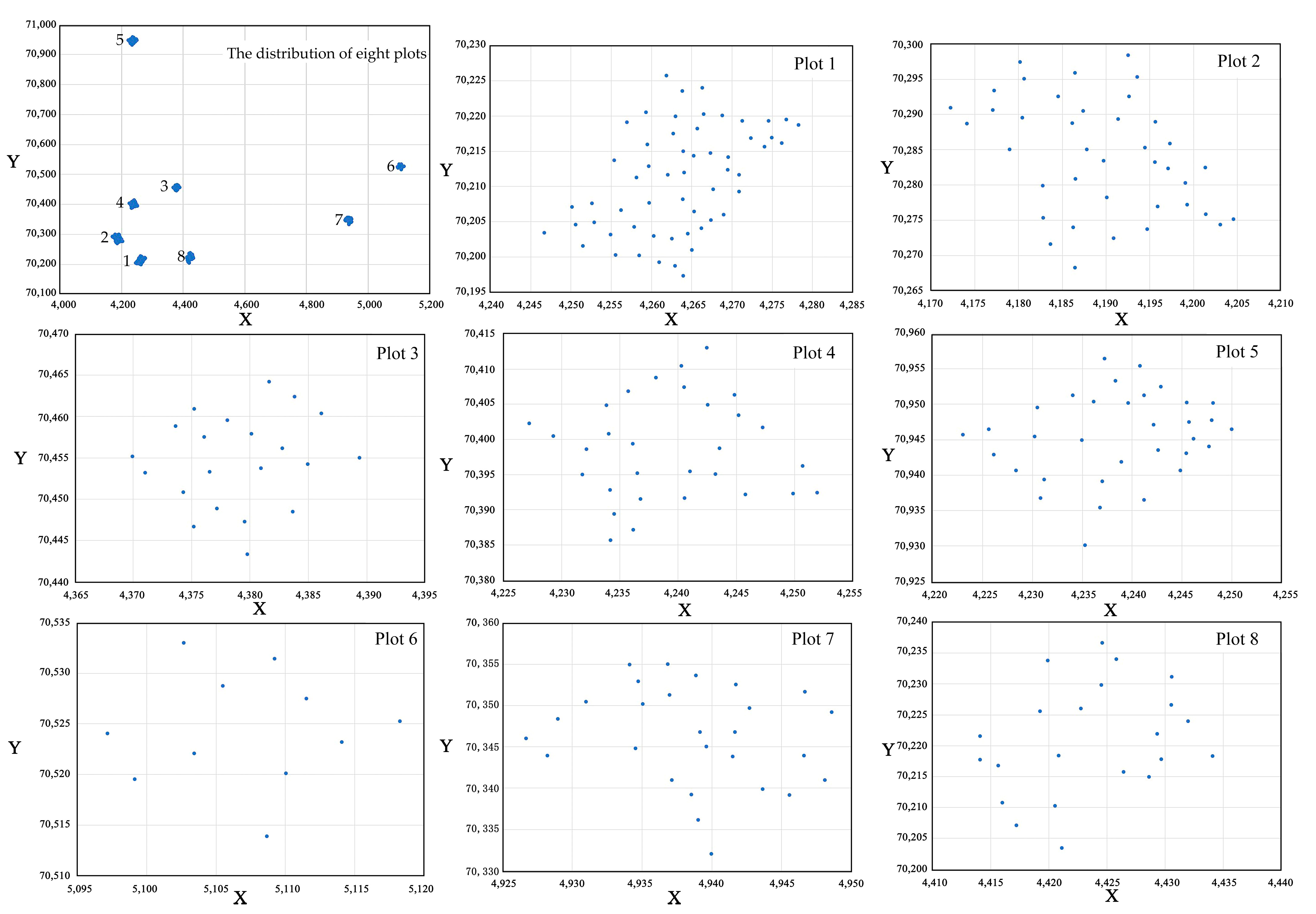
2.1. Data
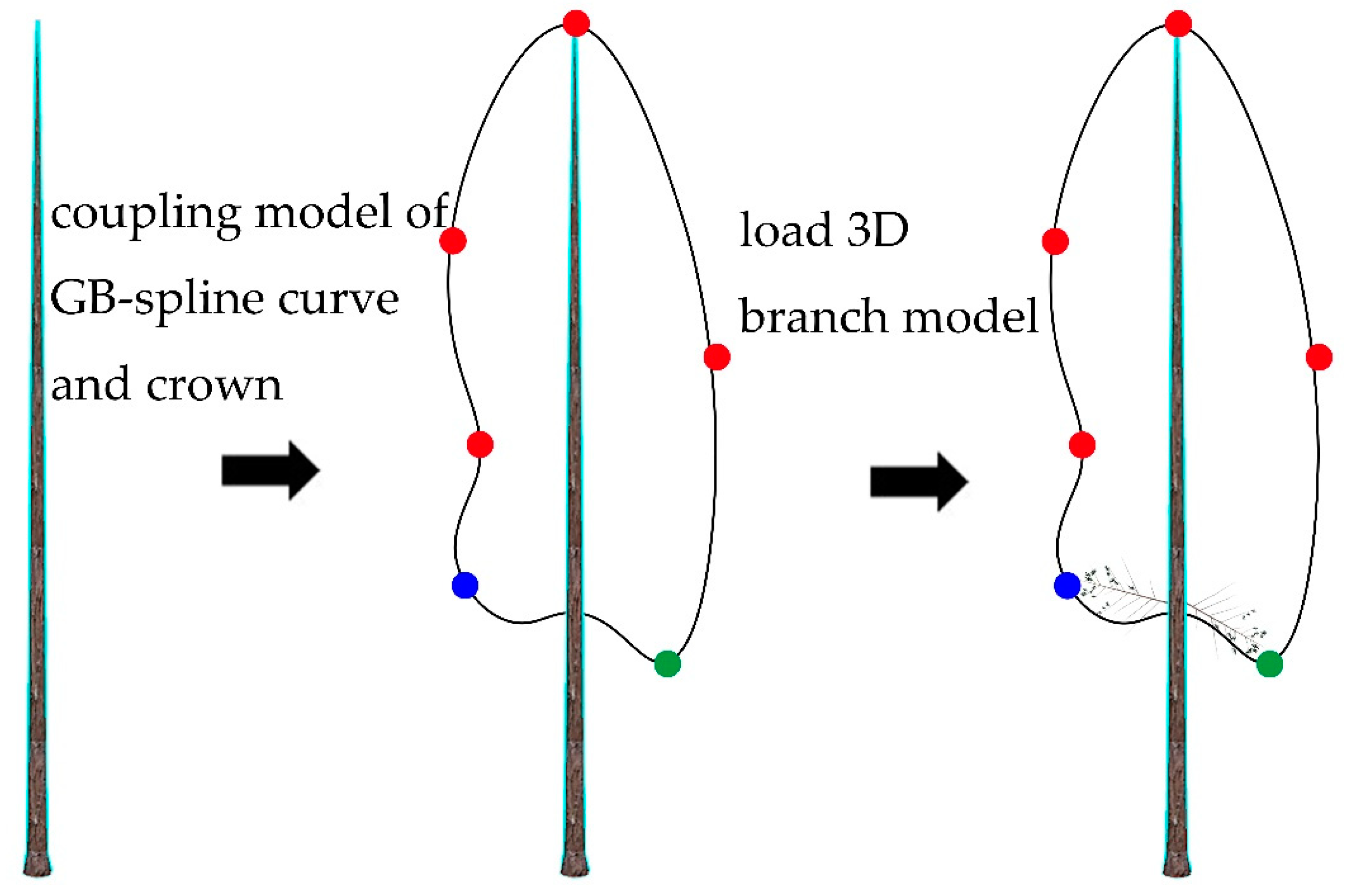
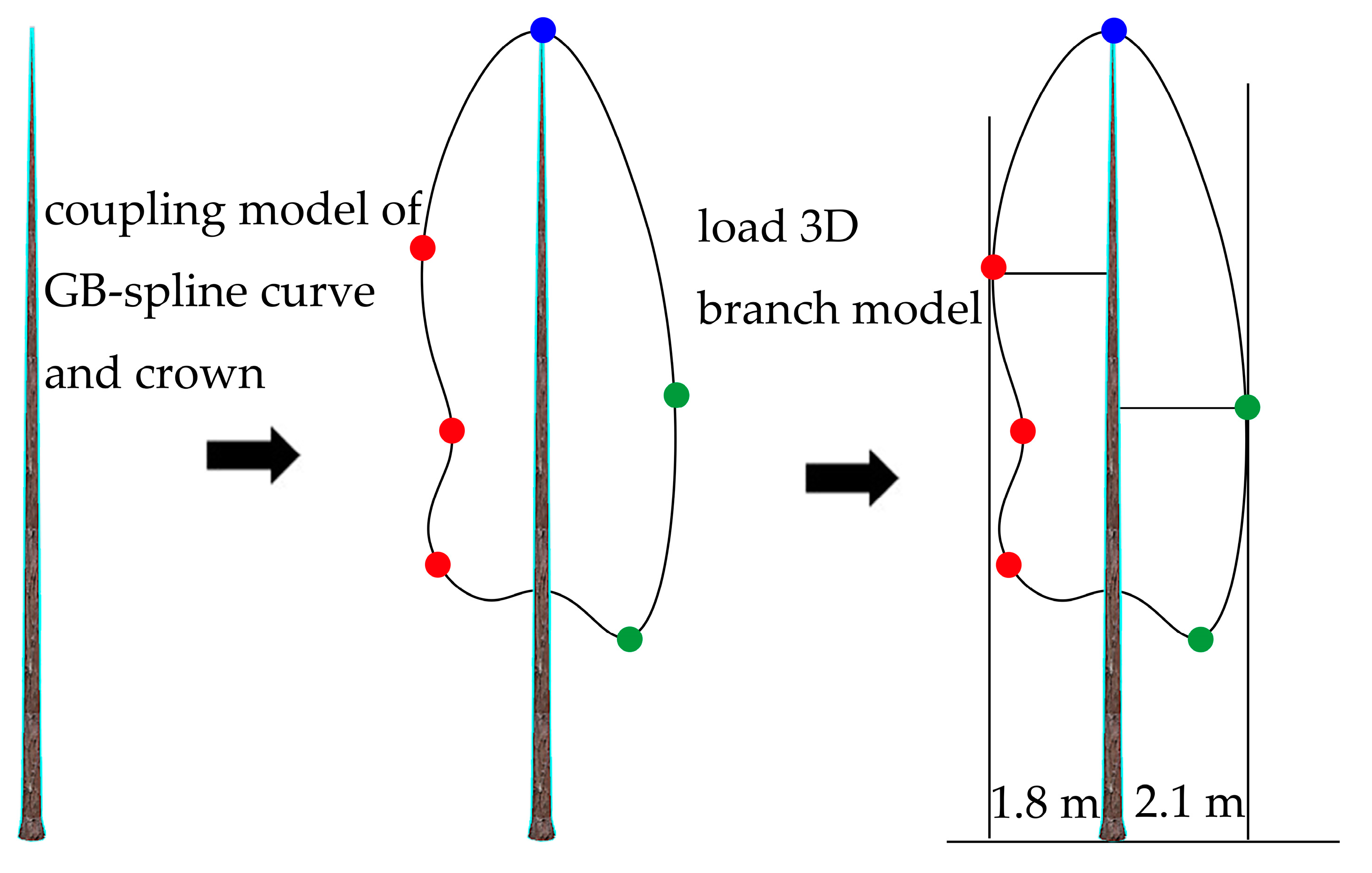
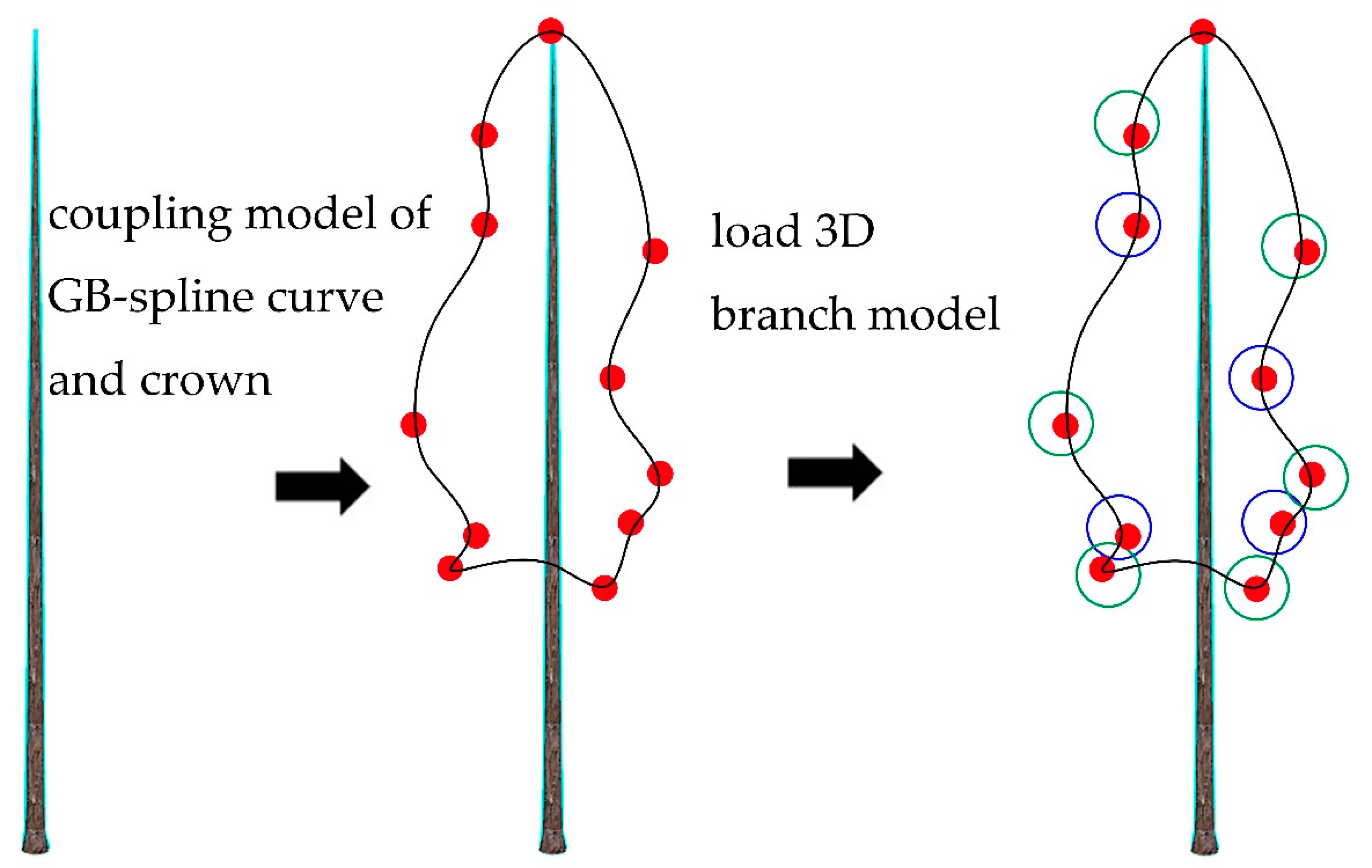
2.2. Constructing CMGBCC
2.3. Constructing Coupling Model of 3D Chinese Fir Trunk, Branches Model and Withered State
2.4. Simulations of Three Types of the Tree Polymorphism
3. Results
3.1. 3D Models of Chinese Fir Trunk and Branch
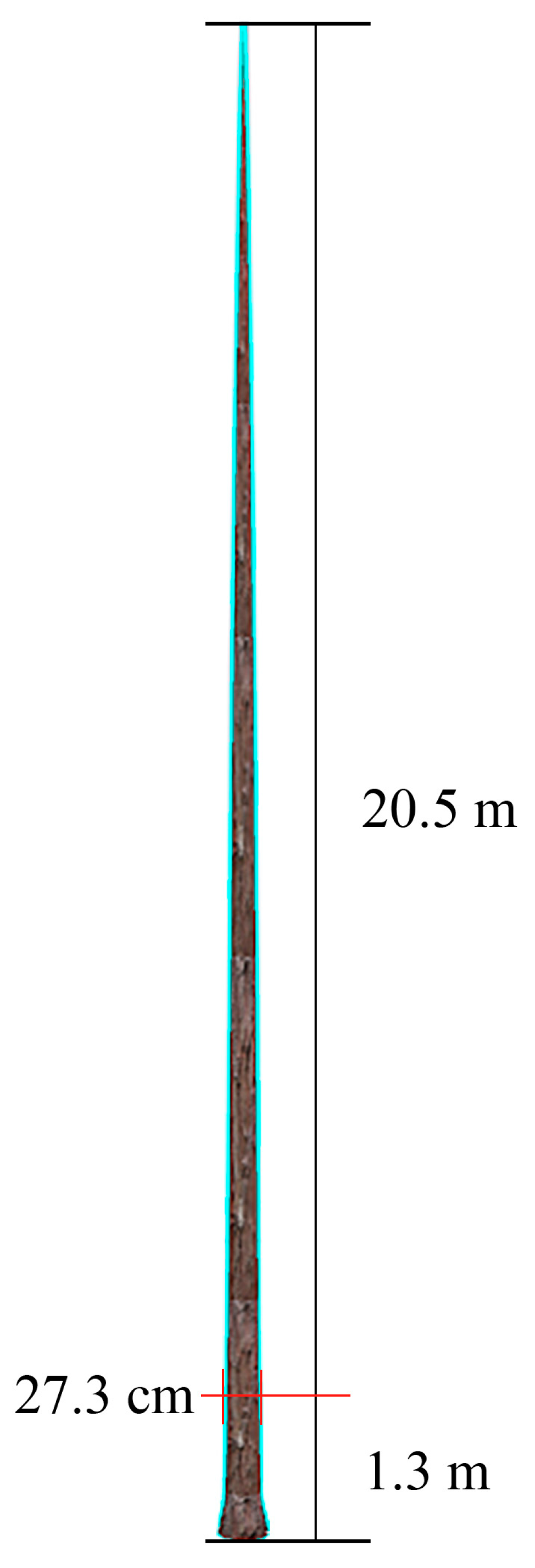
3.1.1. 3D Models of Chinese Fir Trunk
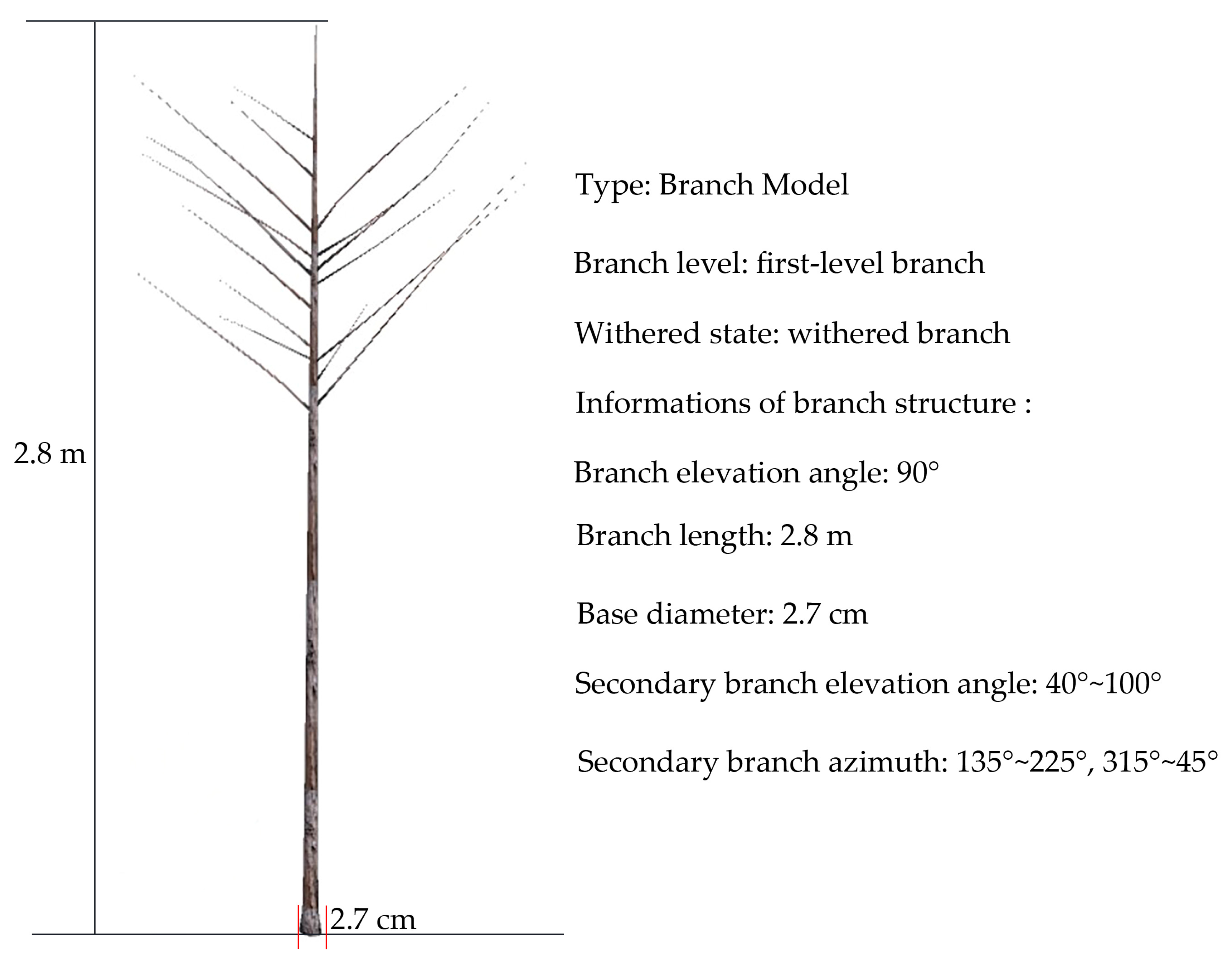
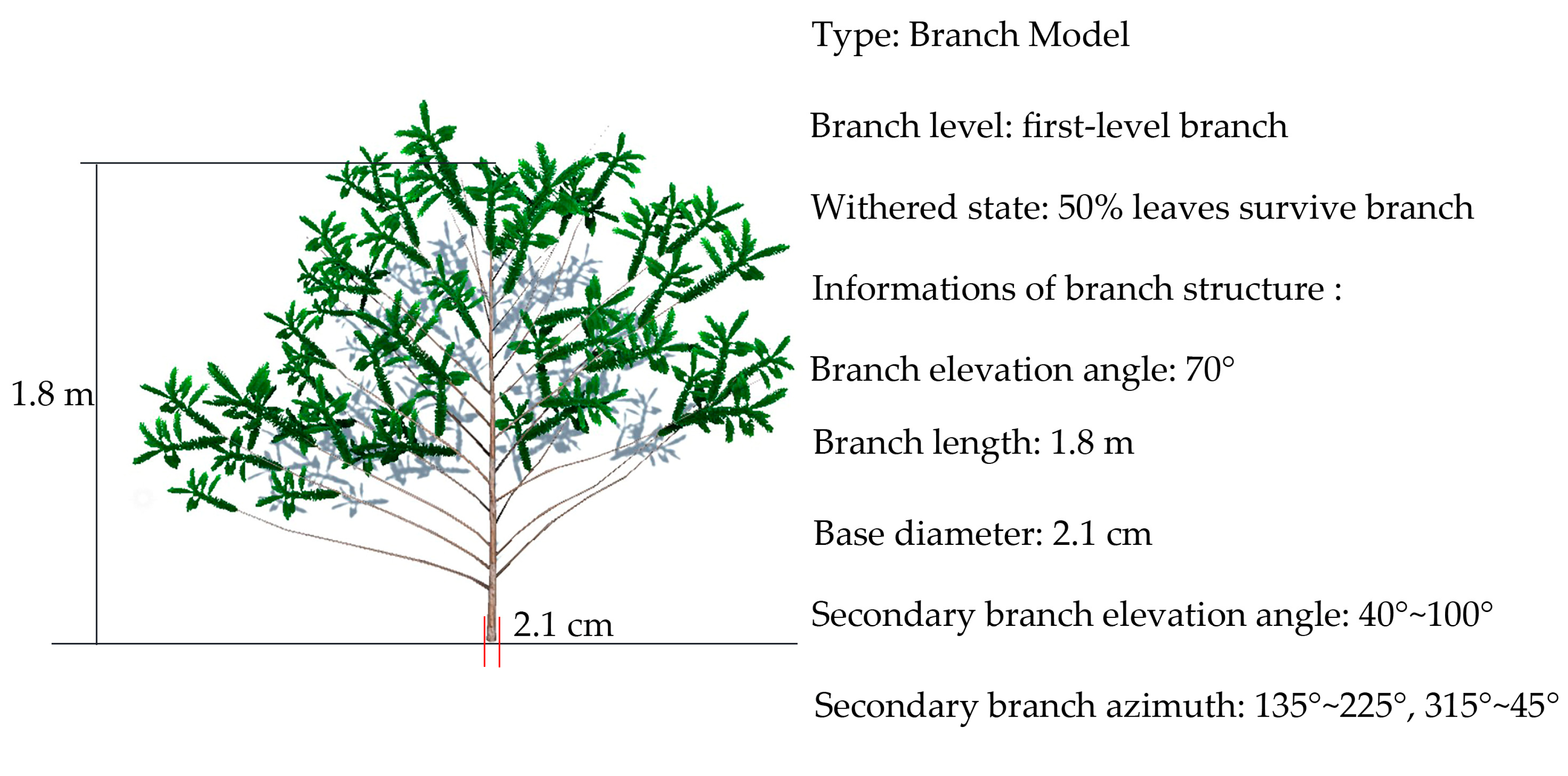
3.1.2. 3D Models of Chinese Fir Branch
3.2. The Result of CMGBCC
3.3. 3D Modeling and Verification of Chinese Fir Polymorphism
4. Discussion
5. Conclusions
- Constructing CMGBCC improved the fitting function for the crown curve.
- We considered the influence of different withered state branches on the whole shape in 3D tree modeling.
- We simulated three types of polymorphisms, including natural pruning, crown displacement, and crown shape difference.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ogawa, K. Size Dependence of Leaf Area and the Mass of Component Organs during a Course of Self-Thinning in a Hinoki (Chamaecyparis obtusa) Seedling Population. Ecol. Res. 2003, 18, 611–618. [Google Scholar] [CrossRef]
- Wang, C.S.; Tang, C.; Hein, S.; Guo, J.J.; Zhao, Z.G.; Zeng, J. Branch Development of Five-Year-Old Betula Alnoides Plantations in Response to Planting Density. Forests 2018, 9, 42. [Google Scholar] [CrossRef]
- Busing, R.T. Disturbance and the Population Dynamics of Liriodendron Tulipifera: Simulations with a Spatial Model of Forest Succession. J. Ecol. 1995, 83, 45. [Google Scholar] [CrossRef]
- Fleck, S.; Mölder, I.; Jacob, M.; Gebauer, T.; Jungkunst, H.F.; Leuschner, C. Comparison of Conventional Eight-Point Crown Projections with LIDAR-Based Virtual Crown Projections in a Temperate Old-Growth Forest. Ann. For. Sci. 2011, 68, 1173–1185. [Google Scholar] [CrossRef]
- Mizunaga, H.; Umeki, T. The Relationships between Tree Size and Spatial Distribution of Foliage-Mass within Crowns of Japanese Cedars (Cryptomeria japonica) in Young Plantations. For. Ecol. Manag. 2001, 149, 129–140. [Google Scholar] [CrossRef]
- Locosselli, G.M.; de Camargo, E.P.; Moreira, T.C.L.; Todesco, E.; Andrade, M.d.F.; de André, C.D.S.; de André, P.A.; Singer, J.M.; Ferreira, L.S.; Saldiva, P.H.N.; et al. The Role of Air Pollution and Climate on the Growth of Urban Trees. Sci. Total Environ. 2019, 666, 652–661. [Google Scholar] [CrossRef] [PubMed]
- Petritan, A.M.; von Lüpke, B.; Petritan, I.C. Influence of Light Availability on Growth, Leaf Morphology and Plant Architecture of Beech (Fagus sylvatica L.), Maple (Acer pseudoplatanus L.) and Ash (Fraxinus excelsior L.) Saplings. Eur. J. For. Res. 2009, 128, 61–74. [Google Scholar] [CrossRef]
- Fang, K.; Chen, D.; Gou, X.; D’Arrigo, R.; Davi, N. Influence of Non-Climatic Factors on the Relationships between Tree Growth and Climate over the Chinese Loess Plateau. Glob. Planet. Change 2015, 132, 54–63. [Google Scholar] [CrossRef]
- Buechling, A.; Martin, P.; Canham, C. Climate and competition effects on tree growth in Rocky Mountain forests. J. Ecol. 2017, 105, 1636–1647. [Google Scholar] [CrossRef]
- Coomes, D.A.; Allen, R.B. Effects of Size, Competition and Altitude on Tree Growth. J. Ecol. 2007, 95, 1084–1097. [Google Scholar] [CrossRef]
- Tucker, G.F.; Lassoie, J.P.; Fahey, T.J. Crown Architecture of Stand-Grown Sugar Maple (Acer saccharum Marsh.) in the Adirondack Mountains. Tree Physiol. 1993, 13, 297–310. [Google Scholar] [CrossRef]
- Turkington, R.; Goldberg, D.E.; Olsvig-Whittaker, L.; Dyer, A.R. Effects of Density on Timing of Emergence and Its Consequences for Survival and Growth in Two Communities of Annual Plants. J. Arid Environ. 2005, 61, 377–396. [Google Scholar] [CrossRef]
- Davies, O.; Pommerening, A. The Contribution of Structural Indices to the Modelling of Sitka Spruce (Picea sitchensis) and Birch (Betula Spp.) Crowns. For. Ecol. Manag. 2008, 256, 68–77. [Google Scholar] [CrossRef]
- Marozau, A.; Kotszan, U.; Nowakowska, J.; Berezovska, D.; Moser, W.K.; Hsiang, T.; Oszako, T. The Influence of the Provenance and Spatial Structure on the Growth of European Silver Fir (Abies alba Mill.) of Autochthonous Origin in a Forest Plantation in the Białowieża Forest. Forests 2022, 13, 831. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Li, Y.; Yang, T.; Chen, Z.; Li, S. Visual Simulation of Chinese Fir Crown Growth Based on Spatial Structure. For. Res. 2018, 13, 150–157. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, N.; Zhang, H.; Cui, Z.; Yang, T.; Li, Y.; Liu, H. Visual Simulation of Chinese Fir under Branch Height in Consideration of Spatial Structure. J. Nanjing For. Univ. Nat. Sci. Ed. 2022, 46, 51–57. (In Chinese) [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, H.; Zuo, Y.; Yang, T.; Liu, Y.; Zhang, J.; Wang, L. The Distribution of under Branch Heights in Various Directions of the Three-Dimensional Chinese Fir Model. J. Nanjing For. Univ. Natural Sci. Ed. 2022, 46, 81–87. (In Chinese) [Google Scholar] [CrossRef]
- Crecente-Campo, F.; Marshall, P.; LeMay, V.; Diéguez-Aranda, U. A Crown Profile Model for Pinus Radiata D. Don in Northwestern Spain. For. Ecol. Manag. 2009, 257, 2370–2379. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, C.; Wu, B. Crown Profile Modeling and Prediction Based on Ensemble Learning. Forests 2022, 13, 410. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, H.Q.; Lu, K.N. Research on Three-Dimensional Simulation of Tree’s Morphology Based on Tree-Crown Growth Model. In Proceedings of the 2010 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 10–12 December 2010; IEEE: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Runions, A.; Lane, B.; Prusinkiewicz, P. Modeling Trees with a Space Colonization Algorithm. Nat. Phenom. 2007, 6, 63–70. [Google Scholar]
- Palubicki, W.; Horel, K.; Longay, S.; Runions, A.; Lane, B.; Měch, R.; Prusinkiewicz, P. Self-Organizing Tree Models for Image Synthesis. ACM Trans. Graph. 2009, 28, 1–10. [Google Scholar] [CrossRef]
- Suzuki, T.; Ohsaki, K.; Sato, H. A representation method for todo-fir shapes using computer graphics. J. Jpn. For. Soc. 1992, 74, 504–508. (In Japanese) [Google Scholar]
- Eilers, P.H.C.; Marx, B.D. Flexible Smoothing with B-Splines and Penalties. Stat. Sci. 1996, 11, 89–102. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, M.; Wang, X. Interactive Modeling of 3D Tree with Ball B-Spline Curves. Int. J. Virtual Real. 2009, 8, 101–107. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Wu, Z.; Zhang, D.; Liu, X. Extending Ball B-Spline by B-Spline. Comput. Aided Geom. Des. 2020, 82, 101926. [Google Scholar] [CrossRef]
- Harmening, C.; Hobmaier, C.; Neuner, H. Laser Scanner–Based Deformation Analysis Using Approximating B-Spline Surfaces. Remote Sens. 2021, 18, 3551. [Google Scholar] [CrossRef]
- Sun, Y. Existence of Triple Positive Solutions for a Third-Order Three-Point Boundary Value Problem. J. Comput. Appl. Math. 2008, 221, 194–201. [Google Scholar] [CrossRef]
- Böhm, W. Generating the Bézier Points of B-Spline Curves and Surfaces. Comput. Des. 1981, 13, 365–366. [Google Scholar] [CrossRef]
- Beccari, C.V.; Casciola, G. A Cox-de Boor-Type Recurrence Relation for C1 Multi-Degree Splines. Comput. Aided Geom. Des. 2019, 75, 101784. [Google Scholar] [CrossRef]
- Fritsch, D.; Kada, M. Visualisation Using Game Engines. Geo-Informations-Systeme 2004, 2004, 32–36. [Google Scholar]
- Tang, X.; Pérez-Cruzado, C.; Fehrmann, L.; Álvarez-González, J.G.; Lu, Y.; Kleinn, C. Development of a Compatible Taper Function and Stand-Level Merchantable Volume Model for Chinese Fir Plantations. PLoS ONE 2016, 11, e0147610. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, J.; Duan, A.; Zhang, J. Variable-Exponent Taper Equation Based on Multilevel Nonlinear Mixed Effect for Chinese Fir in China. Forests 2021, 12, 126. [Google Scholar] [CrossRef]
- Duan, A.; Zhang, S.; Zhang, X.; Zhang, J. Development of a Stem Taper Equation and Modelling the Effect of Stand Density on Taper for Chinese Fir Plantations in Southern China. PeerJ 2016, 2016, e1929. [Google Scholar] [CrossRef] [PubMed]
- Lu, K.; Zhang, H.; Liu, M. Study on Plant Architecture of Cunningham ia lanceolata Based on Measured Data. For. Res. 2011, 24, 132–136. (In Chinese) [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J.; Duan, A.; He, C. Estimation of the Self-Thinning Boundary Line within Even-Aged Chinese Fir (Cunninghamia lanceolata (Lamb.) Hook.) Stands: Onset of Self-Thinning. For. Ecol. Manag. 2011, 261, 1010–1015. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, Z.; Jia, W.; Li, D. Modelling the Tree Height, Crown Base Height, and Effective Crown Height of Pinus Koraiensis Plantations Based on Knot Analysis. Forests 2021, 12, 1778. [Google Scholar] [CrossRef]
- Vovides, A.G.; Berger, U.; Grueters, U.; Guevara, R.; Pommerening, A.; Lara-Domínguez, A.L.; López-Portillo, J. Change in Drivers of Mangrove Crown Displacement along a Salinity Stress Gradient. Funct. Ecol. 2018, 32, 2753–2765. [Google Scholar] [CrossRef]
- Longuetaud, F.; Piboule, A.; Wernsdörfer, H.; Collet, C. Crown Plasticity Reduces Inter-Tree Competition in a Mixed Broadleaved Forest. Eur. J. For. Res. 2013, 132, 621–634. [Google Scholar] [CrossRef]
- Tanveer, M.; Thomas, A.; Wu, X.; Zhu, H. Simulate forest trees by integrating l-system and 3d cad files. In Proceedings of the 2020 3rd International Conference on Information and Computer Technologies (ICICT), San Jose, CA, USA, 9–12 March 2020. [Google Scholar] [CrossRef]
- Wang, Z. Cloud Theory and Fractal Application in Virtual Plants. Int. J. Intell. Syst. Appl. 2011, 3, 17–23. [Google Scholar] [CrossRef]
- Tohru, N.; Tohru, N.; Mitsuo, M. Visualization of Optimized Solution Space Using a Simulation System for the Development of Local Forest Management Planning. Ann. For. Res. 2016, 59, 117–128. [Google Scholar] [CrossRef]
- Peng, F.; Zheng, H.; Lu, S.; Shi, Z.; Liu, X.; Li, L. Growth Model and Visualization of a Virtual Jujube Tree. Comput. Electron. Agric. 2019, 157, 146–153. [Google Scholar] [CrossRef]








| Type | Height/m | DBH/cm | UBH/m | HMCW/m | Crown Width/m | Age/a |
|---|---|---|---|---|---|---|
| Max | 30.4 | 36.5 | 14.6 | 18.1 | 4.0 | 30 |
| Min | 8.8 | 8.3 | 4.5 | 7.2 | 0.4 | 12 |
| Average | 17.8 | 23.6 | 8.0 | 13.9 | 1.7 | 24 |
| The Level of Branch | Index | Description |
|---|---|---|
| first-level branch | withered state | amount of needle cover on branches |
| first-level branch | elevation angle | the angle between the branch and the vertical direction of the trunk |
| first-level branch | branch length | length of branch |
| first-level branch | base diameter | branch base diameter |
| second-level branch | elevation angle | the angle between the branch and the vertical direction of the primary branch |
| second-level branch | azimuth | the angle between the branches in the horizontal direction of the primary branch |
| second-level branch | undershoot | length between the branch point and base |
| Tree Height Range | Model Height/m | DBH/cm |
|---|---|---|
| 8.0~9.0 | 8.8 | 13.5 |
| 14.0~15.0 | 14.5 | 20 |
| 20.0~21.0 | 20.5 | 27.3 |
| 26.0~27.0 | 26.4 | 29.7 |
| 30.0~31.0 | 30.4 | 31.2 |
| Index | b-Spline Interpolation | CMGBCC |
|---|---|---|
| Derivative value at the top point | Add manually and uncontrollable factors of the model | It does not need to manually input the derivative value at the top point, simplifying the model construction process and reducing the error caused by humans |
| Collection rules of type value points | Equal distance acquisition | It can be collected according to the crown shape change rules |
| Collection interval of type value points | Equal distance acquisition | Acquisition at any distance |
| Model complexity | The model form is relatively simple | The model form is relatively complex |
| Type | Height/m | DBH/cm | UBH/m | HMCW/m | Crown Width/m |
|---|---|---|---|---|---|
| Max | 28.3 | 34.2 | 14.2 | 17.0 | 3.8 |
| Min | 9.6 | 9.3 | 4.9 | 8.6 | 0.4 |
| Average | 17.0 | 20.4 | 8.3 | 13.1 | 1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Zhang, H.; Liu, Y.; Zhang, J.; Yang, T.; Zuo, Y.; Lei, K. Constructing Coupling Model of Generalized B-Spline Curve and Crown (CMGBCC) to Explore the 3D Modeling of Chinese Fir Polymorphism. Forests 2023, 14, 1267. https://doi.org/10.3390/f14061267
Cui Z, Zhang H, Liu Y, Zhang J, Yang T, Zuo Y, Lei K. Constructing Coupling Model of Generalized B-Spline Curve and Crown (CMGBCC) to Explore the 3D Modeling of Chinese Fir Polymorphism. Forests. 2023; 14(6):1267. https://doi.org/10.3390/f14061267
Chicago/Turabian StyleCui, Zeyu, Huaiqing Zhang, Yang Liu, Jing Zhang, Tingdong Yang, Yuanqing Zuo, and Kexin Lei. 2023. "Constructing Coupling Model of Generalized B-Spline Curve and Crown (CMGBCC) to Explore the 3D Modeling of Chinese Fir Polymorphism" Forests 14, no. 6: 1267. https://doi.org/10.3390/f14061267
APA StyleCui, Z., Zhang, H., Liu, Y., Zhang, J., Yang, T., Zuo, Y., & Lei, K. (2023). Constructing Coupling Model of Generalized B-Spline Curve and Crown (CMGBCC) to Explore the 3D Modeling of Chinese Fir Polymorphism. Forests, 14(6), 1267. https://doi.org/10.3390/f14061267







