Simulation of Spatial and Temporal Distribution of Forest Carbon Stocks in Long Time Series—Based on Remote Sensing and Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Areas
2.2. Data Acquisition and Treatment
2.2.1. Ground Survey Data
| Forest Types | Biomass Function |
|---|---|
| Birch forest | YS = (H/(−0.7161 + 1.7316H))V |
| YB = (H/(71.1504 + 2.3594H))V | |
| YF = (D/(52.1765 + 31.5260D))V | |
| YR = (D/(−7.7814 + 5.2684D))V | |
| Korean pine forest | YS = (N/(369.6842 + 1.5593N))V |
| YB = 0.1807D0.1196H−0.1086V | |
| YF = 0.2835D−0.2246H−0.2737V | |
| YR = H/(−7.4947 + 5.4H))V) | |
| Larch forest | YS = 0.2638D0.6084H−0.3052V |
| YB = 0.0893D0.5372H−0.5798V | |
| YF = (D/(−0.320.565 + 69.0763D))V | |
| YR = (D/(44.2954 + 1.182D))V | |
| Populus forest | YS = 0.2472D0.134H−0.0461V |
| YB = (D/(70.9902 + 8.7291D))V | |
| YF = (D/(−71.0595 + 22.4834D))V | |
| YR = (D/(−7.72 + 0.1178D))V | |
| Pinus sylvestris forest | YS = 0.3063D0.2638H0.0044V |
| YB = 0.0809D0.3271H−0.282V | |
| YF = (D/(−71.0595 + 22.4834D))V | |
| YR = (D/(−25.67 + 7.3893D))V | |
| Mixed broad-leaved forest | YS = 0.5193D0.1529H−0.0981V |
| YB = (D/(79.2051 + 1.2886D))V | |
| YF = (D/(−84.3635 + 42.2363D))V | |
| YR = (H/(−6.079 + 5.4717H))V | |
| Mixed coniferous broad-leaved forest | YS = (D/(−1.3193 + 2.0249D))V |
| YB = (D/(58.0685 + 5.6768D))V | |
| YF = (D/(−507.269 + 78.1762D))V | |
| YR = (H/(−2.1908 + 5.6433H))V | |
| Mixed coniferous forest | YS = (D/(0.6756 + 2.1D))V |
| YB = 0.0631D0.3538H−0.2781V | |
| YF = (D/(−156.921 + 43.4676D))V | |
| YR = (D/(14.289 + 4.883D))V |
2.2.2. Remote Sensing Data
3. Methodology
3.1. Models
3.1.1. Multiple Linear Regression (MLR)
3.1.2. Deep Neural Networks (DNN)
3.1.3. Convolutional Neural Network (CNN)
3.2. Evaluation Indicators
3.2.1. Model Evaluation Indicators
3.2.2. Spatial Autocorrelation Analysis
3.2.3. Sen’s Slope Estimator
3.2.4. Mann–Kendall Statistical Test
3.2.5. Hurst exponent
4. Results
4.1. Descriptive Statistics
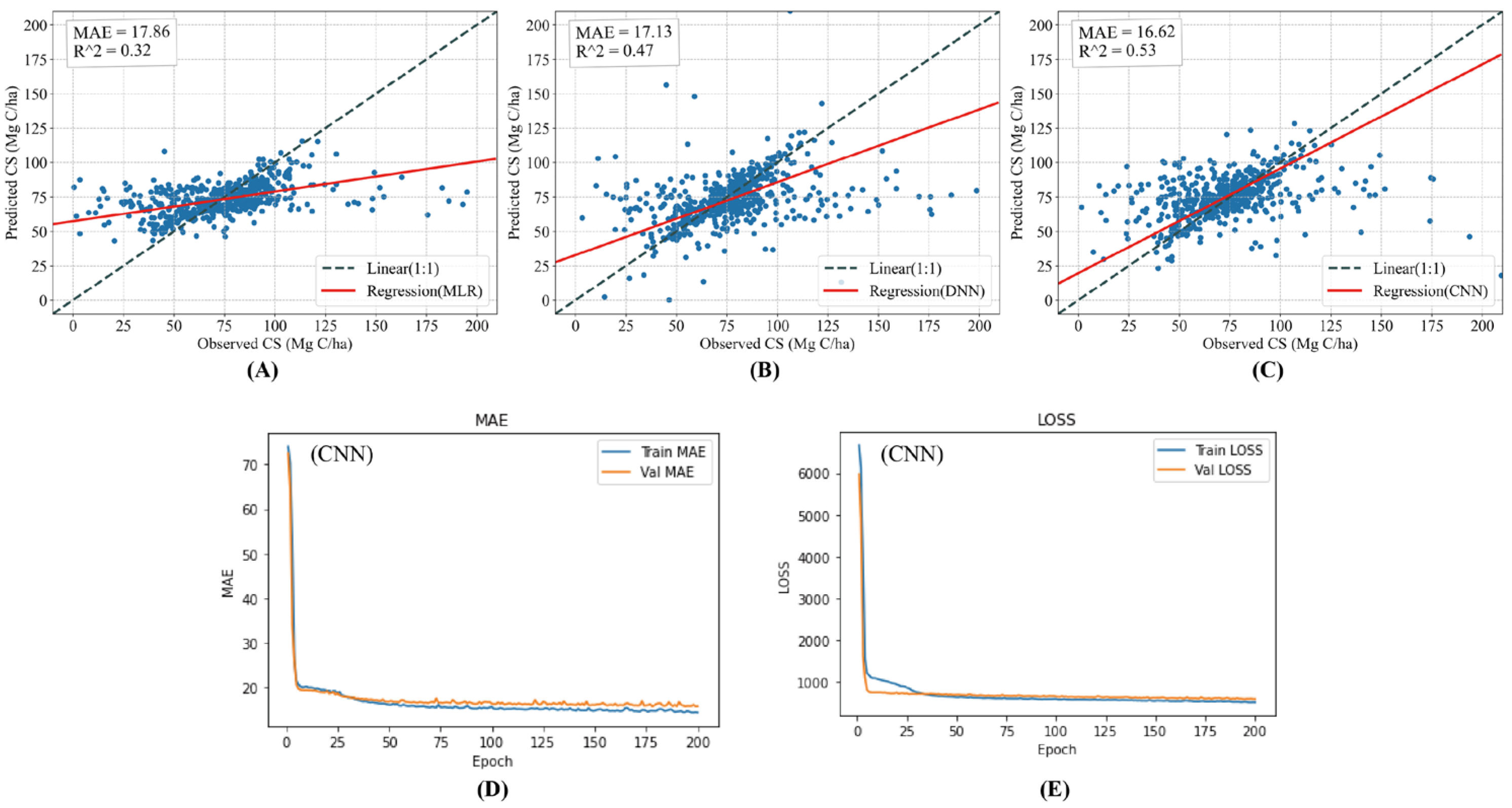
4.2. Evaluation of Models
4.3. Optimal Model for Prediction
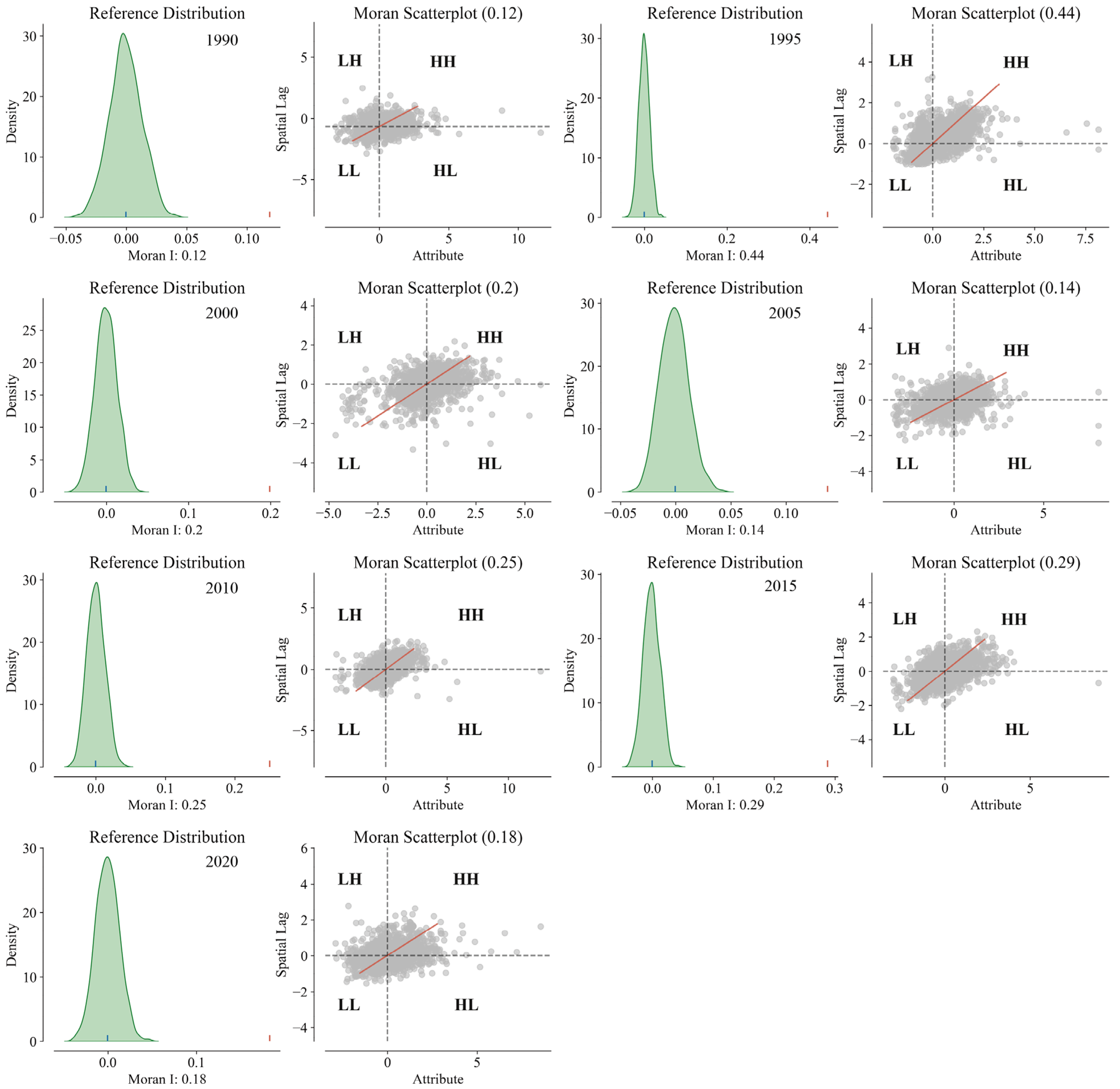
4.4. Spatial Autocorrelation Analysis of Carbon Stocks
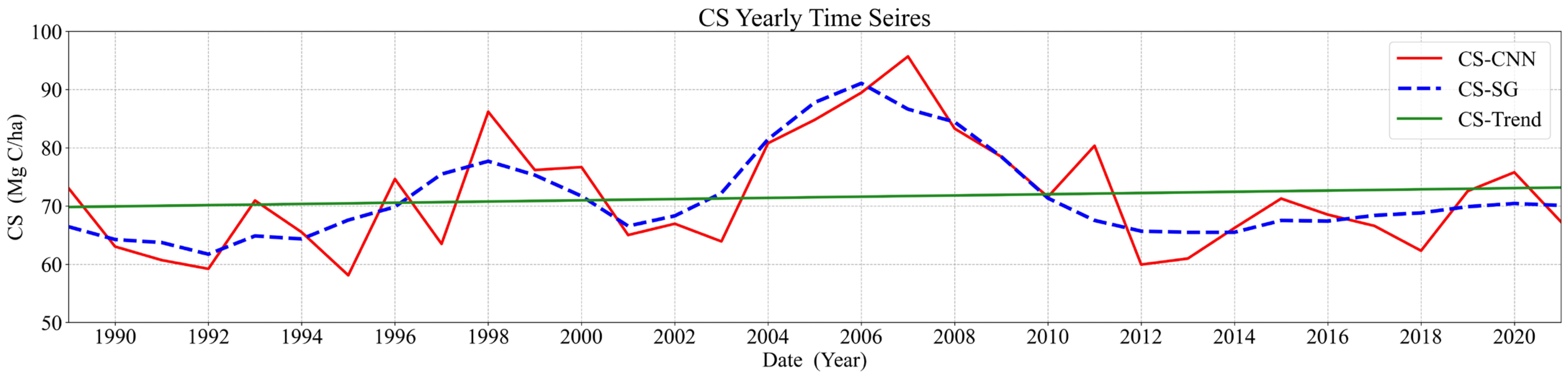
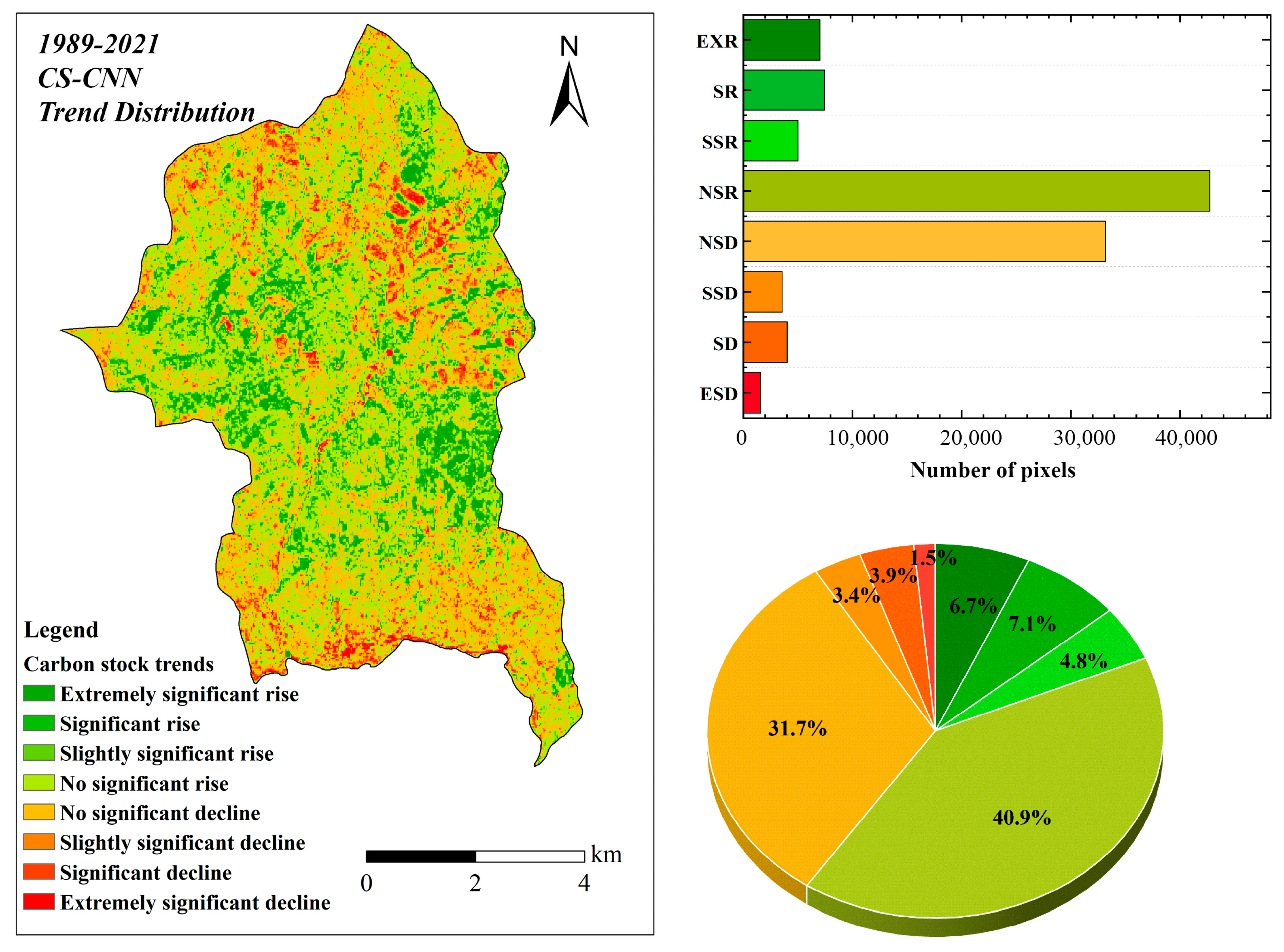
4.5. Trends in the Spatial Transformation of Carbon Stocks
4.6. Future Trends in Forest Carbon Stocks
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zaninovich, S.C.; Gatti, M.G. Carbon Stock Densities of Semi-Deciduous Atlantic Forest and Pine Plantations in Argentina. Sci. Total Environ. 2020, 747, 141085. [Google Scholar] [CrossRef] [PubMed]
- Dalmonech, D.; Marano, G.; Amthor, J.S.; Cescatti, A.; Lindner, M.; Trotta, C.; Collalti, A. Feasibility of Enhancing Carbon Sequestration and Stock Capacity in Temperate and Boreal European Forests via Changes to Management Regimes. Agric. For. Meteorol. 2022, 327, 109203. [Google Scholar] [CrossRef]
- Dulamsuren, C. Organic Carbon Stock Losses by Disturbance: Comparing Broadleaved Pioneer and Late-Successional Conifer Forests in Mongolia’s Boreal Forest. For. Ecol. Manag. 2021, 499, 119636. [Google Scholar] [CrossRef]
- Romanov, A.A.; Tamarovskaya, A.N.; Gloor, E.; Brienen, R.; Gusev, B.A.; Leonenko, E.V.; Vasiliev, A.S.; Krikunov, E.E. Reassessment of Carbon Emissions from Fires and a New Estimate of Net Carbon Uptake in Russian Forests in 2001–2021. Sci. Total Environ. 2022, 846, 157322. [Google Scholar] [CrossRef]
- Xu, C.; Wang, B.; Chen, J. Forest Carbon Sink in China: Linked Drivers and Long Short-Term Memory Network-Based Prediction. J. Clean. Prod. 2022, 359, 132085. [Google Scholar] [CrossRef]
- Fremout, T.; Cobián-De Vinatea, J.; Thomas, E.; Huaman-Zambrano, W.; Salazar-Villegas, M.; Limache-de la Fuente, D.; Bernardino, P.N.; Atkinson, R.; Csaplovics, E.; Muys, B. Site-Specific Scaling of Remote Sensing-Based Estimates of Woody Cover and Aboveground Biomass for Mapping Long-Term Tropical Dry Forest Degradation Status. Remote Sens. Environ. 2022, 276, 113040. [Google Scholar] [CrossRef]
- Ding, Y.; He, X.; Zhou, Z.; Hu, J.; Cai, H.; Wang, X.; Li, L.; Xu, J.; Shi, H. Response of Vegetation to Drought and Yield Monitoring Based on NDVI and SIF. CATENA 2022, 219, 106328. [Google Scholar] [CrossRef]
- Qiu, R.; Li, X.; Han, G.; Xiao, J.; Ma, X.; Gong, W. Monitoring Drought Impacts on Crop Productivity of the U.S. Midwest with Solar-Induced Fluorescence: GOSIF Outperforms GOME-2 SIF and MODIS NDVI, EVI, and NIRv. Agric. For. Meteorol. 2022, 323, 109038. [Google Scholar] [CrossRef]
- Lemoine-Rodríguez, R.; Inostroza, L.; Zepp, H. Does Urban Climate Follow Urban Form? Analysing Intraurban LST Trajectories versus Urban Form Trends in 3 Cities with Different Background Climates. Sci. Total Environ. 2022, 830, 154570. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of Landscape Structure on Surface Urban Heat Islands: A Case Study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Zheng, Z.; Wu, Z.; Chen, Y.; Guo, C.; Marinello, F. Instability of Remote Sensing Based Ecological Index (RSEI) and Its Improvement for Time Series Analysis. Sci. Total Environ. 2022, 814, 152595. [Google Scholar] [CrossRef]
- Wang, Q.; Song, K.; Xiao, X.; Jacinthe, P.-A.; Wen, Z.; Zhao, F.; Tao, H.; Li, S.; Shang, Y.; Wang, Y.; et al. Mapping Water Clarity in North American Lakes and Reservoirs Using Landsat Images on the GEE Platform with the RGRB Model. ISPRS J. Photogramm. Remote Sens. 2022, 194, 39–57. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Parastatidis, D.; Mitraka, Z.; Chrysoulakis, N.; Abrams, M. Online Global Land Surface Temperature Estimation from Landsat. Remote Sens. 2017, 9, 1208. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Jia, W.; Wang, F.; Guo, H.; Ao, Z. Research on the Temporal and Spatial Distributions of Standing Wood Carbon Storage Based on Remote Sensing Images and Local Models. Forests 2022, 13, 346. [Google Scholar] [CrossRef]
- Zhen, Z.; Li, F.; Liu, Z.; Liu, C.; Zhao, Y.; Ma, Z.; Zhang, L. Geographically Local Modeling of Occurrence, Count, and Volume of Downwood in Northeast China. Appl. Geogr. 2013, 37, 114–126. [Google Scholar] [CrossRef]
- Tian, D.; Jiang, L.; Shahzad, M.K.; He, P.; Wang, J.; Yan, Y. Climate-Sensitive Tree Height-Diameter Models for Mixed Forests in Northeastern China. Agric. For. Meteorol. 2022, 326, 109182. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep Learning in Remote Sensing Applications: A Meta-Analysis and Review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Nex, F.; Vosselman, G. Disaster Damage Detection through Synergistic Use of Deep Learning and 3D Point Cloud Features Derived from Very High Resolution Oblique Aerial Images, and Multiple-Kernel-Learning. ISPRS J. Photogramm. Remote Sens. 2018, 140, 45–59. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Tong, S.; Guo, E. Monitoring the Trends of Aeolian Desertified Lands Based on Time-Series Remote Sensing Data in the Horqin Sandy Land, China. CATENA 2017, 157, 286–298. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of Trend Analysis for Monthly Water Quality Data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend Analysis in Turkish Precipitation Data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Tabari, H.; Somee, B.S.; Zadeh, M.R. Testing for Long-Term Trends in Climatic Variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Wang, X.; Li, T.; Ikhumhen, H.O.; Sá, R.M. Spatio-Temporal Variability and Persistence of PM2.5 Concentrations in China Using Trend Analysis Methods and Hurst Exponent. Atmos. Pollut. Res. 2022, 13, 101274. [Google Scholar] [CrossRef]
- Dong, L. Biomass Modeling of Major Tree Species and stAnd Types in the Northeast Forest Region. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2015. [Google Scholar]
- Yu, Y.; Fan, W.; Li, M. Carbon content of forests at different scales in the Northeast Forest Region. J. Appl. Ecol. 2012, 23, 341–346. [Google Scholar] [CrossRef]
- Zhou, B.; Okin, G.S.; Zhang, J. Leveraging Google Earth Engine (GEE) and Machine Learning Algorithms to Incorporate in Situ Measurement from Different Times for Rangelands Monitoring. Remote Sens. Environ. 2020, 236, 111521. [Google Scholar] [CrossRef]
- Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N.; et al. Fifty Years of Landsat Science and Impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
- Martins, V.S.; Roy, D.P.; Huang, H.; Boschetti, L.; Zhang, H.K.; Yan, L. Deep Learning High Resolution Burned Area Mapping by Transfer Learning from Landsat-8 to PlanetScope. Remote Sens. Environ. 2022, 280, 113203. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, e1353691. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and Limits of Vegetation Indices for LAI and APAR Assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Tanre, D.; Holben, B.N.; Kaufman, Y.J. Atmospheric Correction Algorithm for NOAA-AVHRR Products: Theory and Application. IEEE Trans. Geosci. Remote Sens. 1992, 30, 231–248. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W. Application of the WDVI in Estimating LAI at the Generative Stage of Barley. ISPRS J. Photogramm. Remote Sens. 1991, 46, 37–47. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Cristobal, J.; Sobrino, J.A.; Soria, G.; Ninyerola, M.; Pons, X. Revision of the Single-Channel Algorithm for Land Surface Temperature Retrieval From Landsat Thermal-Infrared Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 339–349. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H. A New Remote Sensing Index for Assessing the Spatial Heterogeneity in Urban Ecological Quality: A Case from Fuzhou City, China. Ecol. Indic. 2018, 89, 11–21. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a Tasselled Cap Transformation Based on Landsat 8 At-Satellite Reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Igwe, O.; Omeka, M.E.; Agbasi, J.C. Development of MLR and Variedly Optimized ANN Models for Forecasting the Detachability and Liquefaction Potential Index of Erodible Soils. Geosystems Geoenvironment 2023, 2, 100104. [Google Scholar] [CrossRef]
- Schyns, P.G.; Snoek, L.; Daube, C. Degrees of Algorithmic Equivalence between the Brain and Its DNN Models. Trends Cogn. Sci. 2022, 26, 1090–1102. [Google Scholar] [CrossRef]
- Akbarimajd, A.; Hoertel, N.; Hussain, M.A.; Neshat, A.A.; Marhamati, M.; Bakhtoor, M.; Momeny, M. Learning-to-Augment Incorporated Noise-Robust Deep CNN for Detection of COVID-19 in Noisy X-Ray Images. J. Comput. Sci. 2022, 63, 101763. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- El Bilali, A.; Lamane, H.; Taleb, A.; Nafii, A. A Framework Based on Multivariate Distribution-Based Virtual Sample Generation and DNN for Predicting Water Quality with Small Data. J. Clean. Prod. 2022, 368, 133227. [Google Scholar] [CrossRef]
- Osco, L.P.; Marcato Junior, J.; Marques Ramos, A.P.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A Review on Deep Learning in UAV Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Schmidt, K.; Amirian-Chakan, A.; Rentschler, T.; Zeraatpisheh, M.; Sarmadian, F.; Valavi, R.; Davatgar, N.; Behrens, T.; Scholten, T. Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 2020, 12, 1095. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in Vegetation Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Briechle, S.; Krzystek, P.; Vosselman, G. Silvi-Net—A Dual-CNN Approach for Combined Classification of Tree Species and Standing Dead Trees from Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102292. [Google Scholar] [CrossRef]
- Hamraz, H.; Jacobs, N.B.; Contreras, M.A.; Clark, C.H. Deep Learning for Conifer/Deciduous Classification of Airborne LiDAR 3D Point Clouds Representing Individual Trees. ISPRS J. Photogramm. Remote Sens. 2019, 158, 219–230. [Google Scholar] [CrossRef]
- Zhang, Y.; She, J.; Long, X.; Zhang, M. Spatio-Temporal Evolution and Driving Factors of Eco-Environmental Quality Based on RSEI in Chang-Zhu-Tan Metropolitan Circle, Central China. Ecol. Indic. 2022, 144, 109436. [Google Scholar] [CrossRef]
- Oden, N.L. Spatial Processes: Models & Applications. A. D. Cliff, J.K. Ord. Q. Rev. Biol. 1982, 57, 236–236. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Pelt, R.V.; Carey, A.B.; Thornburgh, D.A.; Berg, D.R.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; et al. Disturbances and Structural Development of Natural Forest Ecosystems with Silvicultural Implications, Using Douglas-Fir Forests as an Example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Xie, D.; Li, X.; Zhou, T.; Feng, Y. Estimating the Contribution of Environmental Variables to Water Quality in the Postrestoration Littoral Zones of Taihu Lake Using the APCS-MLR Model. Sci. Total Environ. 2022, 857, 159678. [Google Scholar] [CrossRef] [PubMed]
- Wadoux, A.M.J.-C. Using Deep Learning for Multivariate Mapping of Soil with Quantified Uncertainty. Geoderma 2019, 351, 59–70. [Google Scholar] [CrossRef]
- Yang, L.; Cai, Y.; Zhang, L.; Guo, M.; Li, A.; Zhou, C. A Deep Learning Method to Predict Soil Organic Carbon Content at a Regional Scale Using Satellite-Based Phenology Variables. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102428. [Google Scholar] [CrossRef]
- Barta, K.A.; Hais, M.; Heurich, M. Characterizing Forest Disturbance and Recovery with Thermal Trajectories Derived from Landsat Time Series Data. Remote Sens. Environ. 2022, 282, 113274. [Google Scholar] [CrossRef]
- Xia, L.; Zhao, F.; Chen, J.; Yu, L.; Lu, M.; Yu, Q.; Liang, S.; Fan, L.; Sun, X.; Wu, S.; et al. A Full Resolution Deep Learning Network for Paddy Rice Mapping Using Landsat Data. ISPRS J. Photogramm. Remote Sens. 2022, 194, 91–107. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, C.; Xu, B.; Zhu, Y.; Zhao, F.; Han, S.; Yang, G.; Yang, H. Predicting Individual Apple Tree Yield Using UAV Multi-Source Remote Sensing Data and Ensemble Learning. Comput. Electron. Agric. 2022, 201, 107275. [Google Scholar] [CrossRef]
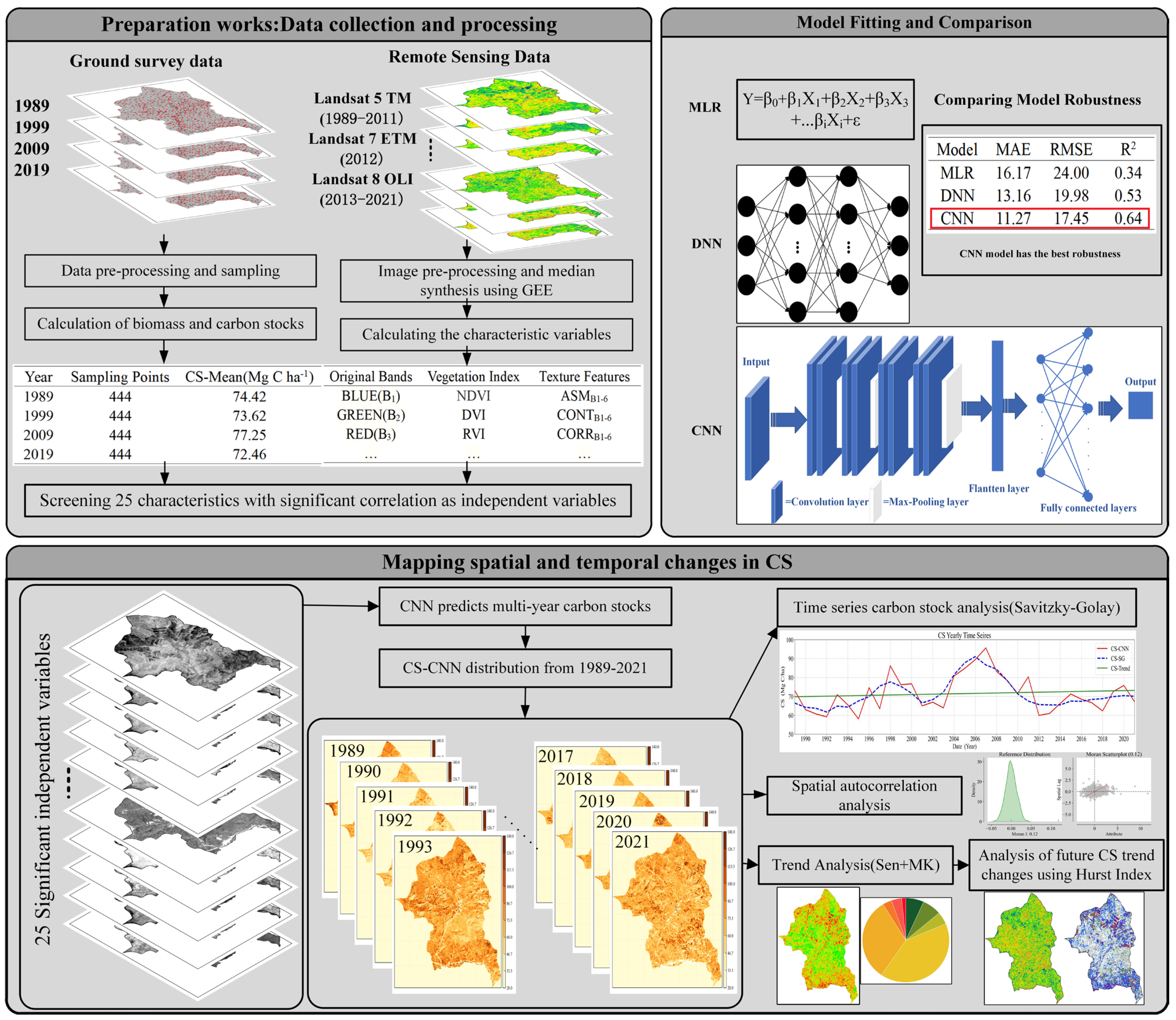
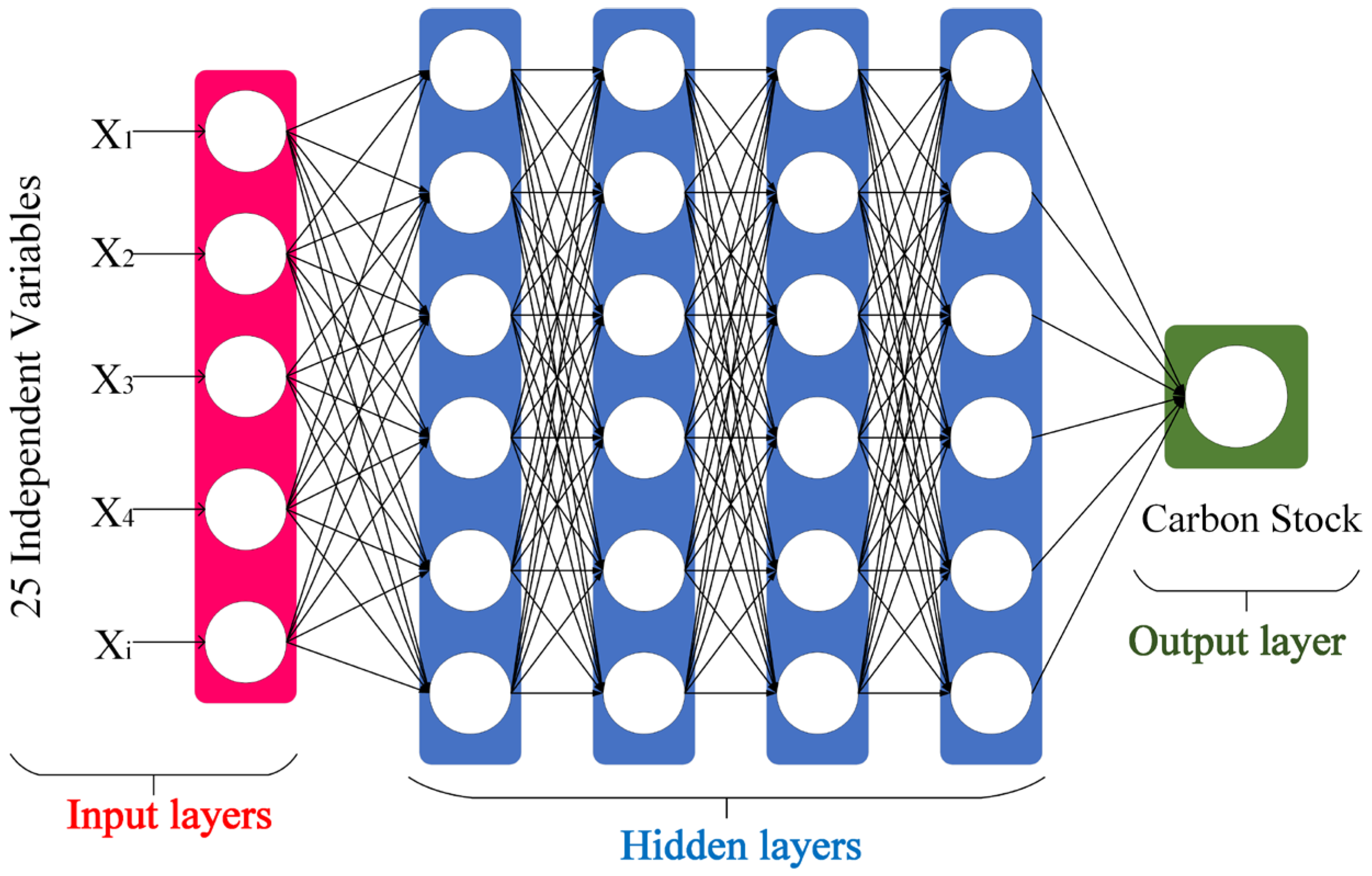
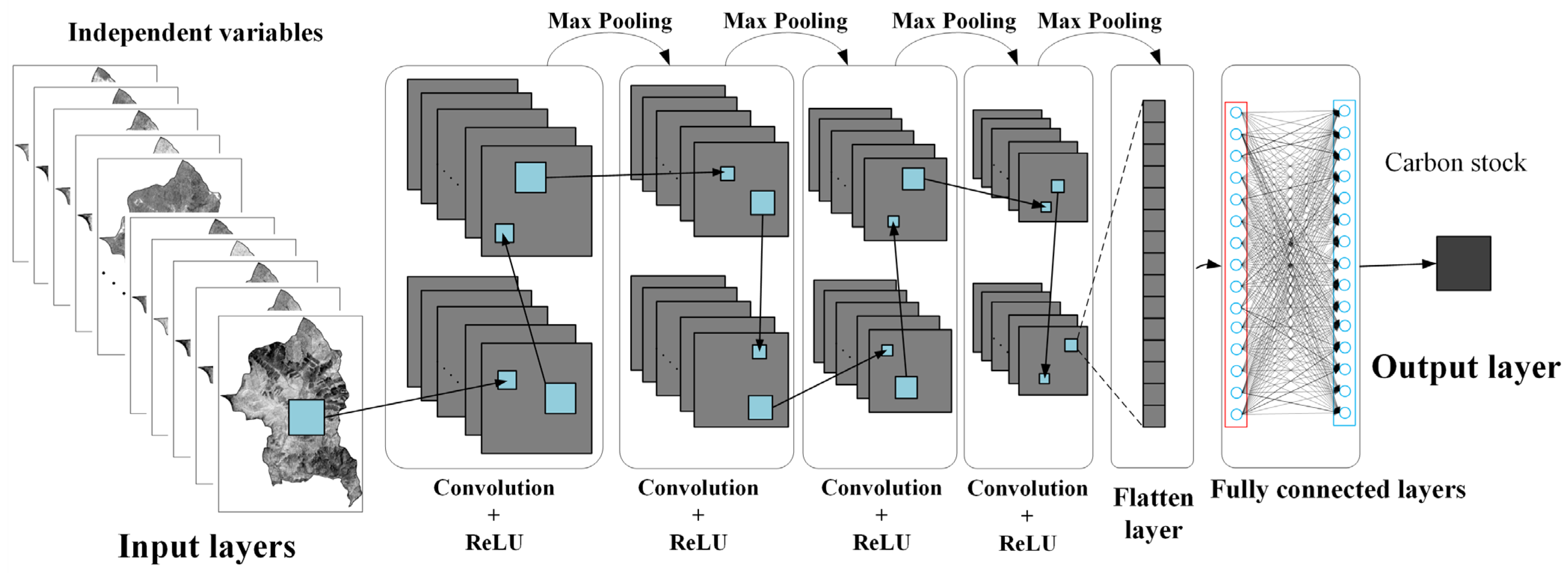
| Remote Sensing Data | Bands, Indices or Parameters | Definition or Calculation Formula |
|---|---|---|
| Original band | BLUE(B1) | Water penetration, distinguishing soil vegetation |
| GREEN(B2) | Distinguishing different vegetation | |
| RED(B3) | Observation of roads, bare soil, and vegetation types | |
| NIR(B4) | Estimating biomass and distinguishing wet soils | |
| SWIR1(B5) | Distinguishing the road, bare leaking soil | |
| SWIR2(B6) | Heat distribution mapping, rock identification | |
| Vegetation Index | Normalized Difference Vegetation Index (NDVI) [35] | (NIR − RED)/(NIR + RED) |
| Difference Vegetation Index (DVI) [36] | NIR − RED | |
| Ratio Vegetation Index (RVI) [37] | NIR/RED | |
| Atmospheric Ratio Vegetation Index (ARVI) [38] | (NIR − (2 × RED − BLUE))/(NIR + (2 × RED − BLUE)) | |
| Soil-Adjusted Vegetation Index (SAVI) [39] | ((NIR − RED)/(NIR + RED + 0.5))(1 + 0.5) | |
| Weighted Difference Vegetation Index (WDVI) [40] | NIR − 0.5 × RED | |
| Modified Soil-Adjusted Vegetation Index (MSAVI) [41] | (2NIR + 1 − ((2 × NIR + 1) − 8 × (NIR − RED))0.5)/2 | |
| Modified Normalized Difference Water Index (MNDWI) [42] | (NIR − GREEN)/(NIR + GREEN) | |
| Land Surface Temperature (LST) [43] | T/(1 + (λT/ρ)lnε); λ is the central wavelength of thermal infrared band, ρ = 1.438 × 10−2 m·k; ε is the surface specific emissivity | |
| Normalized Difference Building and Soil Index (NDBSI) [44] | (SI + IBI)/2; SI and IBI represent the soil index and building index, respectively | |
| Wetness (WET) [45] | β1BLUE + β2GREEN + β3RED + β4NIR + β5SWIR1 + β6SWIR2; β1–6 are the different coefficients corresponding to different sensor types | |
| Texture features | Angular Second Moment (ASMB1–6) | The texture metrics are calculated from the grayscale co-occurrence matrix around each pixel in each band. The grayscale co-occurrence matrix is a list of the frequency of occurrence of different combinations of pixel luminance values (grayscale) in an image. It calculates the number of times a pixel with value X is adjacent to a pixel with value Y in a specific direction and distance, and then derives statistics from this table [46]. |
| Contrast (CONTB1–6) | ||
| Correlation (CORRB1–6) | ||
| Variance (VARB1–6) | ||
| Inverse Difference Moment (IDMB1–6) | ||
| Sum Average (SAVGB1–6) | ||
| Sum Variance (SVARB1–6) | ||
| Sum Entropy (SENTB1–6) | ||
| Entropy (ENTB1–6) | ||
| Difference variance (DVARB1–6) | ||
| Difference entropy (DENTB1–6) | ||
| Information Measure of Corr. 1 (IMCORR1B1–6) | ||
| Information Measure of Corr. 2 (IMCORR2B1–6) | ||
| Max Corr. Coefficient (MAXCORRB1–6) | ||
| Dissimilarity (DISSB1–6) | ||
| Inertia (INERB1–6) | ||
| Cluster Shade (SHADEB1–6) | ||
| Cluster prominence (PROMB1–6) |
| Year | CS-Mean (Mg C ha−1) | CS-Standard Deviation (Mg C ha−1) | CS-Median (Mg C ha−1) |
|---|---|---|---|
| 1989 | 74.42 | 38.35 | 71.65 |
| 1999 | 73.62 | 40.41 | 67.29 |
| 2009 | 77.25 | 24.41 | 78.55 |
| 2019 | 72.46 | 21.87 | 70.57 |
| Combination | MLR | DNN | CNN | |||
|---|---|---|---|---|---|---|
| MAE | R2 | MAE | R2 | MAE | R2 | |
| 1 | 17.58 | 0.34 | 16.87 | 0.51 | 16.32 | 0.54 |
| 2 | 18.16 | 0.29 | 17.09 | 0.48 | 16.87 | 0.52 |
| 3 | 18.01 | 0.35 | 17.32 | 0.42 | 16.34 | 0.54 |
| 4 | 17.96 | 0.31 | 17.29 | 0.45 | 17.11 | 0.49 |
| 5 | 17.60 | 0.34 | 16.84 | 0.51 | 16.38 | 0.53 |
| 6 | 17.87 | 0.32 | 16.98 | 0.49 | 16.90 | 0.51 |
| 7 | 18.21 | 0.28 | 17.13 | 0.47 | 16.23 | 0.57 |
| 8 | 17.54 | 0.35 | 17.28 | 0.46 | 16.27 | 0.56 |
| 9 | 17.71 | 0.32 | 17.32 | 0.41 | 16.97 | 0.50 |
| 10 | 17.97 | 0.31 | 17.19 | 0.43 | 16.84 | 0.52 |
| Mean | 17.86 | 0.32 | 17.13 | 0.46 | 16.62 | 0.53 |
| Change Directions | Future Trends | Percentage |
|---|---|---|
| Continuous decline | Positive significant decline | 0.01 |
| Positive decline | 0.06 | |
| Rise in the past but declining trend in the future | Reverse significant decline | 0.04 |
| Reverse decline | 0.29 | |
| Decline in the past but rising trend in the future | Reverse significant rise | 0.13 |
| Reverse rise | 0.41 | |
| Continuous rise | Positive significant rise | 0.01 |
| Positive rise | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Jia, W.; Sun, Y.; Wang, F.; Miu, Y. Simulation of Spatial and Temporal Distribution of Forest Carbon Stocks in Long Time Series—Based on Remote Sensing and Deep Learning. Forests 2023, 14, 483. https://doi.org/10.3390/f14030483
Zhang X, Jia W, Sun Y, Wang F, Miu Y. Simulation of Spatial and Temporal Distribution of Forest Carbon Stocks in Long Time Series—Based on Remote Sensing and Deep Learning. Forests. 2023; 14(3):483. https://doi.org/10.3390/f14030483
Chicago/Turabian StyleZhang, Xiaoyong, Weiwei Jia, Yuman Sun, Fan Wang, and Yujie Miu. 2023. "Simulation of Spatial and Temporal Distribution of Forest Carbon Stocks in Long Time Series—Based on Remote Sensing and Deep Learning" Forests 14, no. 3: 483. https://doi.org/10.3390/f14030483
APA StyleZhang, X., Jia, W., Sun, Y., Wang, F., & Miu, Y. (2023). Simulation of Spatial and Temporal Distribution of Forest Carbon Stocks in Long Time Series—Based on Remote Sensing and Deep Learning. Forests, 14(3), 483. https://doi.org/10.3390/f14030483





