Calibrating a Process-Based Model to Enhance Robustness in Carbon Sequestration Simulations: The Case of Cedrus atlantica (Endl.) Manetti ex Carrière
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Overall Approach
2.3. Used Data
2.3.1. In-Situ Data
2.3.2. Ex-Situ Data
2.4. Data Preparation and Preprocessing
2.4.1. Model Initialization
2.4.2. Climate Data
2.5. Sensitivity Analysis
2.6. Model Calibration
3. Results
3.1. Stands Characterization
3.1.1. Adjustment of the Height-Circumference Relationship
3.1.2. Results of Stands’ Characterization
3.2. Sensitivity Results
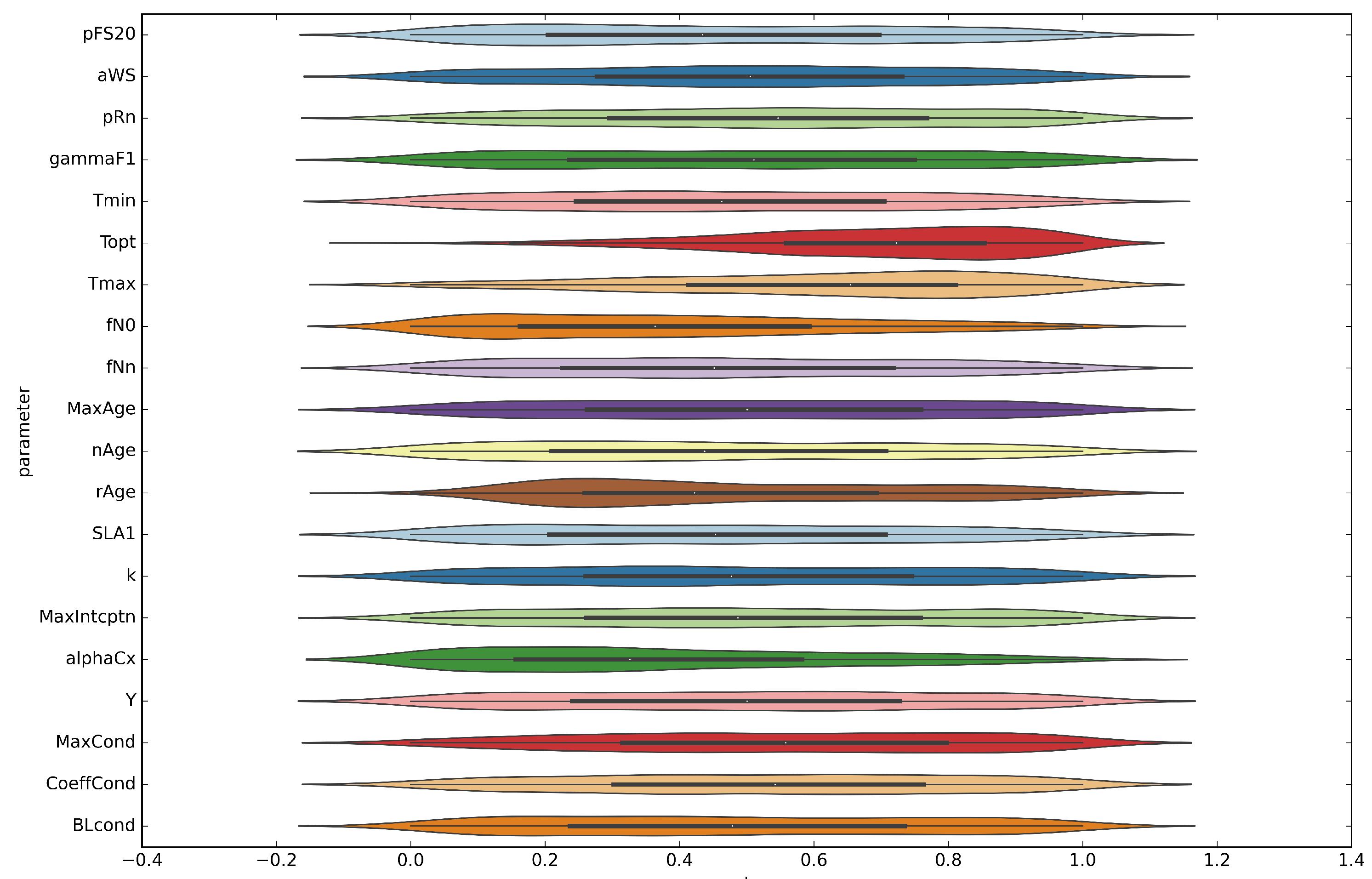
3.3. Calibration
3.4. NPP Simulation
4. Discussion
4.1. Parameter Sensitivity and Optimization
4.1.1. NPP and Canopy Processes and Structure
4.1.2. NPP and Conductance Modifiers
4.1.3. NPP and Carbon Partitioning
4.2. Implications, Future Perspectives, and Limitations
5. Conclusions
- (1)
- Parameters related to stand properties, canopy structure, and processes, as well as biomass partitioning, are the most important or sensitive for the performance of the model.
- (2)
- DE-MC method optimized the values of the 3-PG parameters which was confirmed by the means of Gelman–Rubin convergence test.
- (3)
- According to the predictions of 3-PG, the annual carbon sequestration in the pure Azrou forest varies between 0.35 and 8.82 , it is equal in average to 5.48 , which given the total area corresponds to 7918 .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Zhang, B.; Zhang, S.; Li, X.; Liu, D.; Song, K.; Li, J.; Li, F.; Duan, H. Changes of Land Use and of Ecosystem Service Values in Sanjiang Plain, Northeast China. Environ. Monit. Assess. 2006, 112, 69–91. [Google Scholar] [CrossRef] [PubMed]
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The Value of the World’s Ecosystem Services and Natural Capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Fabrika, M.; Valent, P.; Merganičová, K. Forest Modelling and Visualisation—State of the Art and Perspectives. Cent. Eur. For. J. 2019, 65, 147–165. [Google Scholar] [CrossRef]
- d’Annunzio, R.; Sandker, M.; Finegold, Y.; Min, Z. Projecting Global Forest Area towards 2030. For. Ecol. Manag. 2015, 352, 124–133. [Google Scholar] [CrossRef]
- Cudlín, P.; Seják, J.; Pokorný, J.; Albrechtová, J.; Bastian, O.; Marek, M. Forest Ecosystem Services Under Climate Change and Air Pollution. In Developments in Environmental Science; Matyssek, R., Clarke, N., Cudlin, P., Mikkelsen, T.N., Tuovinen, J.-P., Wieser, G., Paoletti, E., Eds.; Climate Change, Air Pollution and Global Challenges; Elsevier: Amsterdam, The Netherlands, 2013; Volume 13, pp. 521–546. [Google Scholar]
- Benabou, A.; Moukrim, S.; Laaribya, S.; Aafi, A.; Chkhichekh, A.; ElMaadidi, T.; El Aboudi, A. Mapping Ecosystem Services of Forest Stands: Case Study of Maamora, Morocco. Geogr. Environ. Sustain. 2022, 15, 141–149. [Google Scholar] [CrossRef]
- Reid, W.V.; Mooney, H.A.; Cropper, A.; Capistrano, D.; Carpenter, S.R.; Chopra, K.; Dasgupta, P.; Dietz, T.; Duraiappah, A.K.; Hassan, R.; et al. Ecosystems and Human Well-Being-Synthesis: A Report of the Millennium Ecosystem Assessment; Island Press: Washington, DC, USA, 2005; 137p. [Google Scholar]
- Shukla, P.R.; Skea, J.; Calvo Buendia, E.; Masson-Delmotte, V.; Pörtner, H.-O.; Roberts, D.C.; Zhai, P.; Slade, R.; Connors, S.; Van Diemen, R.; et al. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2019. [Google Scholar]
- UNFCCC. Adoption of the Paris Agreement; Report No. FCCC/CP/2015/L.9/Rev.1; UNFCCC: Bonn, Germany, 2015. [Google Scholar]
- Harris, N.; Cook-Patton, S.; Gibbs, D.; Lister, K. Young Forests Capture Carbon Quicker than Previously Thought; WRI: Washington, DC, USA, 2020. [Google Scholar]
- Piao, S.; Fang, J.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The Carbon Balance of Terrestrial Ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef]
- Hartig, F.; Dyke, J.; Hickler, T.; Higgins, S.I.; O’Hara, R.B.; Scheiter, S.; Huth, A. Connecting Dynamic Vegetation Models to Data—An Inverse Perspective. J. Biogeogr. 2012, 39, 2240–2252. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Sands, P. Physiological Ecology of Forest Production: Principles, Processes and Models, 1st ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2016; ISBN 978-0-12-810206-0. [Google Scholar]
- Maréchaux, I.; Langerwish, F.; Huth, A.; Bugmann, H.; Morin, X.; Reyer, C.P.O.; Seidl, R.; Collalti, A.; de Paula, M.D.; Fischer, R.; et al. Modelling forests to address key ecological questions: Lessons learned from different modelling communities and possible future paths. Ecol. Evol. 2021, 11, 3746–3770. [Google Scholar] [CrossRef]
- Rodríguez-Suárez, J.A.; Soto, B.; Iglesias, M.L.; Diaz-Fierros, F. Application of the 3PG Forest Growth Model to a Eucalyptus Globulus Plantation in Northwest Spain. Eur. J. For. Res. 2010, 129, 573–583. [Google Scholar] [CrossRef]
- Dalmonech, D.; Marano, G.; Amthor, J.S.; Cescatti, A.; Lindner, M.; Trotta, C.; Collalti, A. Feasibility of Enhancing Carbon Sequestration and Stock Capacity in Temperate and Boreal European Forests via Changes to Management Regimes. Agric. For. Meteorol. 2022, 327, 109203. [Google Scholar] [CrossRef]
- Testolin, R.; Dalmonech, D.; Marano, G.; Bagnara, M.; D’Andrea, E.; Matteucci, G.; Noce, S.; Collalti, A. Simulating Diverse Forest Management Options in a Changing Climate on a Pinus Nigra Subsp. Laricio Plantation in Southern Italy. Sci. Total Environ. 2023, 857, 159361. [Google Scholar] [CrossRef] [PubMed]
- Mahnken, M.; Cailleret, M.; Collalti, A.; Trotta, C.; Biondo, C.; D’Andrea, E.; Dalmonech, D.; Marano, G.; Mäkelä, A.; Minunno, F.; et al. Accuracy, realism and general applicability of European forest models. Glob. Chang. Biol. 2022, 28, 6921–6943. [Google Scholar] [CrossRef] [PubMed]
- Landsberg, J.J.; Waring, R.H. A Generalised Model of Forest Productivity Using Simplified Concepts of Radiation-Use Efficiency, Carbon Balance and Partitioning. For. Ecol. Manag. 1997, 95, 209–228. [Google Scholar] [CrossRef]
- Almeida, A.C.; Landsberg, J.J.; Sands, P.J. Parameterisation of 3-PG Model for Fast-Growing Eucalyptus Grandis Plantations. For. Ecol. Manag. 2004, 193, 179–195. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Waring, R.H.; Coops, N.C. Performance of the Forest Productivity Model 3-PG Applied to a Wide Range of Forest Types. For. Ecol. Manag. 2003, 172, 199–214. [Google Scholar] [CrossRef]
- Zhao, M.; Xiang, W.; Peng, C.; Tian, D. Simulating Age-Related Changes in Carbon Storage and Allocation in a Chinese Fir Plantation Growing in Southern China Using the 3-PG Model. For. Ecol. Manag. 2009, 257, 1520–1531. [Google Scholar] [CrossRef]
- Stape, J.L.; Ryan, M.G.; Binkley, D. Testing the Utility of the 3-PG Model for Growth of Eucalyptusgrandis×urophylla with Natural and Manipulated Supplies of Water and Nutrients. For. Ecol. Manag. 2004, 193, 219–234. [Google Scholar] [CrossRef]
- Dye, P.J.; Jacobs, S.; Drew, D. Verification of 3-PG Growth and Water-Use Predictions in Twelve Eucalyptus Plantation Stands in Zululand, South Africa. For. Ecol. Manag. 2004, 193, 197–218. [Google Scholar] [CrossRef]
- Esprey, L.; Sands, P.; Smith, C. Understanding 3PG Using a Sensitivity Analysis. For. Ecol. Manag. 2004, 193, 235–250. [Google Scholar] [CrossRef]
- Coops, N.C.; Waring, R.H.; Law, B.E. Assessing the Past and Future Distribution and Productivity of Ponderosa Pine in the Pacific Northwest Using a Process Model, 3-PG. Ecol. Model. 2005, 183, 107–124. [Google Scholar] [CrossRef]
- Wei, L.; Marshall, J.D.; Zhang, J.; Zhou, H.; Powers, R.F. 3-PG Simulations of Young Ponderosa Pine Plantations under Varied Management Intensity: Why Do They Grow so Differently? For. Ecol. Manag. 2014, 313, 69–82. [Google Scholar] [CrossRef]
- Dye, P. Modelling Growth and Water Use in Four Pinus Patula Stands with the 3-PG Model. S. Afr. For. J. 2001, 191, 53. [Google Scholar]
- Landsberg, J.J.; Mäkelä, A.; Sievänen, R.; Kukkola, M. Analysis of Biomass Accumulation and Stem Size Distributions over Long Periods in Managed Stands of Pinus Sylvestris in Finland Using the 3-PG Model. Tree Physiol. 2005, 25, 781–792. [Google Scholar] [CrossRef] [PubMed]
- Xenakis, G.; Ray, D.; Mencuccini, M. Sensitivity and Uncertainty Analysis from a Coupled 3-PG and Soil Organic Matter Decomposition Model. Ecol. Model. 2008, 219, 1–16. [Google Scholar] [CrossRef]
- Minunno, F.; Xenakis, G.; Perks, M.P.; Mencuccini, M. Calibration and Validation of a Simplified Process-Based Model for the Prediction of the Carbon Balance of Scottish Sitka Spruce (Picea Sitchensis) Plantations. Can. J. For. Res. 2010, 40, 2411–2426. [Google Scholar] [CrossRef]
- Nolè, A.; Collalti, A.; Magnani, F.; Duce, P.; Ferrara, A.; Mancino, G.; Marras, S.; Sirca, C.; Spano, D.; Borghetti, M. Assessing Temporal Variation of Primary and Ecosystem Production in Two Mediterranean Forests Using a Modified 3-PG Model. Ann. For. Sci. 2013, 70, 729–741. [Google Scholar] [CrossRef]
- Naggar, M. La Régénération Du Cèdre Dans Le Moyen Atlas Central Au Maroc. For. Méditerranéenne 2013, 34, 25–34. [Google Scholar]
- Fennane, M.; Ibn Tattou, M. Statistiques et Commentaires Sur l’inventaire Actuel de La Flore Vasculaire Du Maroc. Bull. de l’Inst. Sci. 2012, 34, 1–9. [Google Scholar]
- Benabid, A. Biogéographie, Phytosociologie et Phytodynamique Des Cédraies de l’Atlas Cedrus atlantica (Manetti). Ann. De La Rech. For. Au Maroc 1994, 27, 33–60. [Google Scholar]
- HCEFLCD. Etudes D’aménagement Concerté des Forêts et Parcours Collectifs des Forêts de la Province D’Ifrane; d’Azrou, F., Ed.; Report; HCEFLCD: Rabat, Morocco, 2007; p. 7. [Google Scholar]
- M’hirit, O.; Benzyane, M. Le Cèdre De L’Atlas: Mémoire Du Temps; Editions Mardaga: Wavre, Belgium, 2006; ISBN 978-9981-896-72-7. [Google Scholar]
- Moukrim, S.; Lahssini, S.; Naggar, M.; Lahlaoi, H.; Rifai, N.; Arahou, M.; Rhazi, L. Local community involvement in forest rangeland management: Case study of compensation on forest area closed to grazing in Morocco. Rangel. J. 2019, 41, 43–53. [Google Scholar] [CrossRef]
- Derak, M.; M’hirit, O.; Mouflih, B.; Et-tobi, M. Influence de la densité et du type de peuplement sur le dépérissement du Cèdre à Sidi M’Guild (Moyen Atlas Marocain). Forêt Méditerranéenne 2008, 1, 23–32. [Google Scholar]
- Moukrim, S.; Lahssini, S.; Rifai, N.; Menzou, K.; Mharzi-Alaoui, H.; Labbaci, A.; Rhazi, M.; Wahby, I.W.; El Madihi, M.; Rhazi, L. Modélisation de la distribution potentielle de Cedrus atlantica Manetti au Maroc et impacts du changement climatique. Bois Et Forêts Des Trop. 2020, 344, 3–16. [Google Scholar] [CrossRef]
- Joint Research Centre, Institute for Environment and Sustainability; Hiederer, R. Mapping Soil Properties for Europe: Spatial Representation of Soil Database Attributes; Publications Office: Luxembourg, Luxembourg, 2013; Available online: https://data.europa.eu/doi/10.2788/94128 (accessed on 25 May 2021).
- Cochran, W.G. Sampling Techniques, 3rd ed.; Wiley series in probability and mathematical statistics; Wiley: New York, NY, USA, 1977; ISBN 978-0-471-16240-7. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- El Mderssa, M. (Faculté polytechnique de Beni Mellal, Beni Mellal, Morocco). Personal communication, 2019.
- IPCC. Guidelines for National Greenhouse Gas Inventories Volume4 Agriculture, Forestry and Other Land Use. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/vol4.html (accessed on 10 January 2021).
- Lin, J.C.; Pejam, M.R.; Chan, E.; Wofsy, S.C.; Gottlieb, E.W.; Margolis, H.A.; McCaughey, J.H. Attributing uncertainties in simulated biospheric carbon fluxes to different error sources. Glob. Biogeochem. Cycles 2011, 25, 2. [Google Scholar] [CrossRef]
- Luo, Y.; Weng, E.; Wu, X.; Gao, C.; Zhou, X.; Zhang, L. Parameter identifiability, constraint, and equifinality in data assimilation with ecosystem models. Ecol. Appl. Publ. Ecol. Soc. Am. 2009, 19, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Sun, X.; Lu, Z.; Wu, Y. A Novel Multiobjective Optimization Method Based on Sensitivity Analysis. Math. Probl. Eng. 2016, 2016, 6012805. [Google Scholar] [CrossRef]
- Menberg, K.; Heo, Y.; Augenbroe, G.; Choudhary, R. New Extension Of Morris Method For Sensitivity Analysis of Building Energy Models. 2016. Available online: https://www.researchgate.net/publication/308119619_New_extension_of_Morris_method_for_sensitivity_analysis_of_building_energy_models (accessed on 18 May 2021).
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Franczyk, A. Using the Morris sensitivity analysis method to assess the importance of input variables on time-reversal imaging of seismic sources. Acta Geophys. 2019, 67, 1525–1533. [Google Scholar] [CrossRef]
- Collalti, A.; Thornton, P.E.; Cescatti, A.; Rita, A.; Borghetti, M.; Nolè, A.; Trotta, C.; Ciais, P.; Matteucci, G. The Sensitivity of the Forest Carbon Budget Shifts across Processes along with Stand Development and Climate Change. Ecol. Appl. 2019, 29, e01837. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A.; Cariboni, J. From Screening to Quantitative Sensitivity Analysis. A Unified Approach. Comput. Phys. Commun. 2011, 182, 978–988. [Google Scholar] [CrossRef]
- Ren, X.; He, H.; Moore, D.J.P.; Zhang, L.; Liu, M.; Li, F.; Yu, G.; Wang, H. Uncertainty analysis of modeled carbon and water fluxes in a subtropical coniferous plantation. J. Geophys. Res. Biogeosci. 2013, 118, 1674–1688. [Google Scholar] [CrossRef]
- Ricciuto, D.M.; King, A.W.; Dragoni, D.; Post, W.M. Parameter and prediction uncertainty in an optimized terrestrial carbon cycle model: Effects of constraining variables and data record length. J. Geophys. Res. Biogeosci. 2011, 116, G1. [Google Scholar] [CrossRef]
- Zobitz, J.M.; Desai, A.R.; Moore, D.J.P.; Chadwick, M.A. A primer for data assimilation with ecological models using Markov Chain Monte Carlo (MCMC). Oecologia 2011, 167, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zheng, X.; Ren, Y. Parameter Optimization of the 3PG Model Based on Sensitivity Analysis and a Bayesian Method. Forests 2020, 11, 1369. [Google Scholar] [CrossRef]
- Braak, C.J.T. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte-Carlo sampling. Psychon. Bull. Rev. 2018, 25, 143–154. [Google Scholar] [CrossRef]
- Trotsiuk, V.; Hartig, F.; Forrester, D.I. R3PG—An r Package for Simulating Forest Growth Using the 3-PG Process-Based Model. Methods Ecol. Evol. 2020, 11, 1470–1475. [Google Scholar] [CrossRef]
- Hartig, F.; Minunno, F.; Paul, S. BayesianTools: General-Purpose MCMC and SMC Samplers and Tools for Bayesian Statistics. R Package Version 0.1.7. 2019. Available online: https://CRAN.R-project.org/package=BayesianTools (accessed on 18 May 2021).
- ter Braak, C.J.F.; Vrugt, J.A. Differential Evolution Markov Chain with Snooker Updater and Fewer Chains. Stat. Comput. 2008, 18, 435–446. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- McElreath, R. Statistical Rethinking: A Bayesian Course with Examples in R and Stan; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015; ISBN 978-1-4822-5344-3. [Google Scholar]
- Raison, R.J.; Myers, B.J. The Biology of Forest Growth Experiment: Linking Water and Nitrogen Availability to the Growth of Pinus Radiata. For. Ecol. Manag. 1992, 52, 279–308. [Google Scholar] [CrossRef]
- Lu, Y.; Coops, N.C.; Wang, T.; Wang, G. A Process-Based Approach to Estimate Chinese Fir (Cunninghamia Lanceolata) Distribution and Productivity in Southern China under Climate Change. Forests 2015, 6, 360–379. [Google Scholar] [CrossRef]
- Patenaude, G.; Milne, R.; Van Oijen, M.; Rowland, C.S.; Hill, R.A. Integrating Remote Sensing Datasets into Ecological Modelling: A Bayesian Approach. Int. J. Remote Sens. 2008, 29, 1295–1315. [Google Scholar] [CrossRef]
- Navarro-Cerrillo, R.M.; Beira, J.; Suarez, J.; Xenakis, G.; Sánchez-Salguero, R.; Hernández-Clemente, R. Growth Decline Assessment in Pinus Sylvestris L. and Pinus Nigra Arnold. Forest by Using 3-PG Model. For. Syst. 2016, 25, 3. [Google Scholar] [CrossRef]
- Pinjuv, G.L. Hybrid Forest Modelling of Pinus Radiata D. Don in Canterbury, New Zealand; University of Canterbury: Christchurch, New Zealand, 2006. [Google Scholar]
- Forrester, D.I.; Ammer, C.; Annighöfer, P.J.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; del Río, M.; Drössler, L.; et al. Predicting the Spatial and Temporal Dynamics of Species Interactions in Fagus Sylvatica and Pinus Sylvestris Forests across Europe. For. Ecol. Manag. 2017, 405, 112–133. [Google Scholar] [CrossRef]
- Forrester, D.I.; Tang, X. Analysing the Spatial and Temporal Dynamics of Species Interactions in Mixed-Species Forests and the Effects of Stand Density Using the 3-PG Model. Ecol. Model. 2016, 319, 233–254. [Google Scholar] [CrossRef]
- Collalti, A.; Prentice, I.C. Is NPP Proportional to GPP? Waring’s Hypothesis 20 Years on. Tree Physiol. 2019, 39, 1473–1483. [Google Scholar] [CrossRef]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net Primary Production of Forests: A Constant Fraction of Gross Primary Production? Tree Physiol. 1998, 18, 129–134. [Google Scholar] [CrossRef]
- Massoud, E.C.; Xu, C.; Fisher, R.A.; Knox, R.G.; Walker, A.P.; Serbin, S.P.; Christoffersen, B.O.; Holm, J.A.; Kueppers, L.M.; Ricciuto, D.M.; et al. Identification of Key Parameters Controlling Demographically Structured Vegetation Dynamics in a Land Surface Model: CLM4.5(FATES). Geosci. Model Dev. 2019, 12, 4133–4164. [Google Scholar] [CrossRef]
- Collalti, A.; Tjoelker, M.G.; Hoch, G.; Mäkelä, A.; Guidolotti, G.; Heskel, M.; Petit, G.; Ryan, M.G.; Battipaglia, G.; Matteucci, G.; et al. Plant Respiration: Controlled by Photosynthesis or Biomass? Glob. Chang. Biol. 2020, 26, 1739–1753. [Google Scholar] [CrossRef]
- Collalti, A.; Ibrom, A.; Stockmarr, A.; Cescatti, A.; Alkama, R.; Fernández-Martínez, M.; Matteucci, G.; Sitch, S.; Friedlingstein, P.; Ciais, P.; et al. Forest Production Efficiency Increases with Growth Temperature. Nat. Commun. 2020, 11, 5322. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Sharkey, T.D. Stomatal Conductance and Photosynthesis. Annu. Rev. Plant Physiol. 1982, 33, 317–345. [Google Scholar] [CrossRef]
- Paul, K.I.; Polglase, P.J.; Richards, G.P. Sensitivity Analysis of Predicted Change in Soil Carbon Following Afforestation. Ecol. Model. 2003, 164, 137–152. [Google Scholar] [CrossRef]
- Zaehle, S.; Sitch, S.; Smith, B.; Hatterman, F. Effects of Parameter Uncertainties on the Modeling of Terrestrial Biosphere Dynamics. Glob. Biogeochem. Cycles 2005, 19. [Google Scholar] [CrossRef]
- Pappas, C.; Fatichi, S.; Leuzinger, S.; Wolf, A.; Burlando, P. Sensitivity Analysis of a Process-Based Ecosystem Model: Pinpointing Parameterization and Structural Issues. J. Geophys. Res. Biogeosci. 2013, 118, 505–528. [Google Scholar] [CrossRef]
- Tatarinov, F.A.; Cienciala, E. Application of BIOME-BGC Model to Managed Forests: 1. Sensitivity Analysis. For. Ecol. Manag. 2006, 237, 267–279. [Google Scholar] [CrossRef]
- Bontemps, J.-D.; Bouriaud, O. Predictive Approaches to Forest Site Productivity: Recent Trends, Challenges and Future Perspectives. For. Int. J. For. Res. 2014, 87, 109–128. [Google Scholar] [CrossRef]
- Ulrich, D.E.M.; Still, C.; Brooks, J.R.; Kim, Y.; Meinzer, F.C. Investigating Old-Growth Ponderosa Pine Physiology Using Tree-Rings, d13C, d18O, and a Process-Based Model. Ecology 2019, 100, e02656. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martín-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest Disturbances under Climate Change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef]
- Goulden, M.L.; Munger, J.W.; Fan, S.-M.; Daube, B.C.; Wofsy, S.C. Measurements of Carbon Sequestration by Long-Term Eddy Covariance: Methods and a Critical Evaluation of Accuracy. Glob. Change Biol. 1996, 2, 169–182. [Google Scholar] [CrossRef]
- López-Serrano, F.R.; Martínez-García, E.; Dadi, T.; Rubio, E.; García-Morote, F.A.; Lucas-Borja, M.E.; Andrés-Abellán, M. Biomass Growth Simulations in a Natural Mixed Forest Stand under Different Thinning Intensities by 3-PG Process-Based Model. Eur. J. For. Res. 2015, 134, 167–185. [Google Scholar] [CrossRef]
- Zaher, H.; Sabir, M.; Benjelloun, H.; Paul-Igor, H. Effect of forest land use change on carbohydrates, physical soil quality and carbon stocks in Moroccan cedar area. J. Environ. Manag. 2020, 254, 109544. [Google Scholar] [CrossRef] [PubMed]
- M’Hirit, O. Etude Ecologique et Forestiere des Cedraies du Rif Marocain; Essai sur une Approche Multidimensionnelle de la Phytoecologie et de la Productivite du Cedre (Cedrus atlantica Manetti). Ph.D. Thesis, Université de Droit, d’Economie et des Sciences d’Aix-Marseille, Aix-en-Provence, France, 1982. [Google Scholar]
- Toth, J. Première approche de la production potentielle du Cèdre de l’Atlas dans le sud de la France. Rev. For. Fr. 1973, 5, 381. [Google Scholar] [CrossRef]
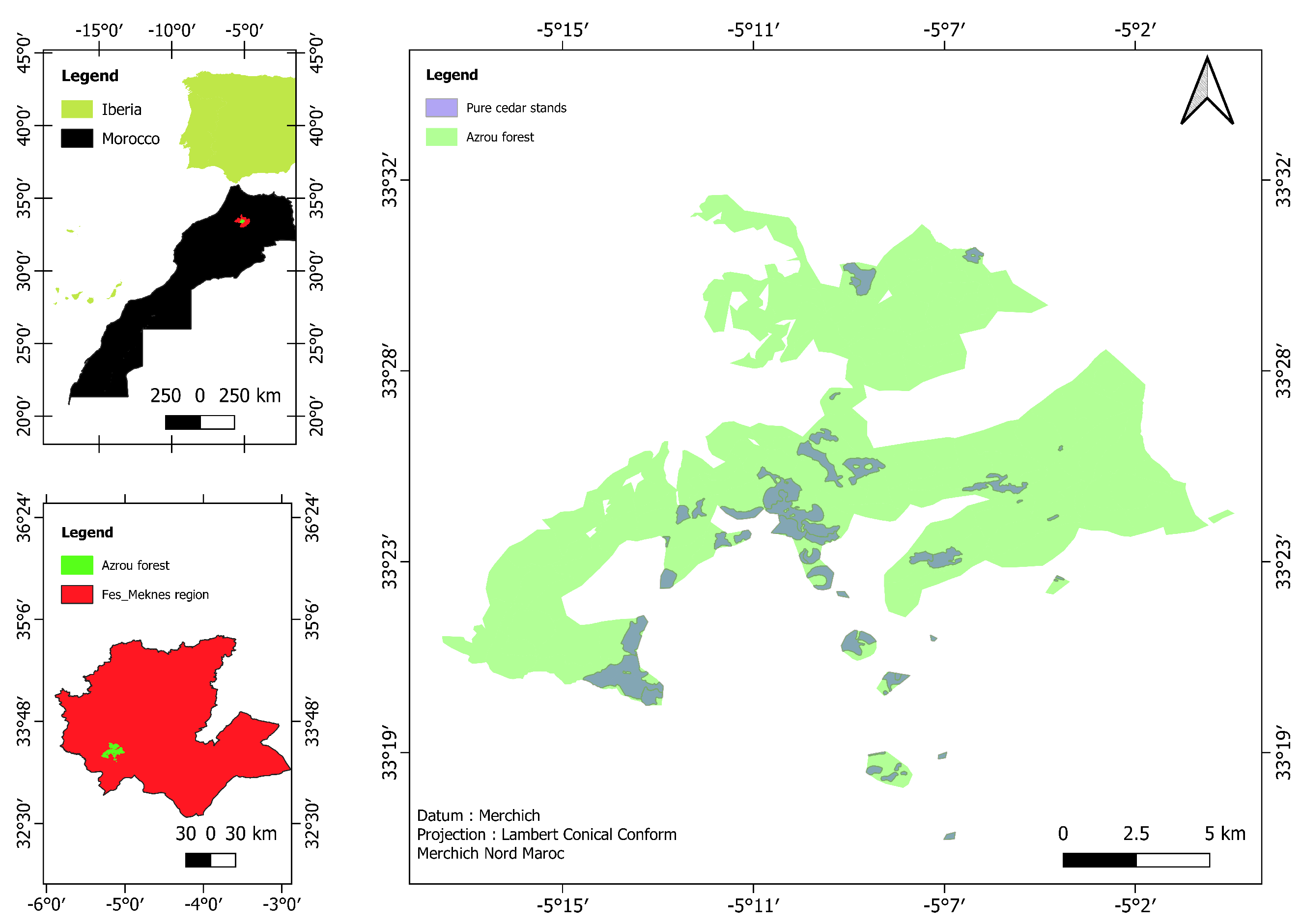
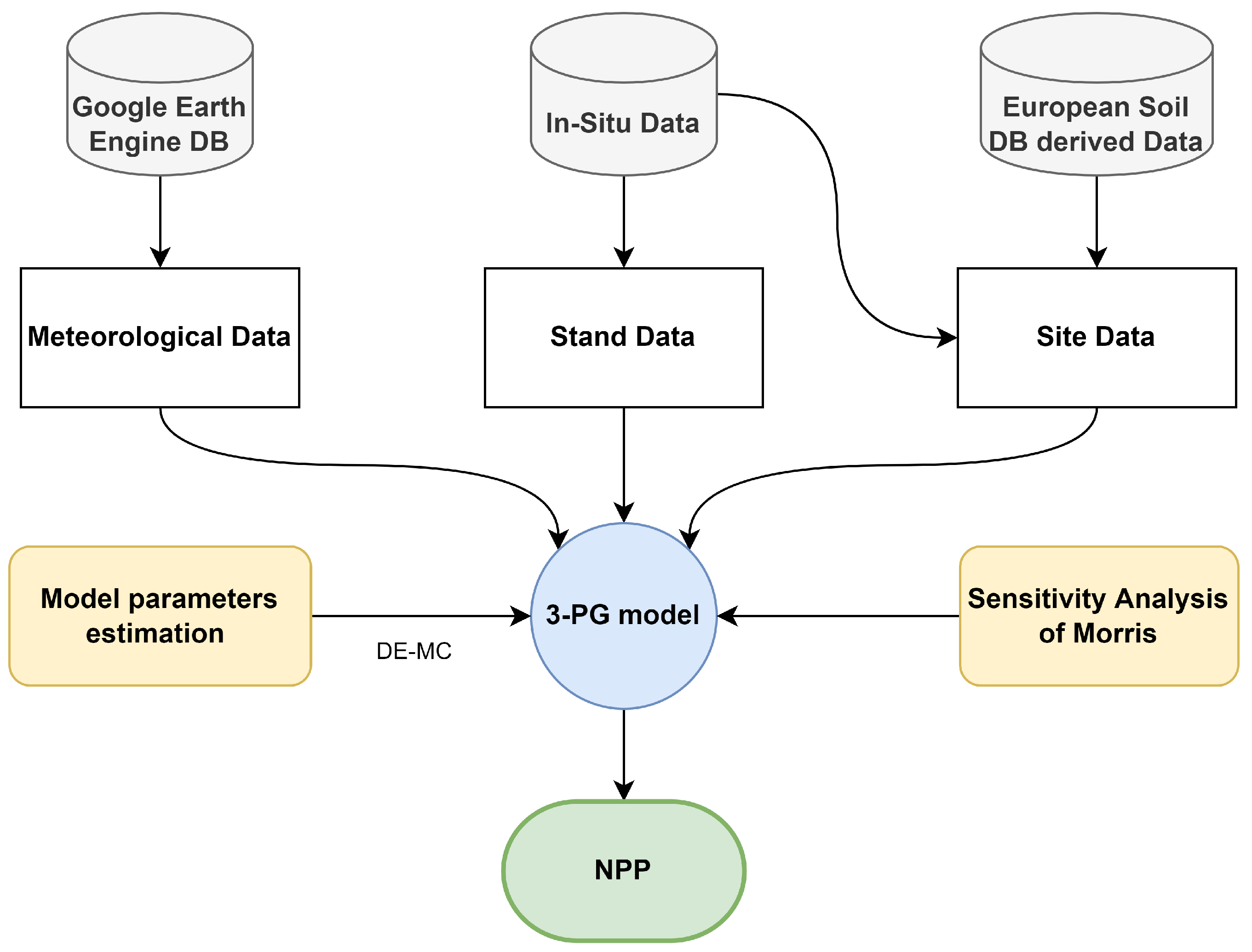
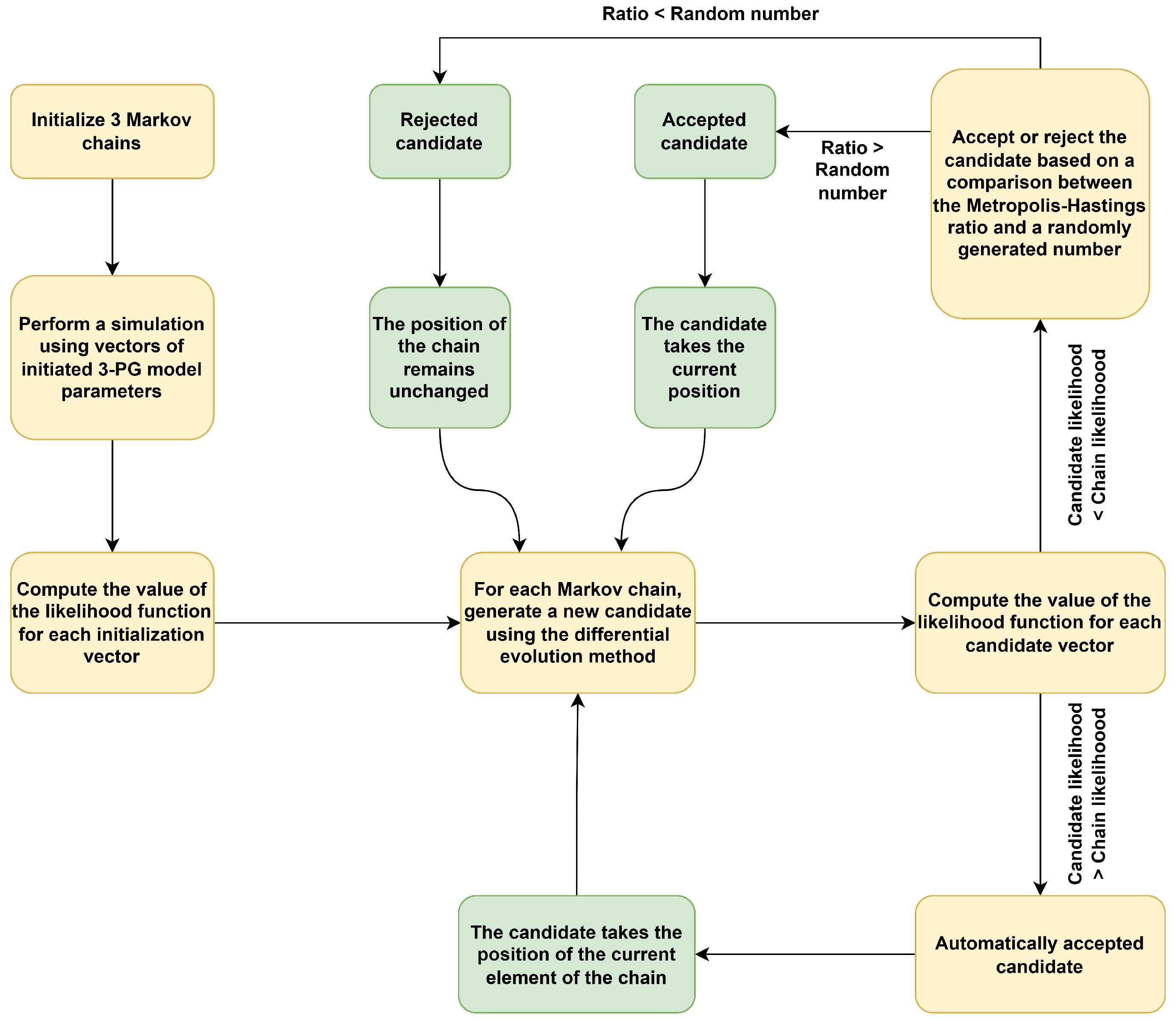
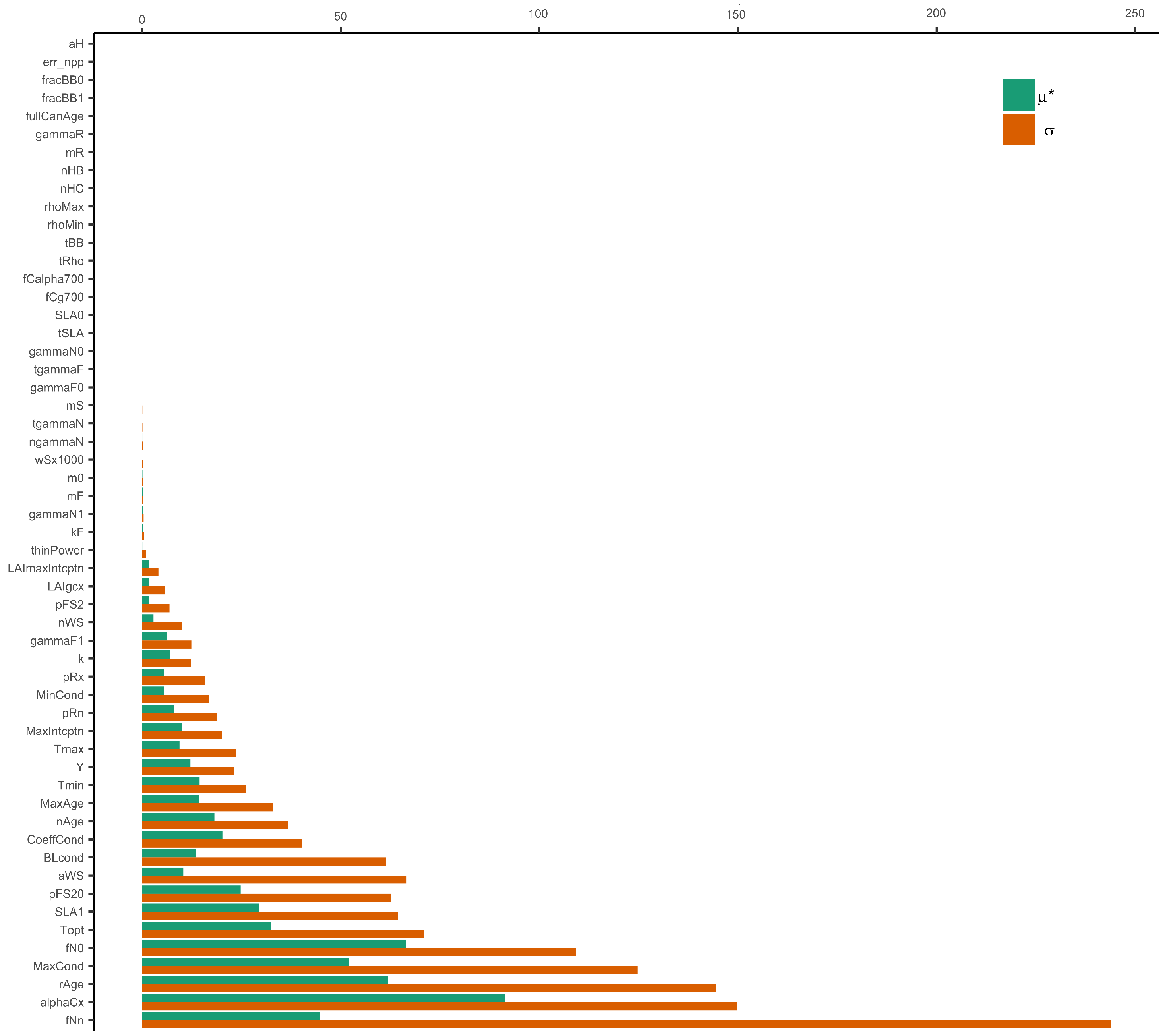
| Stratum | Area (ha) | The Standard Deviation of the Annual Increase in Carbomass () | Number of Selected Plots |
|---|---|---|---|
| Cool exposure/Low density | 368 | 0.55 | 6 |
| Warm exposure/Low density | 675 | 0.24 | 5 |
| Cool exposure/High density | 145 | 1.05 | 5 |
| Warm exposure/High density | 258 | 1.18 | 8 |
| Total | 1446 | 24 |
| Category | Variable | Collection Name | Band Name | Spatial/Temporal Resolution |
|---|---|---|---|---|
| Climate (4) | tmp_min | “ECMWF/ERA5/DAILY” | minimum_2m_air_temperature | 0.25°/1 day |
| tmp_max | “ECMWF/ERA5/DAILY” | maximum_2m_air_temperature | 0.25°/1 day | |
| tmp_mean | “MODIS_006_MOD11A2” | LST_Day_1km | 1000 m/8 days | |
| prcp | “ECMWF/ERA5/MONTHLY” | total_precipitation | 0.25°/1 month | |
| srad | “ECMWF/ERA5_LAND/MONTHLY” | surface_solar_radiation_downwards | 0.1°/1 month | |
| frost_days | “MODIS/006/MOD11A1” | LST_Day_1km | 1000 m/1 day | |
| Site (2) | ASW | European Soil Database [41] | SMU_EU_S_TAWC | 1000 m/- |
| NPP (6) | Npp | “MODIS/006/MOD17A2H” | PsnNet | 500 m/8 days |
| Component | Model |
|---|---|
| Tree (Aboveground part) | |
| Stem | |
| Foliage |
| Compartment | Stem | Foliage | Branches | Mean |
|---|---|---|---|---|
| %Carbon | 57.41 | 57.30 | 54.30 | 56.43 |
| Stratum | N () | D (cm) | Age (yr) | SB ± SD () | FB ± SD () | RB ± SD () | CAI () |
|---|---|---|---|---|---|---|---|
| Cool exposure/High density | 466 | 49 | 174 | 89.25 ± 19.3 | 0.50 ± 0.12 | 48.88 ± 15.3 | 1.1 |
| Cool exposure/Low density | 180 | 35 | 107 | 49.78 ± 10.6 | 0.19 ± 0.05 | 17.62 ± 6.6 | 1.13 |
| Warm exposure/High density | 792 | 46 | 159 | 268.08 ± 52 | 0.92 ± 0.20 | 93.95 ± 13.4 | 0.93 |
| Warm exposure/Low density | 140 | 71 | 149 | 66.68 ± 16.2 | 0.16 ± 0.13 | 22.68 ± 9.3 | 1.96 |
| Default Model | Median Model | Calibrated Model | |
|---|---|---|---|
| MSE | 0.32068 | 0.26213 | 0.26210 |
| Parameter | Unit | Initial Value | Range | Mode | Mean ± Standard Deviation | Description |
|---|---|---|---|---|---|---|
| pFS20 | - | 0.6 | [0.05, 0.8] | 0.29 | 0.39 ± 0.21 | Foliage stem partitioning at D = 20 cm |
| aWS | - | 0.05 | [0, 0.4] | 0.117 | 0.201 ± 0.109 | Constant in stem mass v. diameter relationship |
| pRn | - | 0.2 | [0.0001, 0.5] | 0.466 | 0.267 ± 0.141 | Minimum fraction of NPP to roots |
| gammaF1 | 1/month | 0.049 | [0.0001, 0.04] | 0.0126 | 0.0198 ± 0.0117 | Maximum litterfall rate |
| Tmin | Degree °C | 0 | [, 8] | 3.25 ± 2.45 | Minimum temperature for growth | |
| Topt | Degree °C | 19.5 | [10, 30] | 23.87 | 23.98 ± 4.06 | Optimum temperature for growth |
| Tmax | Degree °C | 35 | [30, 40] | 38.57 | 36.11 ± 2.59 | Maximum temperature for growth |
| fN0 | - | 0.6 | [0.0001, 1] | 0.1300 | 0.3943 ± 0.2648 | Value of fN when FR = 0 |
| fNn | - | 1 | [0, 1] | 0.87 | 0.47 ± 0.28 | Power of (1-FR) in fN |
| MaxAge | Years | 500 | [350, 550] | 461 | 452 ± 57 | Maximum stand age used in age modifier |
| nAge | - | 4 | [1, 4.325] | 2.477 | 2.537 ± 0.970 | Power of relative age in function for fAge |
| rAge | - | 0.95 | [0.0001, 1.4] | 0.2436 | 0.6980 ± 0.3510 | Relative age to give fAge = 0.5 |
| SLA1 | m2/kg | 5.5 | [5, 30] | 22.33 | 16.62 ± 7.15 | Specific leaf area for mature leaves |
| K | - | 0.2921 | [0.4, 0.6] | 0.40 | 0.49 ± 0.06 | Extinction coefficient for absorption of PAR by the canopy |
| MaxIntrcptn | - | 0.25 | [0.1, 0.4] | 0.36 | 0.25 ± 0.087 | Maximum proportion of rainfall evaporated from canopy |
| alphaCx | molC/molPAR | 0.04212129 | [0.02, 0.09] | 0.0493 | 0.0468 ± 0.0188 | Canopy quantum efficiency |
| Y | - | 0.47 | [0.44, 0.51] | 0.48 | 0.47 ± 0.02 | Ratio NPP/GPP |
| MaxCond | m/s | 0.02 | [0.001, 0.03] | 0.022 | 0.016 ± 0.008 | Maximum canopy conductance |
| CoeffCond | 1/mBar | 0.05 | [0.0001, 0.07] | 0.0030 | 0.0367 ± 0.0196 | Defines stomatal response to VPD |
| BLcond | m/s | 0.2 | [0.0001, 0.3] | 0.1105 | 0.1479 ± 0.0861 | Canopy boundary layer conductance |
| Statum | Area (ha) | Unit Carbon Increase ± SD () | Stratum Carbon Increase () |
|---|---|---|---|
| Cool exposure/Low density | 368 | 5.20 ± 0.34 | 1913 |
| Warm exposure/Low density | 675 | 5.08 ± 0.46 | 3429 |
| Cool exposure/High density | 145 | 7.24 ± 0.77 | 1049 |
| Warm exposure/High density | 258 | 5.92 ± 0.41 | 1527 |
| Pure cedar forest | 1446 | 5.47 | 7918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boukhris, I.; Lahssini, S.; Collalti, A.; Moukrim, S.; Santini, M.; Chiti, T.; Valentini, R. Calibrating a Process-Based Model to Enhance Robustness in Carbon Sequestration Simulations: The Case of Cedrus atlantica (Endl.) Manetti ex Carrière. Forests 2023, 14, 401. https://doi.org/10.3390/f14020401
Boukhris I, Lahssini S, Collalti A, Moukrim S, Santini M, Chiti T, Valentini R. Calibrating a Process-Based Model to Enhance Robustness in Carbon Sequestration Simulations: The Case of Cedrus atlantica (Endl.) Manetti ex Carrière. Forests. 2023; 14(2):401. https://doi.org/10.3390/f14020401
Chicago/Turabian StyleBoukhris, Issam, Said Lahssini, Alessio Collalti, Said Moukrim, Monia Santini, Tommaso Chiti, and Riccardo Valentini. 2023. "Calibrating a Process-Based Model to Enhance Robustness in Carbon Sequestration Simulations: The Case of Cedrus atlantica (Endl.) Manetti ex Carrière" Forests 14, no. 2: 401. https://doi.org/10.3390/f14020401
APA StyleBoukhris, I., Lahssini, S., Collalti, A., Moukrim, S., Santini, M., Chiti, T., & Valentini, R. (2023). Calibrating a Process-Based Model to Enhance Robustness in Carbon Sequestration Simulations: The Case of Cedrus atlantica (Endl.) Manetti ex Carrière. Forests, 14(2), 401. https://doi.org/10.3390/f14020401








