Optimizing Bucking Decisions in Korean Red Pine: A Dynamic Programming Approach to Timber Profitability
Abstract
1. Introduction
2. Materials and Methods
2.1. Development of a Log Sawing Simulation Model
2.2. Data Collection
2.3. Profitability Analysis
3. Results
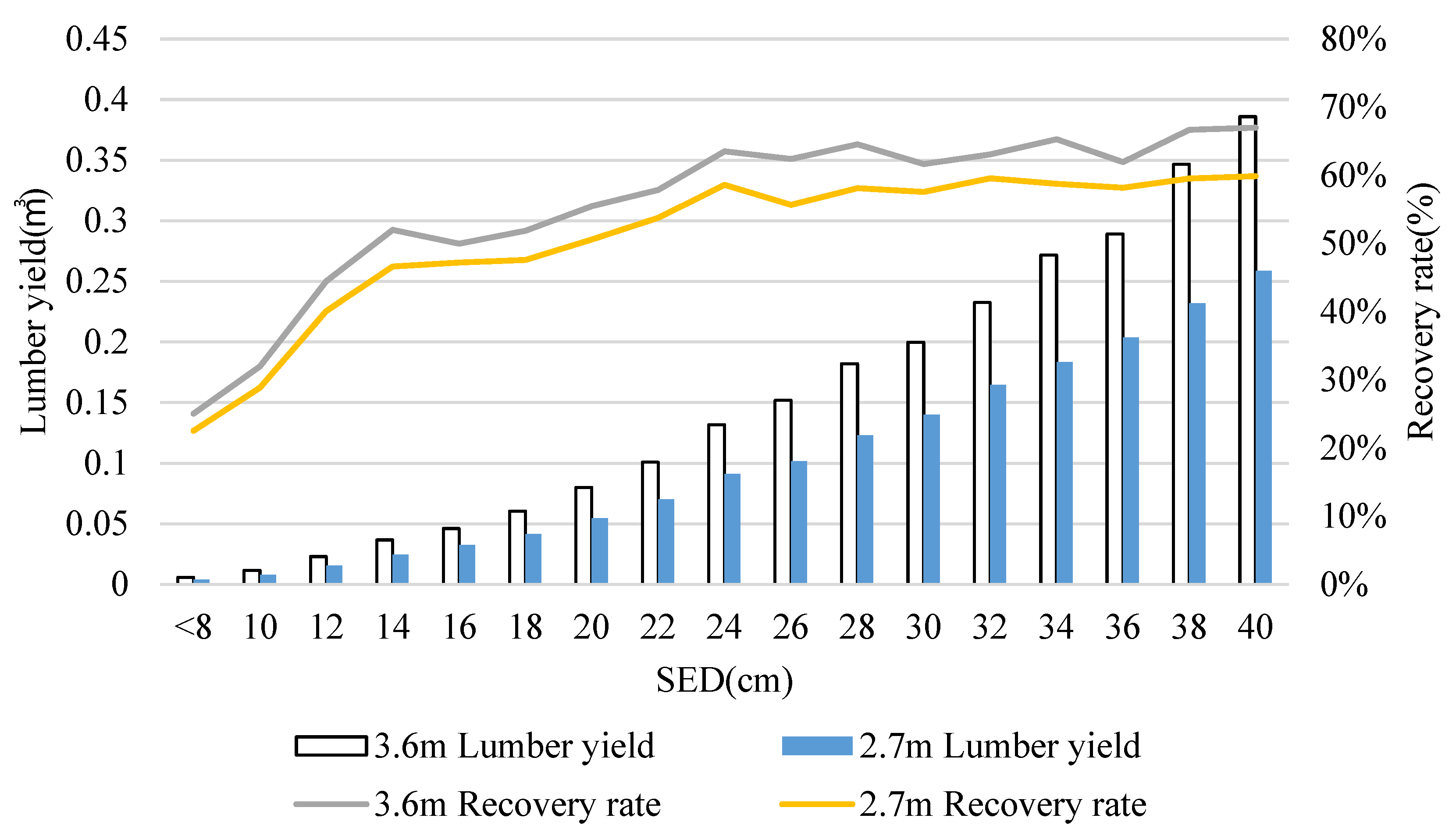
3.1. Lumber Yield and Recovery Rate of Sawing 3.6 m and 2.7 m Logs
3.2. Pulp Chip Yield from Chipping 1.8 m Logs
3.3. Net Profit Comparison between Lumber Production and Pulp Chip Production
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korea Forest Service. Statistical Yearbook of Forestry; Korea Forest Service: Daejeon, Republic of Korea, 2016.
- Seol, A.; Han, H.; Jung, Y.; Chung, H.; Chung, J. Analyzing the Comparative Economic Efficiency of Short-wood Woodgrab Logging and Whole-tree Cable Logging Operations. J. Korean Soc. For. Soc. Sci. 2016, 105, 231–237. [Google Scholar]
- Korea Forest Research Institute. Pine Tree, the Economical Tree Species; Korea Forest Research Institute: Seoul, Republic of Korea, 2011. [Google Scholar]
- Han, H.; Seol, A.; Jung, Y.; Chung, J. Maintaining long-rotation forestry: A new challenge for sustained yield of timber resources in South Korea. Int. For. Rev. 2018, 20, 199–205. [Google Scholar] [CrossRef]
- Scholz, J.; Meyer, A.D.; Marques, A.S.; Pinho, T.M.; Boaventura-Cunha, J.; Orshoven, J.V.; Rosset, C.; Kunzi, J.; Kaarle, J.; Nummila, K. Digital technologies for forest supply chain optimization: Existing solutions and future trends. Environ. Manag. 2018, 62, 1108–1133. [Google Scholar] [CrossRef] [PubMed]
- Vaatainen, K.; Anttila, P.; Eliasson, L.; Enstrom, J.; Laitila, J.; Prinz, R.; Rouata, J. Roundwood and biomass logistics in Finland and Sweden. Croat. J. For. Eng. 2021, 42, 24. [Google Scholar] [CrossRef]
- Kogler, C.; Schimpfhuber, S.; Eichberger, C.; Rauch, P. Benchmarking procurement cost saving strategies for wood supply chains. Forests 2021, 12, 1086. [Google Scholar] [CrossRef]
- Kogler, C.; Rauch, P. Lead time and quality driven transport strategies for the wood supply chain. Res. Transp. Bus. Manag. 2023, 47, 100946. [Google Scholar] [CrossRef]
- Acuna, M.; Sessions, J.; Zamora, R.; Boston, K.; Brown, M.; Ghaffariyan, M.R. Methods to manage and optimize forest biomass supply chains: A review. Curr. For. Rep. 2019, 5, 124–141. [Google Scholar] [CrossRef]
- Peter, R.K.; Bamping, J.H. Theoretical sawing of pine logs. For. Prod. J. 1962, 12, 549–557. [Google Scholar]
- Hallock, H. Mathematical Analysis of the Effect of Kerf Width on Lumber Yield from Small Logs; USDA, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1962.
- Taylor, F.W.; Garton, M.W. The Systematic Evaluation of a Pine Sawmilling Operation. Master’s Thesis, The Mississippi State University, Lee Blvd, MS, USA, 1970. [Google Scholar]
- McAdoo, J. Computer simulation of small-log mill processing. For. Prod. J. 1969, 19, 34–35. [Google Scholar]
- Hallock, H.; Lewis, D.W. Increasing Softwood Dimension Yield from Small Logs-Best Opening Face; USDA, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1971.
- Bellman, R. The Theory of Dynamic Programming. Bull. Am. Math. Soc. 1954, 60, 503–515. [Google Scholar] [CrossRef]
- Briggs, D.G. A Dynamic Programming Approach to Optimizing Stem Conversion. Ph.D. Thesis, The University of Washington, Washington, DC, USA, 1980. [Google Scholar]
- Rönnqvist, M. Optimization in forestry. Math. Program. 2003, 97, 267–284. [Google Scholar] [CrossRef]
- Geerts, J.M.P. Mathematical solution for optimizing the sawing pattern of a log given its dimensions and its defect core. N. Z. J. For. Sci. 1984, 14, 124–134. [Google Scholar]
- Todoroki, C.L.; Ronnqvist, E.M. Secondary log breakdown optimization with dynamic programming. J. Oper. Res. Soc. 1997, 48, 471–478. [Google Scholar] [CrossRef]
- Faaland, B.; Briggs, D. Log Bucking and Lumber Manufacturing Using Dynamic Programming. Manag. Sci. 1984, 30, 245–257. [Google Scholar] [CrossRef]
- Reinders, M.P.; Hendriks, T.H.B. Lumber production optimization. Eur. J. Oper. Res. 1989, 42, 243–253. [Google Scholar] [CrossRef]
- Puumalainen, J. Optimal cross-cutting and sensitivity analysis for various log dimension constraints by using dynamic programming approach. Scand. J. Forest. Res. 1998, 13, 74–82. [Google Scholar] [CrossRef]
- Kwon, S.D. Development of a Simulation Model for Stand-Level Forest Management. Ph.D. Thesis, The Seoul National University, Seoul, Republic of Korea, 2003. [Google Scholar]
- Kwon, S.D.; Kim, H.H.; Chung, J.S. Estimation of Merchantable Volume and Yield Using A Stem Shape Simulation. J. Korean Soc. For. Soc. Sci. 2007, 96, 362–368. [Google Scholar]
- Kwon, K.B.; Han, H.; Seol, A.R.; Chung, H.J.; Chung, J.S. Development of a Wood Recovery Estimation Model for the Tree Conversion Processes of Larix kaempferi. J. Korean Soc. For. Soc. Sci. 2013, 102, 484–490. [Google Scholar] [CrossRef][Green Version]
- Lee, C.T.; Chung, D.J.; Lee, Y.D.; Jo, J.M. A Study on Utilization of the Sawed Products from Black Locust; Korea Forest Research Institute: Seoul, Republic of Korea, 1985. [Google Scholar]
- Lee, C.T.; Chung, D.J.; Park, J.H. A Study on Utilization of Furniture Parts from Alnus; Korea Forest Research Institute: Seoul, Republic of Korea, 1986. [Google Scholar]
- Lee, C.T.; Kwon, J.T.; Han, G.J. A Demonstration Test of the Domestic Timber Using Movable Sawing Machine; Korea Forest Research Institute: Seoul, Republic of Korea, 1989. [Google Scholar]
- Bobrowski, P.M. The Effect of Modeling on Log Bucking Solution Techniques. J. Oper. Res. Soc. 1994, 45, 624–634. [Google Scholar] [CrossRef]
- Korea Forest Service. Report on the State of Forest Products Utilization; Korea Forest Service: Daejeon, Republic of Korea, 2015.
- Bellman, R. Dynamic-Programming and the Numerical-Solution of Variational-Problems. Oper. Res. 1957, 5, 277–288. [Google Scholar]
- Korpunen, H.; Mochan, S.; Uusitalo, J. An activity-based costing method for sawmilling. For. Prod. J. 2010, 60, 420–431. [Google Scholar] [CrossRef]
- Korea Forestry Promotion Institute. The Quarterly Market Prices of Domestic Timber; Korea Forestry Promotion Institute: Seoul, Republic of Korea, 2022. [Google Scholar]
- Korea Forest Research Institute. Tree, Log and Biomass Volume and Yield Table; Korea Forest Research Institute: Seoul, Republic of Korea, 2011. [Google Scholar]
- Jung, H.S. Wood Science; Seoul National University Press: Seoul, Republic of Korea, 1998. [Google Scholar]
- Pinto, I.; Usenius, A.; Song, T.C.; Pereira, H. Sawing simulation of maritime pine (Pinus pinaster Ait.) stems for production of heartwood-containing components. For. Prod. J. 2005, 55, 88–96. [Google Scholar]
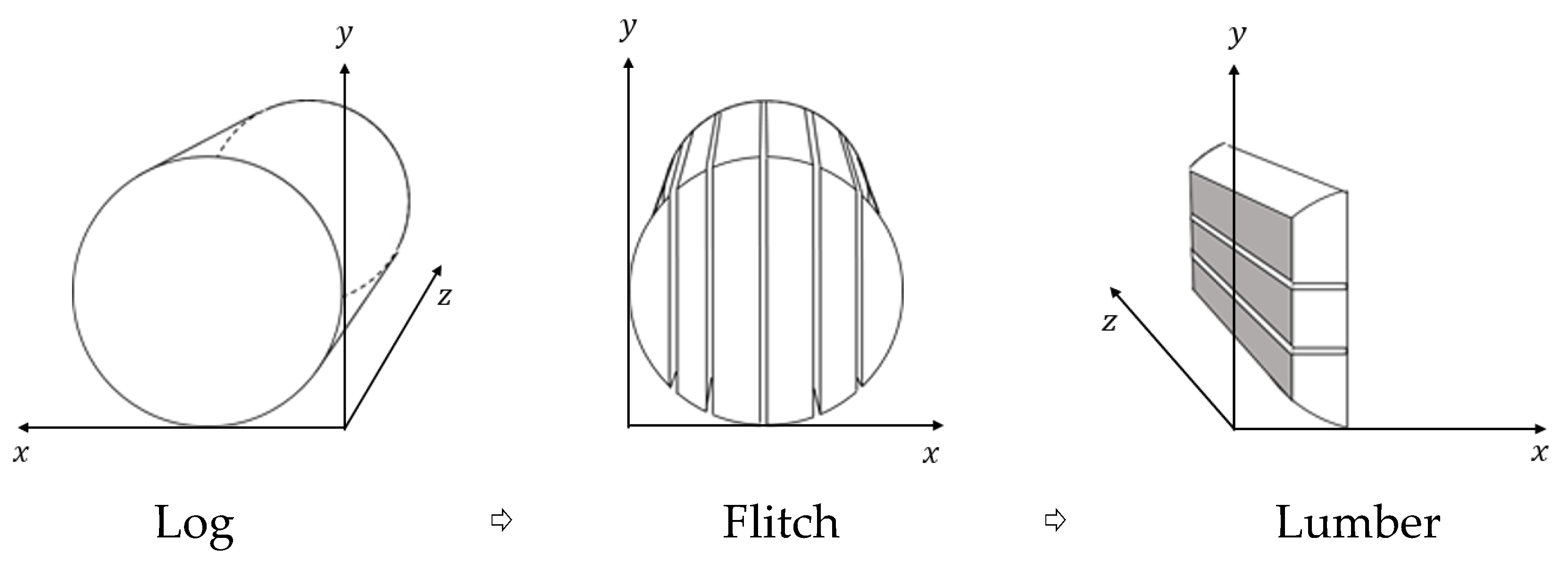

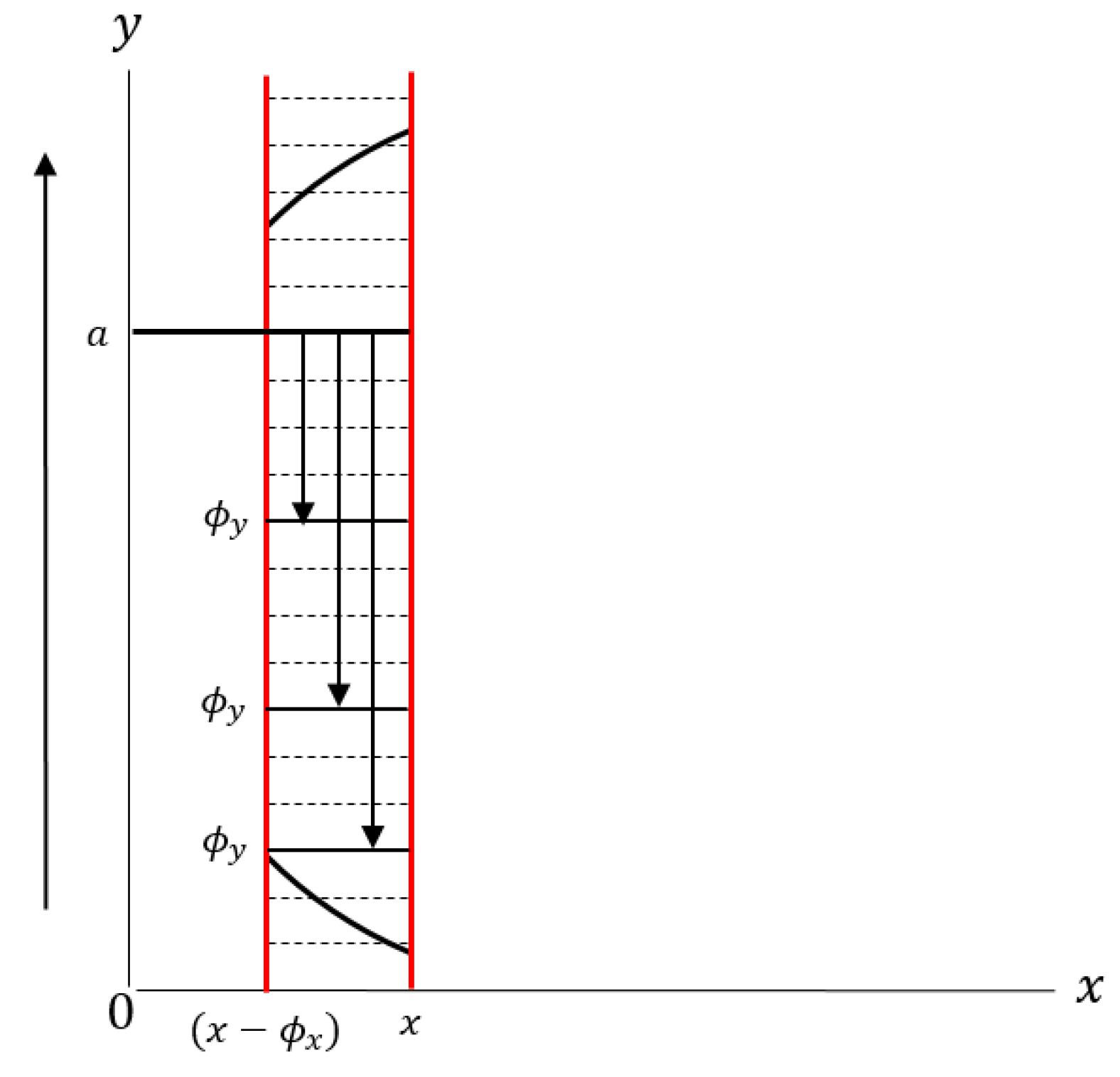
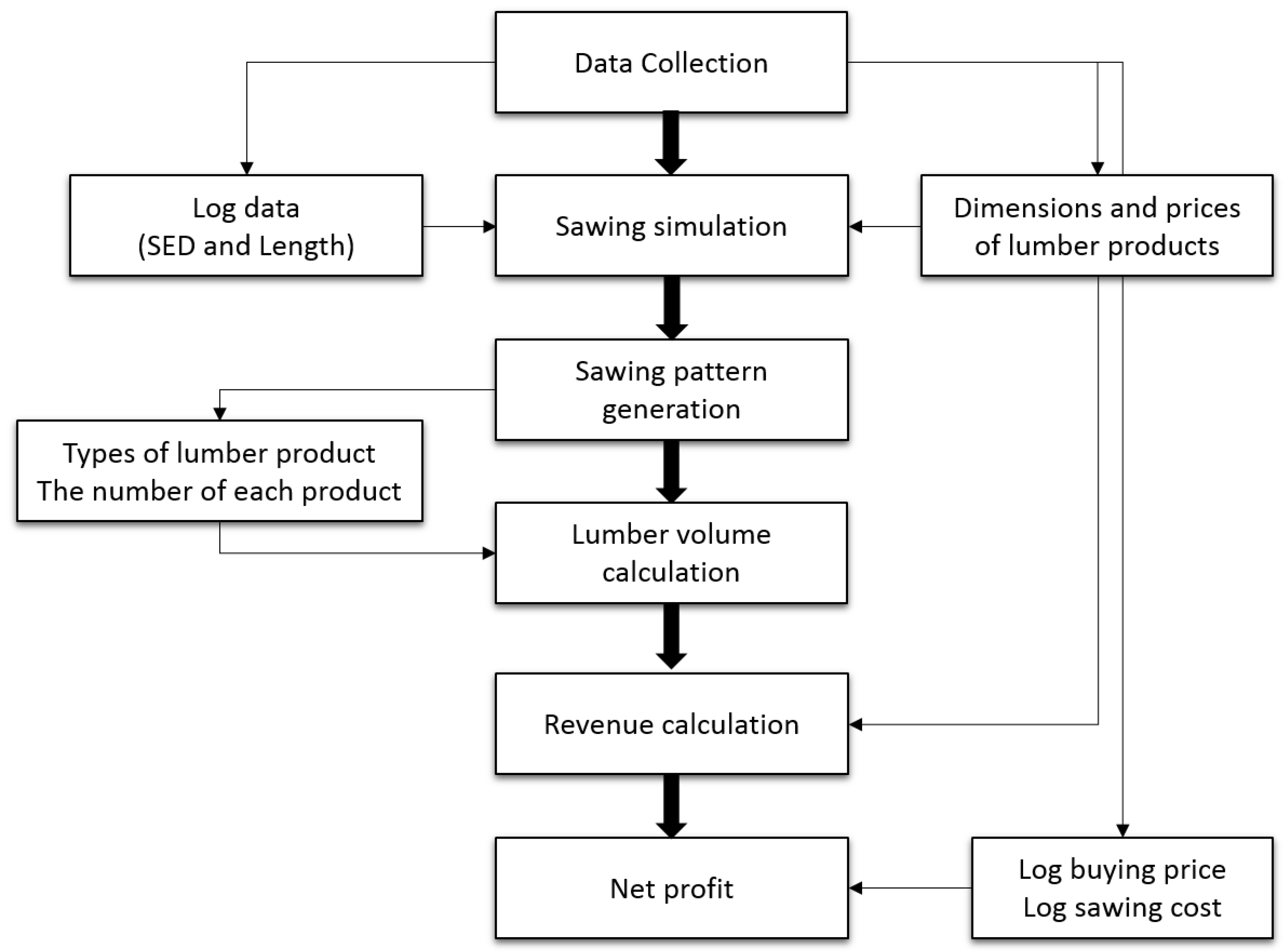
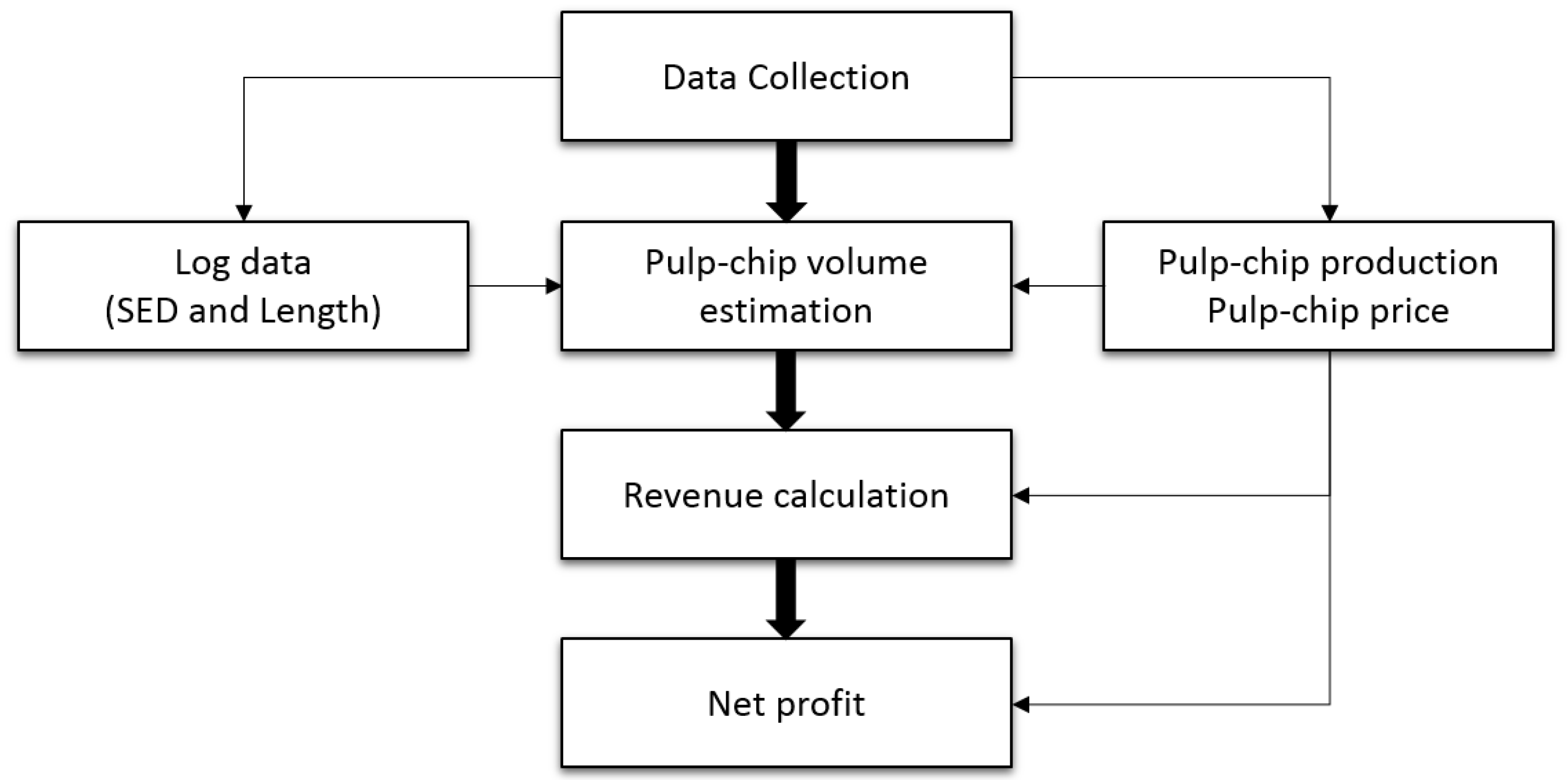

| Type | Lumber Products (3.6 m Type) | Lumber Products (2.7 m Type) | ||
|---|---|---|---|---|
| Dimensions (mm) | Price ($) | Dimensions (mm) | Price ($) | |
| 1 | 27 89 | 8 | 27 89 | 6.1 |
| 2 | 38 38 | 5.2 | 38 38 | 4 |
| 3 | 38 89 | 12.4 | 38 89 | 9.3 |
| 4 | 38 140 | 17.8 | 38 140 | 13.3 |
| 5 | 89 89 | 27.9 | 38 184 | 19.5 |
| 6 | 140 140 | 64 | 38 235 | 29.3 |
| 7 | 180 180 | 108 | 38 285 | 36 |
| 8 | 200 200 | 145.6 | 90 90 | 20.1 |
| 9 | 250 250 | 234.9 | 90 140 | 33.5 |
| 10 | - | - | 140 140 | 48 |
| 11 | - | - | 180 180 | 81 |
| 12 | - | - | 200 200 | 109.3 |
| 13 | - | - | 250 250 | 176.1 |
| Supreme | 1st | 2nd | 3rd | Bolt | Pulp | |
|---|---|---|---|---|---|---|
| SED * (cm) | >42 | >27 | >21 | >18 | >12 | >6 |
| Length (m) | >2.1 | >3.6 | >3.6 | >2.1 | >2.4 | >1.8 |
| Price ($/) | 392.5 | 215.2 | 183.4 | 166.9 | 162 | 58.4 |
| No. | Dimensions | SED * (cm) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | ||
| 1 | 27 89 | - | - | - | - | 2 | - | - | 2 | - | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 1 | - |
| 2 | 38 38 | 1 | 1 | 2 | 4 | 3 | - | 6 | 6 | 4 | 6 | 5 | 8 | - | 5 | 5 | 2 | 10 | 13 |
| 3 | 38 89 | - | - | - | - | - | 2 | 2 | 2 | 6 | 6 | 8 | 9 | 2 | - | 15 | 1 | 20 | 15 |
| 4 | 38 140 | - | - | - | - | - | 1 | - | - | - | - | - | - | 1 | 2 | - | 1 | 1 | - |
| 5 | 89 89 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | - | 4 |
| 6 | 140 140 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 7 | 180 180 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 8 | 200 200 | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | - | - | - | - |
| 9 | 250 250 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | - |
| No. | Dimensions | SED * (cm) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | ||
| 1 | 27 89 | - | - | - | - | 2 | - | - | 2 | - | 2 | 1 | 2 | - | - | - | 1 | 3 | 2 |
| 2 | 38 38 | 1 | 1 | 2 | 4 | 3 | - | 6 | 6 | 11 | 6 | - | - | - | - | - | 1 | 1 | 7 |
| 3 | 38 89 | - | - | - | - | - | 2 | 2 | 2 | 3 | 6 | 1 | - | - | - | 2 | 1 | - | - |
| 4 | 38 140 | - | - | - | - | - | 1 | - | - | - | - | - | - | 1 | 2 | - | - | 1 | - |
| 5 | 38 184 | - | - | - | - | - | - | - | - | - | - | 2 | 2 | 1 | - | - | 1 | 1 | |
| 6 | 38 235 | - | - | - | - | - | - | - | - | - | - | 2 | 3 | 2 | 2 | 2 | 2 | 2 | 1 |
| 7 | 38 285 | - | - | - | - | - | - | - | - | - | - | - | - | 2 | 3 | 4 | 4 | 5 | 6 |
| 8 | 90 90 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 9 | 90 140 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 10 | 140 140 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 11 | 180 180 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 12 | 200 200 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 13 | 250 250 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| SED * (cm) | Green Weight of a Log (ton) | Pulp Chip Yield |
|---|---|---|
| 6 | 0.006 | 0.015 |
| 8 | 0.011 | 0.027 |
| 10 | 0.017 | 0.043 |
| 12 | 0.025 | 0.061 |
| 14 | 0.033 | 0.083 |
| 16 | 0.044 | 0.109 |
| 18 | 0.055 | 0.138 |
| 20 | 0.068 | 0.170 |
| 22 | 0.082 | 0.206 |
| 24 | 0.098 | 0.245 |
| 26 | 0.115 | 0.288 |
| 28 | 0.133 | 0.334 |
| 30 | 0.153 | 0.383 |
| 32 | 0.174 | 0.436 |
| 34 | 0.197 | 0.492 |
| 36 | 0.221 | 0.552 |
| 38 | 0.246 | 0.615 |
| 40 | 0.272 | 0.681 |
| SED * (cm) | Net Profit ($) | ||
|---|---|---|---|
| Lumber | Pulp Chip | ||
| 3.6 m Log | 2.7 m Log | 1.8 m Log | |
| <8 | 1.80 (120%) ** | 1.43 (76%) | 0.82 |
| 10 | 4.92 (285%) | 3.88 (203%) | 1.28 |
| 12 | 12.51 (581%) | 9.75 (431%) | 1.84 |
| 14 | 20.24 (708%) | 15.65 (525%) | 2.50 |
| 16 | 27.75 (748%) | 20.95 (540%) | 3.27 |
| 18 | 36.62 (785%) | 28.09 (579%) | 4.14 |
| 20 | 47.97 (839%) | 36.80 (620%) | 5.11 |
| 22 | 61.24 (891%) | 46.22 (648%) | 6.18 |
| 24 | 80.62 (996%) | 61.42 (735%) | 7.36 |
| 26 | 93.30 (981%) | 77.70 (800%) | 8.63 |
| 28 | 113.23 (1031%) | 97.89 (878%) | 10.01 |
| 30 | 132.63 (1054%) | 116.21 (911%) | 11.49 |
| 32 | 148.37 (1035%) | 139.28 (965%) | 13.08 |
| 34 | 170.98 (1058%) | 160.37 (986%) | 14.76 |
| 36 | 197.18 (1091%) | 173.32 (947%) | 16.55 |
| 38 | 219.05 (1088%) | 198.03 (974%) | 18.44 |
| 40 | 246.70 (1107%) | 220.08 (977%) | 20.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, Y.; Chang, Y.; You, J.; Kim, D.; Han, H. Optimizing Bucking Decisions in Korean Red Pine: A Dynamic Programming Approach to Timber Profitability. Forests 2023, 14, 2450. https://doi.org/10.3390/f14122450
Jung Y, Chang Y, You J, Kim D, Han H. Optimizing Bucking Decisions in Korean Red Pine: A Dynamic Programming Approach to Timber Profitability. Forests. 2023; 14(12):2450. https://doi.org/10.3390/f14122450
Chicago/Turabian StyleJung, Yoonkoo, Yoonseong Chang, Joungwon You, Dayoung Kim, and Hee Han. 2023. "Optimizing Bucking Decisions in Korean Red Pine: A Dynamic Programming Approach to Timber Profitability" Forests 14, no. 12: 2450. https://doi.org/10.3390/f14122450
APA StyleJung, Y., Chang, Y., You, J., Kim, D., & Han, H. (2023). Optimizing Bucking Decisions in Korean Red Pine: A Dynamic Programming Approach to Timber Profitability. Forests, 14(12), 2450. https://doi.org/10.3390/f14122450






