Abstract
The acoustic vibration performance of wood affects the quality of many musical instruments, and the variability of wood causes obvious differences between individual timber samples. To mitigate the variations among the individual timber samples intended for musical instruments, in this study, we combined finite element simulation with experimental testing to investigate the effect of the periodic annular groove structure on the comprehensive acoustic vibration characteristics of wood. The results revealed that there are discernible correlations between the structural parameters of the periodic annular groove and the key acoustic parameters of wood, including the resonant frequency, equivalent dynamic modulus of elasticity, equivalent specific dynamic modulus of elasticity, equivalent acoustic radiation quality constant, and equivalent acoustic impedance. These relationships can be used to fine-tune the overall acoustic vibration performance of wood and harmonize the acoustic vibration characteristics among different timber specimens. The effects of the periodic annular groove structure on the five acoustic vibration parameters obtained through finite element simulations exhibited minimal differences to the corresponding results from experimental tests. Furthermore, there was a remarkably strong correlation between the outcomes of the finite element simulations and the experimental test results, with the coefficient of determination exceeding 0.99.
1. Introduction
Spruce (Picea asperata), Paulownia (Paulownia fortunei), and other wood species possess exceptional acoustic resonance and vibration spectral properties, making them important raw materials for the production of the resonance components of musical instruments [1,2]. The Yueqin, Chinese zither, lute, and various other traditional Chinese musical instruments all employ Paulownia wood as the primary material [3,4]. However, the variability of the structure and properties of the wood greatly affect the acoustic properties, resulting in difficulties in the selection of wood for the production of musical instruments [4]. Consequently, wood that is suitable for the production of musical instruments is very limited [5]. To overcome the lack of musical instrument timber resources for the development of the musical instrument industry, it is necessary to find ways to solve the problem of the intrinsic variability of wood, which causes differences between individual wood samples. Controlling the overall performance of materials through structural design to produce a “metamaterial” provides an idea to solve this problem [6,7,8].
Metamaterials are a novel category of materials that are manufactured with artificial structures as functional units, which can engender unprecedented properties on the macroscopic level of the material that are unattainable for conventional materials [9,10,11]. These attributes usually rely on the geometry and size of the structural units rather than the specific properties of the material components [12,13]. Metamaterials were originally used in optics and electromagnetism to modify the wave properties through their structures [14]. Their usage was later extended to acoustics, where they have the ability to flexibly manipulate acoustic waves and control the vibrational spectral characteristics of materials [15,16]. Thus, the artificial design and production of specific structures to cater to specific needs constitute a crucial aspect of acoustic metamaterials research [17]. Numerical simulation techniques have been widely used for material modeling and property analysis [18,19,20]. This approach can reduce the costs associated with developing new materials and accelerate research into innovative structures.
Research on the soundboards of common stringed instruments, such as guitars, pianos, and violins, has demonstrated that structural changes significantly affect the acoustic characteristics of these soundboards [21,22,23,24]. For instance, adding ribs to a piano’s soundboard can effectively equalize the propagation speeds of vibrations in various directions across the soundboard [25]. Similarly, varying the thickness of a violin’s soundboard can fine-tune its self-resonance frequency, which typically follows a parabolic trend with the board thickness. Additionally, the construction of a speaker box can lower the modal frequency of an instrument’s back and top plates [26]. Research on the structure-related acoustic properties and modifications of soundboards highlights the inescapable influence of the structure on sound generation. This phenomenon bears a striking resemblance to the effects of metamaterials. It provides a sound basis for modifying timber structures to improve their suitability for use in musical instruments and minimizing the disparities arising from the natural variation of wood.
Attempts have been made to control the sound source by machining special structures into the material used for musical instruments. Because drummers stick a mass block to the tympanic membrane to make the drum sound better, Bader et al. [27] designed and constructed a structure for the tympanic membrane. Experiments showed that changing the structure could make the range of the tone made by the drum wider. Oñate et al. [28] investigated the effect of locally coupled mechanical metamaterials on the soundboard of an acoustic guitar. They concluded that this simple mechanism allows for the artificial manipulation of the spectral properties of the instrument. Gonzalez et al. [29] performed numerical simulations to investigate the effect of machining different periodic or elliptical holes in the soundboard on the overall acoustic vibrational properties of the material. They experimentally verified that this approach is a simple and controllable way to equalize the sound quality of the soundboard or expand the range of the timber species. For musical instruments, through-holes can have a detrimental effect on the appearance of the product. A numerical study of the vibration effect of the periodic elliptical groove structure in the soundboard of guitars has been performed [30]. After analyzing the simulation results, it was concluded that metamaterials could be used to meet the specific needs of guitars. However, the existing studies did not comprehensively explore the relationships between the structure and the parameters for evaluating the acoustic vibration performance of wood, and the types of structures involved were limited.
In this study, finite element numerical simulations were performed to investigate the acoustic vibration characteristics of wood featuring periodic annular groove structures with varying structural parameters. The aim is to understand the relationships between five acoustic vibration parameters (the frequency, equivalent dynamic modulus of elasticity (MOE), equivalent specific dynamic MOE, equivalent acoustic radiation quality constant, and equivalent acoustic impedance) and the structural parameters. Subsequently, experimental validation of the simulation findings was performed, with the aim of providing insights into the potential adjustments of the material properties in musical instrument materials through introducing periodic structures. This research provides a valuable reference for fine-tuning the material properties of musical instruments through introducing periodic structures to achieve a harmonious balance between the product quality and timbre of instruments.
2. Materials and Methods
2.1. Structural Design
The four wood specimens used in the experiments were Paulownia wood, which is commonly used for traditional Chinese musical instruments, with a moisture content of approximately 6%. The structural parameters and densities of the four wood specimens are given in Table 1.

Table 1.
Dimensions and densities of experimental wooden specimens.
The annular groove structure has many structural parameters, which facilitate the realization of a variety of structures. To simplify the variables, it was necessary to fix some of the structural parameters and change only some of them to facilitate the investigation of the relationships between the structure and acoustic vibration properties of the wood. Based on the dimensions of the specimens, each individual annular groove of the periodic annular groove structure was located in a rectangular unit of 20 mm × 20 mm × 11 mm. The depth of the groove was fixed to 2 mm, and only the sizes of the outer and inner circles of the annuluses were changed while obtaining multiple ring widths. To ensure a certain material strength, the diameter of the inner cylinder that was formed by the groove was not less than 2 mm. The minimum distance between the outer circle and the edge of the beam was not less than 2 mm. A total of 66 structures were designed. The design values of all of the structures are given in Table 2, and the structure of the unit is shown in Figure 1.

Table 2.
Sixty-six groups of parameters of the annular structures.
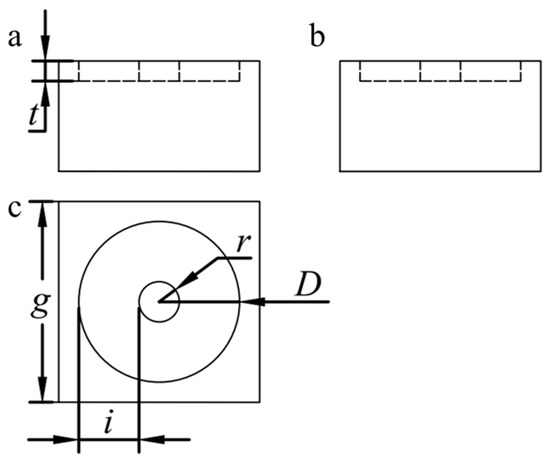
Figure 1.
Three views of the structure of the unit: (a) the main view; (b) the side view; and (c) the top view. D is the radius of the outer circle (mm); r is the radius of the inner circle (mm); i is the width of the annulus (mm); g is the length of the side of the square, which is 20 mm; and t is the depth of the groove, which is 2 mm.
2.2. Finite Element Simulation
Many wood-related studies using finite element simulation techniques have been reported [31,32]. Wood is in the range of linear elastic variation when it is subjected to free vibration. Modal analysis belongs to the category of linear analysis, so computational modal analysis based on a linear elastic material can be carried out on a wood model using ANSYS 2021R1 [33]. Three-dimensional models of all the structures were constructed using AutoCAD 2017, and a beam model without the circular slot structure was constructed as a control. The overall dimensions of the model were set to 240 mm (X) × 20 mm (Y) × 11 mm (Z) based on the specimen dimensions. One of the models generated in the ANSYS Workbench is shown in Figure 2.

Figure 2.
A model with a periodic annular groove structure with R of 8 mm and r of 2 mm.
The correct material properties were also assigned to the model, and appropriate meshing was performed during the pre-processing. Wood is considered to have orthotropic anisotropy, so the model needed to be given material properties in all three directions. The parameters used in the model are given in Table 3.

Table 3.
Material parameters of Paulownia wood used in computational modal analysis.
According to the grain direction of the specimen, the X, Y, and Z directions of the material for the modal analysis were set as the longitudinal (L), radial (R), and tangential (T) directions of the wood, respectively. In real vibration, any system has damping, meaning that the free vibration of the system has a smaller intrinsic frequency than the undamped free vibration. However, the small damping has a very small effect, which can be ignored [35], and the damping of Paulownia wood is very small, so it was ignored in the simulation process.
A multi-area method was used to delineate the mesh of the model, and the size of the grid cells was set to 2 mm. The finite element model was then loaded and solved. During the experimental process, the support locations of the specimens were positioned at nodal points of the first vibrational mode. Impact vibration tests were conducted under free boundary conditions at both ends. This can be considered to be in close proximity to free vibration. Therefore, the modal solution was directly performed on the model after setting the number of vibrational modes in the software, and the modal vibration pattern was obtained through post-processing to obtain the natural frequency f of the first transverse vibrational mode.
2.3. Equations for the Equivalent Parameters
According to Gonzalez et al. [29], wood processed with a periodic structure is still considered to be intact, in which case the overall density of the wood is set to the equivalent density ρ0:
where ρ is the density of Paulownia wood (kg·m−3), V′ is the volume of the excavated periodic annular groove structure (m3), and V is the overall volume of the timber beam when the groove is not excavated (m3).
After defining the equivalent density, the equivalent dynamic MOE E′ was defined based on the dynamic MOE formula [36]:
where l is the overall length of the beam (m), h is the overall thickness of the beam (m), fn is the nth-order transverse free vibration natural frequency of the beam (Hz), and β is a parameter related to fn, determined by the boundary conditions of the beam.
The dynamic MOE is an important physical property of materials that can be used to calculate the parameters for acoustic vibration performance evaluation. These parameters include the specific dynamic MOE, acoustic radiation quality constant, and acoustic impedance [36,37]. Based on the commonly used acoustic vibration performance evaluation parameters, the equivalent specific dynamic MOE Esp′, equivalent acoustic radiation quality constant R′, and equivalent acoustic impedance w′ are derived. The related equations are as follows:
The relationships between the structural parameters and the equivalent parameters can be analyzed by examining the corresponding equivalent parameters for each specific structure.
2.4. Experimental Test
In the experimental test, the specimen was supported by two elastic supports at the nodes of the first-order free vibration, and the excitation was applied with a blade at one end. The microphone at the other end received the vibration signals and input them into a fast Fourier transform (FFT) spectrum analyzer to analyze the signals and determine the f value of the specimen. A schematic of the experimental setup is shown in Figure 3.
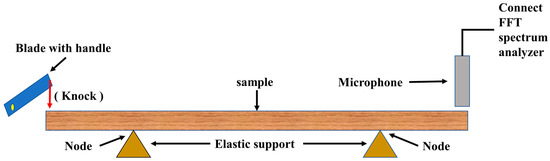
Figure 3.
Schematic diagram of the transverse vibration test.
The f value of the intact wood was determined first, and then different structures were machined on the sample using a computer numerical control carving machine. Vibration tests were performed after each structure was machined to obtain the f value of each structure, and then, the characteristic parameters of the intact wood and the equivalent parameters of the wood with a specific structure were calculated separately. Nine structures of the sixty-six designed structures were processed using four wood specimens, where the A beam was held constant for r, the B beam was held constant for D, and the C beam and F beam were supplemented with two sets of cases, where i = 4 mm. The parameters of the nine structures in the experimental tests are given in Table 4. The three structures obtained during the experimental tests are shown in Figure 4.

Table 4.
Parameters of the experimental test structures.

Figure 4.
The three structures obtained in the experimental tests are, from top to bottom, C0, B2, and A7.
From the properties of metamaterials, it is clear that the changes in the wood properties in this study are caused by the structure alone and not related to the specific properties of the wood. In fact, owing to the variability of the wood, there were considerable differences between the vibration properties of the four specimens, so the experimental tests were concerned with the extent of structure-induced changes in the vibration properties. Based on the above analysis, the rate of change mK′ was defined as follows:
where K′ is f, E′, Esp′, R′, or w′ of wood with a given structure, and K is the corresponding parameter of the intact wood. The magnitude of mK′ can be used to determine the degree of change in the acoustic vibration properties of the wood caused by the structure.
There are bound to be errors between the results from the finite element method and the experimental test, so it is necessary to verify the validity of the finite element results based on the experimental test. The error between the finite element calculation result and the experimental test result was set to XK′, which was calculated as
where m0 is the mK′ value of the f value or equivalent parameter of the structure calculated via finite elements, and m1 is the corresponding result of the experimental test.
3. Results and Discussion
3.1. Results of the Experimental Tests
The mK′ values of the nine structures are given in Table 5. The trends of the mK′ values were analyzed, and the results are shown in Figure 5. When r or i was constant, all five mK′ values increased with increasing D, showing a positive correlation between mK′ and D (Figure 5a,b). The changes from fastest to slowest were in the order mE′, mEsp′, mw′, mf, and mR′. When D was constant, mE′ and mw′ decreased with increasing r, and they showed similar trends. Conversely, mEsp′, mR′, and mf increased with increasing r, and mR′ and mEsp′ increased more rapidly than mf (Figure 5c).

Table 5.
Nine groups of mK′ obtained from the experimental test.
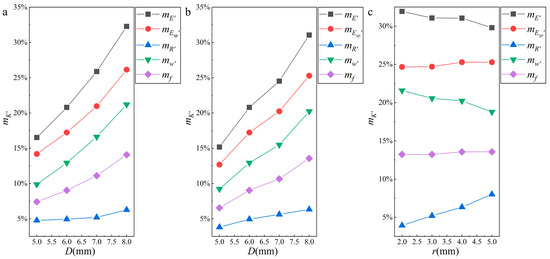
Figure 5.
Relationship between mK′ and structural parameters obtained from the experimental tests: (a) relationship between mK′ and D when r is 2 mm; (b) relationship between mK′ and D when i is 4 mm; (c) relationship between mK′ and r when D is 8 mm.
In the experimental tests, A8 and B2 were structures with D = 8 mm and r = 2 mm, but they had different mK′ values, which may be because the variability of the microstructure of the wood had a different effect on the macroscopically identical structure. Variability is an inherent characteristic of wood, which means that the actual effect of a structure on different individual pieces of wood can easily differ. Nevertheless, it is essential to identify consistent patterns in the effect of the macroscopic periodic annular groove structure on the material’s macroscopic properties. To uncover these patterns and reduce experimental costs, further investigations were performed via finite element simulation. The aim of these simulations is to elucidate the systematic effects of all 66 designed periodic annular groove structures on the acoustic vibration properties of wood.
3.2. Results of Finite Element Simulation
In the finite element simulations, the focus was to analyze the changes in the parameters themselves, because this provides a more intuitive understanding compared with studying the rates of change in the parameters. Specifically, the relationships between f, E′, Esp′, R′, and w′ and the structural parameters of the periodic annular groove were analyzed. This approach allows for a more straightforward and comprehensible assessment of the effects of the structural parameters of the groove on these key material properties.
3.2.1. Relationship between f and Structural Parameters
The vibration patterns of the first vibrational mode and f were obtained from the computational modal results of ANSYS Workbench. The relationships between the structural parameters of the periodic annular groove and f were analyzed, and the results are shown in Figure 6.
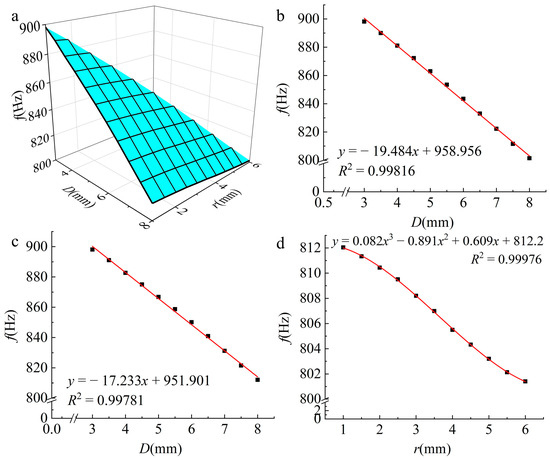
Figure 6.
Relationship between f and structural parameters. (a) Relationship between f and D, r; (b) with i = 2 mm constant, relationship between f and D; (c) with r = 1 mm constant, relationship between f and D; (d) with D = 8 mm constant, relationship between f and r.
Overall, f exhibited a downward-sloping surface with increasing values of both D and r (Figure 6a). This indicates that as D or r increased, f decreased. Three distinct relationships were extracted from the dataset comprising 66 data points, specifically, the relationship between f and D when i = 2 mm (Figure 6b), the relationship between f and D when r = 1 mm (Figure 6c), and the relationship between f and r when D = 8 mm (Figure 6d). These three relationships were then analyzed.
When i = 2 mm and D varied from 3 to 8 mm, f substantially decreased from 898.1 to 801.4 Hz. Notably, there was a linear negative correlation between f and D, with a variation of 10.77%, representing the maximum achievable range within the range of the structural parameter variations.
When r = 1 mm and D varied from 3 to 8 mm, f decreased from 898.1 to 812.0 Hz, a change of 9.59%. In addition, there was a noticeable linear negative correlation between f and D.
For D = 8 mm, as r increased from 1 to 6 mm, f decreased from 812.0 to 801.4 Hz, a decrease of only 1.31%. The trend of the decrease in f with increasing r was best described by a cubic function.
In Figure 6a, apart from the specific values of 898.1 and 801.4 Hz, each given f value corresponds to a certain range of D and r values. This observation suggests that nearly all of the f values can be achieved through multiple combinations of D and r. Variations in D have a more pronounced effect on f than variations in r. Consequently, when a periodic annular groove structure is used to adjust the f parameter of wood, it is advisable to initially determine the appropriate D for a coarse adjustment of f, followed by using r for a finer adjustment to achieve the desired f value.
3.2.2. Relationship between E′ and structural parameters
The finite-element-simulation-derived f was substituted into Equation (2) to obtain E′. The relationships between the structural parameters of the periodic annular groove and E′ are shown in Figure 7.
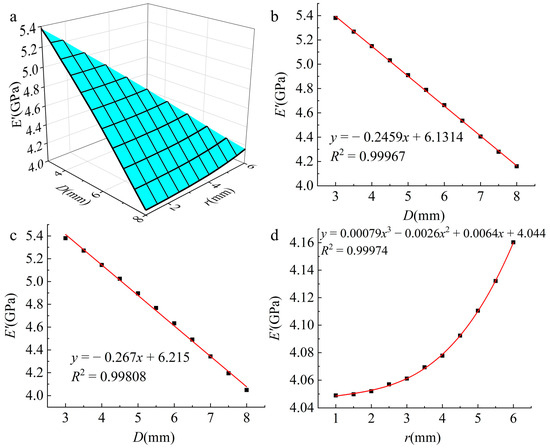
Figure 7.
Relationship between E′ and structural parameters. (a) Relationship between E′ and D, r; (b) with i = 2 mm constant, relationship between E′ and D; (c) with r = 1 mm constant, relationship between E′ and D; (d) with D = 8 mm constant, relationship between E′ and r.
Overall, a skewed surface formed between E′, D, and r (Figure 7a), where E′ decreased with increasing D but increased with increasing r. We extracted the three most prominent relationships from the dataset of 66 data points: the relationship between E′ and D when r = 1 mm (Figure 7b), the relationship between E′ and D when i = 2 mm (Figure 7c), and the relationship between E′ and r when D = 8 mm (Figure 7d). The three extracted relationships were then analyzed.
When r = 1 mm and D increased from 3 to 8 mm, E′ decreased from 5.38 to 4.05 GPa, showing a pronounced linear negative correlation between E′ and D. This decrease in E′ was the largest among the 66 structures, reaching 24.74%.
When i = 2 mm and D increased from 3 to 8 mm, E′ decreased from 5.38 to 4.16 GPa, a decrease of 22.68%. Similarly, there was a noticeable linear negative correlation between E′ and D.
When D = 8 mm and r increased from 1 to 6 mm, E′ increased from 4.05 to 4.16 GPa, a modest increase of only 2.74%. The trend of the increase in E′ with r followed a nearly cubic curve.
In Figure 7a, except for the values of 5.38 and 4.05 GPa, each value of E′ corresponds to a certain range of D and r values, indicating that almost all of the E′ values can be achieved using more than one combination of D and r. It is clear that E′ is more strongly influenced by D than r. Therefore, when adjusting the E′ value of wood using a periodic annular groove structure, it is advisable to first determine the size of D to achieve a preliminary selection of E′ and then fine-tune E′ using r.
3.2.3. Relationship between Esp′ and Structural Parameters
The specific dynamic MOE is an important parameter for assessing the acoustic vibration performance of wood, because it measures the vibrational acceleration of the individual cell wall material. A higher specific dynamic MOE indicates an improved vibrational efficiency and better acoustic vibrational outcomes in wood [1,38]. The relationships between the structural parameters of the periodic annular groove and Esp′ were analyzed, and the results are shown in Figure 8.
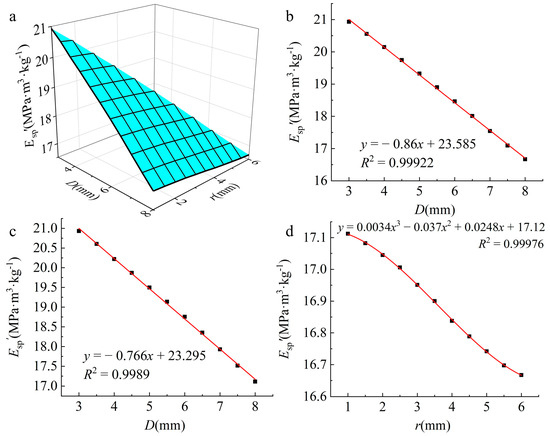
Figure 8.
Relationship between Esp′ and structural parameters. (a) Relationship between Esp′ and D, r; (b) with i = 2 mm constant, relationship between Esp′ and D; (c) with r = 1 mm constant, relationship between Esp′ and D; (d) with D = 8 mm constant, relationship between Esp′ and r.
Esp′ decreased with an increase in either D or r, exhibiting a trend that was similar to that observed for f (Figure 8a). Among the 66 data groups, we selected three specific relationships for further analysis: the relationship between Esp′ and D when i = 2 mm (Figure 8b), the relationship between Esp′ and D when r = 1 mm (Figure 8c), and the relationship between E′ and r when D = 8 mm (Figure 8d).
When i = 2 mm and D increased from 3 to 8 mm, Esp′ noticeably decreased from 20.93 to 16.67 MPa·m3·kg−1. Esp′ exhibited a clear negative linear correlation with D, and the change in Esp′ was the highest among the 66 structures, amounting to 20.35%.
When r = 1 mm and D increased from 3 to 8 mm, Esp′ decreased from 20.93 to 17.11 MPa·m3·kg−1, a decrease of 18.25%. Esp′ also exhibited a noticeable negative linear correlation with D.
When D = 8 mm and r increased from 1 to 6 mm, Esp′ decreased by only 2.57%, and the trend of the decrease in Esp′ with increasing r closely resembled a cubic curve.
Similar to the situation for f (Figure 8a), except for the values of 20.93 and 16.67 MPa·m3·kg−1, each Esp′ value corresponded to a certain range of D and r values. In other words, almost all of the Esp′ values can be achieved with various combinations of D and r. D had a stronger influence on Esp′ than r. Therefore, when adjusting the Esp′ value of wood using a periodic annular groove structure, it is still possible to first determine the initial selection of D and then fine-tune Esp′ using r.
3.2.4. Relationship between w′ and Structural Parameters
The acoustic impedance is also related to the vibrational efficiency of wood, and it can quantify the resistance of wood to the propagation of sound waves. A higher acoustic impedance value indicates that the wood produces a weaker sound, whereas a lower acoustic impedance value leads to a louder sound [37,38,39]. The relationships between the structural parameters of the periodic annular groove and w′ are shown in Figure 9.
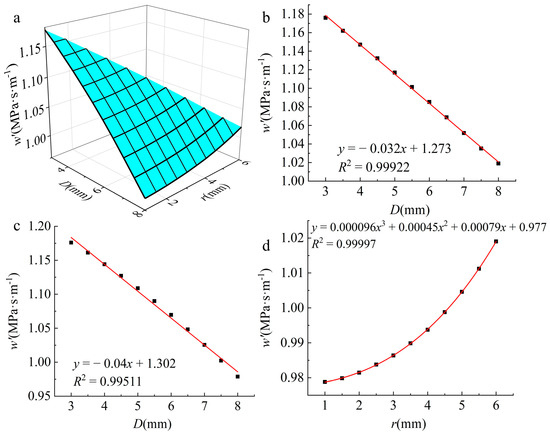
Figure 9.
Relationship between w′ and structural parameters. (a) Relationship between w′ and D, r; (b) with i = 2 mm constant, relationship between w′ and D; (c) with r = 1 mm constant, relationship between w′ and D; (d) with D = 8 mm constant, relationship between w′ and r.
w′ showed a similar overall curved surface relationship with D and r to that of E′ (Figure 9a). The relationships between w′ and D when i = 2 mm (Figure 9b), w′ and r when r = 1 mm (Figure 9c), and w′ and r when D = 8 mm (Figure 9d) were then analyzed.
When r = 1 mm and D increased from 3 to 8 mm, w′ decreased from 1.176 to 0.979 MPa·s·m−1, and there was a noticeable negative linear correlation between w′ and D. The largest degree of change caused by the 66 structures was 16.75%.
When i = 2 mm and D increased from 3 to 8 mm, w′ decreased from 1.176 to 1.019 MPa·s·m−1, a decrease of 13.35%. There was also a noticeable negative linear correlation between w′ and D.
When D = 8 mm and r increased from 1 to 6 mm, w′ increased from 0.979 to 1.019 MPa·s·m−1, an increase of 4.09%. The trend of the increase in w′ with increasing r was close to a cubic curve.
The decrease in w′ indicates that the periodic annular groove structure can improve the transmission of sound waves in wood, resulting in a more resonant acoustic effect. This enhancement can increase the suitability of wood for musical instruments. Similar to the situation observed for E′ (Figure 7a), apart from the values of 1.176 and 0.979 MPa·s·m−1, there was a certain range of D and r values corresponding to a single w′ value. This indicates that nearly all of the w′ values can be achieved using more than one combination of D and r. It is clear that changes in D result in more pronounced variations in w′ than changes in r do. Therefore, when adjusting the w′ value of wood using a periodic annular groove structure, it is advisable to first determine the appropriate D value for coarse adjustments of w′, followed by fine-tuning w′ using r.
3.2.5. Relationship between R′ and Structural Parameters
The acoustic radiation quality constant describes the degree to which the vibration of wood is attenuated by acoustic radiation and measures the amount of acoustic power it radiates into the air, with a higher acoustic radiation quality constant being more likely to produce a louder sound from wood [37,38,39]. The structural parameters of the periodic annular groove were analyzed in terms of R′, and the results are shown in Figure 10.
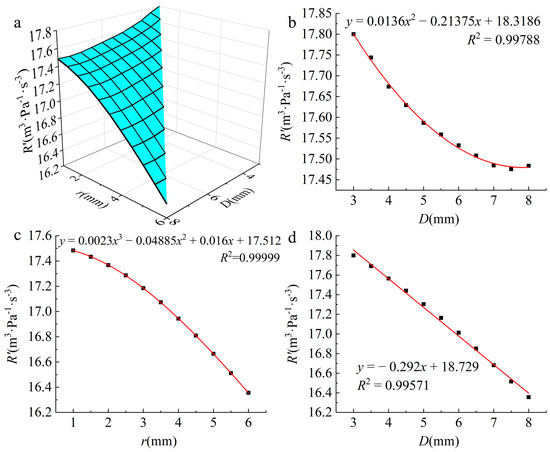
Figure 10.
Relationship between R′ and structural parameters. (a) Relationship between R′ and D, r; (b) with r = 1 mm constant, relationship between w′ and D; (c) with D = 8 mm constant, relationship between R′ and r; (d) with i = 2 mm constant, relationship between R′ and D.
R′ formed a unique surface with D and r (Figure 10a). Three relationships were extracted from the 66 sets of data, including the relationship between R′ and D when r = 1 mm (Figure 10b), the relationship between R′ and r when D = 8 mm (Figure 10c), and the relationship between R′ and D when i = 2 mm (Figure 10d). The three relationships were then analyzed.
When i = 2 mm and D increased from 3 to 8 mm, R′ decreased from 17.800 to 16.356 m3·Pa−1·s−3, and there was a noticeable negative linear correlation between R′ and D. The decrease in R′ was the maximum value among the 66 structures (8.11%).
When D = 8 mm and r increased from 1 to 6 mm, R′ decreased from 17.483 to 16.356 m3·Pa−1·s−3, representing a decrease of 6.45%. The trend of the decrease in R′ with increasing r was best described by a cubic function.
When r = 1 mm and D increased from 3 to 7.5 mm, R′ decreased from 17.800 to 17.476 m3·Pa−1·s−3, a decrease of only 1.82%. This was the maximum decrease in R′ within this relationship, after which it began to increase. Over the entire range, the trend of R′ with increasing D closely resembled a quadratic curve.
The relationship between R′, D, and r was unique. However, apart from the values of 17.800 and 16.356 m3·Pa−1·s−3, a single R′ value still corresponded to a range of D and r values, as shown in Figure 10a. Therefore, almost all of the R′ values can be achieved using more than one combination of D and r. Nevertheless, variation in r had a more pronounced effect on R′ than variation in D (Figure 10b–d). This is distinct from the four parameters discussed earlier. Hence, when adjusting the R′ value of wood using a periodic annular groove structure, it is advisable to first determine the size of r for the initial selection of R′ and then fine-tune R′ using D.
3.3. Reliability Evaluation of the Finite Element Simulation Results
Based on the finite element simulation results of f, E′, Esp′, R′, and w′, when r or i were constant, all of the five parameters decreased as D increased. Correspondingly, from the experimental results in Section 2.1, the corresponding mK′ values for all five parameters increased with increasing D. When D was constant, the relationships between the five parameters and r obtained from finite element simulations closely approximated cubic functions. Specifically, as r increased, its effect on the decrease in f and Esp′ initially increased before decreasing. As r increased, its effect on the decrease in R′ gradually increased, and its effect on the increase in E′ and w′ gradually became more pronounced. The trends in the changes of these five parameters also largely aligned with the corresponding mK′ variations, obtained through experimental tests. Therefore, in terms of the trend, the overall trend of the effect of the annular groove structure on the acoustic vibration performance of wood obtained from the finite element simulation is of reference value.
To evaluate the reliability of the finite element simulation results, we analyzed the correlation between the experimental test results and the finite element simulation results. All of the mK′ results obtained through finite element simulations for the nine structures tested in the experiments are given in Table 6. We specifically investigated the correlation between the experimental and simulation results for three cases: r = 2 mm (Figure 11a), D = 8 mm (Figure 11b), and i = 4 mm (Figure 11c). Owing to the inherent limitations of finite element simulations, such as idealized assumptions and factors related to actual machining precision, finite element simulation results inevitably contain errors. Consequently, the data fitting slopes for all three cases were less than 1. However, the determination coefficients (R2 values) for all three cases exceeded 0.99. This indicates an excellent correlation between the results obtained from both methods, indicating that the finite element simulation method is highly reliable.

Table 6.
mK′ obtained via numerical simulation of the models corresponding to the experimentally tested structures.
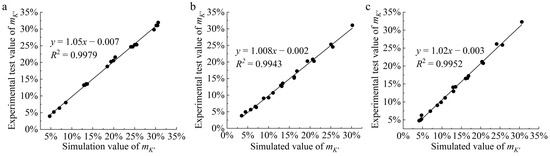
Figure 11.
Correlation of mK′ obtained from experiment and simulation. (a): D = 8 mm; (b): i = 4 mm; (c): r = 2 mm.
The XK′ results for all of the mK′ values are given in Table 7. The majority of the values did not exceed 10%. This indicates that there were minimal differences between the experimental and simulated results, demonstrating a high degree of similarity between the two. The larger errors all appeared in the results of R′, in which the largest error value belonged to structure A8 (−24.59%). This fluctuation in the errors can be attributed to the formula for R′. Unlike the formulas for the other parameters used to assess the equivalent acoustic vibration performance, the formula for R′ includes the cube of the density in addition to E′. This amplifies the effect of density variations in the wood on the calculations. Furthermore, the obtained results suggest that the periodic annular groove structure induces minimal changes in the sound radiation quality factor constant, so even small variations in the rate of change can lead to noticeable errors.

Table 7.
XK′ of finite element simulation.
Taking structure B2 as an example, in the finite element simulation, the equivalent density of structure B2 was 0.238 g·cm−3, which was 91.5% of the density of the wood that was input into the model. In the experimental test, the equivalent density of structure B2 was measured to be 0.184 g·cm−3, which corresponds to 90.2% of the density of specimen B as measured in the experiment. The difference in the density change between the two was only 1.3%. Meanwhile, the difference between the corresponding mR′ values for structure B2 in Table 5 and Table 6 was only 0.79%. Despite these small differences, the error calculated for mR′ was 20.21%. Given the inherent variability of wood itself, fluctuations in the rate of change of R′ are almost inevitable. However, based on the correlation analysis, it can still be considered that overall, finite element simulation techniques can be used to investigate and predict the effect of structures on the acoustic vibration performance of wood.
3.4. Overall Evaluation of Results
After confirming the reliability of the finite element simulations, it can be observed from the simulation results that the periodic annular groove structure causes a decrease in Esp′, indicating a reduction in the overall vibrational efficiency of the wood. The slight decrease in R′ implies a minor attenuation in sound energy radiation, while the decrease in w′ signifies an elevated response of the wood to vibrations [39]. High-quality Paulownia wood inherently possesses elevated values of Esp′ and R′. Thus, even after processing the periodic annular groove structure, Paulownia wood still meets the requirements for serving as a soundboard in musical instruments [40].
In comparison to the scenario where only small-diameter through-holes are individually drilled in the LR direction [41], the changes brought about by the periodic annular groove structure are more pronounced and exhibit a regular pattern. This presents an almost precise programmable method for adjusting the acoustic vibrational performance of wood in musical instrument production. It allows for the deliberate tuning of parts in Paulownia wood that does not meet the acoustic vibrational performance requirements of the target instrument. This intentional adjustment contributes to the consistent acoustic quality of the final product.
Considering that different components of wooden musical instruments have varied requirements for wood properties, it is imperative to explore more periodic structures, such as rectangles, polygons, and their corresponding annular counterparts. Furthermore, the introduction of theories like fractals could be considered for design purposes, allowing for the adjustment of parameters. This approach aims to achieve diverse modifications that are tailored to the specific needs of different instrument components. Additionally, it is crucial to note that the acoustic effects of musical instruments are not solely characterized by the material properties discussed in this paper. The conditions encountered by sound waves as they pass through instrument components, such as reflections [42], also warrant attention. In contrast to a smooth soundboard, when sound waves propagate through periodic structures, they undergo multiple reflections, interferences, and scatterings at the interfaces between wood and air. This results in complex propagation phenomena, including the potential for negative refraction [43]. Therefore, further research is necessary to investigate phenomena such as sound wave reflections within these structures in order to confirm their applicability in musical instruments.
4. Conclusions
We have investigated the variation in the acoustic vibration performance of Paulownia wood with different periodic annular groove structures via finite element techniques in conjunction with experimental tests. The key conclusions can be summarized as follows:
- (1)
- It is feasible to modify the acoustic vibration performance of wood using periodic circular groove structures. When the groove depth and ring width are constant, the wood’s frequency, equivalent dynamic MOE, equivalent specific dynamic MOE, equivalent acoustic radiation quality constant, and equivalent acoustic impedance exhibit noticeable linear negative correlations with the outer circle radius. When the groove depth and outer circle radius are constant, the relationships between the wood’s five acoustic vibration parameters and the inner circle radius are close to cubic functions. When the groove depth and inner circle are constant, except for the relationship between the equivalent sound radiation quality factor and the outer circle radius, which approximates a quadratic function, the other acoustic vibration performance-related parameters are linearly and negatively correlated with the outer circle radius. Therefore, periodic circular groove structures can be used to adjust the acoustic vibration performance of wood, reducing the differences resulting from the variability among individual wood samples.
- (2)
- There are different relationships between various acoustic vibration performance parameters and the periodic annular groove structure parameters. However, apart from the equivalent sound radiation quality factor, the other parameters can first be roughly selected based on the outer circle radius, followed by fine-tuning with the inner circle radius. In contrast, the equivalent sound radiation quality factor is better suited for initial selection based on the inner circle radius, followed by fine-tuning with the outer circle radius, enabling the design of the wood’s acoustic vibration performance.
- (3)
- Following the concept of metamaterials, we experimentally verified the extent to which the frequency, equivalent dynamic MOE, equivalent ratio of dynamic MOE, equivalent sound radiation quality factor, and equivalent acoustic impedance of wood are influenced by structural changes. Overall, the observed trend in each parameter closely aligned with the finite element simulation results. There was a high degree of correlation between the experimental test results and finite element simulation results. Thus, it is considered that finite element techniques can be used to investigate the effect of the structure of periodic annular grooves on the acoustic vibration performance of wood.
Author Contributions
Conceptualization, L.Z. and Z.L.; Methodology, L.Z. and L.H.; Software, L.Z. and Y.L.; Validation, Y.L. and J.Z. (Juncheng Zhang); Investigation, L.Z. and H.Z.; Formal Analysis, J.Z. (Juncheng Zhang); Data Curation, H.C. and M.L.; Writing—Original Draft Preparation, L.Z. and L.H.; Writing—Review and Editing, LZ., Z.L. and Y.M.; Visualization, Y.L.; Supervision, J.Z. (Jing Zhou); Funding Acquisition, Y.M., Z.L., H.C. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the National Natural Science Foundation of China (grant no. 32271781) and National Undergraduate Training Programs for Innovations [grant number. 202310225102].
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, Z.; Deng, L.; Song, R.; Chen, F.; Liu, X. Research Progress on The Acoustic Vibration Performance of Wood and Bamboo. World For. Res. 2021, 34, 1–7. [Google Scholar] [CrossRef]
- Viala, R.; Placet, V.; Cogan, S. Simultaneous Non-Destructive Identification of Multiple Elastic and Damping Properties of Spruce Tonewood to Improve Grading. J. Cult. Herit. 2020, 42, 108–116. [Google Scholar] [CrossRef]
- Yoshikawa, S. Acoustical Classification of Woods for String Instruments. J. Acoust. Soc. Am. 2007, 122, 568–573. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Meng, S.; Zhao, P.; Yue, M. A Method for Identifying Wood Grades of Chinese Zither Panel Based on Near Infrared Spectroscopy. Spectrosc. Spect. Anal. 2019, 39, 723. [Google Scholar] [CrossRef]
- Liu, M.; Peng, L.; Lyu, S.; Lyu, J.; Gao, Y.; Fan, Z. Research Progress of Wood Treatment to Improve Acoustic Vibration Performance for Making Musical Instruments. China Wood Ind. 2020, 34, 29–33. [Google Scholar] [CrossRef]
- Akl, W.; Elsabbagh, A.; Baz, A. Acoustic Metamaterials with Circular Sector Cavities and Programmable Densities. J. Acoust. Soc. Am. 2012, 132, 2857–2865. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Cheng, H.; Tian, J.; Chen, S. Multidimensional Manipulation of Wave Fields Based on Artificial Microstructures. Opto-Electron. Adv. 2020, 3, 200002. [Google Scholar] [CrossRef]
- Dalela, S.; Balaji, P.S.; Jena, D.P. A Review on Application of Mechanical Metamaterials for Vibration Control. Mech. Adv. Mater. Struct. 2022, 29, 3237–3262. [Google Scholar] [CrossRef]
- Liu, X.; Hu, G. Elastic Metamaterials Making Use of Chirality: A Review. J. Mech. Eng. 2016, 62, 403–418. [Google Scholar] [CrossRef]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical Design and Multifunctional Applications of Chiral Mechanical Metamaterials: A Review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.W.; Van Hecke, M.; Wegener, M. 3D Metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Hedayati, R.; Bodaghi, M. Acoustic Metamaterials and Acoustic Foams: Recent Advances. Appl. Sci. 2022, 12, 3096. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical Metamaterials Associated with Stiffness, Rigidity and Compressibility: A Brief Review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Zhou, J.; Li, L.T. Metamaterial technology and its application prospects. Strateg. Study CAE 2018, 20, 69–74. [Google Scholar] [CrossRef]
- Sun, H.; Yan, F.; Gu, H.; Li, Y. Acoustic Metamaterial with Negative Parameter. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9 March 2014. [Google Scholar] [CrossRef]
- Cui, H.; Liu, C.; Hu, H. Research on Low-Frequency Noise Control Based on Fractal Coiled Acoustic Metamaterials. Shock Vib. 2022, 2022, 2083563. [Google Scholar] [CrossRef]
- Kumar, S.; Pueh Lee, H. Recent Advances in Active Acoustic Metamaterials. Int. J. Appl. Mech. 2019, 11, 1950081. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, X.M.; Lin, P.; Lee, H.P. Sound Insulation Properties of Membrane-type Acoustic Metamaterials. Noise Vib. Control 2021, 41, 42–48. [Google Scholar] [CrossRef]
- Mir, F.; Saadatzi, M.; Ahmed, R.U.; Banerjee, S. Acoustoelastic MetaWall Noise Barriers for Industrial Application with Simultaneous Energy Harvesting Capability. Appl. Acoust. 2018, 139, 282–292. [Google Scholar] [CrossRef]
- Zhu, Y.; Assouar, B. Multifunctional Acoustic Metasurface Based on an Array of Helmholtz Resonators. Phys. Rev. B 2019, 99, 174109. [Google Scholar] [CrossRef]
- Viala, R.; Placet, V.; Cogan, S. Model-Based Evidence of the Dominance of the Guitar Brace Design over Material and Climatic Variability for Dynamic Behaviors. Appl. Acoust. 2021, 182, 108275. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Rosca, I.C.; Mihălcică, M.; Bucur, V. Dynamic Response of Wooden Plates in Different Stages of Guitar Manufacturing. Eur. J. Wood Wood Prod. 2022, 80, 997–1013. [Google Scholar] [CrossRef]
- Brauchler, A.; Ziegler, P.; Eberhard, P. An Entirely Reverse-Engineered Finite Element Model of a Classical Guitar in Comparison with Experimental Data. J. Acoust. Soc. Am. 2021, 149, 4450–4462. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A Data-Driven Approach to Violin Making. Sci. Rep. 2021, 11, 9455. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Shen, J.; Liu, M. Effect of Ribs on Vibration Transmission of Piano Soundboard. J. Northeast For. Univ. 2009, 37, 44–45. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Dinulică, F.; Bucur, V.; Gliga, V.G.; Nastac, S.M.; Câmpean, M. Changing the Vibrational Behavior of the Wooden Thin Arched Plates—The Maestro Violins Experimental Study Case. Thin Wall. Struct. 2022, 174, 109042. [Google Scholar] [CrossRef]
- Bader, R.; Fischer, J.; Münster, M.; Kontopidis, P. Metamaterials in Musical Acoustics: A Modified Frame Drum. J. Acoust. Soc. Am. 2019, 145, 3086–3094. [Google Scholar] [CrossRef]
- Oñate, C.E.; Arancibia, A.; Cartes, G.; Beas, C.F. Seeking for Spectral Manipulation of the Sound of Musical Instruments Using Metamaterials. In Proceedings of the 15th International Audio Mostly Conference, Graz, Austria, 15 September 2020. [Google Scholar] [CrossRef]
- Gonzalez, S.; Chacra, E.; Carreño, C.; Espinoza, C. Wooden Mechanical Metamaterials: Towards Tunable Wood Plates. Mater. Des. 2022, 221, 110952. [Google Scholar] [CrossRef]
- Lercari, M.; Gonzalez, S.; Espinoza, C.; Longo, G.; Antonacci, F.; Sarti, A. Using Mechanical Metamaterials in Guitar Top Plates: A Numerical Study. Appl. Sci. 2022, 12, 8619. [Google Scholar] [CrossRef]
- Bui, T.A.; Lardeur, P.; Oudjene, M.; Park, J. Numerical Modelling of the Variability of the Vibration Frequencies of Multi-Layered Timber Structures Using the Modal Stability Procedure. Compos. Struct. 2022, 285, 115226. [Google Scholar] [CrossRef]
- Hawryszków, P.; Biliszczuk, J. Vibration Serviceability of Footbridges Made of the Sustainable and Eco Structural Material: Glued-Laminated Wood. Materials 2022, 15, 1529. [Google Scholar] [CrossRef]
- Wang, F.; Yang, L.Q.; Sun, J.; Zhu, X. Application of Finite Element Method to Modal Analysis of Wood. J. Northeast For. Univ. 2008, 36, 24–25. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, Y.; Miao, Y.; Liu, Z.; Li, Y.; Tian, M.; Li, X.; Wang, C. Vibration Mode of Guzheng Soundboard with Composite Structure. J. Beijing For. Univ. 2022, 44, 132–141. [Google Scholar] [CrossRef]
- Ni, Z. Vibration Mechanics; Xi’an Jiaotong University Press: Xi’an, China, 1989; pp. 65–67. [Google Scholar]
- Brémaud, I.; El Kaïm, Y.; Guibal, D.; Minato, K.; Thibaut, B.; Gril, J. Characterisation and Categorisation of the Diversity in Viscoelastic Vibrational Properties between 98 Wood Types. Ann. Forest. Sci. 2012, 69, 373–386. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Wood for Sound. Am. J. Bot. 2006, 93, 1439–1448. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Adamopoulos, S. Acoustic Properties of Modified Wood under Different Humid Conditions and Their Relevance for Musical Instruments. Appl. Acoust. 2018, 140, 92–99. [Google Scholar] [CrossRef]
- Mania, P.; Gąsiorek, M. Acoustic Properties of Resonant Spruce Wood Modified Using Oil-Heat Treatment (OHT). Materials 2020, 13, 1962. [Google Scholar] [CrossRef]
- Hassan, K.T.S.; Tippner, J. Acoustic Properties Assessment of Neem (Azadirachta Indica A. Juss.) Wood from Trees Irrigated with Secondarily Treated Wastewater. Bioresources 2019, 14, 2919–2930. [Google Scholar] [CrossRef]
- Abdolahian Sohi, A.M.; Khademi-Eslam, H.; Hemmasi, A.H.; Roohnia, M.; Talaiepour, M. Nondestructive Detection of the Effect of Drilling on Acoustic Performance of Wood. Bioresources 2011, 6, 2632–2646. [Google Scholar] [CrossRef]
- Zvoníček, T.; Vašina, M.; Pata, V.; Smolka, P. Three-Dimensional Printing Process for Musical Instruments: Sound Reflection Properties of Polymeric Materials for Enhanced Acoustical Performance. Polymers 2023, 15, 2025. [Google Scholar] [CrossRef]
- Tallarico, D.; Haslinger, S.G. Trapped Modes and Negative Refraction in a Locally Resonant Metamaterial: Transient Insights into Manufacturing Bounds for Ultrasonic Applications. Appl. Sci. 2021, 11, 7576. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).