Causality and Importance of Sustainable Forestry Goals: Strategic and Tactical Assessment by DEMATEL and AHP

Abstract

This paper presents the combined use of standard DEMATEL and AHP methodologies in assessing a selected set of criteria for evaluating sustainable forestry goals. Creating a decision-making framework with two participating individuals (the authors of this research) enabled the comparison of individually obtained solutions with the aggregated solutions derived by two methodologies. The use of DEMATEL enabled strategic viewing of the causality relations among criteria and a limited indication of cardinal information (weights) about their importance. Different from DEMATEL, the use of AHP is considered a control mechanism in tactical decision-making situations such as the usage of standard multi-criteria methods for solving forestry-related allocation or selection problems. AHP’s role is to derive weights of criteria in a very structured environment based on assumption that criteria are independent and only their mutual importance is relevant for further decision-making. Individual solutions and aggregation schemes for creating group solutions are compared for both methodologies. Critical analysis is given for different aspects of their combined use when treating causalities and the importance of criteria in evaluations of long-term sustainable forestry goals.

1. Introduction

Using DEMATEL (Decision Making Trial and Evaluation Laboratory) and AHP (Analytic Hierarchy Process) in individual and combined settings for solving decision-making problems is becoming a hot topic in recent years. Both theoretical and practical issues related to these two multi-criteria decision-making (MCDM) methodologies are broadly discussed in scientific papers. So far there are no significant discussions or controversies regarding the outcomes of their individual or joint usage. Rich pertinent literature elaborates on applications of different versions of these methods in crisp, fuzzy, and rough methodological settings, about uses by groups, managing insufficient (incomplete) and unreliable information, etc. In general, most reported research agrees about the high potential of these two methodologies in supporting strategic and tactical decision-making processes, including the extension of their results to other methods and methodologies positioned sometimes at high levels of management. Interested readers can find more information on the usage of DEMATEL, AHP, and other multicriteria methods in the literature [1,2,3,4,5,6,7,8,9].

To assess sustainable forestry goals there are many methodologically different options. An interesting approach is presented by Nazariani et al. [10] for assessing sustainable management tools in the central Zagros forests of Iran. Following demands for conducting administrative affairs in Near East, DEMATEL is applied in the analysis of sustainable forest management criteria and indicators from the local (Iran) to national level. A total of 7 criteria and 65 sustainable indicators are evaluated by recognized experts via questionnaire, with DEMATEL prioritizing the sustainability criteria and indicating the significant correlations among them. Likert scale was also utilized to rank all the indicators, and in terms of their relative weight, they were compared.

Generally speaking, the goals in forestry depend on the type of forest that is managed and will differ for protected forests and for the forest that is designed for the exploitation of wood and forest products. For protected forests, there are many publications defining goals and guidelines for their management and planning [11,12,13]. In the case of managing protected forests (for example, a part of a national park, or a natural monument), the main goals are oriented towards the protection of wilderness and maintaining biodiversity, along with developing eco-tourism [13,14,15]. In the case of having a forest that is designed for wood production the goals are differently organized, even though biodiversity is a factor in the decision-making process, the focus shifts toward productivity parameters and indicators, such as timber production, net incomes and future value of timber [16] or, similarly, harvesting costs and timber value [17].

In this paper, we have used seven criteria defined in the document “The Montreal Process—Criteria and Indicators for Conservation and Management of Temperate and Boreal Forests”. The first issue of this document was released in 1995 [18] and has been updated from that period on, with the most recent publication in 2015 [19]. The latter document has been used as an outline for this research; the general concept has been adopted with minor modifications of the criteria set. A more detailed explanation of each criterion can be found in Section 3.

One of the key issues in implementing a decision-making methodology for assessing sustainable forestry goals is to recognize the possible causality of goals by recognizing so-called ‘cause’ and ‘effect’ goals and classifying them into ‘prominence’ and ‘relation’ clusters. This kind of initial strategic assessment is best achieved by the use of the DEMATEL methodology developed in the early 70-es of the last century in Switzerland [20,21]. The other approach in the assessment of sustainable forestry goals, which could be understood as the tactical approach is to determine ‘utilities of goals’ expressed as cardinal information and measured by weights of importance, assuming that goals are mutually independent. The presumption that causal relations do not exist is relative but may correspond to clusters of criteria determined by the DEMATEL. This, tactical part of the decision-making process can efficiently be supported by the AHP method [22] developed about the same time as the DEMATEL.

DEMATEL has been developed to study and solve complex and intertwined problems. This technique is based on pairwise comparisons of influential factors of certain systems and identifying their inter-relationships and importance described in the causes-effects setting [23]. By mapping causal relationships, DEMATEL enables the identification of the internal dependencies between factors and makes them understandable [24,25]. In most research, it is pointed out that estimating the opinion of one or more experts in the group with accurate numerical values from a given scale, especially under uncertainty and/or lack of information, is the most commonly difficult and tedious process. Although the comparison scale has only five grades, it is not that easy to distinguish relations among influential factors, especially because the reciprocity or transition rule is not applicable differently from the AHP method. More details on this method will be given in the next section.

AHP has been developed to support hierarchically structured decision-making problems [22]. Without losing in generality, the hierarchy structure with three levels has the goal at the top, the criteria set is positioned at the level below the goal, and at the bottom, there is a set of alternative decisions to be globally weighted by importance regarding the goal via criteria set. By assumption, at a given level of the hierarchy, decision elements are mutually independent, but they are at the same time dependent on elements in the upper level. For instance, alternative solutions to the decision problem are positioned at the bottom level of the hierarchy and by assumption are independent. But, all alternatives are dependent (have utilities) on criteria set in the upper level of a hierarchy. The same logic applies to criteria regarding the overall goal at the top of the hierarchy. The AHP method is extensively applied in many versions for solving decision-making problems in individual and group settings. Similar to DEMATEL, AHP also uses pairwise comparisons, and prioritization of decision elements is performed by a given matrix or optimization method at all levels (except at the top where only the goal exists). The final synthesis of local priorities provides weights (‘utilities’) of alternative decisions versus the goal. Based on derived weights, ranking of solutions may help in a further phase of the decision-making process such as reduction of candidate solutions, grouping solutions into clusters, etc. In recently published papers, there are reports on applying the fuzzy AHP [26,27,28] and grey AHP [29,30], as well as an integrated application of AHP and other MC analysis methods, in a group decision-making context [31,32]. There are also other documents reporting on integrated use of different MC analysis methods in forestry and natural resources management [33,34,35], and the trend of their combing is still very active in recent research [36]. The paper [27] analyses the group decision-making process using fuzzy sets and linear assignment in order to: 1. consider indeterminacy level of evaluations and 2. eliminate subjectivity in responses.

In this study, DEMATEL and AHP are used in a two-members group context. The authors independently applied firstly DEMATEL and then (again independently) AHP to evaluate, respectively, the causality and importance of seven sustainable forestry goals modified from [37], and these were modified from the FAO document [19]. The individually obtained and aggregated results are discussed in both contexts: (a) causality (DEMATEL); and (b) independence (AHP). The main steps of the applied modeling and analysis approach are illustrated in Figure 1.

2. Materials and Methods

2.1. DEMATEL

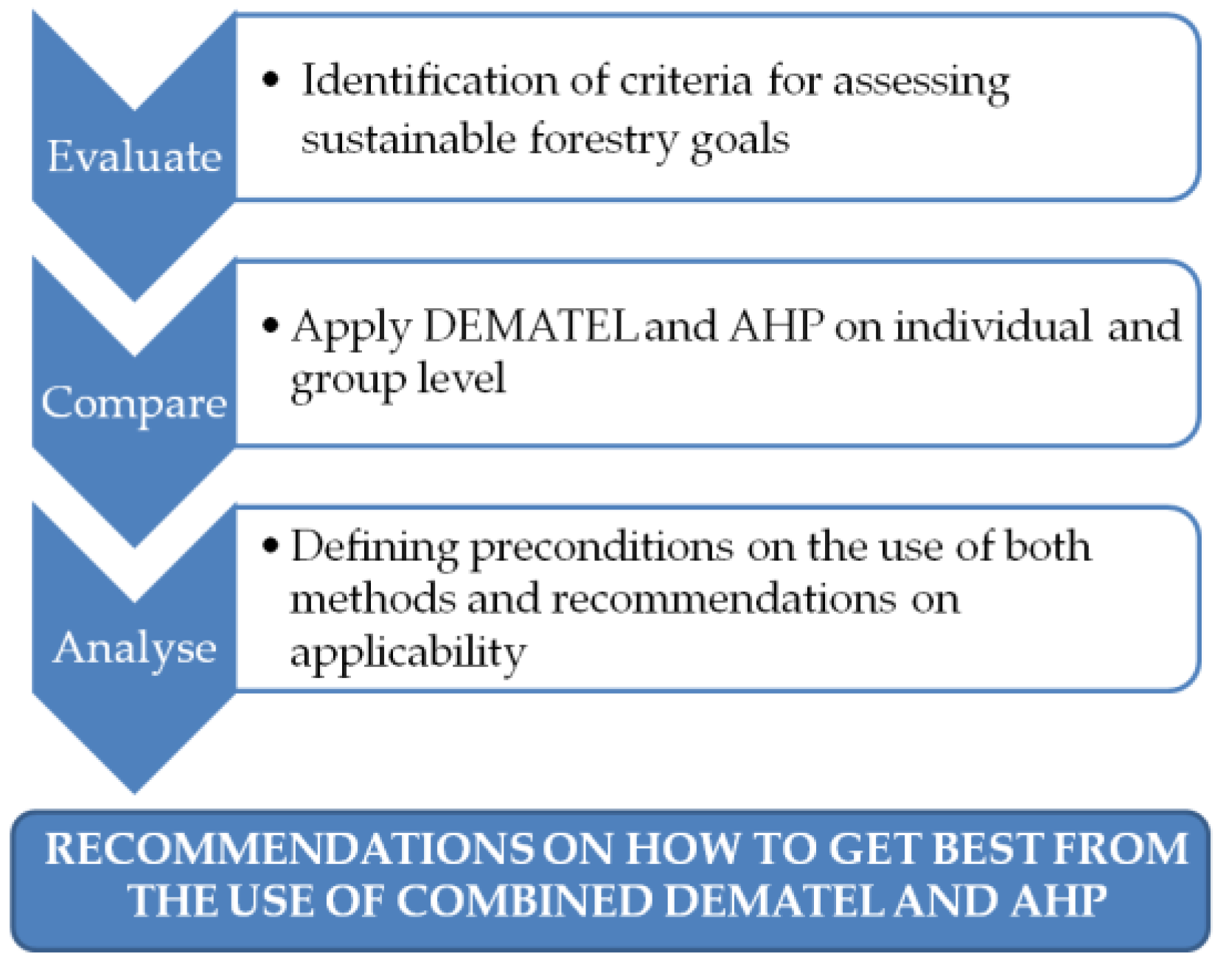
The DEMATEL (DEcision-MAking Trial and Evaluation Laboratory) is developed by the Science and Human Affairs Program of the Battelle Memorial Institute of Geneva between 1972 and 1976. Its original idea was to enable the description and understanding of contextual relations and identify the cause-effect chain of components/factors for a complex decision problem [20,21]. Since its original introduction in the field of societal systems and sciences, the DEMATEL applications extremely dispersed in almost all fields of science and technology. The result is thousands of research and professional reports on its adjustments, mathematical and methodological shifts from crisp to fuzzy and rough representations, combined uses with other multi-criteria methods, individual and group applications, etc. In an analysis of decision problems, DEMATEL is used to recognize the interactions between the factors and to categorize factors into ‘cause’ and ‘effect’ groups [38]. More details about the method are found in the research of Li et al. [39]. For a given system DEMATEL identifies the critical factors that have the greatest influence on other factors and maps relations between factors thus providing the analysts with indicators of how to manage the system, its operation, or divisions into subsystems, better controllable and/or observable. Causal relations between factors, such as cause-effect relations, have fundamental importance for the decision-making process. One of the critical issues in assessing alternative solutions is how they perform concerning a given set of objectives or criteria. In most cases, this is related to solving a multi-criteria optimization problem (MCOP) for which it is required to previously allocate weights to the objectives/criteria respecting their importance regarding certain preference schemes, strategies, or else. Furthermore, the association of weights to objectives/criteria set most often assumes that elements in this set are mutually independent. The decision-maker compares these elements and eventually from afar considers the fact that some elements are “cause” and others are “effect” while playing in the same game which assumes their causal independence.

In the MCOP context, the role of DEMATEL can be understood as an efficient framework to recognize causality among elements (e.g., criteria) within a system (e.g., decision problem). The causal diagram can be acquired in DEMATEL by mapping criteria in a proper way so the decision maker can identify the most influential criteria, distinguish cause from effect criteria and possibly moderate his thinking about how to proceed with solving MCOP.

As stated by Du and Li [38] lots of efforts have been spent on improving and extending the DEMATEL, perspectives changes happened in many directions and research and applications continue.

2.1.1. Procedure

The procedure of DEMATEL is generally divided into the following five steps [38]:

• Step 1: Define quality features and establish a measurement scale;
• Step 2: Extract the direct relation matrix of influential factors;
• Step 3: Normalize the direct relation matrix;
• Step 4: Calculate the total relation matrix;
• Step 5: Calculate the threshold value and construct the DEMATEL map

Preparatory Step 1 and concluding Step 3 do not contain any mathematics, while in Steps 2-4 only simple matrix operations are performed.

In Step 1 influential factors in the system are evidenced and a measurement scale is established as shown in

Table 1. DEMATEL comparison scale [40].

Numeric Value	Definition
0	No influence
1	Very low influence
2	Low influence
3	High influence
4	Very high influence

.

In Step 2 one has to make the comparisons of factors by using the scale in Table 1 and create the relation matrix of influential factors. This matrix is commonly denoted as the direct relation matrix (Z).

The Z matrix has a n × n size with zero values on the main diagonal, while the numeric values in it are labeled as z_ij. The matrix is not symmetrical (z_ij ≠ 1/z_ji) because one factor can strongly influence the other, while that other factor can have no effect back on the first one. Note that this is different from the AHP comparison matrices, generated by the decision maker using a 9-point scale and propagating the effect of inverse (reciprocal) importance of any two compared elements [15].

In Step 3, the direct influence matrix (Z) is normalized by using relations (1) and (2).

$$X=\frac{Z}{s}$$

(1)

$$s=max\left(ma{x}_{1\le i\le n}{{\displaystyle \sum }}_{j=1}^n{z}_{ij, }ma{x}_{1\le i\le n}{{\displaystyle \sum }}_{i=1}^n{z}_{ij}\right)$$

(2)

In relations (1) and (2) the $x_{ij}$ elements of the matrix X fulfill the conditions: $0\le x_{ij}<1$ and $0\le {{\displaystyle \sum }}_{j=1}^n{x}_{ij}\le 1$, while at least one row in Z is such that ${{\displaystyle \sum }}_{j=1}^n{z}_{ij }\le s$.

In Step 4, the total relation matrix (T) is calculated using the Formula (3). This calculation is based on studies by Papoulis [41] where it was shown that a sub-stochastic matrix can be obtained by using normalized direct relation matrix X and absorbing the state of Markov chain matrices shown in relation (3).

$$\mathit{lim}{X}^k=O\mathrm{when} k\to \infty ; \mathrm{and} =X+X^2+X^3+\dots +X^k=X {\left(I-X\right)}^{-1}$$

(3)

In relation (3) O is the null matrix, I is an identity matrix, and ‘−1′ denotes the inverse matrix operator.

In Step 5, to construct the DEMATEL map and indicate relations between factors it is required to calculate the vectors R and C by using relations (4) and (5) and produce so-called an influential relation map shown in Figure 2. The vectors R and C are, respectively, sums of elements in rows and columns in the total relation matrix T.

$$R={\left[r_i\right]}_{n\times 1}= {\left[{{\displaystyle \sum }}_{j=1}^n{t}_{ij}\right]}_{n\times 1}$$

(4)

$$C={\left[c_j\right]}_{1\times n}= {\left[{{\displaystyle \sum }}_{i=1}^n{t}_{ij}\right]}_{1\times n}.$$

(5)

Each r_i summarize both the indirect and direct effects imparted by factor ‘i’ to the other factors, whereas c_j depicts both the indirect and direct effects received by factor ‘j’ from the other factors. If we let i = j, {i,j|1, 2, …, n} then sum (r_i + c_j) known as ‘Prominence’ exhibits the total effects given and received by factor ‘i’. Besides, it also displays the degree of importance of factor ‘i’ in the entire system. On the other hand, the difference (r_i − c_j), called ‘Relation’, displays the net effect through which factor ‘i’ contributes to the system. If the value (r_i − c_j) is positive, then factor ‘i’ is in the net cause group, while factor ‘i’ will be in the net effect (receiver) group if the value (r_i − c_j) is negative [42].

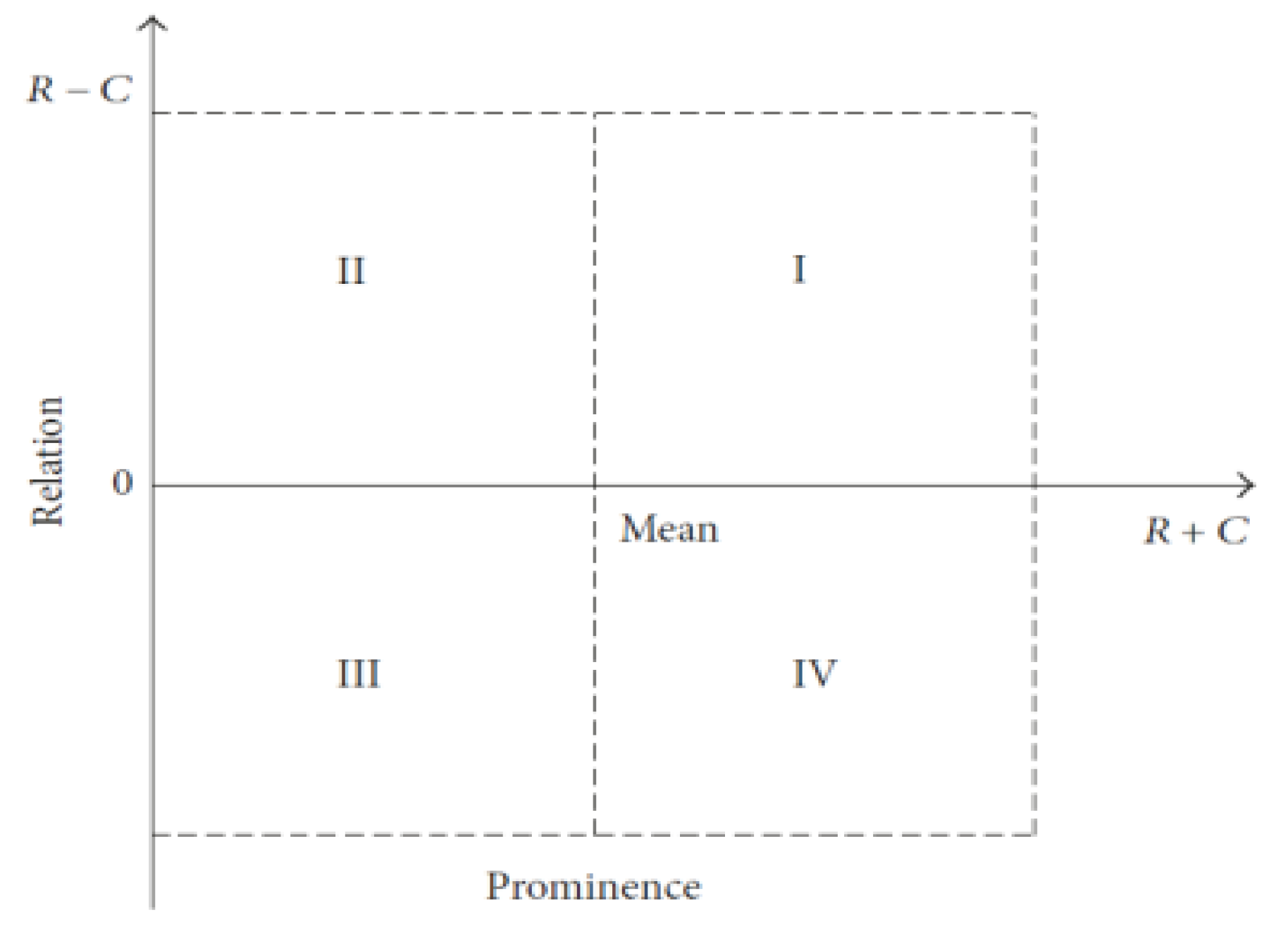
To construct the causal diagram, the threshold value has to be computed in as an average of all elements in the total relation matrix T overall value t_ij in matrix T reflects how one factor (i) influences another factor (j); hence the threshold value assists in distinguishing some important and unimportant effects in the system [43]. Worth mentioning is that in some situations, the causal graph may be too complex to show valuable information for decision-making if all relations among factors are considered. The decision maker has to set a threshold value to indicate the influence level; if there are more decision-makers, this value can be set on a consensus basis, through discussions, or in another way. Most commonly, only the values greater than the threshold value are highlighted and are chosen for portraying in the form of a causal relationship map, acquired by plotting the values of (r + c, r − c) in the graph.

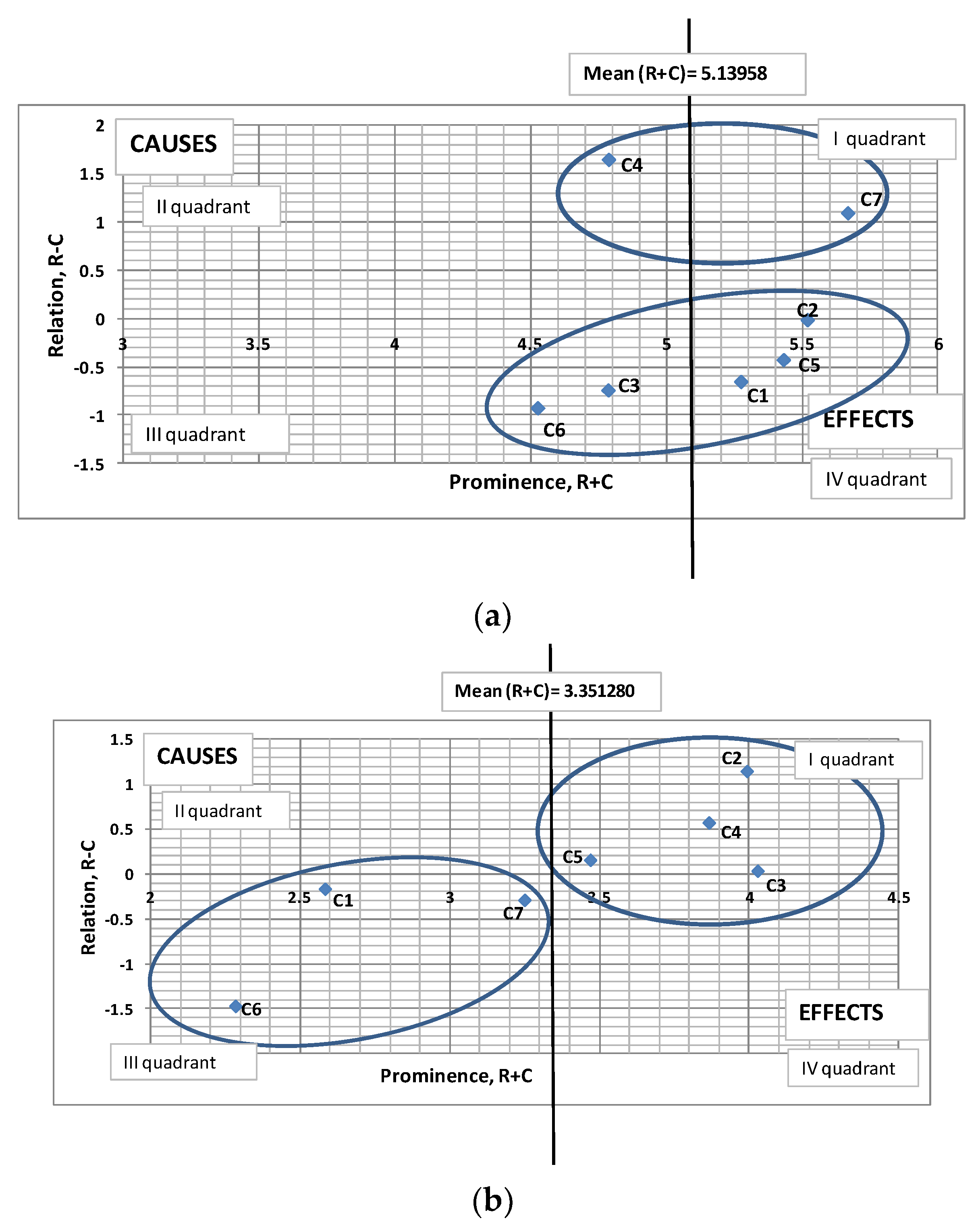
Figure 2, as taken from Si et al. [42] is derived from eight classical DEMATEL studies, and represents a synthesis of the research reported by many authors. Namely, factors in a complex system can be classified with respect to the threshold value. In Figure 1 dash line ‘Mean’ corresponds to the threshold value and divides the graph into four quadrants. The factors in quadrant I correspond to core factors or intertwined givers since they have high prominence and relation. The factors in quadrant II are givers because they have low prominence but high relation. The factors in quadrant III have low prominence and low relation and are relatively disconnected from the system, therefore called independent factors or autonomous receivers. Finally, the factors in quadrant IV have high prominence, but low relation and can be called impact factors or intertwined receivers; these factors are impacted by other factors and cannot be directly improved.

The DEMATEL calculations can be fully performed in the R programming package “dematel”, which also offers a graphical representation of the results in Step 5. The DEMATEL results in this research were processed in this package, while additional computations are performed by the Fortran program which integrates features of both models, DEMATEL and AHP, used in this research.

2.1.2. Importance of Influential Factors (Criteria)

Regarding the weights of factors, there are two reported proposals on how to compute these weights within the DEMATEL framework. First, in studies [2,43,44] classical DEMATEL was used to compute the weights of criteria as ‘factors’ of a given ‘system’, i.e., decision-making problem. The criteria weights are determined based on the prominence (R + C) through a normalization procedure represented by relation (6):

$$w_i=\frac{r_i+c_i}{{{\displaystyle \sum }}_{i=1}^n{r}_i+c_i},\hspace{1em}i=1, \dots , n.$$

(6)

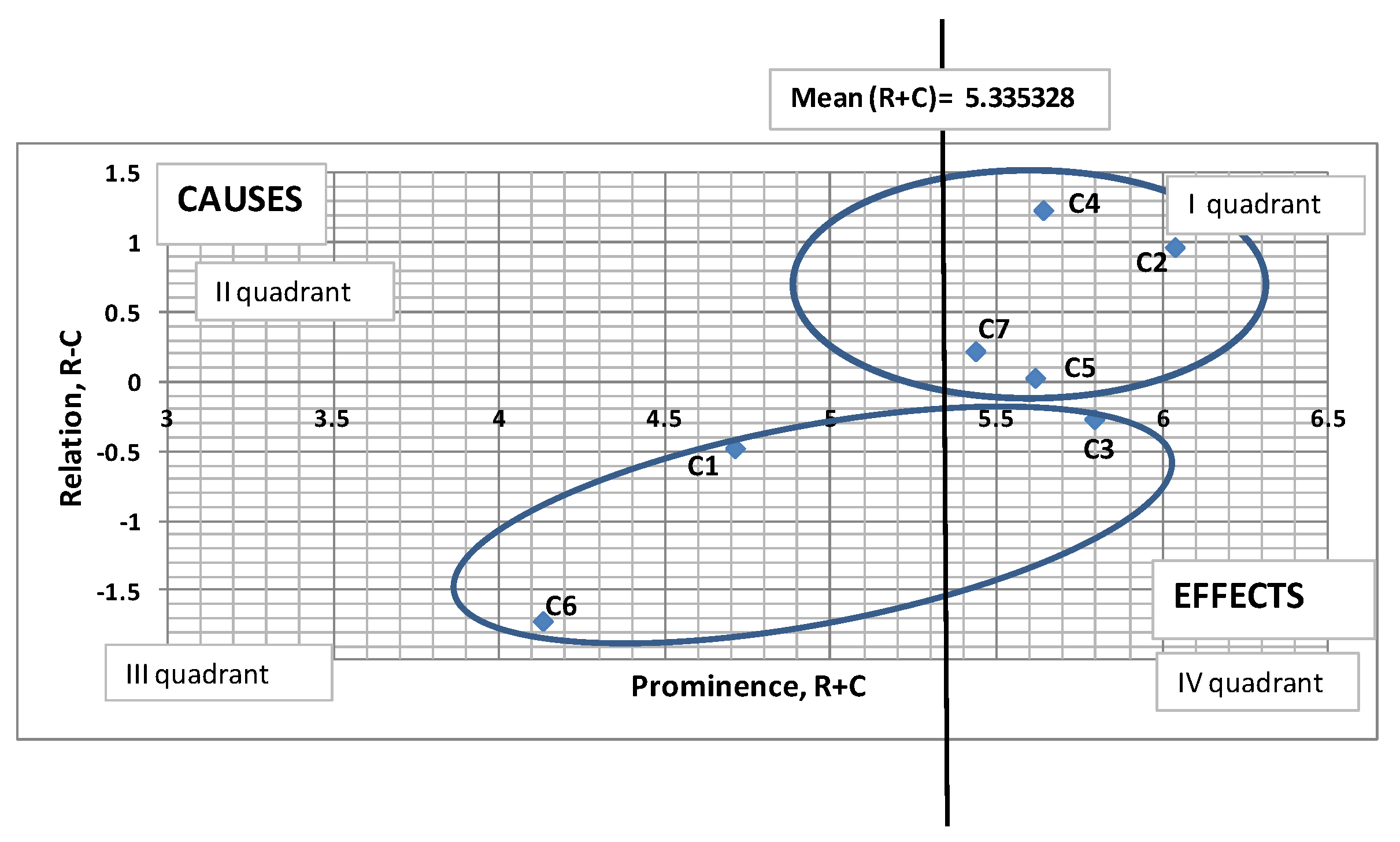
Second, Dalalah et al. [40] proposed Formula (7) to measure the relative importance of a factor (here criterion) which accounts for the interdependence from the cause-effect map and the interrelations between factors. Formula (7) represents the length of the vector in a graph (R + C, R − C) starting from the origin to each criterion (Figure 3).

$$w_i^{\prime }=\sqrt{{\left(r_i+c_i\right)}^2+{\left(r_i-c_i\right)}^2},\hspace{1em}{w}_i=\frac{w_i^{\prime }}{{{\displaystyle \sum }}_{i=1}^n{w}_i^{\prime }}\hspace{1em}i=1, \dots , n$$

(7)

After normalization in (7), the weights w_i (i = 1, …, n) can be used for decision-making by standard MCDM methods such as TOPSIS, CP, and others.

2.2. AHP

If the decision problem is structured as a top-down hierarchy with decision elements at each level, then it is possible to perform a step-by-step procedure of assessing the importance of elements at a given level versus elements in adjacent upper level, to perform prioritization of elements at this level and to finally synthesize all locally obtained weights into the final (global) weights of elements in the bottom level versus the element on the top of the hierarchy. To illustrate the concept, let that three-level hierarchy contains a goal at the top, criteria set on the level below, and alternatives set at the bottom level. First, criteria are evaluated versus the goal to obtain their weights. Then all alternatives are compared versus each criterion to obtain their local weights (regarding criteria). Finally, local weights of criteria and alternatives are synthesized to obtain the final (global) weights of alternatives versus the goal.

2.2.1. Scale and Prioritization

In the standard AHP method, a central point is that in each hierarchy level below the top one (overall goal) pairwise comparison matrices are created to present the multiple preference relation among a given set of decision options versus discriminating decision options in the upper level of the hierarchy; e.g., preference relation among criteria versus goal, or alternatives versus given criterion. Preference relation among any two decision elements is defined by the decision maker (or analyst) using a 9-point scale (

Table 2. Saaty’s importance scale.

Definition	Assigned Value
Equally important	1
Weak importance	3
Strong importance	5
Demonstrated importance	7
Absolute importance	9
Intermediate values	2, 4, 6, 8

) defined in [22].

For the number of elements in one level of hierarchy n, the comparison matrix has the quadratic form (8):

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ \dots & \dots & \dots & \dots \\ a_{n1}& a_{n2}& \dots & a_{nn}\end{array}\right]$$

(8)

Under perfect consistency, each a_ij should be equal to w_i/w_j, where w_i and w_j are the local weights of elements i and j regarding the element in the next upper level. The weight’s vector w = (w₁, w₂, …, w_n)^T corresponding to the matrix (8) comprises the local weights of the elements in the given hierarchy level regarding the element in the next upper level. Further, if the decision-maker is fully consistent, then the transitive rule a_ij‧a_jk = a_ik should apply for all i, j, and k in the range 1 to n. Because in most cases it is not possible to achieve due to inconsistency of the decision maker or limitations of the scale in Table 1, or both at the same time, different measures are introduced to detect such inconsistencies.

Local prioritization of decision elements and deriving the vector w is performed by a selected mathematical model from matrix or optimization theory. Identifying an unknown vector w is not a unique procedure and depends on the method for deriving it. The problem is known as the prioritization problem and there are many procedures to compute this vector.

Most used are matrix methods Eigenvector method (EV) and Additive Normalization method (AN) [22], and optimization methods Logarithmic Least Square method (LLS) [22], Weighted Logarithmic Least Square Method [45], Fuzzy preference programming Method (FPP) [46], and Cosine Maximization Method [47]. Worth mentioning is that there are arguments in favor of some methods versus others and that discussion among researchers is still open in this subject area.

After comparisons of the decision elements are completed by the decision maker and placed in positive reciprocal quadratic matrix A = [a_ij]_n×n (relation 8), the EV method is commonly used to calculate the so-called local priority vector w as the principal eigenvector of a comparison matrix. This method is suggested by Saaty [22], and is considered a part of standard AHP. The standard AHP may be time-consuming and tiresome for the decision makers [48], and therefore we suggest using the abbreviated AHP comparisons (see, for example, [49]) in cases of more combust decision structure.

2.2.2. Consistency Measures

To measure the quality of the vector w, computed by any of the existing methods, one can define several metrics and compare the original matrix A and the corresponding matrix C (9), once the priority vector is already identified by the given prioritization method.

$$C=\left[\begin{array}{cccc}w1/w1& w1/w2& \dots & w1/wn\\ w2/w1& w2/w2& \dots & w2/wn\\ \dots & \dots & \dots & \dots \\ wn/w1& wn/w2& \dots & wn/wn\end{array}\right]$$

(9)

Three most used are also used in this study:

• CR—Consistency ratio applicable when eigenvector prioritization is applied;
• ED—Total Euclidean distance for measuring differences between original judgments and derived weights of decision elements, and
• MV—Minimum violation criterion for recognizing possible rank reversals between compared decision elements.

The CR is part of the standard AHP procedure, with the EV method applied for deriving priority vector w. The consistency index CR is calculated using the consistency index (CI) and random index (RI), and is an average random consistency index derived from a sample of randomly generated reciprocal matrices using the 9-point scale (Table 1):

$$CR=\mathit{CI}/\mathit{RI}=(\lambda -n)/\left(\mathit{RI}\right(n-1\left)\right)$$

(10)

where λ is the principal eigenvalue of the matrix (8) and n is the order of the matrix (8). If CR = 0, the matrix is perfectly consistent. Considering the maximum level of the inconsistency of the decision-maker, as a measure when validating the consistency of a given comparison matrix, Saaty [22] suggested CR values of up to 0.10 as tolerant. Authors [50,51] have shown that values up to 0.30 can in many cases, be adopted as satisfactory, especially if the size of the PCM is 7 or greater. Our research in the group applications of the AHP also indicated that in certain cases, the tolerance level for the CR can be extended up to 0.30. Experiments partly described here showed that in billions of generated matrices of sizes seven and eight, it was possible to find just a few matrices with a CR lower than 0.10. Most frequently, this value ranged from 0.15 to 0.80. Matrices were automatically excluded from further evaluation if the CR was larger than 0.25.

The total ED, also referred to as the total deviation, represents the distance measured between all elements in a comparison matrix (1) and the related ratios of the weights of the derived priority vector:

$$ED={\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\left(a_{ij}-w_i/w_j\right)}^2}}\right]}^{1/2}$$

(11)

This consistency measure is a universal error measure that depends on the priority vector w derived by the prioritization method employed.

The MV measure sums up all violations associated with the priority vector w for any given prioritization method and is expressed as:

$$MV={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{I}_{ij}}}$$

(12)

where:

$$I_{\mathit{ij}}=\left\{\begin{array}{ll}1& \mathrm{if} w_i>w_j \mathrm{and} a_{ji}>1\\ 0.5& \mathrm{if} w_i=w_j \mathrm{and} a_{ji}\ne 1\\ 0.5& \mathrm{if} w_i\ne w_j \mathrm{and} a_{ji}=1\\ 0& \mathrm{otherwise}\end{array}\right.$$

(13)

The ‘conditions of violation’ defined by (13) penalise the possible order reversals as follows. If the j-th alternative is preferred to the i-th one (i.e., a_ji > 1), but the derived priorities are such that w_i > w_j, then there is a ‘violation’ or element preference reversal.

2.2.3. Aggregation of Weights in Group Contexts

The aggregation of individual priorities could be performed by weighted geometric mean method, relation (14), as suggested by Forman and Peniwati [52].

$$w_i^G={{\displaystyle \prod }}_{k=1}^K{\left[w_i\left(k\right)\right]}^{{\alpha }_k},\hspace{1em}i=1, \dots , n$$

(14)

In relation (14) K represents the number of decision-makers, w_i(k) is the priority of i-th decision element for k-th decision-maker, α_k is the ‘weight’ of k-th decision-maker, and w_i^G is the aggregated group priority value. Notice that weights α_k should be additively normalized before their use in (14) and that the final additive normalization of priorities w_i^G is required.

2.3. Combined Use of DEMATEL and AHP

Causal (DEMATEL) and preferential (AHP) methods are conceptually distinct models. They are mostly applied separately, but there is also reported research about attempts to combine their features in complex decision-making frameworks. The role of AHP can be best understood as a tool to generate information on the tactical (short-term or mid-term) importance of goals, while the DEMATEL better fits to strategic analysis of causality relations of goals on a long-term basis and setting the scene for repeatable applications of AHP as a tactical tool. This issue will be broadly elaborated on in the following section.

3. Assessing Sustainable Forestry Goals

3.1. Criteria for Assesing Goals

The assessment of cause-effect relations and mutual importance among sustainable forestry goals are stated as two stages process. The first stage started with the identification of sustainable goals in forestry and setting the group of criteria that would enable the assessment supported by the DEMATEL procedure. Followed by the strategic identification of causal relations among criteria, in the second stage criteria, mutual importance is validated by the pairwise comparison methodology within the framework of the AHP method. Recall that standard complete AHP applies on at least three level hierarchies (goal-criteria-alternatives); in this study, the AHP’s ‘spirit’ is fully preserved by using all its features except the synthesis part (for details, see [22,53]).

The following set of criteria for assessing forestry goals is modified from the document [19] and is as follows:

• C1: Biodiversity conservation;
• C2: Productive capacity of forest ecosystems;
• C3: Maintenance of ecosystem health and vitality;
• C4: Conservation of soil and water resources;
• C5: Maintenance of global carbon cycles;
• C6: Enhancement of socioeconomic benefits;
• C7: Legal and institutional framework.

A brief description of the criteria will help to understand the behavior and differences in attitudes of the two authors while setting their opinions by using two different evaluation scales and acting as real decision-makers while fully applying two involved methods for the same problem. The main characteristics of the selected criteria are as follows:

Biodiversity conservation (C1) is related to the protection of plant and animal species diversity, i.e., their richness and evenness. In this regard, it is important to maintain a high number of different species (richness), but also to preserve their equal distribution (evenness) throughout forest ecosystems [54]. A high share of allochthonous and invasive species may lead to the loss of native species, and the task is to prevent this from happening.

Productive capacity of forest ecosystems (C2) is directly associated with the financial profit from wood and other forest products. The most valuable are forest systems covered with species that are dominantly exploited in the wood industry, for example, oak and beech on the territory of Serbia [55]. This applies to the areas that are not protected as valuable natural assets by the law of nature protection, but to forests that are designed for harvesting and wood production.

Maintenance of ecosystem health and vitality (C3) is associated with maintaining natural ecosystem processes and preventing all disturbances that may happen. This is related to protecting both species and their habitats, and their interrelations, as an integral part of protecting ecosystem vitality and resilience. This applies to forest ecosystems, but also to aquatic ecosystems if there are any.

Conservation of soil and water resources (C4) is an ecological function of forest ecosystems. It is related to the success of forest cover to prevent or control the erosion processes and therefore preserve soil and water quality [56]. A compact forest cover will protect the soil loss caused by wind and/or water erosion, and this indirectly prevents water pollution, as well. Soil and water resources protection also maintains the life processes of living organisms within.

Maintenance to global carbon cycles (C5) is beneficial from two main perspectives; the first one is a process of carbon absorption in tree tissues and forest soil (and its consequential reduction in the air where it represents a pollutant); the second one is a process of “carbon sequestration”—the process related to absorbing carbon by trees for photosynthesis processes. Undisturbed forest cover favors proper maintenance of the global carbon cycle.

Enhancement of social benefits (C6) is related to the potential of forests to fulfill social functions, such as recreation, tourism, education, “forest bathing”, etc. These functions are linked with the overall vitality of forests, as well as with the existence of forest equipment and facilities such as bicycle and walking pathways, the presence of picnic zones, resting areas, etc. These benefits can also profit from the presence of scenic landscapes, with many viewpoints, places for “bird watching” etc.

The legal and institutional framework (C7) is treated differently depending on the forest protection status. If a forest represents a part of a coordinated network of protected areas (for example Natura 2000) the legal requirements are quite strict. When a forest does not hold any protection status, the regulations are more loose, but still should take into account the sustainability concept (for example, in terms that tree cutting should not exceed natural tree growth) to keep the forest system stable.

3.2. Methodology

The goals are assessed by authors in two fundamentally different environments: (1) DEMATEL cause-effect environment; and (2) AHP prioritization in an independency environment. The assessment and decision-making context are partially the same. The criteria set is the same and participants in applications of DEMATEL and AHP are the same, namely authors in this research. What is not the same as that DEMATEL features strategic thinking and derives the importance of criteria based on their causal relationships, while AHP emulates operational (tactical) thinking and direct derivation of criteria importance by their pairwise comparisons as they are mutually independent. The methods use different measurement scales with fundamentally different semantic meanings, and therefore dependency (cause-effect) and independency context are established from different points of view.

The authors are identified hereafter as decision-makers DM1 and DM2, in given authorship orders. Once mutually agreed on the criteria set, the following methodological steps are performed:

• DEMATEL and AHP are applied independently, without consultations, discussions, or consensus of decision-makers. Weights of criteria based on DEMATEL results are obtained by using relations (1)–(5). The weights of criteria for AHP are derived by the eigenvector prioritization method.
• DEMATEL is used in a two-member group version. Individual direct relation matrices set by DM1 and DM2 are aggregated by averaging entries at all positions and then the standard DEMATEL procedure is followed until its very end (creating graph).
• Individually obtained AHP results in Step 1, namely, the vectors containing the weights of criteria, are aggregated to obtain group weights.
• Individual and grouped results of two applied methods are summarized and discussed.

The results of Steps 1-4 are cross-compared to indicate causality and the importance of criteria (described in subSection 4.1) that can be used in further evaluations of long-term sustainable forestry goals with multi-criteria decision-making methods. Worth mentioning is that in the case of the application of either conceptual approach involved in this research (DEMATEL or AHP), the results may bring some controversies, especially in cases of group applications (see, for example, [57]), combined uses, or extensions to fuzzy or rough versions of these and other known techniques multi-criteria techniques.

3.3. Application of DEMATEL—Individual Context

The input data were direct influence matrices for DM1 and DM2 (

Table 3. DEMATEL direct influence matrix—individual assessments.

	DM1							DM2
	C1	C2	C3	C4	C5	C6	C7	C1	C2	C3	C4	C5	C6	C7
C1	0	1	1	1	2	2	2	0	2	1	1	1	3	2
C2	3	0	1	1	2	2	2	4	0	4	4	3	3	3
C3	2	2	0	0	2	1	1	1	3	0	3	3	3	3
C4	2	2	2	0	3	2	2	2	2	4	0	4	3	3
C5	1	3	3	1	0	1	1	2	2	3	3	0	2	2
C6	1	1	2	1	1	0	1	0	0	2	0	0	0	1
C7	3	2	2	2	2	3	0	2	2	2	2	2	1	0

), and these were created by individual assessments (see Table 1).

Starting from the individual direct influence matrices defined by decision-makers DM1 and DM2, DEMATEL procedure generated total relation matrices and calculated sums by rows and columns, R and C respectively (

Table 4. DEMATEL total relation matrix—individual assessments.

DM1						DM2
	R *	C *	R + C	R − C	E/C	R *	C *	R + C	R − C	E/C
C1	2.312	2.961	5.272	−0.650	effect	1.209	1.372	2.581	−0.164	effect
C2	2.753	2.763	5.517	−0.011	effect	2.569	1.422	3.991	1.147	cause
C3	2.023	2.761	4.784	−0.739	effect	2.032	1.995	4.027	0.0376	cause
C4	3.217	1.568	4.785	1.650	cause	2.219	1.645	3.864	0.574	cause
C5	2.503	2.926	5.429	−0.424	effect	1.813	1.654	3.468	0.159	cause
C6	1.801	2.723	4.524	−0.923	effect	0.407	1.875	2.282	−1.468	effect
C7	3.381	2.285	5.665	1.095	cause	1.481	1.767	3.248	−0.287	effect

* R—sums by rows; C—sums by columns.

).

Based on these sums and corresponding values of R + C and R − C, the ‘cause’ or ‘effect’ status is associated with each criterion and presented on the corresponding graph. The results for the individual assessments are presented in Figure 4.

Individual assessment of criteria shows that DM1 believes that criterion C7—Legal and institutional framework is most important on a long-term basis for managing forests, while DM2 thinks that criterion C3—Maintenance of ecosystem health and vitality is more important than the other criteria, Figure 4b. Regarding the importance indication computed by DEMATEL for DM2, the C3 criterion is only a bit advanced compared to the C2 criterion which relates to the productive capacity of forest ecosystems. This fact will be interesting to keep in mind when group results are analyzed. Regarding individual clustering criteria into ‘cause’ and ‘effect’ groups, the results of two decision makers correspond partly, that is: criteria C1 and C6 belong to ‘effects’ and criterion C4 belongs to ‘causes’. The other criteria are clustered by decision-makers in opposite groups ‘causes’ and ‘effects’.

3.4. Application of DEMATEL—Group Context

Group context has been derived by aggregating individual assessments. By aggregating values in Table 3 and Table 4, we have obtained data for

Table 5. DEMATEL direct influence matrix—group context.

Criteria	Group (DM1 and DM2)
	C1	C2	C3	C4	C5	C6	C7
C1	0.0	1.5	1.0	1.0	1.5	2.5	2.0
C2	3.5	0.0	2.0	2.5	2.5	2.5	2.5
C3	1.5	2.5	0.0	2.5	2.5	2.0	2.0
C4	2.0	2.0	3.0	3.5	3.5	2.5	2.5
C5	1.5	2.5	3.0	0.0	0.0	1.5	1.5
C6	0.5	0.5	2.0	0.5	0.5	0.0	1.0
C7	2.5	2.0	2.0	2.0	2.0	2.0	0.0

.

After having direct influence matrix defined, one could calculate total relation matrix for group context (

Table 6. DEMATEL total relation matrix—group context.

Criteria	Group (DM1 and DM2)
	R	C	R + C	R − C	E/C
C1	2.116	2.592	4.708	−0.4760	effect
C2	3.503	2.532	6.035	0.971	cause
C3	2.763	3.029	5.792	−0.266	effect
C4	3.437	2.20126	5.638	1.235	cause
C5	2.821	2.792	5.613	0.0299	cause
C6	1.206	2.923	4.129	−1.717	effect
C7	2.828	2.605	5.433	0.223	cause

).

The final results of DEMATEL application are shown in Figure 5, and represent the values for the group.

The final results of DEMATEL application are shown in Figure 5, and represent the values for the group. After individual direct impact matrices are aggregated, the joint (group) result puts ahead criterion C2—Productive capacity of forest ecosystems as the most important. As the group result, an indication of C2 as the most important criterion in a way stresses the strategic importance of the financial profit from wood and other forest products in global sustainable forest management. The economic aspect represented by C2 in a way overlaps other aspects of managing forests. Besides, DEMATEL puts this criterion into a ‘cause’ cluster for DM2 and group (DM1+DM2). Note that for DM1 (Figure 4a) this criterion is rather ‘effect’, but very close to the delimiting line ‘0′ in the diagram and therefore close to being shifted into the ‘cause’ group. Regarding group clustering criteria, DM1 correspondence with the group is that criteria C1, C3, and C6 belong to the ‘effects’ group; the remaining criteria are clustered within cause and effect groups differently from the group result. In the case of DM2, criteria C2, C4 and C5 belong to ‘causes’ and C1 and C6 to ‘effects’ (Figure 4b) equally as if the group result is considered; cluster positions of the remaining two criteria C1 and C7 differ from the group clustering.

Besides standard DEMATEL application, additional computations are performed by applying Formulas (6) and (7) to derive weights of criteria for possible further uses by multi-criteria methods such as CP, TOPSIS, etc.

Table 7. (a) DEMATEL—Criteria weights obtained by relation (6) [2,45]. (b) DEMATEL—Criteria weights obtained by Formula (7) [46].

DEMATEL Weights (w) and Ranks
DM1	DM2	Aggregated (DM1 and DM2)
(a)
0.147 (4)	0.110 (6)	0.125 (6)
0.153 (2)	0.170 (2)	0.161 (1)
0.133 (5-6)	0.172 (1)	0.153 (2)
0.133 (5-6)	0.165 (3)	0.152 (3)
0.151 (3)	0.148 (4)	0.148 (4)
0.126 (7)	0.097 (7)	0.118 (7)
(b)
0.145 (4)	0.107 (7)	0.126 (6)
0.151 (2)	0.172 (1)	0.162 (1)
0.132 (6)	0.167 (2)	0.155 (2)
0.138 (5)	0.162 (3)	0.151 (3)
0.149 (3)	0.144 (4)	0.150 (4)
0.126 (7)	0.113 (6)	0.111 (7)

a shows that if Formula (6) is applied as proposed by Cebi [45] and Yazdani-Chamzini [2], decision-makers differently weight criteria by importance, and that aggregated ‘group’ weighting is almost the same as this for DM2. Cross-referencing data in Table 7a indicates that criterion C2 is more important than the others. The least important is criterion C6 in all three cases (DM1, DM2, and group). Note that the C2 criterion is identified by DEMATEL as the most important criterion for a group (Cf. Figure 5) and that this criterion can be considered (by the group) as a ‘cause’ criterion.

The application of Formula (7) proposed by Dalalah et al. [46] generates similar weights and ordering of criteria by importance as in the previous case, Table 7b.

Because cardinal and ordinal information in both cases (Formulas (6) and (7)) is similar, one may conclude that either formula can be used for generating the required input for MCDM analyses that might follow initial DEMATEL assessments. Note, however, that weights of top-ranked criteria in both cases are ‘smoothed’, being around a value of 0.150. This may lead to difficulties in discriminating alternatives by importance once the decision matrix is used in standard applications of MCDM models.

3.5. Application of AHP

Acting individually, after the set of seven criteria is agreed to be used, two decision-makers validated the importance of the criteria by using Saaty’s 9-point scale from Table 2. Created matrices are shown in Figure 6; signs ‘-‘ in a lower triangle of two matrices represent reciprocal values of corresponding elements in upper triangles, symmetric to the main diagonals containing values ’1′.

Prioritization of criteria is performed individually by the EV (eigenvector) method and indicators of consistency (CR, ED, and MV) are computed using relations (10)–(13). The results of the computations are shown in Table 4. The last column of the table contains a joint priority vector after geometric averaging is performed by relation (14) and the resulting vector is normalized.

All three vectors containing criteria weights (two individual and one joint vector) indicate a high level of agreement between decision-makers about the importance of criteria. Individually and when grouped the AHP result is that criterion C3—‘Maintenance of ecosystem health and vitality is more important than the others. The second most important in all three vectors is criterion C4—‘Conservation of soil and water resources’ and the third is criterion C5—‘Maintenance of global carbon cycles.’ Both decision makers consider criteria ‘Enhancement of social benefits’ (C6), and ‘Legal and institutional framework’ (C7), as the least important.

Regarding priority vectors obtained individually, DM1 demonstrated inconsistency slightly over tolerant value (CR = 0.146 > 0.100), and DM2 was very consistent with value CR = 0.026. ED values corresponding to the DMs’ inconsistency were measured by CR. Finally, the third indicator, rank reversal indicator MV, is lower for the DM1 (MV = 1) than for DM2 (MV = 3) which indicates that judgments of DM1 were very near to (in)consistency threshold value of CR = 0.100, To conclude, all three indicators confirm acceptable consistency of decision makers considering a relatively large number of criteria and corresponding (7 × 6)/2 = 21 pairwise comparisons each decision maker had to do and insert numbers from the 9-point scale into an upper triangle of a matrix (8).

4. Discussion

Application of two well-known MCDM techniques in assessing sustainable forest management goals, individually and interpreted in a group context, showed that different outcomes may be derived and explained from several different points of view.

First, it is well known that DEMATEL implies a need for a deep understanding of relations between influential factors in the very early stage. That is, creating an initial relation (direct impact) matrix requires the decision maker to apply the causality principle and set numerical values while declaring cause-effect relations between any two factors of the system. In the case of the system being a decision-making problem, and the criteria set proposed in this study being the factors in the system, for evaluating their inter-relations before evaluations of sustainable forestry goals start, the challenge has two faces. One is ‘background information setting’: what are the relations between forestry goals, i.e., how much they are independent, and if there are causality relations among them, what are the intensities expressed with help of a 5-point scale, etc. The other face is ‘front information setting’: how much-selected criteria set is representative (meaningful) for evaluating forestry goals, having in mind that their inter-relations would respect the inter-relations of forestry goals? In this complex situation, the decision maker can be faced with difficulties, inconsistencies, and probable errors while judging decision elements (here, goals and criteria). DEMATEL can only partly discover and help to resolve some of these problems.

Second, the AHP method generally implies mutual independence of compared decision elements at a given level of the hierarchy, versus decision elements in the upper level. In the case of the criteria set which is used in this study, there is just one level of the hierarchy. The AHP philosophy is behind the process of comparing criteria in pairs by using a 9-point scale defined by Saaty and performing prioritization by the eigenvector method to derive the weights of criteria. These weights can later be used for evaluating forestry goals by other standard MCDM methods or forwarded in another way to the next level of decision-making.

As shown in the presented results of this study, the importance of criteria detected by the AHP can be different from those detected by the DEMATEL. For instance, DM1 weighted with AHP criterion C7 as the least important, while the DEMATEL recognized it as the most important one. This difference can be attributed to relative inconsistency demonstrated by the DM1 when applying AHP, and, on the other side, that “importance formulas” used along with DEMATEL are not as confident outcomes as the causality relations detected between criteria. Namely, DEMATEL provides only a limited indication of cardinal information (weights) about criteria importance.

Most of the results of the two methods results coincide with each other or can be used following the similarity principle. With the inspection of information contained in Figure 3 and Figure 4 for inputs to DEMATEL and AHP and the results for these models shown in Table 7 and

Table 8. AHP criteria weights obtained by eigenvector method and aggregated by Formula (14) and consistency measures.

AHP Weights (w) and Ranks
DM1	DM2	Aggregated (DM1 and DM2)
0.071 (5)	0.111 (5)	0.089 (5)
0.116 (4)	0.117 (4)	0.117 (4)
0.304 (1)	0.264 (1)	0.286 (1)
0.254 (2)	0.193 (2)	0.224 (2)
0.158 (3)	0.192 (3)	0.176 (3)
0.052 (6)	0.044 (7)	0.048 (7)
CR = 0.146	CR = 0.026	-
ED = 7.846	ED = 3.223	-
MV = 1.0	MV = 3.0	-

, one can conclude that despite inherent difficulties the two experts participating in this research provided useful information for further studies of sustainable forestry goals.

4.1. Importance of Influential Factors (Criteria)

The importance of criteria is a critical issue if vectors R + C and R − C, derived from the total relation matrix in DEMATEL, are used to calculate the weights of criteria and forward them to certain decision-making models such as CP, TOPSIS, etc. Values of R+C and R − C, and especially graph representation in their coordinate system are very useful for understanding causal relations among criteria. However, our study shows that it is not justified to directly interpret their mutual importance from the graph (R + C)/(R − C) and to insert calculated weights by either Formula (6) or (7) into the decision matrix typical for MCDM, such as those two mentioned.

We argue that positions of criteria in the graph can only serve as an indication of criteria importance, but for deriving their real mutual importance there are more exact methods as was demonstrated by the AHP application. For instance, relations (6) and (7), applicable along with DEMATEL, rank criteria C2, C3, and C4 as the three most important criteria, in that order, Table 7a,b. On the other hand, AHP ranks criteria C3, C4, and C5 as the top 3, while criterion C2 is ranked fourth, Table 8.

For the sake of completeness, it worth mentioning is that the results obtained in this study coincide with conclusions that came out from some earlier studies that DEMATEL and AHP perform in the same direction regarding recognition of the importance of influential factors in the system (here decision problem). Both methods in the group context identified criteria C2 and C5 as more important than the others. This outcome could help to simplify the decision-making process by reducing the number of criteria, or at least clustering them into more and less important ones. In this particular case study, from a strategic point of view DEMATEL obviously, provided that information, while AHP in the tactical part provided necessary contrasting criteria by importance.

4.2. Scales and Matrices

DEMATEL commonly uses a linear 5-point scale for deploying the decision maker’s opinion on causality between compared elements (recall that criteria are ‘factors’ in the decision-making problem understood as a ‘system’). Initially created direct relation matrix is quadratic and not symmetrical. All elements in the matrix are integers. AHP commonly uses a 9-point scale for deploying decision-makers’ judgments on the importance of decision elements (here criteria). Created pairwise comparison matrix is also quadratic, but symmetrical. Because matrix elements in an upper and lower triangle are symmetrical to the main diagonal, elements are integers and real numbers (reciprocals of integers).

Regarding numerical scales used in DEMATEL and AHP applications, their meaning (relation and preference, respectively), size (5 and 9, respectively), and their linear-nonlinear ‘features’ may easily imply differences in the behavior of the decision maker(s) while performing judgments.

4.3. Consistency

To our best knowledge, there is no particular discussion in scientific society related to DEMATEL about the consistency of decision-makers while ‘judging’ causality among influential factors in the system. The same applies to group contexts. If there are more decision-makers, their direct relation matrices are simply additively aggregated and the computation process continues. There are no proposals for geometrical aggregations, commonly used in group scenarios of decision-making, particularly if there are significant differences in individual opinions. No measures of individual or group consistency in DEMATEL are identified in the literature. In the case of AHP, such measures exist and in this paper we have analyzed three of them: Eucleadian distance, Minimum Violation and Consistency Ratio. Concerning consistency, it worth mentioning is that the judgment about causality among factors (DEMATEL), or their mutual importance (AHP) can be tedious and controversial. In some cases, it is not easy to immediately say that some factor is cause or effect regarding all other factors, and with what intensity in each particular relation.

5. Conclusions

This paper illustrates the procedure of evaluating sustainable forestry goals by applying DEMATEL and AHP methodologies. The procedure has been applied in the individual and group context, with the aim of strategic analysis of causality relations among criteria (DEMATEL) and tactical decision-making related to determining the importance of criteria and their “weights” (AHP).

The future research agenda will include several extensions in the combined use of DEMATEL and AHP in forestry planning and management, especially on a global scale. Sustainable goals in forestry will be more precisely treated, including the extension of criteria set for their assessment. Different scenarios of individual and group decision-making employing fuzzy numbers and rough numbers should be analyzed along with versions of these two models based on crisp numbers. Detecting advantages and drawbacks, especially in group settings may better direct future research and indicate more prominent solutions in combining (or not combining) methodologies supported by DEMATEL and AHP.

Being aware that combining the DEMATEL and AHP methods proved to be efficient in this study, we opt for future research in exploring possibilities to achieve synergy (within established common decision-making process) of DEMATEL outputs and the results of other multicriteria models, such as ANP, TOPSIS, VIKOR, and ELECTRE. Group DEMATEL application assumes that once initial relation matrices are collected from participants in the group, at each position of the group matrix, simple averaging of individual judgments is performed before the procedure continues. Equivalent to this in AHP is to aggregate individual judgments in each position of the pairwise comparison matrix. In AHP, this procedure is known as AIJ (aggregation of individual judgments). Future research should include sensitivity analysis of effects that may be expected if various schemes of aggregation of individual judgment are applied; for instance, weighted geometrical instead of simple arithmetic aggregation. This can be important if individual judgments significantly differ, and/or one wants to favor some individuals and allocate appropriate weights different from equalized.

This ‘front’ approach in sensitivity analysis can be compared with the ‘end’ approach, which is to perform aggregations of the final individual results. For instance, in the case of DEMATEL, this means exploring what happens if the final weights of influential factors are aggregated after each individual completed the DEMATEL procedure, with either formula for deriving weights. In the case of AHP, analogous ‘end’ aggregation would be performed with individually obtained weights of factors; this procedure in group AHP applications is known as AIP (aggregation of individual priorities).