Generation Mechanism of Supply and Demand Gap of Forestry Carbon Sequestration Based on Evolutionary Game: Findings from China

Abstract

Aiming at the gap between supply and demand in forestry carbon sequestration trading, an evolutionary game model of forest farmers, emission-controlled enterprises (ECEs), and the government is established, where the purchasing behavior of ECEs is divided into offsetting carbon emission and speculation in the carbon emission trade market. By sorting out the stable conditions of each equilibrium point, the causes of the gap between supply and demand are analyzed to explore the coupling mechanism between financial means and market regulation. At last, a numerical case of actual background is applied to verify the rationality of the conclusions. The study found that: (1) The combination of government financial subsidies with the market mechanism is based on subsidies to ECEs. (2) The best time for the government to reduce financial subsidies to forest farmers is when the carbon quota is tightened and more industries are included in the carbon trading system; the best time for the government to reduce subsidies to ECEs is when the carbon quota tightening policy dominates. (3) The reasons for market imbalance in the early and late stages of forestry carbon neutralization mechanism development are different.

1. Introduction

Implementing emission reduction commitments has become an important way for China to contribute to the construction of the global ecological civilization. Both financial regulation and market mechanism are the most important means applied to protect the forest ecology in most areas. In recent years, the hybrid compensation mode of the market mechanism based on carbon trading and government financial support has been developing rapidly [1]. The carbon trading policy endows carbon emission rights with commodity attributes, which are circulated in the carbon trading market. This mechanism promotes the liquidity and allocation of funds and resources between different industries and regions [2,3,4,5,6,7]. The report of the United Nations Intergovernmental Panel on Climate Change (IPCC) pointed out that negative emission technologies play an important role in the process of reducing emissions. Forestry carbon sinks (FCS) are the cheapest and most accessible technical means [8]. Compared with other emission reduction measures, FCS projects have more advantages in economic, social, and ecological benefits [9]. Therefore, it is included in the China Certified Emission Reduction (CCER) offset mechanism [10,11]. All pilot regions in China use CCER as an offset mechanism for carbon emission quotas and have a preference for FCS. For example, Hubei Province encourages the use of agriculture and forestry in various CCER projects. Shenzhen does not impose geographical restrictions on agriculture and forestry projects [12]. FCS projects not only provide forest farmers with extra income and employment opportunities, but also provide emission control enterprises (ECEs) with emission reduction channels [13,14,15].

However, the FCS projects in China are not developing as well as expected due to low emission reduction, small market share, large initial investment, difficulty in the financing, and insufficient demand [12]. On the one hand, the implementation of FCS requires some basic conditions [16]. The characteristics of FCS projects, such as complex procedures, long cycles, and large investments, restrain forest farmers from participating in FCS projects [17,18], which lead to the stable supply of FCS. On the other hand, the market-oriented supply system of FCS is not yet perfect. Although the number of applied projects is large, the transaction price is unstable [19]. Since the FCS market is greatly affected by the policy, it has a high transaction risk [20], which has restrained the supply of FCS to a certain extent. The development of FCS projects is inseparable from the guidance and promotion of the government, and the intensity of government intervention is proportional to the intensity of carbon emission reduction effects in the trading market [21]. In addition, compared to controlling risks from price fluctuation, stabilizing the fluctuation of market transactions should be paid more attention [20,22]. Therefore, although government financial compensation should be the mainstay at the current stage, the market-based compensation mechanism should also be improved constantly.

The supply and demand of FCS are related dynamically [12]. On the one hand, ECEs must respond to demand based on maximizing their profits [23]. The increase in demand from FCS will send an incentive signal to the supply side, which will boost the supply potential. On the other hand, according to their different demand purposes, the purchase behavior of FCS can be further subdivided into offsetting and speculation. Both of them further constitute supply and demand. Proper speculation can stimulate the carbon trading market. Most studies on FCS explored the supply potential [24,25,26,27] and participation willingness of FCS [28,29,30] based on the characteristics of the project itself and operators or analyzed the factors affecting the demand for FCS [31,32,33]. Therefore, research on the combination of supply and demand under the market mechanism is not sufficient. The core of forest ecological compensation is the transaction of ecological products. The market mechanism is the key to activating farmers’ participation and improving operating efficiency. In addition, forest ecological products have the property of public goods. While the market plays a role, the government’s regulation also plays a decisive role [34]. The research between the government and FCS is mostly aimed at analyzing the trend of policies or exploring the unilateral incentive of the government [35,36] or ECEs [37] to forest farmers. Hence, the role of the market mechanism and the impact of different purchasing behaviors on the market vitality are not considered sufficiently. Moreover, the boundary between government management and market regulation and the relationship between decision-making subjects under different leading roles should be explored as well.

Therefore, most research on FCS is based on the supply or demand side unilaterally and considers use-based demanders only, while the direction of the behavioral decisions of both the supply and demand sides of FCS and the direction of its promotion is unclear. On the one hand, this approach of separating supply and demand cannot explore the spontaneous regulation mechanism of the market and the game relationship between different market behaviors. Thus, it cannot explore the constraint barriers in trading and the interaction between carbon trading market policies and fiscal mechanisms. On the other hand, the demanders of FCS are divided into use-based, voluntary, and speculative types, and speculative demand is generated along with use-based demand. Hence, the incentives for the carbon trading market need to be explored based on considering speculative behavior. In addition, in terms of methodological choice, existing studies have used qualitative analysis methods mostly, but this cannot fully reflect the dynamic decision-making process of the participating actors. Therefore, it is the purpose of this paper to explore how to model the game between trading agents within the market mechanism through quantitative research and thus to explore the right direction to guide the behavior of the FCS market.

The evolutionary game emphasizes the long-term dynamic decision-making process of bounded rationality with incomplete information. Therefore, this paper constructs an evolutionary game model between forest farmers, ECEs, and the government. From the objectives of participation, the behavior of ECEs is divided into offsetting and speculation. By analyzing the early and late stages of forestry carbon neutralization mechanism development, the evolutionary stable strategy (ESS) of participating entities is concluded. Finally, the evolutionary game model is analyzed numerically by taking the Guangdong Chimelong carbon sink afforestation project as a case background [38]. The Guangdong Chimelong FCS project, developed in 2011 and recorded in 2014, is the first forestry CCER project in China that can be traded in the carbon market. The project generates measurable, reportable, and verifiable greenhouse gas emission reductions through afforestation, which plays a pilot and demonstration role for carbon sink afforestation projects and is of great significance in promoting sustainable development.

The marginal contribution of the paper may include: (1) Enriching research on the optimization of forestry carbon trading is examined. The long-term dynamic equilibrium of the FCS market and the reasons for market imbalance in different development stages are analyzed. (2) The coupling mechanism and optimization method of government financial subsidies with the market trade are explored. (3) The conditions for the transition of the forest carbon neutralization mechanism from the early stage to the later stage and the coupling mechanism with other emission reduction policies are studied.

The rest of this paper is organized as follows. In Section 2, the basic problems assumptions are described. Game models of FCS trading are established in Section 3. The stable state of market equilibrium is analyzed in Section 4. A numerical example in FCS trading is presented in Section 5 to verify our results from the models. The main results are discussed in Section 6. Section 7 concludes the paper and examines the main policy implications.

2. Problem Description and Basic Assumptions

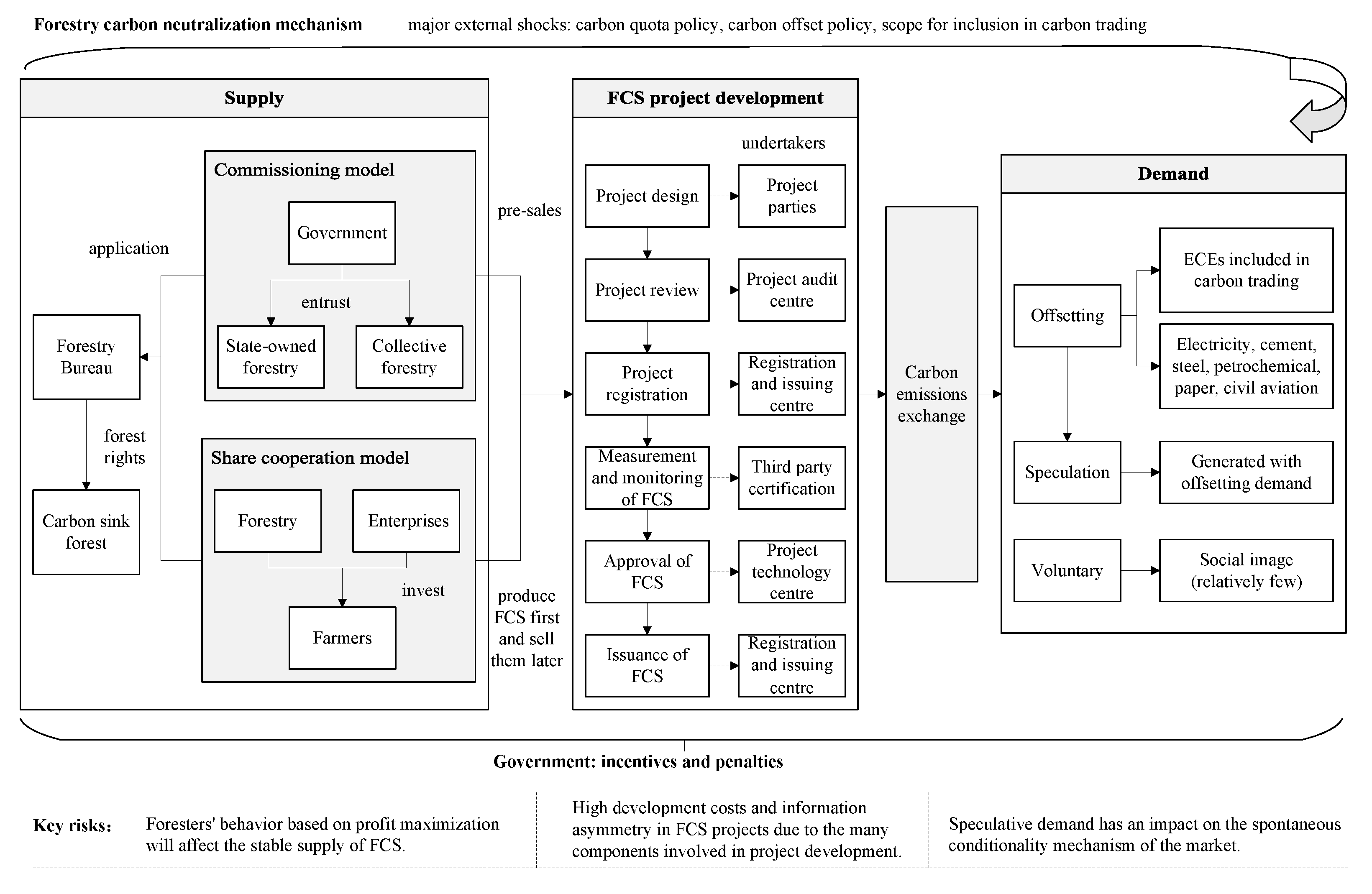
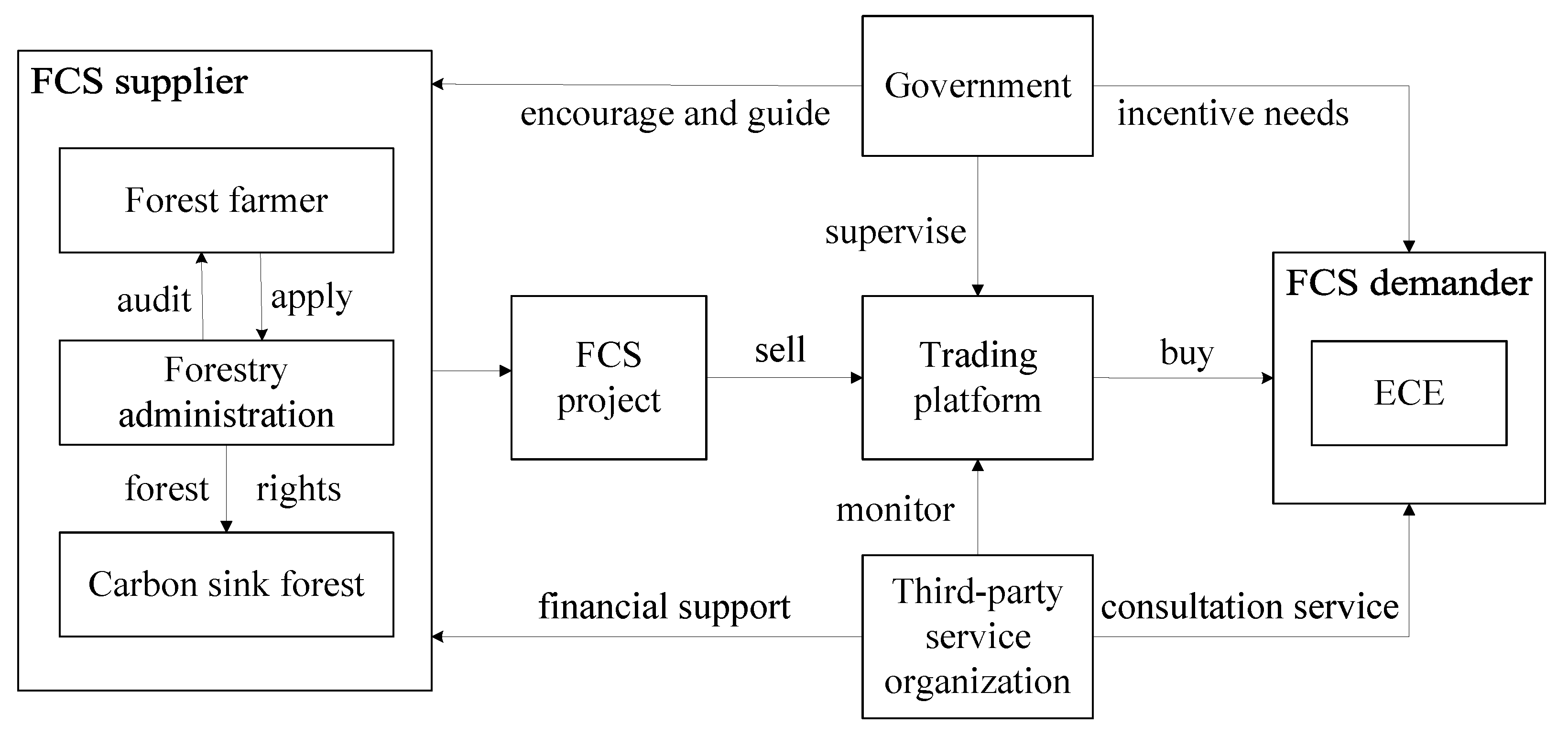
2.1. Problem Description

The market organization structure of FCS trading mainly includes market carriers (FCS project); market elements (subjects, products, and platforms); and market environment (price, market operation mechanism, and policy guarantee mechanism). The FCS trading models include the share cooperation model, the self-management model, the dependency model, and the commission model, among which the share cooperation model and the commission model are used widely. The market structure and key risks of FCS trading are shown in Figure 1.

FCS trading is an innovative mode to marketize forest ecological compensation. In this market, project owners and forest farmers are suppliers of FCS [39]. The key to the project is the supply of farmers’ forest land. Hence, farmers’ decisions will affect the stable supply of FCS directly. Thereafter, the suppliers are referred collectively to as forest farmers. The primary purpose that forest farmers participate in FCS projects is to maximize economic benefits by selling trees at the best time [40,41]. It is necessary for farmers to decide to sell timber to obtain income or to continue to operate the project to increase carbon sequestration. In a broad sense, market ecological compensation mainly refers to the sale of ecosystem services provided by forests together with other products in the market, including the benefits obtained from the development of the under-forest economy [34]. Therefore, this paper assumes that forest farmers participating in FCS projects can obtain benefits by selling carbon sequestration and developing the under-forest economy. (1) When they participate in FCS projects, forest farmers can carry out under-forest economic activities and obtain forest income $R_f$; moreover, the forest farmer can obtain FCS income through the carbon trading market $C_f$. During this process, forest farmers need to bear the initial cost, such as application cost, survey and design cost, carbon sink measurement report, and the cost of arranging the relevant work after the project is adopted in the period, such as the cost of tending and monitoring trees, $C_b$. (2) When they do not participate in FCS projects, forest farmers can obtain timber income $R_w$, and the harvesting cost is $C_w$.

ECEs have two objectives: to meet the requirements of carbon emission allowance and to maximize their profits by two kinds of methods: technological innovation or improvement and carbon trade. FCS provides more diversified emission reduction methods for ECEs. Regardless of the carbon allowance trading between ECEs, ECEs mainly meet the carbon quota requirements through technological innovation for emission reduction and offsetting in combination with the offset mechanism. Therefore, ECEs make emission reduction decisions to maximize their profits based on their own characteristics and the price of carbon sink. The core of the carbon market trading mechanism is to control the total amount of the emission quota. FCS serves as a supplementary offset mechanism; it will increase the total supply in disguise and change the relationship between the supply and demand of emission quotas in the carbon market when the offset ratio is too high. Thus, the market price of the emission quota will be affected accordingly. Therefore, the offset ratio of carbon sink products is usually controlled at five to ten percent in practice. (1) When ECEs choose to purchase FCS to meet the carbon quota requirements and while forest farmers participate in the FCS project, the ECEs need to pay the cost of purchasing FCS $C_f=\theta \tilde{E}{P}_f$, where $\tilde{E}$ is the carbon quota requirement of ECEs, $\theta$ is the ratio of offset by purchasing FCS, $0<\theta <0.1$, and $P_f$ is the unit price of FCS in the carbon trading market. The technological innovation cost incurred by the ECE’s technological emission reduction is assumed to be $C_t$. When forest farmers do not participate in FCS projects, ECEs can meet the carbon quota requirements by purchasing carbon sinks certified by other offset projects and paying $C_e=\theta \tilde{E}{P}_e$, where $P_e$ is the transaction unit price of carbon sinks generated by other offset projects. (2) When ECEs rely entirely on technology to reduce emissions, the cost is assumed to be $C_t^{\prime }=\theta \tilde{E}T$, where T is the unit cost of technical emission reduction, and $C_t^{\prime }>C_t$. The price of carbon sinks is volatile, so ECEs have speculative behaviors. After purchasing FCS with $C_f$, ECEs will sell FCS again to earn the income $R_v$.

The FCS requires a large amount of investment. However, its financing has difficulties. These situations lead to its demand being unstable. Therefore, government support is necessary to affect forest farmers’ decision making. (1) When the government supports reducing the cost of FCS development, assume that the reduction and exemption rate is $\phi$, and the cost to be paid by forest farmers is $(1-\phi )C_b$; the relevant reduction and exemption subsidies for the purchase of FCS by ECEs is M. In the process of promoting the development of FCS projects, the government can obtain ecological and social benefits denoted as $R_e+R_s$ with the fixed cost being $C_g$. (2) When the government does not support FCS projects financially, forest farmers will ignore forest development and management. This may cause stagnation or regression of the FCS project. At this time, the government needs to bear the relevant losses $C_s$ caused by the aggravation of forest degradation. When forest farmers choose other forestry activities, the government can obtain related benefits $R_i$ such as stable employment. At present, the development of FCS projects is still in the stage of financing difficulties. Government support can not only offset part of the cost but also transmit an incentive signal to increase the possibility of financing. The abundance of funds can increase the carbon sequestration capacity of forests and speed up the construction of an information-based talent team to manage forest land scientifically. When the government does not support FCS financially, the funds will be not abundant. The forest management ability will be greatly reduced as well. The ecological and social benefits of the FCS that the government can obtain are assumed to be $\lambda (R_e+R_s)$, where $0<\lambda <1$. The speculative behavior of ECEs will have an impact on the trading market, and the government’s income under the speculative behavior is assumed to be $\zeta (R_e+R_s)$. When $\zeta >1$, the speculative behavior of ECEs will appropriately stimulate the vitality of the trading market; when $\zeta <1$, the speculative behavior of ECEs will cause large fluctuations in carbon sink prices, thereby affecting the stability of the trading market.

The simplified process of FCS trading is shown in Figure 2, where third parties include organizations that provide professional, technical, and financial services.

FCS needs both internal and external drivers. On the one hand, FCS needs external policy and legal protection; on the other hand, various incentives are the endogenous driving force of trading, which can promote the flow of capital within the market. Therefore, FCS cannot be separated from government guidance, regulation, and supervision, nor can it be separated from the spontaneous regulation of the market. Similar to international carbon sink trading, China’s FCS is driven by the government in the initial stage of trading, and then the market is guided to join gradually; in the mature period, the market is driven as the dominant force, and the government withdraws gradually. The driving force and development path of the FCS market is shown in Figure 3.

To reduce the dependence on government subsidies, the ecological compensation must transform from passive to active mode. The hybrid model combining government compensation, such as setting up special funds for forest management and protection, forest farmers’ subsidies, and market-based compensation, has gradually become the mainstream [34]. The essence of forest ecological compensation is the transaction of ecological products, and the market mechanism is the endogenous driving force to encourage forest farmers to participate, thereby realizing ecological and social benefits [7]. In addition, forestry ecological products have the attributes of public goods, which not only require the market to play an independent role in mobilization but also need to continuously strengthen the regulatory role of the government [42]. For the development of the mixed compensation model, government financial compensation supplemented by the market should be the mainstay at the current stage [34,43,44]. Therefore, in the process of realizing market equilibrium, how to effectively clarify the boundary between government management and market mechanism regulation defines the game relationship between various stakeholders, and building a coupling model of government compensation and market compensation is a difficult point that needs to be discussed.

2.2. Assumptions and Model Parameters

According to the factoring process in FCS projects, we make the following assumptions.

(1)

Forest farmers will not suffer losses when they do not participate in FCS projects, i.e., $R_w>C_w$, where $R_w$ is the timber benefits, and $C_w$ is the tending and harvesting costs. FCS projects have high development costs which cannot be offset by the under-forest income, and the main purpose for forest farmers to participate in FCS projects is to obtain carbon sink benefits. Therefore, $R_f<C_b$, where $R_f$ is the forest farmers’ benefit from the under-forest economy, and $C_b$ is the cost for forest farmers to carry out FCS projects. Carbon sink income, timber income, development cost, and felling cost are all calculated by the area of the forest. Natural and man-made risks are not considered.

(2)

ECEs will not reduce emissions voluntarily besides meeting the carbon quota requirements. According to the different purposes of the ECEs, this paper considers two types of demand: forced offsetting and speculation. Since the daily operating income of ECEs does not affect the analysis of the model, the game model only includes the benefits and costs associated with the purchase of FCS by ECEs. ECEs with excessive emissions will be fined at 3–5 times the average carbon market price, and the emission reduction cost of the offset mechanism is generally lower than the transaction price of carbon allowances. Therefore, it is assumed that ECEs are rational economic persons and operate normally so that no default behaviors will occur. It is assumed that the original intention of a company willing to purchase FCS is the low-cost nature of the offset mechanism. In terms of project types and geographical restrictions, each trading pilot in China is inclined to FCS projects. Therefore, compared with other offset projects, under the premise of a stable supply of FCS, ECEs will give priority to purchasing FCS. When FCS is not supplied or the supply is unstable, ECEs will choose to purchase certified emission reductions from other offset projects.

(3)

The development cost of FCS projects is high, and the supporting funds are insufficient. Therefore, it is assumed that in the early development of the forestry carbon neutralization mechanism, government subsidies will be invested effectively in the construction of information technology talent teams to increase the carbon sequestration capacity of forests. In addition, the government needs to bear the resulting loss $C_s$, which is high if the government does not provide sufficient support leading to forest farmers not participating in FCS projects.

Based on the above assumptions, related symbols and definitions are further described as follows:

R_e:

the ecological benefits obtained by the government when the forest farmer participates in the FCS project;

R_s:

the social benefits obtained by the government when the forest farmer participates in the FCS project;

R_i:

other related benefits such as stable employment obtained by the government when forest farmers choose to carry out forestry activities such as wood products;

R_f:

the benefit of forest farmers from the under-forest economy;

R_w:

the timber benefits for forest farmers who do not participate in FCS projects;

R_v:

the income from ECEs purchasing FCS for speculation;

C_w:

the tending and harvesting costs when forest farmers do not participate in FCS projects;

C_b:

the cost for forest farmers to carry out FCS projects;

C_f:

the cost for ECEs to meet the carbon quota requirements by purchasing FCS, which is also the income of forest farmers from carbon sinks;

C_t:

the cost of emission reduction through technology when ECEs purchase FCS;

C′_w:

the cost for ECEs not to purchase FCS and to rely solely on technical emission reduction to meet carbon quota requirements;

C_e:

the cost of other offset methods chosen by ECEs under the condition of stable supply of FCS, ${\displaystyle C_e>C_f}$;

C_g:

the fixed costs for the government to support FCS;

C_s:

related losses caused by project stagnation or regression when both the government and forest farmers do not care about the forest development and management;

M:

the financial subsidies that ECEs can obtain by purchasing FCS;

P_f:

the unit price of FCS;

P_e:

the unit price of other carbon sink products;

T:

the unit cost of technical emission reduction of ECEs;

Ẽ:

carbon quotas for ECEs;

θ:

the proportion of the offset by the ECE;

x:

the probability that the government chooses to support the FCS project;

y:

the probability that ECEs choose to purchase the FCS;

z:

the probability that forest farmers choose to participate in the FCS project;

α:

the probability that ECEs choose to offset when they purchase FCS;

ζ:

the influence coefficient of the speculative behavior of ECEs on the carbon trading market;

λ:

the influence coefficient of the government’s lack of support for forest management;

φ:

the proportion of government subsidies for FCS project costs.

3. The Model

3.1. Construction of the Game Matrix

Each participant has three actions in the game model. The government may or may not support the FCS project with the probability x and $1-x$, respectively. The ECEs may or may not purchase the FCS with the probability y and $1-y$. In addition, the ECEs have two purposes, i.e, offsetting or speculating with the probability $\alpha$ and $1-\alpha$, when the ECEs decide to participate in FCS trade. The farmers may or may not participate in the FCS project with probability z and $1-z$, respectively. To sum up, there are nine possible scenes. The return matrix of the government, forest farmers, and the ECEs under different situations is concluded in

Table 1. The return matrix.

		ECE
		(y)		($1-y$)
		($\alpha$)	($1-\alpha$)
	(x)	$R-M-\phi C_b-C_g$	$\zeta R-M-\phi C_b-C_g$	$R_e-\phi C_b-C_g$	(z)
G		$-C_t-C_f+M$	$R_v-C_t^{\prime }-C_f+M$	$-C_t^{\prime }$
O		$R^{\prime }-(1-\phi )C_b$	$R^{\prime }-(1-\phi )C_b$	$R_f-(1-\phi )C_b$		F
V		$R_i-C_g$	$R_i-C_g$	$R_i-C_g$	($1-z$)	O
E		$-C_t-C_e$	$-C_t^{\prime }$	$-C_t^{\prime }$		R
R		$R_w-C_w$	$R_w-C_w$	$R_w-C_w$		E
N	($1-x$)	$\lambda R$	$\zeta \lambda R$	$\lambda R_e$	(z)	S
M		$-C_t-C_f$	$R_v-C_t^{\prime }-C_f$	$-C_t^{\prime }$		T
E		$R^{\prime }-C_b$	$R^{\prime }-C_b$	$R_f-C_b$		E
N		$R_i-C_s$	$R_i-C_s$	$R_i-C_s$	($1-z$)	R
T		$-C_t-C_e$	$-C_t^{\prime }$	$-C_t^{\prime }$
		$R_w-C_w$	$R_w-C_w$	$R_w-C_w$

Note: R = R_e + R_s; R′ = C_f + R_f; C_t = (1 − θ) ẼT; C_f = θẼP_f; C′_t = ẼT; C_e = θẼP_e.

. In Table 1, each cell of the return matrix has three rows. Each row represents the return of the government, the ECEs, and the farmers, respectively, based on their chosen strategy. For an explanation of the return matrix, see Appendix A for details.

3.2. Solution and Discrimination of Equilibrium Point

The government, ECEs, and forest farmers will continuously adjust their decisions to achieve the expected benefits. Next, we will analyze the main influencing factors of the profit function which guide the game subject to choosing the strategy.

(1)

Replicator dynamics equation of the government

The expected return of the government is assumed to be $E_{\left(x\right)}$ when it supports FCS projects and $E_{(1-x)}$ when it does not. The average return is denoted as ${\overline{E}}_x$. Then,

$$\begin{array}{cc}{E}_{\left(x\right)}=& yz[\alpha (R_e+R_s)+(1-\alpha )\zeta (R_e+R_s)-M-\phi C_b-C_g]\hfill \\ & +y(1-z)(R_i-C_g)+(1-y)z(R_e-\phi C_b-C_g)\hfill \\ & +(1-y)(1-z)(R_i-C_g)\hfill \end{array}$$

(1)

$$\begin{array}{cc}{E}_{(1-x)}=& yz[\alpha \lambda (R_e+R_s)+(1-\alpha )\zeta \lambda (R_e+R_s)]\hfill \\ & +y(1-z)(R_i-C_s)+(1-y)z\lambda R_e+(1-y)(1-z)(R_i-C_s)\hfill \end{array}$$

(2)

$$\begin{array}{cc}{\overline{E}}_x=& x{E}_{\left(x\right)}+(1-x)E_{(1-x)}\hfill \end{array}$$

(3)

The replicator dynamics equation is

$$\begin{array}{cc}F\left(x\right)& ={\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=x(E_{\left(x\right)}-{\overline{E}}_x)\hfill \\ & =x(1-x)\left\{yz[(1-\lambda )(R_e+R_s)(\alpha +\zeta -\alpha \zeta )-M-\phi C_b-C_g]\right.\hfill \\ & +y(1-z)(C_s-C_g)+(1-y)z[(1-\lambda )R_e-\phi C_b-C_g]\hfill \\ & \left.+(1-y)(1-z)(C_s-C_g)\right\}\hfill \end{array}$$

(4)

(2)

Replicator dynamics equation of the ECE

The expected return of the ECE is assumed to be $E_{\left(y\right)}$ when they purchase FCS and $E_{(1-y)}$ when they do not. The average return is denoted as ${\overline{E}}_y$. Then,

$$\begin{array}{cc}{E}_{\left(y\right)}=& xz[\alpha (-C_t-C_f+M)+(1-\alpha )(R_v-C_t^{\prime }-C_f+M)]\hfill \\ & +x(1-z)[\alpha (-C_t-C_e)+(1-\alpha )(-C_t^{\prime })]\hfill \\ & +(1-x)z[\alpha (-C_t-C_f)+(1-\alpha )(R_v-C_t^{\prime }-C_f)]\hfill \\ & +(1-x)(1-z)[\alpha (-C_t-C_e)+(1-\alpha )(-C_t^{\prime })]\hfill \end{array}$$

(5)

$$\begin{array}{cc}{E}_{(1-y)}=& -xz{C}_t^{\prime }-x(1-z)C_t^{\prime }\hfill \\ & -(1-x)z{C}_t^{\prime }-(1-x)(1-z)C_t^{\prime }\hfill \end{array}$$

(6)

$$\begin{array}{cc}{\overline{E}}_y=& y{E}_{\left(y\right)}+(1-y)E_{(1-y)}\hfill \end{array}$$

(7)

The replicator dynamics equation is

$$\begin{array}{cc}F\left(y\right)& ={\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=y(E_{\left(y\right)}-{\overline{E}}_y)\hfill \\ & =y(1-y)\left\{xz[C_t^{\prime }-\alpha C_t+(1-\alpha )(R_v-C_t^{\prime })-C_f+M]\right.\hfill \\ & +x(1-z)\alpha (C_t^{\prime }-C_t-C_e)\hfill \\ & +(1-x)z[R_v-\alpha (C_t+R_v-C_t^{\prime })-C_f]\hfill \\ & \left.+(1-x)(1-z)\alpha (C_t^{\prime }-C_t-C_e)\right\}\hfill \end{array}$$

(8)

(3)

Replicator dynamics equation of the forest farmer

The expected return of the forest farmers is assumed to be $E_{\left(z\right)}$ when they participate in the FCS project and $E_{(1-z)}$ when they do not. The average return is denoted as ${\overline{E}}_z$. Then,

$$\begin{array}{cc}{E}_{\left(z\right)}=& xy[C_f+R_f-(1-\phi )C_b]+x(1-y)[R_f-(1-\phi )C_b]\hfill \\ & +(1-x)y(C_f+R_f-C_b)+(1-x)(1-y)(R_f-C_b)\hfill \end{array}$$

(9)

$$\begin{array}{cc}{E}_{(1-z)}=& xy(R_w-C_w)+x(1-y)(R_w-C_w)\hfill \\ & +(1-x)y(R_w-C_w)+(1-x)(1-y)(R_w-C_w)\hfill \end{array}$$

(10)

$$\begin{array}{cc}{\overline{E}}_z=& z{E}_{\left(z\right)}+(1-z)E_{(1-z)}\hfill \end{array}$$

(11)

The replicator dynamics equation is

$$\begin{array}{cc}F\left(z\right)& ={\displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}}=z(E_{\left(z\right)}-{\overline{E}}_z)\hfill \\ & =z(1-z)\left\{xy[C_f+R_f-(1-\phi )C_b-R_w+C_w]\right.\hfill \\ & +x(1-y)[R_f-(1-\phi )C_b-R_w+C_w]\hfill \\ & +(1-x)y(C_f+R_f-C_b-R_w+C_w)\hfill \\ & \left.+(1-x)(1-y)(R_f-C_b-R_w+C_w)\right\}\hfill \end{array}$$

(12)

4. Analysis of Equilibrium State and Stability Strategy of Evolutionary Game

Through the system composed of Equations (4), (8), and (12), the evolutionary game system has eight pure strategy equilibrium points: $E_1(0,0,0)$, $E_2(1,0,0)$, $E_3(0,1,0)$, $E_4(0,0,1)$, $E_5(1,0,1)$, $E_6(1,1,0)$, $E_7(0,1,1)$, and $E_8(1,1,1)$ and five mixed strategy equilibrium points. ESS is a strict Nash equilibrium (pure strategy equilibrium). Therefore, ESS only exists in eight pure strategy equilibrium points, and it is necessary to discuss their asymptotic stability.

According to the Lyapunov stability theory [45], the method of judging the asymptotic stability of pure-strategy equilibrium points is to construct a Jacobian matrix. Then, the evolutionary stability of each pure strategy equilibrium point is determined by the sign of the eigenvalues of the Jacobian matrix. Taking the derivatives of Equations (4), (8), and (12) respectively, we can obtain the following Jacobian matrix.

$$J=\left[\begin{array}{ccc}{\displaystyle \frac{\partial F\left(x\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(x\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(x\right)}{\partial z}}\\ {\displaystyle \frac{\partial F\left(y\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(y\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(y\right)}{\partial z}}\\ {\displaystyle \frac{\partial F\left(z\right)}{\partial x}}& {\displaystyle \frac{\partial F\left(z\right)}{\partial y}}& {\displaystyle \frac{\partial F\left(z\right)}{\partial z}}\end{array}\right]$$

(13)

The eigenvalues of the Jacobian matrix of the eight equilibrium points are represented by ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$, respectively. According to the Lyapunov discrimination method, the equilibrium point is an asymptotically stable point, and the corresponding strategy is ESS when ${\lambda }_1<0$, ${\lambda }_2<0$, and ${\lambda }_3<0$. See Appendix B for the solution of the Jacobian matrix and the judgment of the equilibrium point.

Assuming that when ECEs purchase FCS and forest farmers participate in FCS projects, the income difference between the government choosing to support and not support is $\Delta {\pi }_1=(1-\lambda )(R_e+R_s)[\alpha +(1-\alpha )\zeta ]-M-\phi C_b-C_g$. When the government supports FCS and forest farmers participate in FCS projects, the income difference between ECEs choosing to purchase and not purchase is $\Delta {\pi }_2=[\alpha (-C_t-C_f+M)+(1-\alpha )(R_v-C_t^{\prime }-C_f+M)]-(-C_t^{\prime })$. When the government supports FCS and the ECE purchases FCS, the income difference between forest farmers choosing to participate and not participate is $\Delta {\pi }_3=[C_f+R_f-(1-\phi )C_b)]-(R_w-C_w)$. By assumption (1), there is $R_f-C_b-R_w+C_w<0$.

4.1. Stability Analysis in the Early Stage of Development of Forestry Carbon Neutralization Mechanism

The government plays a leading role in the early development of the forestry carbon neutralization mechanism. Therefore, when the government does not support FCS, forest farmers who do not participate in the FCS project will suffer a great loss $C_s$, which is much higher than the business cost $C_g$ when the government supports FCS, i.e., $C_s>C_g$. Since the development of the FCS program itself requires high costs, the financing of the FCS program will be more difficult if there is no government support. This will lead to the lack of funds for the development of the FCS program, which will lead to a significant decline in forest management capabilities.

4.1.1. The Stable State of Market Equilibrium in the Early Stage of Forestry Carbon Neutralization Mechanism Development

When $\Delta {\pi }_1>0$, $\Delta {\pi }_2>0$, $\Delta {\pi }_3>0$, and, $C_t^{\prime }>C_t+C_e$, the stability of each equilibrium point is shown in

Table 2. Stability judgment and analysis of equilibrium point (market equilibrium).

Equilibrium Point	Sign of ${\mathit{\lambda }}_1$	Sign of ${\mathit{\lambda }}_2$	Sign of ${\mathit{\lambda }}_3$	Judgement
$E_1(0,0,0)$	+	+	−	SP
$E_2(1,0,0)$	−	+	U	SP
$E_3(0,1,0)$	+	−	U	SP
$E_4(0,0,1)$	U	U	+	UP
$E_5(1,0,1)$	U	+	U	UP
$E_6(1,1,0)$	−	−	+	SP
$E_7(0,1,1)$	+	U	U	UP
$E_8(1,1,1)$	−	−	−	ESS

Note: U—uncertain; SP—saddle point; UP—unstable point; ESS—evolutionary stable strategy.

. It can be found that $E_8(1,1,1)$ is the only evolutionary stable point.

At the beginning of the development of the forest carbon neutralization mechanism,

$$\lambda <1-{\displaystyle \frac{M+\phi C_b+C_g}{(R_e+R_s)[\alpha +(1-\alpha )\zeta ]}}$$

The lack of government support will seriously dampen the enthusiasm of forest farmers. On the one hand, the high development cost delay of returns of FCS projects will reduce forest farmers’ willingness to participate in FCS projects; on the other hand, when the forestry carbon neutralization mechanism cooperates with various environmental policies, such as financial subsidies, it will send incentive signals to financial institutions and investors, which will influence their investment and financing decision-making behavior by adjusting the expectations of financial supporters under the implementation of the policy. When financial institutions tend to accept financing applications or investors tend to invest, FCS projects will be supported financially, which will improve the operational capabilities of FCS projects indirectly. When $\Delta {\pi }_3>0$, the income of forest farmers participating in the FCS project is higher than when they do not participate. There is a time lag in the implementation of ECEs emission reduction strategies. Therefore, when the supply of FCS is unstable and $C_t^{\prime }>C_t+C_e$ exists, ECEs will choose candidate emission reduction plans to maximize profits.

Proposition 1.

Speculation and offsetting are interchangeable for ECEs, and the turning point to the spontaneous adjustment of the market mechanism is at $C_f-M\to C_t^{\prime }-C_t$.

Proof. 

See Appendix C.1. □

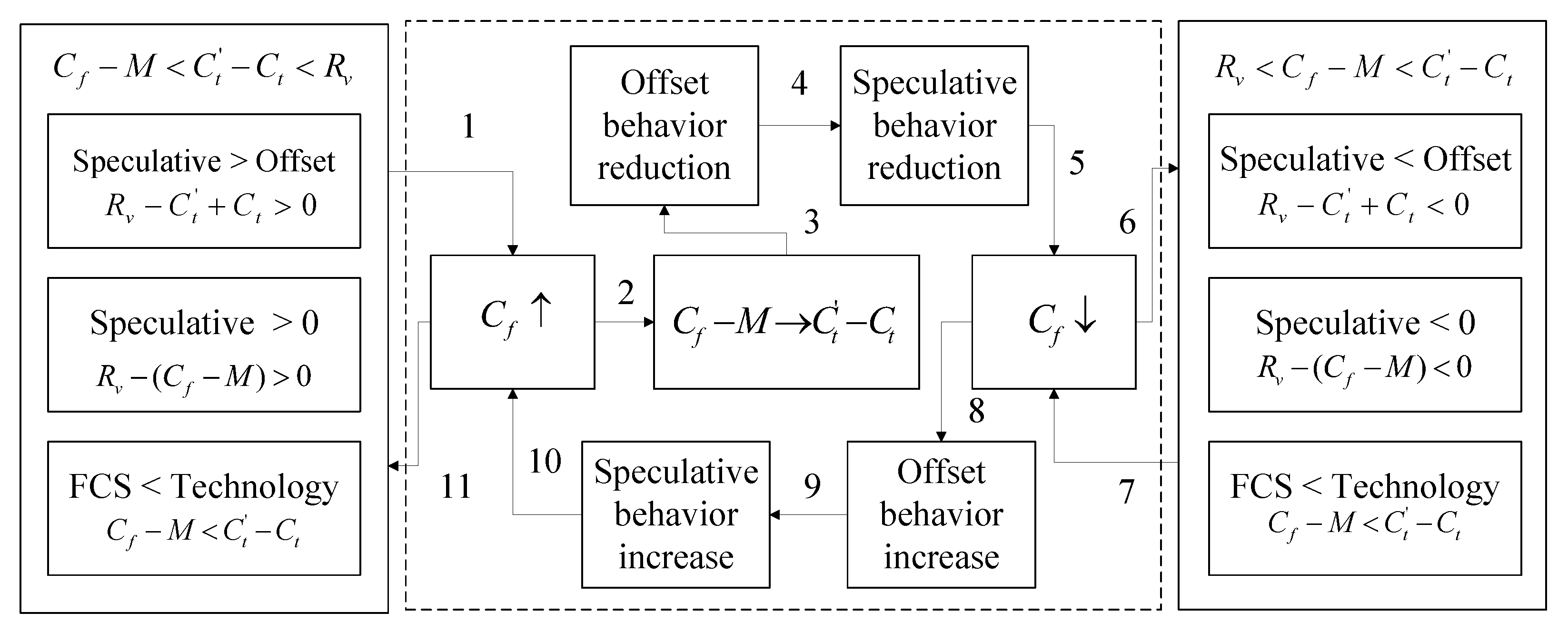
4.1.2. The Stable State of Market Imbalance in the Early Stage of Forestry Carbon Neutralization Mechanism Development

(1)

The reason for the steady state of oversupply

When $(1-\lambda )R_e-\phi C_b-C_g>0$, $\Delta {\pi }_2<0$, and $\Delta {\pi }_3-C_f>0$, the stability of each equilibrium point is shown in

Table 3. Stability judgment and analysis of equilibrium point (oversupply).

Equilibrium Point	Sign of ${\mathit{\lambda }}_1$	Sign of ${\mathit{\lambda }}_2$	Sign of ${\mathit{\lambda }}_3$	Judgement
$E_1(0,0,0)$	+	U	−	SP
$E_2(1,0,0)$	−	U	+	SP
$E_3(0,1,0)$	+	U	U	UP
$E_4(0,0,1)$	+	−	+	SP
$E_5(1,0,1)$	−	−	−	ESS
$E_6(1,1,0)$	−	U	+	SP
$E_7(0,1,1)$	U	+	U	UP
$E_8(1,1,1)$	U	+	−	SP

. In this case, $E_5(1,0,1)$ is the only evolutionary stable point.

Proposition 2.

Market risk is the key reason for oversupply in the early development of the forestry carbon neutralization mechanism. To increase the demand for FCS, i.e., to make sure $R_v+M-C_f>\alpha (R_v+C_t-C_t^{\prime })$ exist, it is necessary to

1.

Increase M and $C_t^{\prime }-C_t$, where $C_t^{\prime }=\tilde{E}T$, $C_t=(1-\theta )\tilde{E}T$, so $C_t^{\prime }-C_t=\theta \tilde{E}T$;

2.

Adjust subsidies appropriately for forest farmers and transfer them to subsidies for ECEs to increase the endogenous power of forest farmers and reduce the financial burden of the government.

Proof. 

See Appendix C.2. □

(2)

The reason for the steady state of short supply

When $C_t^{\prime }>C_t+C_e$ and $\Delta {\pi }_3<0$, the stability of each equilibrium point is shown in

Table 4. Stability judgment and analysis of equilibrium point (in short supply).

Equilibrium Point	Sign of ${\mathit{\lambda }}_1$	Sign of ${\mathit{\lambda }}_2$	Sign of ${\mathit{\lambda }}_3$	Judgement
$E_1(0,0,0)$	+	+	−	SP
$E_2(1,0,0)$	−	+	−	SP
$E_3(0,1,0)$	+	−	−	SP
$E_4(0,0,1)$	U	U	+	UP
$E_5(1,0,1)$	U	U	+	UP
$E_6(1,1,0)$	−	−	−	ESS
$E_7(0,1,1)$	U	U	+	UP
$E_8(1,1,1)$	U	U	+	UP

. In this case, $E_6(1,1,0)$ is the only evolutionary stable point.

Proposition 3.

Market risk and project development are the key reasons for the shortage of supply in the early development of the forestry carbon neutralization mechanism. To improve the forest farmers’ enthusiasm to participate in the FCS project, it is necessary to adjust carbon allowances appropriately and increase the proportion of cost subsidies φ to forest farmers.

Proof. 

See Appendix C.3. □

4.2. Stability Analysis in the Later Stage of Development of Forestry Carbon Neutralization Mechanism

The market plays a leading role in the late development of the forestry carbon neutralization mechanism, where $\lambda$ is close to one. The possibility of forest farmers not participating in FCS projects due to a lack of government support means $C_s$ is small and $C_s<C_g$.

4.2.1. The Stable State of Market Equilibrium in the Later Stage of Forestry Carbon Neutralization Mechanism Development

When $\Delta {\pi }_1<0$, $\Delta {\pi }_2-M>0$, $\Delta {\pi }_3-\phi C_b>0$, and $C_t^{\prime }>C_t+C_e$, the stability of each equilibrium point is shown in

Table 5. Stability judgment and analysis of equilibrium point (market equilibrium).

Equilibrium Point	Sign of ${\mathit{\lambda }}_1$	Sign of ${\mathit{\lambda }}_2$	Sign of ${\mathit{\lambda }}_3$	Judgement
$E_1(0,0,0)$	−	+	−	SP
$E_2(1,0,0)$	+	+	U	UP
$E_3(0,1,0)$	−	−	+	SP
$E_4(0,0,1)$	U	+	+	UP
$E_5(1,0,1)$	U	+	U	UP
$E_6(1,1,0)$	−	−	+	SP
$E_7(0,1,1)$	−	−	−	ESS
$E_8(1,1,1)$	+	−	−	SP

. It can be found that $E_7(0,1,1)$ is the only evolutionary stable point.

The stable development and benefits of the FCS project will stimulate more forest farmers to participate and related enterprises or financial institutions to invest, which will broaden financing channels and reduce the pressure on the government. Therefore, the income gap between the government not supporting FCS projects and supporting FCS projects narrows, where

$$\lambda >1-{\displaystyle \frac{M+\phi C_b+C_g}{(R_e+R_s)[\alpha +(1-\alpha )\zeta ]}}$$

When $\lambda$ is close to one, the benefit that the government can obtain by supporting FCS projects is equal approximately to the benefits obtained by not supporting FCS projects. It can be obtained that $\Delta {\pi }_1=-M-\phi C_b-C_g<0$ exists, and the FCS trading is self-regulated by the market to equilibrium completely.

Proposition 4.

In the later development of the forestry carbon neutralization mechanism, $C_f\to C_t^{\prime }-C_t$ is a turning point in the spontaneous adjustment of the market mechanism.

Proof. 

See Appendix C.4. □

4.2.2. The Stable State of Market Imbalance in the Later Stage of Forestry Carbon Neutralization Mechanism Development

In the $E_4(0,0,1)$ scenario, it can be derived that ${\lambda }_3=-(R_f-C_b-R_w+C_w)>0$ exists. Therefore, $E_4(0,0,1)$ will not be an evolutionary stable point. It means that in the later development of the forestry carbon neutralization mechanism, there will be no stable situation of oversupply in FCS trading.

When $C_t^{\prime }>C_t+C_e$, $\Delta {\pi }_3-\phi C_b<0$, $R_f-(1-\phi )C_b-R_w+C_w<0$, and $\Delta {\pi }_2<0$, the stability of each equilibrium point is shown in

Table 6. Stability judgment and analysis of equilibrium point (in short supply).

Equilibrium Point	Sign of ${\mathit{\lambda }}_1$	Sign of ${\mathit{\lambda }}_2$	Sign of ${\mathit{\lambda }}_3$	Judgement
$E_1(0,0,0)$	−	+	−	SP
$E_2(1,0,0)$	+	+	U	UP
$E_3(0,1,0)$	−	−	−	ESS
$E_4(0,0,1)$	U	U	+	UP
$E_5(1,0,1)$	U	−	+	SP
$E_6(1,1,0)$	+	−	U	SP
$E_7(0,1,1)$	U	+	+	UP
$E_8(1,1,1)$	U	+	U	UP

. It can be found that $E_3(0,1,0)$ is the only evolutionary stable point.

Proposition 5.

Market risk and operational risk are the key reasons for the shortage of supply in the early development of the forestry carbon neutralization mechanism, and the dislocation between the reduction of financial subsidies and the increase of carbon allowances is the cause of the market imbalance.

Proof. 

See Appendix C.5. □

5. A Numerical Example

In this section, based on the case in the Guangdong Chimelong FCS project [38], we discuss the FCS trade to verify the above results.

5.1. Background

Guangdong Cuifeng Landscaping Co., Ltd. (CF) implemented the Guangdong Chimelong FCS project with the support of the China Green Carbon Foundation (CGCF) and the Guangdong Provincial Forestry Department. (1) CF is responsible for financial investment, development, and carbon sink trading. (2) Each village committee is responsible for providing forest land to obtain land funds, supervising and managing the forest land, and stipulating that trees cannot be cut down during the project period. Thereafter, each village enjoys the right to output and ownership of forest land and participates in the distribution of FCS income. (3) Guangdong Provincial Forestry Department provides strategic guidance and coordination. The costs and incomes of the Guangdong Chimelong FCS project are detailed in Appendix D. To sum up, $C_b=12.5$ million, $R_e=1.3$ billion, $R_s=100$ million, $R_w-C_w=70$ million, and $R_f=0$. The 10 million donated by Guangdong Chimelong through CGCF can be regarded as a financial subsidy, so $\phi =0.8$. Other variables are uncertain variables related to the stability of the carbon trading market. They will be assigned according to the division of the scenario in the model.

5.2. Stability Analysis

5.2.1. Market Equilibrium in the Early Stage of Forestry Carbon Neutralization Mechanism Development

In this case, $E_8(1,1,1)$ is ESS, i.e., $\Delta {\pi }_1>0$, $\Delta {\pi }_2>0$, $\Delta {\pi }_3>0$, and $C_t^{\prime }>C_t+C_e$. Therefore, let $C_g=100$ million, $C_t^{\prime }=5$ billion, $C_t=4.5$ billion, $C_s=1$ billion, $C_e=490$ million, and $\lambda =0.6$.

(1)

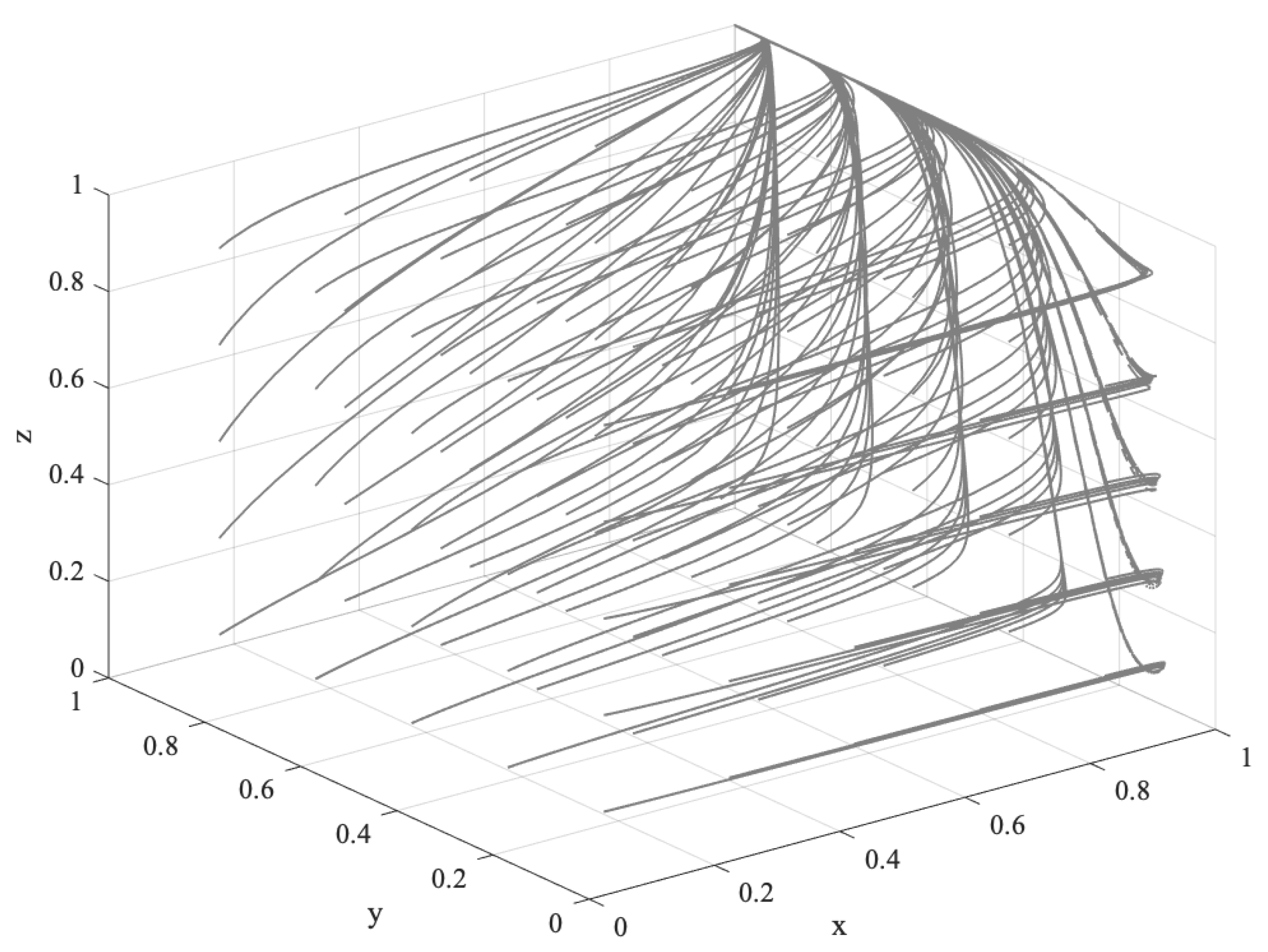
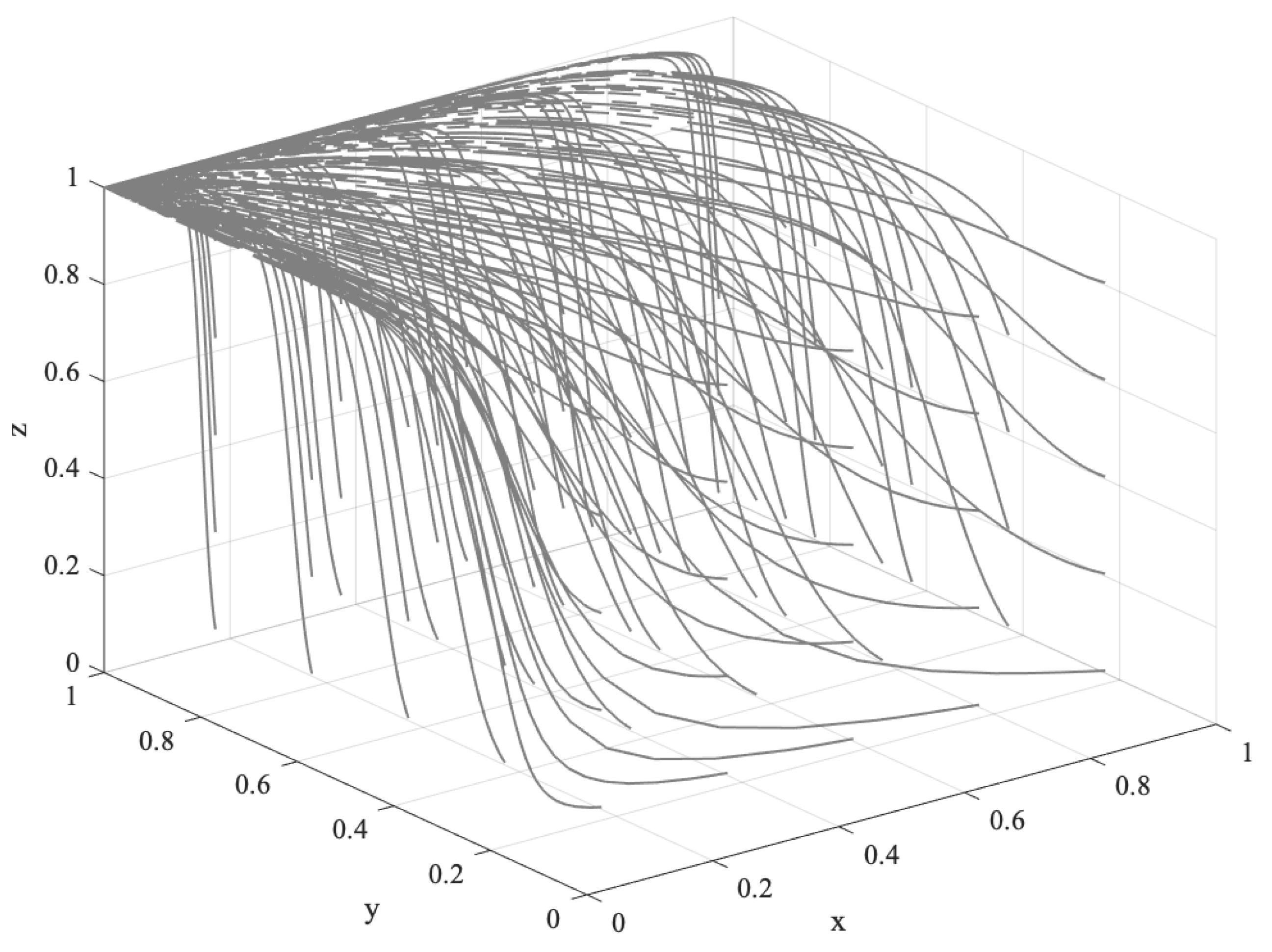
When the income from speculation is higher than the income from offsetting, the FCS price is on the rise, and speculation will be profitable, which means $R_v+C_t-C_t^{\prime }>0$ and $R_v-(C_f-M)>0$. At this time, the cost of ECEs to purchase FCS is lower than the cost of technical emission reduction, i.e., $C_f-M<C_t^{\prime }-C_t$. ECEs have a high probability of purchasing FCS for speculation. The speculative behavior will stimulate market vitality, so $\zeta >1$. In the case of a stable supply of FCS, the cost of purchasing FCS $C_f-M$ is lower than the cost of purchasing other carbon sequestration products $C_e$. Therefore, let $C_f=5.2$ billion, $M=40$ million, $R_v=5.4$ billion, $\alpha =0.4$, and $\zeta =1.1$. The evolution track of the system is shown in Figure 4. After repeated decision making and evolution, the behaviors of the government, ECEs, and forest farmers tend to “support”, “purchase”, and “participate”, respectively.

(2)

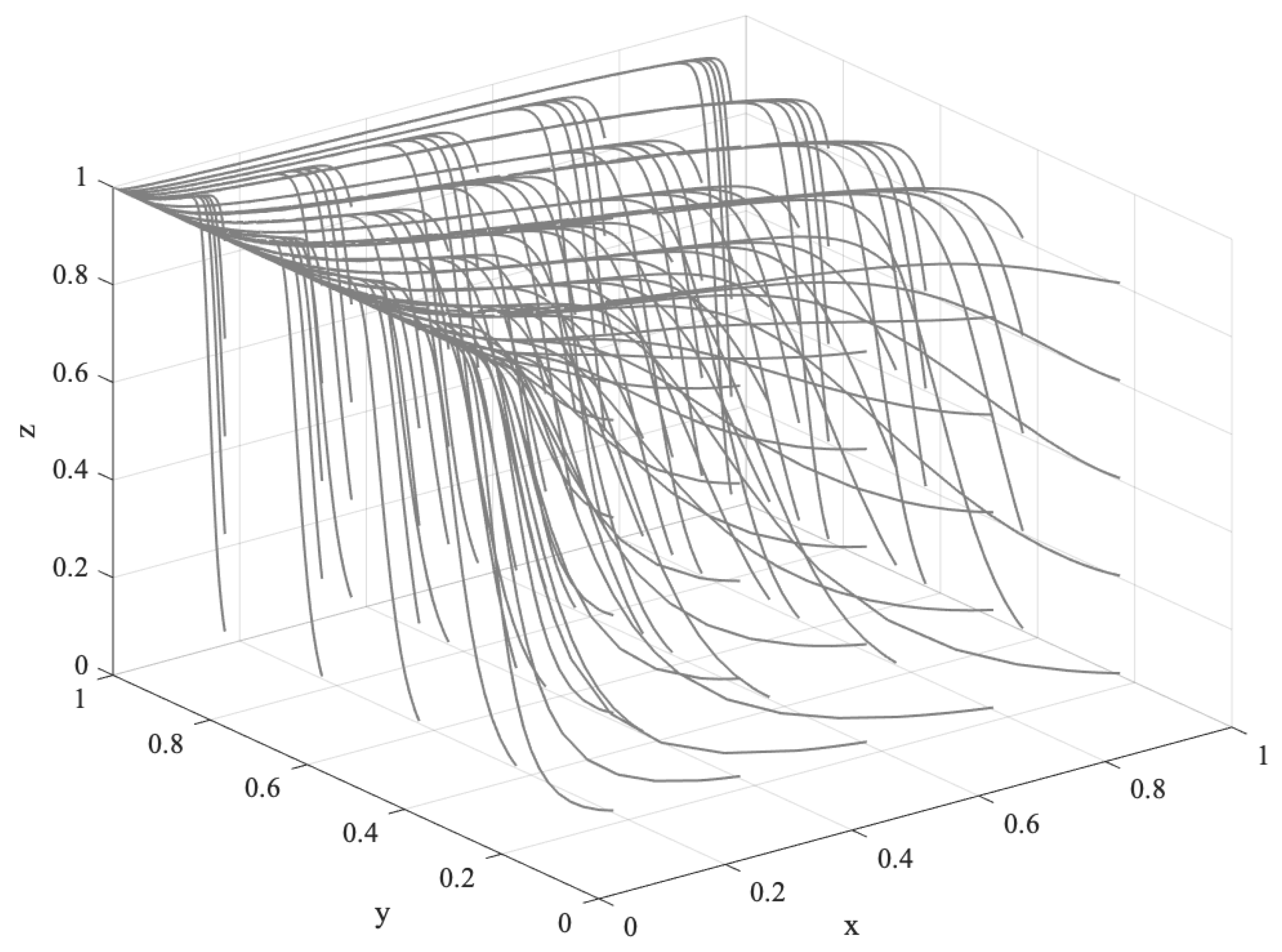
When the offsetting income is higher than the speculative income, the FCS price is in decline, and speculation falls, which means $R_v+C_t-C_t^{\prime }<0$ and $R_v-(C_f-M)<0$. At this time, the cost of ECEs to purchase FCS is lower than the cost of technical emission reduction, i.e., $C_f-M<C_t^{\prime }-C_t$. ECEs have a high probability of purchasing FCS for offset, and speculation will affect the carbon trading market adversely, so $\zeta <1$. Therefore, let $C_f=5.3$ billion, $M=40$ million, $R_v=4.8$ billion, $\alpha =0.6$, and $\zeta =0.9$. The evolution track of the system is shown in Figure 5. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “support”, “purchase”, and “participate”.

In Figure 4 and Figure 5, “x”, “y”, and “z” represent the probability of government supporting FCS projects, ECEs purchasing FCS, and foresters participating in FCS projects, respectively. Comparing the different scenarios in the same equilibrium (Figure 4 and Figure 5), ECEs evolve more quickly to the strategy of purchasing FCS if the benefits of offsetting through purchasing FCS are higher than the benefits of speculation. In addition, foresters’ willingness to participate in FCS projects (z) decreases gradually and then increases again as demand increases if government support is strong and ECEs’ purchase intentions are small, i.e., $(x,y)\to (1,0)$. Therefore, the market instead of government support is the key to stimulating long-term participation in FCS projects. In the short term, government support may be effective in motivating foresters to participate in FCS projects. In the long term, the key to influencing foresters’ decisions is the demand for FCS from ECEs. Therefore, in the current situation where FCS supply is important to be able to make policy adjustments as soon as possible to switch to a simultaneous balance between supply and demand.

5.2.2. Market Equilibrium in the Later Stage of Forestry Carbon Neutralization Mechanism Development

In this case, $E_7(0,1,1)$ is ESS, i.e., $\Delta {\pi }_1<0$, $\Delta {\pi }_2-M>0$, $\Delta {\pi }_3-\phi C_b>0$, and $C_t^{\prime }>C_t+C_e$. Therefore, let $C_g=1$ billion, $C_t^{\prime }=10$ billion, $C_t=90$ billion, $C_s=20$ million, $C_e=9.8$ billion, $M=10$ million, $\lambda =0.95$, and $\phi =0.2$.

(1)

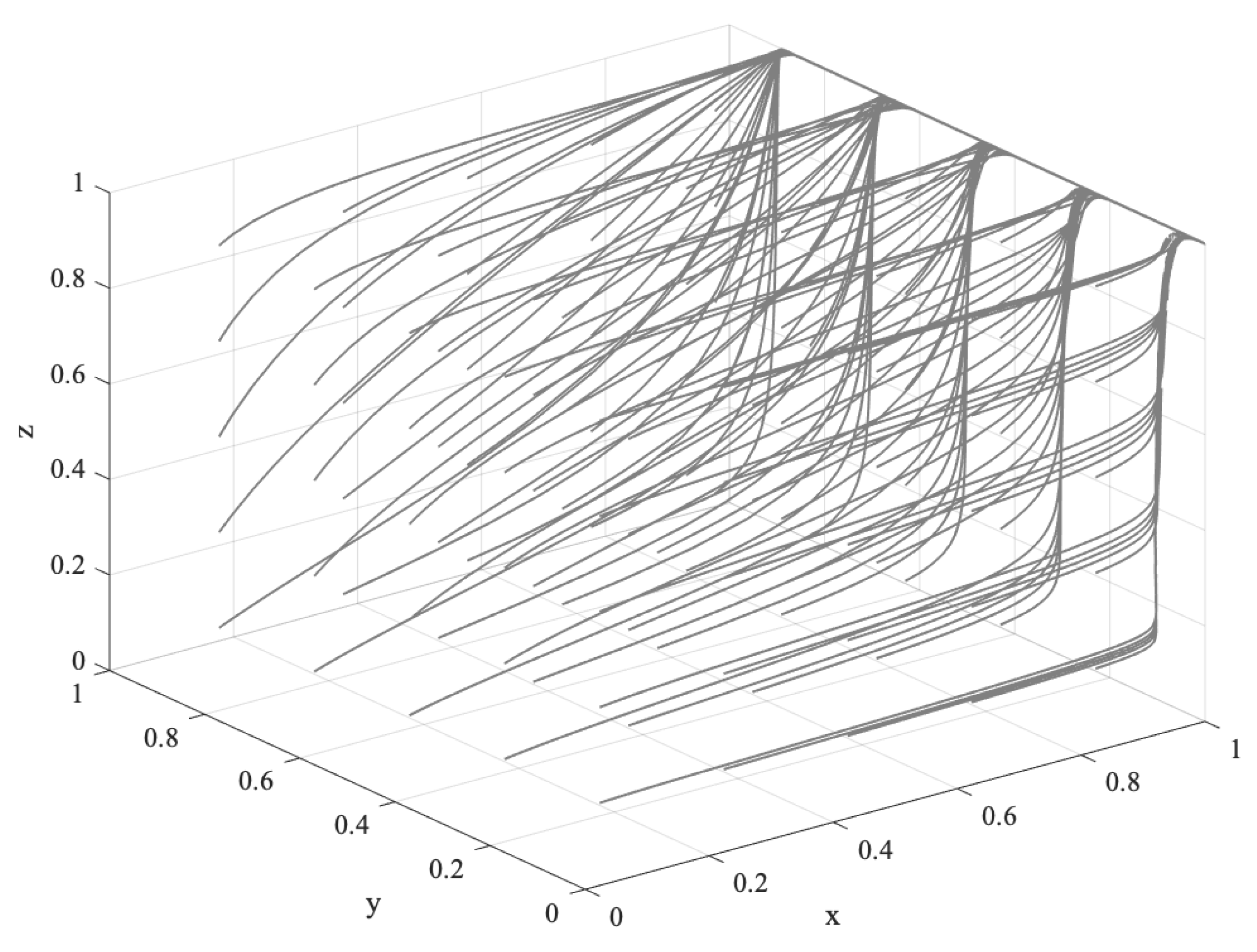
When the speculative income is higher than the offsetting income, the FCS price is on the rise, and speculation can be profitable, which means $R_v+C_t-C_t^{\prime }>0$ and $R_v-C_f>0$. At this time, the cost of ECEs to purchase FCS is lower than the cost of technical emission reduction, i.e., $C_f<C_t^{\prime }-C_t$. ECEs have a high probability of purchasing FCS for speculation, and speculation will stimulate market vitality, so $\zeta >1$. In the case of a stable supply of FCS, the cost of purchasing FCS $C_f-M$ is lower than the cost of purchasing other carbon sequestration products $C_e$. Therefore, let $C_f=9.5$ million, $R_v=10.2$ billion, $\alpha =0.4$, and $\zeta =1.1$. The evolution track of the system is shown in Figure 6. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “not support”, “purchase”, and “participate”.

(2)

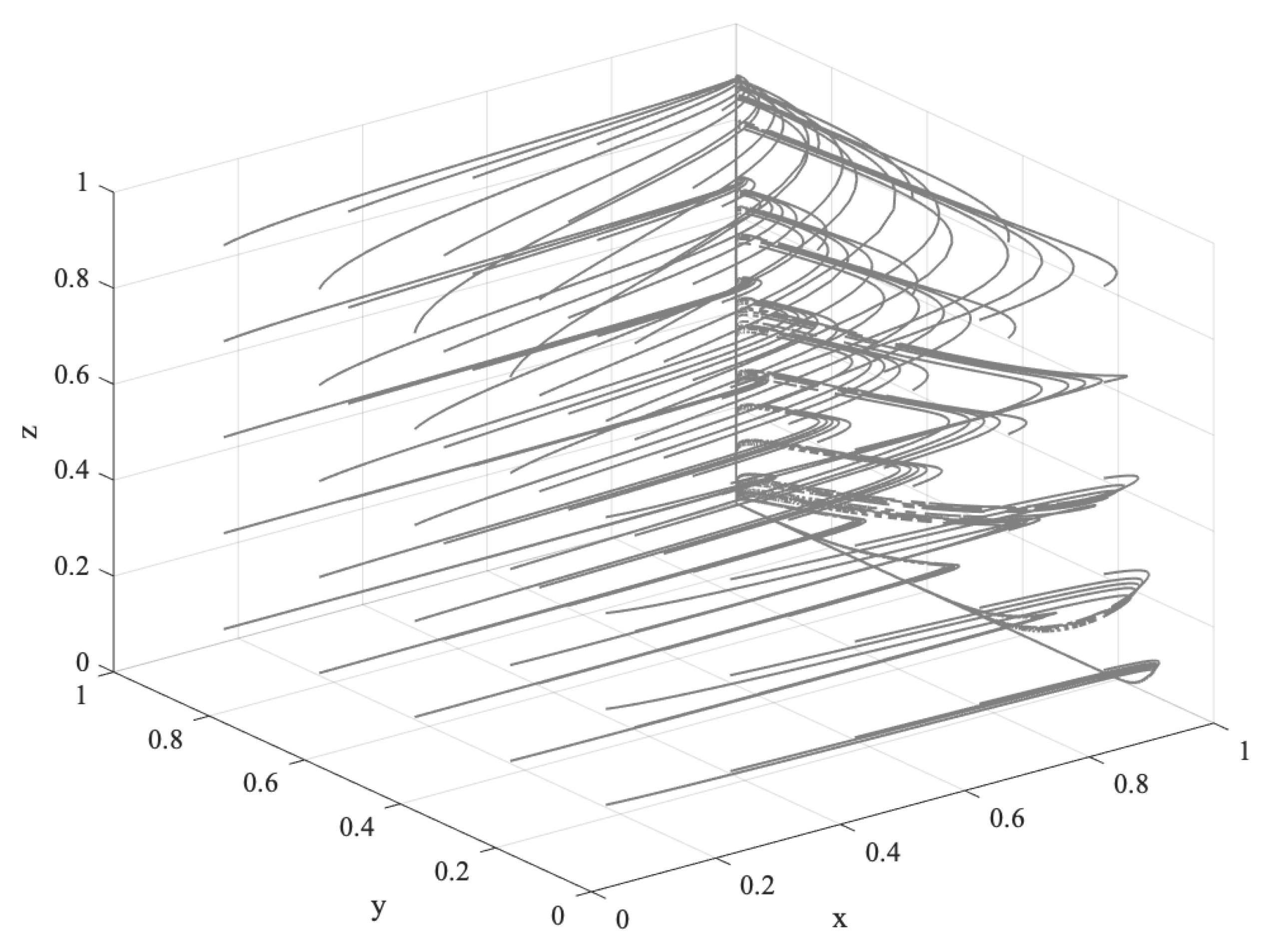
When the offsetting income is higher than the speculative income, the FCS price is in decline, and speculation falls, which means $R_v+C_t-C_t^{\prime }<0$ and $R_v-C_f<0$. At this time, the cost of ECEs to purchase FCS is lower than the cost of technical emission reduction, i.e., $C_f<C_t^{\prime }-C_t$. ECEs have a high probability of purchasing FCS for offset, and speculation will affect the carbon trading market adversely, so $\zeta <1$. Therefore, let $C_f=9.5$ billion, $R_v=9$ billion, $\alpha =0.6$, and $\zeta =0.9$. The evolution track of the system is shown in Figure 7. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “not support”, “purchase”, and “participate”.

Comparing Figure 6 and Figure 7, the system converges better if the ECE generates higher returns through purchasing FCS for offsetting than speculating. Unlike the comparison results in Section 5.2.1, the increase in the convergence effect of the system at this point is reflected in the decision making of the foresters, which also indicates that the sensitivity between demand and supply is greater at the later stage.

5.2.3. Market Imbalance with Oversupply

In this case, $E_5(1,0,1)$ is ESS, i.e., $(1-\lambda )R_e-\phi C_b-C_g>0$, $\Delta {\pi }_2<0$, and $\Delta {\pi }_3-C_f>0$. Therefore, let $C_g=1$ billion, $R_f=80$ million, $C_t^{\prime }=5$ billion, $C_t=4.5$ billion, $C_s=1$ billion, $C_e=490$ million, $C_f=550$ million, $M=40$ million, $R_v=500$ million, $\lambda =0.6$, $\alpha =0.5$, and $\phi =1$. The evolution track of the system is shown in Figure 8. As can be seen from Figure 8, the government will choose to support the project because of the huge ecological losses that would be incurred by not supporting it. Although high government financial subsidies can incentivize foresters to participate in FCS projects, they cannot improve endogenous motivation. At this point, neither purchasing FCS by ECEs for offsetting nor speculation can outweigh the benefits that ECEs can obtain through technological innovation in emissions reduction. Even if speculating can obtain positive returns, it will only involve a part of the enterprise. For example, if ECEs’ emission reduction plan fails to meet carbon quota requirements, the ECE will face high fines and a negative external image. Though the price of FCS is higher than its technical abatement costs, ECEs will still purchase FCS due to time. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “support”, “not purchase”, and “participate”.

5.2.4. Market Imbalance in Short Supply

(1)

In the early stage of the development of forestry carbon neutralization mechanism

In this case, $E_6(1,1,0)$ is ESS, i.e., $C_t^{\prime }>C_t+C_e$ and $\Delta {\pi }_3<0$. Therefore, let $C_g=100$ million, $C_t^{\prime }=5$ billion, $C_t=4.5$ billion, $C_s=1$ billion, $C_e=490$ million, $C_f=80$ million, $M=40$ million, $R_v=500$ million, $\lambda =0.6$, $\alpha =0.5$, and $\phi =1$. The evolution track of the system is shown in Figure 9. As can be seen in Figure 9, market activity is low. On the one hand, the government’s financial subsidy ratio $\phi$ is low. On the other hand, the market-based compensation mechanism is not well developed, and the range of volatility of the overall FCS price can be increased by adjusting the government subsidy M for ECE and the offsettable carbon emission allowances $\theta \tilde{E}$. Then $C_f$ increases. In addition, extra attention needs to be paid at this stage to losses arising from lower-than-expected FCS emission reductions caused by poor operations. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “support”, “purchase”, and “not participate”.

(2)

In the later stage of the development of forestry carbon neutralization mechanism

In this case, $E_3(0,1,0)$ is ESS, i.e., $C_t^{\prime }>C_t+C_e$, $\Delta {\pi }_3-\phi C_b<0$, $R_f-(1-\phi )C_b-R_w+C_w<0$, and $\Delta {\pi }_2<0$. Therefore, let $C_g=100$ million, $C_t^{\prime }=1$ billion, $C_t=900$ million, $C_s=20$ billion, $C_e=95$ million, $C_f=80$ million, $M=10$ million, $R_v=35$ million, $\lambda =0.95$, $\phi =1$, and $\alpha =0.5$. The evolution track of the system is shown in Figure 10. As can be seen from Figure 10, at this stage, the government’s financial subsidies to foresters play a minor role, and the market takes the lead. The supply and demand of FCS are regulated by the market spontaneously. On the one hand, FCS has commodity properties, and therefore it is substitutable. A large misalignment with the price fluctuation cycles of other carbon sink products should be avoided. On the other hand, too much reduction in government subsidies M for ECE or premature removal of them in the process of an upward adjustment of offsettable carbon emission allowances $\theta \tilde{E}$ will reduce foresters’ incentive to participate indirectly. After repeated decision making and long-term evolution, the behaviors of the government, ECEs, and forest farmers tend to “not support”, “purchase”, and “not participate”.

6. Discussion

Based on the above analysis, it can be found that the combination of government financial subsidies with the market mechanism is based on subsidies to ECEs. At present, the research shows that the government’s subsidy for ECEs to purchase FCS should be coordinated with carbon trading policies [23]. However, it does not reveal the specific mechanism and the impact of speculation on the carbon trading market. Based on the above analysis, the combination of government and market mechanisms is concluded in Figure 11.

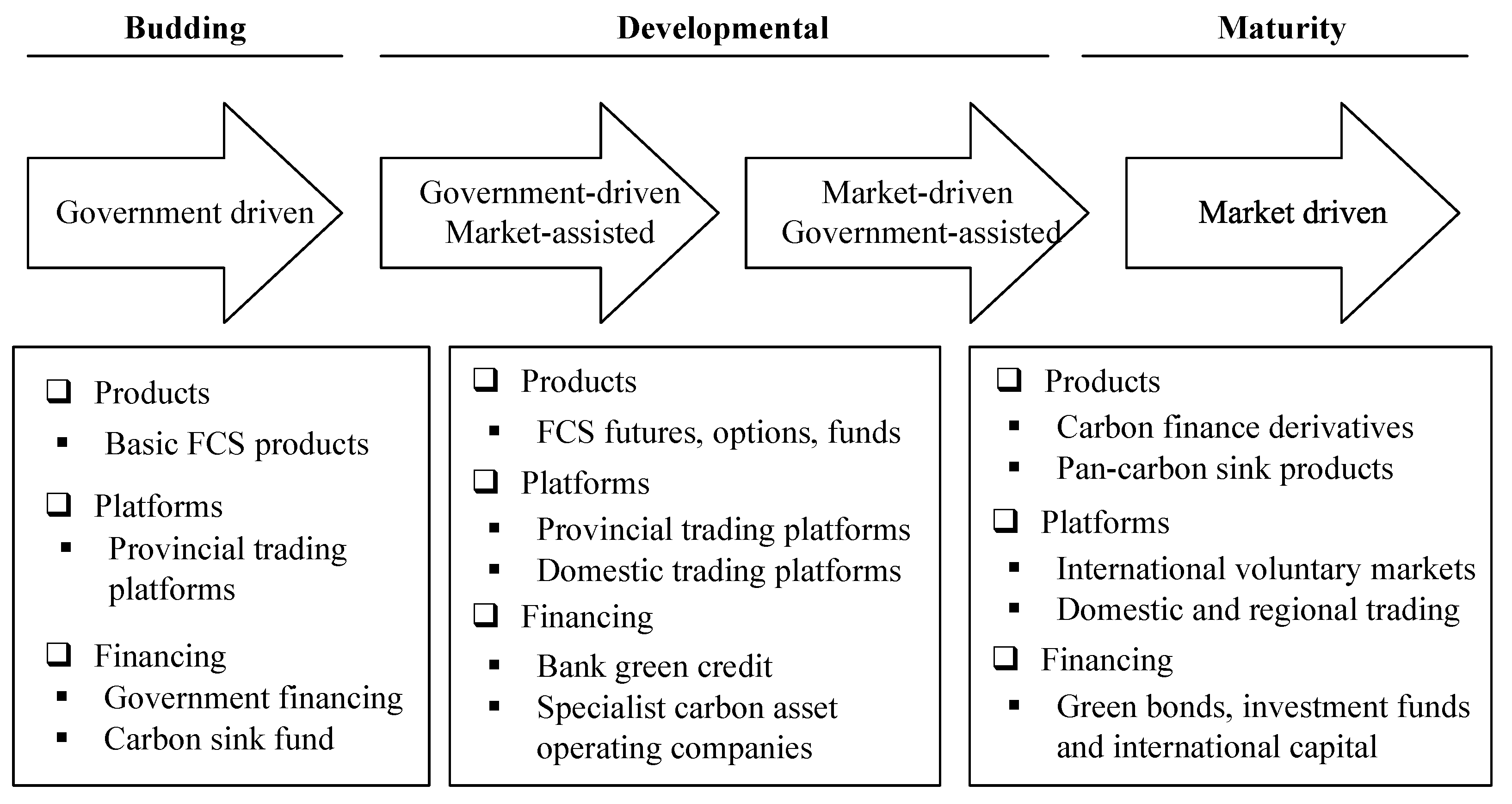
6.1. Transformation Conditions of Forestry Carbon Neutralization Mechanism from Early Stage to Later Stage

(1)

Supply side. With the reduction of government subsidies, the key to the transition from $C_f+R_f-(1-\phi )C_b-R_w+C_w>0$ to $C_f+R_f-C_b-R_w+C_w>0$ is to increase FCS income $C_f$, where $C_f=\theta \tilde{E}{P}_f$. $P_f$ fluctuates with the spontaneous adjustment of the market and is jointly determined by both supply and demand. Moreover, $\theta \tilde{E}$ not only affects $C_f$ directly but also affects $C_f$ indirectly through $P_f$. Therefore, $\theta \tilde{E}$ has the greatest impact.

(2)

Demand side. With the reduction of government subsidies, the key to the transition from $C_f-M<C_t^{\prime }-C_t$ to $C_f<C_t^{\prime }-C_t$ is to increase FCS income $C_f$. $C_f-M<C_t^{\prime }-C_t$, i.e., $P_f-{\displaystyle \frac{M}{\theta \tilde{E}}}<T$, where $\theta \tilde{E}$ is the most important breakthrough, and its changes will affect T and $P_f$.

The key to the transition from early to late market equilibrium is that $(1-\phi )C_b+(R_w-C_w)-R_f<C_f<C_t^{\prime }-C_t+M$ to $C_b+(R_w-C_w)-R_f<C_f<C_t^{\prime }-C_t$. Therefore, $C_f$ connects supply and demand, in which carbon allowances are the key to market equilibrium and transition from the early stage to the later stage. Most studies show that carbon trading should be promoted by adjusting carbon allowance policies [23,31,46], but they do not explain the specific mechanism and the coordination relationship between carbon allowance adjustment and government subsidies. There are two main ways to adjust carbon quotas: (1) Carbon quotas can be tightened. The reduction of $\tilde{E}$ will lead to the increase in emission reduction cost T of ECEs. Since $P_f-{\displaystyle \frac{M}{\theta \tilde{E}}}<T$, when M does not not change, $P_f$ will increase. (2) More industries can be included into the carbon trading system and trade across regions. The increase in $\tilde{E}$ will lead to an increase in emission reduction costs for the group of ECEs. Since $P_f-{\displaystyle \frac{M}{\theta \tilde{E}}}<T$, the sign of $P_f$ is uncertain.

From $C_f=\theta \tilde{E}{P}_f$, it can be found that reducing the government’s financial subsidies to forest farmers gradually is more efficient when implementing the above two carbon quota policies at the same time. In addition, because of the scale effect, if only reducing carbon quotas, ECEs will only rely on technological innovation to achieve emission reduction targets at the cost of the economy. In addition, since $P_f-{\displaystyle \frac{M}{\theta \tilde{E}}}<T$, to maintain an unequal balance in reducing the M subsidy to ECEs, the best time to reduce M is when tightening the carbon allowance policy takes the lead. The impact of carbon allowance policy adjustment is shown in Figure 12.

A combination of supply and demand, until $C_b+(R_w-C_w)-R_f<C_f<C_t^{\prime }-C_t$ exists, which means the price fluctuation range of FCS is ${\displaystyle \frac{C_b+(R_w-C_w)-R_f}{\theta \tilde{E}}}<P_f<T$. At this time, $\phi \to 0$, $M\to 0$, and $\lambda >1-{\displaystyle \frac{M+\phi C_b+C_g}{(R_e+R_s)[\alpha +(1-\alpha )\zeta ]}}\to 1$.

6.2. Reasons for Imbalance in FCS Market

Most studies show that the complexity of project development and the instability of the trading market are the reasons that hinder the development of forestry carbon neutralization mechanism [20,31,35], but they do not analyze the reasons for market imbalances at different stages. In addition, the impact of market risk at different stages of development varies.

Market risk and project development are the most important risk sources in the early stage of the development of the forestry carbon neutralization mechanism. At this time, the government should increase financial subsidies for FCS projects and introduce supporting financing strategies to share financial pressures. An FCS transaction has three characteristics of high asset specificity, high uncertainty, and low transaction frequency based on transaction cost theory, which leads to higher FCS transaction costs than other CCER projects [47]. (1) The dedicated assets of FCS projects cannot be used for other purposes, so the cost of assets includes “irretrievable costs” or “sunk costs”. (2) The credit period of FCS projects is 20–60 years, which means that the longer the project period, the higher the risks of policies, markets, and natural disasters. (3) Transactions can only be carried out after regular monitoring, certification, and issuance. Therefore, the trading frequency of FCS is relatively low, which cannot bring benefits in time to make up for the early development costs.

Market risk and operational risk are the most important risk sources in the later stage of the development of the forestry carbon neutralization mechanism. (1) Market risk: The adjustment of carbon quotas needs to be coordinated with government support, which is also the key to the transition from the early stage to the later stage. (2) Operational risk: In the case of high demand in the later period, if the FCS is much lower than expected, it will lead to a supply fault and affect the balance of the market.

Based on the above comparative analysis of different stages, we can obtain the following main results. (1) The steady state of oversupply only occurs in the early stages of the forestry carbon neutralization mechanism when high government subsidies can maintain the supply of FCS. However, it is unable to achieve market-based compensation. Therefore, the market equilibrium cannot achieve an effective transition to the later stages. (2) The reasons for the stable state of oversupply differ between the early and late stages of the development of the forestry carbon neutralization mechanism. The demand and price of FCS are lower in the early stages of the development of the forestry carbon neutralization mechanism, Moreover, risk-averse foresters will choose not to participate in FCS projects because FCS projects have high transaction risk and operational risk due to their long cycle. In addition, due to the unstable supply of FCS, it is difficult to ensure that FCS has a cost advantage over other carbon sink products while ensuring that foresters are profitable. In the later stages of the development of the forestry carbon neutralization mechanism, the market plays a dominant role, and the reasons for the oversupply are the increase in demand under the tightening of carbon quotas and the foresters’ management problems with the forests. In summary, the essential cause of market imbalance in either case is $P_f-{\displaystyle \frac{M}{\theta \tilde{E}}}>T$, i.e., $C_f-M>C_t^{\prime }-C_t$.

7. Conclusions and Policy Implications

This paper executes a game analysis of the dynamic evolution process of FCS trading. We find the following main conclusions.

(1)

The government plays a leading role in the early development of the forestry carbon neutralization mechanism, and market risk and project development are critical. The government’s incentive to participate plays an important role in the regulation of market behavior. Firstly, financial subsidies make up for some of the high development costs for forest farmers; purchasing FCS can obtain corresponding subsidies and positive external effects for ECEs. Secondly, the cost of purchasing FCS by ECEs is close to their technical emission reduction costs, which is a turning point in the market’s spontaneous adjustment. Therefore, at this stage, the government’s subsidies to ECEs have increased the purchase willingness of ECEs and the fluctuation range of the overall price of FCS.

(2)

The key to the transition of the forestry carbon neutralization mechanism from the early stage to the later stage is to increase the FCS income by adjusting the carbon quota policy. Tightening carbon quotas can increase the price of FCS indirectly; including more industries in the carbon trading system can increase the number of transactions directly. Therefore, reducing the government’s financial subsidies to forest farmers gradually is more efficient when implementing the above two carbon quota policies at the same time, and the best time to reduce financial subsidies to ECEs is when tightening the carbon allowance policy takes the lead. The market plays a leading role in the late stage of forestry carbon neutralization mechanism development, and market risk and operational risk are the keys. At this time, the price cap of FCS is only related to the emission reduction cost of ECEs.

(3)

The steady state of oversupply of FCS will occur only in the early stage. The essential reason for the oversupply is that the cost of ECEs purchasing FCS is higher than the cost of technical emission reduction. The reason for the shortage of supply in the early stage is the negative supply of forest farmers driven by profit. On the one hand, the financial subsidy is low; on the other hand, the demand and price are low, and participation has high transaction risks and operational risks due to the long-term cycle. In addition, it is difficult to guarantee the cost advantage of FCS compared with other carbon sink products when FCS cannot be supplied stably. The reason for the shortage of supply in the later stage is the relationship between the increase in carbon allowances and the reduction in ECEs purchase subsidies when more industries are included in carbon trading.

This paper clarified the conditions for the existence of equilibrium in FCS markets and the causes of market imbalances. It still has some limitations. Firstly, the development and trading of FCS is the most critical stage that affects its emission reduction effect. With the increase in FCS fever, more and more enterprises are getting involved in developing FCS projects. However, most companies promise unrealistic conditions and sign a large number of cooperative development contracts with forestry units, which are subsequently subcontracted to companies with lower development strength, disrupting the market order and reducing foresters’ willingness to participate. Future research could therefore incorporate the transaction and development phases into the same system and analyze the coupling between the different segments and how risks can be mitigated. Secondly, this paper examines the synergy of policies at different stages of development from a dynamic evolutionary perspective, while prices guide supply and demand, and different policies drive prices from different perspectives. Therefore, the impact of different policy changes on the mean and variance of prices can be studied in the future. Finally, as China’s FCS started late and relevant data is scarce, future research can build on the analysis of this paper’s model to design further studies to assess the specific implementation effects of the policy and angles for improvement.