Estimating Carbon Stocks and Biomass Expansion Factors of Urban Greening Trees Using Terrestrial Laser Scanning
Abstract
:1. Introduction
2. Materials and Methods
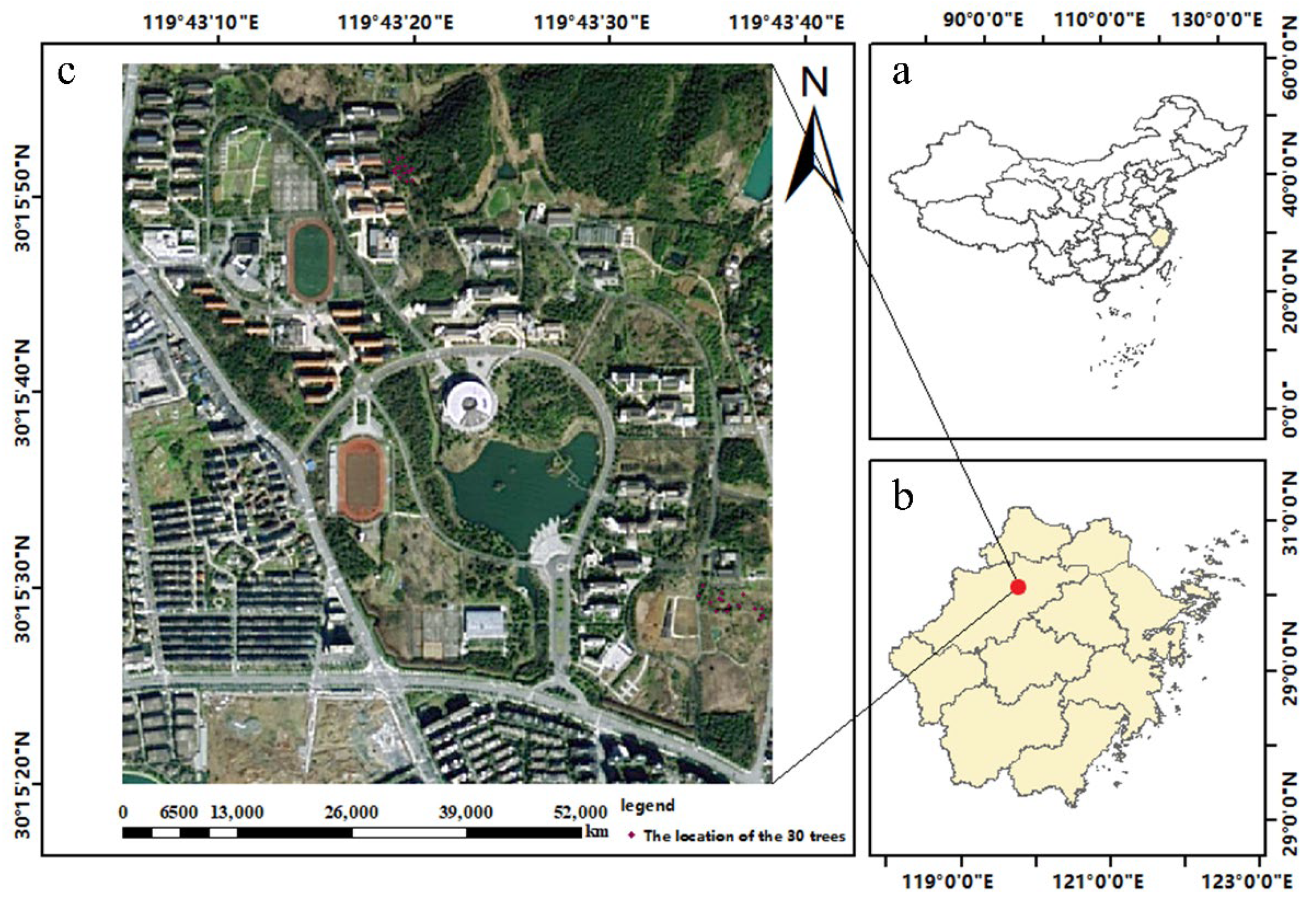
2.1. Study Area and Instrumentation
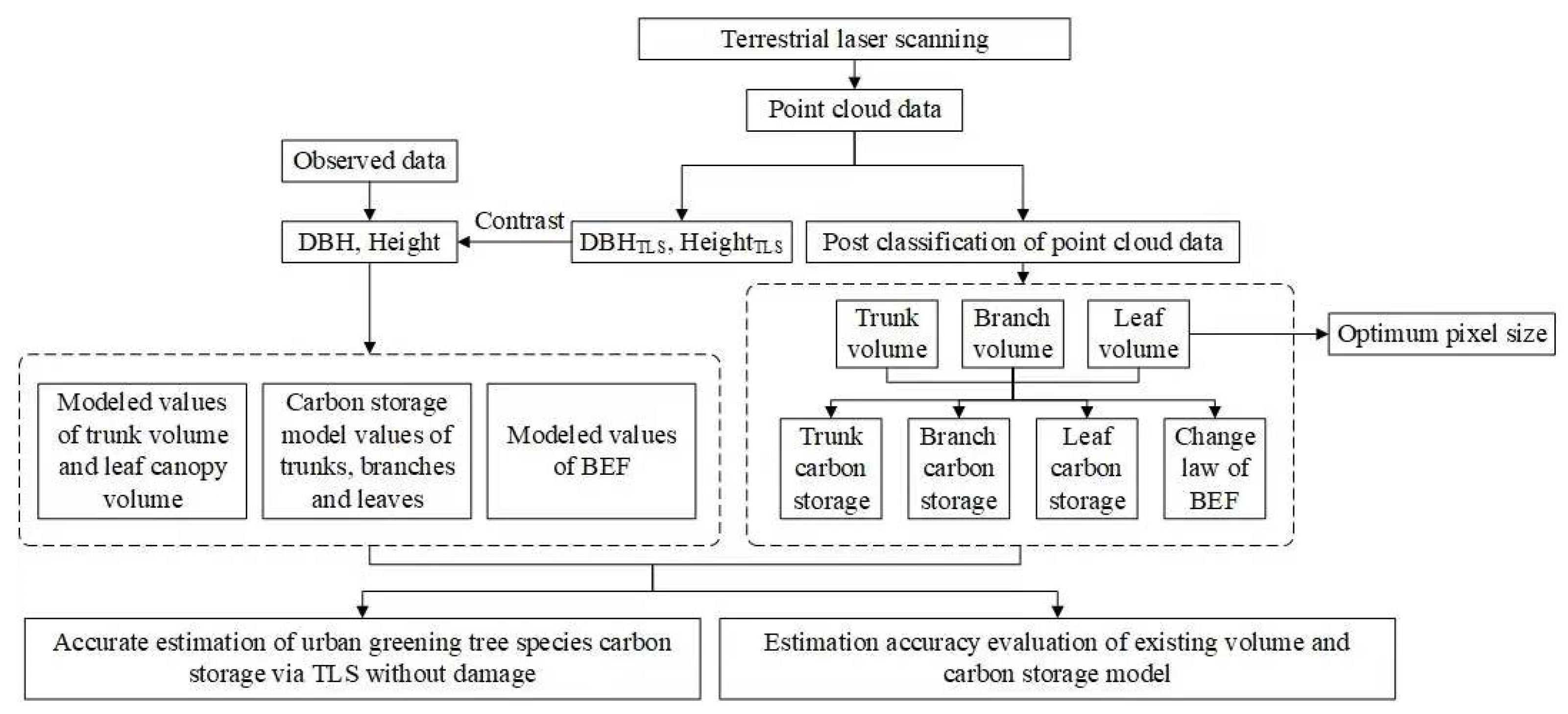
2.2. Research Technique
2.3. Data Acquisition
2.3.1. Single-Stand Point Cloud Data Acquisition
2.3.2. Sample Collection
- (1)
- Trunk sample collection
- (2)
- Crown sample collection
2.4. Data Pre-Processing
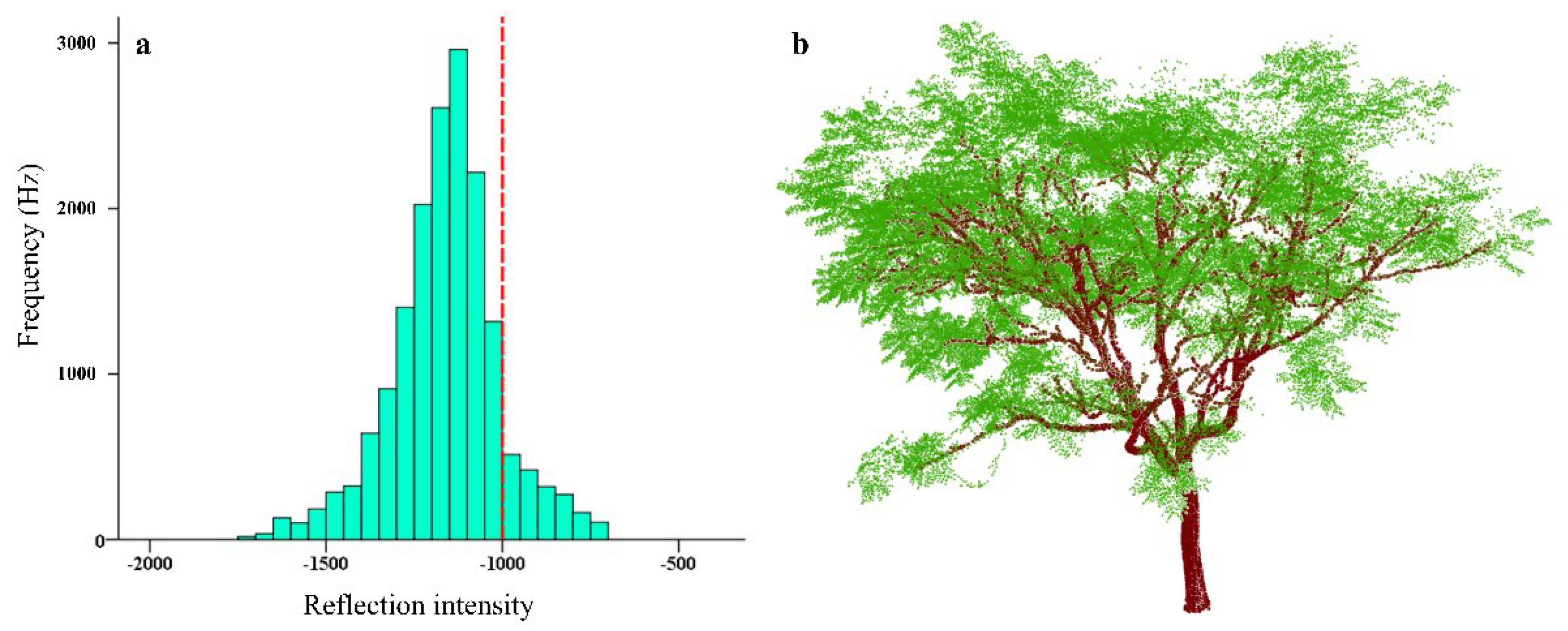
2.4.1. Point Cloud Data
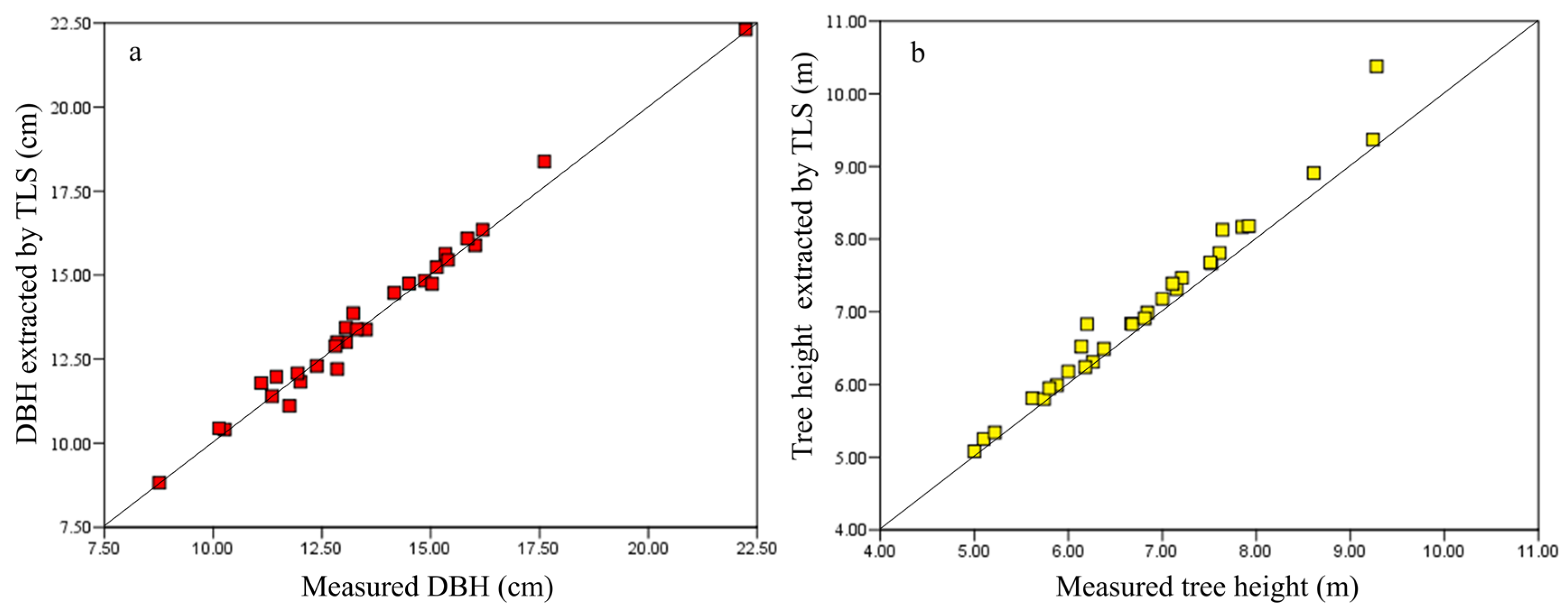
2.4.2. Tree Measurement Factors
2.4.3. Voxel Size
2.5. Measurement Methods
2.5.1. TLS-Derived Carbon Stock Measurements
- Calculation of trunk carbon stock
- 2.
- Calculation of branch carbon stock
- 3.
- Calculation of leaf carbon stock
2.5.2. Volume and Carbon Storage Model Measurements
- Trunk and canopy volume model measurement methods
- 2.
- Carbon stocks of various organs model measurement methods
2.5.3. BEF Measurement
2.5.4. Analysis of Variance and Accuracy Assessment Methods
3. Results
3.1. Comparative Analysis of Basic Tree Measurement Factors
3.2. Analysis of Trunk Volume and Carbon Stocks Measured by Different Methods
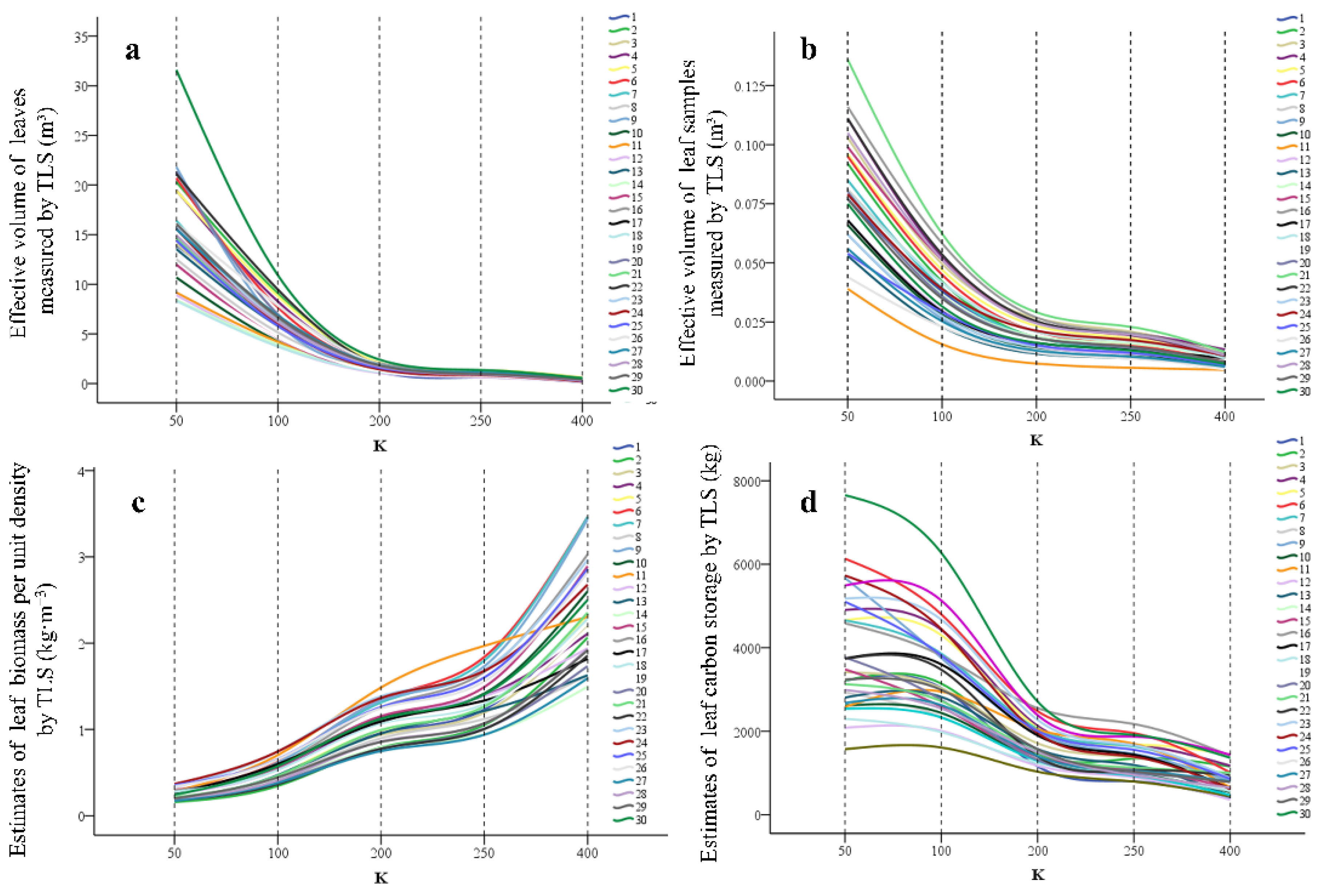
3.3. Leaf Volume and Carbon Stock Based on TLS Measurements
3.4. Analysis of Canopy Volume and Carbon Stock Calculated by Different Methods
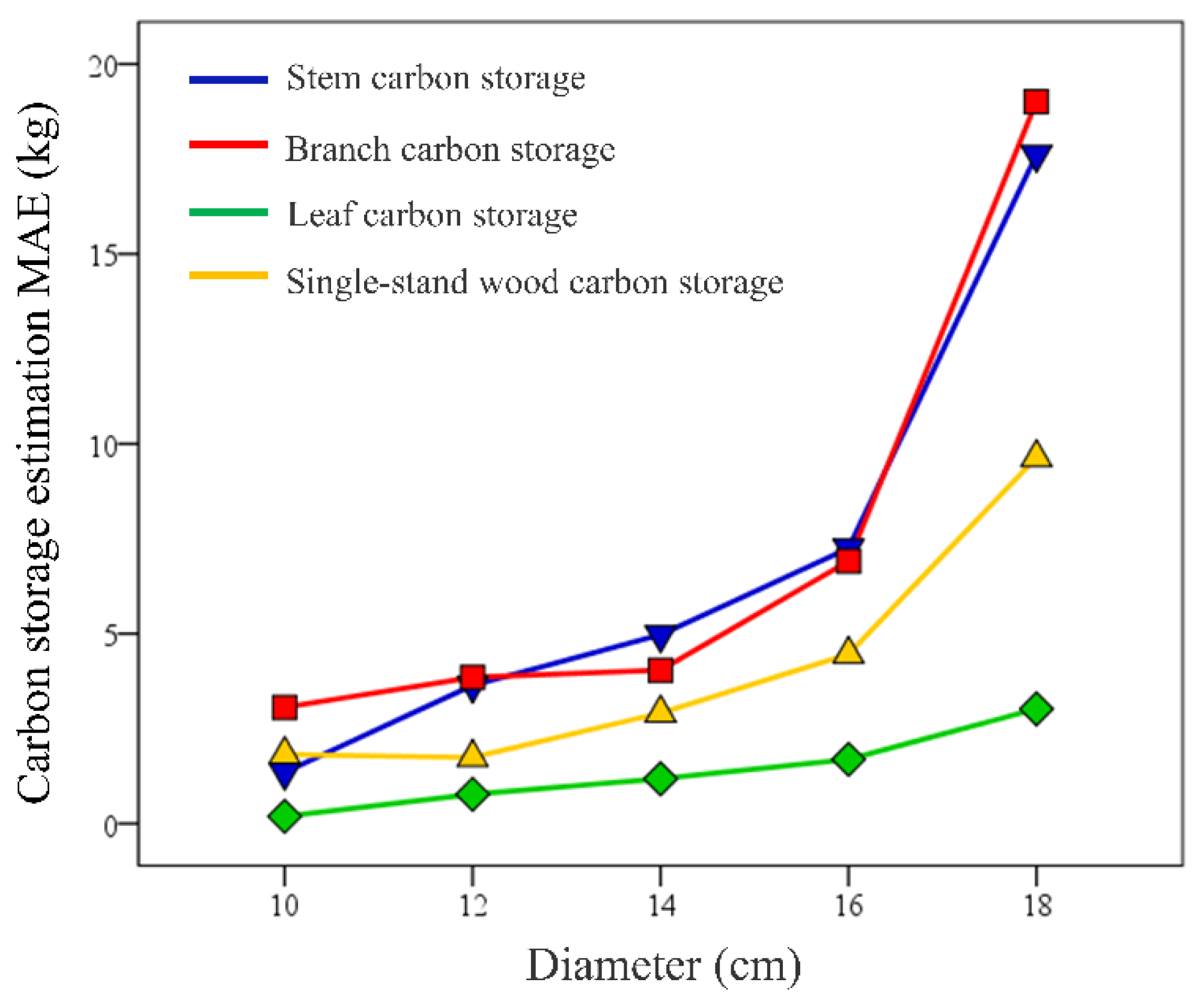
3.5. Estimating Carbon Stocks of Individual Organs and Individual Trees by Different Methods
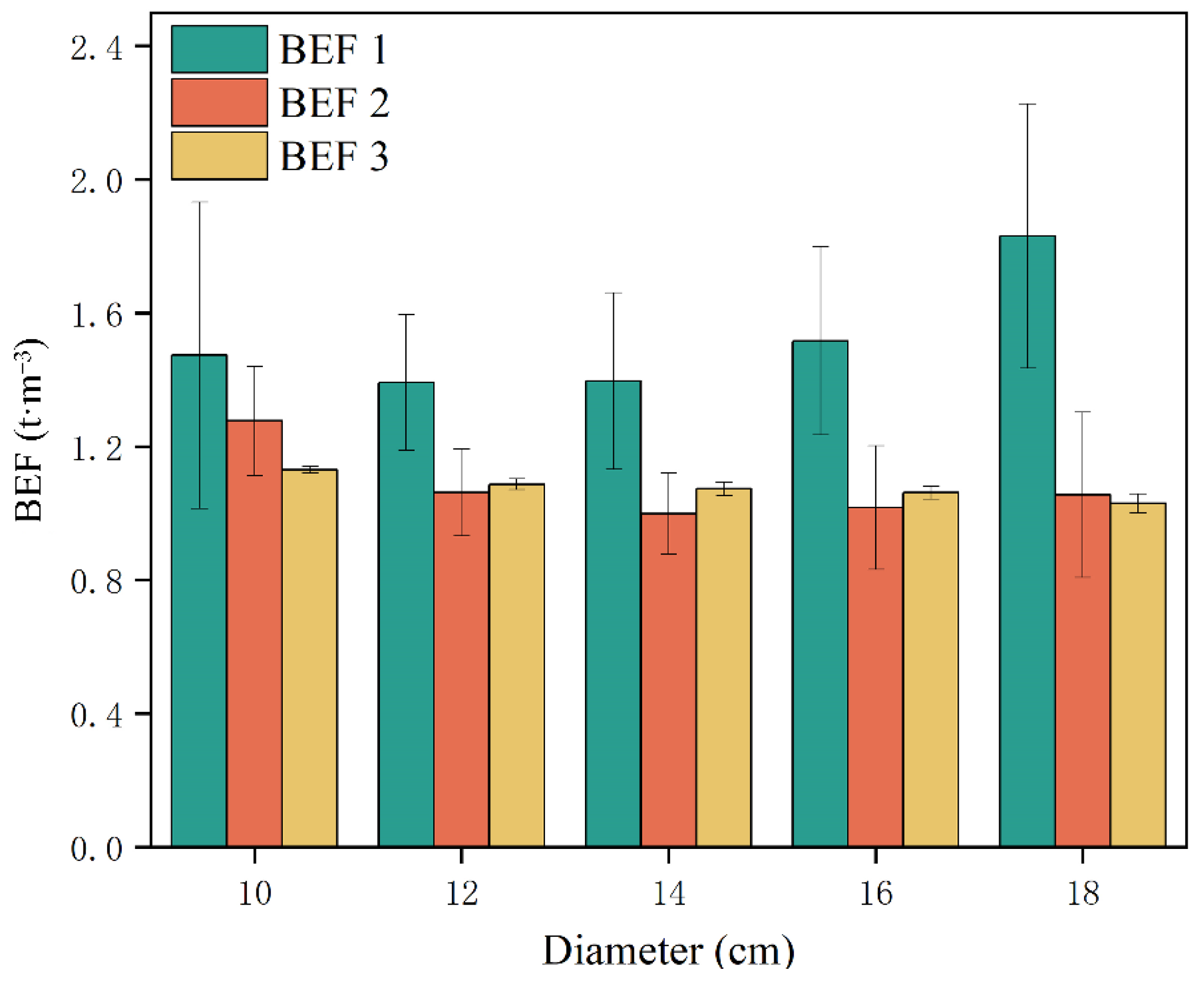
3.6. Measurement and Analysis of BEF by Different Methods
3.6.1. Comparison of Different BEF Measurement Methods
3.6.2. Accuracy Comparison of Carbon Stocks Measured by Different BEF
3.6.3. Correlation Analysis of BEF and Tree Measurement Factors
4. Discussion
4.1. TLS-Based Carbon Stock Measurements
4.2. Differences in the Accuracy of Trunk Carbon Stocks by Model
4.3. Leaf Carbon Stocks Influenced by the Voxel Size
4.4. Differences between Urban Greening Tree Species and Wild Stands
4.5. TLS Accuracy in Measuring Wood Volume, Carbon Stocks, and BEF of Urban Greening Trees
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Díaz-Porras, D.F.; Gaston, K.J.; Evans, K.L. 110 Years of Change in Urban Tree Stocks and Associated Carbon Storage. Ecol. Evol. 2014, 4, 1413–1422. [Google Scholar] [CrossRef] [PubMed]
- Soulé, M.; Kyereh, B.; Kuyah, S.; Tougiani, A.; Saadou, M. Azadirachta Indica A. Juss. a Multi-Purpose Tree as a Leading Species in Carbon Stocking in Two Sahelian Cities of Niger. Urban Ecosyst. 2022, 25, 51–64. [Google Scholar] [CrossRef]
- Pregitzer, C.C.; Hanna, C.; Charlop-Powers, S.; Bradford, M.A. Estimating Carbon Storage in Urban Forests of New York City. Urban Ecosyst. 2022, 25, 617–631. [Google Scholar] [CrossRef]
- Li, X.; Yi, M.J.; Son, Y.; Park, P.S.; Lee, K.H.; Son, Y.M.; Kim, R.H.; Jeong, M.J. Biomass Expansion Factors of Natural Japanese Red Pine (Pinus Densiflora) Forests in Korea. J. Plant Biol. 2010, 53, 381–386. [Google Scholar] [CrossRef]
- Muumbe, T.P.; Baade, J.; Singh, J.; Schmullius, C.; Thau, C. Terrestrial Laser Scanning for Vegetation Analyses with a Special Focus on Savannas. Remote Sens. 2021, 13, 507. [Google Scholar] [CrossRef]
- Stovall, A.E.L.; Vorster, A.G.; Anderson, R.S.; Evangelista, P.H.; Shugart, H.H. Non-Destructive Aboveground Biomass Estimation of Coniferous Trees Using Terrestrial LiDAR. Remote Sens. Environ. 2017, 200, 31–42. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest Inventory with Terrestrial LiDAR: A Comparison of Static and Hand-Held Mobile Laser Scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Brown, S.L.; Schroeder, P.; Kern, J.S. Spatial Distribution of Biomass in Forests of the Eastern USA. For. Ecol. Manag. 1999, 123, 81–90. [Google Scholar] [CrossRef]
- Fang, J.; Wang, G.G.; Liu, G.; Xu, S. Forest Biomass of China: An Estimate Based on the Biomass–Volume Relationship. Ecol. Appl. 1998, 8, 1084–1091. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial Laser Scanning in Forest Inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Qiu, T.; Song, C.; Zhang, Y.; Liu, H.; Vose, J.M. Urbanization and Climate Change Jointly Shift Land Surface Phenology in the Northern Mid-Latitude Large Cities. Remote Sens. Environ. 2020, 236, 111477. [Google Scholar] [CrossRef]
- Jiang, M.; He, Y.; Song, C.; Pan, Y.; Qiu, T.; Tian, S. Disaggregating Climatic and Anthropogenic Influences on Vegetation Changes in Beijing-Tianjin-Hebei Region of China. Sci. Total Environ. 2021, 786, 147574. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X. TLS Laser Intensity Correction Based on Polynomial Model. Zhongguo Jiguang Chin. J. Lasers 2015, 42, 314002. [Google Scholar] [CrossRef]
- Ma, J.; Li, X.; Baoquan, J.; Liu, X.; Li, T.; Zhang, W.; Liu, W. Spatial Variation Analysis of Urban Forest Vegetation Carbon Storage and Sequestration in Built-up Areas of Beijing Based on i-Tree Eco and Kriging. Urban For. Urban Green. 2021, 66, 127413. [Google Scholar] [CrossRef]
- Boucher, P.B.; Paynter, I.; Orwig, D.A.; Valencius, I.; Schaaf, C. Sampling Forests with Terrestrial Laser Scanning. Ann. Bot. 2021, 128, 689–708. [Google Scholar] [CrossRef]
- Gao, X.; Li, C.; Cai, Y.; Ye, L.; Xiao, L.; Zhou, G.; Zhou, Y. Influence of Scale Effect of Canopy Projection on Understory Microclimate in Three Subtropical Urban Broad-Leaved Forests. Remote Sens. 2021, 13, 3786. [Google Scholar] [CrossRef]
- Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning. Remote Sens. 2020, 12, 2672. [Google Scholar] [CrossRef]
- Wang, F.; Lin, H.; Changhui, L.I. Application of Terrestrial 3D Laser Scanning Technology in Urban Surveying. Bull. Surv. Mapp. 2012, 9, 47–49. [Google Scholar]
- Hauglin, M.; Gobakken, T.; Astrup, R.; Ene, L.; Næsset, E. Estimating Single-Tree Crown Biomass of Norway Spruce by Airborne Laser Scanning: A Comparison of Methods with and without the Use of Terrestrial Laser Scanning to Obtain the Ground Reference Data. Forests 2014, 5, 384–403. [Google Scholar] [CrossRef]
- Sanz, R.; Rosell, J.R.; Llorens, J.; Gil, E.; Planas, S. Relationship between Tree Row LIDAR-Volume and Leaf Area Density for Fruit Orchards and Vineyards Obtained with a LIDAR 3D Dynamic Measurement System. Agric. For. Meteorol. 2013, 171–172, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; De Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Indirabai, I.; Nair, M.V.H.; Jaishanker, R.N.; Nidamanuri, R.R. Terrestrial Laser Scanner Based 3D Reconstruction of Trees and Retrieval of Leaf Area Index in a Forest Environment. Ecol. Inform. 2019, 53, 100986. [Google Scholar] [CrossRef]
- Sun, J.; Wang, P.; Gao, Z.; Liu, Z.; Li, Y.; Gan, X.; Liu, Z. Wood–Leaf Classification of Tree Point Cloud Based on Intensity and Geometric Information. Remote Sens. 2021, 13, 4050. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, W.; Wang, Q.; Huang, X. Deriving Individual-Tree Biomass from Effective Crown Data Generated by Terrestrial Laser Scanning. Remote Sens. 2019, 11, 2793. [Google Scholar] [CrossRef]
- Han, G.S.; Feng, Z.K.; Liu, Y.X.; Wang, X.K. Tree measurement principle and accuracy analysis of three-dimensional laser scanning system. J. Beijing For. Univ. 2005, S2, 187–190. (In Chinese) [Google Scholar]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass Estimation Methods for Tropical Forests with Applications to Forest Inventory Data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
- Deng, X.R.; Feng, Z.K.; Luo, X. Application of three-dimensional laser scanning system in forestry. J. Beijing For. Univ. 2005, 27, 43–47. (In Chinese) [Google Scholar]
- Li, F.; Li, M.; Feng, X. High-Precision Method for Estimating the Three-Dimensional Green Quantity of an Urban Forest. J. Indian Soc. Remote Sens. 2021, 49, 1407–1417. [Google Scholar] [CrossRef]
- Heinzel, J.; Huber, M.O. Detecting Tree Stems from Volumetric TLS Data in Forest Environments with Rich Understory. Remote Sens. 2017, 9, 9. [Google Scholar] [CrossRef]
- Feng, Z.K.; Luo, X.; Ma, Q.Y.; Hao, X.; Chen, X.; Zhao, L. An Estimation of Tree Canopy Biomass Based on 3D Laser Scanning Imaging System. J. Beijing For. Univ. 2007, 29, 52–56. (In Chinese) [Google Scholar]
- Lin, W.; Meng, Y.; Qiu, Z.; Zhang, S.; Wu, J. Measurement and Calculation of Crown Projection Area and Crown Volume of Individual Trees Based on 3D Laser-Scanned Point-Cloud Data. Int. J. Remote Sens. 2017, 38, 1083–1100. [Google Scholar] [CrossRef]
- Chen, S.; Feng, Z.; Chen, P.; Khan, T.U.; Lian, Y. Nondestructive Estimation of the Above-Ground Biomass of Multiple Tree Species in Boreal Forests of China Using Terrestrial Laser Scanning. Forests 2019, 10, 936. [Google Scholar] [CrossRef]
- Brolly, G.; Kiraly, G. Algorithms for Stem Mapping by Means of Terrestrial Laser Scanning. Acta Silv. Lignaria Hung. 2009, 5, 119–130. [Google Scholar]
- Lalonde, J.F.; Vandapel, N.; Hebert, M. Automatic Three-Dimensional Point Cloud Processing for Forest Inventory; CMU-RI-TR-06-21; Carnegie Mellon University: Pittsburgh, PA, USA, 2006; pp. 1–16. [Google Scholar]
- Tanhuanpää, T.; Kankare, V.; Setälä, H.; Yli-Pelkonen, V.; Vastaranta, M.; Niemi, M.T.; Raisio, J.; Holopainen, M. Assessing Above-Ground Biomass of Open-Grown Urban Trees: A Comparison between Existing Models and a Volume-Based Approach. Urban For. Urban Green. 2017, 21, 239–246. [Google Scholar] [CrossRef] [Green Version]
- Abd Rahman, M.Z.; Abu Bakar, M.A.; Razak, K.A.; Rasib, A.W.; Kanniah, K.D.; Wan Kadir, W.H.; Omar, H.; Faidi, A.; Kassim, A.R.; Abd Latif, Z. Non-Destructive, Laser-Based Individual Tree Aboveground Biomass Estimation in a Tropical Rainforest. Forests 2017, 8, 86. [Google Scholar] [CrossRef]
- Hu, M.; Pitkänen, T.P.; Minunno, F.; Tian, X.; Lehtonen, A.; Mäkelä, A. A New Method to Estimate Branch Biomass from Terrestrial Laser Scanning Data by Bridging Tree Structure Models. Ann. Bot. 2021, 128, 737–752. [Google Scholar] [CrossRef]
- Estornell, J.; Velázquez-Martí, B.; Fernández-Sarría, A.; Martí, J. Lidar Methods for Measurement of Trees in Urban Forests. J. Appl. Remote Sens. 2018, 12, 1–17. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- de Conto, T.; Olofsson, K.; Görgens, E.B.; Rodriguez, L.C.E.; Almeida, G. Performance of Stem Denoising and Stem Modelling Algorithms on Single Tree Point Clouds from Terrestrial Laser Scanning. Comput. Electron. Agric. 2017, 143, 165–176. [Google Scholar] [CrossRef]
- Hu, H.Q.; Luo, B.Z.; Wei, S.J.; Wei, S.W.; Sun, L.; Luo, S.S.; Ma, H.B. Biomass Carbon Density and Carbon Sequestration Capacity in Seven Typical Forest Types of the Xiaoxing’an Mountains, China. Chin. J. Plant Ecol. 2015, 39, 140–158. (In Chinese) [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kankare, V.; Holopainen, M. Stem Curve Measurement Using Terrestrial Laser Scanning. In Proceedings of the 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Tasmania, Australia, 16–20 October 2011; pp. 1–6. [Google Scholar]
- Zheng, G.; Ma, L.; He, W.; Eitel, J.U.H.; Moskal, L.M.; Zhang, Z. Assessing the Contribution of Woody Materials to Forest Angular Gap Fraction and Effective Leaf Area Index Using Terrestrial Laser Scanning Data. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1475–1487. [Google Scholar] [CrossRef]
- Donovan, S.D.; MacLean, D.A.; Kershaw, J.A.; Lavigne, M.B. Quantification of Forest Canopy Changes Caused by Spruce Budworm Defoliation Using Digital Hemispherical Imagery. Agric. For. Meteorol. 2018, 262, 89–99. [Google Scholar] [CrossRef]
- Seidel, D.; Fleck, S.A.; Suarez, L.; Jones, S.D.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M. Validating Canopy Clumping Retrieval Methods Using Hemispherical Photography in a Simulated Eucalypt Forest. Agric. For. Meteorol. 2017, 247, 181–193. [Google Scholar] [CrossRef]
- Li, H.K.; Lei, Y.C. Estimation of Forest Vegetation Biomass and Carbon Storage in China; China Forestry Publishing House: Beijing, China, 2010; pp. 26–29. [Google Scholar]
- Fang, J.Y.; Chen, A.P.; Zhao, S.Q.; Ci, L.J. Estimating Biomass Carbon of China’s Forests: Supplementary Notes on Report Published in Science (291:2320−2322) by Fang et al. (2001). J. Plant Ecol. 2002, 26, 243–249. (In Chinese) [Google Scholar]
- Xu, S.Y.; Shi, Y.J.; Feng, S.G. Nondestructive and Accurate Measurement of Volume and Stem Carbon storage for Urban Greening Tree Species Based on Terrestrial Laser Scanning Point Cloud. J. Zhejiang AF Univ. 2018, 35, 1062–1069. (In Chinese) [Google Scholar] [CrossRef]
- Witzmann, S.; Matitz, L.; Gollob, C.; Ritter, T.; Kraßnitzer, R.; Tockner, A.; Stampfer, K.; Nothdurft, A. Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation. Remote Sens. 2022, 14, 1923. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A. Reliable Estimates of Merchantable Timber Volume from Terrestrial Laser Scanning. Remote Sens. 2021, 13, 3610. [Google Scholar] [CrossRef]
- Luck, L.; Hutley, L.B.; Calders, K.; Levick, S.R. Exploring the Variability of Tropical Savanna Tree Structural Allometry with Terrestrial Laser Scanning. Remote Sens. 2020, 12, 3893. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual Tree Biomass Estimation Using Terrestrial Laser Scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Wei, X.H.; Wang, Y.G.; Zheng, J.; Wang, M.; Feng, Z.K. Calculation method of canopy volume based on 3D laser scanning point cloud. Trans. Chin. Soc. Agric. Mach. 2013, 7, 235–240. (In Chinese) [Google Scholar]
- Schraik, D.; Hovi, A.; Rautiainen, M. Crown Level Clumping in Norway Spruce from Terrestrial Laser Scanning Measurements. Agric. For. Meteorol. 2021, 296, 108238. [Google Scholar] [CrossRef]
- Herold, A.; Zell, J.; Rohner, B.; Didion, M.; Thürig, E.; Rösler, E. State and Change of Forest Resources. In Swiss National Forest Inventory–Methods and Models of the Fourth Assessment; Springer: Berlin/Heidelberg, Germany, 2019; pp. 205–230. [Google Scholar]
- McHale, M.R.; Burke, I.C.; Lefsky, M.A.; Peper, P.J.; McPherson, E.G. Urban Forest Biomass Estimates: Is It Important to Use Allometric Relationships Developed Specifically for Urban Trees? Urban Ecosyst. 2009, 12, 95–113. [Google Scholar] [CrossRef]
- Velasco, E.; Chen, K.W. Carbon Storage Estimation of Tropical Urban Trees by an Improved Allometric Model for Aboveground Biomass Based on Terrestrial Laser Scanning. Urban For. Urban Green. 2019, 44, 126387. [Google Scholar] [CrossRef]
- Dhyani, S.; Singh, A.; Gujre, N.; Joshi, R.K. Quantifying Tree Carbon Stock in Historically Conserved Seminary Hills Urban Forest of Nagpur, India. Acta Ecol. Sin. 2021, 41, 193–203. [Google Scholar] [CrossRef]
- Shi, Y. Vegetation Structure Characteristics and Carbon Uptake of Urban Built-Up Area in China; Zhejiang University: Hangzhou, China, 2013. (In Chinese) [Google Scholar]
- Ji, H.X.; Shi, Y.; Zhu, Y.M. Tree growth and carbon sequestration in different land-use types in Hangzhou City. Chin. J. Ecol. 2011, 11, 2405–2412. (In Chinese) [Google Scholar]
- Nowak, D.J.; Greenfield, E.J.; Hoehn, R.E.; Lapoint, E. Carbon Storage and Sequestration by Trees in Urban and Community Areas of the United States. Environ. Pollut. 2013, 178, 229–236. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Sun, X.; Xu, S.; Hua, W.; Tian, J.; Xu, Y. Feasibility Study on the Estimation of the Living Vegetation Volume of Individual Street Trees Using Terrestrial Laser Scanning. Urban For. Urban Green. 2022, 71, 127553. [Google Scholar] [CrossRef]
- Côté, J.-F.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. The structural and radiative consistency of three-dimensional tree reconstructions from terrestrial lidar. Remote Sens. Environ. 2009, 113, 1067–1081. [Google Scholar] [CrossRef]




| Methods | Volume·dm−3 | Carbon Stock·kg−1 |
|---|---|---|
| TLS_0.1 m sectional measurement | 37.61 ± 11.01 c | 12.26 ± 5.71 d |
| TLS_1.0 m sectional measurement | 40.22 ± 11.49 c | 13.11 ± 5.64 cd |
| One- dimensional volume model | 69.12 ± 34.67 ab | 21.89 ± 10.67 a |
| Binary volume model | 53.12 ± 30.86 b | 16.98 ± 10.11 bc |
| Carbon stock model | NA | 17.89 ± 9.62 bc |
| Calculation Method | Canopy Volume·m−3 | Canopy Carbon Stock·kg−1 |
|---|---|---|
| Canopy volume model | 20.24 ± 11.87 a | 3.52 ± 1.81 b |
| k = 100 voxel | 6.63 ± 1.79 b | 2.48 ± 0.86 b |
| Branch and leaf (k = 100 voxel) were calculated separately | 6.63 ± 1.79 b | 14.26 ± 8.94 a |
| Measured Value of TLS (kg) | Model Values (kg) | t | p | RMSE (kg) | Bias (kg) | |
|---|---|---|---|---|---|---|
| Trunk | 12.26 ± 5.71 | 17.89 ± 9.62 | −2.729 | 0.008 | 7.08 | −5.53 |
| Branch | 12.49 ± 8.22 | 7.01 ± 4.26 | −2.310 | 0.024 | 6.55 | 5.11 |
| Leaf | 1.82 ± 0.71 | 2.96 ± 1.27 | −4.102 | 0.001 | 1.47 | −1.16 |
| Single tree | 26.79 ± 13.82 | 27.91 ± 15.16 | −0.309 | 0.756 | 4.36 | −1.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Shi, Y.; Zhang, F.; Zhou, Y.; Ding, Z.; Lv, S.; Xu, L. Estimating Carbon Stocks and Biomass Expansion Factors of Urban Greening Trees Using Terrestrial Laser Scanning. Forests 2022, 13, 1389. https://doi.org/10.3390/f13091389
Wu L, Shi Y, Zhang F, Zhou Y, Ding Z, Lv S, Xu L. Estimating Carbon Stocks and Biomass Expansion Factors of Urban Greening Trees Using Terrestrial Laser Scanning. Forests. 2022; 13(9):1389. https://doi.org/10.3390/f13091389
Chicago/Turabian StyleWu, Linlin, Yongjun Shi, Fanyi Zhang, Yufeng Zhou, Zhentian Ding, Shixin Lv, and Lin Xu. 2022. "Estimating Carbon Stocks and Biomass Expansion Factors of Urban Greening Trees Using Terrestrial Laser Scanning" Forests 13, no. 9: 1389. https://doi.org/10.3390/f13091389
APA StyleWu, L., Shi, Y., Zhang, F., Zhou, Y., Ding, Z., Lv, S., & Xu, L. (2022). Estimating Carbon Stocks and Biomass Expansion Factors of Urban Greening Trees Using Terrestrial Laser Scanning. Forests, 13(9), 1389. https://doi.org/10.3390/f13091389






