Semi-Empirical Models and Revision of Predicting Approaches of Tree Aboveground Biomass Assessments
Abstract
1. Introduction
2. Materials and Methods
2.1. Tree Aboveground Biomass Allometric Models
2.1.1. The Conventional Allometric Model
2.1.2. The Fractal Model
2.2. Bio-Physics of Volume and Mass of Tree Boles
2.2.1. Shapes of Tree Boles
2.2.2. Ontogenetic Principles
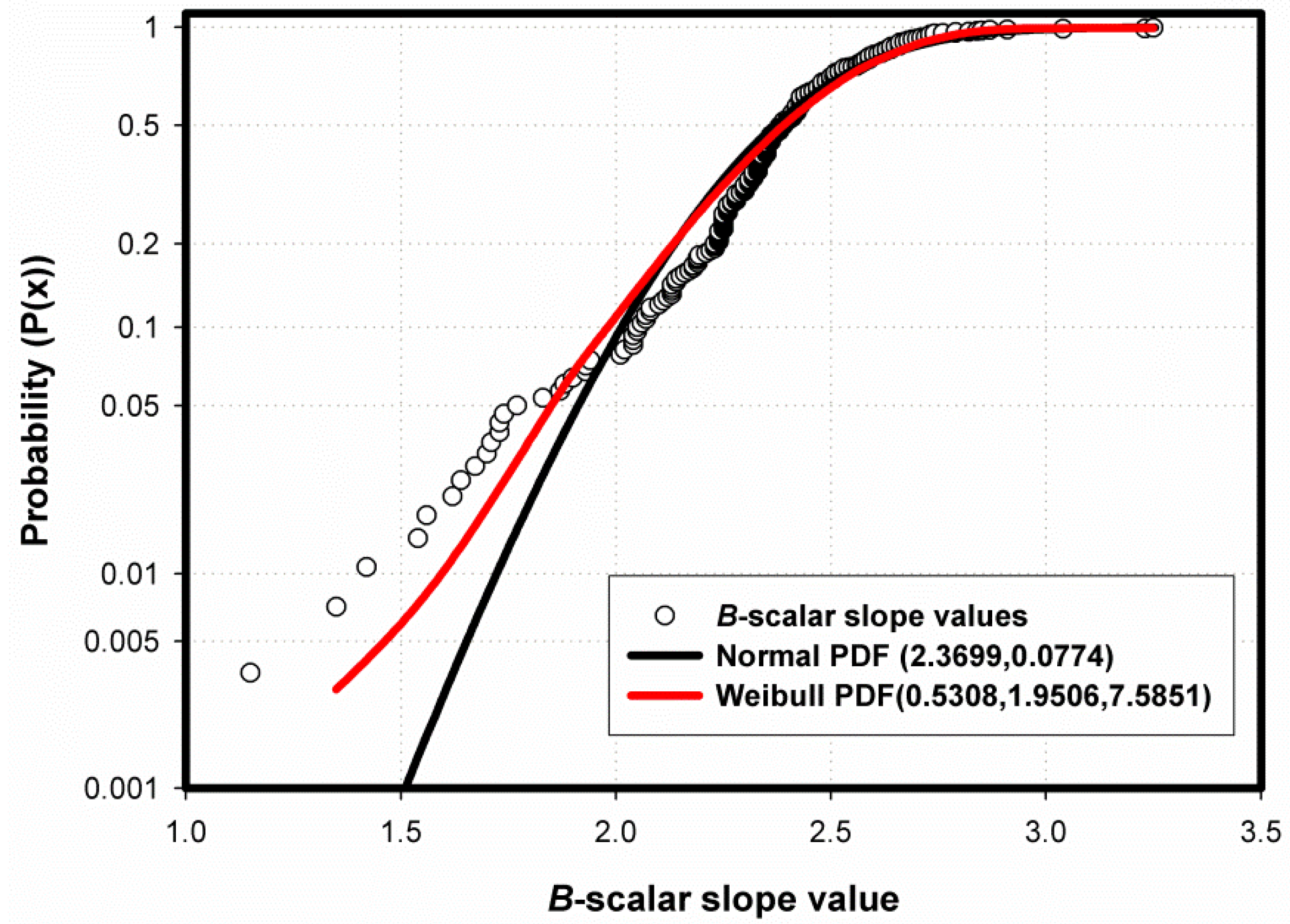
2.2.3. Further Empirical Evidence of Ontogenetie of Scalar Coefficient Values
2.3. Proposed Semi-Empirical Non-Ddestructive Models of M Assessments
2.3.1. The Reduced MNR Model
Allometric Data for Testing the MNR Model
Testing the MNR Model
2.3.2. The Shape-Dimensional Model
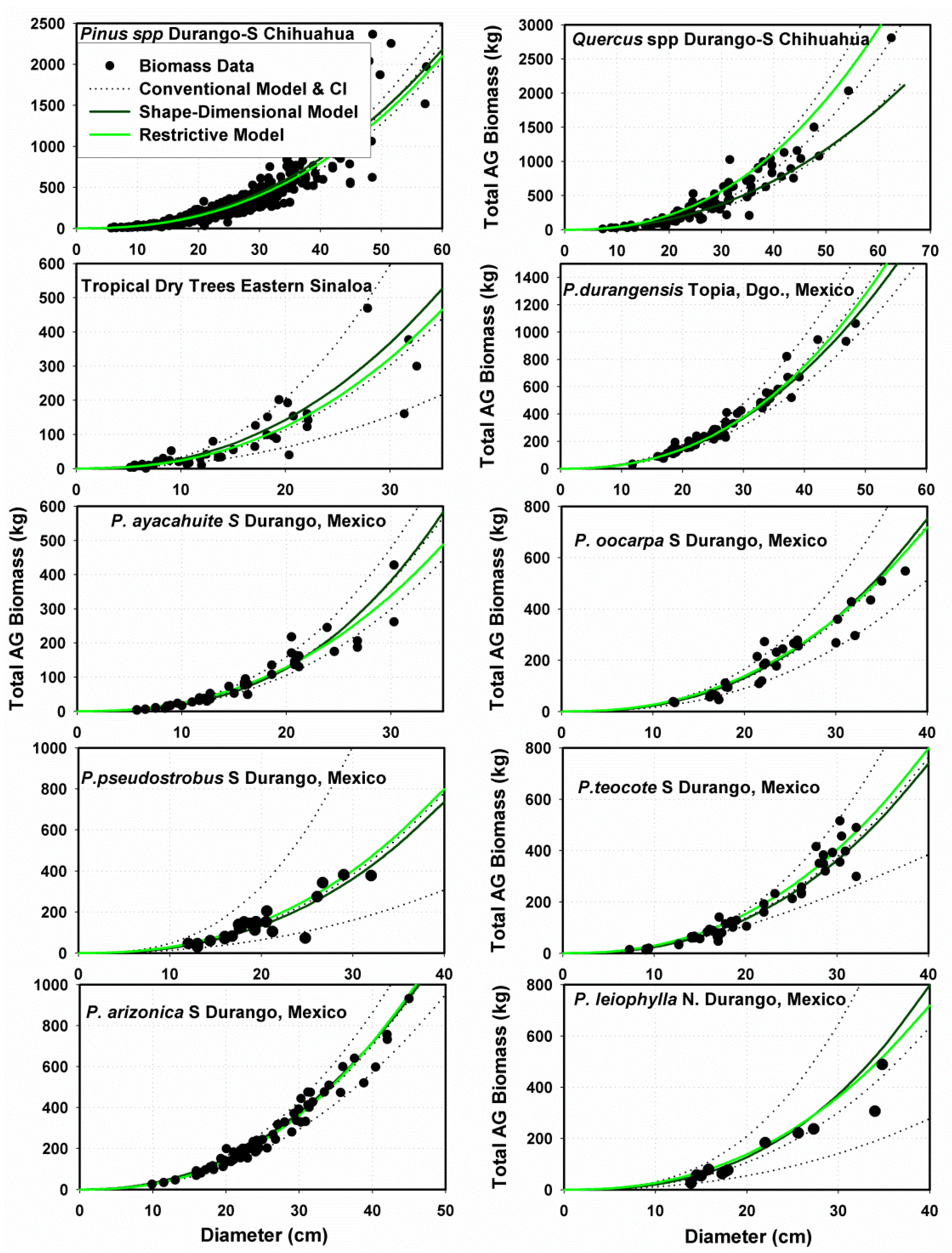
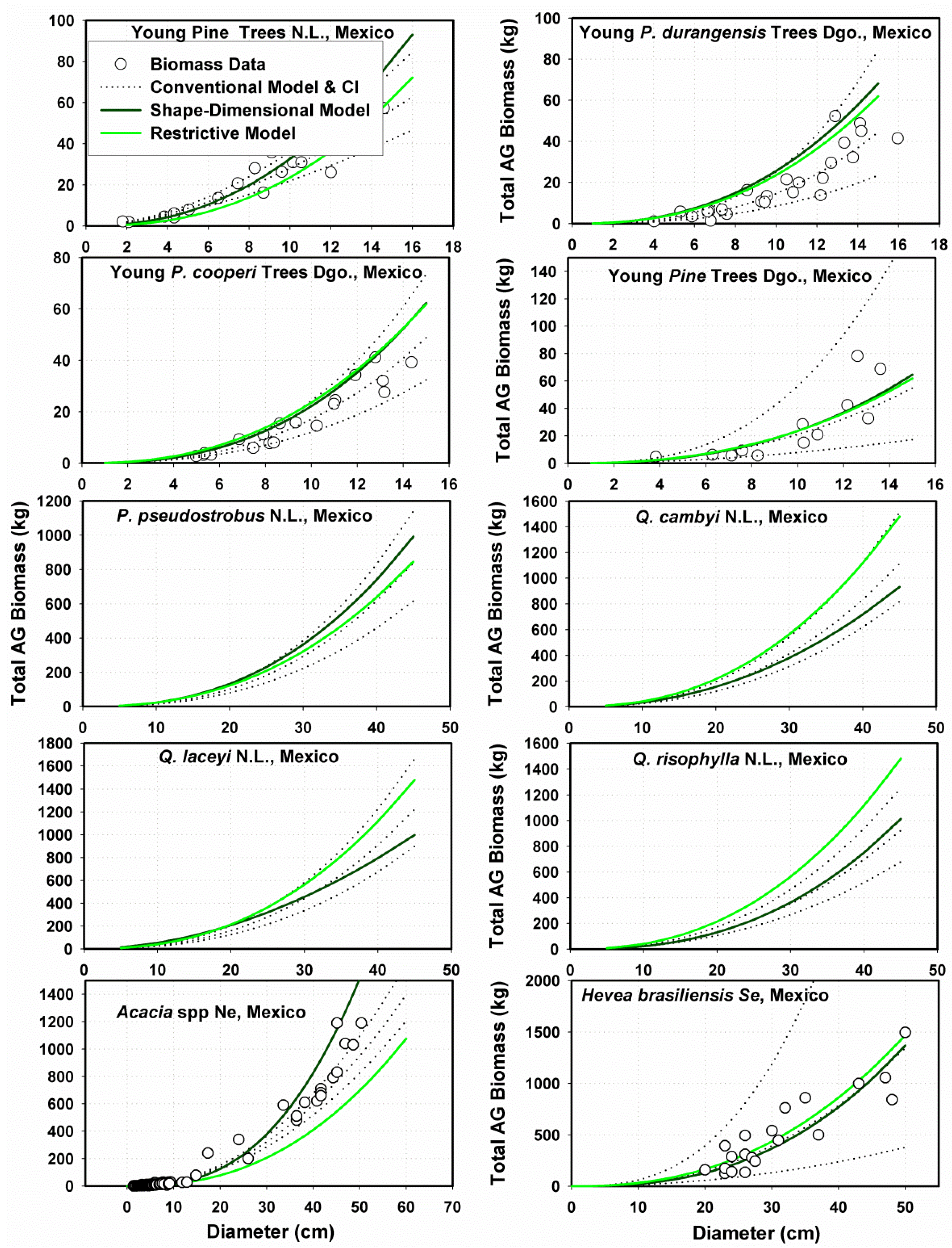
Allometric Data for Testing the MSD Model
Allometric Data for Validating the MSD Model
2.3.3. Model Fitting Statistics
3. Results
3.1. The MNR Model
3.2. The MSD Model
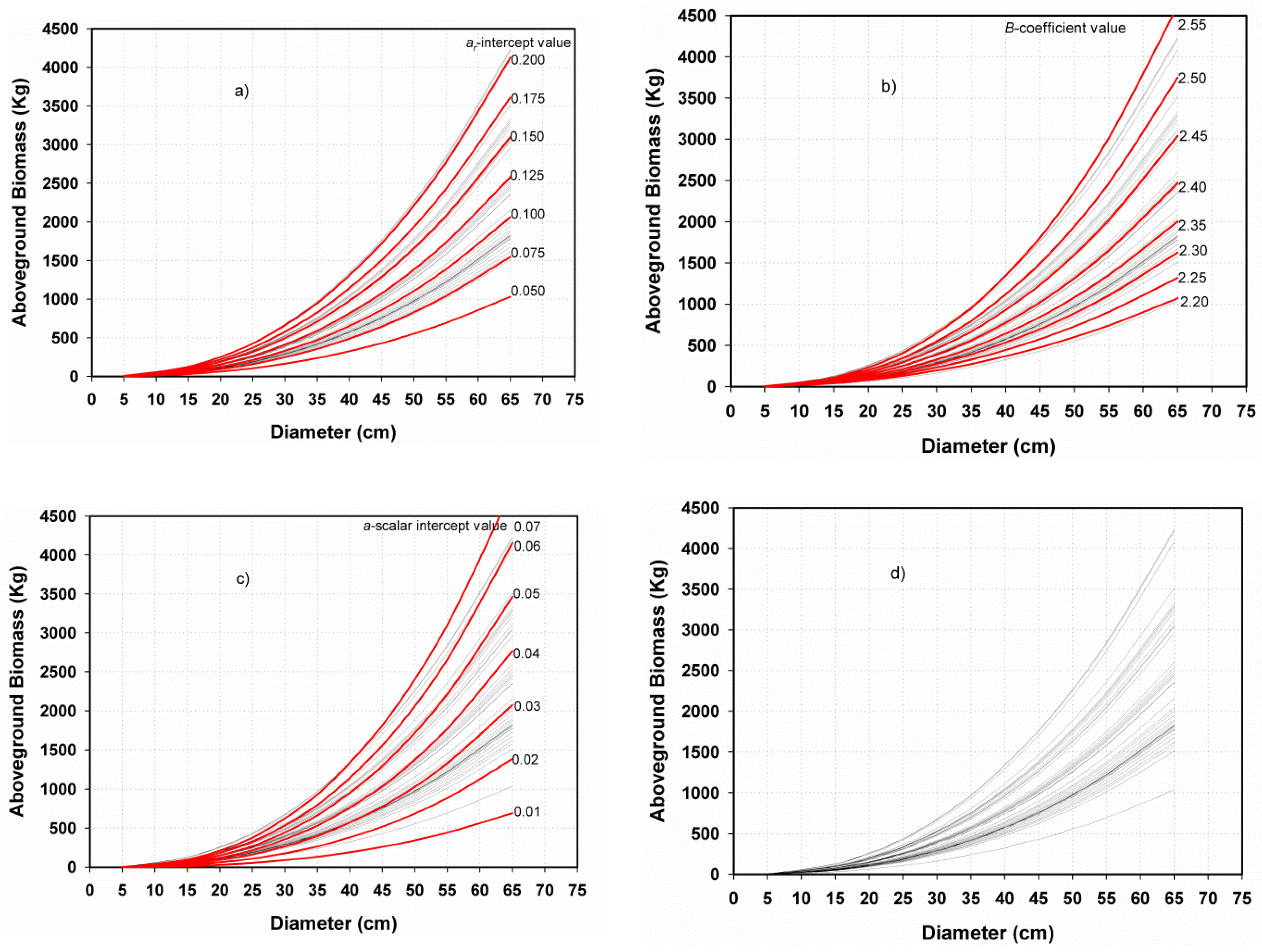
3.2.1. Preliminary Parameter Assessments and Relationships
Testing the Association of Equation Parameters
The a-Scalar Intercept
3.2.2. Performance of Fitting and Validation of the MSD Model
3.3. Contrasting the Performance of MSD and MNR Models
4. Discussion
4.1. The Performance of Semi-Empirical Models
4.2. Major Assumptions of Semi-Empirical Models
4.2.1. A Constant B-Scalar Exponent
4.2.2. The Variable B-Scalar Exponent
4.3. Ontogeneity
4.4. Improving Scalar Parameter Assessments
4.4.1. Scalar Coefficients
4.4.2. The Wood Specific Gravity Value
4.4.3. Proper a- and B-Scalar Coefficient Values
4.5. Remarks
4.6. Summary of Allometric Models to Evaluate Tree Aboveground Biomass
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests; Forest Resources Assessment Publication; Forestry Papers 134; FAO: Rome, Italy, 1997; p. 55. [Google Scholar]
- Ketterings, Q.M.; Noordwijk, C.M.Y.; Ambagau, R.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
- Chave, J.; Muller-Landau, H.; Baker, T.R.; Easdale, T.; Ter Steege, H.; Webb, C. Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecol. Appl. 2006, 16, 2356–2367. [Google Scholar] [CrossRef]
- Pilli, R.; Anfodillo, T.; Carrer, M. Towards a functional and simplified allometry for estimating forest biomass. For. Ecol. Manag. 2006, 237, 583–593. [Google Scholar] [CrossRef]
- Návar, J. Measurement and assessment methods of forest aboveground biomass: A literature Review and the Challenges Ahead. In Biomass; Momba, M., Bux, F., Eds.; 2010; Available online: http://sciyo.com/articles/show/title/biomass (accessed on 30 March 2022).
- Návar, J. The regulation of the water cycle by forests. J. Hydrol. 2022; on review. [Google Scholar]
- Návar, J. Modeling rainfall interception of forests: Extending drip equations. Agric. For. Meteorol. 2019, 279, 107704. [Google Scholar]
- Brown, S.; Gillespie, A.J.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar]
- Chave, J.; Riéra, B.; Dubois, M.-A. Estimation of biomass in a neotropical forest of French Guiana: Spatial and temporal variability. J. Trop. Ecol. 2001, 17, 79–96. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Návar, J.; Gonzalez, N.; Maldonado, D.; Graciano, J.; Dale, V.; Parresol, B. Biomass equations for pine species of forest plantations of Durango, Mexico. Madera Y Bosques 2004, 10, 17–28. [Google Scholar] [CrossRef]
- Návar, J.; Rodríguez-Flores, F.J.; Domínguez-Calleros, P.A. Taper functions and merchantable timber for températe forests of Northwestern Mexico. Ann. For. Res. 2013, 56, 165–178. [Google Scholar]
- Návar, J. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. For. Ecol. Manag. 2009, 257, 427–434. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef]
- Návar, J. Biomass component equations for Latin American species and groups of species. Ann. For. Sci. 2009, 66, 208. [Google Scholar] [CrossRef]
- Baskerville, G.L. Estimation of Dry Weight of Tree Components and Total Standing Crop in Conifer Stands. Ecology 1965, 46, 867–869. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A General Model for the Origin of Allometric Scaling Laws in Biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Enquist, B.; Brown, J.H.; West, G.B. Allometric scaling of plant energetics and population density. Nature 1998, 395, 163–165. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B. A general model for the structure and allometry of plant vascular systems. Nature 1999, 400, 664–667. [Google Scholar] [CrossRef]
- Paz-Pellat, F.; Velázquez-Rodríguez, A.; Sánchez-Sanchez, C.; Salas-Aguilar, V.; Méndez-González, J.; Acosta-Mireles, M.; Nájera-Luna, J.A. Alometría generalizada para la estimación de biomasa aérea total de plantas leñosas, marco teórico general y aplicaciones. Madera Y Bosques 2021, 27. [Google Scholar] [CrossRef]
- Genet, A.; Wernsdorfer, H.; Jonrad, M.; Pretzsch, H.; Rauch, M.; Ponette, Q.; Nys, C.; Legout, A.; Ranger, J.; Vallet, P.; et al. Ontogeny partially explains the apparent heterogeneity of published biomass equations for Fagussylvatica in central Europe. For. Ecol. Manag. 2011, 261, 1188–1202. [Google Scholar] [CrossRef]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States trees species. Forest Sci. 2003, 49, 12–35. [Google Scholar]
- Baskerville, G.L. Use of Logarithmic Regression in the Estimation of Plant Biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Sprugel, D.G. Correcting for Bias in Log-Transformed Allometric Equations. Ecology 1983, 64, 209–210. [Google Scholar] [CrossRef]
- Husch, B.; Miller, C.I.; Beers, T.W. Forest Mensuration, 3rd ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Cunia, T.; Briggs, R.D. Forcing additivity of biomass tables—Some empirical results. Can. J. For. Res. 1984, 14, 376–384. [Google Scholar] [CrossRef]
- Cunia, T.; Briggs, R.D. Forcing additivity of biomass tables—Use of the generalized least-square method. Can. J. For. Res. 1985, 15, 23–28. [Google Scholar] [CrossRef]
- Parresol, B. Assesing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Parresol, B.R. Additivity of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Návar, J.; Dominguez-Calleros, P.A.; Contreras-Aviña, J.C.; Estrada-Márquez, C. Ajuste de siete modelos de ahusamiento a los perfiles fustales de Pinus hartwegii Lindl. Del NorestedeMéxico. Agrociencia 1997, 31, 73–81. [Google Scholar]
- Fehrmann, L.; Kleinn, C. General considerations about the use of allometric equations for biomass estimation on the example of Norway spruce in central Europe. For. Ecol. Manag. 2006, 236, 412–421. [Google Scholar] [CrossRef]
- Mandelbrot, B. Fractal Geometry of Nature; Freeman: New York, NY, USA, 1982. [Google Scholar]
- Schumacher, F.X.; Hall, F.S. Logarthmic expression of timber-tree volume. J. Agric. Res. 1933, 47, 719–734. [Google Scholar]
- McMahon, T. Size and Shape in Biology: Elastic criteria impose limits on biological proportions, and consequently on metabolic rates. Science 1973, 179, 1201–1204. [Google Scholar] [CrossRef]
- Burkhardt, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, Germany, 2012; 457p. [Google Scholar]
- King, D.A. The Adaptive Significance of Tree Height. Am. Nat. 1990, 135, 809–828. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Allometry: The Scaling of Form and Process; University of Chicago Press: Chicago, IL, USA; London, UK, 1994. [Google Scholar]
- Overman, J.P.M.; Witte, H.J.L.; Saldarriaga, J.G. Evaluation of regression models for above-ground biomass determination in Amazon rainforest. J. Trop. Ecol. 1994, 10, 207–218. [Google Scholar] [CrossRef]
- Araujo, T.M.; Highughi, N.; Carvalho, J.A. Comparison of formulae for biomass content determination in a tropical rain forest in the state of Para. Braz. For. Ecol. Manag. 1999, 117, 43–52. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Lao, S.; Caspersen, J.P.; Fosterand, R.B.; Hubbell, S.P. Spatial and temporal variation of biomass in a tropical forest: Results from a large census plot in Panama. J. Ecol. 2003, 91, 240–252. [Google Scholar] [CrossRef]
- Colorado, G.J. Ecuaciones de biomasa aérea para los árboles de los bosques secundarios del área de influencia de la Central hidroeléctrica Porce II. Trabajo de grado para optar por el título de Ingeniero Forestal. Bachelor’s Thesis, Universidad Nacional de Colombia, Medellín, Colombia, 2001. [Google Scholar]
- Feldpausch, T.R.; McDonald, A.J.; Passos, C.A.M.; Lehmann, J.; Riha, S.J. Biomasa, harvestable area, and forest structure estimated from commercial forest inventories and remote sensed imagery in Southern Amazonia. For. Ecol. Manag. 2006, 233, 121–132. [Google Scholar] [CrossRef]
- Monroy, C.R.; Návar, J. Ecuaciones de aditividad para estimar componentes de biomasa de Hevea brasiliensis Muell Arg. En Veracruz, México. Madera Y Bosques 2004, 10, 29–43. [Google Scholar] [CrossRef][Green Version]
- Rojo-Martínez, G.E.; Jasso-Mata, J.; Vargas-Hernández, J.; Palma-López, D.J.; Velásquez-Martínez, A. Biomasa aérea en plantaciones comerciales de hule (Hevea brasiliensis Mull Arg.) en el estado de Oaxaca, México. Agrociencia 2005, 39, 449–456. [Google Scholar]
- Cairns, M.A.; Olmsted, I.; Granados, J.; Argaez, J. Composition and aboveground tree biomass of a dry semi-evergreen forest on Mexico’s Yucatan Peninsula. For. Ecol. Manag. 2003, 186, 125–132. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modeling Forest Growth and Yield; Applications to Mixed Tropical Forest; International Center for Agriculture and Biosciences: Wallingford, UK, 1994; 312p. [Google Scholar]
- Parolin, P. Radial gradients in wood specific gravity in trees of central Amazonian floodplains. IAWA J. 2002, 23, 449–457. [Google Scholar] [CrossRef]
- Silva-Arredondo, M.; Návar, J. Estimacion de la densidad de la madera en árboles de comunidades forestales templadas del norte del estado de Durango, México. Madera Y Bosques, 2010; in press. [Google Scholar] [CrossRef]
- Miles, P.D.; Smith, W.B. Specific Gravity and Other Properties of Wood and Bark for 156 Tree Species Found in North America; Research Note NRS-38; USDA, FS, Northern Research Station: Delware, OH, USA, 2009. [Google Scholar]
- Spurr, S.H.; Barnes, B.V. Forest Ecology, 2nd ed.; AGT Editor. S.A.: Miguel Hidalgo, Mexico, 1995; 690p. [Google Scholar]





| A | a-Re-Escalated | B | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Σ | CI | σ | CI | σ | CI | ||||
| Jenkins et al. [23] | 10 (2456) | 0.11 | 0.03 | 0.02 | 0.12 | 0.03 | 0.02 | 2.40 | 0.07 | 0.05 |
| Ter Mikaelian and Korzukhin [15] | 41 | 0.15 | 0.08 | 0.03 | 0.11 | 0.04 | 0.01 | 2.33 | 0.17 | 0.05 |
| Fehrmann and Klein [32] | 28 | 0.17 | 0.16 | 0.06 | 0.12 | 0.02 | 0.01 | 2.40 | 0.25 | 0.09 |
| Návar [16] | 78 | 0.16 | 0.15 | 0.03 | 0.14 | 0.09 | 0.02 | 2.38 | 0.23 | 0.05 |
| Návar [12] | 34 | 0.10 | 0.11 | 0.04 | 0.12 | 0.05 | 0.02 | 2.42 | 0.25 | 0.08 |
| Zianis and Mencuccini [3] | 277 | 0.15 | 0.13 | 0.01 | 0.12 | 0.04 | 0.01 | 2.37 | 0.28 | 0.03 |
| Μean Values | 0.14 | 0.11 | 0.03 | 0.12 | 0.05 | 0.01 | 2.38 | 0.21 | 0.06 | |
| Coefficient Values of Equation (1) | Diameter Statistics (cm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Location | Species (n) | a | B | SB | r2 | MSE | Min | Max | Mean |
| DATA FOR MODEL DEVELOPMENT (n = 21) | |||||||||
| 1. S. Chihuahua | P. arizonica (n = 30) | −1.482 | 2.129 | 0.1697 | 0.84 | 0.026 | 16.20 | 32.90 | 25.70 |
| 2. S. Chihuahua | P. durangensis (n = 30) | −3.532 | 2.731 | 0.1478 | 0.92 | 0.054 | 12.10 | 46.00 | 27.40 |
| 3. S. Chihuahua | Qurcus spp. (n = 45) | −2.144 | 2.403 | 0.1275 | 0.89 | 0.060 | 15.40 | 48.70 | 29.10 |
| 4. El Salto, Dgo | P. cooperi (n = 20) | −1.922 | 2.321 | 0.1596 | 0.93 | 0.068 | 12.50 | 57.40 | 31.70 |
| 5. El Salto, Dgo | Q. sideroxylla (n = 30) | −2.592 | 2.585 | 0.1093 | 0.95 | 0.061 | 9.80 | 62.50 | 27.80 |
| 6. Tepehuanes, Dgo | P. arizonica (n = 36) | −3.573 | 2.746 | 0.0897 | 0.96 | 0.038 | 10.00 | 45.00 | 22.60 |
| 7. Tepehuanes, Dgo | P. durangensis (n = 15) | −3.416 | 2.715 | 0.1405 | 0.96 | 0.039 | 11.80 | 57.20 | 24.30 |
| 8. Tepehuanes, Dgo | P. leiophylla (n = 12) | −3.039 | 2.523 | 0.2237 | 0.92 | 0.058 | 13.90 | 34.80 | 21.30 |
| 9. Altares, Dgo | P. arizonica (n = 60) | −0.877 | 1.980 | 0.0560 | 0.81 | 0.094 | 9.90 | 45.00 | 25.70 |
| 10. San Dimas, Dgo | P. ayacahuite (45) | −3.066 | 2.646 | 0.0690 | 0.97 | 0.044 | 5.70 | 30.30 | 15.40 |
| 11. San Dimas, Dgo | P. cooperi (n = 12) | −3.264 | 2.707 | 0.1100 | 0.90 | 0.274 | 8.20 | 38.10 | 18.40 |
| 12. San Dimas, Dgo | P. durangensis (n = 71) | −2.084 | 2.323 | 0.0680 | 0.94 | 0.074 | 6.20 | 48.50 | 18.70 |
| 13. San Dimas, Dgo | P. leiophylla (n = 15) | −3.549 | 2.787 | 0.1020 | 0.94 | 0.065 | 9.60 | 29.00 | 20.20 |
| 14. Mezquital, Dgo | P. oocarpa (31) | −3.065 | 2.625 | 0.1030 | 0.93 | 0.061 | 12.20 | 44.80 | 25.20 |
| 15. Mezquital, Dgo | P. pseudostrobus (n = 24) | −2.611 | 2.531 | 0.2700 | 0.88 | 0.047 | 12.00 | 32.00 | 19.60 |
| 16. Mezquital, Dgo | P. teocote (n = 49) | −3.182 | 2.702 | 0.0690 | 0.96 | 0.050 | 7.30 | 43.30 | 21.90 |
| 17. Mezquital, Dgo | Quercus spp. (n = 17) | −2.754 | 2.574 | 0.0700 | 0.94 | 0.089 | 7.30 | 41.20 | 21.10 |
| 18. Topia, Dgo | P. durangensis (n = 60) | −2.108 | 2.373 | 0.0606 | 0.96 | 0.019 | 11.80 | 48.40 | 26.00 |
| 19. E. Sinaloa | Tropical Dry trees (n = 40) | −2.523 | 2.437 | 0.1993 | 0.80 | 0.443 | 5.20 | 32.60 | 14.80 |
| 20. Dgo.-S.Chih. | Pinus spp. (n = 520) | −2.818 | 2.574 | 0.0260 | 0.94 | 0.076 | 5.70 | 57.40 | 23.50 |
| 21. Dgo.-S.Chih. | Quercus spp. (n = 106) | −2.874 | 2.631 | 0.0807 | 0.93 | 0.078 | 7.30 | 62.50 | 26.80 |
| Average | −2.69 | 2.53 | 0.12 | 0.92 | 0.09 | 10.00 | 44.65 | 23.20 | |
| C.I. | 0.30 | 0.09 | 0.03 | 0.02 | 0.04 | 1.38 | 4.50 | 1.89 | |
| DATA FOR MODEL MODEL VALIDATION (n = 11) | |||||||||
| 22. Iturbide, N.L. | P. pseudostrobus (n = 8) | −3.164 | 2.599 | 0.0807 | 0.98 | NA | 5.00 | 42.40 | 2.32 |
| 23. Iturbide, N.L. | Q. cambyi (n = 8) | −2.311 | 2.449 | 0.0807 | 0.97 | NA | 5.00 | 39.50 | 23.10 |
| 24. Iturbide, N.L. | Q. laceyi (n = 7) | −2.434 | 2.507 | 0.0807 | 0.98 | NA | 6.00 | 35.20 | 20.20 |
| 25. Iturbide, N.L. | Q. risophylla (n = 8) | −2.209 | 2.374 | 0.0807 | 0.97 | NA | 7.40 | 40.60 | 23.90 |
| 26. El Salto, Dgo | Y. Pine trees N.L. (n = 17) | −0.610 | 1.713 | 0.1073 | 0.94 | 0.068 | 1.80 | 14.60 | 7.70 |
| 27. El Salto, Dgo | Y. P. durangensis (n = 25) | −3.642 | 2.746 | 0.2370 | 0.85 | 0.168 | 4.00 | 15.00 | 10.00 |
| 28. El Salto, Dgo | Y. P. cooperi (n = 19) | −3.119 | 2.588 | 0.1515 | 0.94 | 0.047 | 5.00 | 14.40 | 9.20 |
| 29. El Salto, Dgo | Y. Pinus spp. (n = 12) | −2.397 | 2.364 | 0.4276 | 0.73 | 0.281 | 3.80 | 13.60 | 9.70 |
| 30. NE Mexico | Acacia spp. (n = 190) | −1.414 | 2.114 | 0.0360 | 0.95 | 0.144 | 1.40 | 57.30 | 8.30 |
| 31. NE Mexico | Prosopis spp. (n = 62) | −1.871 | 2.320 | 0.0880 | 0.92 | 0.213 | 2.70 | 21.80 | 9.10 |
| 32. Ver., Mexico | Hevea brasiliensis (n = 20) | −2.199 | 2.404 | 0.3246 | 0.74 | 0.152 | 20.00 | 50.00 | 31.10 |
| Average | −2.31 | 2.38 | 0.15 | 0.91 | 0.15 | 5.65 | 31.31 | 14.06 | |
| C.I. | 0.50 | 0.16 | 0.07 | 0.05 | 0.05 | 3.00 | 9.44 | 5.29 | |
| D-H Relationship; Ln(H) = a + BLn(D); H = BoDB* | V-D,H Relation; Ln(V) = a + BLn(D) + B1Ln(H); V = BoDB1HB2 | |||||||
|---|---|---|---|---|---|---|---|---|
| (Equation No) ah(Bo) | B = H* | r2 | MSE | Ln (av(Bo)) | d(B1) | h(B2) | r2 | MSE |
| EQUATIONS FOR MODEL DEVELOPMENT (n = 21) | ||||||||
| (1) 1.6270 | 0.3040 | 0.22 | 0.0090 | −8.8600 | 1.8300 | 0.7700 | 0.92 | 0.0115 |
| (2) 0.7560 | 0.5440 | 0.43 | 0.0310 | −9.6600 | 2.0100 | 0.8600 | 0.98 | 0.0120 |
| (3) 0.5070 | 0.5630 | 0.34 | 0.0490 | −9.4300 | 1.9800 | 0.7200 | 0.98 | 0.0108 |
| (4) 1.0490 | 0.5620 | 0.73 | 0.0160 | −9.3200 | 1.8700 | 0.9360 | 0.96 | 0.0320 |
| (5) 0.7520 | 0.5650 | 0.62 | 0.0330 | −9.6700 | 1.7900 | 1.0270 | 0.98 | 0.0180 |
| (6) 0.4540 | 0.6780 | 0.47 | 0.0680 | −9.5600 | 1.8560 | 0.9990 | 0.99 | 0.0077 |
| (7) −0.0020 | 0.8420 | 0.75 | 0.0330 | −9.7600 | 2.0470 | 0.8570 | 0.99 | 0.0057 |
| (8) 0.7530 | 0.5690 | 0.69 | 0.0150 | −10.0900 | 2.2300 | 0.7530 | 0.99 | 0.0085 |
| (9) 1.7280 | 0.3230 | 0.33 | 0.0205 | −9.5370 | 1.9678 | 0.8590 | 0.99 | 0.0047 |
| (10) −0.0470 | 0.9070 | 0.87 | 0.0250 | −9.6370 | 1.6870 | 1.1710 | 0.99 | 0.0087 |
| (11) 0.6630 | 0.6260 | 0.89 | 0.0160 | −9.8870 | 2.0960 | 0.8770 | 0.99 | 0.0057 |
| (12) 1.3090 | 0.4730 | 0.62 | 0.0330 | −9.6960 | 1.9280 | 0.9560 | 0.99 | 0.0160 |
| (13) 0.7780 | 0.5980 | 0.75 | 0.0150 | −9.7920 | 2.1790 | 0.6940 | 0.99 | 0.0061 |
| (14) 0.7740 | 0.5750 | 0.47 | 0.0400 | −9.8440 | 1.9890 | 0.9350 | 0.99 | 0.0047 |
| (15) 0.9600 | 0.5950 | 0.75 | 0.0070 | −9.9590 | 1.6930 | 1.2910 | 0.99 | 0.0028 |
| (16) 0.9630 | 0.5360 | 0.66 | 0.0240 | −9.6320 | 2.0510 | 0.7890 | 0.99 | 0.0103 |
| (17) 1.2430 | 0.4410 | 0.53 | 0.0390 | −9.5500 | 1.8230 | 0.9760 | 0.98 | 0.0209 |
| (18) 1.2150 | 0.4660 | 0.46 | 0.0240 | −9.2170 | 1.9200 | 0.8040 | 0.99 | 0.0067 |
| (19) 0.5717 | 0.3750 | 0.14 | 0.2130 | −9.7344 | 2.0163 | 0.8150 | 0.98 | 0.1726 |
| (20) 1.3392 | 0.4430 | 0.25 | 0.1010 | −10.0750 | 1.7284 | 1.3466 | 0.98 | 0.0230 |
| (21) 1.1537 | 0.4119 | 0.29 | 0.0610 | −9.3906 | 1.8961 | 0.8129 | 0.98 | 0.0160 |
| Average | 0.54 | 0.54 | 0.04 | −9.63 | 1.93 | 0.92 | 0.98 | 0.02 |
| C.I. | 0.06 | 0.09 | 0.02 | 0.12 | 0.06 | 0.07 | 0.01 | 0.02 |
| EQUATIONS FOR MODEL VALIDATION (n = 11) | ||||||||
| (22) 0.9890 | 0.5540 | 0.60 | 0.0350 | −9.7105 | 2.0068 | 0.8562 | 0.99 | 0.0160 |
| (23) 1.1187 | 0.4209 | 0.79 | 0.0480 | −10.1246 | 1.6824 | 1.2601 | 0.91 | NA |
| (24) 1.2810 | 0.3330 | 0.78 | 0.0320 | −9.5341 | 1.5731 | 1.0773 | 0.86 | NA |
| (25) 0.9560 | 0.5090 | 0.89 | 0.0320 | −10.7150 | 1.7917 | 1.4429 | 0.95 | NA |
| (26) 1.9633 | 0.3842 | 0.91 | 0.0200 | −7.8209 | 2.5891 | −0.9378 | 0.96 | 0.0500 |
| (27) 1.2347 | 0.4750 | 0.50 | 0.0400 | −9.6237 | 2.0354 | 0.7972 | 0.99 | 0.0150 |
| (28) 0.6372 | 0.6680 | 0.80 | 0.0230 | −9.6414 | 1.8232 | 1.0820 | 0.99 | 0.0190 |
| (29) 0.9770 | 0.5530 | 0.57 | 0.0380 | −9.7418 | 2.0047 | 0.8757 | 0.99 | 0.0149 |
| (30) −0.4290 | 0.6180 | 0.45 | 0.0820 | −9.4756 | 1.9902 | 1.1737 | 0.99 | 0.0066 |
| (31) −0.4732 | 0.6272 | 0.57 | 0.0715 | −9.4756 | 1.9902 | 1.1737 | 0.98 | 0.0115 |
| (32) 0.5430 | 0.7450 | 0.63 | 0.0255 | −9.8310 | 1.8370 | 1.0010 | 0.93 | 0.0430 |
| Average | 0.54 | 0.68 | 0.04 | −9.61 | 1.94 | 0.89 | 0.96 | 0.020 |
| C.I. | 0.07 | 0.09 | 0.01 | 0.41 | 0.16 | 0.38 | 0.03 | 0.010 |
| Name | Equation or Model | Parameters | Calculation Method | Spatial Range | Author |
|---|---|---|---|---|---|
| Conventional | Ln(M) = Ln(a) + BLn(D) M = aDB | a,B | Statistics | Species, Local | Baskerville [17] |
| Fractals (MWBE) | M = CρD2.67 | C, B = 2.67 | Statistics, Mathematics | Forests, Worldwide | West et al. [18] |
| Restrictive (MNR) | M = CρD2.38 ar = Cρw; ar ≠ a | C, B = 2.38 | Statistics, Mathematics | Forests, Worldwide | This Report |
| Shape-Dimensional (MSD) | M = CρDd+hH* V = avDdHh; H = ahDdH* C = avah | d,h,H*,av,ah 2.33 ≤ B ≤ 2.5 H* ≈ 0.54 | Statistics, Mathematics, Physics | Forests, Worldwide | This Report |
| Genet (MGE) | M = a + ρF(D2H)γ | a,F,γ γ ≤ 0.95 | Statistics, Mathematics | Groups of Species | Genet et al. [22] |
| Ketterings (MKE) | M = CρD2+H* | C,H* H* ≈ 0.53 B ≈ 2.53 | Statistics, Mathematics | Tropical Forests | Ketterings et al. [2] |
| Chave (MCH) | M = C(pwD2H)γ | C,γ γ ≤ 0.95 | Statistics, | Tropical Forests | Chavé et al. [10] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corral-Rivas, S.; Luján-Soto, J.E.; Domínguez-Gómez, T.G.; Corral-Rivas, J.J.; Rodríguez-Flores, F.d.J.; Colín, J.-G.; Graciano-Luna, J.d.J.; Návar, J. Semi-Empirical Models and Revision of Predicting Approaches of Tree Aboveground Biomass Assessments. Forests 2022, 13, 999. https://doi.org/10.3390/f13070999
Corral-Rivas S, Luján-Soto JE, Domínguez-Gómez TG, Corral-Rivas JJ, Rodríguez-Flores FdJ, Colín J-G, Graciano-Luna JdJ, Návar J. Semi-Empirical Models and Revision of Predicting Approaches of Tree Aboveground Biomass Assessments. Forests. 2022; 13(7):999. https://doi.org/10.3390/f13070999
Chicago/Turabian StyleCorral-Rivas, Sacramento, José Encarnación Luján-Soto, Tilo Gustavo Domínguez-Gómez, José Javier Corral-Rivas, Felipa de Jesús Rodríguez-Flores, José-Guadalupe Colín, José de Jesús Graciano-Luna, and José Návar. 2022. "Semi-Empirical Models and Revision of Predicting Approaches of Tree Aboveground Biomass Assessments" Forests 13, no. 7: 999. https://doi.org/10.3390/f13070999
APA StyleCorral-Rivas, S., Luján-Soto, J. E., Domínguez-Gómez, T. G., Corral-Rivas, J. J., Rodríguez-Flores, F. d. J., Colín, J.-G., Graciano-Luna, J. d. J., & Návar, J. (2022). Semi-Empirical Models and Revision of Predicting Approaches of Tree Aboveground Biomass Assessments. Forests, 13(7), 999. https://doi.org/10.3390/f13070999







