Additive Root Biomass Equations for Betula platyphylla Suk. Plantations in Northeast China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Description
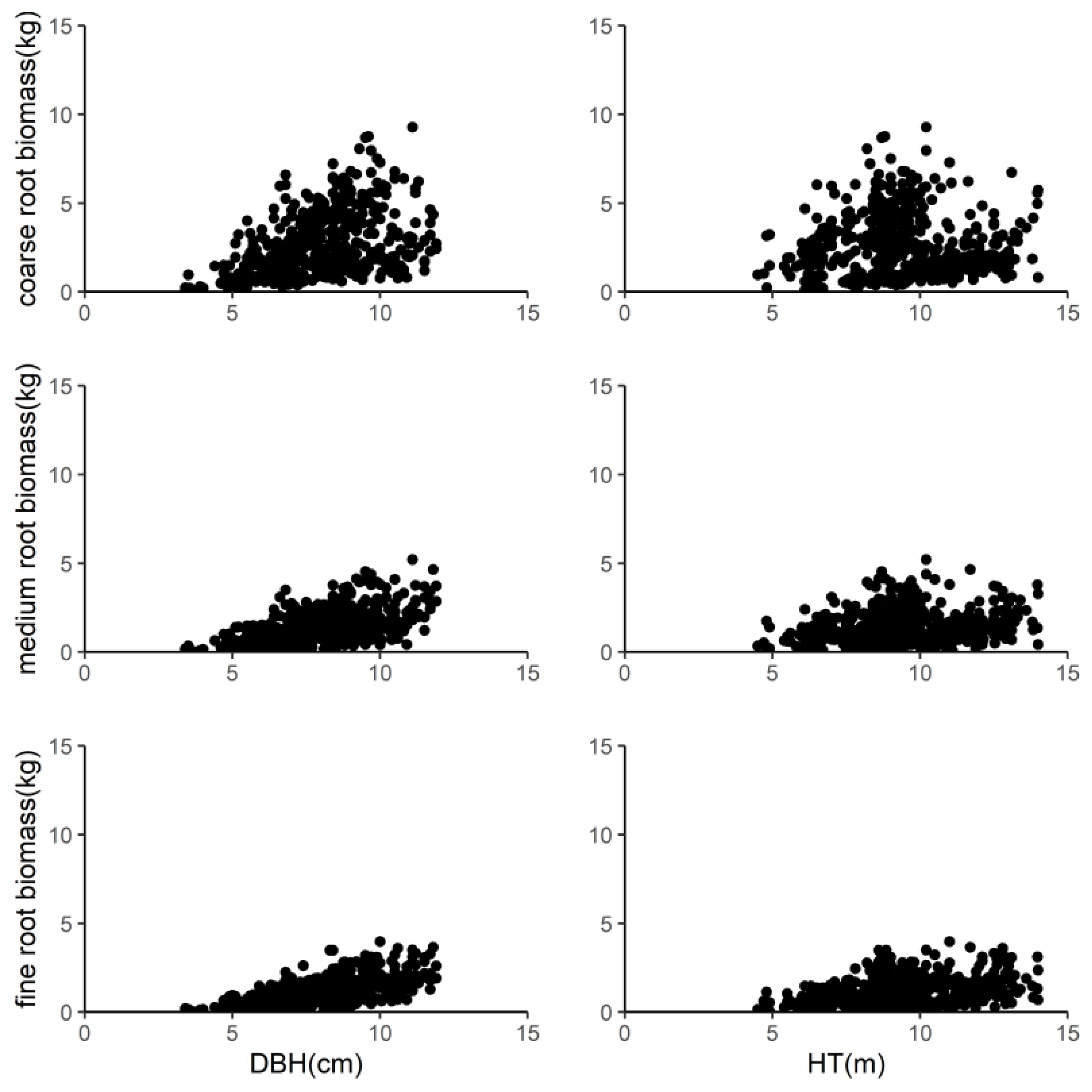
2.2. Measurement of Belowground Root Biomass
2.3. Selection of Allometric Equations and Error Structures
2.4. Additive and Disaggregated Models of Biomass Equations
2.5. Model Assessment and Evaluation
3. Results
3.1. Selection of Biomass Models
3.2. Additive Biomass Equations
3.3. Disaggregated Model Equations
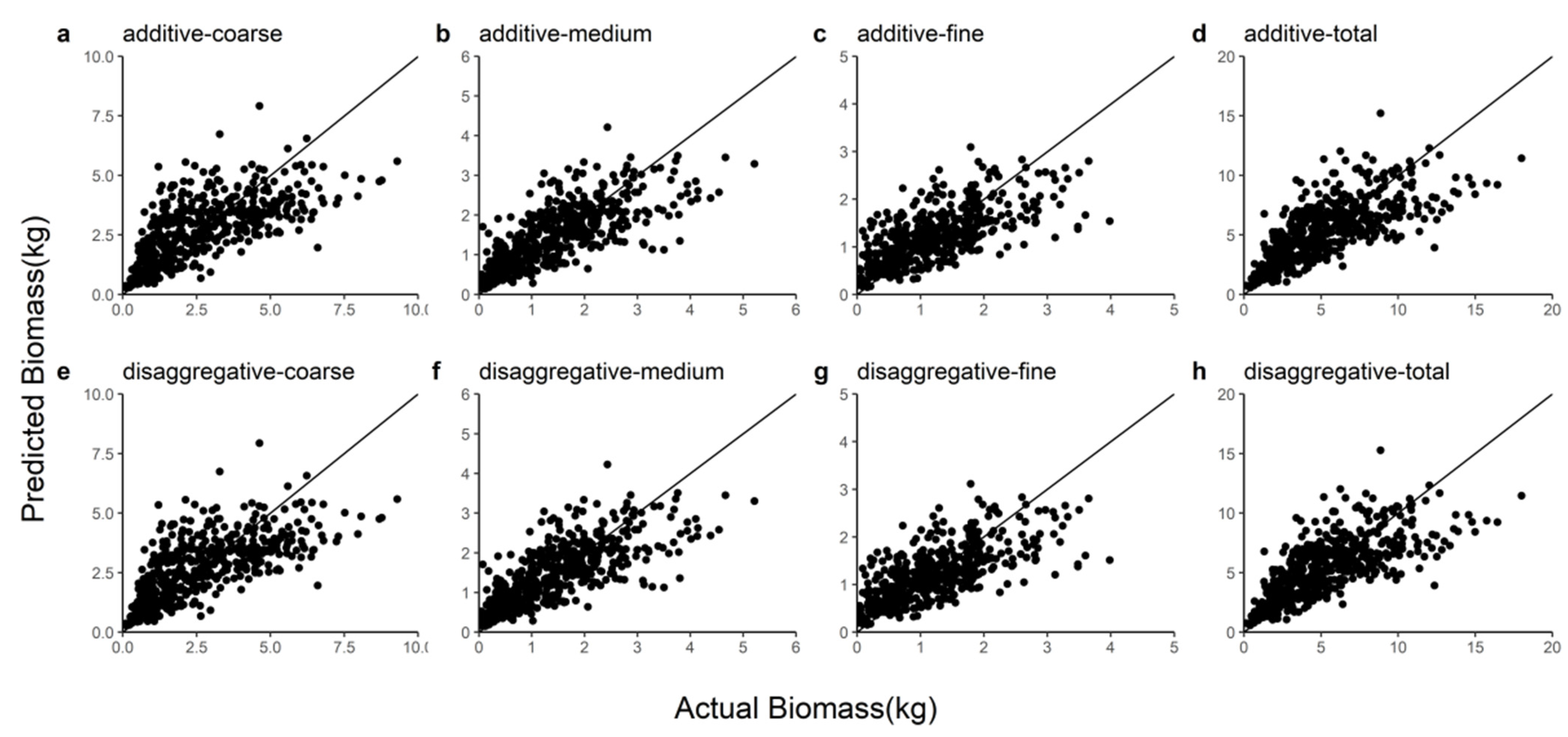
3.4. Biomass Model Validation and Comparison
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, D.; Wang, X.; Yin, Y.; Zhan, J.; Lewis, B.J.; Tian, J.; Bao, Y.; Zhou, W.; Zhou, L.; Dai, L. Estimates of Forest Biomass Carbon Storage in Liaoning Province of Northeast China: A Review and Assessment. PLoS ONE 2014, 9, e89572. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Kane, M.; Markewitz, D.; Teskey, R.; Clutter, M. Additive Tree Biomass Equations for Midrotation Loblolly Pine Plantations. For. Sci. 2015, 61, 613–623. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Zhang, L.; Li, F. A Three-Step Proportional Weighting System of Nonlinear Biomass Equations. For. Sci. 2015, 61, 35–45. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. Aboveground Biomass Relationships for Beech (Fagus Moesiaca Cz.) Trees in Vermio Mountain, Northern Greece, and Generalised Equations for Fagus sp. Ann. For. Sci. 2003, 60, 439–448. [Google Scholar] [CrossRef] [Green Version]
- Quint, T.C.; Dech, J.P. Allometric Models for Predicting the Aboveground Biomass of Canada Yew (Taxus Canadensis Marsh.) from Visual and Digital Cover Estimates. Can. J. For. Res. 2010, 40, 2003–2014. [Google Scholar] [CrossRef]
- Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U.; Barrio-Anta, M.; Crecente-Campo, F. Aboveground Stand-Level Biomass Estimation: A Comparison of Two Methods for Major Forest Species in Northwest Spain. Ann. For. Sci. 2012, 69, 735–746. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, Y.C.; Zeng, W.S. Uncertainty Analysis for Regional-Level above-Ground Biomass Estimates Based on Individual Tree Biomass Model. Acta Ecol. Sin. 2015, 35, 7738–7747. [Google Scholar] [CrossRef]
- McCormack, M.L.; Dickie, I.A.; Eissenstat, D.M.; Fahey, T.J.; Fernandez, C.W.; Guo, D.; Helmisaari, H.-S.; Hobbie, E.A.; Iversen, C.M.; Jackson, R.B.; et al. Redefining Fine Roots Improves Understanding of Below-Ground Contributions to Terrestrial Biosphere Processes. New Phytol. 2015, 207, 505–518. [Google Scholar] [CrossRef]
- Fogel, R. Root Turnover and Productivity of Coniferous Forests. Plant Soil 1983, 71, 75–85. [Google Scholar] [CrossRef]
- Brassard, B.W.; Chen, H.Y.H.; Bergeron, Y. Influence of Environmental Variability on Root Dynamics in Northern Forests. Crit. Rev. Plant Sci. 2009, 28, 179–197. [Google Scholar] [CrossRef]
- Zheng, C.; Mason, E.G.; Jia, L.; Wei, S.; Sun, C.; Duan, J. A Single-Tree Additive Biomass Model of Quercus Variabilis Blume Forests in North China. Trees 2015, 29, 705–716. [Google Scholar] [CrossRef] [Green Version]
- Dutcă, I.; Mather, R.; Blujdea, V.N.B.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-Effects on Biomass Allometric Models for Early Growth Plantations of Norway Spruce (Picea Abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Norby, R.J.; Ledford, J.; Reilly, C.D.; Miller, N.E.; O’Neill, E.G. Fine-Root Production Dominates Response of a Deciduous Forest to Atmospheric CO2 Enrichment. Proc. Natl. Acad. Sci. USA 2004, 101, 9689–9693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Gao, X. Community structure and driving factors for rhizosphere ectomycorrhizal fungi of Betula platyphylla in Daqing Mountain. Chin. J. Ecol. 2021, 40, 1244–1252. [Google Scholar]
- Parresol, B.R. Additivity of Nonlinear Biomass Equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Dong, L.; Li, F.; Jia, W. Compatible Tree Biomass Models for Natural White Birch (Betula platyphylla) in Northeast China Forest Area. Sci. Silvae Sin. 2013, 49, 75–85. [Google Scholar]
- Dong, L.; Zhang, L.; Li, F. Developing Additive Systems of Biomass Equations for Nine Hardwood Species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D.; Liu, G.; Yang, C.; Teskey, R.O. Additive Tree Biomass Equations for Betula Platyphylla Suk. Plantations in Northeast China. Ann. For. Sci. 2018, 75, 60. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Zhang, H.; Shu, H. Study on establish and estimate method of compatible biomass model. Sci. Silvae Sin. 2000, S1, 19–27. [Google Scholar]
- Lima, A.J.N.; Suwa, R.; de Mello Ribeiro, G.H.P.; Kajimoto, T.; dos Santos, J.; da Silva, R.P.; de Souza, C.A.S.; de Barros, P.C.; Noguchi, H.; Ishizuka, M.; et al. Allometric Models for Estimating Above- and below-Ground Biomass in Amazonian Forests at São Gabriel Da Cachoeira in the Upper Rio Negro, Brazil. For. Ecol. Manag. 2012, 277, 163–172. [Google Scholar] [CrossRef]
- Monika, V.; Daniel, Z.; Tomáš, Č.; Vít, Š. Models for Predicting Aboveground Biomass of European Beech (Fagus Sylvatica L.) in the Czech Republic. J. For. Sci. 2016, 61, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Meng, S.; Jia, Q.; Liu, Q.; Zhou, G.; Wang, H.; Yu, J. Aboveground Biomass Allocation and Additive Allometric Models for Natural Larix Gmelinii in the Western Daxing’anling Mountains, Northeastern China. Forests 2019, 10, 150. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests 2019, 10, 862. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Aboveground Biomass Allometric Models for Evergreen Broad-Leaved Forest Damaged by a Serious Ice Storm in Southern China. Forests 2020, 11, 320. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, C.; Fan, X.; Zhao, Y. Biomass Allocation Patterns and Allometric Models of Abies Nephrolepis Maxim. Shengtai Xuebao Acta Ecol. Sin. 2011, 31, 3918–3927. [Google Scholar]
- Chen, D.; Sun, X.; Jin, Y.; Zhang, Y.; Zhang, S. Effects of Stand Age and Competition on Allometric Relationships for Biomass Partitioning in Larixkaempferi Plantation. Acta Ecol. Sin. 2019, 40, 843–853. [Google Scholar]
- Finér, L.; Ohashi, M.; Noguchi, K.; Hirano, Y. Factors Causing Variation in Fine Root Biomass in Forest Ecosystems. For. Ecol. Manag. 2011, 261, 265–277. [Google Scholar] [CrossRef]
- Akburak, S.; Oral, H.V.; Ozdemir, E.; Makineci, E. Temporal Variations of Biomass, Carbon and Nitrogen of Roots under Different Tree Species. Scand. J. For. Res. 2013, 28, 8–16. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Weng, Y.H.; Zhang, H.G.; Meng, F.R.; Major, J.E. Comparing Fast- and Slow-Growing Provenances of Picea Koraiensis in Biomass, Carbon Parameters and Their Relationships with Growth. For. Ecol. Manag. 2013, 307, 178–185. [Google Scholar] [CrossRef]
- Rutishauser, E.; Noor’an, F.; Laumonier, Y.; Halperin, J.; Rufi’ie; Hergoualc’h, K.; Verchot, L. Generic Allometric Models Including Height Best Estimate Forest Biomass and Carbon Stocks in Indonesia. For. Ecol. Manag. 2013, 307, 219–225. [Google Scholar] [CrossRef]
- Xiao, X.; White, E.P.; Hooten, M.B.; Durham, S.L. On the Use of Log-Transformation vs. Nonlinear Regression for Analyzing Biological Power Laws. Ecology 2011, 92, 1887–1894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Affleck, D.L.R.; Diéguez-Aranda, U. Additive Nonlinear Biomass Equations: A Likelihood-Based Approach. For. Sci. 2016, 62, 129–140. [Google Scholar] [CrossRef]
- Bengio, Y.; Grandvalet, Y. No Unbiased Estimator of the Variance of K-Fold Cross-Validation. J. Mach. Learn. Res. 2004, 5, 1089–1105. [Google Scholar]
- Dutcă, I. The Variation Driven by Differences between Species and between Sites in Allometric Biomass Models. Forests 2019, 10, 976. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, H.; Hosen, M.F.; Siddiqui, M.R.H.; Abdullah, S.M.R.; Islam, S.M.Z.; Matieu, H.; Iqbal, M.Z.; Akhter, M. Allometric Biomass Model for Aquilaria Malaccensis Lam. in Bangladesh: A Nondestructive Approach. J. Sustain. For. 2021, 40, 594–606. [Google Scholar] [CrossRef]
- Rizvi, R.H.; Khare, D.; Dhillon, R.S. Statistical Models for Aboveground Biomass of Populus Deltoides Planted in Agroforestry in Haryana. Trop. Ecol. 2008, 49, 35–42. [Google Scholar]
- Dong, L.-H.; Li, F.-R.; Song, Y.-W. Error Structure and Additivity of Individual Tree Biomass Model for Four Natural Conifer Species in Northeast China. Chin. J. Appl. Ecol. 2015, 26, 704–714. [Google Scholar]
- Cao, L.; Li, H. Analysis of Error Structure for Additive Biomass Equations on the Use of Multivariate Likelihood Function. Forests 2019, 10, 298. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Li, F. Additive Stand-Level Biomass Models for Natural Larch Forest in the East of Daxing’an Mountains. Linye Kexue Sci. Silvae Sin. 2016, 52, 13–21. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Allometry and Partitioning of Individual Tree Biomass and Carbon of Abies Nephrolepis Maxim in Northeast China. Scand. J. For. Res. 2016, 31, 399–411. [Google Scholar] [CrossRef]
- Atkinson, C.L.; Parr, T.B.; van Ee, B.C.; Knapp, D.D.; Winebarger, M.; Madoni, K.J.; Haag, W.R. Length-Mass Equations for Freshwater Unionid Mussel Assemblages: Implications for Estimating Ecosystem Function. Freshw. Sci. 2020, 39, 377–390. [Google Scholar] [CrossRef]
- Xie, L.; Fu, L.; Widagdo, F.R.A.; Dong, L.; Li, F. Improving the Accuracy of Tree Biomass Estimations for Three Coniferous Tree Species in Northeast China. Trees 2021, 36, 451–469. [Google Scholar] [CrossRef]
- Cui, Y.; Bi, H.; Liu, S.; Hou, G.; Wang, N.; Ma, X.; Zhao, D.; Wang, S.; Yun, H. Developing Additive Systems of Biomass Equations for Robinia Pseudoacacia L. in the Region of Loess Plateau of Western Shanxi Province, China. Forests 2020, 11, 1332. [Google Scholar] [CrossRef]
- Meng, S.; Yang, F.; Hu, S.; Wang, H.; Wang, H. Generic Additive Allometric Models and Biomass Allocation for Two Natural Oak Species in Northeastern China. Forests 2021, 12, 715. [Google Scholar] [CrossRef]
- Usoltsev, V.A.; Shobairi, S.O.R.; Chasovskikh, V.P. Additive Allometric Models of Single-Tree Biomass of Sp. as a Basis of Regional Taxation Standards for Eurasia. Civ. Environ. Eng. 2018, 14, 105–115. [Google Scholar] [CrossRef] [Green Version]
- Bijak, S.; Zasada, M.; Agnieszka, B.; Bronisz, K.; Czajkowski, M.; Ludwisiak, Ł.; Tomusiak, R.; Wojtan, R. Estimating Coarse Roots Biomass in Young Silver Birch Stands on Post-Agricultural Lands in Central Poland. Silva Fenn. 2013, 47, 963. [Google Scholar] [CrossRef]
- Kapeluck, P.R.; Lear, D.H.V. A Technique for Estimating Below-Stump Biomass of Mature Loblolly Pine Plantations. Can. J. For. Res. 1995, 25, 355–360. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, FAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Xiao, C.W.; Sang, W.G.; Wang, R.-Z. Fine Root Dynamics and Turnover Rate in an Asia White Birch Forest of Donglingshan Mountain, China. For. Ecol. Manag. 2008, 255, 765–773. [Google Scholar] [CrossRef]
- Leuschner, C.; Hertel, D.; Schmid, I.; Koch, O.; Muhs, A.; Hölscher, D. Stand Fine Root Biomass and Fine Root Morphology in Old-Growth Beech Forests as a Function of Precipitation and Soil Fertility. Plant Soil 2004, 258, 43–56. [Google Scholar] [CrossRef]
- Burke, M.K.; Raynal, D.J. Fine Root Growth Phenology, Production, and Turnover in a Northern Hardwood Forest Ecosystem. Plant Soil 1994, 162, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Albaugh, T.J. Leaf Area and Above- and Belowground Growth Responses of Loblolly Pine to Nutrient and Water Additions. For. Sci. 1996, 44, 317–328. [Google Scholar]
- Zhang, Y.; Wen, Z. Root Biomass of Pinus massoniana Plantations under Different Planting Densities. Sci. Silvae Sin. 2011, 47, 75–81. [Google Scholar]
- Varik, M.; Aosaar, J.; Ostonen, I.; Lõhmus, K.; Uri, V. Carbon and Nitrogen Accumulation in Belowground Tree Biomass in a Chronosequence of Silver Birch Stands. For. Ecol. Manag. 2013, 302, 62–70. [Google Scholar] [CrossRef]
- Yang, L.; Wu, S.; Zhang, L. Fine Root Biomass Dynamics and Carbon Storage along a Successional Gradient in Changbai Mountains, China. Forestry 2010, 83, 379–387. [Google Scholar] [CrossRef]
- Wang, N.; Wang, C.; Quan, X. Variations in fine root dynamics and turnover rates in five forest types in northeastern China. J. For. Res. 2019, 31, 871–884. [Google Scholar] [CrossRef]

| Site | Latitude (°) | Longitude (°) | MAT (°C) | T max (°C) | T min (°C) | MAP (mm) | Samples |
|---|---|---|---|---|---|---|---|
| Heilongjiang | 45.42 | 127.63 | 2.56 | 25.88 | −25.88 | 596.00 | 333 |
| Jinlin | 43.66 | 126.66 | 3.05 | 24.49 | −26.44 | 707.00 | 26 |
| Liaoning | 40.85 | 123.92 | 6.64 | 26.26 | −17.52 | 904.00 | 134 |
| Parameter | DBH (cm) | HT (m) | Coarse Root (kg) | Medium Root (kg) | Fine Root (kg) | Total Biomass (kg) |
|---|---|---|---|---|---|---|
| Mean | 7.98 | 9.41 | 2.65 | 1.48 | 1.20 | 5.34 |
| SD | 1.71 | 1.97 | 1.79 | 0.96 | 0.75 | 3.23 |
| Max | 11.90 | 14.00 | 9.29 | 10.19 | 3.98 | 20.27 |
| Min | 3.40 | 4.50 | 0.10 | 0.02 | 0.02 | 0.14 |
| Equation | Coarse Root | Medium Root | Fine Root | Total Biomass |
|---|---|---|---|---|
| 187.29 | 50.42 | 8.53 | 140.43 | |
| 163.58 | 41.98 | 8.68 | 115.03 | |
| 195.21 | 45.54 | 9.45 | 142.31 |
| Model | Biomass Component | R2 | E | MABE | RMSE |
|---|---|---|---|---|---|
| Coarse | 0.3728 | 0.3150 | 1.1087 | 1.4819 | |
| Medium | 0.4975 | 0.1047 | 0.5382 | 0.7120 | |
| Fine | 0.3695 | 0.1922 | 0.4714 | 0.6225 | |
| Total | 0.4627 | 0.4605 | 1.8767 | 2.4789 | |
| Coarse | 0.3181 | 0.3411 | 1.1646 | 1.5445 | |
| Medium | 0.4203 | 0.1082 | 0.5823 | 0.7645 | |
| Fine | 0.3065 | 0.1901 | 0.4974 | 0.6547 | |
| Total | 0.3850 | 0.4918 | 2.0232 | 2.6515 | |
| Coarse | 0.4907 | 0.2626 | 0.9805 | 1.3336 | |
| Medium | 0.5615 | 0.1222 | 0.4849 | 0.6639 | |
| Fine | 0.4825 | 0.1253 | 0.4248 | 0.5656 | |
| Total | 0.5509 | 0.3627 | 1.6711 | 2.6416 |
| Biomass Component | Parameter | Asymptotic Estimate | Asymptotic Standard Error | p Value |
|---|---|---|---|---|
| Coarse | −0.9679 | 0.2008 | 0.0000 | |
| 2.2547 | 0.1435 | 0.0000 | ||
| −1.1789 | 0.1369 | 0.0000 | ||
| 0.2733 | 0.0932 | 0.0034 | ||
| −0.8561 | 0.0943 | 0.0000 | ||
| Medium | −2.7028 | 0.1985 | 0.0000 | |
| 2.2534 | 0.1356 | 0.0000 | ||
| −0.6586 | 0.1282 | 0.0000 | ||
| −0.3815 | 0.1287 | 0.0031 | ||
| −0.7157 | 0.0746 | 0.0000 | ||
| Fine | −3.7903 | 0.2251 | 0.0000 | |
| 2.313 | 0.1463 | 0.0000 | ||
| −0.361 | 0.1446 | 0.0126 | ||
| −0.3346 | 0.1323 | 0.0116 | ||
| −0.2382 | 0.0572 | 0.0000 |
| Equation | Parameter | Asymptotic Estimate | Asymptotic Standard Error | p Value |
|---|---|---|---|---|
| −1.0113 | 0.1807 | 0.0000 | ||
| 2.2706 | 0.1251 | 0.0000 | ||
| −0.8676 | 0.12 | 0.0000 | ||
| −0.0108 | 0.0946 | 0.9088 | ||
| −0.6541 | 0.0682 | 0.0000 | ||
| 1.5647 | 0.1545 | 0.0000 | ||
| −0.0272 | 0.1063 | 0.7983 | ||
| −0.6669 | 0.1021 | 0.0000 | ||
| 0.6444 | 0.085 | 0.0000 | ||
| −0.3682 | 0.0663 | 0.0000 | ||
| 1.1035 | 0.1793 | 0.0000 | ||
| −0.0653 | 0.1182 | 0.5810 | ||
| −0.2995 | 0.1142 | 0.0088 | ||
| −0.045 | 0.1053 | 0.6693 | ||
| −0.4775 | 0.0564 | 0.0000 |
| Model | Biomass Component | R2 | E | MAER | RMSE |
|---|---|---|---|---|---|
| Additive | Coarse | 0.4970 | −0.0463 | 0.9953 | 1.3281 |
| Medium | 0.5706 | −0.0155 | 0.4883 | 0.6596 | |
| Fine | 0.5044 | −0.0109 | 0.4209 | 0.5547 | |
| Total | 0.5480 | −0.0725 | 1.7155 | 2.2782 | |
| Disaggregated | Coarse | 0.5043 | −0.0387 | 0.9865 | 1.3178 |
| Medium | 0.5762 | −0.0123 | 0.4846 | 0.6551 | |
| Fine | 0.5062 | −0.0096 | 0.4211 | 0.5537 | |
| Total | 0.5548 | −0.0605 | 1.6990 | 2.2601 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Wang, X. Additive Root Biomass Equations for Betula platyphylla Suk. Plantations in Northeast China. Forests 2022, 13, 661. https://doi.org/10.3390/f13050661
Pan L, Wang X. Additive Root Biomass Equations for Betula platyphylla Suk. Plantations in Northeast China. Forests. 2022; 13(5):661. https://doi.org/10.3390/f13050661
Chicago/Turabian StylePan, Li, and Xiuwei Wang. 2022. "Additive Root Biomass Equations for Betula platyphylla Suk. Plantations in Northeast China" Forests 13, no. 5: 661. https://doi.org/10.3390/f13050661
APA StylePan, L., & Wang, X. (2022). Additive Root Biomass Equations for Betula platyphylla Suk. Plantations in Northeast China. Forests, 13(5), 661. https://doi.org/10.3390/f13050661






