Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Taper Models
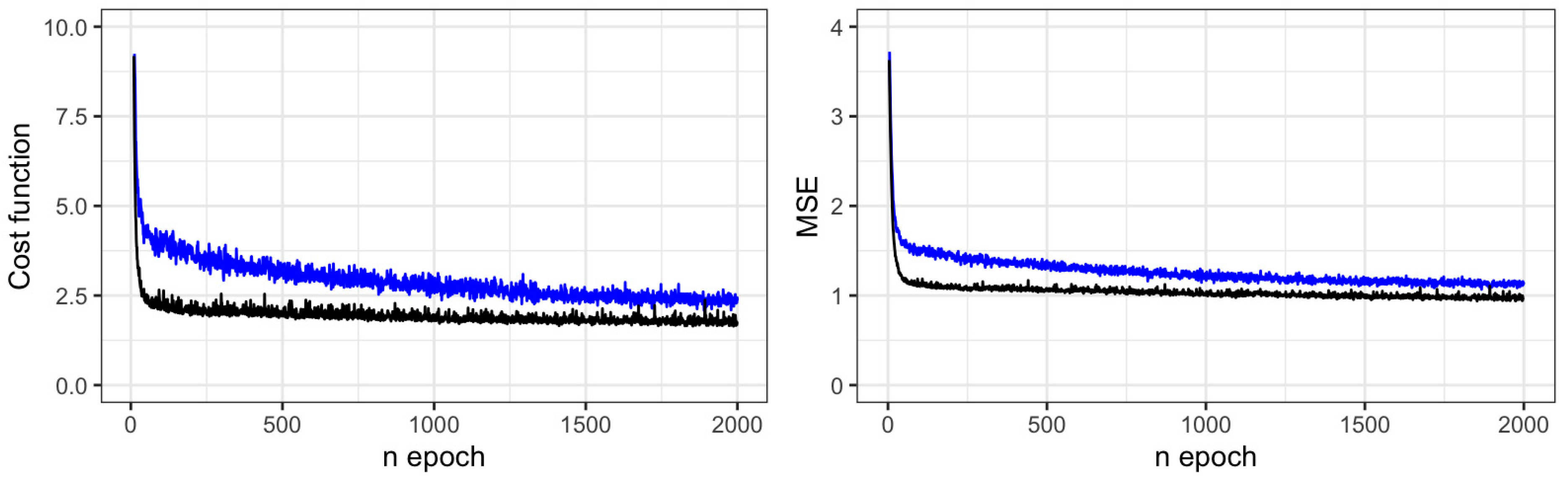
2.3. Modeling with Artificial Neural Networks
2.4. Artificial Neural Networks Structure
2.5. Performance Metrics and Cross-Validation
2.6. Generation of Estimated Volume
2.7. Proof of Methods Performance
3. Results
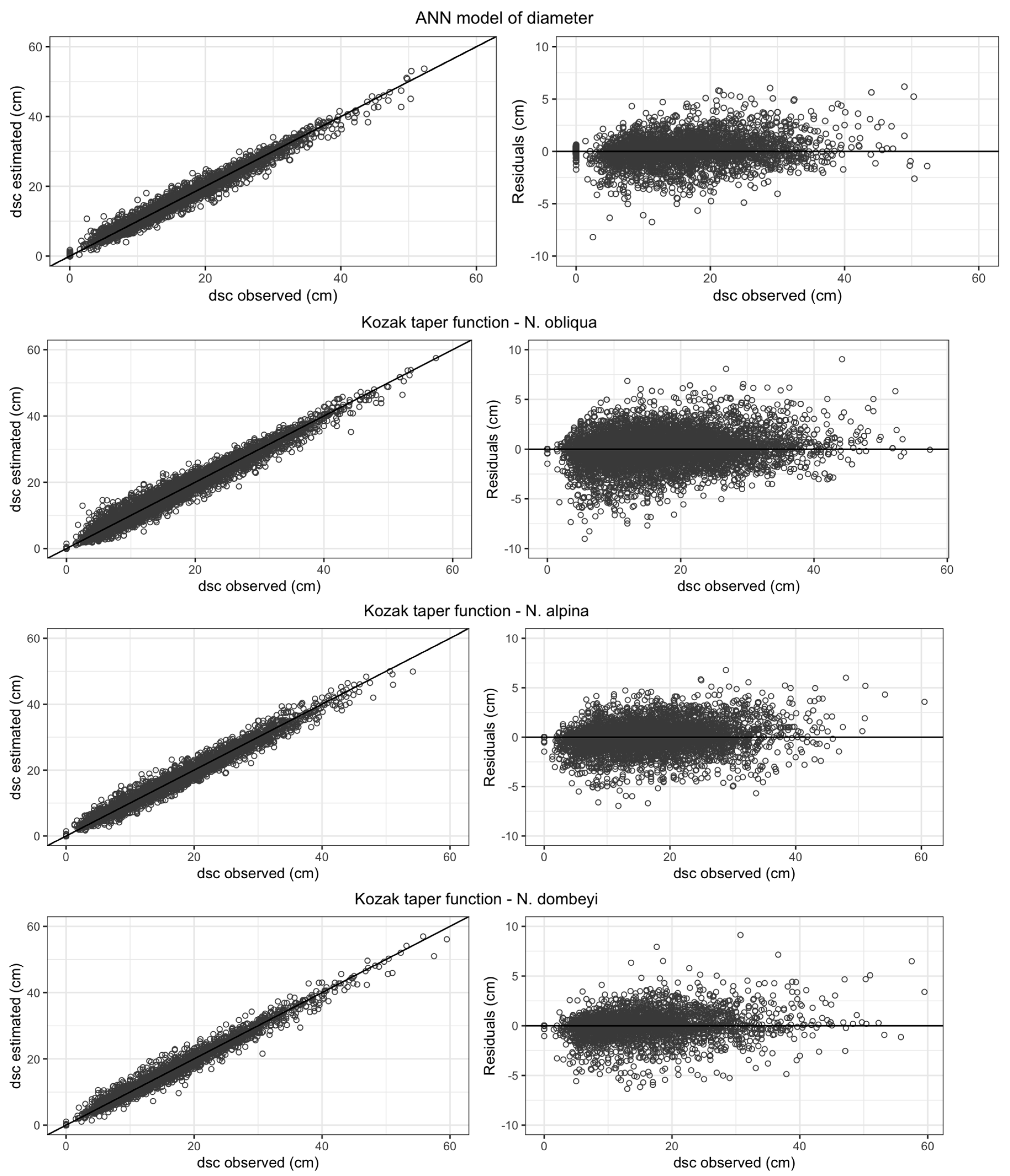
3.1. Stem Diameter Modeling
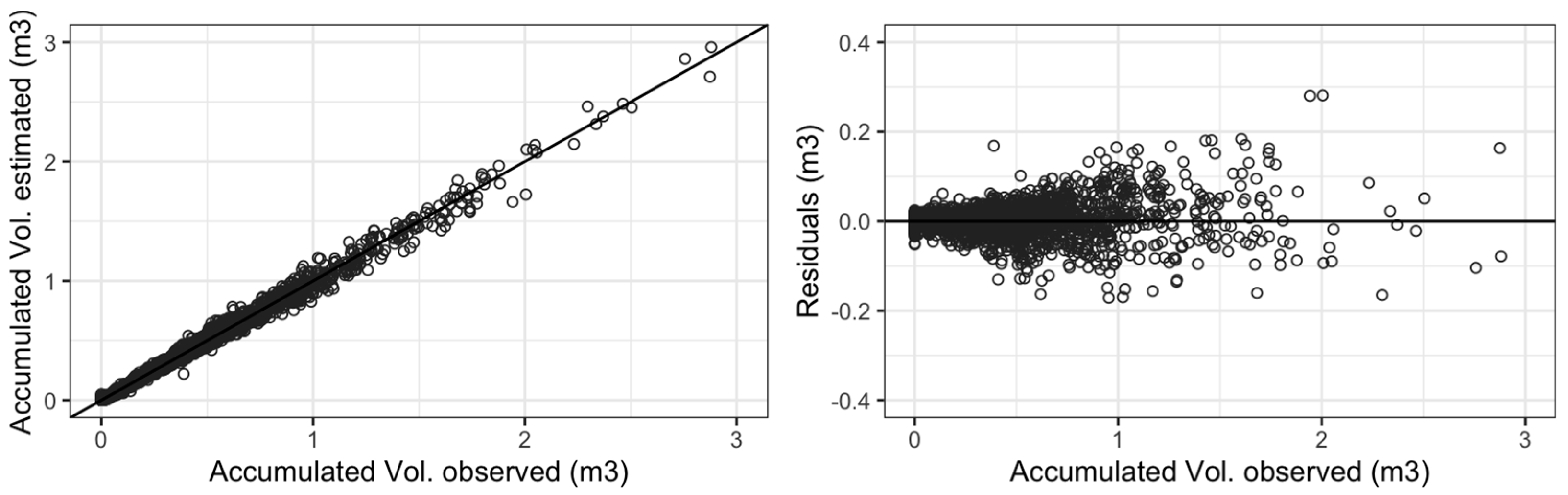
3.2. Modeling for the Accumulated Volume
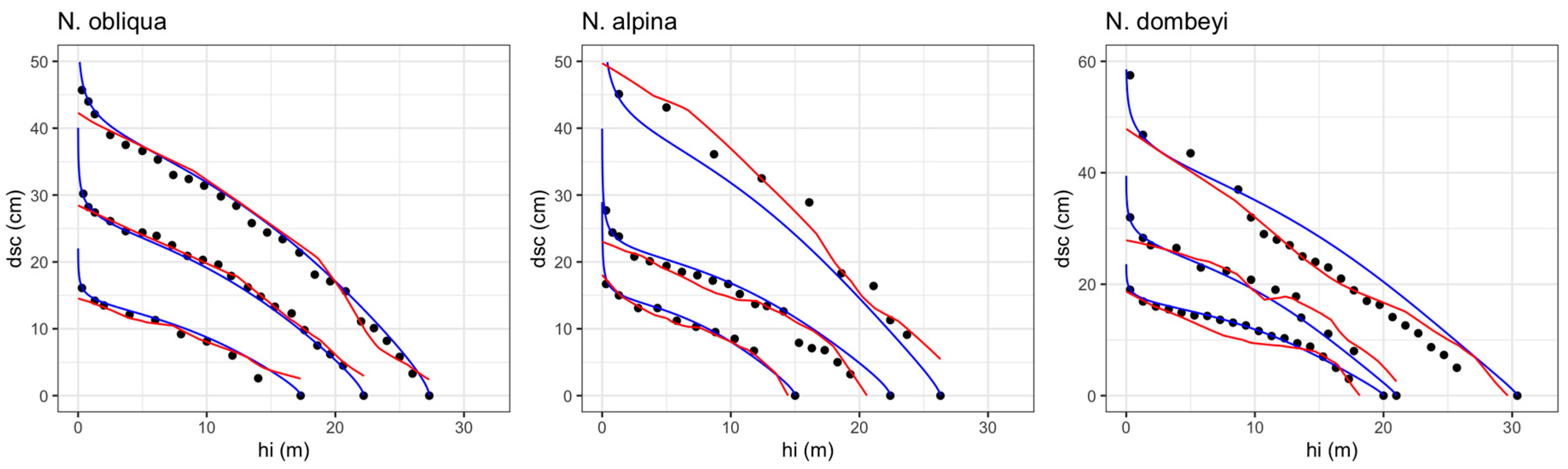
3.3. Individual Volume Estimation
3.4. Proof of Methods Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- # Setting callbacks and creating routes
- name <- "model_name"
- root0 <- "directory_path/Callbacks_Weights/"
- dir.create(paste0(root0,name,"/"), showWarnings = FALSE)
- root <- file.path(paste0(root0,name),"weights.{epoch:02d}-{val_loss:.2f}.hdf5")
- # Creating Artificial Neural Network (ANN)
- model <- keras_model_sequential()
- # Create architecture for diameter estimates using eight predictor variables
- model %>% layer_dense(units = 30, activation = "relu", input_shape = c(8)) %>%
- layer_dense(units = 25, activation = "relu", input_shape = c(8)) %>%
- layer_dropout(0.1) %>%
- layer_dense(units = 1)
- # Compile ANN
- modelo %>% compile(loss='mse',
- optimizer = 'adam',
- metrics = 'mae')
- # Create Callback
- cp_callback <- callback_model_checkpoint(filepath = root,
- save_best_only = TRUE,
- save_weights_only = TRUE,
- save_freq = "epoch",
- monitor = "val_loss")
- # Training ANN
- history <- model %>% fit(data_train,
- y_train,
- epochs=2000,
- batch_size=32,
- validation_split=0.2,
- callbacks=list(cp_callback))
- # Summary of ANN architecture
- summary(model)
- # Evaluation performance ANN using testing data
- model %>% evaluate(data_test, y_test)
- # Generating performance indices
- loss <- history[["metrics"]][["loss"]]
- val_loss <- history[["metrics"]][["val_loss"]]
- mae <- history[["metrics"]][["mae"]]
- val_mae <- history[["metrics"]][["val_mae"]]
- epoch <- seq(1:length(loss))
- # Setting a dataframe with performance indices
- data_epochs <- as.data.frame(cbind(epoch,loss,val_loss,mae,val_mae))
- # Writting a csv file with performance índices
- write.csv(data_epochs, paste0("directory_path/Models_save/epochs_my_",name,".csv"),
- row.names = FALSE)
- # Save ANN architecture
- model %>% save_model_hdf5(paste0("directory_path/Models_save/my_",name,".h5"))
- # Load ANN architecture and best weights
- best_file <- "weights.1860-1.95.hdf5"
- root2 <- paste0("directory_path/Callbacks_Weights/",name,"/",best_file)
- model <- keras_model_sequential()
- model %>% layer_dense(units = 30, activation = "relu", input_shape = c(8)) %>%
- layer_dense(units = 25, activation = "relu", input_shape = c(8)) %>%
- layer_dense(units = 1)
- model_load <- load_model_weights_hdf5(object=model, filepath = root2)
- # Predictions and performance índices in new dataset testing
- y_est <- model_load %>% predict(data_test_new)
- error <- (y_obs - y_est)
- sesgo <- mean(error)
- RMSE_test <- sqrt(mean(error^2))
- RMSE_test_p <- (RMSE_test/mean(y_test))*100
References
- Schikowski, A.B.; Corte, A.P.D.; Ruza, M.S.; Sanquetta, C.R.; Montano, R. Modeling of stem form and volume through machine learning. Anais da Academia Brasileira de Ciências 2018, 90, 3389–3401. [Google Scholar] [CrossRef] [PubMed]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Socha, J.; Netzel, P.; Cywicka, D. Stem taper approximation by artificial neural network and a regression set models. Forests 2020, 11, 79. [Google Scholar] [CrossRef]
- Amarioarei, A.; Paun, M.; Strimbu, B. Development of nonlinear parsimonious forest models using efficient expansion of the taylor series: Applications to site productivity and taper. Forests 2020, 11, 458. [Google Scholar] [CrossRef]
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, C.; Wei, X.; Blanco, J.A.; Trancoso, R. Tree profile equations are significantly improved when adding tree age and stocking degree: An example for Larix gmelinii in the Greater Khingan Mountains of Inner Mongolia, northeast China. Eur. J. For. Res. 2020, 139, 443–458. [Google Scholar] [CrossRef]
- Jiang, L.; Brooks, J.R. Taper, volume, and weight equations for Red Pine in West Virginia. North. J. Appl. For. 2008, 25, 151–153. [Google Scholar] [CrossRef]
- Valenzuela, C.; Acuña, E.; Ortega, A.; Quiñonez-Barraza, G.; Corral-Rivas, J.; Cancino, J. Variable-top stem biomass equations at tree-level generated by a simultaneous density-integral system for second growth forests of roble, raulí, and coigüe in Chile. J. For. Res. 2019, 30, 993–1010. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Eskandari, S.; Reza Jaafari, M.; Oliva, P.; Ghorbanzadeh, O.; Blaschke, T. Mapping land cover and tree canopy cover in Zagros Forests of Iran: Application of Sentinel-2, Google Earth, and field data. Remote Sens. 2020, 12, 1912. [Google Scholar] [CrossRef]
- Garg, R.; Aggarwal, H.; Centobelli, P.; Cerchione, R. Extracting knowledge from big data for sustainability: A comparison of machine learning techniques. Sustainability 2019, 11, 6669. [Google Scholar] [CrossRef]
- Rex, F.E.; Silva, C.A.; Dalla Corte, A.P.; Klauberg, C.; Mohan, M.; Cardil, A.; Silva, V.S.d.; Almeida, D.R.A.d.; Garcia, M.; Broadbent, E.N.; et al. Comparison of statistical modelling approaches for estimating tropical forest aboveground biomass stock and reporting their changes in low-intensity logging areas using multi-temporal LiDAR data. Remote Sens. 2020, 12, 1498. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, D.; Zhou, R.; Fang, L.; Zheng, X.; Lou, X. Estimation of DBH at forest stand level based on multi-parameters and generalized regression neural network. Forests 2019, 10, 778. [Google Scholar] [CrossRef]
- Ercanlı, İ. Innovative deep learning artificial intelligence applications for predicting relationships between individual tree height and diameter at breast height. For. Ecosyst. 2020, 7, 2. [Google Scholar] [CrossRef]
- Sylvain, J.-D.; Drolet, G.; Brown, N. Mapping dead forest cover using a deep convolutional neural network and digital aerial photography. ISPRS J. Photogramm. Remote Sens. 2019, 156, 14–26. [Google Scholar] [CrossRef]
- Verly Lopes, D.J.; Burgreen, G.W.; Entsminger, E.D. North American hardwoods identification using machine-learning. Forests 2020, 11, 298. [Google Scholar] [CrossRef]
- Bulanadi, J.; Tumibay, G.; Quioc, M.A. Spatiotemporal Data Analysis and Forecasting Model for Forestland Rehabilitation. Int. J. Comput. Sci. Res. 2019, 3, 229–245. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Trincado, G. Evaluation of potential modeling approaches for Scots pine stem diameter prediction in north-eastern Turkey. Comput. Electron. Agric. 2019, 162, 773–782. [Google Scholar] [CrossRef]
- Shen, J.; Hu, Z.; Sharma, R.P.; Wang, G.; Meng, X.; Wang, M.; Wang, Q.; Fu, L. Modeling height–diameter relationship for poplar plantations using combined-optimization multiple hidden layer back propagation neural network. Forests 2020, 11, 442. [Google Scholar] [CrossRef]
- Diamantopoulou, M.J.; Milios, E. Modelling total volume of dominant pine trees in reforestations via multivariate analysis and artificial neural network models. Biosyst. Eng. 2010, 105, 306–315. [Google Scholar] [CrossRef]
- Martins Silva, J.P.; Marques da Silva, M.L.; Ferreira da Silva, E.; Fernandes da Silva, G.; Ribeiro de Mendonca, A.; Cabacinha, C.D.; Araujo, E.F.; Santos, J.S.; Vieira, G.C.; Felix de Almeida, M.N.; et al. Computational techniques applied to volume and biomass estimation of trees in Brazilian savanna. J. Environ. Manag. 2019, 249, 109368. [Google Scholar] [CrossRef] [PubMed]
- Castaño-Santamaría, J.; Crecente-Campo, F.; Fernández-Martínez, J.L.; Barrio-Anta, M.; Obeso, J.R. Tree height prediction approaches for uneven-aged beech forests in northwestern Spain. For. Ecol. Manag. 2013, 307, 63–73. [Google Scholar] [CrossRef]
- Scrinzi, G.; Marzullo, L.; Galvagni, D. Development of a neural network model to update forest distribution data for managed alpine stands. Ecol. Model. 2007, 206, 331–346. [Google Scholar] [CrossRef]
- Mauro, F.; Frank, B.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Prediction of diameter distributions and tree-lists in southwestern Oregon using LiDAR and stand-level auxiliary information. Can. J. For. Res. 2019, 49, 775–787. [Google Scholar] [CrossRef]
- Nunes, M.H.; Gorgens, E.B. Artificial intelligence procedures for tree taper estimation within a complex vegetation mosaic in Brazil. PLoS ONE 2016, 11, e0154738. [Google Scholar] [CrossRef]
- Dolácio, C.J.F.; de Oliveira, T.W.G.; Oliveira, R.S.; Cerqueira, C.L.; Costa, L.R.R. Different approaches for modeling Swietenia macrophylla commercial volume in an Amazon agroforestry system. Agrofor. Syst. 2019, 94, 1011–1022. [Google Scholar] [CrossRef]
- Sakici, O.E.; Ozdemir, G. Stem taper estimations with artificial neural networks for mixed Oriental Beech and KazdaĞi Fir stands in Karabük Region, Turkey. Cerne 2018, 24, 439–451. [Google Scholar] [CrossRef]
- Şenyurt, M.; Ercanli, I. A comparison of artificial neural network models and regression models to predict tree volumes for crimean black pine trees in Cankiri forests. Sumar. List 2019, 143, 423. [Google Scholar] [CrossRef]
- Donoso, P.; Donoso, C.; Sandoval, V. Proposición de zonas de crecimiento de renovales de roble (Nothofagus obliqua) y raulí (Nothofagus alpina) en su rango de distribución natural. Bosque 1993, 14, 37–55. [Google Scholar] [CrossRef]
- Lara, A.; Donoso, C.; Donoso, P.; Nuñez, P.; Cavieres, A. Normas de manejo para raleo de renovales del tipo forestal roble–raulí–coigüe. In Silvicultura de los Bosques Nativos de Chile; Donoso, C., Lara, A., Eds.; Editorial Universitaria: Santiago, Chile, 1999; pp. 129–144. [Google Scholar]
- CONAF. Catastro de los Recursos Vegetacionales Nativos de Chile: Monitoreo de Cambios y Actualizaciones Periodo 1997–2011; Corporación Nacional Forestal (CONAF): Santiago, Chile, 2011; p. 29. [Google Scholar]
- Kershaw, J.A.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; p. 613. [Google Scholar]
- Bruce, D.; Curtis, R.O.; Vancoevering, C. Development of a system of taper and volume tables for Red Alder. For. Sci. 1968, 14, 339–350. [Google Scholar] [CrossRef]
- Demaerschalk, J.P. Converting volume equations to compatible taper equations. For. Sci. 1972, 18, 241–245. [Google Scholar] [CrossRef]
- Biging, G.S. A compatible volume- taper function for Alberta trees. For. Sci. 1984, 14, 339–350. [Google Scholar]
- Lee, W.-K.; Seo, J.-H.; Son, Y.-M.; Lee, K.-H.; von Gadow, K. Modeling stem profiles for Pinus densiflora in Korea. For. Ecol. Manag. 2003, 172, 69–77. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic gradient descent. Proceedings of THE 3rd International Conference on Learning Representations, ICLR 2015, Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Chollet, F. Keras. Available online: https://github.com/fchollet/keras (accessed on 29 October 2020).
- Qi, M.; Zhang, G.P. An investigation of model selection criteria for neural network time series forecasting. Eur. J. Oper. Res. 2001, 132, 666–680. [Google Scholar] [CrossRef]
- Hjelm, B. Stem taper equations for poplars growing on farmland in Sweden. J. For. Res. 2013, 24, 15–22. [Google Scholar] [CrossRef]
- Liu, Y.; Trancoso, R.; Ma, Q.; Yue, C.; Wei, X.; Blanco, J.A. Incorporating climate effects in Larix gmelinii improves stem taper models in the Greater Khingan Mountains of Inner Mongolia, northeast China. For. Ecol. Manag. 2020, 464, 118065. [Google Scholar] [CrossRef]
- Yang, S.-I.; Burkhart, H.E. Robustness of parametric and nonparametric fitting procedures of tree-stem taper with alternative definitions for validation data. J. For. 2020, 118, 576–583. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Brooks, J.R.; Wiant, H.V., Jr. Estimating tree bole volume using artificial neural network models for four species in Turkey. J. Environ. Manag. 2010, 91, 742–753. [Google Scholar] [CrossRef]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar] [CrossRef]
- Leite, H.G.; da Silva, M.L.M.; Binoti, D.H.B.; Fardin, L.; Takizawa, F.H. Estimation of inside-bark diameter and heartwood diameter for Tectona grandis Linn. trees using artificial neural networks. Eur. J. For. Res. 2011, 130, 263–269. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Brooks, J.R. The use of tree crown variables in over-bark diameter and volume prediction models. iForest 2014, 7, 132–139. [Google Scholar] [CrossRef]
- Sanquetta, C.R.; Piva, L.R.O.; Wojciechowski, J.; Corte, A.P.D.; Schikowski, A.B. Volume estimation of Cryptomeria japonica logs in southern Brazil using artificial intelligence models. South. For. 2017, 80, 29–36. [Google Scholar] [CrossRef]
- da Silva, E.M.; Maia, R.D.; Cabacinha, C.D. Bee-inspired RBF network for volume estimation of individual trees. Comput. Electron. Agric. 2018, 152, 401–408. [Google Scholar] [CrossRef]


| Species | n | Diameter (cm) | Height (m) | Volume (m3 tree−1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Av | SD | Min | Max | Av | SD | Min | Max | Av | SD | Min | Max | ||
| N. obliqua | 635 | 24.3 | 9.4 | 4.9 | 54.7 | 20.5 | 5.6 | 6.0 | 36.8 | 0.512 | 0.444 | 0.006 | 3.138 |
| N. alpina | 459 | 24.5 | 8.9 | 4.6 | 52.0 | 21.7 | 4.6 | 7.0 | 33.4 | 0.529 | 0.383 | 0.007 | 2.368 |
| N. dombeyi | 286 | 22.7 | 10.0 | 4.9 | 53.2 | 19.7 | 6.0 | 5.6 | 33.7 | 0.481 | 0.500 | 0.007 | 2.839 |
| Model | Model Structure | Cite |
|---|---|---|
| 1 | Bruce et al. [33] | |
| 2 | Bruce et al. [33] | |
| 3 | Demaerschalk [34] | |
| 4 | Biging [35] | |
| 5 | Lee et al. [36] | |
| 6 | Kozak [5] |
| Species | Model | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | Bias (cm) | AIC | BIC | RMSE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm) | (%) | |||||||||||||
| N. obliqua | 1 | 0.9793 * | −0.0079 * | 0.0013 * | 0.082 | 6.51 | 1.61 | 1.66 | 10.8 | |||||
| 2 | 0.9541 * | 0.0157 * | −0.0035 * | 0.179 | 6.49 | 1.59 | 1.64 | 10.7 | ||||||
| 3 | 0.1240 * | 0.9806 * | −0.7845 * | 0.7204 * | 0.029 | 8.50 | 1.89 | 1.65 | 10.7 | |||||
| 4 | 1.1601 * | 0.3885 * | 0.119 | 4.48 | 1.18 | 1.62 | 10.5 | |||||||
| 5 | 1.2676 * | 0.9473 * | 1.3716 * | −1.8155 * | 1.3268 * | 0.036 | 10.48 | 2.09 | 1.61 | 10.4 | ||||
| 6 | 0.9850 * | 0.9917 * | 1.0001 * | 0.4059 * | −0.1256 * | 0.5402 * | −0.1274 * | 0.0208 * | 0.018 | 16.43 | 2.51 | 1.54 | 10.0 | |
| N. alpina | 1 | 1.0015 * | −0.0195 * | 0.0015 ns | 0.025 | 6.47 | 1.57 | 1.60 | 10.5 | |||||
| 2 | 0.9634 * | 0.0260 * | −0.0078 * | 0.141 | 6.45 | 1.55 | 1.57 | 10.2 | ||||||
| 3 | 0.1072 * | 0.9497 * | −0.7479 * | 0.7318 * | 0.023 | 8.46 | 1.85 | 1.59 | 10.4 | |||||
| 4 | 1.1710 * | 0.3985 * | 0.107 | 4.43 | 1.12 | 1.53 | 10.0 | |||||||
| 5 | 1.3108 * | 0.9414 * | 1.9184 * | −2.4435 * | 1.5119 * | 0.032 | 10.41 | 2.01 | 1.50 | 9.8 | ||||
| 6 | 0.8925 * | 1.0267 * | 0.9994 * | 1.0690 * | −0.2439 * | 1.3983 * | −0.7274 * | 0.1219 * | 0.002 | 16.32 | 2.40 | 1.38 | 9.0 | |
| N. dombeyi | 1 | 0.9891 * | 0.0015 * | 0.0000 ns | −0.044 | 6.41 | 1.51 | 1.51 | 10.5 | |||||
| 2 | 0.9821 * | 0.0047 * | −0.0010 * | −0.009 | 6.41 | 1.50 | 1.50 | 10.5 | ||||||
| 3 | 0.0957 * | 0.9604 * | −0.7890 * | 0.7760 * | 0.017 | 8.40 | 1.79 | 1.49 | 10.4 | |||||
| 4 | 1.1989 * | 0.4342 * | 0.121 | 4.42 | 1.11 | 1.52 | 10.6 | |||||||
| 5 | 1.2683 * | 0.9504 * | 1.5661 * | −1.8257 * | 1.2954 * | 0.027 | 10.36 | 1.97 | 1.43 | 10.0 | ||||
| 6 | 0.8236 * | 1.0669 * | 0.9982 * | 0.5046 * | −0.0820 * | 0.3046 * | −0.0852 * | 0.1123 * | 0.008 | 16.30 | 2.38 | 1.35 | 9.5 | |
| Variable | Optimizer | Batch Size | Layer | Units | n pars. | Bias Test | RMSE Train | AIC | BIC | RMSE Test | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm) | (%) | (cm) | (%) | |||||||||
| Dsc | Adam | 32 | 2 | 30–25 | 1071 | −0.0812 | 1.1503 | 7.5 | 16.14 | 2.22 | 1.1643 | 7.7 |
| Adam | 32 | 2 | 30–20 | 911 | 0.0324 | 1.2508 | 8.1 | 16.22 | 2.30 | 1.2596 | 8.3 | |
| Adam | 32 | 3 | 30–25–10 | 1316 | 0.1282 | 1.2037 | 7.8 | 16.19 | 2.26 | 1.2963 | 8.5 | |
| (m3) | (%) | (m3) | (%) | |||||||||
| Volume | Adam | 32 | 3 | 40–20–10 | 1441 | −0.0001 | 0.0266 | 8.2 | 14.37 | −1.43 | 0.0296 | 9.0 |
| Adam | 32 | 3 | 40–30–20 | 2271 | 0.0008 | 0.0269 | 8.3 | 14.38 | −1.42 | 0.0318 | 9.7 | |
| Adam | 32 | 2 | 30–25 | 1101 | 0.0012 | 0.0284 | 8.8 | 14.44 | −1.36 | 0.0327 | 10.1 | |
| Species | Model | RMSE | |
|---|---|---|---|
| (m3 tree−1) | (%) | ||
| N. obliqua | Kozak | 0.0378 | 11.6 |
| One-phase ANN | 0.0336 | 10.2 | |
| Two-phase ANN | 0.0332 | 9.8 | |
| N. alpina | Kozak | 0.0266 | 9.9 |
| One-phase ANN | 0.0245 | 8.9 | |
| Two-phase ANN | 0.0236 | 8.3 | |
| N. dombeyi | Kozak | 0.0301 | 10.3 |
| One-phase ANN | 0.0294 | 9.3 | |
| Two-phase ANN | 0.0278 | 8.6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandoval, S.; Acuña, E. Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest. Forests 2022, 13, 2143. https://doi.org/10.3390/f13122143
Sandoval S, Acuña E. Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest. Forests. 2022; 13(12):2143. https://doi.org/10.3390/f13122143
Chicago/Turabian StyleSandoval, Simón, and Eduardo Acuña. 2022. "Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest" Forests 13, no. 12: 2143. https://doi.org/10.3390/f13122143
APA StyleSandoval, S., & Acuña, E. (2022). Stem Taper Estimation Using Artificial Neural Networks for Nothofagus Trees in Natural Forest. Forests, 13(12), 2143. https://doi.org/10.3390/f13122143







