Prediction of Static Bending Properties of Eucalyptus Clones Using Stress Wave Measurements on Standing Trees, Logs and Small Clear Specimens
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Origin
2.2. Sampling and Measurements
2.3. Data Analysis
3. Results and Discussion
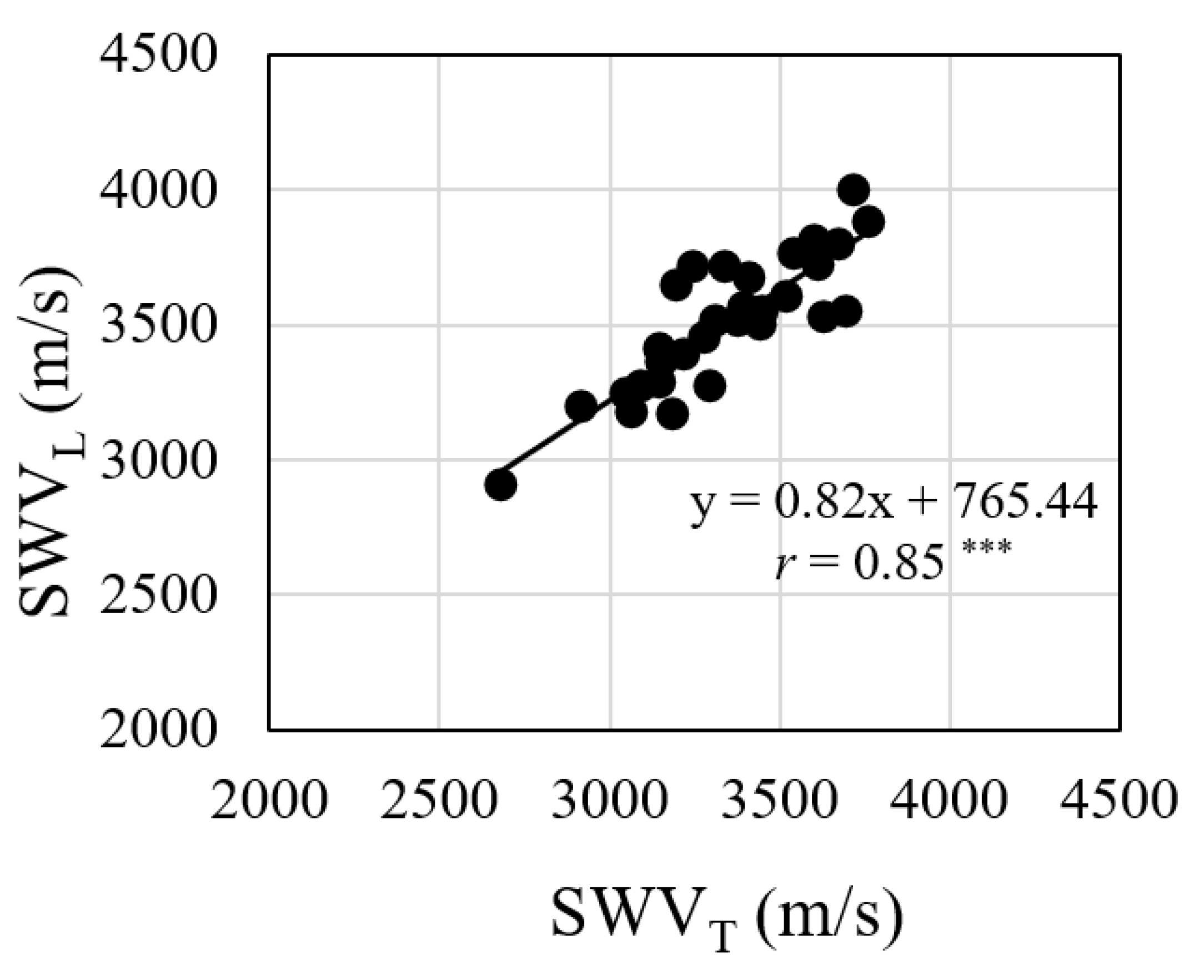
3.1. Stress Wave Measurements in Trees and Logs
3.2. Radial and Among-Clonal Variations of SWVS and Wood Properties
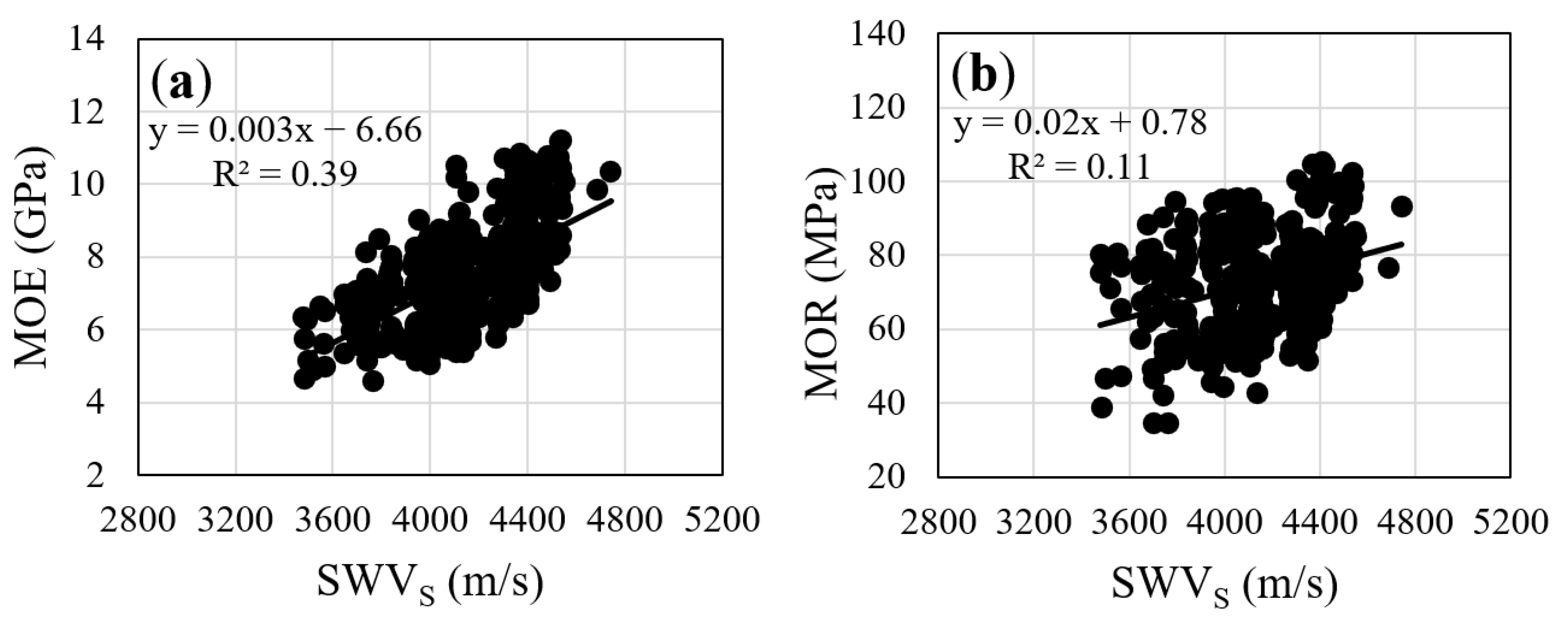
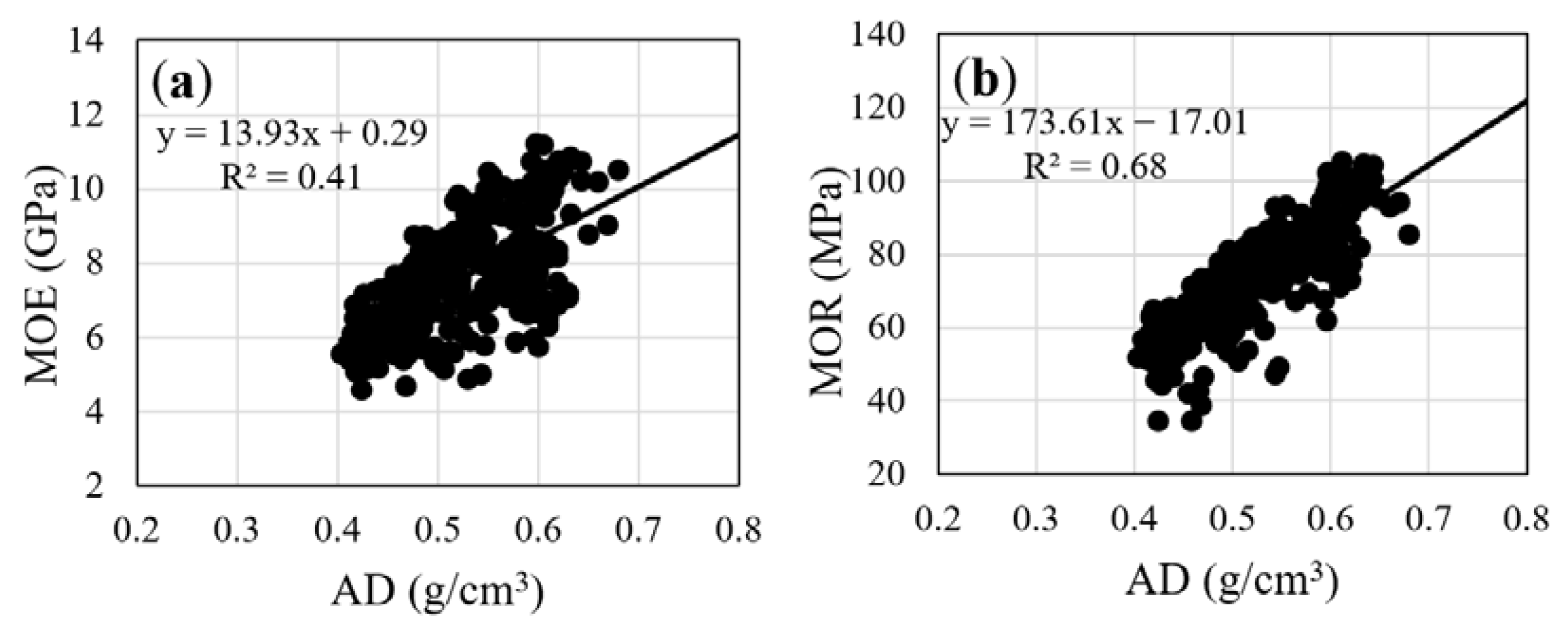
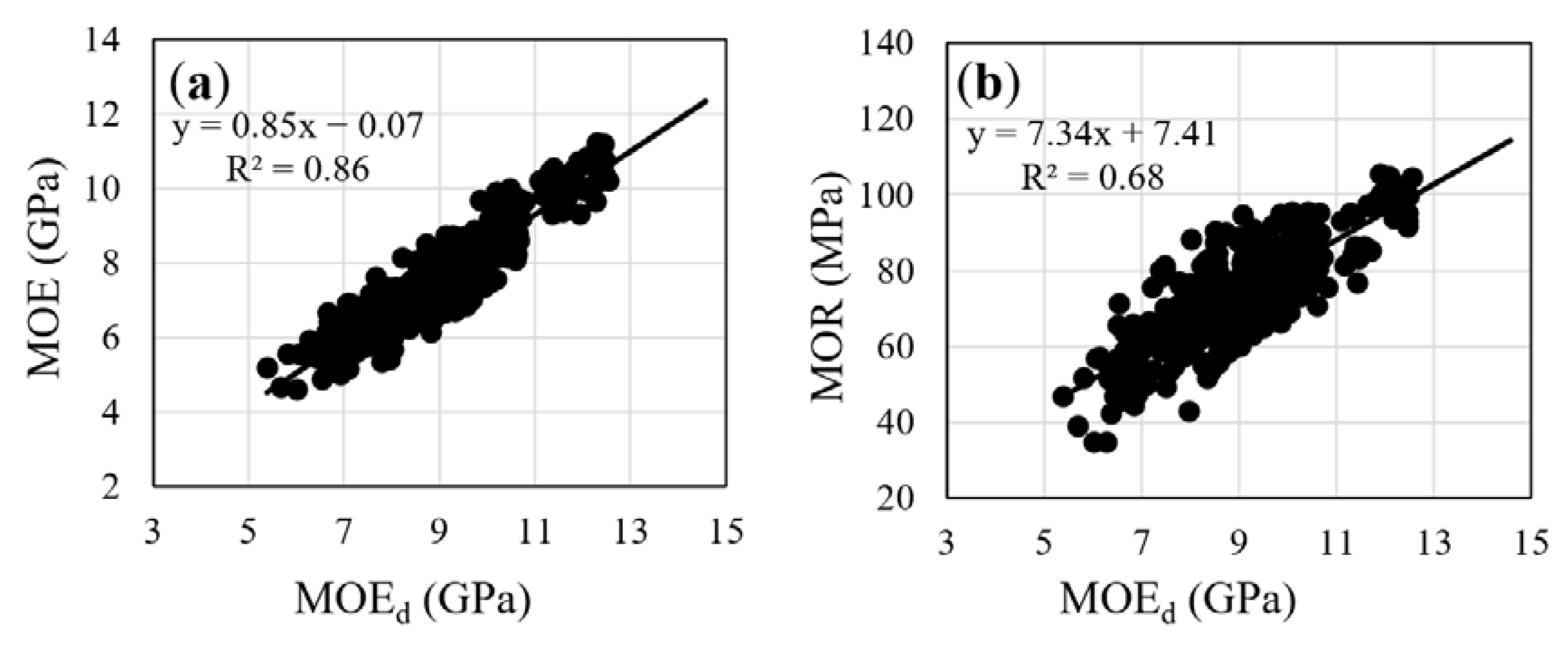
3.3. Prediction of Static Bending Properties Using Stress Wave Measurements on Standing Trees, Logs, and Small Specimens
4. Conclusions
- There was a significant difference in density and static properties in radial location and among Eucalyptus clones. Clones 3 and 5 had significantly higher AD, MOR, and MOE than other clones. Therefore, clones 3 and 5 might be appropriate for Eucalyptus tree breeding programs focused on improving wood quality, specifically for lumber production in the north central region or similar sites of Vietnam.
- SWVT and SWVL had positive correlations with both average MOE- and MOR-determined by static bending tests of small specimens. This implies that stress wave velocities measured using time of flight gives a good indication of static bending properties in Eucalyptus clones planted in Vietnam.
- At the specimen level, SWVS and AD were significantly correlated with static bending properties. Improved prediction of stiffness can be achieved when both SWVS and AD of specimens are used together to calculate dynamic modulus of elasticity (MOEd), while this combination does not improve predictions of bending strength, compared to using AD alone.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vietnam Ministry of Agriculture and Rural Development. The National Forest Status; Decision no. 1558/QD-BNN-TCLN; Vietnam Ministry of Agriculture and Rural Development: Hanoi, Vietnam, 2021. (In Vietnamese) [Google Scholar]
- Blackburn, D.; Huong, V.D.; Mendham, D. Returns to Vietnamese smallholder farmers from managing acacia plantations for sawn wood over 4–10 year rotations. For. Policy Econ. 2020, 121, 1023128. [Google Scholar] [CrossRef]
- Viet Nam News: Viet Nam’s Wood Industry Continues to Grow. Available online: https://link.gov.vn/R4BMAG4m (accessed on 15 May 2022).
- Eldridge, K.G.; Davidson, J.; Hardwood, C.E.; Van Wyk, G. Eucalypt Domestication and Breeding; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Kha, L.D.; Thinh, H.H.; Cuong, N.V. Improvement of Eucalypts for reforestation in Vietnam. In Eucalyptus in Asia, Proceedings of an International Conference Held in Zhanjiang, Guangdong, China, 7-11 April 2003; Turnbull, J.W., Ed.; Australian Centre for International Agricultural Research: Canberra, Australia, 2003. [Google Scholar]
- Vietnam Ministry of Agriculture and Rural Development. Decision Approving: Planning on Conversion of Forest Plant Species to Serve the Project on Restructuring the Forestry Sector; No. 23/QD-BNN-TCLN; Vietnam Ministry of Agriculture and Rural Development: Ha Noi, Vietnam, 2017. (In Vietnamese) [Google Scholar]
- Wu, S.; Xu, J.; Li, G.; Risto, V.; Du, Z.; Lu, Z.; Li, B.; Wang, W. Genotypic variation in wood properties and growth traits of Eucalyptus hybrid clones in southern China. New For. 2011, 42, 35–50. [Google Scholar] [CrossRef]
- Thinh, H.H.; Kien, N.D.; Hai, P.H.; Mai, D.T.; Kien, M.T.; Son, L.; Son, D.H. Research on Selection and Breeding of High-Yield and High-Quality Varieties for Some Main Tree Species in the 2006—2010 period; Technical Report; Vietnamese Academy of Forest Sciences: Ha Noi, Vietnam, 2010. (In Vietnamese) [Google Scholar]
- Washusen, R.; Ades, P.; Evans, R.; Ilic, J.; Vinden, P. Relationships between density, shrinkage, extractives content and microfibril angle in tension wood from three provenances of 10-year-old Eucalyptus globulus Labill. Holzforschung 2001, 55, 176–182. [Google Scholar] [CrossRef]
- McKenzie, H.M.; Shelbourne, C.J.A.; Kimberley, M.O.; McKinley, R.B.; Britton, R.A.J. Processing young plantation-grown Eucalyptus nitens for solid-wood products. 2: Predicting product quality from tree, increment core, disc, and 1-m billet properties. N. Zeal. J. For. Sci. 2003, 33, 79–113. [Google Scholar]
- Wentzel-Vietheer, M.; Washusen, R.; Downes, G.M.; Harwood, C.; Ebdon, N.; Ozarska, B.; Baker, T. Prediction of non-recoverable collapse in Eucalyptus globulus from near infrared scanning of radial wood samples. Eur. J. Wood Wood Prod. 2013, 71, 755–768. [Google Scholar] [CrossRef]
- Walker, J.C.F.; Butterfield, B.G.; Harris, J.M.; Langrish, T.A.G.; Uprichar, J.M. Primary Wood Processing: Principles and Practice; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Schimleck, L.; Dahlen, J.; Apiolaza, L.A.; Downes, G.; Emms, G.; Evans, R.; Moore, J.; Paques, L.; Van den Bulcke, J.; Wang, X. Non-destructive evaluation techniques and what they tell us about wood property variation. Forests 2019, 10, 718. [Google Scholar] [CrossRef]
- Wang, X.; Verrill, S.; Lowell, E.; Ross, R.J.; Herian, V.L. Acoustic sorting models for improved log segregation. Wood Fiber Sci. 2013, 45, 343–352. Available online: https://wfs.swst.org/index.php/wfs/article/view/1587 (accessed on 20 March 2022).
- Butler, M.A.; Dahlen, J.; Eberhardt, T.L.; Montes, C.; Antony, F.; Daniels, R.F. Acoustic evaluation of loblolly pine tree- and lumber-length logs allows for segregation of lumber modulus of elasticity, not for modulus of rupture. Ann. For. Sci. 2017, 74, 20. [Google Scholar] [CrossRef]
- Tumenjargal, B.; Ishiguri, F.; Takahashi, Y.; Nezu, I.; Baasan, B.; Chultem, G.; Aiso-Sanada, H.; Ohshima, J.; Yokota, S. Predicting the bending properties of Larix sibirica lumber using nondestructive testing method. Int. Wood Prod. J. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Van Duong, D.; Schimleck, L.; Tran, D.L.; Vo, H.D. Radial and among-clonal variations of the stress-wave velocity, wood density, and mechanical properties in 5-year-old Acacia auriculiformis clones. BioResources 2022, 17, 2084–2096. [Google Scholar] [CrossRef]
- Vo, D.H.; Tran, L.D.; Nguyen, V.B.; Hoang, V.T.; Tran, A.H.; Duong, Q.T. Site and Productivity Management of Multi-Rotation Plantations of Acacia Mangium, Acacia Auriculiformis and Eucalyptus Hybrids for Saw-Log Production in Vietnam; Technical Report; Vietnamese Academy of Forest Sciences: Ha Noi, Vietnam, 2018. (In Vietnamese) [Google Scholar]
- Ishiguri, F.; Diloksumpun, S.; Tanabe, J.; Iizuka, K.; Yokota, S. Stress-wave velocity of trees and dynamic Young’s modulus of logs of 4-year-old Eucalyptus camaldulensis trees selected for pulpwood production in Thailand. J. Wood Sci. 2013, 59, 506–511. [Google Scholar] [CrossRef]
- JIS Z2101:1994; Methods of Test for Woods. Japanese Standard Association: Tokyo, Japan, 2000. (In Japanese)
- R A Language and Environment for Statistical Computing—R Foundation for Statistical Computing. 2020. Available online: https://www.R-project.org/ (accessed on 3 January 2022).
- Blackburn, D.; Hamilton, M.; Hardwood, C.; Innes, T.; Potts, B.; Williams, D. Stiffness and checking of Eucalyptus nitens sawn boards: Genetic variation and potential for genetic improvement. Tree Genet. Genomes 2010, 6, 757–765. [Google Scholar] [CrossRef]
- Mora, C.R.; Schimleck, L.R.; Isik, F.; Mahon, J.M.; Clark, A.; Daniels, R.F. Relationships between acoustic variables and different measures of stiffness in standing Pinus taeda trees. Can. J. For. Res. 2009, 39, 1421–1429. [Google Scholar] [CrossRef]
- Ishiguri, F.; Matsui, R.; Iizuka, K.; Yokota, S.; Yoshizawa, N. Prediction of the mechanical properties of lumber by stress-wave velocity and Pilodyn penetration of 36-year-old Japanese larch trees. Holz Als Roh Werkst. 2008, 66, 275–280. [Google Scholar] [CrossRef]
- Dickson, R.L.; Raymond, C.A.; Joe, W.; Wilkinson, C.A. Segregation of Eucalyptus dunnii log using acoustics. For. Ecol. Manage. 2003, 179, 243–251. [Google Scholar] [CrossRef]
- De Melo, R.R.; Barbosa, K.T.; Beltrame, R.; Acosta, A.P.; Pimenta, A.S.; Mascarenhas, A.R.P. Ultrasound to determine physical-mechanical properties of Eucalyptus camaldulensis wood. Wood Mater. Sci. Eng. 2020, 16, 1–7. [Google Scholar] [CrossRef]
- Kothiyal, V.; Raturi, A. Estimating mechanical properties and specific gravity for five-year-old Eucalyptus tereticornis having board moisture content range by NIR spectroscopy. Holzforschung 2011, 65, 757–762. [Google Scholar] [CrossRef]
- Zobel, B.J.; van Buijtenen, J.P. Wood Variation, Its Causes and Control; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Van Duong, D.; Schimleck, L.; Lam Tran, D. Variation in Wood Density and Mechanical Properties of Acacia mangium Provenances Planted in Vietnam. J. Sus. For. 2022, 1–15. [Google Scholar] [CrossRef]
- Ilic, J. Relatioship among the dynamic and static elastic properties of air-dry Eucalyptus delegatensis R. Baker. Holz Als Roh Werkst. 2001, 59, 169–175. [Google Scholar] [CrossRef]
- De Oliveira, F.G.R.; de Campos, J.A.O.; Sales, A. Ultrasonic measurements in Brazilian hardwood. Mater. Res. 2002, 5, 51–55. [Google Scholar] [CrossRef]
- Wang, X.; Ross, R.J.; McClellan, M.; Barbour, R.J.; Erickson, J.R.; Forsman, J.W.; McGinnis, G.D. Nondestructive evaluation of standing trees with a stress wave method. Wood Fiber Sci. 2001, 33, 522–533. Available online: https://wfs.swst.org/index.php/wfs/article/view/1014 (accessed on 8 March 2022).
- Sharma, S.K.; Rao, R.V.; Shukla, S.R.; Kumar, P.; Sudheendra, R.; Sujatha, M.; Dubey, Y.M. Wood quality of coppiced Eucalyptus tereticornis for value addition. IAWA J. 2005, 26, 137–147. [Google Scholar] [CrossRef]
- Sales, A.; Candian, M.; Cardin, V.S. Evaluation of the mechanical properties of Brazilian lumber (Goupia glabra) by nondestructive techniques. Constr. Build. Mater. 2011, 25, 1450–1454. [Google Scholar] [CrossRef]
- Vazquez, C.; Goncalves, R.; Bertoldo, C.; Bano, V.; Vega, A.; Crespo, J.; Guaita, M. Determination of the mechanical properties of Castanea sativa Mill. using ultrasonic wave propagation and comparison with static compression and bending methods. Wood Sci. Technol. 2015, 49, 607–622. [Google Scholar] [CrossRef]
- Van Duong, D.; Ridley-Ellis, D. Estimating mechanical properties of clear wood from ten-year-old Melia azedarach trees using the stress wave method. Eur. J. Wood Wood Prod. 2021, 79, 941–949. [Google Scholar] [CrossRef]


| Clone | Species | Code | n | DBH (cm) | Tree Height (m) |
|---|---|---|---|---|---|
| UP54 | E. urophylla × E. pellita | 1 | 5 | 14.24 ± 0.88 | 18.81 ± 0.54 |
| UP95 | E. urophylla × E. pellita | 2 | 5 | 15.43 ± 0.58 | 20.01 ± 0.38 |
| UP99 | E. urophylla × E. pellita | 3 | 5 | 13.17 ± 0.93 | 18.40 ± 0.60 |
| U892 | E. urophylla | 4 | 5 | 14.18 ± 1.96 | 18.08 ± 0.63 |
| U1427 | E. urophylla | 5 | 5 | 14.06 ± 1.09 | 16.48 ± 0.65 |
| PN14 | E. urophylla | 6 | 5 | 13.83 ± 1.18 | 15.23 ± 0.30 |
| Clone | n | SWVT (m/s) | SWVL (m/s) | ||||
|---|---|---|---|---|---|---|---|
| Mean | SD | Range | Mean | SD | Range | ||
| 1 | 5 | 3151 cd | 101 | 3047–3299 | 3229 c | 55 | 3166–3285 |
| 2 | 5 | 3559 ab | 129 | 3399–3704 | 3569 b | 85 | 3498–3714 |
| 3 | 5 | 3662 a | 86 | 3546–3759 | 3844 a | 91 | 3762–3989 |
| 4 | 5 | 3375 bc | 95 | 3279–3521 | 3588 b | 106 | 3449–3706 |
| 5 | 5 | 3288 c | 123 | 3160–3450 | 3553 b | 137 | 3354–3714 |
| 6 | 5 | 3013 d | 214 | 2686–3219 | 3231 c | 206 | 2989–3404 |
| Mean | 30 | 3341 | 256 | 2686–3759 | 3503 | 246 | 2898–3989 |
| Variable | Description | n | SWVS (m/s) | AD (g/cm3) | MOEd (GPa) | MOE (GPa) | MOR (MPa) | |
|---|---|---|---|---|---|---|---|---|
| Radial positions | 1 | Near pith | 40 | 4021 b ± 128 | 0.43 b ± 0.02 | 6.99 b ± 0.62 | 5.96 b ± 0.51 | 56.50 b ± 4.63 |
| Near bark | 40 | 4244 a ± 168 | 0.48 a ± 0.02 | 8.71 a ± 0.84 | 7.38 a ± 0.69 | 69.59 a ± 4.69 | ||
| 2 | Near pith | 40 | 4229 b ± 131 | 0.46 b ± 0.02 | 8.27 b ± 0.70 | 6.57 b ± 0.57 | 62.37 b ± 7.01 | |
| Near bark | 40 | 4353 a ± 57 | 0.51 a ± 0.01 | 9.69 a ± 0.39 | 7.92 a ± 0.60 | 76.22 a ± 4.88 | ||
| 3 | Near pith | 28 | 4226 b ± 122 | 0.53 b ± 0.07 | 9.52 b ± 1.86 | 8.24 b ± 1.71 | 77.45 b ± 14.60 | |
| Near bark | 28 | 4421 a ± 122 | 0.58 a ± 0.05 | 11.42 a ± 1.28 | 9.73 a ± 1.23 | 92.50 a ± 11.71 | ||
| 4 | Near pith | 28 | 4234 b ± 153 | 0.47 b ± 0.03 | 8.39 b ± 1.08 | 7.30 b ± 0.92 | 65.09 b ± 6.36 | |
| Near bark | 28 | 4360 a ± 125 | 0.52 a ± 0.03 | 9.84 a ± 0.89 | 8.63 a ± 1.02 | 76.36 a ± 4.90 | ||
| 5 | Near pith | 32 | 3744 b ± 149 | 0.59 a ± 0.02 | 8.32 b ± 0.74 | 7.02 b ± 0.77 | 80.42 b ± 6.16 | |
| Near bark | 32 | 4016 a ± 83 | 0.60 a ± 0.03 | 9.61 a ± 0.67 | 8.39 a ± 0.66 | 87.47 a ± 4.63 | ||
| 6 | Near pith | 28 | 3772 b ± 144 | 0.50 b ± 0.03 | 7.07 b ± 0.77 | 5.97 b ± 0.78 | 57.01 b ± 11.10 | |
| Near bark | 28 | 4034 a ± 186 | 0.57 a ± 0.02 | 9.25 a ± 0.72 | 7.50 a ± 0.83 | 76.13 a ± 6.10 | ||
| Clones | 1 | 80 | 4133 b ± 186 | 0.46 e ± 0.03 | 7.85 c ± 1.14 | 6.67 d ± 0.94 | 63.05 c ± 8.05 | |
| 2 | 80 | 4291 a ± 118 | 0.49 d ± 0.03 | 8.98 b ± 0.91 | 7.24 bc ± 0.89 | 69.30 b ± 9.20 | ||
| 3 | 56 | 4323 a ± 194 | 0.56 b ± 0.06 | 10.47 a ± 1.85 | 8.98 a ± 1.65 | 84.98 a ± 15.15 | ||
| 4 | 56 | 4297 a ± 152 | 0.49 d ± 0.04 | 9.12 b ± 1.22 | 7.97 b ± 1.17 | 70.73 b ± 8.00 | ||
| 5 | 64 | 3880 c ± 182 | 0.60 a ± 0.03 | 8.97 b ± 0.96 | 7.70 b ± 0.99 | 83.94 a ± 6.47 | ||
| 6 | 56 | 3903 c ± 211 | 0.53 c ± 0.05 | 8.16 c ± 1.33 | 6.73 cd ± 1.11 | 66.57 bc ± 13.11 | ||
| Mean | 392 | 4142 ± 249 | 0.52 ± 0.06 | 8.86 ± 1.48 | 7.48 ± 1.36 | 72.47 ± 13.11 | ||
| Reference | Species | Country | Stand Age | AD (g/cm3) | MOEd (GPa) | MOE (GPa) | MOR (MPa) |
|---|---|---|---|---|---|---|---|
| This study | Eucalyptus | Vietnam | 6 | 0.46–0.60 | 7.85–10.47 | 6.67–8.98 | 63.05–84.98 |
| De Melo et al. [26] | E. camaldulensis | Brazil | 5 | 0.56 | 7.01 | 77.95 | |
| Kothiyal and Raturi [27] | E. tereticornis | India | 5 | 0.58 | 7.98 | 84.80 | |
| Duong et al. [17] | A. auriculiformis | Vietnam | 5 | 0.50–0.59 | 8.70–10.95 | 7.37–9.14 | 83.81–101.43 |
| Duong et al. [29] | A. mangium | Vietnam | 5 | 0.44–0.50 | 7.73–8.92 | 7.03–8.23 | 66.63–84.19 |
| Source of Variation | df | SWVS | AD | MOEd | MOE | MOR | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| p Value | Var (%) | p Value | Var (%) | p Value | Var (%) | p Value | Var (%) | p Value | Var (%) | ||
| Clone (C) | 5 | 0.001 | 40.38 | 0.001 | 43.22 | 0.001 | 16.47 | 0.001 | 19.54 | 0.001 | 24.00 |
| Ramet (T)/Clone | 24 | 0.001 | 2.18 | 0.001 | 2.23 | 0.001 | 2.33 | 0.001 | 2.90 | 0.001 | 2.00 |
| Radial position (R) | 1 | 0.001 | 55.92 | 0.001 | 52.44 | 0.001 | 80.15 | 0.001 | 76.92 | 0.001 | 72.39 |
| C × R | 5 | 0.001 | 0.86 | 0.001 | 1.72 | 0.001 | 0.63 | 0.677 | 0.10 | 0.001 | 1.17 |
| T × R | 23 | 0.001 | 0.46 | 0.001 | 0.29 | 0.001 | 0.31 | 0.001 | 0.39 | 0.001 | 0.31 |
| Residuals | 333 | 0.20 | 0.10 | 0.12 | 0.15 | 0.13 | |||||
| Level | Y | X | n | Equation | r | p-Value |
|---|---|---|---|---|---|---|
| Tree level | MOE | SWVT | 30 | Y = 0.003X − 1.27 | 0.61 | <0.001 |
| MOR | 30 | Y = 0.021X + 2.50 | 0.53 | 0.003 | ||
| Log level | MOE | SWVL | 30 | Y = 0.003X − 4.42 | 0.76 | <0.001 |
| MOR | 30 | Y = 0.030X − 31.03 | 0.71 | <0.001 |
| Clone | Variables | MOE | MOR | ||
|---|---|---|---|---|---|
| Equation | r | Equation | r | ||
| 1 | SWVS | MOE = 0.004SWVS − 10.51 | 0.83 *** | MOR = 0.03SWVS − 57.24 | 0.67 *** |
| AD | MOE = 25.46AD − 4.96 | 0.85 *** | MOR = 229.26AD − 41.67 | 0.89 *** | |
| MOEd | MOE = 0.76MOEd + 0.69 | 0.92 *** | MOR = 5.94MOEd + 16.43 | 0.84 *** | |
| 2 | SWVS | MOE = 0.005SWVS − 15.22 | 0.69 *** | MOR = 0.05SWVS − 131.10 | 0.60 *** |
| AD | MOE = 22.42AD − 43.66 | 0.75 *** | MOR = 248.15AD − 51.40 | 0.81 *** | |
| MOEd | MOE = 0.82MOEd − 0.11 | 0.83 *** | MOR = 8.29MOEd − 5.17 | 0.82 *** | |
| 3 | SWVS | MOE = 0.007SWVS − 20.79 | 0.81 *** | MOR = 0.06SWVS − 166.60 | 0.74 *** |
| AD | MOE = 23.40AD − 4.03 | 0.92 *** | MOR = 217.08AD − 35.74 | 0.93 *** | |
| MOEd | MOE = 0.85MOEd + 0.03 | 0.96 *** | MOR = 7.65MOEd + 4.87 | 0.93 *** | |
| 4 | SWVS | MOE = 0.006SWVS − 18.12 | 0.79 *** | MOR = 0.04SWVS − 79.81 | 0.67 *** |
| AD | MOE = 26.76AD − 5.21 | 0.88 *** | MOR = 160.32AD − 8.17 | 0.78 *** | |
| MOEd | MOE = 0.88MOEd − 0.06 | 0.92 *** | MOR = 5.16MOEd + 23.71 | 0.79 *** | |
| 5 | SWVS | MOE = 0.005SWVS − 10.18 | 0.84 *** | MOR = 0.02SWVS − 1.68 | 0.62 *** |
| AD | MOE = 13.01AD − 0.04 | 0.36 ** | MOR = 74.11AD + 39.81 | 0.31 * | |
| MOEd | MOE = 0.93MOEd − 0.60 | 0.89 *** | MOR = 4.61MOEd + 42.59 | 0.68 *** | |
| 6 | SWVS | MOE = 0.004SWVS − 10.17 | 0.82 *** | MOR = 0.04SWVS − 10.86 | 0.72 *** |
| AD | MOE = 15.15AD − 1.32 | 0.63 *** | MOR = 215.42AD − 47.95 | 0.76 *** | |
| MOEd | MOE = 0.74MOEd + 0.71 | 0.88 *** | MOR = 8.59MOEd − 3.55 | 0.87 *** | |
| Combined | SWVS | MOE = 0.003SWVS − 6.66 | 0.63 *** | MOR = 0.02SWVS + 0.78 | 0.33 *** |
| AD | MOE = 13.93AD + 0.29 | 0.64 *** | MOR = 173.61AD − 17.01 | 0.82 *** | |
| MOEd | MOE = 0.85MOEd − 0.07 | 0.93 *** | MOR = 7.34MOEd + 7.41 | 0.83 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Duong, D.; Schimleck, L. Prediction of Static Bending Properties of Eucalyptus Clones Using Stress Wave Measurements on Standing Trees, Logs and Small Clear Specimens. Forests 2022, 13, 1728. https://doi.org/10.3390/f13101728
Van Duong D, Schimleck L. Prediction of Static Bending Properties of Eucalyptus Clones Using Stress Wave Measurements on Standing Trees, Logs and Small Clear Specimens. Forests. 2022; 13(10):1728. https://doi.org/10.3390/f13101728
Chicago/Turabian StyleVan Duong, Doan, and Laurence Schimleck. 2022. "Prediction of Static Bending Properties of Eucalyptus Clones Using Stress Wave Measurements on Standing Trees, Logs and Small Clear Specimens" Forests 13, no. 10: 1728. https://doi.org/10.3390/f13101728
APA StyleVan Duong, D., & Schimleck, L. (2022). Prediction of Static Bending Properties of Eucalyptus Clones Using Stress Wave Measurements on Standing Trees, Logs and Small Clear Specimens. Forests, 13(10), 1728. https://doi.org/10.3390/f13101728








