Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs
Abstract
:1. Introduction
2. Materials and Methods
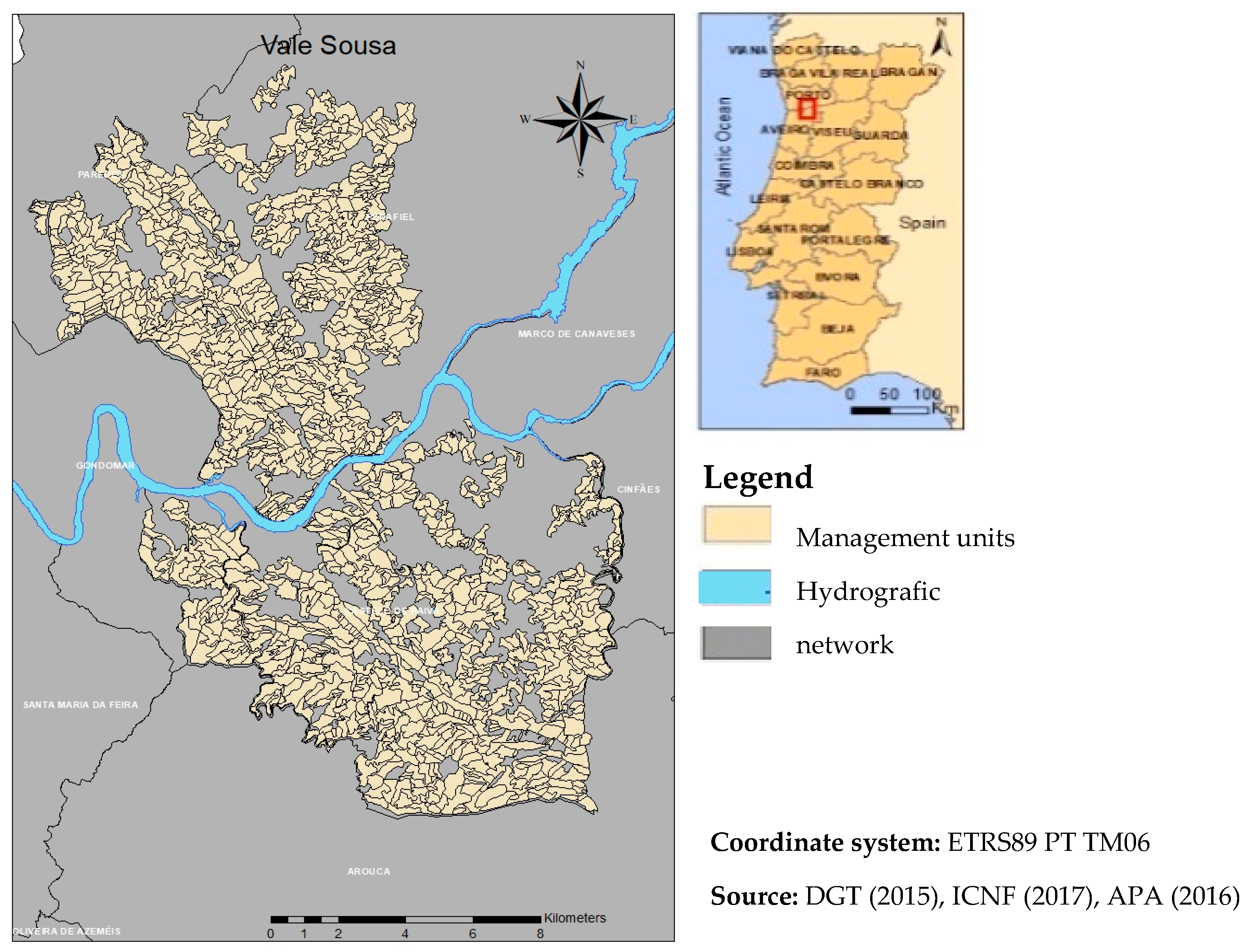
2.1. Study Area and Materials
2.2. Growth and Yield Modeling and Simulation
2.3. The MOIP Formulation
- TWOOD—total amount of wood flows;
- CARB—average carbon stock;
- CORK—total adult cork yield;
- EROS—total erosion;
- BIOD—biodiversity indicator;
- FRES—fire resistance indicator.
δ → min, EROS → min
2.4. Solving the MOIP
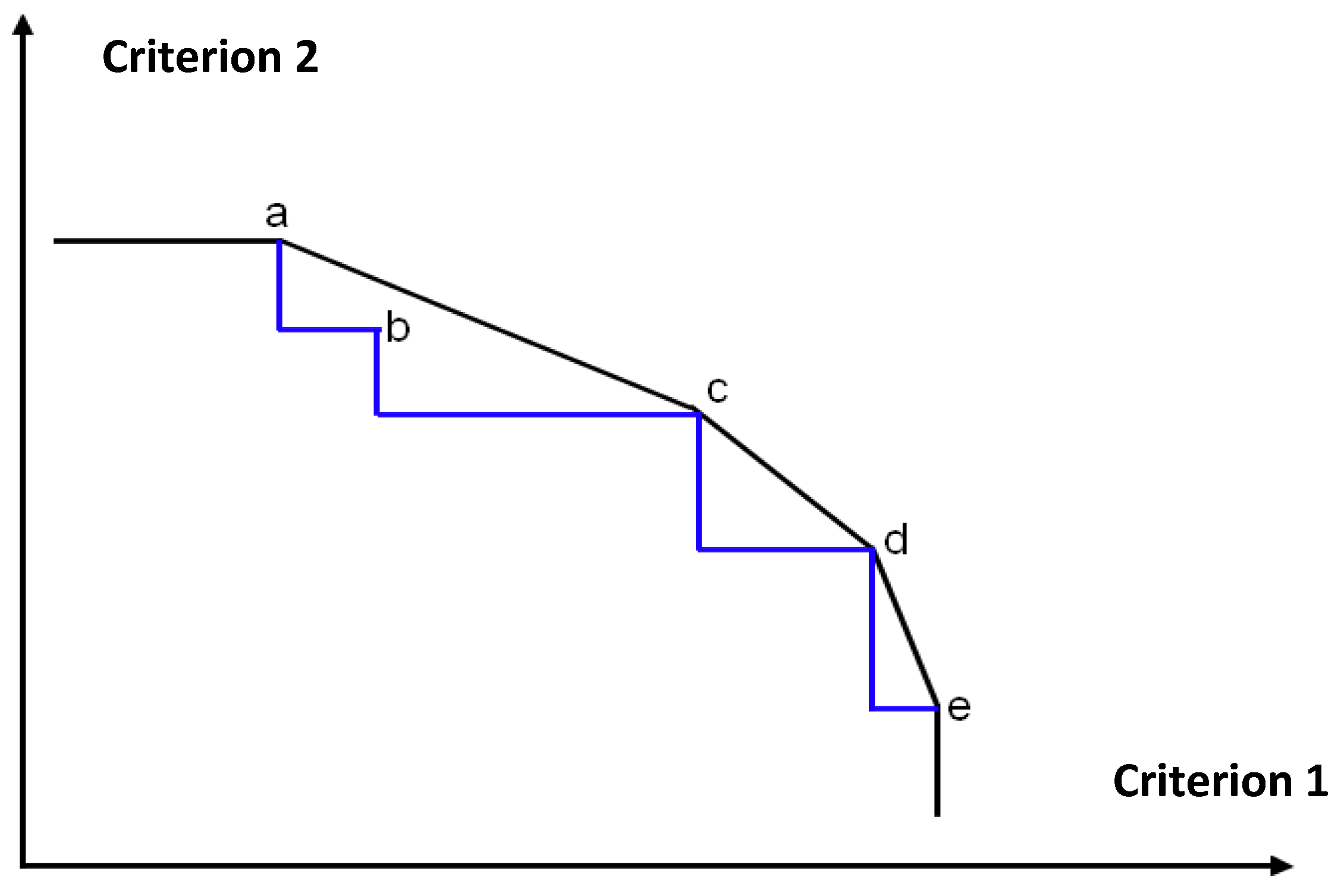
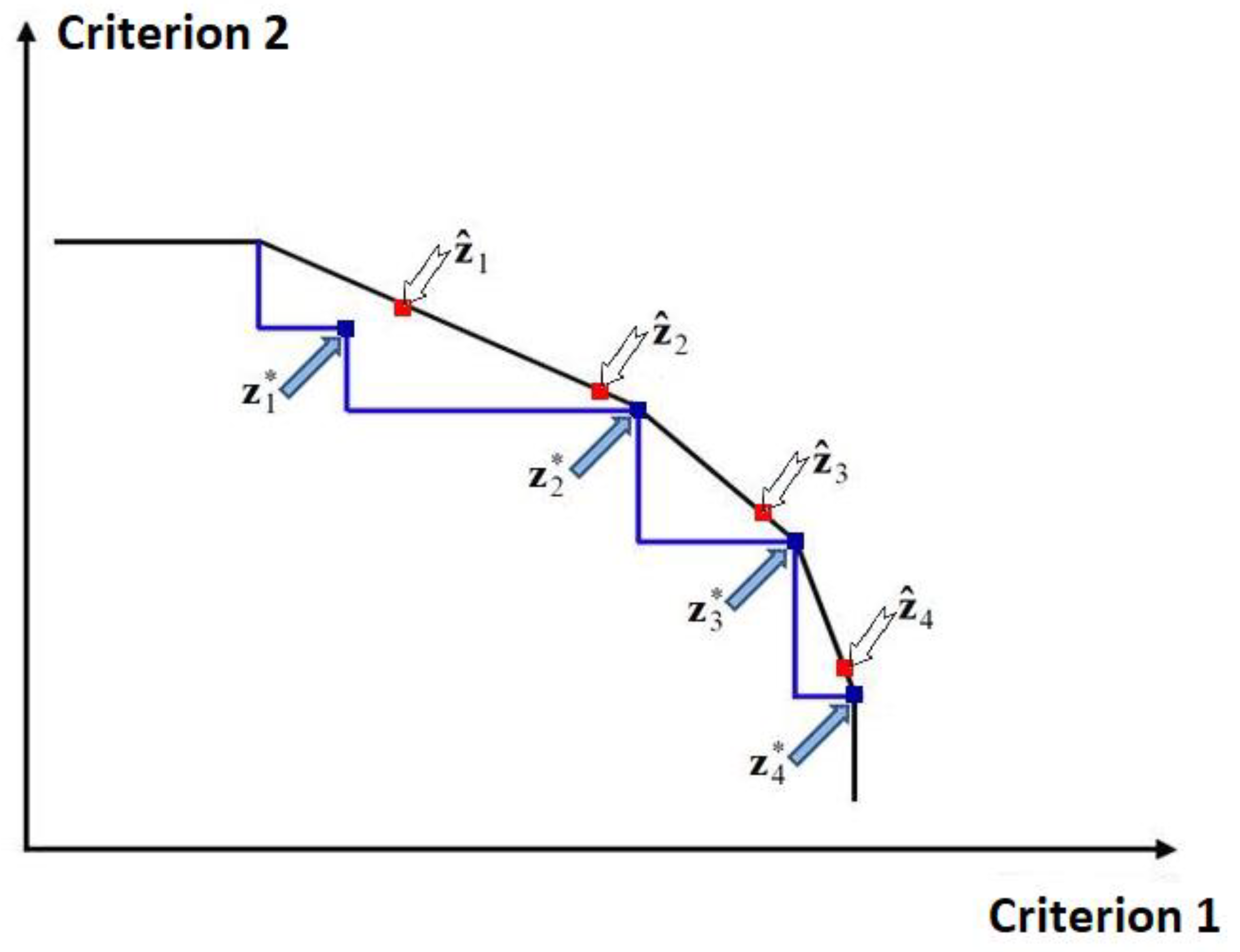
2.5. Decomposition Approach to Constructing Pareto Frontier with MOIP Problems
3. Results
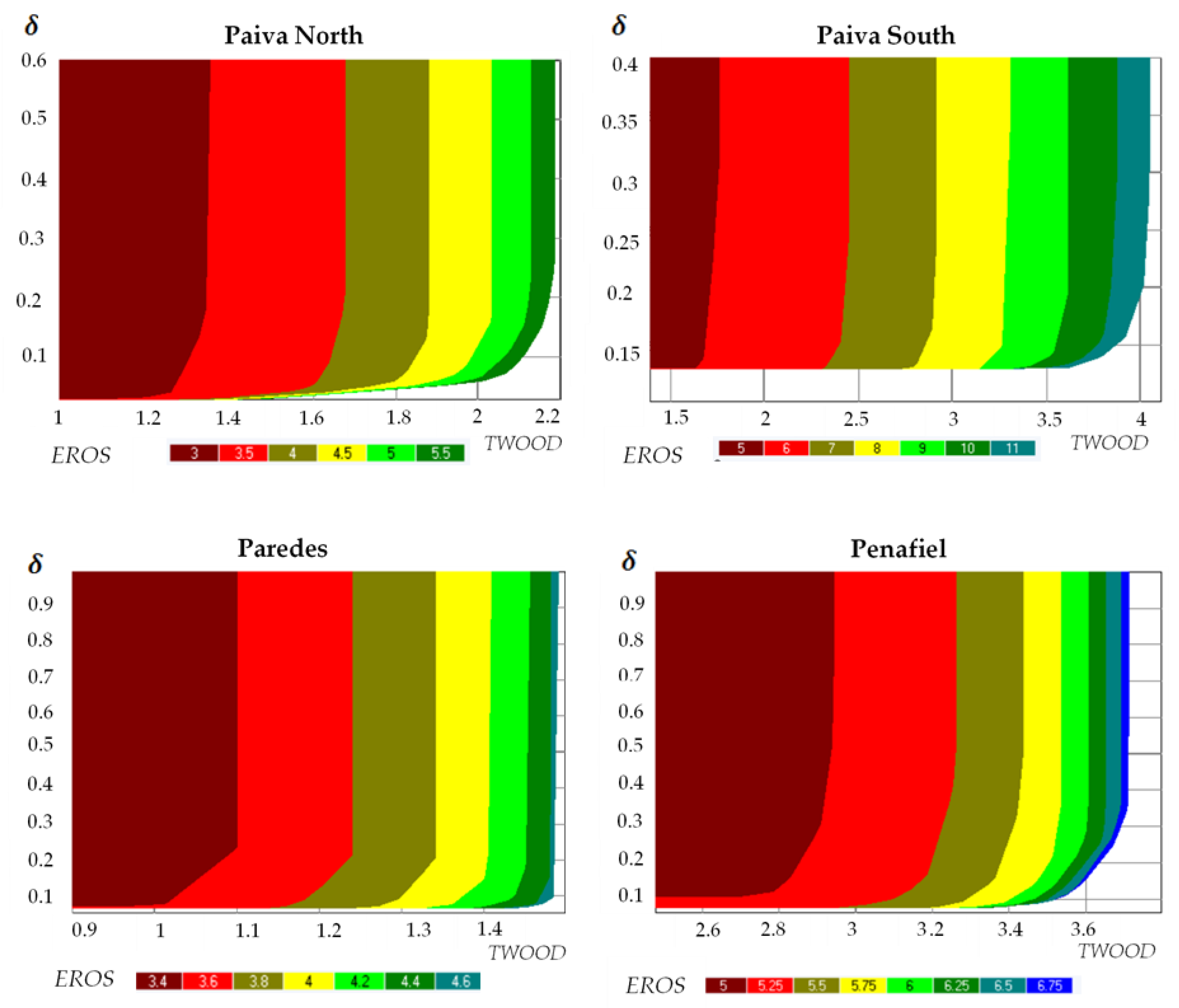
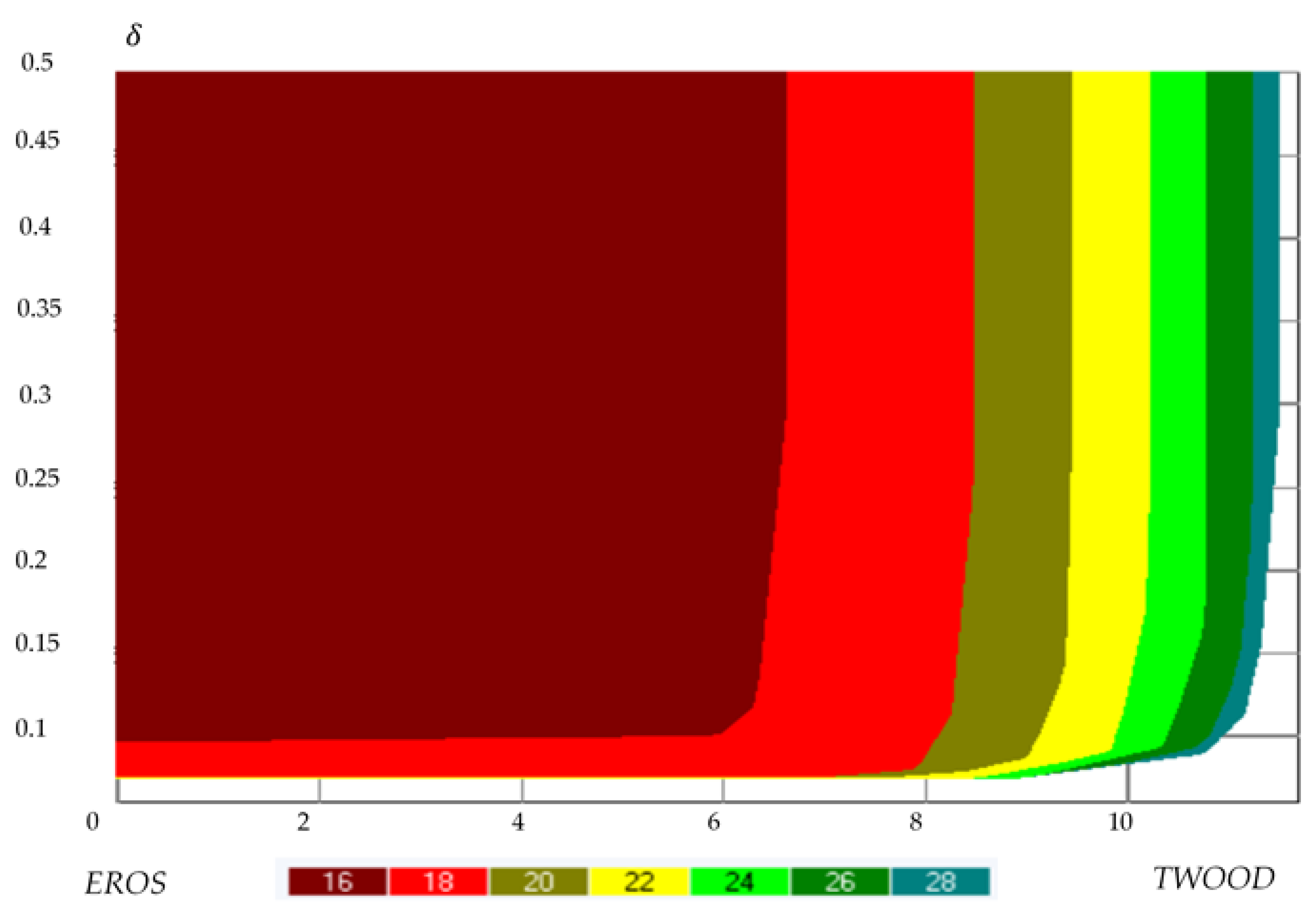
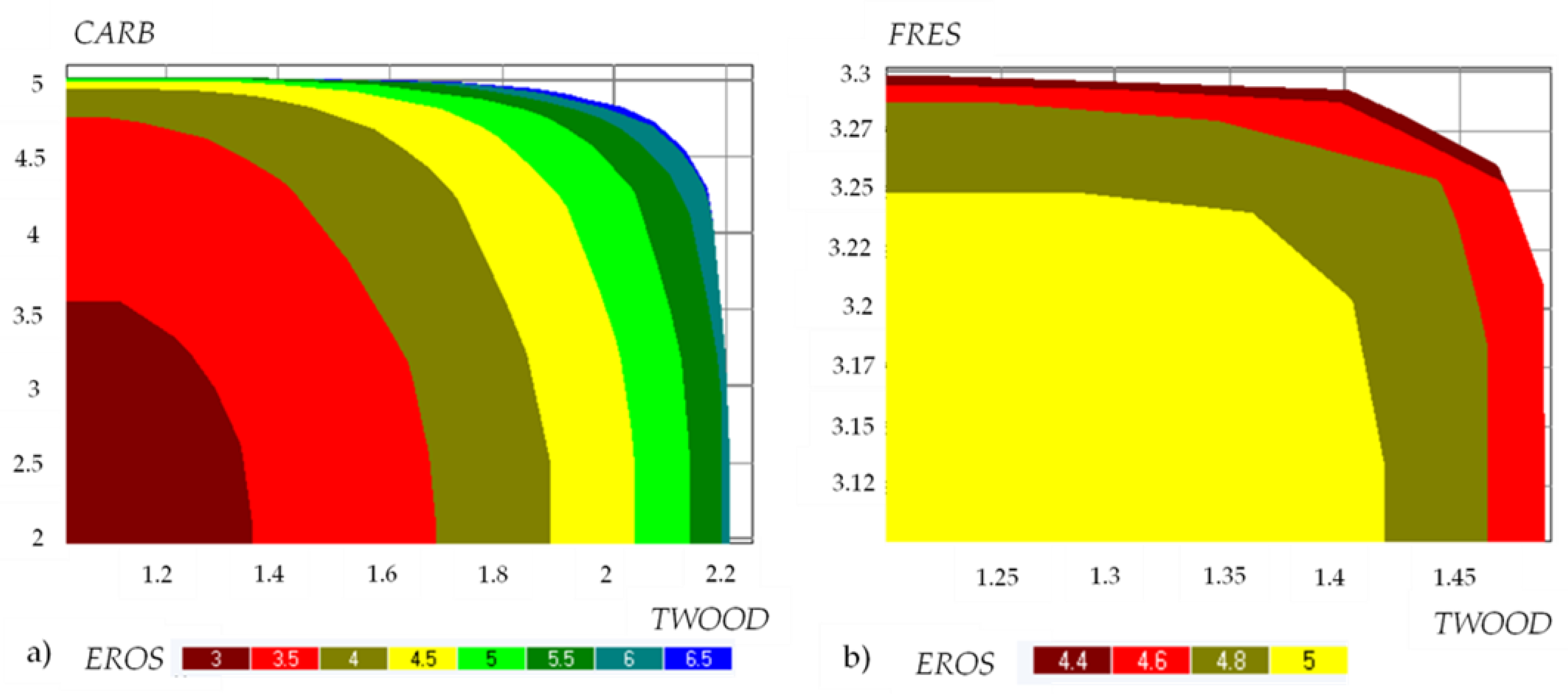
3.1. Tradeoff Analysis for the Sub-Problems
3.2. Tradeoff Analysis for the Master Problem after Merging the tradeoffs from All Subareas
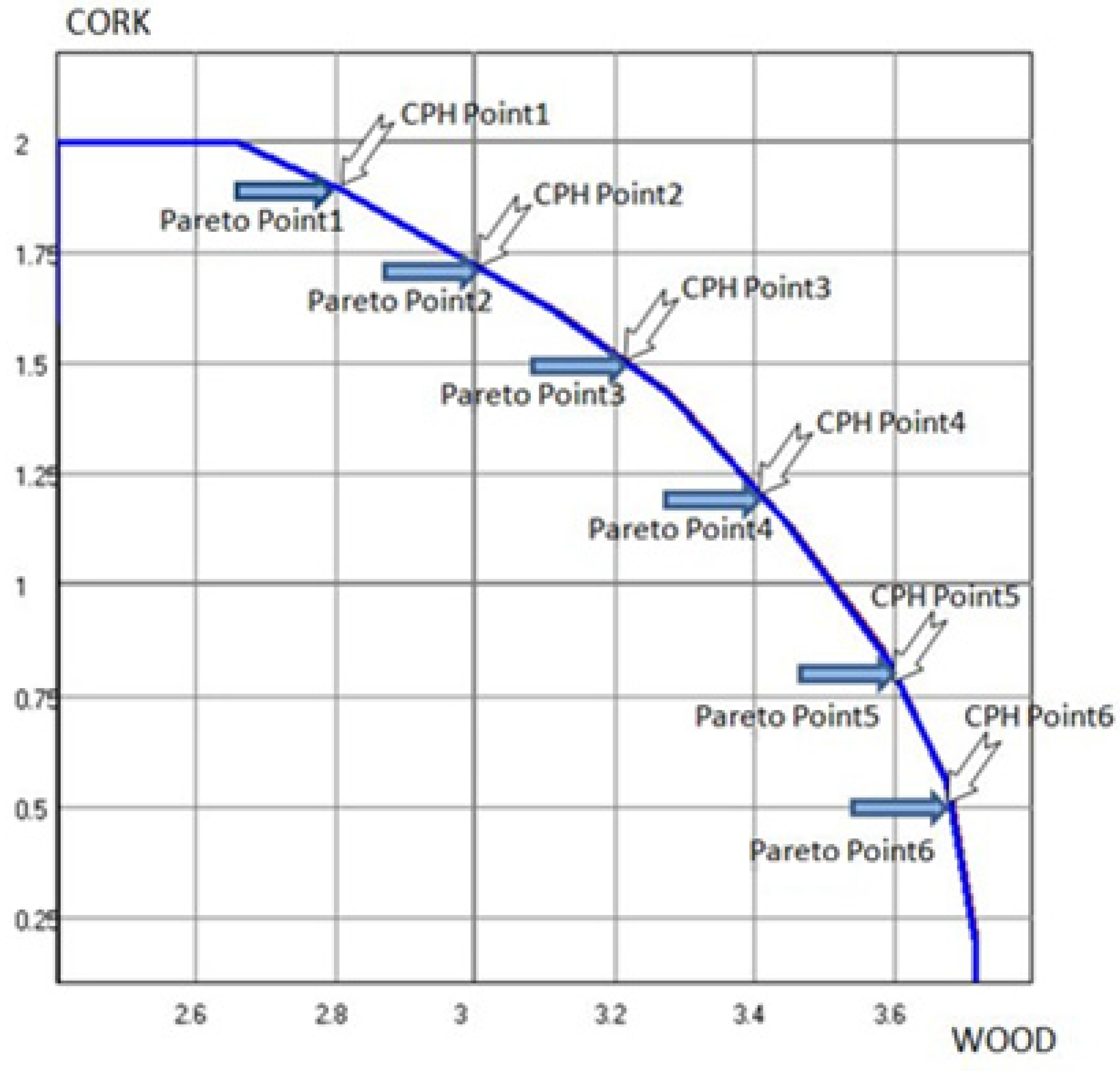
3.3. Surrogate Pareto Frontier Accuracy
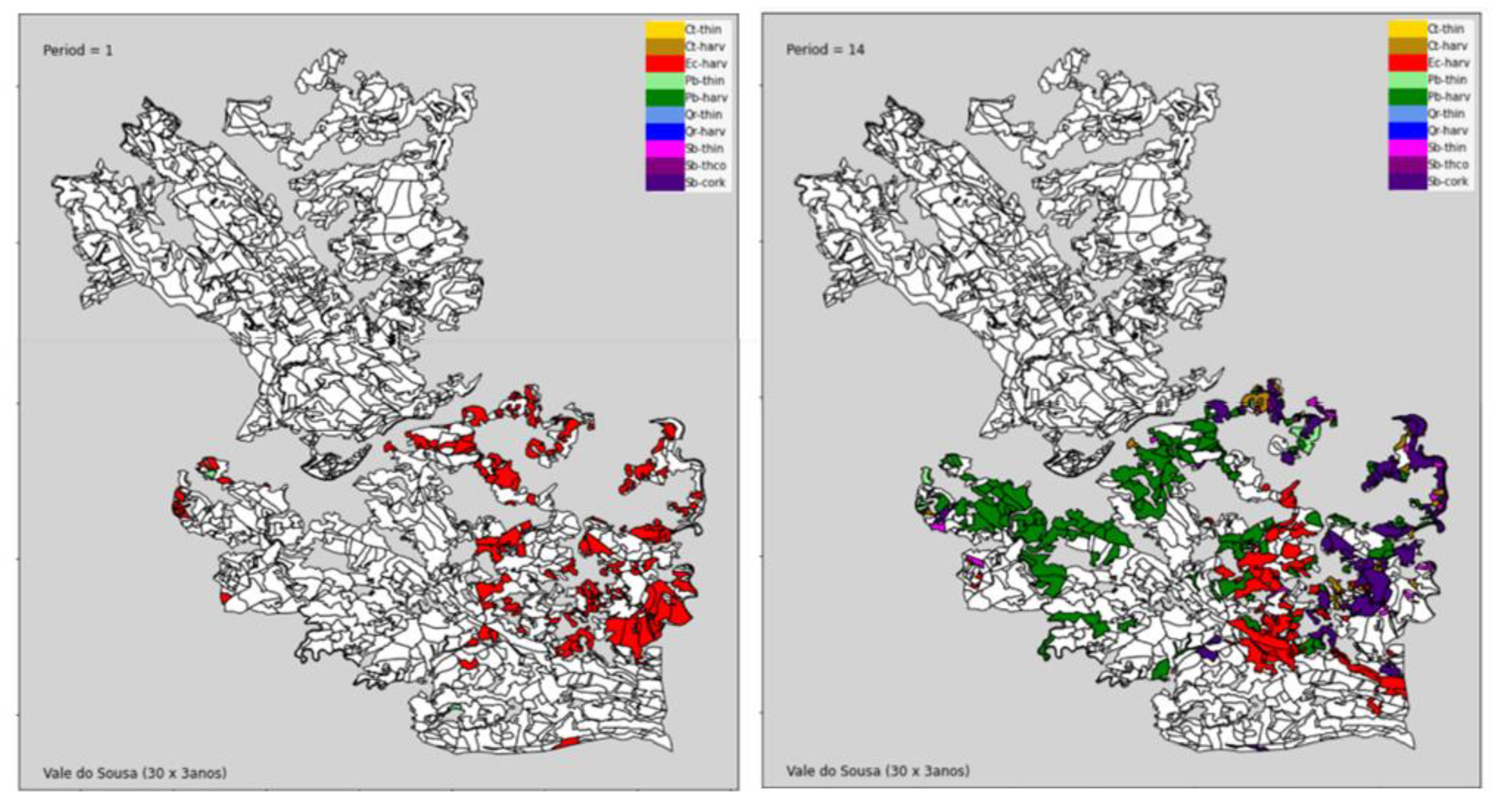
3.4. Spatialization of the Solution in Each Block or for All Area
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| (A1) | ||
| (A2) | ||
| (A3) | ||
| (A4) | ||
| (A5) | ||
| (A6) | ||
| (A7) | ||
| (A8) | ||
| (A9) | ||
| (A10) | ||
| (A11) | ||
| (A12) | ||
| (A13) | ||
| (A14) | ||
| (A15) | ||
| (A16) | ||
| (A17) | ||
| (A18) | ||
| (A19) | ||
| (A20) | ||
| (A21) | ||
| (A22) | ||
| (A23) | ||
| (A24) | ||
| (A25) | ||
| (A26) | ||
| (A27) | ||
| (A28) | ||
| (A29) |
- if prescription j is applied in management unit i, or 0 otherwise;
- T = the number of planning periods (t = 1…30);
- F = the number of forest management models (8);
- = the set of prescriptions that were classified as belonging to a cover type;
- = total forested area in each subarea;
- = the area occupied by each species in the management unit i;
- = the pine timber flow in period t that results from assigning prescription j to stand i;
- = the eucalyptus timber flow in period t that results from assigning prescription j to stand i;
- = the chestnut timber flow in period t that results from assigning prescription j to stand i;
- = the pedunculated oak timber flow in period t that results from assigning to stand i the prescription j;
- = the cork oak flow in period t that results from assigning to stand i the prescription j;
- = the cork timber flow that results from assigning prescription j to stand i in period t;
- the standing volume (in m3) in the ending inventory in stand i when assigning prescription j in t;
- = average yearly carbon stock (Mg ha−1) in period t that results from assigning prescription j to stand i;
- = fire resistance indicator in period t that results from assigning to stand i prescription j, ranging from 1 (less resistance) to 5 (highest resistance);
- = biodiversity indicator in period t that results from assigning to stand i prescription j, ranging from 0 (bare land or no biodiversity) to 8 (highest level of biodiversity);
- = RAFL index or cultural services indicator in period t that results from assigning to stand i prescription j, ranging from 1 (low cultural interest) to 5 (highest cultural and recreation interest);
- = the soil erosion in Mg in period t that results from assigning to stand i the prescription j;
- = the area assigned to cover type f;
- Equation (A1) states that only one prescription is assigned to each stand in the MOIP model.
- Equations (A2)–(A6) define, respectively, the pine, eucalypt, chestnut, pedunculated oak and cork oak timber yield.
- Equation (A7) defines the adult cork yield in each planning period.
- Equation (A8) defines the total amount of wood thinned and harvested in each period.
- Equation (A9) was included to define the standing volume in the case study area at the end of the planning horizon.
- Equation (A10) defines the average carbon stock in the study area in each planning period.
- Equations (A11) to (A14) define, respectively, the fire resistance indicator, biodiversity indicator, cultural services indicators and soil erosion.
- Equations (A15) defines the area assigned to each cover type.
- Equations (A16) to (A27) represent, respectively, the total pine sawlog yield, total eucalyptus pulpwood yield, total chestnut sawlog yield, total pedunculate oak sawlog yield, total cork oak sawlog yield, total adult cork yield, average over the 30 planning periods of carbon stock, fire resistance indicator, biodiversity indicator, cultural services indicator and total erosion across the planning horizon. These equations thus define the values of the criteria considered for testing purposes in each subarea.
- Equations (A28) and (A29) establish a maximum fluctuation of between periods in the amount of wood thinned and harvested.
References
- Baskent, E.Z.; Keleş, S. Spatial forest planning: A review. Ecol. Model. 2005, 188, 145–173. [Google Scholar] [CrossRef]
- Tóth, S.F.; McDill, M.E.; Rebain, S. Finding the efficient frontier of a bi-criteria, spatially explicit, harvest scheduling problem. Forest Sci. 2006, 52, 93–107. [Google Scholar] [CrossRef]
- Rönnqvist, M.; D’Amours, S.; Weintraub, A.; Jofre, A.; Gunn, E.; Haight, R.G.; Martell, D.; Murray, A.; Romero, C. Operations Research challenges in forestry: 33 open problems. Ann. Oper. Res. 2015, 232, 1–30. [Google Scholar] [CrossRef]
- Weintraub, A.; Murray, A.T. Review of combinatorial problems induced by spatial forest harvesting planning. Discret. Appl. Math. 2006, 154, 867–879. [Google Scholar] [CrossRef]
- Tóth, S.F.; McDill, M.E. Finding efficient harvest schedules under three conflicting objectives. Forest Sci. 2009, 55, 117–131. [Google Scholar] [CrossRef]
- Mavrotas, G.; Florios, K. An improved version of the augmented ε-constraint method (AUGMECON2) for finding the exact pareto set in multi-objective integer programming problems. Appl. Math. Comput. 2013, 219, 9652–9669. [Google Scholar] [CrossRef]
- Benson, H.P. Multi-Objective Optimization: Pareto Optimal Solutions, Properties. In Encyclopedia of Optimization; Floudas, C.A., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Branke, J.; Deb, K.; Miettinen, K.; Slowinski, R.; Miettinen, K. Preface. In Multiobjective Optimization; Branke, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. V–XII. [Google Scholar]
- Miettinen, K. A Posteriori Methods. In Nonlinear Multiobjective Optimization. International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 1998; Volume 12. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Lotov, A.; Miettinen, K. Visualizing the Pareto Frontier. In Computer Vision; Branke, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 213–243. [Google Scholar]
- Marques, S.; Marto, M.; Bushenkov, V.; McDill, M.; Borges, J. Addressing Wildfire Risk in Forest Management Planning with Multiple Criteria Decision Making Methods. Sustainability 2017, 9, 298. [Google Scholar] [CrossRef] [Green Version]
- Trautmann, H.; Mehnen, J. Preference-based Pareto optimization in certain and noisy environments. Eng. Optim. 2009, 41, 23–38. [Google Scholar] [CrossRef]
- Miettinen, K. Introduction to Multiobjective Optimization: Noninteractive Approaches. In Multiobjective Optimization; Branke, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–26. [Google Scholar]
- Geoffrion, A.M. Proper efficiency and the theory of vector maximization. J. Math. Anal. Appl. 1968, 22, 618–630. [Google Scholar] [CrossRef] [Green Version]
- Eswaran, P.K.; Ravindran, A.; Moskowitz, H. Algorithms for nonlinear integer brcriterion problems. J. Optim. Theory Appl. 1989, 63, 261–279. [Google Scholar] [CrossRef]
- Borges, J.G.; Garcia-Gonzalo, J.; Bushenkov, V.; McDill, M.E.; Marques, S.; Oliveira, M. Addressing Multicriteria Forest Management with Pareto Frontier Methods: An Application in Portugal. For. Sci. 2014, 60, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Borges, J.G.; Marques, S.; Garcia-Gonzalo, J.; Rahman, A.U.; Bushenkov, V.; Sottomayor, M.; Carvalho, P.O.; Nordström, E.-M. A Multiple Criteria Approach for Negotiating Ecosystem Services Supply Targets and Forest Owners’ Programs. For. Sci. 2017, 63, 49–61. [Google Scholar] [CrossRef]
- Marto, M.; Reynolds, K.M.; Borges, J.G.; Bushenkov, V.A.; Marques, S. Combining Decision Support Approaches for Optimizing the Selection of Bundles of Ecosystem Services. Forests 2018, 9, 438. [Google Scholar] [CrossRef] [Green Version]
- Lotov, A.V. Decomposition methods for the Edgeworth-Pareto hull approximation. Comput. Math. Math. Phys. 2015, 55, 1653–1664. [Google Scholar] [CrossRef]
- Marques, S.; Bushenkov, V.A.; Lotov, A.V.; Marto, M.; Borges, J.G. Bi-Level Participatory Forest Management Planning Supported by Pareto Frontier Visualization. For. Sci. 2019, 66, 490–500. [Google Scholar] [CrossRef]
- Marto, M.; Reynolds, K.M.; Borges, J.G.; Bushenkov, V.A.; Marques, S.; Marques, M.; Barreiro, S.; Botequim, B.; Tomé, M. Web-Based Forest Resources Management Decision Support System. Forests 2019, 10, 1079. [Google Scholar] [CrossRef] [Green Version]
- Gómez-García, E.; Crecente-Campo, F.; Anta, M.B.; Diéguez-Aranda, U. A disaggregated dynamic model for predicting volume, biomass and carbon stocks in even-aged pedunculate oak stands in Galicia (NW Spain). Eur. J. For. Res. 2015, 134, 569–583. [Google Scholar] [CrossRef]
- Gómez-García, E.; Diéguez-Aranda, U.; Cunha, M.; Rodríguez-Soalleiro, R. Comparison of harvest-related removal of aboveground biomass, carbon and nutrients in pedunculate oak stands and in fast-growing tree stands in NW Spain. For. Ecol. Manag. 2016, 365, 119–127. [Google Scholar] [CrossRef]
- Almeida, A.M.; Tomé, J.; Tomé, M. Development of a system to predict the evolution of individual tree mature cork caliber over time. For. Ecol. Manag. 2010, 260, 1303–1314. [Google Scholar] [CrossRef]
- Paulo, J.A.; Tomé, M. Equações para Estimação do Volume e Biomassa de Duas Espécies de Carvalhos: Quercus suber e Quercus ilex; Publicações GIMREF—RC1/2006; Departamento de Engenharia Florestal, Instituto Superior de Agronomia: Lisboa, Portugal, 2006; p. 21. Available online: http://hdl.handle.net/10400.5/1730Â (accessed on 10 August 2021).
- Paulo, J.A.; Tomé, M. Predicting mature cork biomass with t years of growth based in one measurement taken at any other age. For. Ecol. Manag. 2010, 259, 1993–2005. [Google Scholar] [CrossRef]
- Paulo, J.A. Desenvolvimento de um Sistema para Apoio à Gestão Sustentável de Montados de Sobro. Ph.D. Thesis, Universidade Técnica de Lisboa, Instituto Superior de Agronomia, Lisboa, Portugal, 2011. Available online: http://hdl.handle.net/10400.5/3850 (accessed on 10 August 2021).
- Paulo, J.A.; Tomé, J.; Tomé, M. Nonlinear fixed and random generalized height–diameter models for Portuguese cork oak stands. Ann. For. Sci. 2011, 68, 295–309. [Google Scholar] [CrossRef] [Green Version]
- Paulo, J.A.; Palma, J.; Gomes, A.A.; Faias, S.P.; Tomé, J.; Tomé, M. Predicting site index from climate and soil variables for cork oak (Quercus suber L.) stands in Portugal. New For. 2015, 46, 293–307. [Google Scholar] [CrossRef] [Green Version]
- Tomé, J.; Tomé, M.; Barreiro, S.; Paulo, J.A. Age-independent difference equations for modelling tree and stand growth. Can. J. For. Res. 2006, 36, 1621–1630. [Google Scholar] [CrossRef]
- Claessens, H.; Oosterbaan, A.; Savill, P.; Rondeux, J. A review of the characteristics of black alder (Alnus glutinosa (L.) Gaertn.) and their implications for silvicultural practices. Forests 2010, 83, 163–175. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-González, P.M.; Stella, J.; Campelo, F.; Ferreira, M.T.; Albuquerque, A. Subsidy or stress? Tree structure and growth in wetland forests along a hydrological gradient in Southern Europe. For. Ecol. Manag. 2010, 259, 2015–2025. [Google Scholar] [CrossRef]
- Quercus Robur Simulator for Galicia. Available online: https://manuelar.shinyapps.io/Quercusrobur_SimGaliza/ (accessed on 14 July 2021).
- Barreiro, S.; Rua, J.; Tomé, M. StandsSIM-MD: A Management Driven forest SIMulator. For. Syst. 2016, 25, 7. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, L.; Constantino, M.; Borges, J.; Garcia-Gonzalo, J. Addressing Wildfire Risk in a Landscape-Level Scheduling Model: An Application in Portugal. For. Sci. 2015, 61, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, A.R.; Marques, S.; Botequim, B.; Marto, M.; Borges, J.G. Forest management for optimizing soil protection: A land-scape-level approach. For. Ecosyst. 2021, 8, 50. [Google Scholar] [CrossRef]
- Botequim, B.; Zubizarreta-Gerendiain, A.; Garcia-Gonzalo, J.; Silva, A.; Marques, S.; Fernandes, P.; Pereira, J.M.C.; Tomé, M.; Fernandes, P. A model of shrub biomass accumulation as a tool to support management of Portuguese forests. iForest—Biogeosci. For. 2015, 8, 114–125. [Google Scholar] [CrossRef] [Green Version]
- Biber, P.; Maarten, T.N.; Black, K.; Borga, M.; Borges, J.G.; Felton, A.; Hoogstra-Klein, M.; Lindbladh, M.; Zoccatelli, D. ALTERFOR WP3; Deliverable 3.2.—Synthesis Report: Discrepancies between ES Needs and ES Outputs under Current FMMs. 2018, p. 44. Available online: https://alterfor-project.eu/files/alterfor/download/Deliverables/D3.2%20Synthesis%20report.pdf (accessed on 5 July 2019).
- Nieuwenhuis, M.; Biber, P. Milestone 11—Projections with Current FMMs Per Case Study; University College Dublin: Dublin, Ireland; Technical University of Munich: Munich, Germany, 2018. [Google Scholar]
- Botequim, B.; Bugalho, M.N.; Rodrigues, A.R.; Marques, S.; Marto, M.; Borges, J.G. Combining Tree Species Composition and Understory Coverage Indicators with Optimization Techniques to Address Concerns with Landscape-Level Biodiversity. Land 2021, 10, 126. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest dynamics, growth and yield. In Forest Dynamics; Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–39. [Google Scholar]
- Lotov, A.V.; Bushenkov, V.A.; Kamenev, G.K. Interactive Decision Maps: Approximation and Visualization of Pareto Frontier; Kluwer Academic Publishers: Norwell, MA, USA, 2004; p. 319. [Google Scholar]
- Wierzbicki, A.P. A Mathematical Basis for Satisficing Decision Making. In Organizations: Multiple Agents with Multiple Criteria; Springer: Berlin/Heidelberg, Germany, 1981; pp. 465–486. [Google Scholar]
- Romero, C.; Tamiz, M.; Jones, D.F. Goal programming; compromise programming and reference point method formulations: Linkages and utility interpretations. J. Oper. Res. Soc. 1998, 49, 986–991. [Google Scholar] [CrossRef]
- Ogryczak, W. On goal programming formulations of the reference point method. J. Oper. Res. Soc. 2001, 52, 691–698. [Google Scholar] [CrossRef]
- Colapinto, C.; Jayaraman, R.; Marsiglio, S. Multi-criteria decision analysis with goal programming in engineering; manage-ment and social sciences: A state-of-the art review. Ann. Oper. Res. 2017, 251, 7–40. [Google Scholar] [CrossRef] [Green Version]
- Tamiz, M.; Mirrazavi, S.; Jones, D.F. Extensions of Pareto efficiency analysis to integer goal programming. Omega-Int. J. Manag. S 1999, 27, 179–188. [Google Scholar] [CrossRef]
- T’Kindt, V.; Billaut, J. Multicriteria Scheduling: Theory, Models and Algorithms; Springer: New York, NY, USA, 2002; p. 303. [Google Scholar]
- Hwang, C.L.; Masud, A.I. Multiple Objective Decision Making. Methods and Applications: A State of the Art Survey; Lecture Notes in Economics and Mathematical Systems 164; Springer: Berlin, Germany, 1979. [Google Scholar]
- Nordström, E.-M.; Eriksson, O.; Öhman, K. Integrating multiple criteria decision analysis in participatory forest planning: Experience from a case study in northern Sweden. For. Policy Econ. 2010, 12, 562–574. [Google Scholar] [CrossRef] [Green Version]
- Haimes, Y. On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Trans. Syst. Man Cybern. 1971, 1, 296–297. [Google Scholar]
- Ehrgott, M.; Ruzika, S. Improved ε-Constraint Method for Multiobjective Programming. J. Optim. Theory Appl. 2008, 138, 375–396. [Google Scholar] [CrossRef]
- Zhang, W.; Reimann, M. A simple augmented ∊-constraint method for multi-objective mathematical integer programming problems. Eur. J. Oper. Res. 2014, 234, 15–24. [Google Scholar] [CrossRef]
- Soylu, B.; Yıldız, G.B. An exact algorithm for biobjective mixed integer linear programming problems. Comput. Oper. Res. 2016, 72, 204–213. [Google Scholar] [CrossRef]
- Burachik, R.S.; Kaya, C.Y.; Rizvi, M.M. Algorithms for generating Pareto fronts of multi-objective integer and mixed-integer programming problems. Eng. Optim. 2021, 1–13. [Google Scholar] [CrossRef]
- Guignard, M.; Kim, S. Lagrangean decomposition: A model yielding stronger lagrangean bounds. Math. Program. 1987, 39, 215–228. [Google Scholar] [CrossRef]
- Hoganson, H.; Rose, D. A Simulation Approach for Optimal Timber Management Scheduling. For. Sci. 1984, 30, 220–238. [Google Scholar] [CrossRef]
- Nordström, E.-M.; Romero, C.; Eriksson, O.; Öhman, K. Aggregation of preferences in participatory forest planning with multiple criteria: An application to the urban forest in Lycksele, Sweden. Can. J. For. Res. 2009, 39, 1979–1992. [Google Scholar] [CrossRef]
- Diaz-Balteiro, L.; Gonzalez-Pachon, J.; Romero, C. Forest management with multiple criteria and multiple stakeholders: An application to two public forests in Spain. Scand. J. For. Res. 2009, 24, 87–93. [Google Scholar] [CrossRef]
- Eyvindson, K.; Kangas, A. Evaluating the required scenario set size for stochastic programming in forest management planning: Incorporating inventory and growth model uncertainty. Can. J. For. Res. 2016, 46, 340–347. [Google Scholar] [CrossRef] [Green Version]
- Koschke, L.; Fürst, C.; Frank, S.; Makeschin, F. A multi-criteria approach for an integrated land-cover-based assessment of ecosystem services provision to support landscape planning. Ecol. Indic. 2012, 21, 54–66. [Google Scholar] [CrossRef]
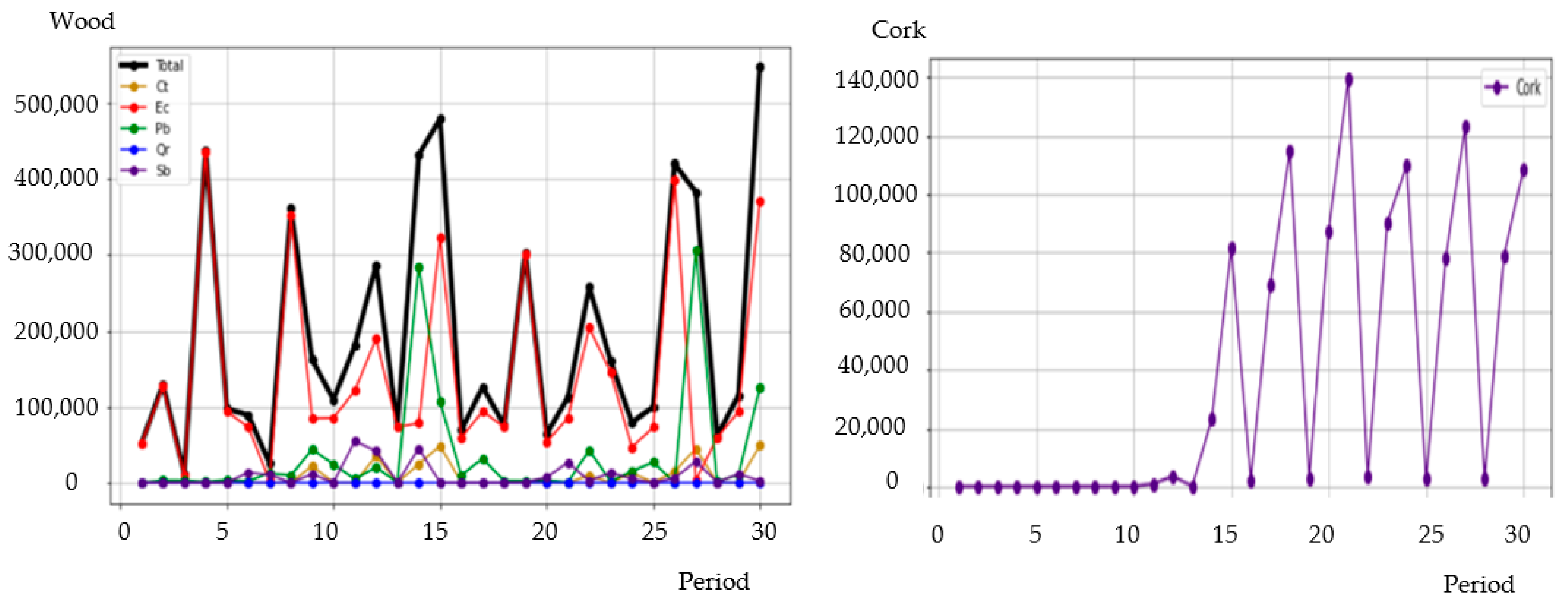
| Paiva | Paredes | Penafiel | EDSCP | ||
|---|---|---|---|---|---|
| North | South | ||||
| Area (ha) | 2936 | 4638 | 2156 | 5067 | 14,838 |
| Number of stands | 362 | 352 | 181 | 458 | 1373 |
| Number of. prescriptions | 73,900 | 70,050 | 20,200 | 85,950 | 250,100 |
| Species | Pedunculate Oak | Cork Oak | Riparian | |
|---|---|---|---|---|
| Prescriptions-Silvicultural operations | Plantation (a) | 1600 | 1600 | - |
| Replanting (b) | 20 | 20 | - | |
| Pruning (c,d) | 23 | - | - | |
| Thinning (d) | 27, 37, 45 | 15, 30, 40, 58, 76 | - | |
| Wilson Factor | 0.2 | - | - | |
| Debarking (d,e) | - | 30, 40, +(9) | - | |
| Final Harvest (d) | 40 to 60 (10) | - | - | |
| Type management | Even-aged | Even-aged | Even-aged | |
| Growth model | [23,24] | SUBER [25,26,27,28,29,30] | [31,32,33] | |
| Simulator | [34] | StandSIM/MD [35] | Yield table | |
| Ecosystem Service | Range | References |
|---|---|---|
| Fire resistance | 1–5 | [12,36] |
| Soil erosion | - | [37] |
| Biodiversity | 0–8 | [38,39,40,41] |
| Cultural services | 1–5 | [42] |
| Target Level of Each Criterion in the EDSCP Problem | Contribution of Each Subarea to the Target Level of Each Criterion | |||||
|---|---|---|---|---|---|---|
| Paiva North | Paiva South | Paredes | Penafiel | |||
| Optimized Criteria | TWOOD (×106 m3) | 9.1661 | 1.6738 | 2.7574 | 1.2747 | 3.4602 |
| δ (×106 m3) | 0.1135 | 0.0560 | 0.1712 | 0.0816 | 0.1464 | |
| EROS (×106 Mg) | 19.8151 | 3.6524 | 66511 | 3.7878 | 5.7238 | |
| Solution in the subareas | ||||||
| PF generation time (in seconds) | 3327 | 1359 | 484 | 4367 | ||
| Optimized Criteria | TWOOD (×106 m3) | 1.6657 | 2.7504 | 1.2704 | 3.4611 | |
| δ (×106 m3) | 0.0539 | 0.1617 | 0.0837 | 0.1375 | ||
| EROS (×106 Mg) | 3.6582 | 6.6496 | 3.7789 | 5.7218 | ||
| Other criteria | CARB (×106 Mg ha−1) | 2.0264 | 2.6791 | 0.3621 | 2.6061 | |
| Cork (×105 arroba) | 0.0316 | 0.0000 | 0.0000 | 0.0162 | ||
| CULTSERV (-) | 0.8824 | 1.2801 | 2.9342 | 3.3211 | ||
| FRES (-) | 2.6197 | 2.0456 | 2.0869 | 2.1123 | ||
| BIOD (-) | 3.1401 | 2.9815 | 2.6467 | 2.7561 | ||
| Area_Ct (ha) | 64 | 17 | 3 | 119 | ||
| Area_Ec (ha) | 726 | 1833 | 542 | 865 | ||
| Area_Mp (ha) | 1315 | 1300 | 1569 | 3824 | ||
| Area_Po (ha) | 774 | 1439 | 18 | 203 | ||
| Area_Rp (ha) | 22 | 48 | 23 | 8 | ||
| Area_Co (ha) | 34 | 0 | 0 | 18 | ||
| Convex Edgeworth–Pareto Hull | Nearest Pareto Frontier Point | |||
|---|---|---|---|---|
| TWOOD | CORK | TWOOD | CORK | |
| Point 1 | 2.800 | 1.885 | 2.801 | 1.885 |
| Point 2 | 2.996 | 1.711 | 3.000 | 1.711 |
| Point 3 | 3.200 | 1.509 | 3.200 | 1.523 |
| Point 4 | 3.399 | 1.199 | 3.399 | 1.201 |
| Point 5 | 3.598 | 0.795 | 3.599 | 0.802 |
| Point 6 | 3.669 | 0.565 | 3.670 | 0.570 |
| Model | Criteria | Point1 | Point2 | Point3 | Point4 | Point5 | Point6 | Point7 | Point8 | Point9 | Point10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Paiva North | TWOOD | SF | 1.2824 | 1.3298 | 1.5247 | 1.4154 | 1.7287 | 2.0747 | 2.1202 | 2.1676 | 2.1749 | 1.8575 |
| FP | 1.2826 | 1.3299 | 1.5199 | 1.4115 | 1.7287 | 2.0747 | 2.1204 | 2.1676 | 2.1749 | 1.8561 | ||
| CARB | SF | 2.9741 | 2.5704 | 3.8064 | 4.3027 | 4.0904 | 3.7861 | 4.2018 | 3.4197 | 3.9327 | 4.9365 | |
| FP | 2.9959 | 2.5915 | 3.8098 | 4.3027 | 4.1563 | 3.8564 | 4.2230 | 3.5113 | 4.0648 | 4.9351 | ||
| EROS | SF | 3.0000 | 3.0000 | 3.5000 | 3.5000 | 4.0000 | 5.0000 | 5.5000 | 5.5000 | 6.0000 | 6.5000 | |
| FP | 2.9999 | 3.0000 | 3.5047 | 3.4999 | 3.9998 | 5.0000 | 5.4822 | 5.5000 | 5.9080 | 6.4702 | ||
| Paredes | TWOOD | SF | 1.4163 | 1.4021 | 1.3837 | 1.4519 | 1.2946 | 1.4120 | 1.4550 | 1.4347 | 1.3696 | 1.2811 |
| FP | 1.4162 | 1.4030 | 1.3852 | 1.4520 | 1.2950 | 1.4123 | 1.4553 | 1.4347 | 1.3696 | 1.2817 | ||
| FRES | SF | 3.1345 | 3.2027 | 3.2195 | 3.2171 | 3.2829 | 3.2787 | 3.2796 | 3.2763 | 3.2930 | 3.2960 | |
| FP | 3.1348 | 3.2027 | 3.2197 | 3.2172 | 3.2829 | 3.2796 | 3.2693 | 3.2763 | 3.2930 | 3.2961 | ||
| EROS | SF | 5.0000 | 5.0000 | 5.0000 | 4.8000 | 4.8000 | 4.6000 | 4.6000 | 4.4000 | 4.4000 | 4.4000 | |
| FP | 5.0000 | 5.0001 | 5.0009 | 4.8005 | 4.8010 | 4.6008 | 4.6151 | 4.4420 | 4.4025 | 4.4193 |
| Model Alias | Pareto Frontier Generation (in Seconds) | |
|---|---|---|
| 2 Criteria | 3 Criteria | |
| Paiva North | 223 | 5219 |
| Paiva South | 313 | 3836 |
| Penafiel | 436 | 6255 |
| Paredes | 47 | 442 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marques, S.; Bushenkov, V.; Lotov, A.; G. Borges, J. Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs. Forests 2021, 12, 1244. https://doi.org/10.3390/f12091244
Marques S, Bushenkov V, Lotov A, G. Borges J. Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs. Forests. 2021; 12(9):1244. https://doi.org/10.3390/f12091244
Chicago/Turabian StyleMarques, Susete, Vladimir Bushenkov, Alexander Lotov, and José G. Borges. 2021. "Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs" Forests 12, no. 9: 1244. https://doi.org/10.3390/f12091244
APA StyleMarques, S., Bushenkov, V., Lotov, A., & G. Borges, J. (2021). Building Pareto Frontiers for Ecosystem Services Tradeoff Analysis in Forest Management Planning Integer Programs. Forests, 12(9), 1244. https://doi.org/10.3390/f12091244








