Disentangling the Relationship between Tree Biomass Yield and Tree Diversity in Mediterranean Mixed Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Biomass Estimation
2.2. Tree Species Diversity Estimation
2.3. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scarascia-Mugnozza, G.; Oswald, H.; Piussi, P.; Radoglou, K. Forests of the Mediterranean region: Gaps in knowledge and research needs. For. Ecol. Manag. 2000, 132, 97–109. [Google Scholar] [CrossRef]
- Del Río, M.; Barbeito, I.; Bravo-Oviedo, A.; Calama, R.; Cañellas, I.; Herrero, C.; Bravo, F. Mediterranean Pine Forests: Management Effects on Carbon Stocks. In Managing Forest Ecosystems: The Challenge of Climate Change, 2nd ed.; Bravo, F., LeMay, V., Jandl, R., Eds.; Springer: Cham, Switzerland, 2017; pp. 301–327. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H.; Schütze, G. Size-structure dynamics of mixed versus pure forest stands. For. Syst. 2014, 23, 560–572. [Google Scholar] [CrossRef] [Green Version]
- Riofrío, J.; Del Río, M.; Bravo, F. Mixing effects on growth efficiency in mixed pine forests. Forestry 2017, 90, 381–392. [Google Scholar] [CrossRef] [Green Version]
- Bravo-Oviedo, A.; Pretzsch, H.; Ammer, C.; Andenmatten, E.; Barbati, A.; Barreiro, S.; Brang, P.; Bravo, F.; Coll, L.; Corona, P.; et al. European Mixed Forests: Definition and research perspectives. For. Syst. 2014, 23, 518–533. [Google Scholar] [CrossRef]
- Knoke, T.; Stimm, B.; Ammer, C.; Moog, M. Mixed forests reconsidered: A forest economics contribution on an ecological concept. For. Ecol. Manag. 2005, 213, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Crowther, T.W.; Picard, N.; Wiser, S.; Zhou, M.; Alberti, G.; Schulze, E.D.; McGuire, A.D.; Bozzato, F.; Pretzsch, H.; et al. Positive biodiversity-productivity relationship predominant in global forests. Science 2016, 354. [Google Scholar] [CrossRef] [Green Version]
- Baeten, L.; Bruelheide, H.; van der Plas, F.; Kambach, S.; Ratcliffe, S.; Jucker, T.; Allan, E.; Ampoorter, E.; Barbaro, L.; Bastias, C.C.; et al. Identifying the tree species compositions that maximize ecosystem functioning in European forests. J. Appl. Ecol. 2019, 56, 733–744. [Google Scholar] [CrossRef]
- Hooper, D.U.; Adair, E.C.; Cardinale, B.J.; Byrnes, J.E.K.; Hungate, B.A.; Matulich, K.L.; O’Connor, M.I. A global synthesis reveals biodiversity loss as a major driver of ecosystem change. Nature 2012, 486, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Szwagrzyk, J.; Gazda, A. Above-ground standing biomass and tree species diversity in natural stands of Central Europe. J. Veg. Sci. 2007, 18, 555–562. [Google Scholar] [CrossRef]
- Baskin, Y. Ecologists Dare to Ask: How Much Does Diversity Matter? Science 1994, 264, 202–203. [Google Scholar] [CrossRef]
- Fraser, L.H.; Pither, J.; Jentsch, A.; Sternberg, M.; Zobel, M.; Askarizadeh, D.; Bartha, S.; Beierkuhnlein, C.; Bennett, J.A.; Bittel, A.; et al. Worldwide evidence of a unimodal relationship between productivity and plant species richness. Science 2015, 349, 302–305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gamfeldt, L.; Snäll, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Fröberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher levels of multiple ecosystem services are found in forests with more tree species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef] [PubMed]
- Mori, A.S.; Lertzman, K.P.; Gustafsson, L. Biodiversity and ecosystem services in forest ecosystems: A research agenda for applied forest ecology. J. Appl. Ecol. 2017, 54, 12–27. [Google Scholar] [CrossRef]
- Grace, J.B.; Hautier, Y.; Hillebrand, H.; Lind, E.M.; Pärtel, M.; Bakker, J.D.; Buckley, Y.M. Integrative modelling reveals mechanisms linking productivity and plant species richness. Nature 2016, 529, 1–10. [Google Scholar] [CrossRef]
- Sala, O.E.; Chapin, F.S.; Armesto, J.J.; Berlow, E.; Bloomfield, J.; Dirzo, R.; Huber-Sanwald, E.; Huenneke, L.F.; Jackson, R.B.; Kinzig, A.; et al. Global biodiversity scenarios for the year 2100. Science 2000, 287, 1770–1774. [Google Scholar] [CrossRef]
- Daily, G.C. Nature’s Services: Societal Dependence on Natural Ecosystems; Island Press: Washington, DC, USA, 1997; 392p. [Google Scholar]
- Iranah, P.; Lal, P.; Wolde, B.T.; Burli, P. Valuing visitor access to forested areas and exploring willingness to pay for forest conservation and restoration finance: The case of small island developing state of Mauritius. J. Environ. Manag. 2018, 223, 868–877. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, R. Tree species diversity of natural mixed stands in eastern Black sea and western Mediterranean region of Turkey. J. Environ. Biol. 2009, 30, 761–766. [Google Scholar]
- Liu, C.L.C.; Kuchma, O.; Krutovsky, K.V. Mixed-species versus monocultures in plantation forestry: Development, benefits, ecosystem services and perspectives for the future. Glob. Ecol. Conserv. 2018, 15, e00419. [Google Scholar] [CrossRef]
- Tilman, D.; Lehman, C.L.; Thomson, K.T. Plant diversity and ecosystem productivity: Theoretical considerations. Proc. Natl. Acad. Sci. USA 1997, 94, 1857–1861. [Google Scholar] [CrossRef] [Green Version]
- Cardinale, B.J.; Wright, J.P.; Cadotte, M.W.; Carroll, I.T.; Hector, A.; Srivastava, D.S.; Loreau, M.; Weis, J.J. Impacts of plant diversity on biomass production increase through time because of species complementarity. Proc. Natl. Acad. Sci. USA 2007, 104, 18123–18128. [Google Scholar] [CrossRef] [Green Version]
- Tilman, D. The ecological consequences of changes in biodiversity: A search for general principles. Ecology 1999, 80, 1455–1474. [Google Scholar] [CrossRef]
- Hamilton, N.; Ferry, M. ggtern: Ternary Diagrams Using ggplot2. J. Stat. Softw. 2018, 87, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Atlas Agroclimático de Castilla y León—ITACYL-AEMET. 2013. Available online: http://atlas.itacyl.es (accessed on 10 March 2021).
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106 2015; FAO: Rome, Italy, 2015; Available online: http://www.fao.org/3/i3794en/I3794en.pdf (accessed on 10 March 2021).
- Ruiz-Peinado, R.; del Rio, M.; Montero, G. New models for estimating the carbon sink capacity of Spanish softwood species. For. Syst. 2011, 20. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Peinado Gertrudix, R.; Montero, G.; del Rio, M. Biomass models to estimate carbon stocks for hardwood tree species. For. Syst. 2012, 21. [Google Scholar] [CrossRef]
- Brockerhoff, E.G.; Barbaro, L.; Castagneyrol, B.; Forrester, D.I.; Gardiner, B.; González-Olabarria, J.R.; Jactel, H. Forest biodiversity, ecosystem functioning and the provision of ecosystem services. Biodivers. Conserv. 2017, 26, 3005–3035. [Google Scholar] [CrossRef] [Green Version]
- Bohn, F.J.; Huth, A. The importance of forest structure to biodiversity–productivity relationships. R. Soc. Open Sci. 2017, 4, 160521. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Hui, G.; Hu, Y.; Zhao, Z. Spatial structural characteristics of forests dominated by Pinus tabulaeformis Carr. PLoS ONE 2018, 13, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhang, G.; Hui, G.; Li, Y.; Hu, Y.; Zhao, Z. The influence of sampling unit size and spatial arrangement patterns on neighborhood-based spatial structure analyses of forest stands. For. Syst. 2016, 25. [Google Scholar] [CrossRef] [Green Version]
- Bravo, F.; Guerra, B. Forest Structure and Diameter Growth in Maritime Pine in a Mediterranean Area; Gadow, K., von Nagel, J., Saborowski, J., Eds.; Springer: Dordrecht, The Nederlands, 2002; pp. 123–134. [Google Scholar] [CrossRef]
- Simpson, E.H. Measurement of Diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Berger, W.H.; Parker, F.L. Diversity of Planktonic Foraminifera in Deep-Sea Sediments. Science 1970, 168, 1345–1347. [Google Scholar] [CrossRef]
- Pielou, E.C. Ecological Diversity; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Gadow, K.V.; Hui, G.Y. Characterizing forest spatial structure and diversity. In Sustainable Forestry in Temperate Regions; University of Lund: Lund, Sweden, 2002; pp. 20–30. [Google Scholar]
- Pielou, E.C. Mathematical Ecology; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Füldner, K. Strukturbeschreibung von Buchen-Edellaubholz-Mischwäldern [Describing Forest Structures in Mixed Beech-Ash-Maple-Sycamore Stands]. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, 1977. [Google Scholar]
- Gadow, K.V.; Hui, G.Y.; Albert, M. Das Winkelmaß–ein Strukturparameter zur Beschreibung der Individualverteilung in Waldbesta¨nden [The uniform angle index—A structural parameter for describing tree distribution in forest stands]. Centralbl. Ges. Forstwes. 1998, 115, 1–10. [Google Scholar]
- Pretzsch, H. Zum Einfluss des Baumvertielungsmusters auf den Bestandszuwachs. [(On the effect of the spatial distribution of trees on the stand growth]. Allg. Forst-und Jagdztg. 1995, 166, 190–201. [Google Scholar]
- Gadow, K.V. Zur Bestandesbeschreibung in der Forsteinrichtung. Forst Holz 1993, 48, 601–606. [Google Scholar]
- Morris, E.K.; Caruso, T.; Buscot, F.; Fischer, M.; Hancock, C.; Maier, T.S.; Meiners, T.; Müller, C.; Obermaier, E.; Prati, D.; et al. Choosing and using diversity indices: Insights for ecological applications from the German Biodiversity Exploratories. Ecol. Evol. 2014, 4, 3514–3524. [Google Scholar] [CrossRef] [Green Version]
- Biber, P.; Weyerhaeuser, H. Numerical methods for characterizing structure and diversity applied to a natural tropical forest and an even aged teak stand. In Natural And Socioeconomic Analysis and Modelling of Forest and Agroforestry Systems in Southeast Asia; Mies, E., Ed.; German Foundation for Development, Food and Agriculture Development Centre, 1988; pp. 83–104. Available online: https://www.waldwachstum.wzw.tum.de/fileadmin/publications/482.pdf (accessed on 31 December 1998).
- Pretzsch, H. Forest Dynamics, Growth, and Yield. In Forest Dynamics, Growth and Yield: From Measurement to Model; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–39. [Google Scholar] [CrossRef]
- Wei, T.; Simko, V. R package “corrplot”: Visualization of a Correlation Matrix. 2017. Available online: https://github.com/taiyun/corrplot (accessed on 31 December 2017).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Wambsganss, J.; Beyer, F.; Freschet, G.T.; Scherer-Lorenzen, M.; Bauhus, J. Tree species mixing reduces biomass but increases length of absorptive fine roots in European forests. J. Ecol. 2021, 1–14. [Google Scholar] [CrossRef]
- Aponte, C.; Kasel, S.; Nitschke, C.R.; Tanase, M.A.; Vickers, H.; Parker, L.; Fedrigo, M.; Kohout, M.; Ruiz-Benito, P.; Zavala, M.A.; et al. Structural diversity underpins carbon storage in Australian temperate forests. Glob. Ecol. Biogeogr. 2020, 29, 789–802. [Google Scholar] [CrossRef]
- Himes, A.; Puettmann, K. Tree species diversity and composition relationship to biomass, understory community, and crown architecture in intensively managed plantations of the coastal pacific northwest, USA. Can. J. For. Res. 2020, 50, 1–12. [Google Scholar] [CrossRef]
- Puettmann, K.J.; Hibbs, D.E. Ecology and dynamics of mixed red alder conifer stands. In Silviculture of Temperate and Boreal Broadleaf–Conifer Mixtures; Comeau, P.G., Thomas, K.D., Eds.; British Columbia Ministry of Forests: Vancouver, BC, Canada, 1996; pp. 82–96. [Google Scholar]
- Kelty, M.J. The role of species mixtures in plantation forestry. For. Ecol. Manag. 2006, 233, 195–204. [Google Scholar] [CrossRef]
- Pretzsch, H. Individual tree structure and growth in mixed compared with monospecific stands. In Mixed-Species Forests; Springer: Berlin/Heidelberg, Germany, 2017; pp. 271–336. [Google Scholar] [CrossRef]
- Puerta-Piñero, C.; Gómez, J.M.; Valladares, F. Irradiance and oak seedling survival and growth in a heterogeneous environment. For. Ecol. Manag. 2007, 242, 462–469. [Google Scholar] [CrossRef]
- Con, T.; Van Thang, N.T.; Ha, D.T.T.; Khiem, C.C.; Quy, T.H.; Lam, V.T.; Van Do, T.; Sato, T. Relationship between aboveground biomass and measures of structure and species diversity in tropical forests of Vietnam. For. Ecol. Manag. 2013, 310, 213–218. [Google Scholar] [CrossRef]
- Poudel, K.P.; Temesgen, H. Methods for estimating aboveground biomass and its components for Douglas-fir and lodgepole pine trees. In New Directions in Inventory Techniques and Applications: Forest Inventory and Analysis (FIA), Proceedings of the Symposium 2015, Portland, OR, USA, 8–10 December 2015; Oregon. Gen. Tech. Rep. PNW-GTR-931; US Department of Agriculture, Forest Service, Pacific Northwest, R: Portland, OR, USA, 2015. [Google Scholar] [CrossRef] [Green Version]
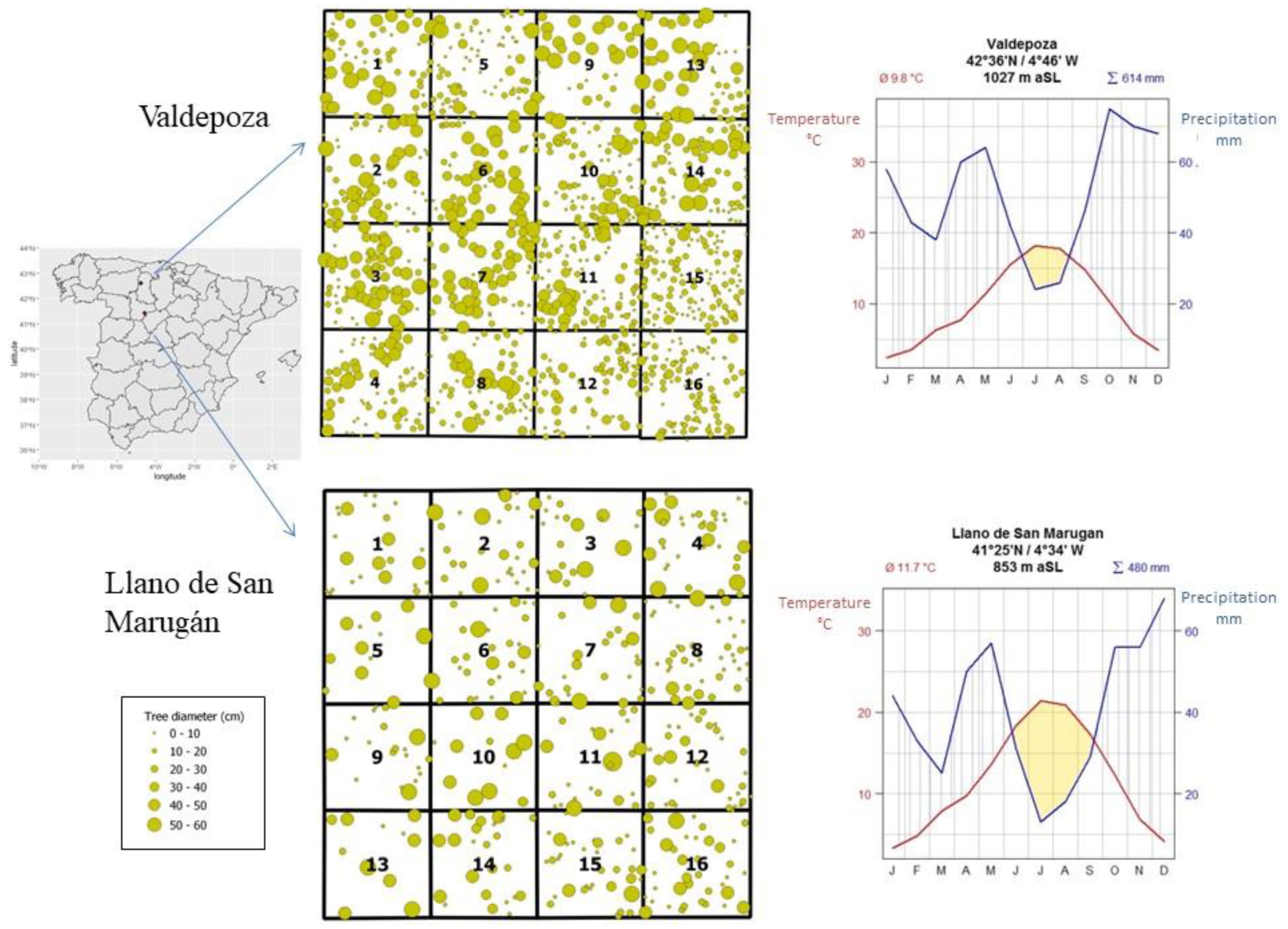
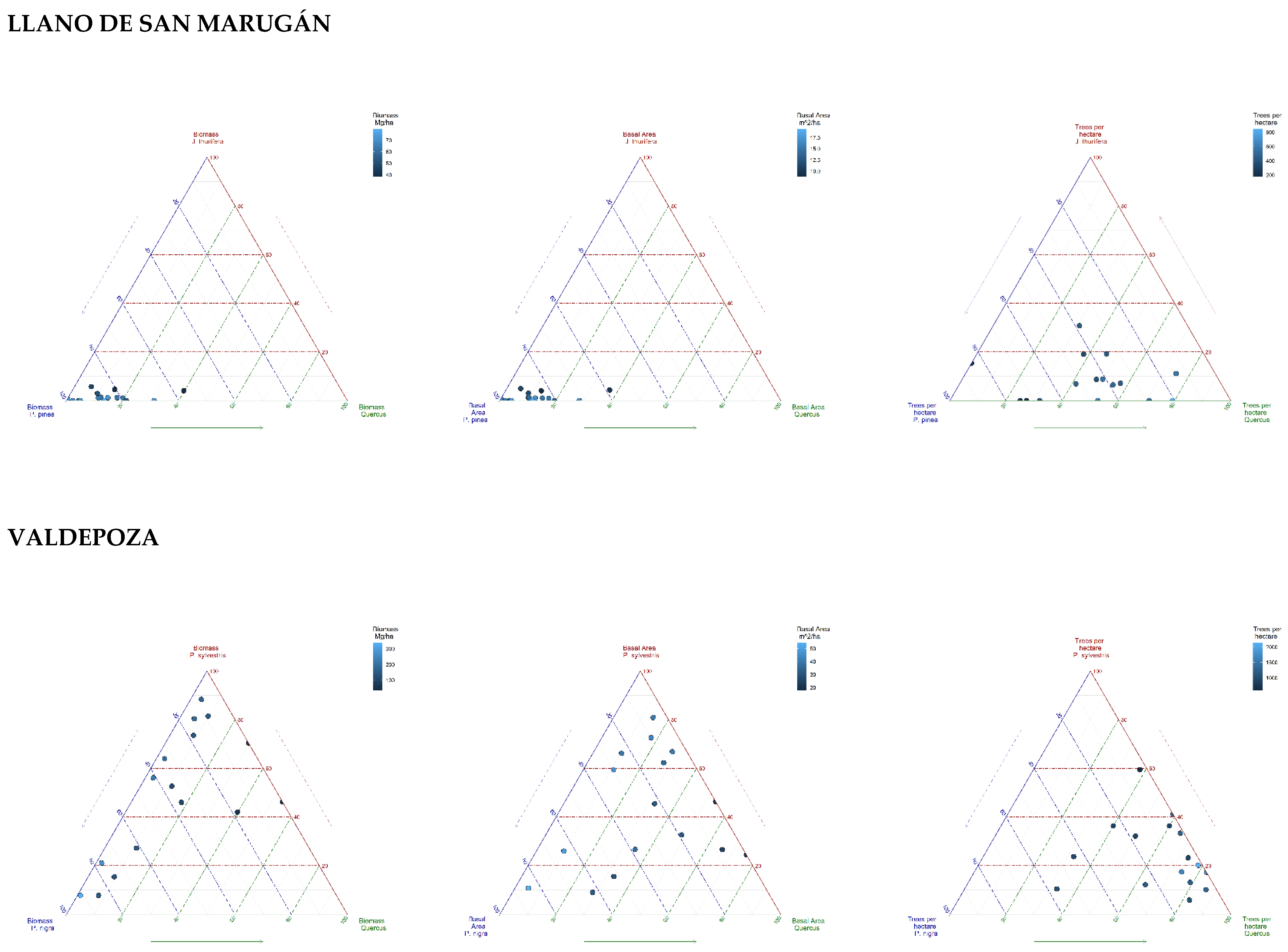
| Llano de San Marugán (437 trees/ha) | Valdepoza (1178 trees/ha) | |||||||
|---|---|---|---|---|---|---|---|---|
| Variables | Mean | St.Dev | Min | Max | Mean | St. Dev | Min | Max |
| B | 134.4 | 196.7 | 2.9 | 1067.5 | 129.6 | 223.7 | 4.4 | 1139.6 |
| d | 16.6 | 11.7 | 3.0 | 50.5 | 16.5 | 10.5 | 4.7 | 49.3 |
| h | 5.8 | 2.5 | 2.0 | 13.0 | 10.6 | 5.5 | 1.5 | 23.9 |
| V | 0.13 | 0.2 | 0.001 | 1.2 | 0.24 | 0.37 | 0.002 | 1.8 |
| G | 14.3 | 35.6 | ||||||
| Sm | 1.0 | 0.02 | 0.9 | 1.0 | 0.9 | 0.0 | 0.9 | 0.9 |
| Sn | 3.3 | 0.4 | 2.4 | 3.9 | 4.3 | 0.3 | 3.5 | 4.8 |
| E | 1.0 | 0.01 | 1.0 | 1.0 | 0.9 | 0.01 | 0.9 | 0.9 |
| D | 2.1 | 0.4 | 1.2 | 2.6 | 1.5 | 0.3 | 1.1 | 2.5 |
| Mi | 0.6 | 0.3 | 0.0 | 1.0 | 0.2 | 0.3 | 0.0 | 1.0 |
| MS | 0.3 | 0.1 | 0.0 | 0.6 | 0.1 | 0.1 | 0.0 | 0.5 |
| W | 0.5 | 0.2 | 0.0 | 1.0 | 0.6 | 0.2 | 0.0 | 1.0 |
| S | 0.3 | 0.2 | 0.1 | 0.9 | 0.7 | 0.1 | 0.5 | 0.8 |
| A | 2.5 | 0.8 | 0.0 | 3.7 | 3.4 | 0.7 | 0.0 | 4.6 |
| TH | 0.3 | 0.1 | 0.0 | 0.7 | 0.2 | 0.1 | 0.02 | 0.8 |
| Species | N | d (cm) | h (m) | v (m3) | g (m2) | B (kg) | Sm | Sn | D | E | Mi | MS | S | W | A | TH |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Llano de San Marugán site | ||||||||||||||||
| Pinus pinea | 177 | 27.51 | 8.16 | 0.25 | 0.07 | 290.11 | 0.95 | 3.21 | 1.98 | 0.98 | 0.54 | 0.25 | 0.19 | 0.48 | 1.90 | 0.36 |
| Quercus faginea | 157 | 9.60 | 4.18 | 0.01 | 0.008 | 38.75 | 0.96 | 3.39 | 2.14 | 0.98 | 0.56 | 0.26 | 0.23 | 0.49 | 2.96 | 0.26 |
| Quercus ilex | 69 | 9.10 | 4.12 | 0.01 | 0.007 | 27.12 | 0.96 | 3.54 | 2.13 | 0.98 | 0.55 | 0.27 | 0.61 | 0.44 | 3.13 | 0.22 |
| Juniperus thurifera | 34 | 7.62 | 4.33 | 0.27 | 0.005 | 21.76 | 0.95 | 3.20 | 2.18 | 0.98 | 0.76 | 0.31 | 0.24 | 0.50 | 2.68 | 0.25 |
| Valdepoza site | ||||||||||||||||
| Pinus nigra | 139 | 30.77 | 19.13 | 0.74 | 0.08 | 518.65 | 0.98 | 4.12 | 1.81 | 0.98 | 0.42 | 0.21 | 0.60 | 0.68 | 3.00 | 0.25 |
| Pinus sylvestris | 266 | 24.11 | 14.02 | 0.49 | 0.06 | 259.01 | 0.98 | 4.24 | 1.63 | 0.99 | 0.53 | 0.22 | 0.65 | 0.65 | 3.20 | 0.24 |
| Quercus pyrenaica | 773 | 11.39 | 8.02 | 0.05 | 0.01 | 15.14 | 0.99 | 4.36 | 1.45 | 0.99 | 0.19 | 0.09 | 0.88 | 0.88 | 3.63 | 0.29 |
| # | Fitted Models | Predictor Variable | ||
|---|---|---|---|---|
| x1 | x2 | x3 | ||
| Single Predictor (22 Alternative Models) | ||||
| 1. | Gi, Sm, Sn, D, E, Mi, MS, S, A, TH, W | |||
| 2. | ||||
| Multivariate models with 2 predictors (413 alternative models) | ||||
| 3. | Gi Sm, Sn, D, E | D, E, Sm, Sn, Mi, MS, S, A, TH, W | ||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | Mi, MS, S | A, TH, W | ||
| 8. | ||||
| 9. | ||||
| Multivariate models with 3 predictors (188 alternative models) | ||||
| 10. | Gi | TH, A | Sm, Sn, D, E, Mi, MS, S, A, W | |
| 11. | ||||
| 12. | D, E, A, Sm, S, TH | MS, S, TH, S, W | ||
| Model | M1 | M2 | M3 | V1 | V2 | V3 |
|---|---|---|---|---|---|---|
| Intercept | 0.747 | 1.011 | 1.303 | 1.843 | 0.398 | 1.414 |
| lnG | 1.289 | 1.057 | ||||
| ln(Mi+1) | 0.509 | |||||
| ln (G*TH) | 0.411 | |||||
| lnS | −2.398 | |||||
| ln G*(Mi+1) | 0.468 | 1.224 | ||||
| ln G*(W+1) | 0.936 | |||||
| R adj | 0.964 | 0.976 | 0.945 | 0.91 | 0.956 | 0.898 |
| AIC | −73.23 | −254.38 | 114.19 | 1606.42 | 747.96 | 1745.14 |
| Models | Qf1 | Qf2 | Qf3 | Qi1 | Qi2 | Qi3 | Jt1 | Jt2 | Jt3 |
|---|---|---|---|---|---|---|---|---|---|
| Intercept | 1.502 | −1.006 | 1.28 | 1.629 | 1.102 | 1.57 | −1.182 | −1.025 | −1.887 |
| lnG | 0.981 | ||||||||
| ln(A+1) | 0.029 | ||||||||
| ln G*TH | 0.36 | ||||||||
| lnG²*(MS+1) | 0.475 | 0.482 | |||||||
| lnG*S | 0.961 | ||||||||
| lnG²*S | 0.495 | ||||||||
| ln G*(Mi+1) | 0.548 | ||||||||
| ln G*(W+1) | 0.582 | ||||||||
| ln G²*TH | 0.158 | ||||||||
| R adj | 0.998 | 0.364 | 0.981 | 0.957 | 0.975 | 0.989 | 0.695 | 0.758 | 0.421 |
| AIC | −883.67 | 113.95 | −442.9 | −131.35 | −168.54 | −224.84 | −29.02 | −36.86 | −7.16 |
| Models | Qp1 | Qp2 | Qp3 | Ps1 | Ps2 | Ps3 | Ps4 | Pn1 | Pn2 | Pn3 | Pn4 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | −1.718 | −1.367 | −1.304 | 1.74 | 2.21 | 1.199 | 1.612 | −0.09 | 1.515 | 5.076 | 0.307 |
| lnG | 1.145 | ||||||||||
| lnG*(W+1) | 0.712 | ||||||||||
| lnS | −0.225 | ||||||||||
| lnG*TH | 0.433 | ||||||||||
| lnG²*(A+1) | 0.387 | 0.603 | |||||||||
| lnG²*(MS+1) | 0.587 | ||||||||||
| lnG²*(W+1) | 0.58 | ||||||||||
| G | 6.868 | 6.85 | 6.83 | 6.81 | |||||||
| D | 0.036 | ||||||||||
| E | −1.573 | ||||||||||
| Sm | −5.19 | ||||||||||
| Sn | −0.08 | ||||||||||
| R adj | 0.539 | 0.907 | 0.9272 | 0.99 | 0.982 | 0.984 | 0.984 | 0.967 | 0.967 | 0.969 | 0.968 |
| AIC | 693.28 | −544.98 | −732.77 | −284.42 | −119.63 | −144.31 | −148.94 | −471.22 | −472.14 | −479.02 | −475.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bravo, F.; Martín Ariza, A.; Dugarsuren, N.; Ordóñez, C. Disentangling the Relationship between Tree Biomass Yield and Tree Diversity in Mediterranean Mixed Forests. Forests 2021, 12, 848. https://doi.org/10.3390/f12070848
Bravo F, Martín Ariza A, Dugarsuren N, Ordóñez C. Disentangling the Relationship between Tree Biomass Yield and Tree Diversity in Mediterranean Mixed Forests. Forests. 2021; 12(7):848. https://doi.org/10.3390/f12070848
Chicago/Turabian StyleBravo, Felipe, Ana Martín Ariza, Narangarav Dugarsuren, and Cristóbal Ordóñez. 2021. "Disentangling the Relationship between Tree Biomass Yield and Tree Diversity in Mediterranean Mixed Forests" Forests 12, no. 7: 848. https://doi.org/10.3390/f12070848
APA StyleBravo, F., Martín Ariza, A., Dugarsuren, N., & Ordóñez, C. (2021). Disentangling the Relationship between Tree Biomass Yield and Tree Diversity in Mediterranean Mixed Forests. Forests, 12(7), 848. https://doi.org/10.3390/f12070848








