Modelling the Spatial Structure of White Spruce Plantations and Their Changes after Various Thinning Treatments
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
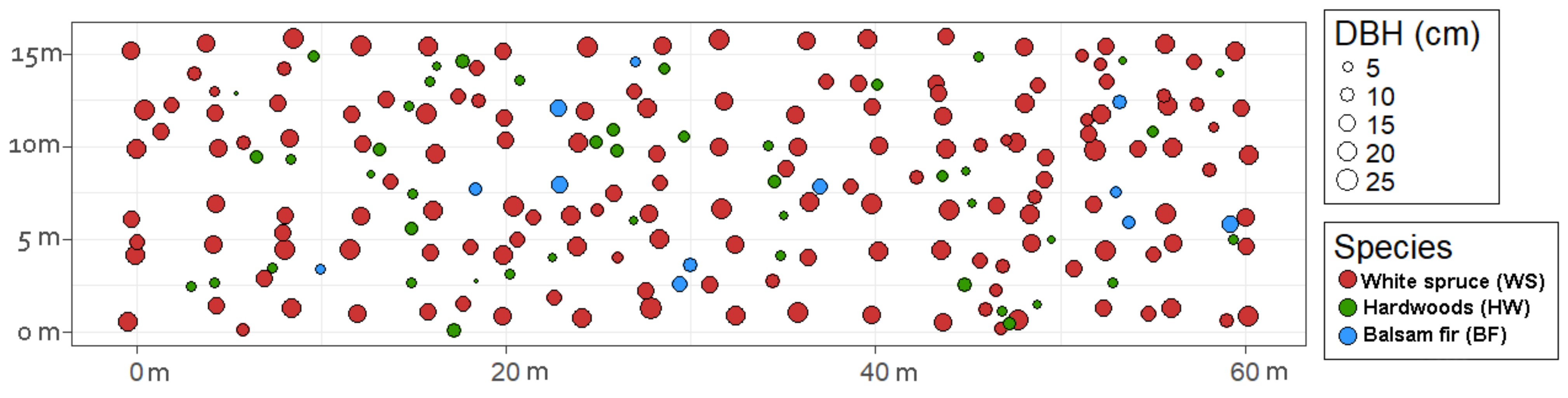
2.2. Data Acquisition
2.3. Modelling Spatial Stand Structure
2.3.1. Clark and Evans index
2.3.2. Spatial Interactions between Individual Trees
2.3.3. Spatial Interactions within Species Groups
2.3.4. Model Validation
2.4. Spatial Stand Structure Simulation
2.4.1. Spatial Stand Structure Generator
- Trees were ordered by DBH.
- For the Gsp where RGsp < 1, the number of clusters (NClusHaGsp) was calculated.
- For all trees, we repeated the following steps, depending on Gsp.
- For trees with RGsp ≥ 1, we generated a random position, identified the 2 closest competitors and, knowing the characteristics (Gsp and DBH) of the neighbours, calculated the theoretical minimum distance with these 2 trees (i.e., MinDistT1 and MinDistT2). If the 2 measured distances were greater than the 2 theoretical values, the point was kept as a potential valid position.
- For trees with RGsp < 1, if the number of trees of the same Gsp already positioned was less than the predicted NClusHaGsp, the tree was positioned randomly. If the number of trees of the same Gsp was greater than NClusHaGsp, we randomly selected a tree of the same Gsp that was already positioned and used it as an anchor for a cluster. From this anchor position, we generated a random point around the anchor point at a distance equal to the modelled DistGsp. Finally, this position was then evaluated in the same way as in the previous point, i.e., by comparing the distances between the target tree and the 2 closest neighbours.
- The generator could start from an empty stand. However, a plantation scheme describing the spacing between planted trees and the presence of planting rows could be used to place planted trees species in these positions. A thinning path could also be added.
2.4.2. Performance Tests of the “Spatialiser”
2.4.3. Thinning Treatment Simulations
3. Results
3.1. Modelling Spatial Stand Structure
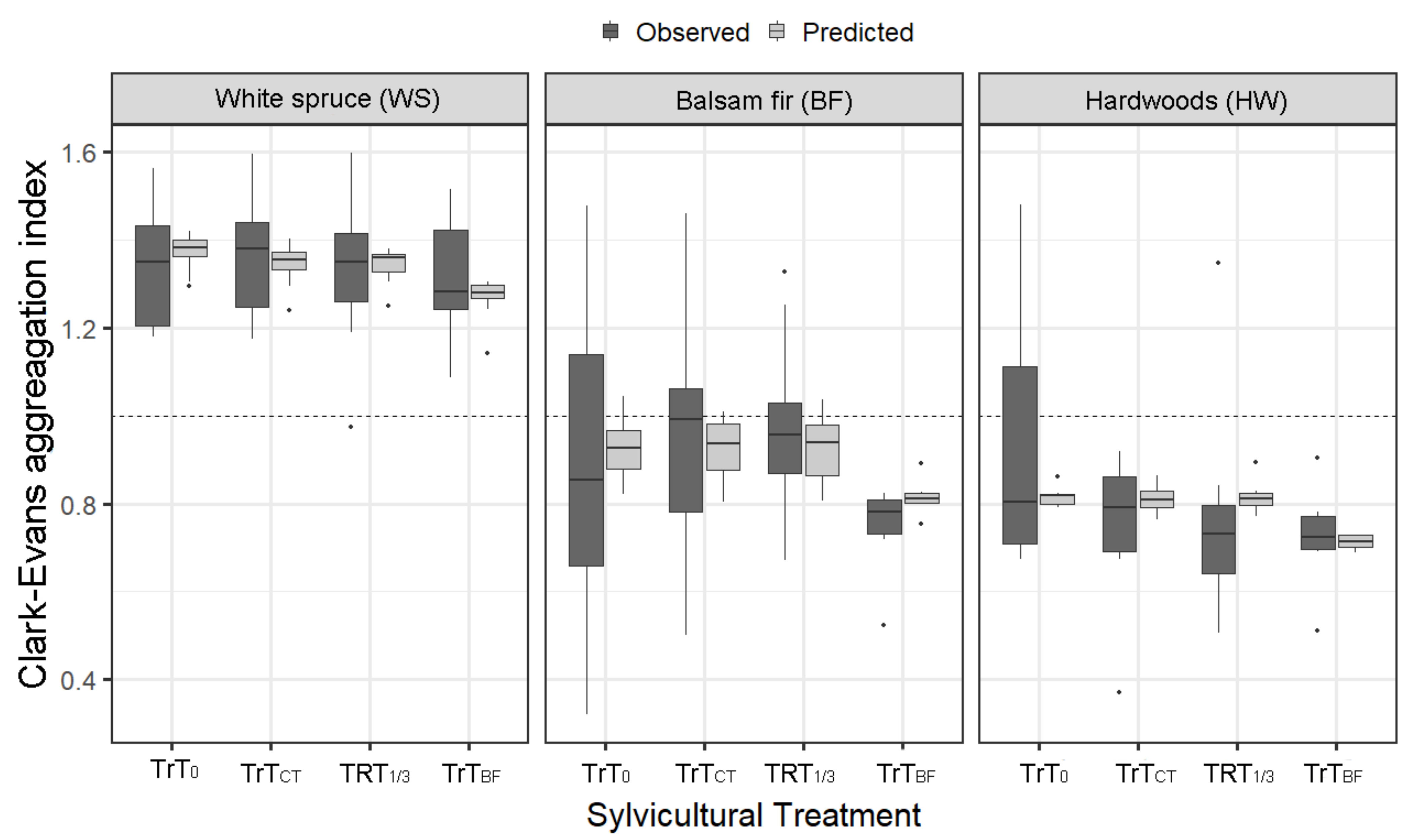
3.1.1. Clark and Evans Index
3.1.2. Spatial Interactions between Individual Trees
3.1.3. Spatial Interactions within Species Groups
3.2. Spatial Stand Structure Simulation
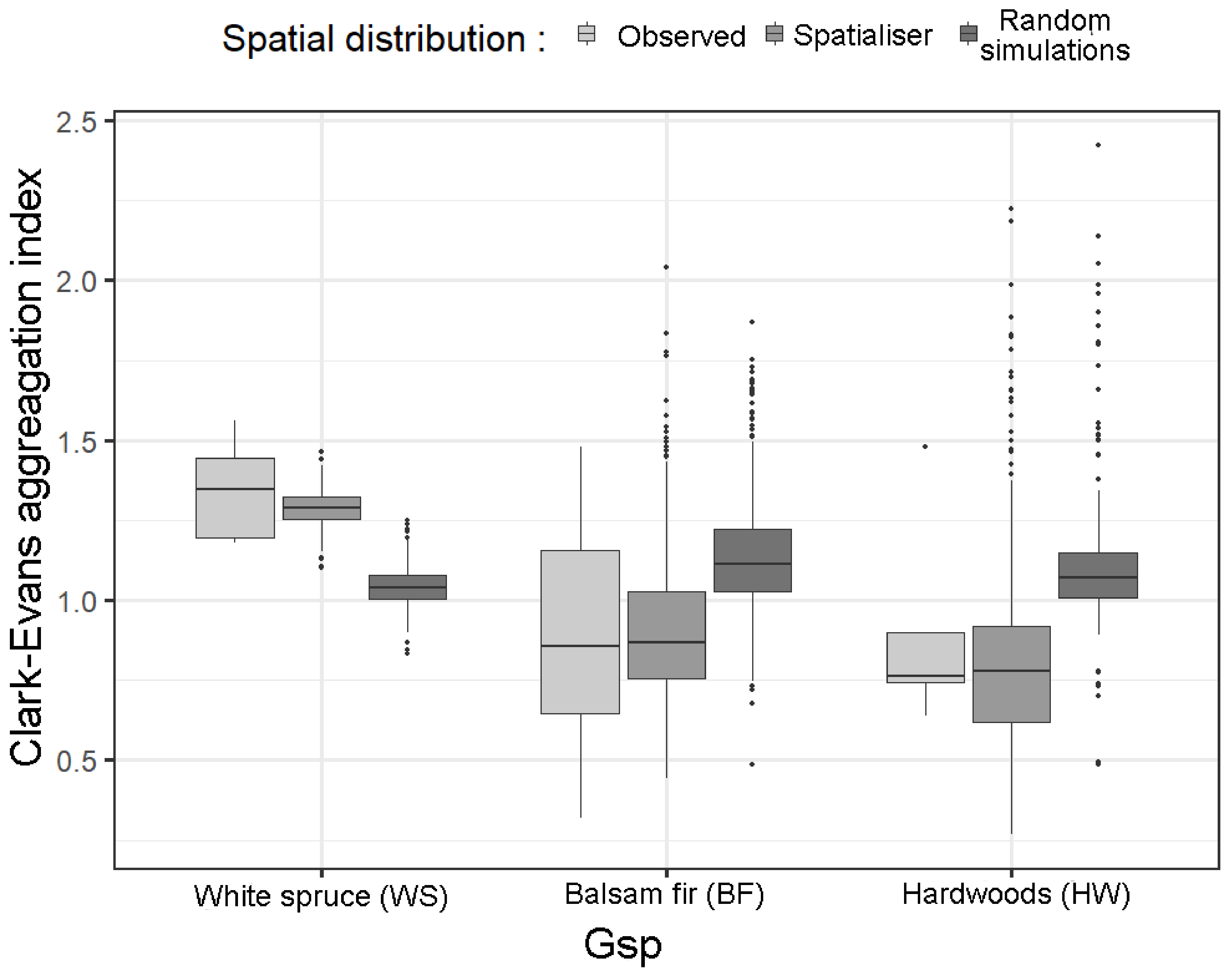
3.2.1. Performance Tests of the “Spatialiser”
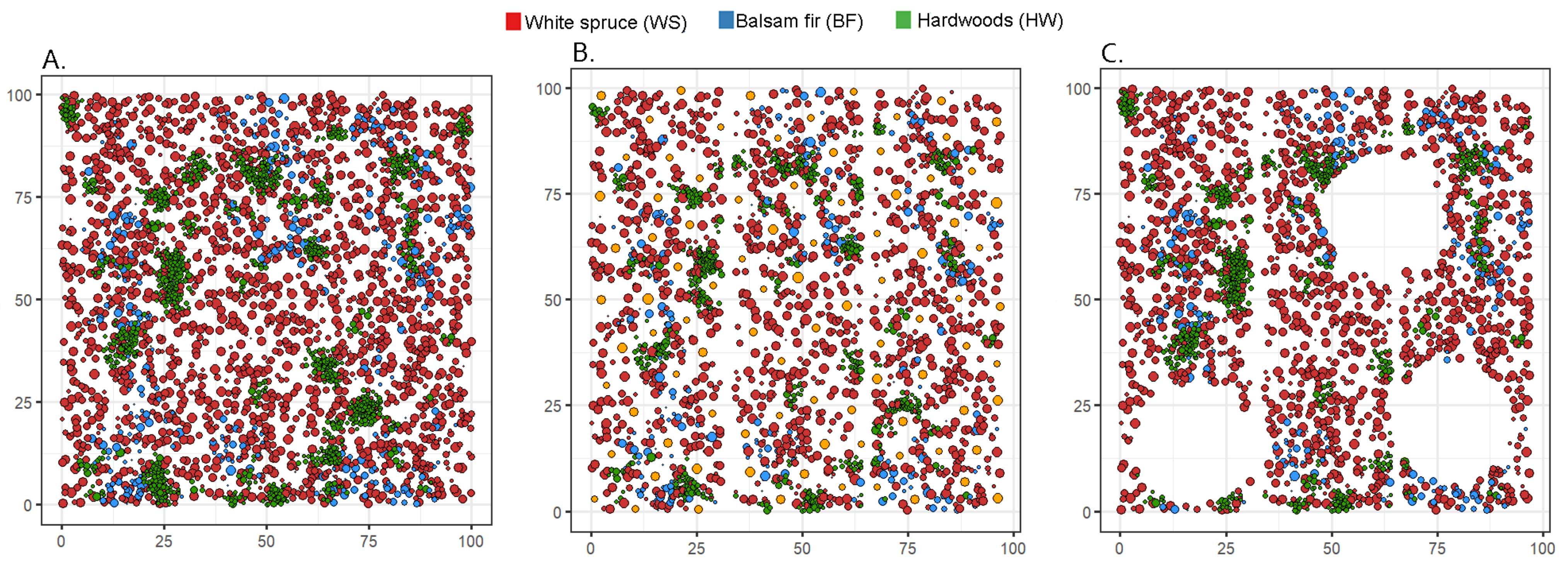
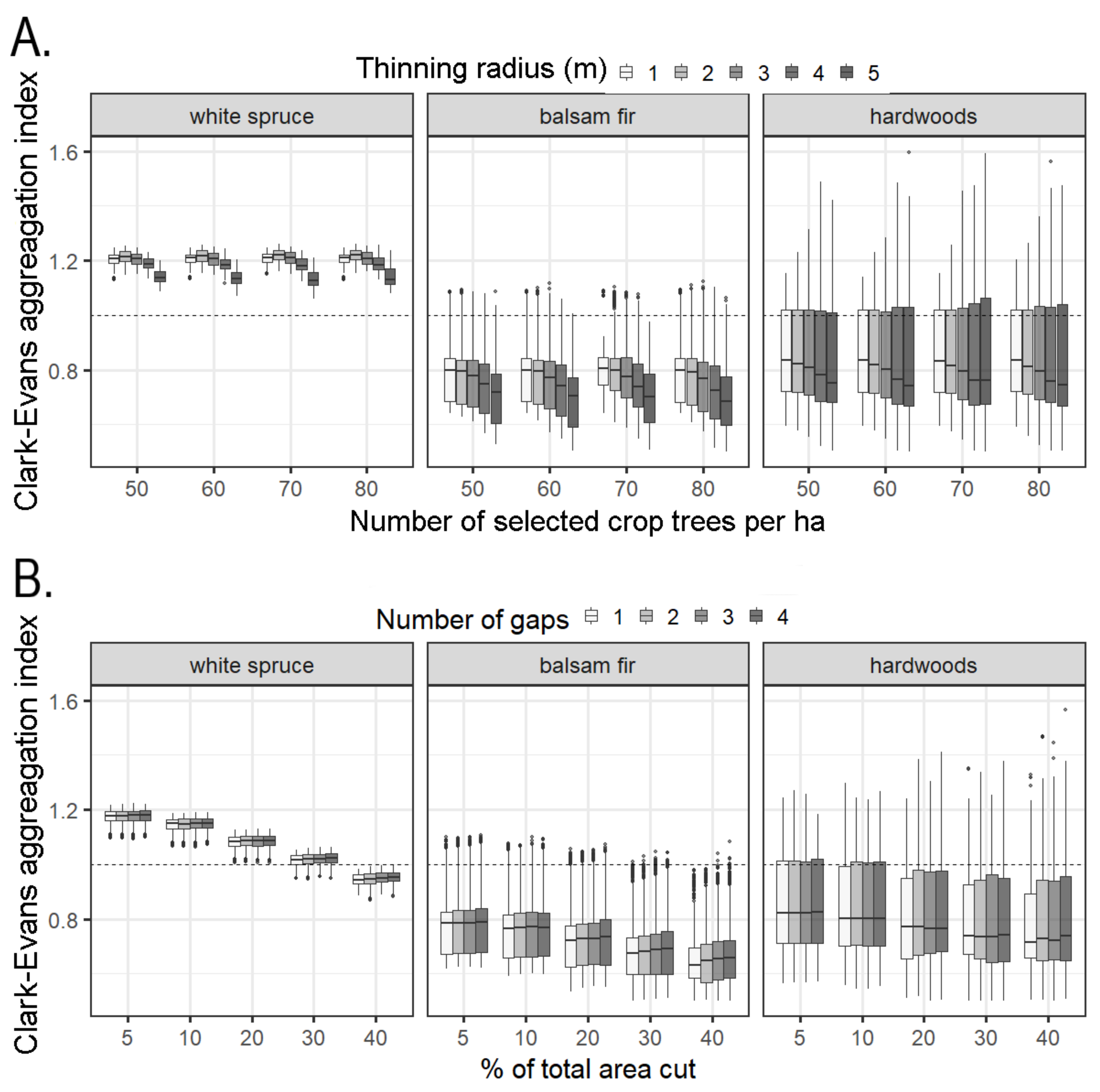
3.2.2. Thinning Treatment Simulations
4. Discussion
4.1. Modelling Spatial Stand Structure
4.2. Spatial Interactions between Individual Trees
4.3. Thinning Treatment Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Batista, J.L.F.; Maguire, D.A. Modelling the spatial structure of tropical forests. For. Ecol. Manag. 1998, 110, 293–314. [Google Scholar] [CrossRef]
- Pommerening, A.; Stoyan, D. Reconstructing spatial tree point patterns from nearest neighbour summary statistics measured in small subwindows. Can. J. For. Res. 2008, 38, 1110–1122. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Forest Growth and Yield Modelling; John Wiley & Sons: Chichester, UK, 2011; ISBN 9781119998518. [Google Scholar]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994; p. 537. [Google Scholar]
- Pommerening, A. Evaluating structural indices by reversing forest structural analysis. For. Ecol. Manag. 2006, 224, 266–277. [Google Scholar] [CrossRef]
- Pretzsch, H. Analysis and modeling of spatial stand structures. Methodological considerations based on mixed beech-larch stands in Lower Saxony. For. Ecol. Manag. 1997, 97, 237–253. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Pacala, S.W.; Deutschman, D.H. Details That Matter: The Spatial Distribution of Individual Trees Maintains Forest Ecosystem Function. Oikos 2017, 74, 357–365. [Google Scholar] [CrossRef]
- Law, R.; Illian, J.; Burslem, D.F.R.P.; Gratzer, G.; Gunatilleke, C.V.S.; Gunatilleke, I. Ecological information from spatial patterns of plants: Insights from point process theory. J. Ecol. 2009, 97, 616–628. [Google Scholar] [CrossRef]
- Bärring, U. On the reproduction of aspen (Populus tremula L.) with emphasis on its suckering ability. Scand. J. For. Res. 1988, 3, 229–240. [Google Scholar] [CrossRef]
- Hibbs, D.E.; Fischer, B.C. Sexual and vegetative reproduction of striped maple (Acer pensylvanicum L.). Bull. Torrey Bot. Club 1979, 106, 222–227. [Google Scholar] [CrossRef]
- Koop, H. Vegetative reproduction of trees in some European natural forests. Vegetatio 1987, 72, 103–110. [Google Scholar] [CrossRef]
- Gray, A.N.; Spies, T.A. Microsite controls on tree seedling establishment in conifer forest canopy gaps. Ecology 1997, 78, 2458–2473. [Google Scholar] [CrossRef]
- Yamamoto, S.-I. Forest gap dynamics and tree regeneration. J. For. Res. 2000, 5, 223–229. [Google Scholar] [CrossRef]
- Wiegand, T.; Moloney, K.A. Handbook of Spatial Point-Pattern Analysis in Ecology; CRC: Boca Raton, FL, USA, 2013; ISBN 1420082558. [Google Scholar]
- Diggle, P.J. Statistical Analysis of Spatial and Spatio-Temporal Point Patterns; CRC: Boca Raton, FL, USA, 2013; ISBN 146656024X. [Google Scholar]
- Fortin, M.; Dale, M.R.T.; Ver Hoef, J.M. Spatial analysis in ecology. Wiley StatsRef Stat. Ref. Online 2014. [Google Scholar] [CrossRef]
- Genet, A.; Grabarnik, P.; Sekretenko, O.; Pothier, D. Incorporating the mechanisms underlying inter-tree competition into a random point process model to improve spatial tree pattern analysis in forestry. Ecol. Model. 2014, 288, 143–154. [Google Scholar] [CrossRef]
- Diggle, P.J.; Fiksel, T.; Grabarnik, P.; Ogata, Y.; Stoyan, D.; Tanemura, M. On parameter estimation for pairwise interaction point processes. Int. Stat. Rev. 1994, 62, 99–117. [Google Scholar] [CrossRef]
- Grabarnik, P.; Särkkä, A. Interacting neighbour point processes: Some models for clustering. J. Stat. Comput. Simul. 2001, 68, 103–125. [Google Scholar] [CrossRef]
- Obiang, N.L.E.; Ngomanda, A.; Mboma, R.; Nzabi, T.; Ngoye, A.; Atsima, L.; Ndjélé, L.; Mate, J.; Lomba, C.; Picard, N. Spatial pattern of central African rainforests can be predicted from average tree size. Oikos 2010, 119, 1643–1653. [Google Scholar] [CrossRef]
- Grabarnik, P.; Särkkä, A. Modelling the spatial and space-time structure of forest stands: How to model asymmetric interaction between neighbouring trees. Procedia Environ. Sci. 2011, 7, 62–67. [Google Scholar] [CrossRef]
- Franklin, J.F.; Van Pelt, R. Remote sensing of structural complexity indices for habitat and species distribution modeling. J. For. 2004, 3, 22–28. [Google Scholar]
- Estes, L.D.; Reillo, P.R.; Mwangi, A.G.; Okin, G.S.; Shugart, H.H. Remote sensing of structural complexity indices for habitat and species distribution modeling. Remote Sens. Environ. 2010, 4, 792–804. [Google Scholar] [CrossRef]
- Gouvernement du Québec. Du Loi sur L’Aménagement Durable du Territoire Forestier; Gouvernement du Québec: Quebec, QC, Canada, 2015.
- Gauthier, S.; Vaillancourt, M.-A.; Leduc, A.; De Grandpré, L.; Kneeshaw, D.; Morin, H.; Drapeau, P.; Bergeron, Y. Ecosystem Management in the Boreal Forest; Presses de l’Université du Québec: Québec, QC, Canada, 2009; ISBN 2760523829. [Google Scholar]
- Harvey, B.D.; Leduc, A.; Gauthier, S.; Bergeron, Y. Stand-landscape integration in natural disturbance-based management of the southern boreal forest. For. Ecol. Manag. 2002, 155, 369–385. [Google Scholar] [CrossRef]
- Franklin, J.F.; Mitchell, R.J.; Palik, B. Natural Disturbance and Stand Development Principles for Ecological Forestry; US Department of Agriculture: Washington, DC, USA, 2007.
- Schütz, J. Silvicultural tools to develop irregular and diverse forest structures. Forestry 2002, 75, 329–337. [Google Scholar] [CrossRef]
- Ruel, J.-C.; Roy, V.; Lussier, J.-M.; Pothier, D.; Meek, P.; Fortin, D. Mise au point d’une sylviculture adaptée à la forêt boréale irrégulière. For. Chron. 2007, 83, 367–374. [Google Scholar] [CrossRef]
- Boucher, Y.; Arseneault, D.; Sirois, L.; Blais, L. Logging pattern and landscape changes over the last century at the boreal and deciduous forest transition in Eastern Canada. Landsc. Ecol. 2009, 24, 171–184. [Google Scholar] [CrossRef]
- Dupuis, S.; Arseneault, D.; Sirois, L. Change from pre-settlement to present-day forest composition reconstructed from early land survey records in eastern Québec, Canada. J. Veg. Sci. 2011, 22, 564–575. [Google Scholar] [CrossRef]
- Boucher, Y.; Arseneault, D.; Sirois, L. Logging-induced change (1930–2002) of a preindustrial landscape at the northern range limit of northern hardwoods, eastern Canada. Can. J. For. Res. 2006, 36, 505–517. [Google Scholar] [CrossRef]
- Grondin, P.; Cimon, A. Les Enjeux de Biodiversité Relatifs à la Composition Forestière; Gouvernement du Québec, Ministère des Ressources Naturelles, de la Faune et des Parcs: Quebec, QC, Canada, 2003.
- Eriksson, S.; Hammer, M. The challenge of combining timber production and biodiversity conservation for long-term ecosystem functioning—A case study of Swedish boreal forestry. For. Ecol. Manag. 2006, 237, 208–217. [Google Scholar] [CrossRef]
- O’Hara, K.L. The historical development of uneven-aged silviculture in North America. Forestry 2002, 75, 339–346. [Google Scholar] [CrossRef]
- Pretzsch, H. Transitioning Monocultures to Complex Forest Stands in Central Europe: Principles and Practice; Burleigh Dodds Science Publishing Limited: Cambridge, UK, 2019. [Google Scholar]
- Schütz, J.-P. Opportunities and strategies of transforming regular forests to irregular forests. For. Ecol. Manag. 2001, 151, 87–94. [Google Scholar] [CrossRef]
- Robitaille, A.; Saucier, J.-P. Forestiers, Québec (Province). Direction de la gestion des stocks; [Québec]. In Paysages Régionaux Du Québec Méridional; Gouvernement du Québec, Ministère des Ressources naturelles: Quebec, QC, Canada, 1998. [Google Scholar]
- Grondin, F.; Drouin, N. Optitek Sawmill Simulator-User’s Guide; Forintek Canada Corporation: Québec, QC, Canada, 1998. [Google Scholar]
- Gagné, L.; Sirois, L.; Lavoie, L. Comparaison du volume et de la valeur des bois résineux issus d’éclaircies par le bas et par dégagement d’arbres-élites dans l’Est du Canada. Can. J. For. Res. 2016, 11, 1320–1329. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Trochta, J.; Krůček, M.; Vrška, T.; Král, K. 3D Forest: An application for descriptions of three-dimensional forest structures using terrestrial LiDAR. PLoS ONE 2017, 12, e0176871. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Sánchez Meador, A.; Bourdon, J.F.; De Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Hahsler, M.; Piekenbrock, M.; Arya, S.; Mount, D. dbscan: Density Based Clustering of Applications with Noise (DBSCAN) and Related Algorithms. R Package Version. 2019. Available online: https://CRAN.R-project.org/package=dbscan (accessed on 28 May 2021).
- Clark, P.J.; Evans, F.C. Distance to nearest neighbour as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: Berlin/Heidelberg, Germany, 2002; Volume 172, p. 488. [Google Scholar]
- Arya, S.; Mount, D.; Kemp, S.E.; Jefferis, G. RANN: Fast Nearest Neighbour Search (Wraps ANN Library) Using L2 Metric. R Package Version 2.6.1. 2019. Available online: https://CRAN.R-project.org/package=RANN (accessed on 28 May 2021).
- Faraway, J.J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models; CRC Press: Boca Raton, FL, USA, 2016; Volume 124, ISBN 1498720986. [Google Scholar]
- Frey, B.J. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Coates, K.D. Tree recruitment in gaps of various size, clearcuts and undisturbed mixed forest of interior British Columbia, Canada. For. Ecol. Manag. 2002, 155, 387–398. [Google Scholar] [CrossRef]
- Choi, J.; Lorimer, C.G.; Vanderwerker, J.; Cole, W.G.; Martin, G.L. A crown model for simulating long-term stand and gap dynamics in northern hardwood forests. For. Ecol. Manag. 2001, 152, 235–258. [Google Scholar] [CrossRef]
- Schneider, R.; Berninger, F.; Ung, C.H.; Bernier, P.Y.; Swift, D.E.; Zhang, S.Y. Calibrating jack pine allometric relationships with simultaneous regressions. Can. J. For. Res. 2008, 38, 2566–2578. [Google Scholar] [CrossRef]
- St-Laurent, M.H.; Ferron, J.; Hins, C.; Gagnon, R. Effects of stand structure and landscape characteristics on habitat use by birds and small mammals in managed boreal forest of eastern Canada. Can. J. For. Res. 2007, 37, 1298–1309. [Google Scholar] [CrossRef]
- Duchateau, E.; Schneider, R.; Tremblay, S.; Dupont-Leduc, L. Density and diameter distributions of saplings in naturally regenerated and planted coniferous stands in Quebec after various approaches of commercial thinning. Ann. For. Sci. 2020, 77, 38. [Google Scholar] [CrossRef]
- Pommerening, A. Approaches to quantifying forest structures. Forestry 2002, 75, 305–324. [Google Scholar] [CrossRef]
- Wilson, B.F. Red Maple Stump Sprouts: Development the First Year; Harvard University: Harvard, MA, USA, 1968; Volume 10. [Google Scholar]
- Dupont-Leduc, L.; Schneider, R.; Sirois, L. Preliminary results from a structural conversion thinning trial in Eastern Canada. J. For. 2020, 118, 515–533. [Google Scholar] [CrossRef]
- Gauthier, M.-M.; Barrette, M.; Tremblay, S. Commercial thinning to meet wood production objectives and develop structural heterogeneity: A case study in the spruce-fir forest, Quebec, Canada. Forests 2015, 6, 510–532. [Google Scholar] [CrossRef]
- Pretzsch, H. Diversity and productivity in forests: Evidence from long-term experimental plots. In Forest Diversity and Function; Springer: Berlin/Heidelberg, Germany, 2005; pp. 41–64. ISBN 3540221913. [Google Scholar]
- Greene, D.F.; Kneeshaw, D.D.; Messier, C.; Lieffers, V.; Cormier, D.; Doucet, R.; Coates, K.D.; Groot, A.; Grover, G.; Calogeropoulos, C. Modelling silvicultural alternatives for conifer regeneration in boreal mixedwood stands (aspen/white spruce/balsam fir). For. Chron. 2002, 78, 281–295. [Google Scholar] [CrossRef]

| TrT0 (Control) | TrTCT (Crop Tree Release Thinning) | ||||||||
| Total | White Spruce | Balsam Fir | Hardwoods | Total | White Spruce | Balsam Fir | Hardwoods | ||
| Quadratic diameter (cm) | All trees | 15.1 [11.8–17.2] | 15.5 [13.3–17.5] | 14.0 [8.8–21.6] | 8.5 [5.5–13.5] | 15.4 [13.4–18.4] | 15.8 [14.2–18.2] | 15.2 [7.8–22.9] | 8.0 [5.3–10.8] |
| Saplings | 6.4 [4.8–7.6] | 6.7 [5.5–7.5] | 5.9 [3.6–8.0] | 5.3 [3.7–7.0] | 7.0 [5.2–7.9] | 7.2 [5.5–8.4] | 6.4 [2.1–8.7] | 6.0 [4.2–7.7] | |
| Merchantable trees | 16.8 [14.8–17.8] | 16.7 [14.9–18.1] | 16.3 [12.4–21.6] | 14.5 [9.8–22.9] | 16.6 [15.0–19.0] | 16.4 [15.1–18.6] | 17.6 [10.4–22.9] | 12.6 [9.2–16.0] | |
| Stand density (trees per ha) | All trees | 2247 [1544–3134] | 1719 [951–2283] | 360 [94–1054] | 168 [0–886] | 1994 [1166–2754] | 1524 [827–2270] | 377 [42–1317] | 93 [0–497] |
| Saplings | 537 [121–1715] | 301 [55–714] | 105 [0–219] | 131 [0–781] | 344 [67–801] | 164 [28–333] | 106 [0–532] | 74 [0–436] | |
| Merchantable trees | 1702 [1364–2161] | 1418 [806–2007] | 255 [54–909] | 37 [0–159] | 1649 [1082–2098] | 1360 [785–1937] | 270 [21–785] | 19 [0–121] | |
| Stand basal area (m2 per ha) | All trees | 39.1 [34–45.4] | 32.0 [17.7–42.9] | 6.1 [0.9–24.7] | 0.9 [0.0–5.3] | 36.5 [29.1–44.0] | 29.2 [20.5–38.5] | 6.8 [0.4–21.0] | 0.5 [0.0–2.5] |
| Saplings | 1.5 [0.4–3.1] | 1.0 [0.2–1.8] | 0.3 [0.0–0.8] | 0.2 [0.0–1.0] | 1.3 [0.3–2.4] | 0.7 [0.1–1.4] | 0.4 [0.0–2.0] | 0.2 [0.0–1.2] | |
| Merchantable trees | 37.7 [31.1–44.9] | 31.1 [17.2–42.3] | 5.9 [0.8–24.2] | 0.7 [0.0–4.3] | 35.3 [27.2–42.6] | 28.5 [20–37.1] | 6.5 [0.2–20.9] | 0.3 [0.0–1.7] | |
| Clark and Evans aggregation index | All trees | 1.23 [1.03–1.50] | 1.34 [1.18–1.56] | 0.90 [0.32–1.48] | 0.94 [0.67–1.48] | 1.32 [1.03–1.49] | 1.36 [1.17–1.60] | 0.93 [0.50–1.46] | 0.74 [0.37–0.92] |
| Saplings | 1.02 [0.83–1.19] | 0.99 [0.82–1.34] | 0.96 [0.55–1.28] | 0.85 [0.69–0.95] | 1.00 [0.26–1.52] | 1.16 [0.88–1.35] | 1.00 [0.32–1.42] | 0.77 [0.43–1.02] | |
| Merchantable trees | 1.34 [1.19–1.51] | 1.34 [1.17–1.54] | 0.91 [0.51–1.34] | 1.05 [0.65–1.46] | 1.35 [1.14–1.52] | 1.34 [1.14–1.57] | 0.94 [0.47–1.48] | 1.25 [0.70–1.74] | |
| TrT1/3 (Thinning From Below) | TrTBF (all Balsam Fir Trees are Harvested) | ||||||||
| Total | White Spruce | Balsam Fir | Hardwoods | Total | White Spruce | Balsam Fir | Hardwoods | ||
| Quadratic diameter (cm) | All trees | 15.8 [13.5–19.9] | 16.0 [14.3–18.5] | 16.4 [8.6–24.6] | 9.0 [5.6–13.2] | 14.3 [11.5–15.6] | 14.8 [14–15.8] | 13.1 [1.2–23.7] | 11.4 [5.2–39.1] |
| Saplings | 6.3 [5.0–7.5] | 6.5 [5.5–7.7] | 5.9 [4.4–7.2] | 5.0 [3.5–7.9] | 5.9 [5.5–7.0] | 6.3 [5.5–7.4] | 4.5 [1.2–8.4] | 4.8 [2.2–6.7] | |
| Merchantable trees | 17.2 [14.9–20.9] | 17.0 [14.8–19.2] | 18.6 [10.5–24.6] | 14.9 [11.6–23.5] | 16.4 [14.7–18.2] | 16.3 [15.0–18.0] | 17.4 [14.1–23.7] | 19.0 [11.7–47.8] | |
| Stand density (trees per ha) | All trees | 1706 [1040–2585] | 1345 [631–2178] | 219 [0–1066] | 141 [0–635] | 2254 [1313–3892] | 1809 [1053–2237] | 106 [11–271] | 339 [9–1662] |
| Saplings | 341 [49–889] | 181 [0–489] | 55 [0–406] | 105 [0–508] | 657 [226–1755] | 334 [200–458] | 39 [0–109] | 284 [9–1445] | |
| Merchantable trees | 1365 [686–2159] | 1164 [580–2017] | 165 [0–660] | 36 [0–127] | 1597 [890–2137] | 1475 [749–1900] | 67 [0–219] | 55 [0–217] | |
| Stand basal area (m2 per ha) | All trees | 31.9 [19.5–46.2] | 26.2 [16.5–38.6] | 4.8 [0.0–15.0] | 0.9 [0.0–5.0] | 34.6 [24.3–40.5] | 31.2 [17.1–36.4] | 1.6 [0.0–5.4] | 1.7 [0.0–5.3] |
| Saplings | 1.0 [0.1–2.0] | 0.6 [0.0–1.5] | 0.2 [0.0–1.5] | 0.2 [0.0–0.9] | 1.6 [0.9–4.1] | 1.0 [0.7–1.5] | 0.1 [0.0–0.4] | 0.5 [0.0–2.8] | |
| Merchantable trees | 30.9 [18.4–45] | 25.6 [16.3–37.5] | 4.6 [0.0–15.0] | 0.7 [0.0–4.5] | 33.1 [23.1–36.4] | 30.2 [16.4–35.2] | 1.6 [0.0–5.3] | 1.2 [0.0–3.9] | |
| Clark and Evans aggregation index | All trees | 1.26 [1.00–1.55] | 1.33 [0.98–1.60] | 0.96 [0.67–1.33 | 0.77 [0.51–1.35] | 1.22 [1.11–1.45] | 1.31 [1.09–1.52] | 0.74 [0.52–0.83] | 0.72 [0.51–0.90] |
| Saplings | 1.08 [0.68–1.56] | 1.14 [0.95–1.39] | 1.04 [0.64–1.51] | 0.76 [0.46–0.90] | 0.92 [0.74–1.13] | 1.05 [0.87–1.24] | 0.92 [0.27–1.44] | 0.68 [0.43–0.90] | |
| Merchantable trees | 1.34 [1.02–1.55] | 1.32 [1.04–1.60] | 1.02 [0.69–1.33] | 1.17 [0.34–2.33] | 1.30 [1.10–1.49] | 1.30 [1.01–1.50] | 0.83 [0.48–1.25] | 1.03 [0.82–1.13] | |
| Category | Variable | Description |
|---|---|---|
| Plot-level | TrT | General notation of the sylvicultural treatment affecting the stand |
| TrT0 | Control (no treatment) | |
| TrTBF | Thinning with priority selection of balsam fir, in which all the balsam fir are harvested | |
| TrT1/3 | Thinning from below, in which the smallest trees are cut while ensuring equal spacing between the remaining trees | |
| TrTCT | Crop tree release thinning to remove competition 3 m around a selected number of crop trees on observed data (from 0 to 4.5 m on simulated data) | |
| Gsp | General group notation for trees being regrouped by species (WS, BF, HW, or total) | |
| WS | Group containing all white spruce (Picea glauca) trees | |
| BF | Group containing all balsam fir (Abies balsamea) trees | |
| HW | Group containing all commercial hardwood species (described in text) | |
| Tot | Group containing all the trees from WS, BF, and HW | |
| NHaGsp | Tree density per hectare for a given Gsp | |
| RGsp | Aggregation index for a given Gsp | |
| Species-level | NClusHaGsp | Number of clusters per hectare for a given Gsp (calculated using the affinity propagation clustering method) |
| DistBF | Closest distance between 2 BF trees inside a cluster | |
| DistHW | Closest distance between 2 HW trees inside a cluster | |
| Tree-level | T0 | Target tree (i.e., tree to be positioned) |
| T1 | Closest competitor tree to T0 | |
| T2 | Second closest competitor tree to T0 | |
| DBHDiff | Absolute difference in diameter at breast height between T0 and T1 | |
| MinDistComp | Closest distance between two trees (where Competitor can be T1 or T2) |
| Coefficient | Variable † | RGsp | ||
|---|---|---|---|---|
| a0 | (Intercept) | 1.69069 | (0.18456) | *** |
| a1 | NHaGsp | 0.00022 | (0.00007) | ** |
| a2 | NHatot | −0.00030 | (0.00007) | *** |
| a3 | BF | −0.04347 | (0.11409) | |
| HW | −0.12414 | (0.11901) | ||
| a4 | TrTCT | −0.47603 | (0.23238) | * |
| TrT1/3 | −0.44839 | (0.19339) | * | |
| TrTBF | −0.91933 | (0.23554) | *** | |
| a5 | BF: NHaGsp | −0.00030 | (0.00011) | ** |
| HW: NHaGsp | −0.00031 | (0.00013) | * | |
| a6 | TrTCT: NHatot | 0.00020 | (0.00010) | |
| TrT1/3: NHatot | 0.00017 | (0.00009) | ||
| TrTBF: NHatot | 0.00034 | (0.00010) | *** | |
| Coefficient | Variable † | MinDistT1 | MinDistT2 | ||||
|---|---|---|---|---|---|---|---|
| b0 | (Intercept) | −0.46104 | (0.04497) | *** | 0.11132 | (0.03626) | ** |
| b1 | RGsp | 0.60337 | (0.03083) | *** | 0.36470 | (0.02402) | *** |
| b2 | DBHT0 | 0.00018 | (0.00001) | *** | 0.00012 | (0.00001) | *** |
| b3 | BFT0 | −0.07628 | (0.02564) | ** | −0.09724 | (0.01971) | *** |
| HWT0 | −0.22557 | (0.02938) | *** | −0.17750 | (0.02261) | *** | |
| b4 | DBHT1 | 0.00015 | (0.00001) | *** | 0.00010 | (0.00001) | *** |
| b5 | BFT1 | −0.19511 | (0.01360) | *** | −0.10188 | (0.01071) | *** |
| HWT1 | −0.27708 | (0.01469) | *** | −0.15679 | (0.01151) | *** | |
| b6 | NHaGsp | −0.00008 | (0.00002) | *** | −0.00011 | (0.00001) | *** |
| b7 | NHatot | −0.00011 | (0.00001) | *** | −0.00007 | (0.00001) | *** |
| b8 | DBHT2 | 0.00007 | (0.00001) | *** | |||
| b9 | BFT2 | −0.08173 | (0.01148) | *** | |||
| HWT2 | −0.11974 | (0.01253) | *** | ||||
| b10 | TrTCT | 0.02701 | (0.00948) | ** | |||
| TrT1/3 | 0.04731 | (0.00964) | *** | ||||
| TrTBF | 0.01166 | (0.00979) | |||||
| Coefficient | Variable † | NClusHaGsp | DistBF | DistHW | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| c0 | (Intercept) | 3.56105 | (0.07538) | *** | 0.49974 | (0.10200) | *** | 0.85028 | (0.31248) | ** |
| c1 | HW | 0.42423 | (0.09695) | *** | ||||||
| c2 | DBHDiff | 0.00113 | (0.00041) | ** | ||||||
| c3 | DBHT0 | 0.00287 | (0.00066) | *** | ||||||
| c4 | DBHT1 | 0.00109 | (0.00031) | *** | 0.00215 | (0.00070) | * | |||
| c5 | R | 0.94840 | (0.09473) | *** | 1.24419 | (0.16511) | *** | |||
| c6 | NHaGsp | −0.00107 | (0.00006) | *** | −0.00279 | (0.00039) | *** | |||
| c7 | NHatot | −0.00022 | (0.00011) | * | ||||||
| c8 | TrTCT | −0.14880 | (0.12912) | 0.04792 | (0.05024) | |||||
| TrT1/3 | −0.31400 | (0.10601) | ** | 0.12117 | (0.05391) | * | ||||
| TrTBF | −0.12706 | (0.10144) | 0.16893 | (0.07865) | * | |||||
| c9 | DBHT0: DBHT1 | −0.00002 | (0.00001) | * | ||||||
| c10 | NHatot: NHaGsp | 5.6e-07 | (0.00000) | *** | ||||||
| c11 | HW: TrTCT | 0.15866 | (0.16286) | |||||||
| HW: TrT1/3 | 0.32693 | (0.13133) | * | |||||||
| HW: TrTBF | 0.32710 | (0.12721) | * | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duchateau, E.; Schneider, R.; Tremblay, S.; Dupont-Leduc, L.; Pretzsch, H. Modelling the Spatial Structure of White Spruce Plantations and Their Changes after Various Thinning Treatments. Forests 2021, 12, 740. https://doi.org/10.3390/f12060740
Duchateau E, Schneider R, Tremblay S, Dupont-Leduc L, Pretzsch H. Modelling the Spatial Structure of White Spruce Plantations and Their Changes after Various Thinning Treatments. Forests. 2021; 12(6):740. https://doi.org/10.3390/f12060740
Chicago/Turabian StyleDuchateau, Emmanuel, Robert Schneider, Stéphane Tremblay, Laurie Dupont-Leduc, and Hans Pretzsch. 2021. "Modelling the Spatial Structure of White Spruce Plantations and Their Changes after Various Thinning Treatments" Forests 12, no. 6: 740. https://doi.org/10.3390/f12060740
APA StyleDuchateau, E., Schneider, R., Tremblay, S., Dupont-Leduc, L., & Pretzsch, H. (2021). Modelling the Spatial Structure of White Spruce Plantations and Their Changes after Various Thinning Treatments. Forests, 12(6), 740. https://doi.org/10.3390/f12060740






