The Contribution of Trees Outside of Forests to Landscape Carbon and Climate Change Mitigation in West Africa
Abstract
:1. Introduction
2. Materials and Methods
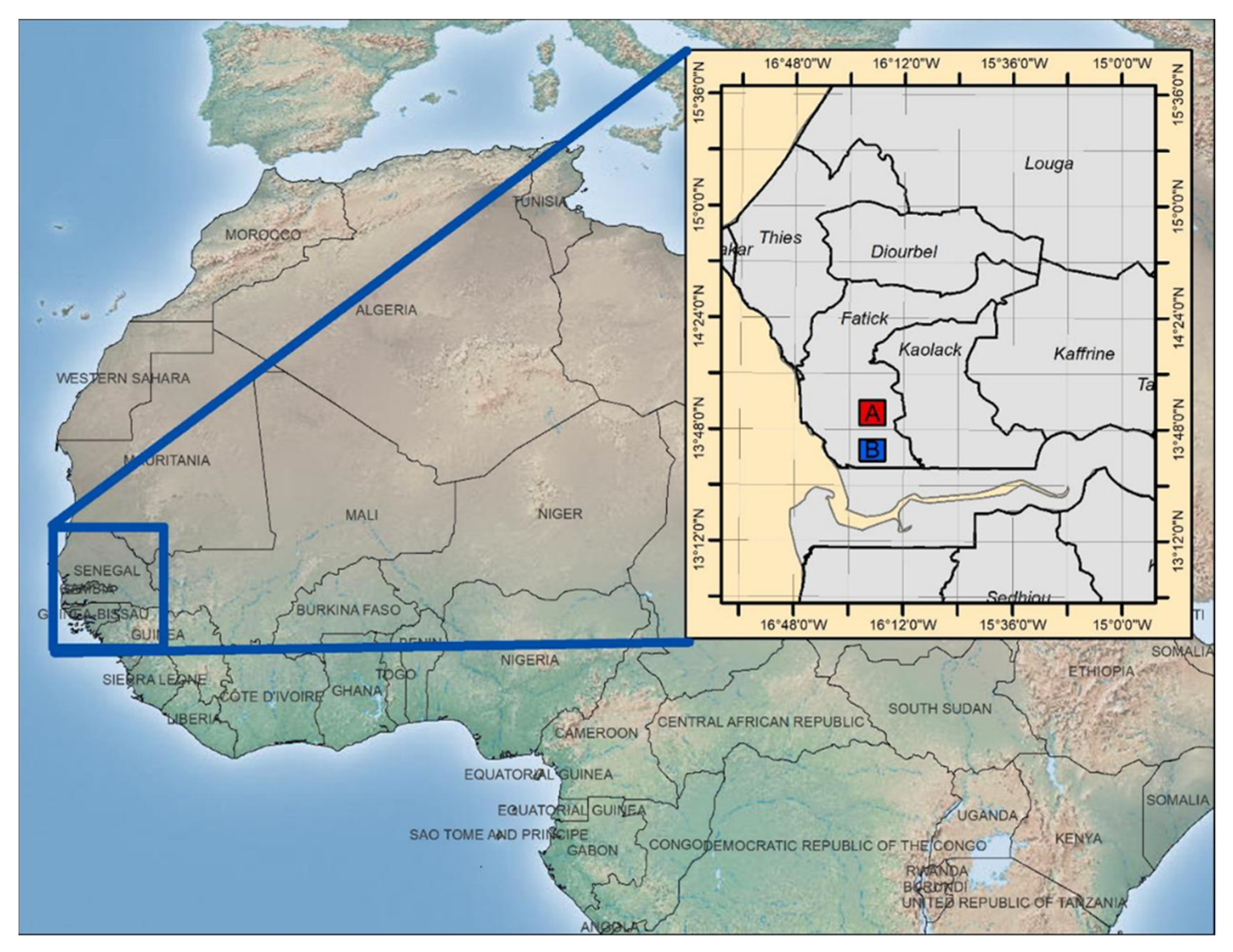
2.1. Study Region
2.2. Basic Approach: Mapping Individual Trees and Estimating Diameter from Crown Area
2.3. Tree Cover Mapping with Very High Resolution Remote Sensing Data
2.4. Field Sampling
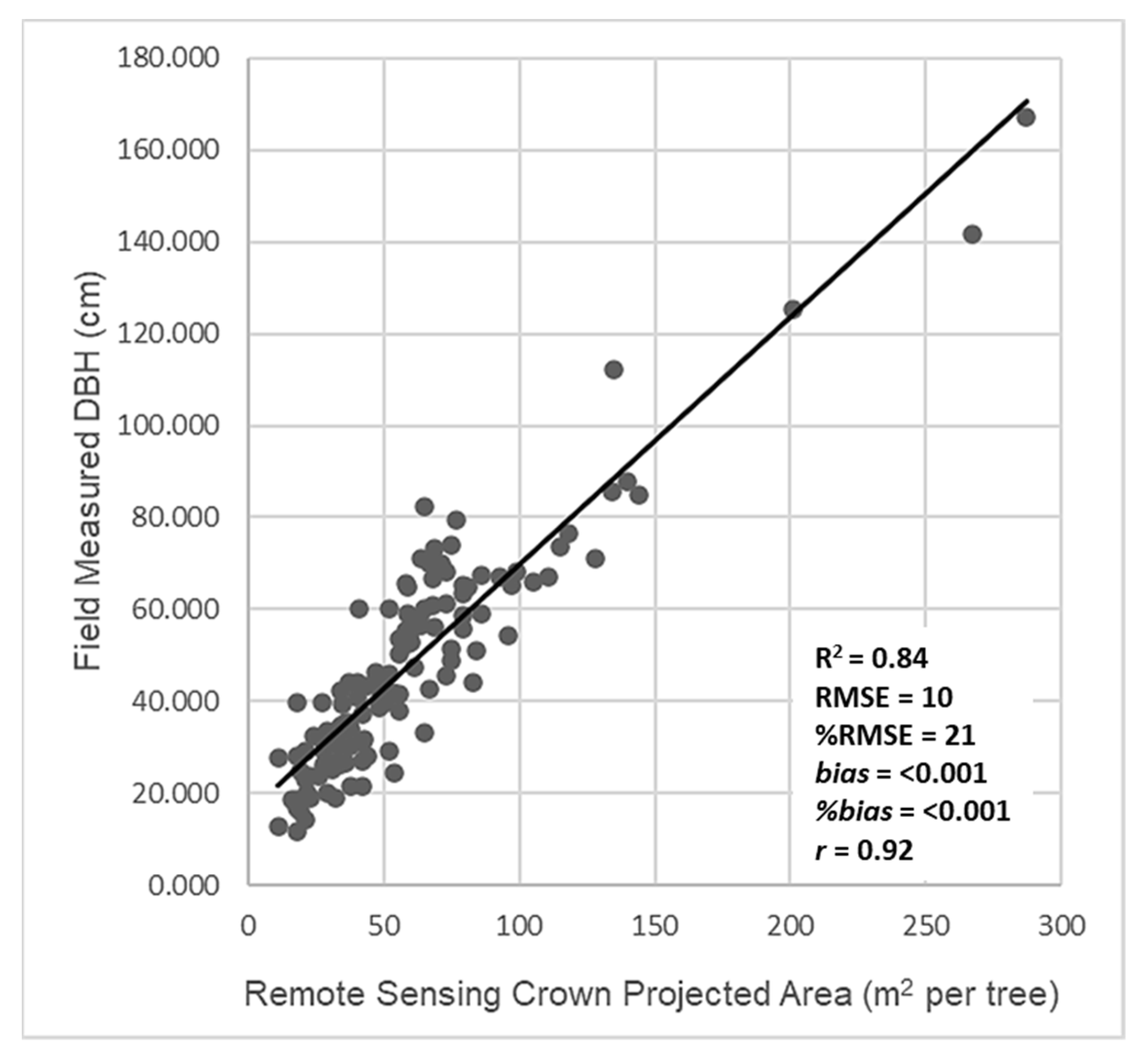
2.5. Estimation of Tree Stem Diameters from Crown Projected Area
2.6. Statistical Metrics
3. Results
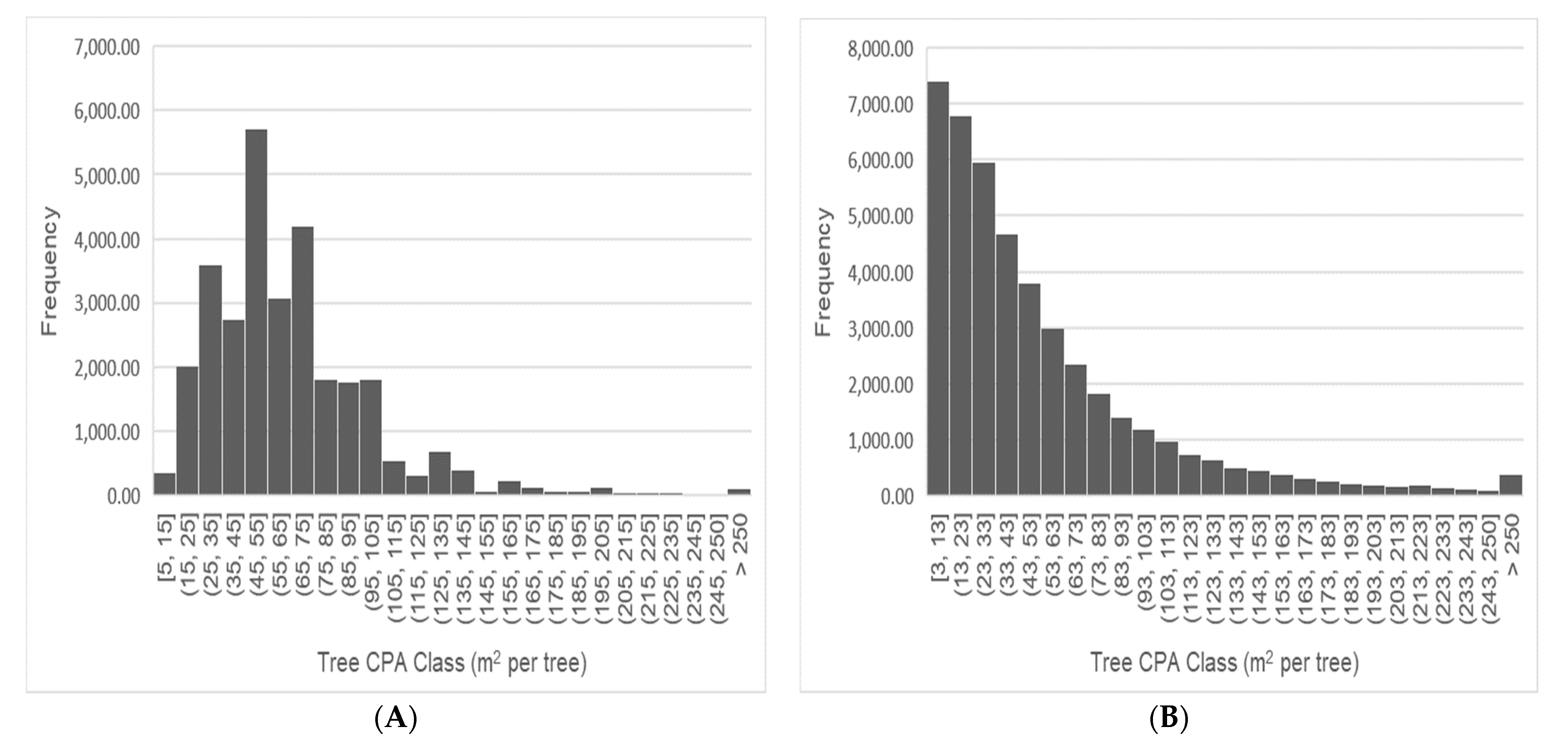
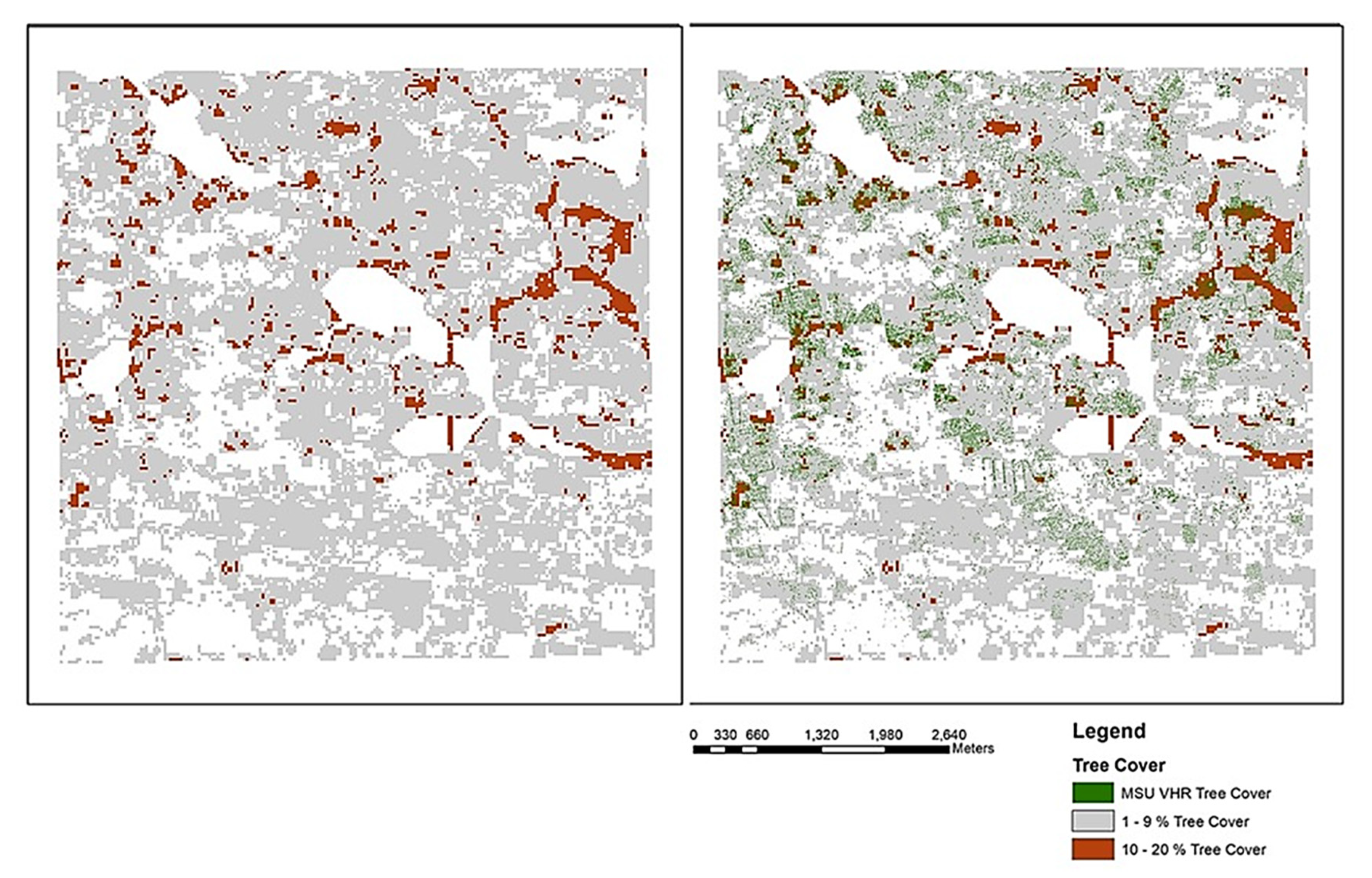
3.1. Landscape Mapping of TOF Cover
3.2. Estimation of Tree Diameter from Remote Sensing Crown Projected Area
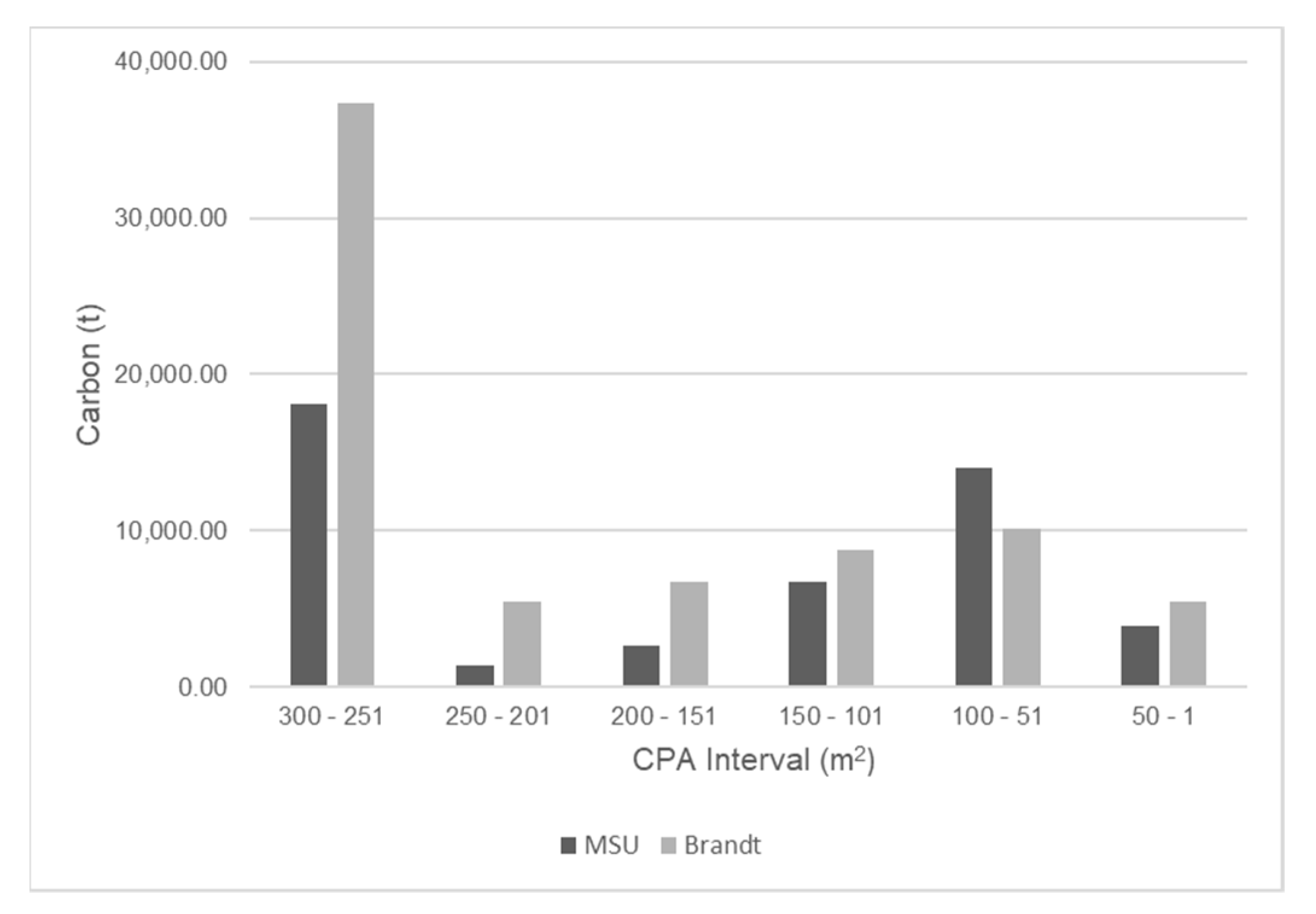
3.3. Carbon Stocks of Landscape Wide TOF
4. Discussion
4.1. Application of Standard Allometric Equations for Carbon Estimation
4.2. Other Studies and Other Tree Parameters
4.3. Comparison of Our Dataset with That of Brandt et al.
4.4. Comparison with Prominent Medium and Coarse Resolution Biomass Datasets
4.5. Limitations and Other Remarks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [Green Version]
- Fischer, R.; Taubert, F.; Müller, M.S.; Groeneveld, J.; Lehmann, S.; Wiegand, T.; Huth, A. Accelerated forest fragmentation leads to critical increase in tropical forest edge area. Sci. Adv. 2021, 7, 7012. [Google Scholar] [CrossRef]
- Vancutsem, C.; Achard, F.; Pekel, J.F.; Vieilledent, G.; Carboni, S.; Simonetti, D.; Gallego, J.; Aragao, L.E.; Nasi, R. Long-term (1990–2019) monitoring of forest cover changes in the humid tropics. Sci. Adv. 2021, 7, 1603. [Google Scholar] [CrossRef]
- Miller, D.C.; Muñoz-Mora, J.C.; Christiaensen, L. Prevalence, economic contribution, and determinants of trees on farms across Sub-Saharan Africa. Forest Policy Econ. 2017, 84, 47–61. [Google Scholar] [CrossRef] [Green Version]
- Zomer, R.J.; Neufeldt, H.; Xu, J.; Ahrends, A.; Bossio, D.; Trabucco, A.; Van Noordwijk, M.; Wang, M. Global Tree Cover and Biomass Carbon on Agricultural Land: The contribution of agroforestry to global and national carbon budgets. Sci. Rep. 2016, 6, 29987. [Google Scholar] [CrossRef] [PubMed]
- Schnell, S.; Altrell, D.; Ståhl, G.; Kleinn, C. The contribution of trees outside forests to national tree biomass and carbon stocks—a comparative study across three continents. Environ. Monit. Assess. 2015, 187, 4197. [Google Scholar] [CrossRef] [PubMed]
- Mbow, C.; Van Noordwijk, M.; Luedeling, E.; Neufeldt, H.; Minang, P.A.; Kowero, G. Agroforestry solutions to address food security and climate change challenges in Africa. Curr. Opin. Environ. Sustain. 2014, 6, 61–67. [Google Scholar] [CrossRef] [Green Version]
- Beckschäfer, P.; Schnell, S.; Kleinn, C. Monitoring and Assessment of Trees Outside Forests (TOF). In Agroforestry; Dagar, J.C., Tewari, V.P., Eds.; Springer Nature: Singapore, 2017; pp. 137–161. [Google Scholar]
- Brandt, M.; Rasmussen, K.; Hiernaux, P.; Herrmann, S.; Tucker, C.J.; Tong, X.; Tian, F.; Mertz, O.; Kergoat, L.; Mbow, C.; et al. Reduction of tree cover in West African woodlands and promotion in semi-arid farmlands. Nat. Geosci. 2018, 11, 328–333. [Google Scholar] [CrossRef] [PubMed]
- Zomer, R.J.; Trabucco, A.; Coe, R.; Place, F. Trees on Farm: Analysis of Global Extent and Geographical Patterns of Agroforestry; ICRAF Working Paper-World Agroforestry Centre 89; World Agroforestry Centre: Nairobi, Kenya, 2009. [Google Scholar]
- Mbow, C.; Smith, P.; Skole, D.; Duguma, L.; Bustamante, M. Achieving mitigation and adaptation to climate change through sustainable agroforestry practices in Africa. Curr. Opin. Environ. Sustain. 2014, 6, 8–14. [Google Scholar] [CrossRef] [Green Version]
- Verchot, L.V.; Van Noordwijk, M.; Kandji, S.; Tomich, T.; Ong, C.; Albrecht, A.; Mackensen, J.; Bantilan, C.; Anupama, K.V.; Palm, C. Climate change: Linking adaptation and mitigation through agroforestry. Mitig. Adapt. Strateg. Glob. Chang. 2007, 12, 901–918. [Google Scholar] [CrossRef] [Green Version]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C.J. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ. 2014, 140, 350–364. [Google Scholar] [CrossRef]
- Sitch, S.; Friedlingstein, P.; Gruber, N.; Jones, S.D.; Murray-Tortarolo, G.; Ahlström, A.; Doney, S.C.; Graven, H.; Heinze, C.; Huntingford, C.; et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 2015, 12, 653–679. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.; Mbow, C.; Diouf, A.A.; Verger, A.; Samimi, C.; Fensholt, R. Ground-and satellite-based evidence of the biophysical mechanisms behind the greening Sahel. Glob. Chang. Biol. 2015, 21, 1610–1620. [Google Scholar] [CrossRef] [Green Version]
- Mbow, C.; Brandt, M.; Ouedraogo, I.; De Leeuw, J.; Marshall, M. What four decades of earth observation tell us about land degradation in the Sahel? Remote Sens. 2015, 7, 4048–4067. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.; Rasmussen, K.; Peñuelas, J.; Tian, F.; Schurgers, G.; Verger, A.; Mertz, O.; Palmer, J.R.; Fensholt, R. Human population growth offsets climate-driven increase in woody vegetation in sub-Saharan Africa. Nat. Ecol. Evol. 2017, 1, 81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brandt, M.; Tappan, G.; Diouf, A.A.; Beye, G.; Mbow, C.; Fensholt, R. Woody vegetation die off and regeneration in response to rainfall variability in the West African Sahel. Remote Sens. 2017, 9, 39. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.; Hiernaux, P.; Rasmussen, K.; Tucker, C.J.; Wigneron, J.P.; Diouf, A.A.; Herrmann, S.M.; Zhang, W.; Kergoat, L.; Mbow, C.; et al. Changes in rainfall distribution promote woody foliage production in the Sahel. Commun. Biol. 2019, 2, 133. [Google Scholar] [CrossRef]
- Zhang, W.; Brandt, M.; Guichard, F.; Tian, Q.; Fensholt, R. Using long-term daily satellite based rainfall data (1983–2015) to analyze spatio-temporal changes in the Sahelian rainfall regime. J. Hydrol. 2017, 550, 427–440. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.; Wigneron, J.P.; Chave, J.; Tagesson, T.; Penuelas, J.; Ciais, P.; Rasmussen, K.; Tian, F.; Mbow, C.; Al-Yaari, A.; et al. Satellite passive microwaves reveal recent climate-induced carbon losses in African drylands. Nat. Ecol. Evol. 2018, 2, 827–835. [Google Scholar] [CrossRef] [Green Version]
- Brandt, M.; Tucker, C.J.; Kariryaa, A.; Rasmussen, K.; Abel, C.; Small, J.; Chave, J.; Rasmussen, L.V.; Hiernaux, P.; Diouf, A.A.; et al. An unexpectedly large count of trees in the West African Sahara and Sahel. Nature 2020, 587, 78–82. [Google Scholar] [CrossRef]
- Walker, S.M.; Pearson, T.R.H.; Casarim, F.M.; Harris, N.; Petrova, S.; Grais, A.; Swails, E.; Netzer, M.; Goslee, K.M.; Brown, S. Standard Operating Procedures for Terrestrial Carbon Measurement; Version February 2018; Winrock International: Washington, DC, USA, 2012. [Google Scholar]
- Dons, K.; Smith-Hall, C.; Meilby, H.; Fensholt, R. Operationalizing measurement of forest degradation: Identification and quantification of charcoal production in tropical dry forests using very high resolution satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 18–27. [Google Scholar] [CrossRef]
- Niang-Diop, F.; Christensen, S.N.; Barfod, A.S.; Sambou, B.; Diop, M.; Goudiaby, A.; Padonou, E.A.; Lykke, A.M. Trees on farmlands in the western central part of Senegal: Implications for a carbon project. Int. J. Biol. Chem. Sci. 2020, 14, 1294–1307. [Google Scholar] [CrossRef]
- Mbow, C.; Verstraete, M.M.; Sambou, B.; Diaw, A.T.; Neufeldt, H. Allometric models for aboveground biomass in dry savanna trees of the Sudan and Sudan–Guinean ecosystems of Southern Senegal. J. For. Res. 2014, 19, 340–347. [Google Scholar] [CrossRef]
- Rasmussen, M.O.; Göttsche, F.M.; Diop, D.; Mbow, C.; Olesen, F.S.; Fensholt, R.; Sandholt, I. Tree survey and allometric models for tiger bush in northern Senegal and comparison with tree parameters derived from high resolution satellite data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 517–527. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: II. Aboveground biomass. Agric. Ecosyst. Environ. 2012, 158, 216–224. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; Forestry Paper 134; Food and Agriculture Organization of the United Nations: Rome, Italy, 1997. [Google Scholar]
- IPCC. Good Practice Guidance for Land Use, Land-Use Change and Forestry; Penman, J., Gytarsky, M., Hiraishi, T., Krug, T., Kruger, D., Pipatti, R., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., et al., Eds.; IPCC National Greenhouse Gas Inventories Programme, Institute for Global Environmental Strategies: Hayama, Japan, 2003; 593p. [Google Scholar]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Eggleston, H.S., Buendia, L., Miwa, K., Ngara, T., Tanabe, K., Eds.; IPCC National Greenhouse Gas Inventories Programme, Institute for Global Environmental Strategies: Hayama, Japan, 2006. [Google Scholar]
- Chabi, A.; Lautenbach, S.; Tondoh, J.E.; Orekan, V.O.A.; Adu-Bredu, S.; Kyei-Baffour, N.; Mama, V.J.; Fonweban, J. The relevance of using in situ carbon and nitrogen data and satellite images to assess aboveground carbon and nitrogen stocks for supporting national REDD+ programmes in Africa. Carbon Balance Manag. 2019, 14, 12. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.; Valentini, R.; Bernoux, M.; Saint-André, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef] [Green Version]
- Balima, L.H.; Nacoulma, B.M.I.; Bayen, P.; Dimobe, K.; Kouamé, F.N.G.; Thiombiano, A. Aboveground biomass allometric equations and distribution of carbon stocks of the African oak (Afzelia africana Sm.) in Burkina Faso. J. For. Res. 2020, 31, 1699–1711. [Google Scholar] [CrossRef] [Green Version]
- Ganamé, M.; Bayen, P.; Ouédraogo, I.; Balima, L.H.; Thiombiano, A. Allometric models for improving aboveground biomass estimates in West African savanna ecosystems. Trees For. People 2021, 4, 100077. [Google Scholar] [CrossRef]
- Sawadogo, L.; Savadogo, P.; Tiveau, D.; Dayamba, S.D.; Zida, D.; Nouvellet, Y.; Oden, P.C.; Guinko, S. Allometric prediction of above-ground biomass of eleven woody tree species in the Sudanian savanna-woodland of West Africa. J. For. Res. 2010, 21, 475–481. [Google Scholar] [CrossRef]
- Chabi, A.; Lautenbach, S.; Orekan, V.O.A.; Kyei-Baffour, N. Allometric models and aboveground biomass stocks of a West African Sudan Savannah watershed in Benin. Carbon Balance Manag. 2016, 11, 16. [Google Scholar] [CrossRef] [Green Version]
- Bayen, P.; Noulèkoun, F.; Bognounou, F.; Lykke, A.M.; Djomo, A.; Lamers, J.P.; Thiombiano, A. Models for estimating aboveground biomass of four dryland woody species in Burkina Faso, West Africa. J. Arid. Environ. 2020, 180, 104205. [Google Scholar] [CrossRef]
- Moussa, M.; Mahamane, L.; Saadou, M. Allometric equations for biomass estimation of woody species and organic soil carbon stocks of agroforestry systems in West African: State of current knowledge. Int. J. Res. 2015, 2, 17–33. [Google Scholar]
- Kuyah, S.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Neufeldt, H.; Dietz, J. Crown area allometries for estimation of aboveground tree biomass in agricultural landscapes of western Kenya. Agrofor. Syst. 2012, 86, 267–277. [Google Scholar] [CrossRef]
- Leite, R.V.; Silva, C.A.; Mohan, M.; Cardil, A.; Almeida, D.R.A.D.; Jaafar, W.S.W.M.; Guerra-Hernández, J.; Weiskittel, A.; Hudak, A.T.; Broadbent, E.N. Individual Tree Attribute Estimation and Uniformity Assessment io Fast-Growiog Eucalyptus spp. Forest Plantations Usiog Lidar and Lioear Mixed-Effects Models. Remote Sens. 2020, 12, 3599. [Google Scholar] [CrossRef]
- Woomer, P.L.; Touré, A.; Sall, M. Carbon stocks in Senegal’s Sahel transition zone. J. Arid. Environ. 2004, 59, 499–510. [Google Scholar] [CrossRef]
- Lutz, J.A.; Furniss, T.J.; Johnson, D.J.; Davies, S.J.; Allen, D.; Alonso, A.; Anderson-Teixeira, K.J.; Andrade, A.; Baltzer, J.; Becker, K.M.; et al. Global importance of large-diameter trees. Glob. Ecol. Biogeogr. 2018, 27, 849–864. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Lin, S.L.; He, J.K.; Kong, F.M.; Yu, J.H.; Jiang, H.S. Big-sized trees overrule remaining trees’ attributes and species richness as determinants of aboveground biomass in tropical forests. Glob. Chang. Biol. 2019, 25, 2810–2824. [Google Scholar] [CrossRef]
- Latifi, H.; Heurich, M. Multi-scale remote sensing-assisted forest inventory: A glimpse of the state-of-the-art and future prospects. Remote Sens. 2019, 11, 1260. [Google Scholar] [CrossRef] [Green Version]
- Almeida, D.R.A.D.; Stark, S.C.; Chazdon, R.; Nelson, B.W.; César, R.G.; Meli, P.; Gorgens, E.B.; Duarte, M.M.; Valbuena, R.; Moreno, V.S.; et al. The effectiveness of lidar remote sensing for monitoring forest cover attributes and landscape restoration. For. Ecol. Manag. 2019, 438, 34–43. [Google Scholar] [CrossRef]
- Muller-Landau, H.C.; Condit, R.S.; Chave, J.; Thomas, S.C.; Bohlman, S.A.; Bunyavejchewin, S.; Davies, S.; Foster, R.; Gunatilleke, S.; Gunatilleke, N.; et al. Testing metabolic ecology theory for allometric scaling of tree size, growth and mortality in tropical forests. Ecol. Lett. 2006, 9, 575–588. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
- Hemery, G.E.; Savill, P.S.; Pryor, S.N. Applications of the crown diameter–stem diameter relationship for different species of broadleaved trees. For. Ecol. Manag. 2005, 215, 285–294. [Google Scholar] [CrossRef]
- Loubota Panzou, G.J.; Fayolle, A.; Jucker, T.; Phillips, O.L.; Bohlman, S.; Banin, L.F.; Lewis, S.L.; Affum-Baffoe, K.; Alves, L.F.; Antin, C.; et al. Pantropical variability in tree crown allometry. Glob. Ecol. Biogeogr. 2021, 30, 459–475. [Google Scholar] [CrossRef]
- Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Dong, H. A first map of tropical Africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 045011. [Google Scholar] [CrossRef] [Green Version]
- Zarin, D.J.; Harris, N.L.; Baccini, A.; Aksenov, D.; Hansen, M.C.; Azevedo-Ramos, C.; Azevedo, T.; Margono, B.A.; Alencar, A.C.; Gabris, C.; et al. Can carbon emissions from tropical deforestation drop by 50% in 5 years? Glob. Chang. Biol. 2016, 22, 1336–1347. [Google Scholar] [CrossRef] [Green Version]
- Baccini, A.G.S.J.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spawn, S.A.; Sullivan, C.C.; Lark, T.J.; Gibbs, H.K. Harmonized global maps of above and belowground biomass carbon density in the year 2010. Sci. Data 2020, 7, 112. [Google Scholar] [CrossRef] [PubMed]
- Skole, D.L.; Mbow, C.; Mugabowindekwe, M.; Brandt, M.S.; Samek, J.H. Trees outside of forests as natural climate solutions. Nat. Clim. Chang. 2021, 11. [Google Scholar] [CrossRef]
- Verdone, M.; Seidl, A. Time, space, place, and the Bonn Challenge global forest restoration target. Restor. Ecol. 2017, 25, 903–911. [Google Scholar] [CrossRef]
- Stanturf, J.A.; Kleine, M.; Mansourian, S.; Parrotta, J.; Madsen, P.; Kant, P.; Burns, J.; Bolte, A. Implementing forest landscape restoration under the Bonn Challenge: A systematic approach. Ann. For. Sci. 2019, 76, 50. [Google Scholar] [CrossRef]
- Guariguata, M.R.; Evans, K. A diagnostic for collaborative monitoring in forest landscape restoration. Restor. Ecol. 2020, 28, 742–749. [Google Scholar] [CrossRef]
- Mansourian, S.; Dudley, N.; Vallauri, D. Forest landscape restoration: Progress in the last decade and remaining challenges. Ecol. Restor. 2017, 35, 281–288. [Google Scholar] [CrossRef]





| Estimate of Tree Diameter, DBH | DBH = 0.5389 × Crs + 15.835 |
|---|---|
| Aboveground Biomass [26] | AGB = 1.929 × DBH − 0.116 × DBH2 + 0.013 × DBH3 |
| Aboveground Biomass [29,30,31] | AGB = EXP(−1.996 + 2.32 × ln(DBH)) |
| Aboveground Biomass [28] | AGB = 0.091 × DBH2.472 |
| Belowground Biomass Factor | BGB = AGB × 0.26 |
| Biomass–Carbon Conversion | C = (AGB + BGB) × 0.5 |
| Study Area (ha) | Total Trees | Total Tree Cover (m2) | Stem Density (trees ha−1) | Tree Cover Percent | Carbon Density (MgC ha−1) | Total Carbon (MgC) 1 | |
|---|---|---|---|---|---|---|---|
| This study | 3336 | 29,835 | 1.923 × 106 | 8 | 5.0 | 13 | 44.28 × 103 |
| Brandt et al. [22] | 3336 | 44,070 | 2.416 × 106 | 12 | 7.0 | 22 | 73.35 × 103 |
| Brown [29] | 9 | 29.60 × 103 | |||||
| Kuyah et al. [28] | 11 | 37.72 × 103 |
| This Study | Brandt et al. 2020 | |||||
|---|---|---|---|---|---|---|
| Tree Crown | Tree Diameter | Tree Carbon | Tree Crown | Tree Diameter | Tree Carbon | |
| Mean | 64.48 | 50.59 | 1.48 | 52.61 | 44.18 | 1.67 |
| Standard Error | 0.208 | 0.112 | 0.017 | 0.238 | 0.128 | 0.019 |
| Median | 56.07 | 46.05 | 0.70 | 36.75 | 35.64 | 0.30 |
| Mode | 49.23 | 42.37 | 0.54 | 5.50 | 19.07 | 0.03 |
| Kurtosis | 5.821 | 5.82 | 67.49 | 4.321 | 4.32 | 23.813 |
| Skewness | 1.86 | 1.86 | 7.08 | 1.94 | 1.94 | 4.515 |
| Minimum | 5.47 | 18.78 | 0.05 | 3.00 | 17.45 | 0.022 |
| Maximum | 298.13 | 176.50 | 42.97 | 299.50 | 177.24 | 35.17 |
| Sum | 1,924,000 | 1,509,281 | 44,283 | 2,318,555 | 1,947,318 | 73,912 |
| Count | 29,835 | 29,835 | 29,835 | 44,070 | 44,070 | 44,070 |
| CPA Size Class (m2) | Number of Brandt Trees | Number of Brandt Trees also Mapped by This Study | % of Brandt Trees also Mapped by This Study | MSU Centroids That Overlap Brandt |
|---|---|---|---|---|
| 251–300 | 380 | 322 | 84.7% | 514 |
| 201–250 | 738 | 582 | 78.8% | 846 |
| 151–200 | 1445 | 967 | 66.9% | 1207 |
| 101–150 | 3473 | 1591 | 45.8% | 1735 |
| 51–100 | 10,484 | 1923 | 18.3% | 2010 |
| 1–50 | 27,550 | 894 | 3.2% | 899 |
| CPA Size Class (m2) | 1 Tree with Overlap (MgC) Case 2: Size Measure | 2 Trees with Overlap (MgC) Case 3: Clustering | 3–5 Trees with Overlap (MgC) Case 3: Clustering |
|---|---|---|---|
| 250–300 | 4540 | 3095 | 1408 |
| 200–250 | 5078 | 2747 | 868 |
| 150–200 | 4915 | 1432 | 232 |
| 100–150 | 3435 | 304 | 33 |
| 50–100 | 158 | −11 | 2 |
| 0–50 | −486 | −4 | −1 |
| Total | 17640 | 7563 | 2542 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skole, D.L.; Samek, J.H.; Dieng, M.; Mbow, C. The Contribution of Trees Outside of Forests to Landscape Carbon and Climate Change Mitigation in West Africa. Forests 2021, 12, 1652. https://doi.org/10.3390/f12121652
Skole DL, Samek JH, Dieng M, Mbow C. The Contribution of Trees Outside of Forests to Landscape Carbon and Climate Change Mitigation in West Africa. Forests. 2021; 12(12):1652. https://doi.org/10.3390/f12121652
Chicago/Turabian StyleSkole, David L., Jay H. Samek, Moussa Dieng, and Cheikh Mbow. 2021. "The Contribution of Trees Outside of Forests to Landscape Carbon and Climate Change Mitigation in West Africa" Forests 12, no. 12: 1652. https://doi.org/10.3390/f12121652
APA StyleSkole, D. L., Samek, J. H., Dieng, M., & Mbow, C. (2021). The Contribution of Trees Outside of Forests to Landscape Carbon and Climate Change Mitigation in West Africa. Forests, 12(12), 1652. https://doi.org/10.3390/f12121652








