Live Crown Ratio Models for Loblolly Pine (Pinus taeda) with Beta Regression
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods and Models
2.3. Beta Regression
2.4. Model Evaluation and Additional Predictors
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, M.W.; Hann, D.W. Equations for Predicting Height to Crown Base for Fourteen Tree Species in Southwest Oregon; Oregon State University, Forestry Research Laboratory: Corvallis, OR, USA, 1987; pp. 1–14. [Google Scholar]
- Ibrahim, E.M.; Osman, E.H. Diameter at Breast Height-Crown Width Prediction Models for Anogeissus Leiocarpus (DC.) Guill &Perr and Combretum Hartmannianum Schweinf. J. For. Prod. Ind. 2014, 3, 2325–4513. [Google Scholar]
- Sharma, R.P.; Vacek, Z.; Vacek, S.; Podrázský, V.; Jansa, V. Modelling individual tree height to crown base of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.). PLoS ONE 2017, 12, e0186394. [Google Scholar] [CrossRef] [Green Version]
- Burkhart, H.E.; Amateis, R.L.; Westfall, J.A.; Daniels, R.F. PTAEDA4.0: Simulation of Individual Tree Growth, Stand Development and Economic Evaluation in Loblolly Pine Plantations; Division of Forestry and Wildlife Research, Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2008; p. 27. [Google Scholar]
- Oliver, C.D.; Larson, B.C. Forest Stand Dynamics: Update Edition; John Wiley & Sons: New York, NY, USA, 1996; p. 520. [Google Scholar]
- Leites, L.; Robinson, A.; Crookston, N. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Can. J. For. Res. 2009, 39, 655–665. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Dordrecht, The Netherlands, 2012; p. 485. [Google Scholar]
- Patton, S.R.; Russell, M.B.; Windmuller-Campione, M.A.; Edgar, C.B. Modeled diameter growth response to intermediate treatments of planted white spruce (Picea glauca) affected by eastern spruce budworm (Choristoneura fumiferana) in Minnesota, USA. Can. J. For. Res. 2019, 49, 1633–1637. [Google Scholar] [CrossRef]
- Larson, P.R. Stem form development of forest trees. For. Sci. Monograph. 1963, 9, 1–42. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Walton, S.B. Incorporating crown ratio into taper equations for loblolly pine trees. For. Sci. 1985, 31, 478–484. [Google Scholar]
- Leites, L.P.; Robinson, A.P. Improving taper equations of loblolly pine with crown dimensions in a mixed-effects modeling framework. For. Sci. 2004, 50, 204–212. [Google Scholar]
- Poudel, K.P.; Temesgen, H.; Gray, A.N. Evaluation of sampling strategies to estimate crown biomass. For. Ecosyst. 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, W.; Zeng, W.; Wang, J.; Meng, J. Development of crown ratio and height to crown base models for Mason pine in southern China. Forests 2020, 11, 1216. [Google Scholar] [CrossRef]
- Zhao, D.; Kane, M.; Borders, B. Crown ratio and relative spacing relationships for loblolly pine plantations. Open J. For. 2012, 2, 110–115. [Google Scholar] [CrossRef]
- Dean, T.J. Using live-crown ratio to control wood quality: An example of quantitative silviculture. In Proceedings of the Paper presented at the Tenth Biennial Southern Silvicultural Research Conference, Shreveport, LA, USA, 16 February 1999. [Google Scholar]
- Akers, M.K.; Daniels, R.F.; Kane, M.; Teskey, R.O.; Zhao, D. Effects of planting density and cultural intensity on stand and crown attributes of mid-rotation loblolly pine plantations. For. Ecol. Manag. 2013, 310, 468–475. [Google Scholar] [CrossRef]
- Land, S.B., Jr.; Belli, K.L.; Duzan, H.W. Family, spacing, and family-by-spacing effects on loblolly pine during five years after planting. In General Technical Report SE-70, Proceedings of the Sixth Biennial Southern Silvicultural Research Conference, Memphis, TN, USA, 30 October–1 November 1990; Coleman, S.S., Neary, D.G., Eds.; U.S. Department of Agriculture, Forest Service, Southeastern Forest Experiment Station: Asheville, NC, USA, 1991. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 14 October 2021).
- Soares, P.; Tomé, M. A tree crown ratio prediction equation for eucalypt plantations. Ann. For. Sci. 2001, 58, 193–202. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Zeileis, A. Beta regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Korhonen, L.; Korhonen, K.T.; Stenberg, P.; Maltamo, M.; Rautiainen, M. Local models for forest canopy cover with beta regression. Silva Fenn. 2007, 41, 671–685. [Google Scholar] [CrossRef] [Green Version]
- Eskelson, B.N.; Madsen, L.; Hagar, J.C.; Temesgen, H. Estimating riparian understory vegetation cover with Beta regression and copula models. For. Sci. 2011, 57, 212–221. [Google Scholar]
- Poudel, K.P.; Temesgen, H. Methods for estimating aboveground biomass and its components for Douglas-fir and lodgepole pine trees. Can. J. For. Res. 2016, 46, 77–87. [Google Scholar] [CrossRef] [Green Version]
- Hoe, M.S.; Dunn, C.J.; Temesgen, H. Multitemporal LiDAR improves estimates of fire severity in forested landscapes. Int. J. Wildl. Fire. 2018, 27, 581–594. [Google Scholar] [CrossRef]
- Smith, J.H.G.; Reukema, D.L. Effects of plantation and juvenile spacing on tree and stand development. In Douglas-Fir: Stand Management for the Future, Proceedings of a Symposium, 18–20 June 1985, Seattle, WA, USA; Oliver, C.D., Hanley, D.P., Johnson, J.A., Eds.; College of Forest Resources, University of Washington: Seattle, WA, USA, 1986; pp. 239–245. [Google Scholar]
- Fu, L.; Zhang, H.; Lu, J.; Zang, H.; Lou, M.; Wang, G. Multilevel nonlinear mixed-effect crown ratio models for individual trees of Mongolian Oak (Quercus mongolica) in Northeast China. PLoS ONE 2015, 10, e0133294. [Google Scholar] [CrossRef]
- Liu, J.; Burkhart, H.E. Spatial characteristics of diameter and total height in juvenile loblolly pine (Pinus taeda L.) plantations. For. Sci. 1993, 40, 774–786. [Google Scholar]
- Chumra, D.J.; Tjoelker, M.G.; Martin, T.A. Environmental and genetic effects on crown shape in young loblolly pine plantations. Can. J. Res. For. 2009, 39, 691–698. [Google Scholar] [CrossRef]


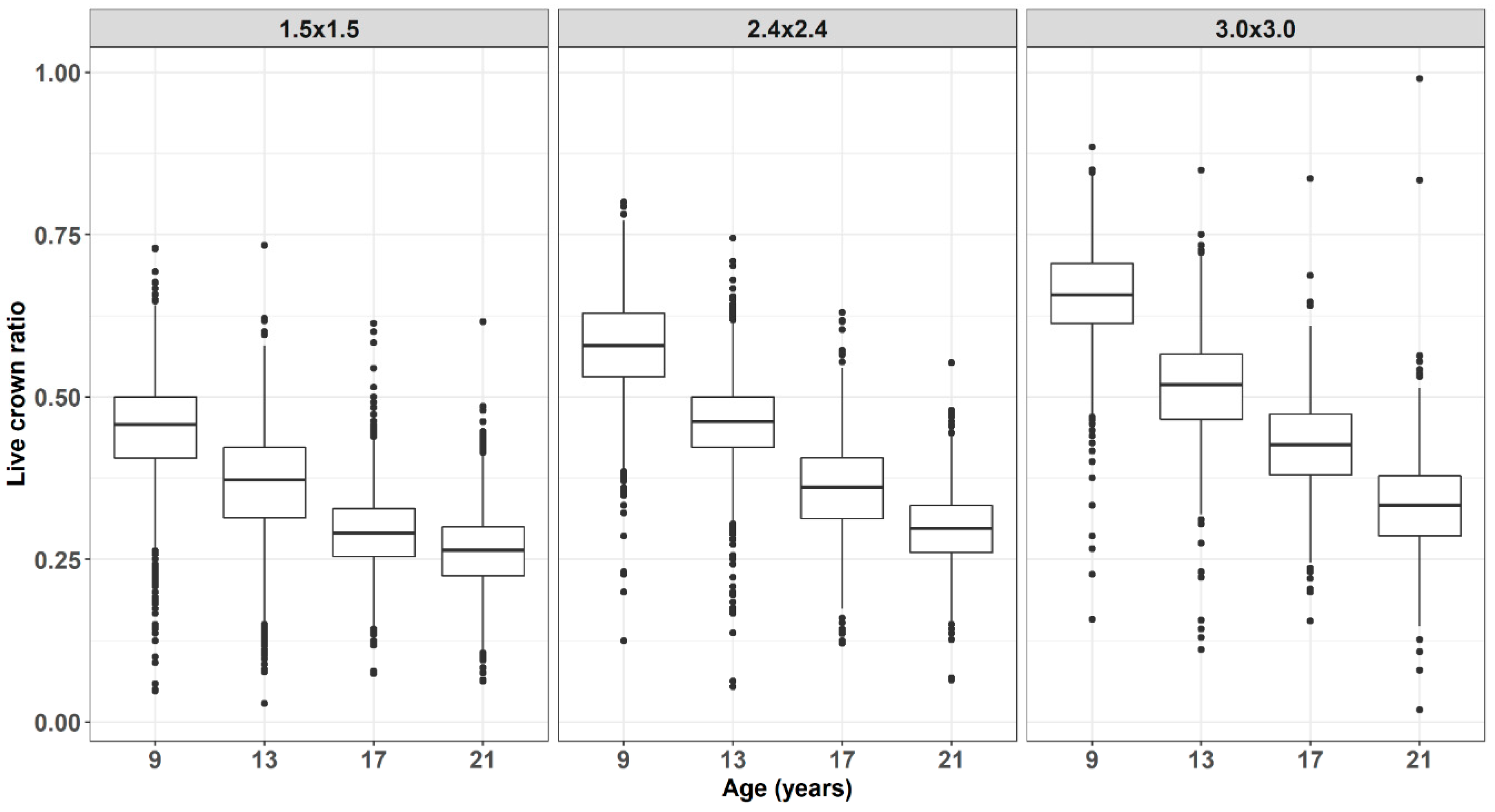
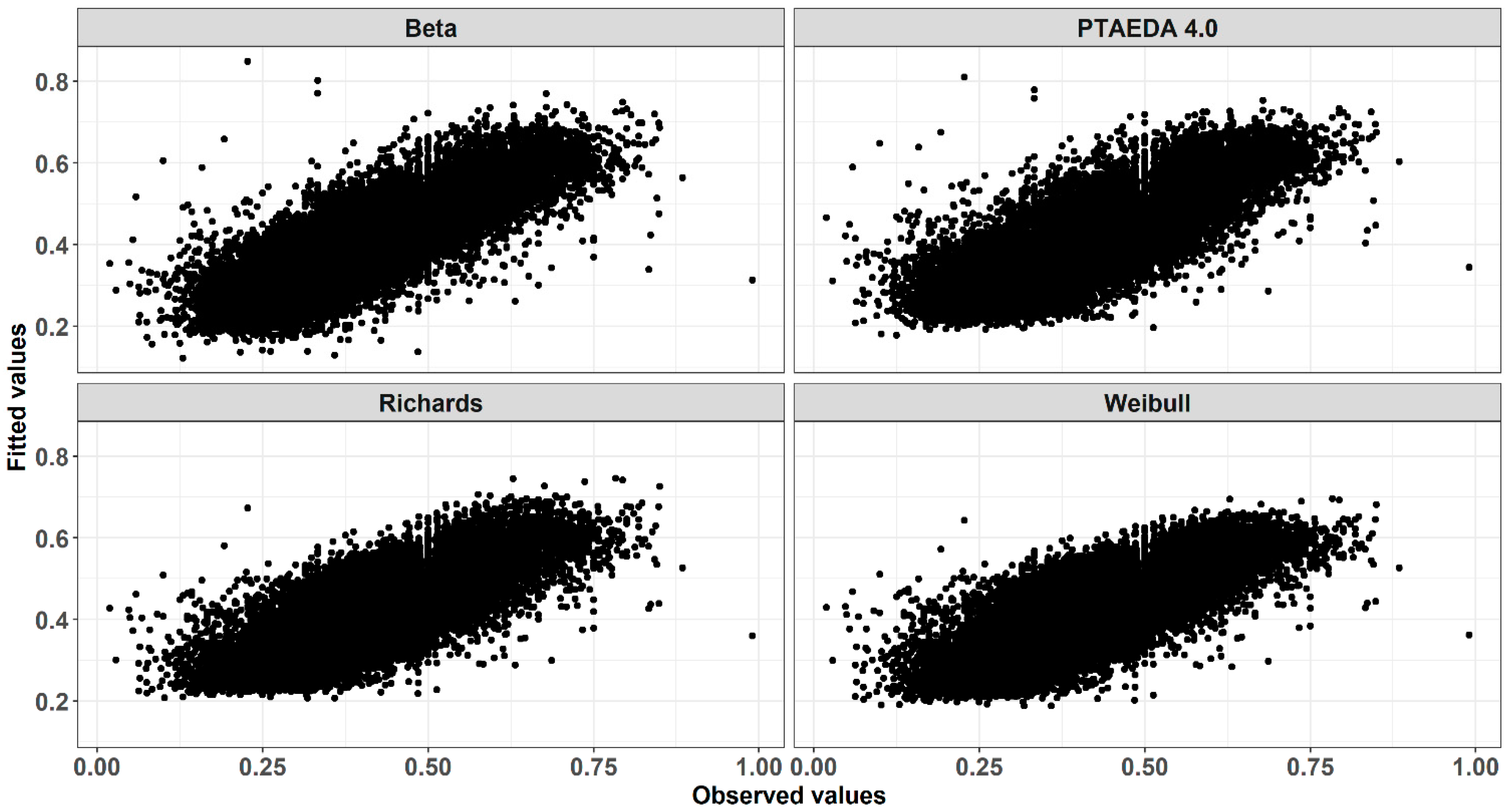
| Family | dbh (cm) | Height (m) | Live Crown Ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.5 × 1.5 | 2.4 × 2.4 | 3.0 × 3.0 | 1.5 × 1.5 | 2.4 × 2.4 | 3.0 × 3.0 | 1.5 × 1.5 | 2.4 × 2.4 | 3.0 × 3.0 | |
| NC1 | 13.26 (3.29) | 18.45 (4.06) | 21.24 (4.78) | 15.09 (3.83) | 16.79 (4.58) | 16.81 (4.70) | 0.37 (0.10) | 0.44 (0.13) | 0.48 (0.14) |
| NC2 | 13.35 (3.58) | 18.19 (4.56) | 21.36 (5.42) | 14.82 (4.06) | 16.32 (4.76) | 16.28 (4.94) | 0.36 (0.11) | 0.44 (0.13) | 0.51 (0.15) |
| NC3 | 13.33 (3.56) | 18.44 (4.47) | 20.97 (4.83) | 14.48 (3.94) | 15.83 (4.65) | 16.08 (4.88) | 0.37 (0.10) | 0.46 (0.13) | 0.51 (0.14) |
| NC4 | 13.51 (3.59) | 18.27 (4.05) | 21.50 (4.79) | 14.86 (4.00) | 16.41 (4.51) | 16.74 (4.74) | 0.36 (0.10) | 0.41 (0.12) | 0.47 (0.14) |
| NC5 | 13.16 (3.52) | 17.94 (4.35) | 20.76 (5.52) | 14.58 (4.11) | 15.91 (4.79) | 15.96 (5.14) | 0.35 (0.10) | 0.43 (0.13) | 0.49 (0.15) |
| NC6 | 13.11 (3.53) | 18.17 (4.45) | 20.20 (4.89) | 14.16 (3.96) | 15.49 (4.56) | 15.27 (4.70) | 0.35 (0.10) | 0.43 (0.11) | 0.49 (0.13) |
| NC7 | 13.69 (3.55) | 18.89 (4.43) | 20.89 (5.39) | 15.23 (4.15) | 16.72 (4.97) | 16.23 (5.02) | 0.36 (0.10) | 0.44 (0.12) | 0.50 (0.14) |
| NC8 | 13.81 (3.72) | 18.67 (4.82) | 21.94 (6.10) | 14.98 (4.16) | 16.56 (4.91) | 16.29 (5.29) | 0.37 (0.11) | 0.44 (0.13) | 0.50 (0.14) |
| LCK | 13.37 (3.86) | 18.52 (4.66) | 21.50 (5.18) | 13.87 (3.95) | 15.14 (4.60) | 15.33 (4.66) | 0.38 (0.11) | 0.46 (0.14) | 0.52 (0.14) |
| Model | Prediction Equation | |
|---|---|---|
| PTAEDA 4.0 | (1) | |
| Richards | (2) | |
| Weibull | (3) | |
| Beta | (4) |
| Model | Parameter Estimate * (Standard Error) | R2 | ||||
|---|---|---|---|---|---|---|
| b0 | b1 | b2 | b3 | b4 | ||
| PTAEDA 4.0 | −0.1823 (0.0029) | 3.9966 (0.0364) | - | - | - | 0.65 |
| Richards | −15.9744 (0.1858) | 66.4144 (0.9222) | 0.0728 (0.0075) | 0.1010 (0.0100) | 2.3063 (0.099) | 0.66 |
| Weibull | −0.7719 (0.0030) | −1.403 (0.0191) | −0.0048 (0.0001) | 0.0016 (0.0001) | - | 0.65 |
| Beta | −1.3176 (0.0357) | −0.1175 (0.0014) | −0.0389 (0.0022) | 0.1006 (0.0028) | 1.5514 (0.0312) | 0.69 |
| Model | MAE | MAPE | RMSE | RMSE % |
|---|---|---|---|---|
| PTAEDA 4.0 | 0.06 | 16.84 | 0.08 | 18.79 |
| Weibull | 0.06 | 16.72 | 0.08 | 18.81 |
| Richards | 0.06 | 16.58 | 0.08 | 18.44 |
| Beta | 0.05 | 15.45 | 0.07 | 17.58 |
| Method | RMSE Percent | MAPE | ||||||
|---|---|---|---|---|---|---|---|---|
| Age 9 | Age 13 | Age 17 | Age 21 | Age 9 | Age 13 | Age 17 | Age 21 | |
| Beta | 15.78 | 17.70 | 18.41 | 20.91 | 13.51 | 16.45 | 15.77 | 16.97 |
| PTAEDA 4.0 | 16.11 | 20.00 | 19.75 | 22.26 | 14.48 | 17.90 | 16.54 | 19.71 |
| Richards | 15.93 | 19.44 | 18.26 | 23.51 | 14.30 | 16.90 | 15.19 | 21.74 |
| Weibull | 16.85 | 18.94 | 18.32 | 24.16 | 15.43 | 16.72 | 15.01 | 20.98 |
| Method | RMSE Percent | MAPE | ||||||
|---|---|---|---|---|---|---|---|---|
| Age 9 | Age 13 | Age 17 | Age 21 | Age 9 | Age 13 | Age 17 | Age 21 | |
| Base Model | 15.78 | 17.7 | 18.41 | 20.91 | 13.51 | 16.45 | 15.77 | 16.97 |
| Base + BAL | 15.78 | 17.68 | 18.35 | 20.91 | 13.52 | 16.45 | 15.72 | 16.97 |
| Base + TPH | 14.23 | 16.91 | 18.08 | 21.33 | 12.30 | 15.94 | 15.68 | 16.97 |
| Base + BAL + TPH | 13.99 | 16.76 | 18.26 | 21.43 | 12.14 | 15.72 | 15.98 | 16.99 |
| Family | b0 | b1 | b2 | b3 | b4 |
|---|---|---|---|---|---|
| NC1 | −1.5167 (0.1031) | −0.1252 (0.0038) | −0.0619 (0.0063) | 0.1274 (0.0082) | 1.8206 (0.0927) |
| NC2 | −1.7774 (0.1138) | −0.1186 (0.0045) | −0.0671 (0.0069) | 0.1245 (0.0091) | 2.1049 (0.1011) |
| NC3 | −1.5013 (0.1101) | −0.1059 (0.0044) | −0.0487 (0.0070) | 0.1029 (0.0092) | 1.7306 (0.0959) |
| NC4 | −0.9988 (0.1094) | −0.1433 (0.0042) | −0.0209 (0.0068) | 0.1057 (0.0088) | 1.1797 (0.0965) |
| NC5 | −1.0764 (0.1047) | −0.1174 (0.0042) | −0.0234 (0.0065) | 0.082 (0.00840) | 1.3402 (0.0911) |
| NC6 | −1.4602 (0.1102) | −0.0979 (0.0043) | −0.0368 (0.0071) | 0.0926 (0.0093) | 1.4788 (0.0955) |
| NC7 | −1.3677 (0.1079) | −0.1072 (0.0039) | −0.0348 (0.0065) | 0.0882 (0.0082) | 1.5712 (0.0951) |
| NC8 | −1.1268 (0.0975) | −0.1173 (0.0040) | −0.0357 (0.0059) | 0.0923 (0.0075) | 1.4463 (0.0856) |
| LCK | −1.4793 (0.1087) | −0.1377 (0.0043) | −0.0477 (0.0067) | 0.1359 (0.0090) | 1.6572 (0.0900) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poudel, K.P.; Avery, S.C.; Granger, J.J. Live Crown Ratio Models for Loblolly Pine (Pinus taeda) with Beta Regression. Forests 2021, 12, 1409. https://doi.org/10.3390/f12101409
Poudel KP, Avery SC, Granger JJ. Live Crown Ratio Models for Loblolly Pine (Pinus taeda) with Beta Regression. Forests. 2021; 12(10):1409. https://doi.org/10.3390/f12101409
Chicago/Turabian StylePoudel, Krishna P., Samantha C. Avery, and Joshua J. Granger. 2021. "Live Crown Ratio Models for Loblolly Pine (Pinus taeda) with Beta Regression" Forests 12, no. 10: 1409. https://doi.org/10.3390/f12101409
APA StylePoudel, K. P., Avery, S. C., & Granger, J. J. (2021). Live Crown Ratio Models for Loblolly Pine (Pinus taeda) with Beta Regression. Forests, 12(10), 1409. https://doi.org/10.3390/f12101409





