A Band Model of Cambium Development: Opportunities and Prospects
Abstract
1. Introduction
- The cambial zone is considered as an “elastic band” within which there is non-uniformity in the rate of its radial enlargement, i.e., the wider the cambial zone, the higher the production rate per time unit in the enlargement zone;
- The growth and division of individual cells in the meristem are not considered;
- The specific incremental production within the cambial zone is determined at the outer border with the xylem, and the cell production (absolute linear increment of cell tissue as μm in the enlargement zone per time unit) is characterized by the kinetic parameters of the zone as a whole.
2. Materials and Methods
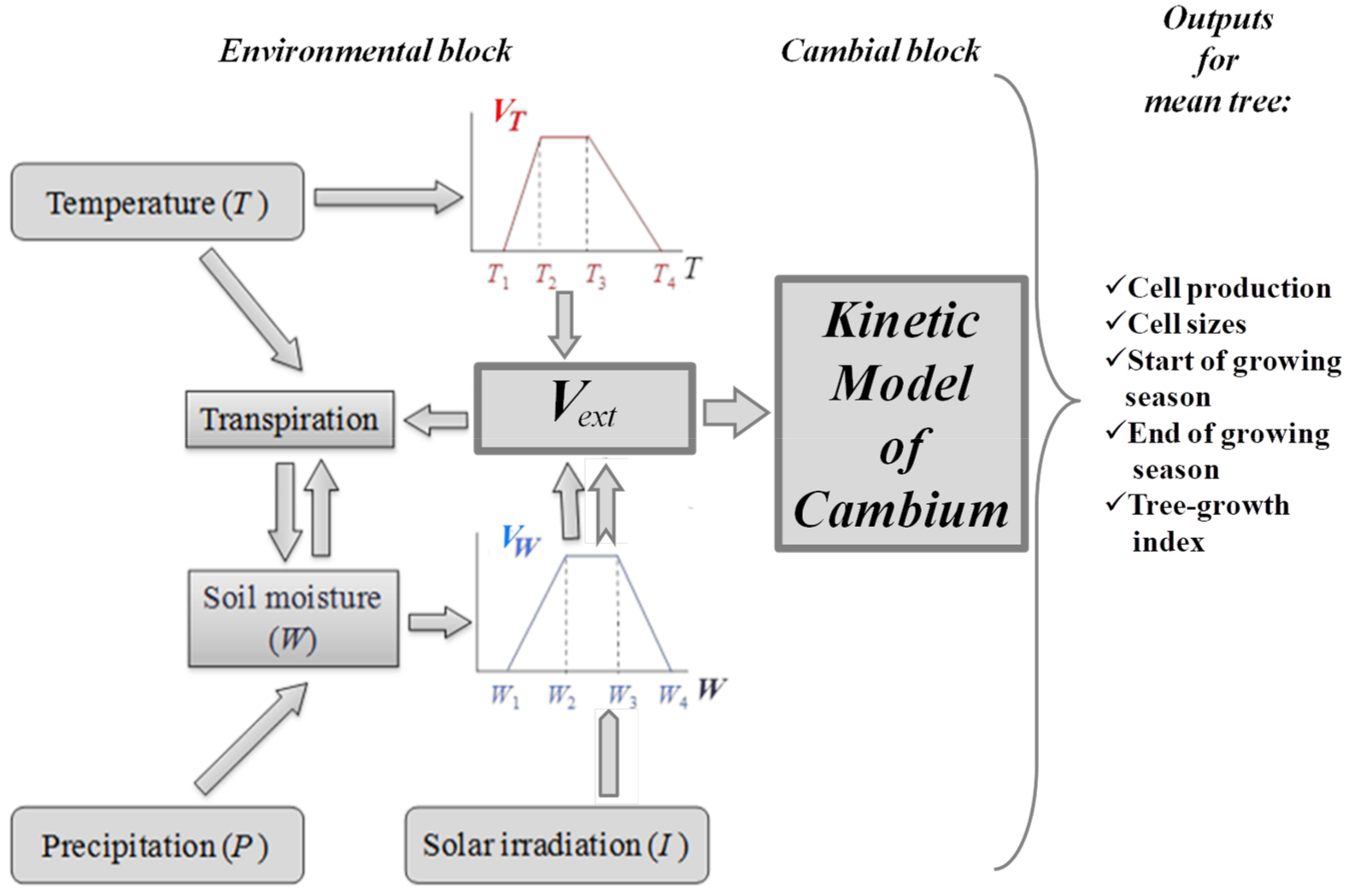
2.1. Brief Description of the VS-Model
2.2. The Band Model of Cambium Development
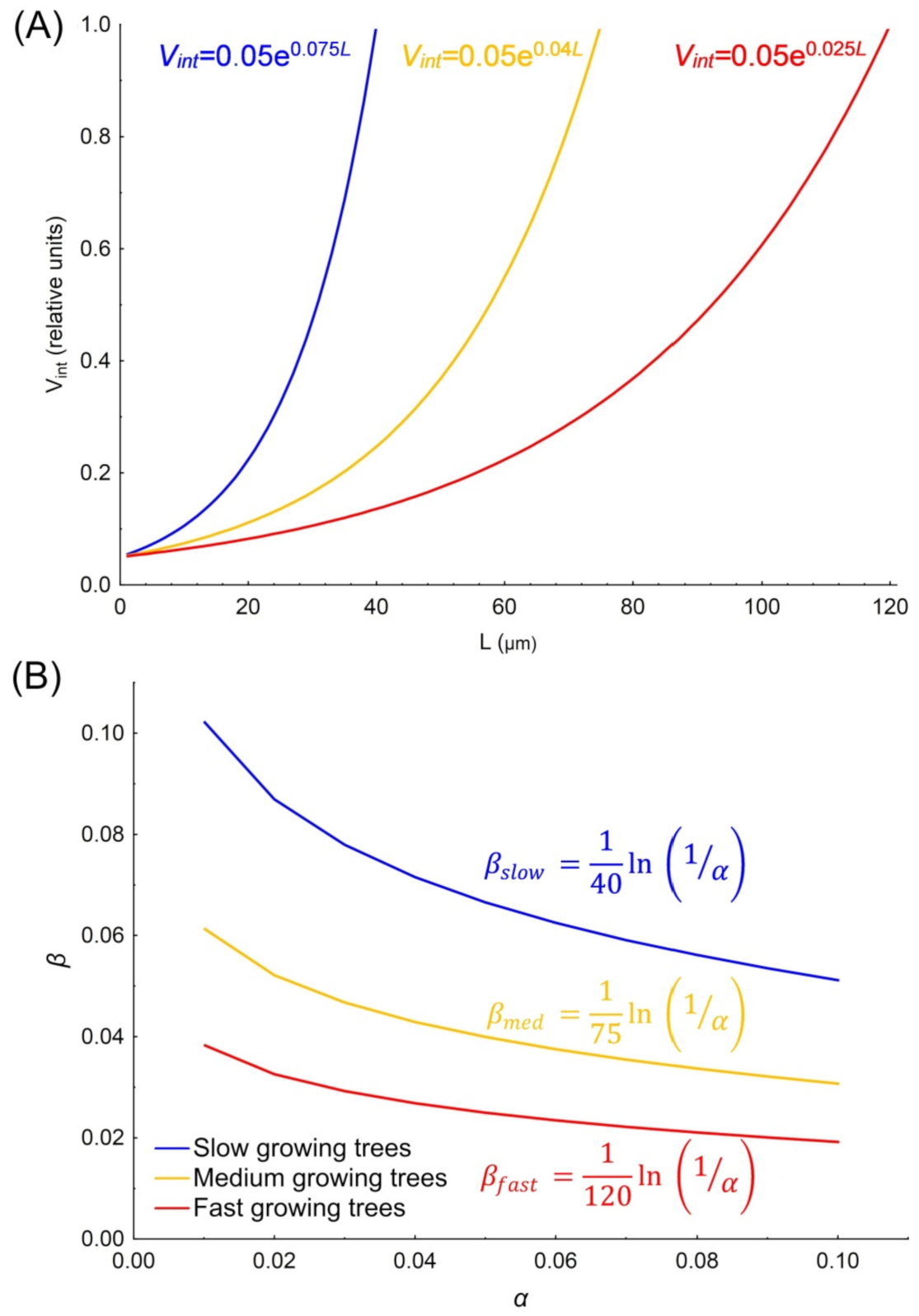
2.3. Two-Step Estimation Procedure of β
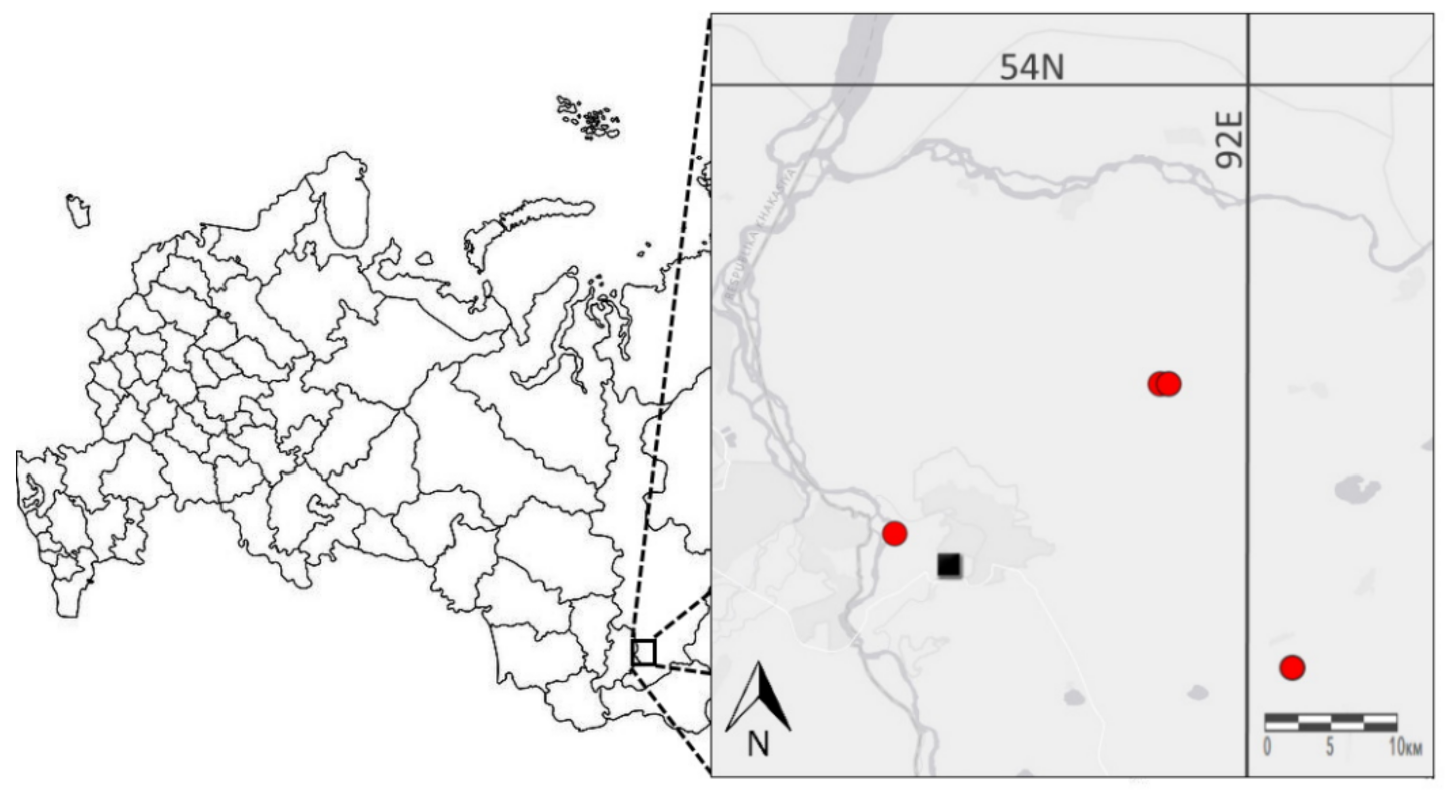
2.4. Data Description
2.5. Parameterization of VS-Model for the Simulation of External Rates
3. Results
3.1. Estimation of the Integral Growth Rate Vext
3.2. Analysis of Cambium Activity Simulations for Synthetic Trees
3.3. Model Testing in Cold Semi-Arid Southern Siberia
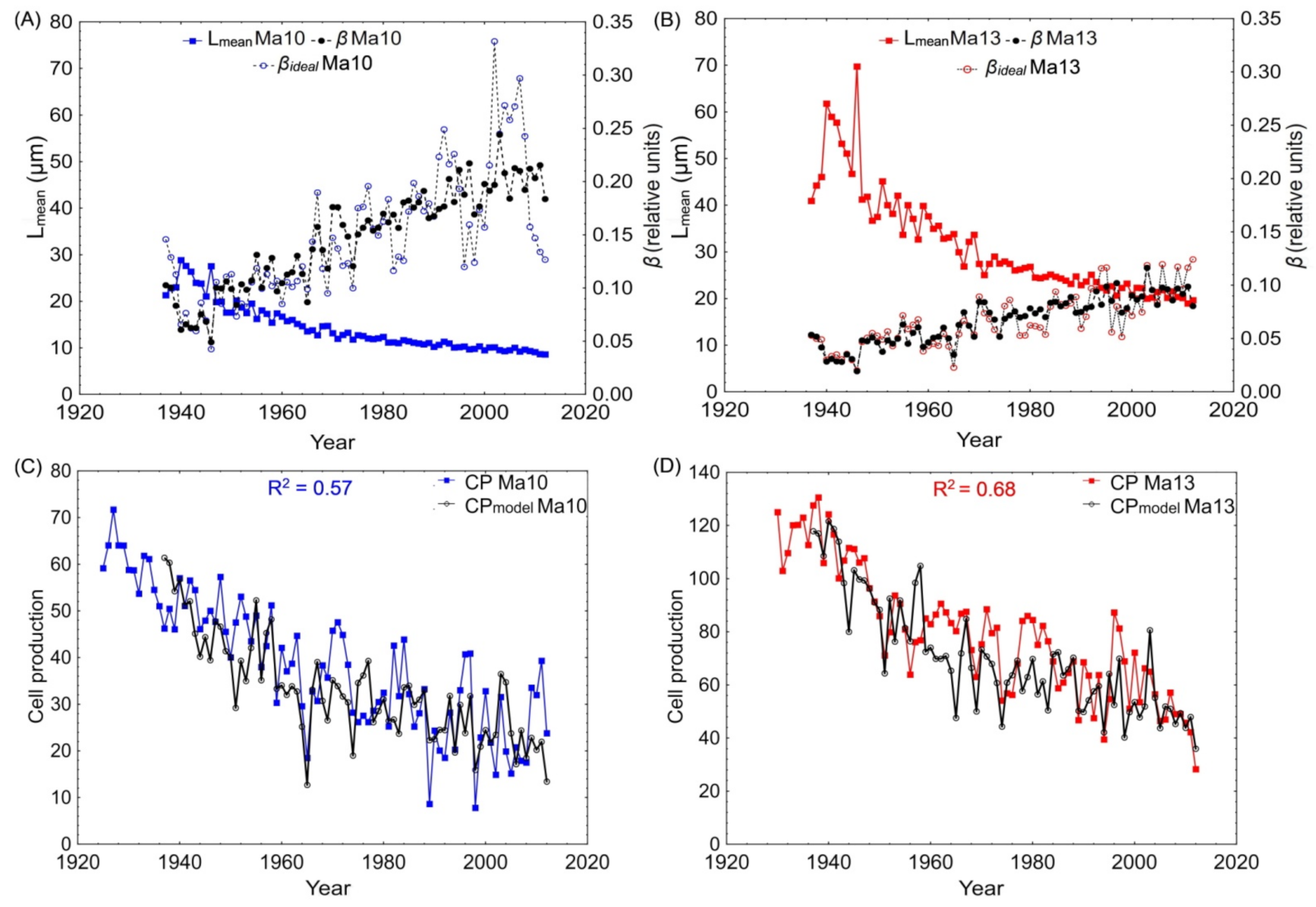
3.4. Long-Term Estimation of Cell Production and Respective Tree-Ring Width for Individual Trees
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chavchavadze, E.S. Drevesina Khvoynykh: Morfologicheskie Osobennosti, Diagnosticheskoe Znachenie. In Wood of Coniferous Plants: Morphological Traits, Diagnostic Value; Nauka: St. Petersburg, Russia, 1979. (In Russian) [Google Scholar]
- Larson, P.R. The Vascular Cambium: Development and Structure; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lanner, R.M.; Connor, K.F. Does bristlecone pine senesce? Exp. Gerontol. 2001, 36, 675–685. [Google Scholar] [CrossRef]
- Lanner, R.M. Why do trees live so long? Ageing Res. Rev. 2002, 1, 653–671. [Google Scholar] [CrossRef]
- Rossi, S.; Deslauriers, A.; Anfodillo, T.; Carrer, M. Age-dependent xylogenesis in timberline conifers. New Phytol. 2008, 177, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Bhalerao, R.P.; Fischer, U. Environmental and hormonal control of cambial stem cell dynamics. J. Exp. Bot. 2017, 68, 79–87. [Google Scholar] [CrossRef]
- Fischer, U.; Kucukoglu, M.; Helariutta, Y.; Bhalerao, R.P. The dynamics of cambial stem cell activity. Annu. Rev. Plant Biol. 2019, 70, 293–319. [Google Scholar] [CrossRef]
- Su, Y.H.; Liu, Y.B.; Zhang, X.S. Auxin-cytokinin interaction regulates meristem development. Mol. Plant 2011, 4, 616–625. [Google Scholar] [CrossRef]
- Schaller, G.E.; Bishopp, A.; Kieber, J.J. The Yin-Yang of hormones: Cytokinin and auxin interactions in plant development. Plant Cell 2015, 27, 44–63. [Google Scholar] [CrossRef]
- Immanen, J.; Nieminen, K.; Smolander, O.-P.; Kojima, M.; Serra, J.A.; Koskinen, P.; Zhang, J.; Elo, A.; Mahonen, A.P.; Street, N.; et al. Cytokinin and auxin display distinct but interconnected distribution and signaling profiles to stimulate cambial activity. Curr. Biol. 2016, 26, 1990–1997. [Google Scholar] [CrossRef]
- Sang, Y.L.; Cheng, Z.J.; Zhang, X.S. Plant stem cells and de novo organogenesis. New Phytol. 2018, 218, 1334–1339. [Google Scholar] [CrossRef]
- Chen, J.J.; Wang, L.Y.; Immanen, J.; Nieminen, K.; Spicer, R.; Helariutta, Y.; Zhang, J.; He, X.Q. Differential regulation of auxin and cytokinin during the secondary vascular tissue regeneration in Populus trees. New Phytol. 2019, 224, 188–201. [Google Scholar] [CrossRef]
- Butto, V.; Deslauriers, A.; Rossi, S.; Rozenberg, P.; Shishov, V.; Morin, H. The role of plant hormones in tree-ring formation. Trees-Struct. Funct. 2020, 34, 315–335. [Google Scholar] [CrossRef]
- Uggla, C.; Mellerowicz, E.J.; Sundberg, B. Indole-3-acetic acid controls cambial growth in Scots pine by positional signaling. Plant Physiol. 1998, 117, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Uggla, C.; Magel, E.; Moritz, T.; Sundberg, B. Function and dynamics of auxin and carbohydrates during earlywood/latewood transition in Scots pine. Plant Physiol. 2001, 125, 2029–2039. [Google Scholar] [CrossRef] [PubMed]
- Perrot-Rechenmann, C. Cellular responses to auxin: Division versus expansion. Cold Spring Harb. Perspect. Biol. 2010, 2. [Google Scholar] [CrossRef]
- Brackmann, K.; Qi, J.Y.; Gebert, M.; Jouannet, V.; Schlamp, T.; Grunwald, K.; Wallner, E.S.; Novikova, D.D.; Levitsky, V.G.; Agusti, J.; et al. Spatial specificity of auxin responses coordinates wood formation. Nat. Commun. 2018, 9, 15. [Google Scholar] [CrossRef]
- Schrader, J.; Nilsson, J.; Mellerowicz, E.; Berglund, A.; Nilsson, P.; Hertzberg, M.; Sandberg, G. A high-resolution transcript profile across the wood-forming meristem of poplar identifies potential regulators of cambial stem cell identity. Plant Cell 2004, 16, 2278–2292. [Google Scholar] [CrossRef]
- Nieminen, K.; Immanen, J.; Laxell, M.; Kauppinen, L.; Tarkowski, P.; Dolezal, K.; Tahtiharju, S.; Elo, A.; Decourteix, M.; Ljung, K.; et al. Cytokinin signaling regulates cambial development in poplar. Proc. Natl. Acad. Sci. USA 2008, 105, 20032–20037. [Google Scholar] [CrossRef]
- Tank, J.G.; Thaker, V.S. Cyclin dependent kinases and their role in regulation of plant cell cycle. Biol. Plant. 2011, 55, 201–212. [Google Scholar] [CrossRef]
- Komaki, S.; Sugimoto, K. Control of the plant cell cycle by developmental and environmental cues. Plant Cell Physiol. 2012, 53, 953–964. [Google Scholar] [CrossRef]
- Campbell, L.; Turner, S. Regulation of vascular cell division. J. Exp. Bot. 2017, 68, 27–43. [Google Scholar] [CrossRef]
- Hartmann, F.P.; Rathgeber, C.B.K.; Fournier, M.; Moulia, B. Modelling wood formation and structure: Power and limits of a morphogenetic gradient in controlling xylem cell proliferation and growth. Ann. For. Sci. 2017, 74. [Google Scholar] [CrossRef]
- Bossinger, G.; Spokevicius, A.V. Sector analysis reveals patterns of cambium differentiation in poplar stems. J. Exp. Bot. 2018, 69, 4339–4348. [Google Scholar] [CrossRef] [PubMed]
- Luck, J.; Barlow, P.W.; Luck, H.B. Deterministic patterns of cellular growth and division within a meristem. Ann. Bot. 1994, 73, 1–11. [Google Scholar] [CrossRef]
- Deleuze, C.; Houllier, F. A simple process-based xylem growth model for describing wood microdensitometric profiles. J. Theor. Biol. 1998, 193, 99–113. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future Environments; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hartmann, F.P.; Rathgeber, C.B.K.; Badel, E.; Fournier, M.; Moulia, B. Modelling the spatial crosstalk between two biochemical signals explains wood formation dynamics and tree-ring structure. J. Exp. Bot. 2020. [Google Scholar] [CrossRef]
- Rathgeber, C.B.K.; Rossi, S.; Bontemps, J.D. Cambial activity related to tree size in a mature silver-fir plantation. Ann. Bot. 2011, 108, 429–438. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Kiesse, T.S.; Hartmann, F.P.; Barbeito, I.; Fournier, M. Generalized additive models reveal the intrinsic complexity of wood formation dynamics. J. Exp. Bot. 2013, 64, 1983–1994. [Google Scholar] [CrossRef] [PubMed]
- Rossi, S.; Morin, H.; Deslauriers, A. Causes and correlations in cambium phenology: Towards an integrated framework of xylogenesis. J. Exp. Bot. 2012, 63, 2117–2126. [Google Scholar] [CrossRef] [PubMed]
- Babushkina, E.A.; Zhirnova, D.E.; Belokopytova, L.V.; Tychkov, I.I.; Vaganov, E.A.; Krutovsky, K.V. Response of four tree species to changing climate in a moisture-limited area of South Siberia. Forests 2019, 10, 999. [Google Scholar] [CrossRef]
- Fonti, M.V.; Fakhrutdinova, V.V.; Kalinina, E.V.; Tychkov, I.I.; Popkova, M.I.; Shishov, V.V.; Nikolaev, A.N. Long-term variability of anatomic features of annual tree rings of larch, pine and spruce in the permafrost zone in central Siberia. Contemp. Probl. Ecol. 2019, 12, 692–702. [Google Scholar] [CrossRef]
- Fonti, M.V.; Babushkina, E.A.; Zhirnova, D.F.; Vaganov, E.A. Xylogenesis of scots pine in an uneven-aged stand of the Minusinsk Depression (Southern Siberia). J. Sib. Fed. Univ. Biol. 2020, 13, 197–207. [Google Scholar] [CrossRef]
- Butto, V.; Shishov, V.; Tychkov, I.; Popkova, M.; He, M.H.; Rossi, S.; Deslauriers, A.; Morin, H. Comparing the cell dynamics of tree-ring formation observed in microcores and as predicted by the Vaganov-Shashkin model. Front. Plant Sci. 2020, 11, 16. [Google Scholar] [CrossRef]
- Popkova, M.I.; Shishov, V.V.; Vaganov, E.A.; Fonti, M.V.; Kirdyanov, A.V.; Babushkina, E.A.; Huang, J.G.; Rossi, S. Contribution of xylem anatomy to tree-ring width of two larch species in permafrost and non-permafrost zones of Siberia. Forests 2020, 11, 1343. [Google Scholar] [CrossRef]
- Evans, M.N.; Reichert, B.K.; Kaplan, A.; Anchukaitis, K.J.; Vaganov, E.A.; Hughes, M.K.; Cane, M.A. A forward modeling approach to paleoclimatic interpretation of tree-ring data. J. Geophys. Res.-Biogeosci. 2006, 111. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Evans, M.N.; Kaplan, A.; Vaganov, E.A.; Hughes, M.K.; Grissino-Mayer, H.D.; Cane, M.A. Forward modeling of regional scale tree-ring patterns in the southeastern United States and the recent influence of summer drought. Geophys. Res. Lett. 2006, 33, 4. [Google Scholar] [CrossRef]
- Anchukaitis, K.J.; Evans, M.N.; Hughes, M.K.; Vaganov, E.A. An interpreted language implementation of the Vaganov-Shashkin tree-ring proxy system model. Dendrochronologia 2020, 60. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Anchukaitis, K.J.; Evans, M.N. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. Dendroclimatol. Prog. Prospect. 2011, 11, 37–75. [Google Scholar] [CrossRef]
- Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Ilyin, V.A.; Bryukhanova, M.V.; Kirdyanov, A.V. VS-oscilloscope: A new tool to parameterize tree radial growth based on climate conditions. Dendrochronologia 2016, 39, 42–50. [Google Scholar] [CrossRef]
- Shishov, V.V.; Arzac, A.; Popkova, M.I.; Yang, B.; He, M.; Vaganov, E.A. “Experimental and theoretical analysis of tree-ring growth in cold climates,” in Boreal Forests in the Face of Climate Change-Sustainable Management. In Advances in Global Change Research; Girona, M., Gauthier, S., Morin, S., Bergeron, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; (Accepted to print). [Google Scholar]
- Tumajer, J.; Kaspar, J.; Kuzelova, H.; Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Vaganov, E.A.; Treml, V. Forward modeling reveals multidecadal trends in cambial kinetics and phenology at treeline. Front. Plant Sci. 2021, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Popkova, M.I.; Vaganov, E.A.; Shishov, V.V.; Babushkina, E.A.; Rossi, S.; Fonti, M.V.; Fonti, P. Modeled tracheidograms disclose drought influence on Pinus sylvestris tree-rings structure from Siberian forest-steppe. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Tychkov, I.I.; Sviderskaya, I.V.; Babushkina, E.A.; Popkova, M.I.; Vaganov, E.A.; Shishov, V.V. How can the parameterization of a process-based model help us understand real tree-ring growth? Trees-Struct. Funct. 2019, 33, 345–357. [Google Scholar] [CrossRef]
- Kirdyanov, A.V.; Krusic, P.J.; Shishov, V.V.; Vaganov, E.A.; Fertikov, A.I.; Myglan, V.S.; Barinov, V.V.; Browse, J.; Esper, J.; Ilyin, V.A.; et al. Ecological and conceptual consequences of Arctic pollution. Ecol. Lett. 2020, 23, 1827–1837. [Google Scholar] [CrossRef]
- Savidge, R.A. Cell biology of bordered-pit formation in balsam-fir trees. Botany 2014, 92, 495–511. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Frank, D.; Fonti, P.; Makinen, H.; Prislan, P.; Rossi, S.; del Castillo, E.M.; Campelo, F.; Vavrcik, H.; et al. Woody biomass production lags stem-girth increase by over one month in coniferous forests. Nat. Plants 2015, 1, 6. [Google Scholar] [CrossRef] [PubMed]
- Lupi, C.; Morin, H.; Deslauriers, A.; Rossi, S. Xylem phenology and wood production: Resolving the chicken-or-egg dilemma. Plant Cell Environ. 2010, 33, 1721–1730. [Google Scholar] [CrossRef] [PubMed]
- Rossi, S.; Morin, H.; Deslauriers, A.; Plourde, P.Y. Predicting xylem phenology in black spruce under climate warming. Glob. Chang. Biol. 2011, 17, 614–625. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990; Volume 23. [Google Scholar]
- Babushkina, E.A.; Vaganov, E.A.; Belokopytova, L.V.; Shishov, V.V.; Grachev, A.M. Competitive strength effect in the climate response of scots pine radial growth in south-central Siberia forest-steppe. Tree-Ring Res. 2015, 71, 106–117. [Google Scholar] [CrossRef]
- Shah, S.K.; Touchan, R.; Babushkina, E.; Shishov, V.V.; Meko, D.M.; Abramenko, O.V.; Belokopytova, L.V.; Hordo, M.; Jevsenak, J.; Kedziora, W.; et al. August to July precipitation from tree rings in the forest-steppe zone of central Siberia (Russia). Tree-Ring Res. 2015, 71, 37–44. [Google Scholar] [CrossRef]
- Magda, V.N.; Vaganov, E.A. Climatic response of tree growth in mountain forest-steppes of the Altai-Sayan region. Izv. RAN. Seriya Geogr. Proc. RAS. Geogr. Ser. 2006, 5, 92–100. (In Russian) [Google Scholar]
- Babushkina, E.A.; Knorre, A.A.; Vaganov, E.A.; Bryukhanova, M.V. Transformation of climatic response in radial increment of trees depending on topoecological conditions of their occurrence. Geogr. Nat. Resour. 2011, 32, 80. [Google Scholar] [CrossRef]
- Cook, E.R.; Krusic, P.J. Program Arstan: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: Palisades, NY, USA, 2005. [Google Scholar]
- Jevsenak, J.; Tychkov, I.; Gricar, J.; Levanic, T.; Tumajer, J.; Prislan, P.; Arnic, D.; Popkova, M.; Shishov, V.V. Growth-limiting factors and climate response variability in Norway spruce (Picea abiesL.) along an elevation and precipitation gradients in Slovenia. Int. J. Biometeorol. 2021, 65, 311–324. [Google Scholar] [CrossRef]
- Buras, A.; Wilmking, M. Correcting the calculation of Gleichlaufigkeit. Dendrochronologia 2015, 34, 29–30. [Google Scholar] [CrossRef]
- Ehlers, K.; Kollmann, R. Primary and secondary plasmodesmata: Structure, origin, and functioning. Protoplasma 2001, 216, 1–30. [Google Scholar] [CrossRef]
- Roberts, A.G.; Oparka, K.J. Plasmodesmata and the control of symplastic transport. Plant Cell Environ. 2003, 26, 103–124. [Google Scholar] [CrossRef]
- Lucas, W.J.; Lee, J.Y. Plant cell biology—Plasmodesmata as a supracellular control network in plants. Nat. Rev. Mol. Cell Biol. 2004, 5, 712–726. [Google Scholar] [CrossRef]
- Fuchs, M.; van Bel, A.J.E.; Ehlers, K. Season-associated modifications in symplasmic organization of the cambium in Populus nigra. Ann. Bot. 2010, 105, 375–387. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wayne, R. (Ed.) Plasmodesmata. In Plant Cell Biology: From Astronomy to Zoology; Elsevier Science Bv: Amsterdam, The Netherlands, 2009; pp. 51–60. [Google Scholar]
- Burch-Smith, T.M.; Stonebloom, S.; Xu, M.; Zambryski, P.C. Plasmodesmata during development: Re-examination of the importance of primary, secondary, and branched plasmodesmata structure versus function. Protoplasma 2011, 248, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Haywood, V.; Kragler, F.; Lucas, W.J. Plasmodesmata: Pathways for protein and ribonucleoprotein signaling. Plant Cell 2002, 14, S303–S325. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, K.; van Bel, A.J.E. Dynamics of plasmodesmal connectivity in successive interfaces of the cambial zone. Planta 2010, 231, 371–385. [Google Scholar] [CrossRef]
- Barnett, J.R. Plasmodesmata and pit development in secondary xylem elements. Planta 1982, 155, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Jansen, S.; Lamy, J.B.; Burlett, R.; Cochard, H.; Gasson, P.; Delzon, S. Plasmodesmatal pores in the torus of bordered pit membranes affect cavitation resistance of conifer xylem. Plant Cell Environ. 2012, 35, 1109–1120. [Google Scholar] [CrossRef] [PubMed]
- Lamarche, V.C.; Hirschboeck, K.K. Frost rings in trees as records of major volcanic-eruptions. Nature 1984, 307, 121–126. [Google Scholar] [CrossRef]
- Gurskaya, M.A.; Shiyatov, S.G. Distribution of frost injuries in the wood of conifers. Russ. J. Ecol. 2006, 37, 7–12. [Google Scholar] [CrossRef]
- Montwe, D.; Isaac-Renton, M.; Hamann, A.; Spiecker, H. Cold adaptation recorded in tree rings highlights risks associated with climate change and assisted migration. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Carteni, F.; Deslauriers, A.; Rossi, S.; Morin, H.; De Micco, V.; Mazzoleni, S.; Giannino, F. The physiological mechanisms behind the earlywood-to-latewood transition: A process-based modeling approach. Front. Plant Sci. 2018, 9, 12. [Google Scholar] [CrossRef]






| Characteristic | Value |
|---|---|
| Duration of chronology, years | 167 |
| Number of trees | 194 |
| Sensitivity coefficient | 0.23 |
| Expressed population signal, EPS | 0.99 |
| Average inter-series correlation coefficient, R-bar | 0.41 |
| ΔL (μm) | Vext (Relative Units) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | |
| slow | 12.68 | 11.35 | 10.01 | 8.68 | 7.34 | 6.01 | 4.67 | 3.34 | 2.00 | 0.67 |
| medium | 23.78 | 21.28 | 18.78 | 16.27 | 13.77 | 11.27 | 8.76 | 6.26 | 3.76 | 1.25 |
| fast | 38.05 | 34.05 | 30.04 | 26.04 | 22.03 | 18.03 | 14.02 | 10.01 | 6.01 | 2.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shishov, V.V.; Tychkov, I.I.; Anchukaitis, K.J.; Zelenov, G.K.; Vaganov, E.A. A Band Model of Cambium Development: Opportunities and Prospects. Forests 2021, 12, 1361. https://doi.org/10.3390/f12101361
Shishov VV, Tychkov II, Anchukaitis KJ, Zelenov GK, Vaganov EA. A Band Model of Cambium Development: Opportunities and Prospects. Forests. 2021; 12(10):1361. https://doi.org/10.3390/f12101361
Chicago/Turabian StyleShishov, Vladimir V., Ivan I. Tychkov, Kevin J. Anchukaitis, Grigory K. Zelenov, and Eugene A. Vaganov. 2021. "A Band Model of Cambium Development: Opportunities and Prospects" Forests 12, no. 10: 1361. https://doi.org/10.3390/f12101361
APA StyleShishov, V. V., Tychkov, I. I., Anchukaitis, K. J., Zelenov, G. K., & Vaganov, E. A. (2021). A Band Model of Cambium Development: Opportunities and Prospects. Forests, 12(10), 1361. https://doi.org/10.3390/f12101361








