Estimating Individual Conifer Seedling Height Using Drone-Based Image Point Clouds
Abstract
1. Introduction
- How accurately can conifer seedling height be estimated in drone surveys for survival (small seedlings) and establishment (older and taller seedlings)?
- Does the accuracy of DIPC differ much from that of softcopy (manual) photogrammetry?
- What is the impact of height-estimation error on counting errors in seedling surveys?
- What is the effect of spatial resolution, season, ground determination method, and seedling size on the accuracy of seedling height estimates?
- What factors contribute to outliers?
2. Materials
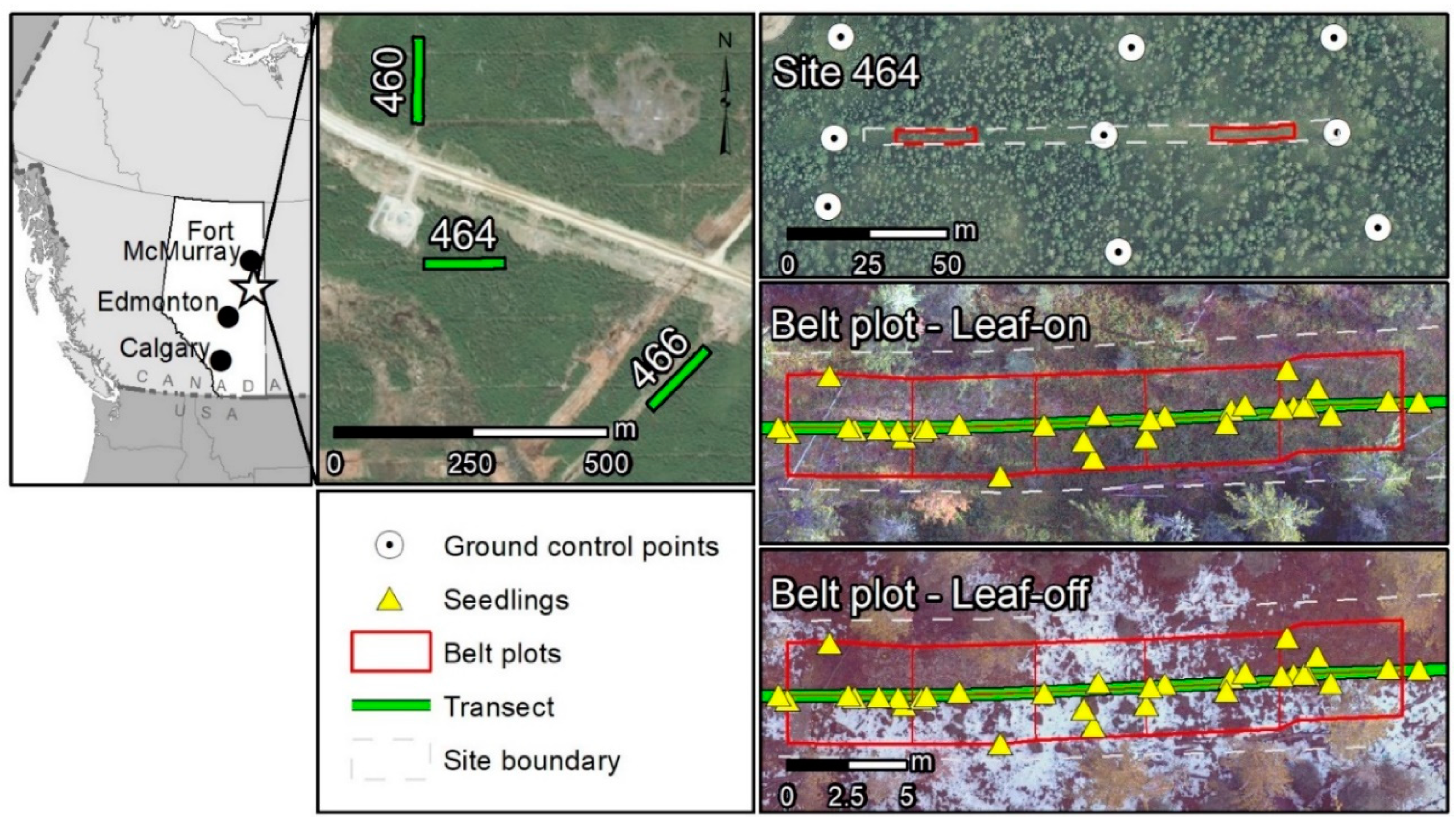
2.1. Study Area
2.2. Field Data
2.3. Drone Data
2.3.1. Acquisition
2.3.2. Drone-Based Image Point Cloud (DIPC) Generation
2.3.3. Softcopy Photogrammetry
2.4. Ancillary Data
3. Methods
3.1. Height Estimation
3.1.1. DIPC
3.1.2. Softcopy Photogrammetry
3.2. Accuracy Assessment
4. Results
4.1. Height Estimation
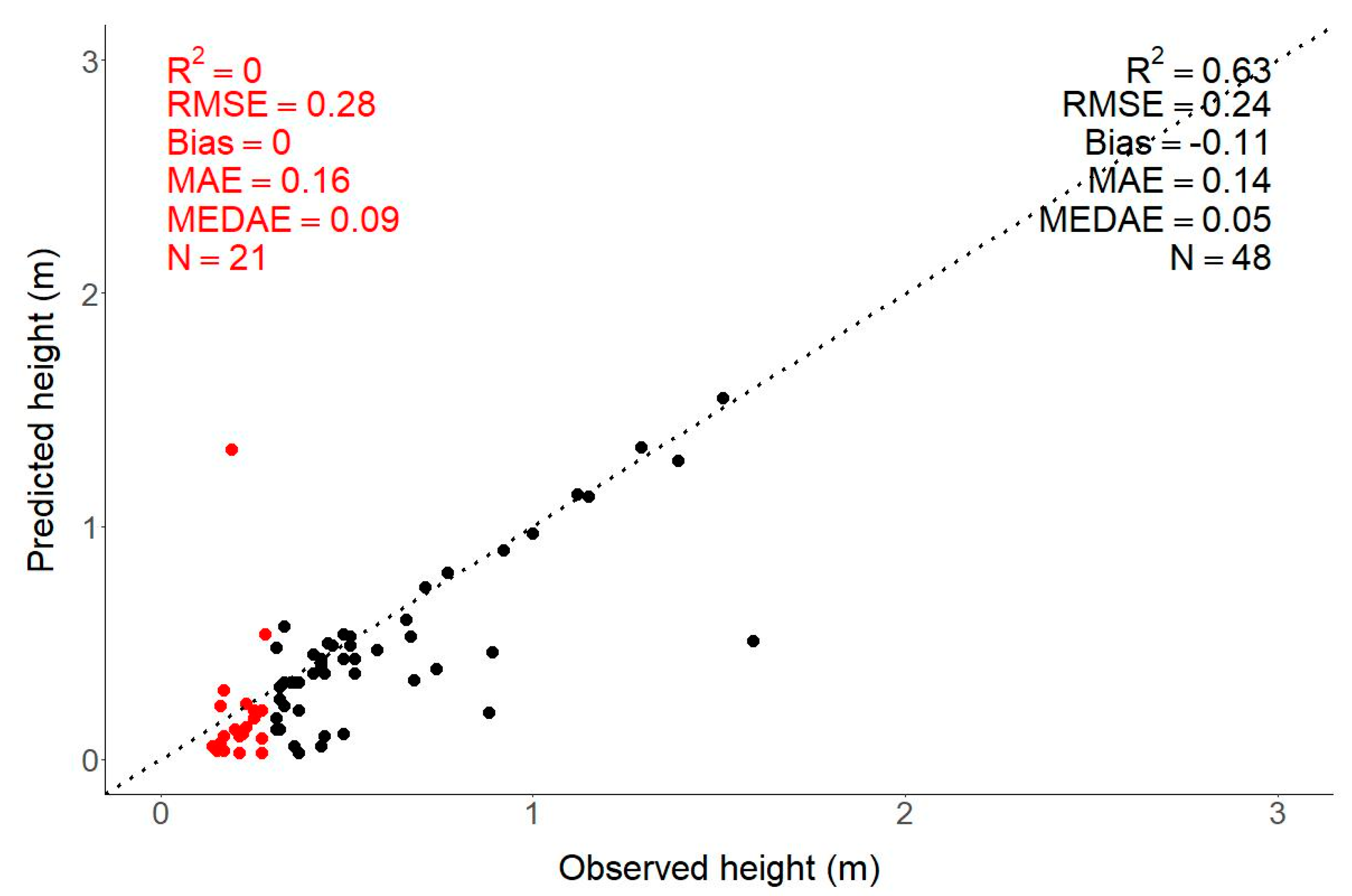
4.1.1. DIPC, Seedlings ≤30 cm
4.1.2. DIPC, Seedlings >30 cm
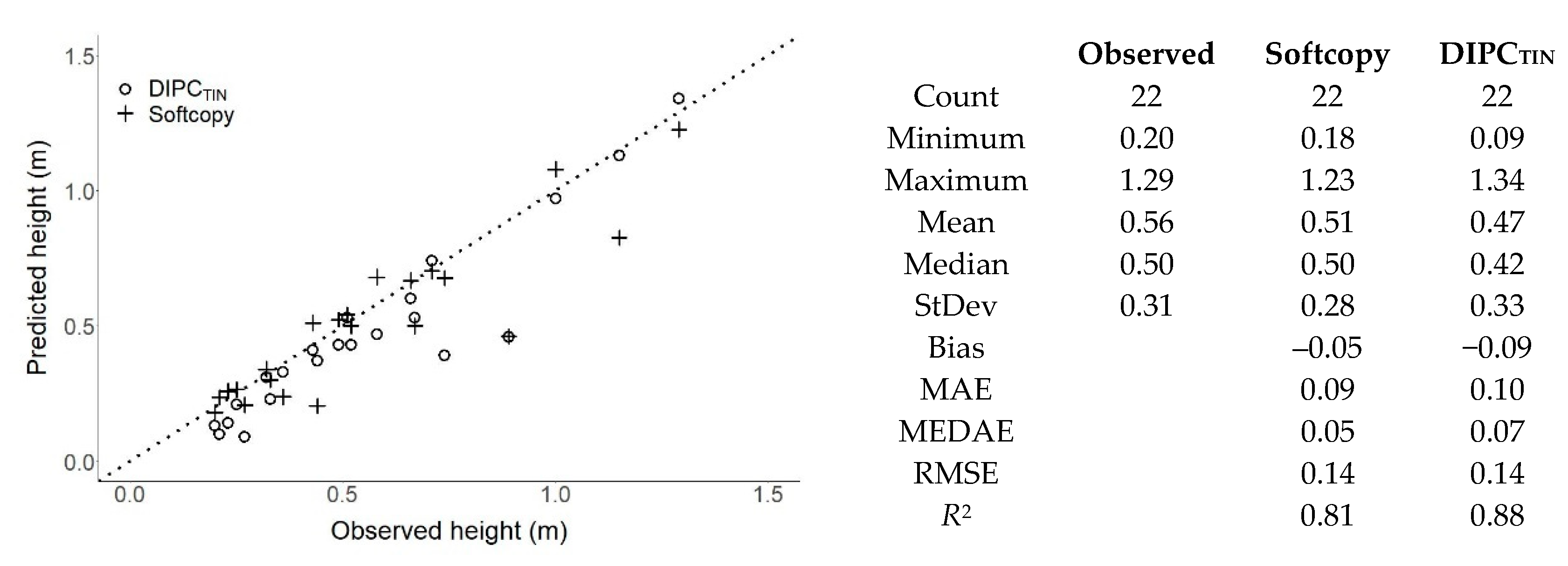
4.1.3. Softcopy Photogrammetry
4.2. Counting Errors in Seedling Surveys
5. Discussion
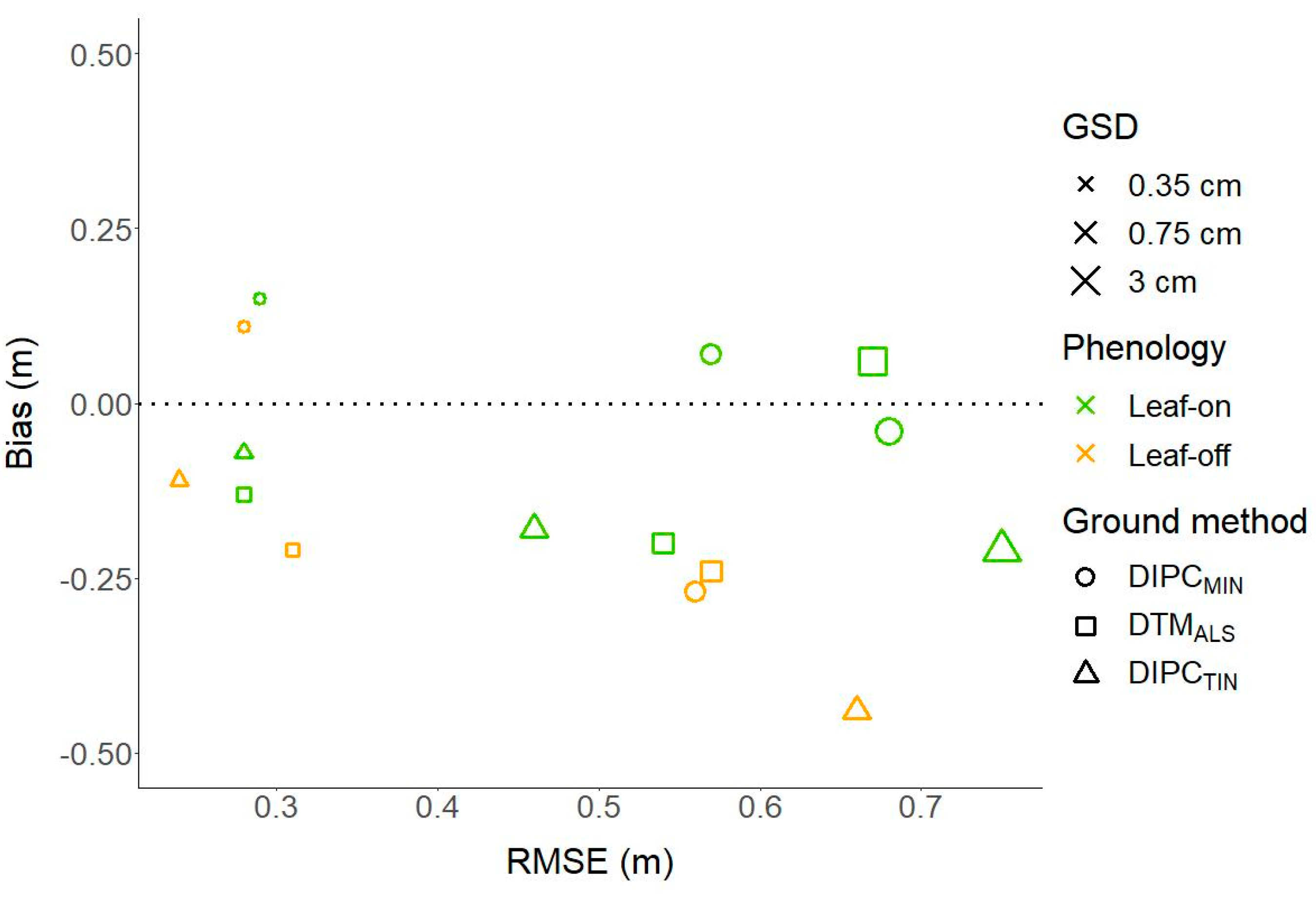
5.1. Effect of Ground Sampling Distance (GSD)
5.2. Effect of Leaf Phenology
5.3. Effect of Ground Determination Method
5.4. Effect of Seedling Size
5.5. Errors Contributing to Outliers
- Location error—all seedlings locations were visually checked to determine which of them did not align with their apparent position in the orthomosaics. Seventeen of the 189 seedlings in this study had an offset greater than 20 cm in at least one orthomosaic. There were several instances where the seedling could not be found at their measured location within any of the orthomosaics. However, most of those seedlings were obstructed from view by adjacent trees so we could not assess their location error. Location errors greater than 20 cm are likely to cause an outlier in the height estimation, which only considers DIPC points within a 20 cm radius of the reported locations. Location error is expected through the DIPC workflow, where XYZ coordinates can be shifted from their true geographic location because of complexities within the SfM process [28,29]. This was demonstrated by slight shifts found between orthomosaics of the different DIPC datasets, as well as between the orthomosaics and their input GCPs. Fortunately, in an operational drone survey, seedling locations will come directly from semi-automated seedling detection on the orthomosaic [5], so these locational offsets will be absent.
- Field measurement or data entry error—seedlings that corresponded to obvious outliers in the 0.35 cm GSD leaf-off dataset were checked in relevant field photos or videos. Figure 8a shows an example of such an error where “observed” height is 0.19 cm, but orthomosaics and field photos show this value is probably incorrect. This type of errors inflates the observed RMSE, but we decided to include them because removing outliers is hardly justifiable except for the limited purposes of a sensitivity analysis such as the one we did on seedling size (Section 5.1).
- 3D reconstruction error—for the finest GSD there was below-ground noise (discussed in Section 5.2). Whatever the source of below-ground noise is, it probably also creates spurious points elsewhere in the DIPC, which will affect height estimation if they happen to be local maxima. Additionally, seedlings can be occluded by adjacent taller vegetation, preventing a full reconstruction in the point cloud. As described earlier, wind will also have an impact on 3D reconstruction where the DIPC workflow will have trouble matching the image pixels of swaying objects. Species phenology and morphology also affect 3D reconstruction; bare twigs from deciduous larches will be difficult to fully capture (e.g., Figure 8b). It also seems that jack pine seedlings are harder to reconstruct, perhaps because of their narrow shape. All these effects lead to underestimation bias and are unlikely to be reduced in an operational drone survey, except perhaps by limiting the maximum ambient wind allowed for acquisitions, as suggested by Frey et al. [25].
- Non-seedling point errors—in a naturally regenerating linear disturbance there will be a lot of vegetation present that interferes with height estimation of nearby seedlings. There were several instances where a seedling’s height was overestimated because of neighboring tall shrubs or adjacent mature trees. To reduce this effect, we limited the DIPC extraction to a narrow vertical cylinder design, which is simple, but the inclusion of some points from neighboring vegetation inevitably occurred. A procedure that included point cloud segmentation [30], wherein clusters of points belonging to the same plant are given a unique ID—thus allowing for the removal of neighboring points belonging to an adjacent plant—would solve this problem, although tuning such an algorithm for short vegetation is not trivial.
5.6. Study Contributions and Limitations
5.7. Outlook
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dabros, A.; Pyper, M.; Castilla, G. Seismic lines in the boreal and arctic ecosystems of North America: Environmental impacts, challenges, and opportunities. Environ. Rev. 2018, 26, 214–229. [Google Scholar] [CrossRef]
- Hebblewhite, M. Billion dollar boreal woodland caribou and the biodiversity impacts of the global oil and gas industry. Biol. Conserv. 2017, 206, 102–111. [Google Scholar] [CrossRef]
- Government of Alberta. Provincial Restoration and Establishment Framework for Legacy Seismic Lines in Alberta; Alberta Environment and Parks, Land and Environment Planning Branch, Government of Alberta: Edmonton, AB, Canada, 2017.
- Feduck, C.; McDermid, G.; Castilla, G. Detection of coniferous seedlings in UAV imagery. Forests 2018, 9, 432. [Google Scholar] [CrossRef]
- Fromm, M.; Schubert, M.; Castilla, G.; Linke, J.; McDermid, G. Automated detection of conifer seedlings in drone imagery using convolutional neural networks. Remote Sens. 2019, 11, 2585. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. Remote sensing of vegetation structure using computer vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef]
- Järnstedt, J.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Holopainen, M.; Viitala, R. Forest variable estimation using a high-resolution digital surface model. ISPRS J. Photogramm. Remote Sens. 2012, 74, 78–84. [Google Scholar] [CrossRef]
- Vastaranta, M.; Wulder, M.A.; White, J.C.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H. Airborne laser scanning and digital stereo imagery measures of forest structure: Comparative results and implications to forest mapping and inventory update. Can. J. Remote Sens. 2013, 39, 382–395. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Chen, S.; McDermid, G.J.; Castilla, G.; Linke, J. Measuring vegetation height in linear disturbances in the boreal forest with UAV photogrammetry. Remote Sens. 2017, 9, 1257. [Google Scholar] [CrossRef]
- Kotivuori, E.; Kukkonen, M.; Mehtätalo, L.; Maltamo, M.; Korhonen, L.; Packalen, P. Forest inventories for small areas using drone imagery without in-situ field measurements. Remote Sens. Environ. 2020, 237, 111404. [Google Scholar] [CrossRef]
- Goodbody, T.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; Crawford, P. Assessing the status of forest regeneration using digital aerial photogrammetry and unmanned aerial systems. Int. J. Remote Sens. 2018, 39, 5246–5264. [Google Scholar] [CrossRef]
- Röder, M.; Latifi, H.; Hill, S.; Wild, J.; Svoboda, M.; Brůna, J.; Macek, M.; Nováková, M.H.; Gülch, E.; Heurich, M. Application of optical unmanned aerial vehicle-based imagery for the inventory of natural regeneration and standing deadwood in post-disturbed spruce forests. Int. J. Remote Sens. 2018, 39, 5288–5309. [Google Scholar] [CrossRef]
- Puliti, S.; Solberg, S.; Granhus, A. Use of UAV photogrammetric data for estimation of biophysical properties in forest stands under regeneration. Remote Sens. 2019, 11, 233. [Google Scholar] [CrossRef]
- Imangholiloo, M.; Saarinen, N.; Markelin, L.; Rosnell, T.; Näsi, R.; Hakala, T.; Honkavaara, E.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Characterizing seedling stands using leaf-off and leaf-on photogrammetric point clouds and hyperspectral imagery acquired from unmanned aerial vehicle. Forests 2019, 10, 415. [Google Scholar] [CrossRef]
- Natural Regions Committee. Natural Regions and Subregions of Alberta; Downing, D.J., Pettapiece, W.W., Eds.; Publ. No. T/852; Government of Alberta: Edmonton, AB, Canada, 2006.
- Agriculture and Agri-food Canada. National Ecological Framework for Canada. 2013. Available online: https://open.canada.ca/data/en/dataset/3ef8e8a9-8d05-4fea-a8bf-7f5023d2b6e1 (accessed on 14 January 2020).
- Lopes Queiroz, G.; McDermid, G.J.; Castilla, G.; Linke, J.; Rahman, M.M. Mapping coarse woody debris with random forest classification of centimetric aerial imagery. Forests 2019, 10, 471. [Google Scholar] [CrossRef]
- Dietmaier, A.; McDermid, G.J.; Rahman, M.M.; Linke, J.; Ludwig, R. Comparison of LiDAR and digital aerial photogrammetry for characterizing canopy openings in the Boreal Forest of Northern Alberta. Remote Sens. 2019, 11, 1919. [Google Scholar] [CrossRef]
- Rahman, M.M.; McDermid, G.J.; Strack, M.; Lovitt, J. A new method to map groundwater table in peatlands using unmanned aerial vehicles. Remote Sens. 2020, 9, 1057. [Google Scholar] [CrossRef]
- Isenburg, M. Scripting LAStools to Create a Clean DTM from Noisy Photogrammetric Point Cloud. Available online: https://rapidlasso.com/2018/12/27/scripting-lastools-to-create-a-clean-dtm-from-noisy-photogrammetric-point-cloud/ (accessed on 24 July 2019).
- R Core Team. The Wilcox.Test Function of the Stats R Package. 2020. Available online: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/wilcox.test (accessed on 1 May 2020).
- R Core Team. The SIGN.Test Function of the BSDA R Package. 2020. Available online: https://www.rdocumentation.org/packages/BSDA/versions/1.2.0/topics/SIGN.test (accessed on 1 May 2020).
- R Core Team. The Theilsen Function Deming R Package. 2020. Available online: https://www.rdocumentation.org/packages/deming/versions/1.3/topics/thielsen (accessed on 1 May 2020).
- Frey, J.; Kovach, K.; Stemmier, S.; Kock, K. UAV photogrammetry of forests as a vulnerable process. A sensitivity analysis for a structure from motion RGB-image pipeline. Remote Sens. 2018, 10, 912. [Google Scholar] [CrossRef]
- Salach, A.; Bakula, K.; Pilarska, M.; Ostrowski, W.; Górski, K.; Kurczyński, Z. Accuracy assessment of point clouds from LiDAR and dense image matching acquired using the UAV platform for DTM creation. Int. J. Geo-Inf. 2018, 7, 342. [Google Scholar] [CrossRef]
- Gianetti, F.; Chirici, G.; Gobakken, T.; Naesset, E.; Travaglini, D.; Pulitli, S. A new approach with DTM-independent metrics for forest growing stock prediction using UAV photogrammetric data. Remote Sens. Environ. 2018, 213, 195–205. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmann, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2016, 280, 51–56. [Google Scholar] [CrossRef]
- Graham, A.; Coops, N.C.; Wilcox, M.; Plowright, A. Evaluation of ground surface models derived from unmanned aerial systems with digital aerial photogrammetry in a disturbed conifer forest. Remote Sens. 2019, 11, 84. [Google Scholar] [CrossRef]
- Grilli, E.; Menna, F.; Remondino, F. A review of point clouds segmentation and classification algorithms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 339. [Google Scholar] [CrossRef]
- Næsset, E.; Nelson, R. Using airborne laser scanning to monitor tree migration in the boreal–alpine transition zone. Remote Sens. Environ. 2007, 110, 357–369. [Google Scholar] [CrossRef]
- Vepakomma, U.; Cormier, D.; Thiffault, N. Potential of UAV based convergent photogrammetry in monitoring regeneration standards. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Toronto, ON, Canada, 30 August–2 September 2015. [Google Scholar]



| Acquisition Parameters | No. of Seedlings | Seedling Height Statistics (m) | Species | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Phenology | GSD (cm) | Min | Max | Mean | Median | StDev | %Sb | %Pj | %Lt | |
| Leaf-on | 0.35 | 69 | 0.16 | 1.59 | 0.49 | 0.37 | 0.34 | 80 | 13 | 7 |
| 0.75 | 176 | 0.15 | 2.38 | 0.59 | 0.43 | 0.44 | 82 | 6 | 13 | |
| 3 | 189 | 0.15 | 2.38 | 0.6 | 0.46 | 0.43 | 79 | 5 | 15 | |
| Leaf-off | 0.35 | 69 | 0.15 | 1.59 | 0.49 | 0.37 | 0.33 | 78 | 13 | 9 |
| 0.75 | 189 | 0.15 | 2.38 | 0.6 | 0.46 | 0.43 | 79 | 5 | 15 | |
| 3 | – | |||||||||
| Site | Acq. Date | Mean AGL (m) | Flight Conditions | Drone | Camera | Focal Len. (mm) | SfM GCP Err. (cm) | GSD (cm) | Approx. Density (pts/m2) |
|---|---|---|---|---|---|---|---|---|---|
| 460 | 3 August 2017 | 5 | Overcast; variable light winds | DJI Mavic Pro | FC220 | 4.73 | 21.5 | 0.35 | 25,000 |
| 31.5 | DJI Inspire 2 | FC6510 | 8.8 | 20.9 | 0.75 | 7000 | |||
| 122 | Variable sun | eBee Sensefly | S.O.D.A | 10.2 | 3 | 3 | 650 | ||
| 19 October 2017 | 5 | Sunny; gentle wind gusts | DJI Mavic Pro | FC220 | 4.73 | 22.3 | 0.35 | 32,000 | |
| 31.7 | DJI Inspire 2 | FC6510 | 8.8 | 12.1 | 0.75 | 5000 | |||
| 464 | 3 August 2017 | 4.7 | Sunny; scattered cloud | DJI Mavic Pro | FC220 | 4.73 | 25.9 | 0.35 | 30,000 |
| 4 August 2017 | 30.4 | Occasional sun; increasing winds | DJI Inspire 2 | FC6510 | 8.8 | 27.2 | 0.75 | 5000 | |
| 3 August 2017 | 122 | Variable sun | eBee Sensefly | S.O.D.A | 10.2 | 5.7 | 3 | 940 | |
| 20 October 2017 | 4.5 | Sunny; gentle wind gusts | DJI Mavic Pro | FC220 | 4.73 | 11.3 | 0.35 | 30,000 | |
| 30.2 | DJI Inspire 2 | FC6510 | 8.8 | 78 | 0.75 | 4600 | |||
| 466 | 3 August 2017 | 5 | Occasional sun | DJI Mavic Pro | FC220 | 4.73 | 12.8 | 0.35 | 25,000 |
| 31 | DJI Inspire 2 | FC6510 | 8.8 | 19 | 0.75 | 4000 | |||
| 122 | eBee Sensefly | S.O.D.A | 10.2 | 5.6 | 3 | 735 | |||
| 19 October 2017 | 5 | Sunny; gentle wind gusts | DJI Mavic Pro | FC220 | 4.73 | 8 | 0.35 | 38,000 | |
| 30.5 | DJI Inspire 2 | FC6510 | 8.8 | 9.2 | 0.75 | 3700 |
| Rank | GSD (cm) | Phenology | Ground Method | N | RMSE (m) | BIAS (m) | MAE (m) | MEDAE (m) | R2 | %om | %com | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.0 | 0.35 | leaf-off | DIPCTIN | 48 | 0.61 | 0.24 | −0.11 | 0.14 | 0.05 | 0.63 | 67 | 13 | 0 |
| 3.2 | 0.35 | leaf-on | DIPCTIN | 48 | 0.61 | 0.28 | −0.07 | 0.18 | 0.11 | 0.43 | 65 | 8 | 6 |
| 3.8 | 0.35 | leaf-off | DIPCMIN | 48 | 0.61 | 0.28 | 0.10 | 0.20 | 0.18 * | 0.67 | 57 | 4 | 19 |
| 5.3 | 0.35 | leaf-on | DTMALS | 46 | 0.61 | 0.29 | −0.14 | 0.21 | 0.14 * | 0.51 | 52 | 7 | 0 |
| 5.8 | 0.75 | leaf-on | DIPCMIN | 123 | 0.75 | 0.57 | 0.06 | 0.33 | 0.13 * | 0.26 | 64 | 10 | 9 |
| 6.8 | 0.35 | leaf-on | DIPCMIN | 46 | 0.61 | 0.29 | 0.15 | 0.24 | 0.22 * | 0.52 | 47 * | 4 | 28 |
| 7.3 | 0.35 | leaf-off | DTMALS | 48 | 0.61 | 0.32 | −0.22 | 0.24 | 0.20 * | 0.59 | 44 * | 15 | 0 |
| 7.3 | 3.00 | leaf-on | DTMALS | 135 | 0.75 | 0.67 | 0.06 | 0.39 | 0.18 * | 0.13 | 61 | 12 | 7 |
| 8.8 | 0.75 | leaf-on | DIPCTIN | 123 | 0.75 | 0.47 | −0.19 | 0.34 | 0.24 * | 0.37 | 39 * | 22 | 5 |
| 9.8 | 0.75 | leaf-off | DTMALS | 135 | 0.75 | 0.57 | −0.25 | 0.38 | 0.19 * | 0.07 | 58 | 30 | 2 |
| 10.3 | 3.00 | leaf-on | DIPCMIN | 135 | 0.75 | 0.68 | −0.04 | 0.45 | 0.28 * | 0.10 | 45 * | 19 | 7 |
| 10.5 | 0.75 | leaf-off | DIPCMIN | 135 | 0.75 | 0.57 | −0.28 | 0.40 | 0.27 * | 0.12 | 54 | 33 | 1 |
| 10.8 | 0.75 | leaf-on | DTMALS | 123 | 0.75 | 0.54 | −0.20 | 0.41 | 0.34 * | 0.22 | 35 * | 20 | 16 |
| 13.8 | 0.75 | leaf-off | DIPCTIN | 135 | 0.75 | 0.67 | −0.45 | 0.54 | 0.39 * | 0.10 | 22 * | 40 | 0 |
| 14.2 | 3.00 | leaf-on | DIPCTIN | 135 | 0.75 | 0.75 | −0.22 | 0.57 | 0.41 * | 0.09 | 23 * | 33 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castilla, G.; Filiatrault, M.; McDermid, G.J.; Gartrell, M. Estimating Individual Conifer Seedling Height Using Drone-Based Image Point Clouds. Forests 2020, 11, 924. https://doi.org/10.3390/f11090924
Castilla G, Filiatrault M, McDermid GJ, Gartrell M. Estimating Individual Conifer Seedling Height Using Drone-Based Image Point Clouds. Forests. 2020; 11(9):924. https://doi.org/10.3390/f11090924
Chicago/Turabian StyleCastilla, Guillermo, Michelle Filiatrault, Gregory J. McDermid, and Michael Gartrell. 2020. "Estimating Individual Conifer Seedling Height Using Drone-Based Image Point Clouds" Forests 11, no. 9: 924. https://doi.org/10.3390/f11090924
APA StyleCastilla, G., Filiatrault, M., McDermid, G. J., & Gartrell, M. (2020). Estimating Individual Conifer Seedling Height Using Drone-Based Image Point Clouds. Forests, 11(9), 924. https://doi.org/10.3390/f11090924







