Economic Performance of Genetically Improved Reforestation Material in Joint Production of Timber and Carbon Sequestration: A Case Study from Finland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Stands
2.2. The Optimization Problem
2.3. Stand Projections
2.4. Financial Data
2.5. Sensitivity Analysis
3. Results
3.1. Main Results
3.2. Sensitivity Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mullin, T.J.; Andersson, B.; Bastien, J.C.; Beaulieu, J.; Burdon, R.D.; Dvorak, W.S.; King, J.N.; Kondo, T.; Krakowski, J.; Lee, S.J.; et al. Economic importance, breeding objectives and achievements. In Genomics of Conifers; Plomion, C., Bousquet, J., Eds.; Science Publishers: New Hampshire, UK, 2012; pp. 40–127. [Google Scholar]
- Ruotsalainen, S. Increased forest production through forest tree breeding. Scand. J. For. Res. 2014, 29, 333–344. [Google Scholar] [CrossRef]
- Jansson, G.; Hansen, J.K.; Haapanen, M.; Kvaalen, H.; Steffenrem, A. The genetic and economic gains from forest tree breeding programmes in Scandinavia and Finland. Scand. J. For. Res. 2016, 32, 273–286. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Salminen, H.; Ojansuu, R.; Hynynen, J.; Kärkkäinen, K.; Haapanen, M. Optimizing stand management involving the effect of genetic gain: Preliminary results for Scots pine in Finland. Can. J. For. Res. 2013, 43, 299–305. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Haapanen, M.; Hynynen, J.; Karhu, J.; Kärkkäinen, K. Genetically improved reforestation stock provides simultaneous benefits for growers and a sawmill, a case study in Finland. Scand. J. For. Res. 2018, 33, 484–492. [Google Scholar] [CrossRef]
- Kimberley, M.O.; Moore, J.R.; Dungey, H. Quantification of realized genetic gain in radiata pine and its incorporation into growth and yield modeling systems. Can. J. For. Res. 2015, 45, 1676–1687. [Google Scholar] [CrossRef]
- Haapanen, M.; Hynynen, J.; Ruotsalainen, S.; Siipilehto, J.; Kilpeläinen, M.L. Realised and projected gains in growth, quality and simulated yield of genetically improved Scots pine in southern Finland. Eur. J. For. Res. 2016, 135, 997–1009. [Google Scholar] [CrossRef]
- Chang, W.Y.; Wang, S.; Gaston, C.; Cool, J.; An, H.; Thomas, B.R. Economic evaluations of tree improvement for planted forests: A systematic review. Bioprod. Bus. 2019, 4, 1–14. [Google Scholar]
- Metz, B.; Davidson, O.R.; Bosch, P.R.; Dave, R.; Meyer, L.A. Change 2007: Mitigation of Climate Change, Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Collins, S.; Larry, E. Caring For Our Natural Assets: An Ecosystem Services Perspective. In Pacific Northwest Research Station, Forest Service; U.S. Department of Agriculture: Portland, OR, USA, 2012. [Google Scholar]
- Latta, G.S.; Adams, D.M.; Bell, K.B.; Kline, J.D. Evaluating land-use and private forest management responses to a potential forest carbon offset sales program in western Oregon (USA). For. Policy Econ. 2016, 65, 1–8. [Google Scholar] [CrossRef]
- Aspinwall, M.J.; McKeand, S.E.; King, J.S. Carbon sequestration from 40 years of planting genetically improved Loblolly pine across the Southeast United States. For. Sci. 2012, 58, 446–456. [Google Scholar] [CrossRef]
- Van Kooten, G.; Binkley, C.; Delcourt, G. Effect of carbon taxes and subsidies on optimal forest rotation age and supply of carbon services. Am. J. Agric. Econ. 1995, 77, 365–374. [Google Scholar] [CrossRef] [Green Version]
- Olschewski, R.; Benitez, P.C. Optimizing joint production of timber and carbon sequestration of afforestation projects. J. For. Econ. 2010, 16, 1–10. [Google Scholar]
- Hoel, M.; Holtsmark, B.; Holtsmark, K. Faustmann and the climate. J. For. Econ. 2014, 20, 192–210. [Google Scholar] [CrossRef]
- Assmuth, A.; Tahvonen, O. Optimal carbon storage in even- and uneven-aged forestry. For. Policy Econ. 2018, 87, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Jayawickrama, K.J.S. Potential genetic gains for carbon sequestration: A preliminary study on radiata pine plantations in New Zealand. For. Ecol. Manag. 2001, 152, 313–322. [Google Scholar] [CrossRef]
- Willis, K.J.; Bennet, K.D.; Birks, H.J.B. The late quarternary dynamics of pines in Europe. In Ecology and Biogeoraphy of Pinus; Richardson, D.M., Ed.; Cambridge Univ Press: Cambridge, UK, 1998; pp. 107–121. [Google Scholar]
- Volosyanchuk, R.T. Pinus sylvestris L. In CABI International (Comp) Pines o Silvicultural Importance; CABI Publ: Wallingford, Oxon, UK, 2002; pp. 449–466. [Google Scholar]
- Straka, T.J. Financial breakeven for competition control in longleaf pine (Pinus palustris Mill.) reestablishment. New For. 2010, 40, 165–173. [Google Scholar] [CrossRef]
- Chang, S.J. Forest valuation under generalized Faustmann formula. Can. J. For. Res. 2013, 44, 56–63. [Google Scholar] [CrossRef]
- Cao, T.; Hyytiäinen, K.; Tahvonen, O.; Valsta, L. Effects of initial stand states on optimal thinning regime and rotation of Picea abies stands. Scand. J. For. Res. 2006, 21, 388–398. [Google Scholar] [CrossRef]
- Charbonneau, P.; Knapp, B. A User’s Guide to PIKAIA 1.0, NCAR Technical Note 418+IA; High Altitude Observatory, National Center for Atmospheric Research: Boulder, CO, USA, 1995; p. 121. [Google Scholar]
- Metcalfe, T.S.; Charbonneau, P. Stellar structure modeling using a parallel genetic algorithm for objective global optimization. J. Comput. Phys. 2003, 185, 176–193. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Li, M.; Chen, D.S.; Wang, F.; Li, Y.; Zhou, Y.; Lang, J.L. Optimizing emission inventory for chemical transport models by using genetic algorithm. Atmos Environ 2010, 44, 3926–3934. [Google Scholar] [CrossRef]
- Juutinen, A.; Ahtikoski, A.; Lehtonen, M.; Mäkipää, R.; Ollikainen, M. The impact of a short-term carbon payment scheme on forest management. For. Policy Econ. 2018, 90, 115–127. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Hökkä, H. Intensive forest management—Does it financially pay off on drained peatlands? Can. J. For. Res. 2019, 49, 1101–1111. [Google Scholar] [CrossRef]
- Matala, J.; Hynynen, J.; Miina, J.; Ojansuu, R.; Peltola, H.; Sievänen, R.; Väisänen, H.; Kellomäki, S. Comparison of a physiological model and a statistical model for prediction of growth and yield in boreal forests. Ecol. Model. 2003, 161, 95–116. [Google Scholar] [CrossRef]
- Salminen, H.; Lehtonen, M.; Hynynen, J. Reusing legacy FORTRAN in the MOTTI growth and yield simulator. Comput. Electron. Agric. 2005, 49, 103–113. [Google Scholar] [CrossRef]
- Hynynen, J.; Salminen, H.; Huuskonen, S.; Ahtikoski, A.; Ojansuu, R.; Siipilehto, J.; Lehtonen, M.; Rummukainen, A.; Kojola, S.; Eerikäinen, K. Scenario Analysis for the Biomass Supply Potential and the Future Development of Finnish Forest Resources; Working Papers of the Finnish Forest Research Institute 302; Finnish Forest Research Institute: Vantaa, Finland, 2014. [Google Scholar]
- Valsta, L. An optimization model for Norway spruce management based on individual-tree growth models. Acta For. Fenn. 1992, 232. [Google Scholar] [CrossRef] [Green Version]
- Niinimäki, S.; Tahvonen, O.; Mäkelä, A. Applying a process-based model in Norway spruce management. For. Ecol. Manag. 2012, 265, 102–115. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Pukkala, T.; Gonzalez-Conzalez, J.M.; Barrio-Anta, M.; Dieguez-Aranda, U. Use of depth-first search and direct search methods to optimize even-aged stand management: A case study involving maritime pine in Asturias (northwest Spain). Can. J. For. Res. 2015, 45, 1269–1279. [Google Scholar] [CrossRef]
- Tonteri, T.; Hotanen, J.P.; Kuusipalo, J. The Finnish forest site type approach: Ordination and classification studies of mesic forest sites in southern Finland. Vegetatio 1990, 87, 85–98. [Google Scholar] [CrossRef]
- Ahtikoski, A.; Ojansuu, R.; Haapanen, M.; Hynynen, J.; Kärkkäinen, K. Financial performance of using genetically improved regeneration material of Scots pine (Pinus sylvestris L.) in Finland. New For. 2012, 43, 335–348. [Google Scholar] [CrossRef]
- Tahvonen, O. Net national emissions, CO2 taxation and the role of forestry. Resour. Energy Econ. 1995, 17, 307–315. [Google Scholar] [CrossRef] [Green Version]
- Geng, A.; Yang, H.; Chen, J.; Hong, Y. Review of carbon storage function of harvested wood products and the potential of wood substitution in greenhouse gas mitigation. For. Policy Econ. 2017, 85, 192–200. [Google Scholar] [CrossRef]
- Tol, R.S. The social cost of carbon. Ann. Rev. Resour. Econ. 2011, 3, 419–443. [Google Scholar] [CrossRef]
- Davies, O.; Kerr, G. Comparing the costs and revenues of transformation to continuous cover forestry for Sitka spruce in Great Britain. Forests 2015, 6, 2424–2449. [Google Scholar] [CrossRef] [Green Version]
- Knoke, T.; Paul, C.; Härtl, F. A critical view on benefit-cost analyses of silvicultural management options with declining discount rates. For. Policy Econ. 2017, 83, 58–69. [Google Scholar] [CrossRef]
- Price, C. Declining discount rate and the social cost of carbon: Forestry consequences. J. For. Econ. 2018, 3, 9–45. [Google Scholar] [CrossRef]
- Pohjola, J.; Valsta, L. Carbon credits and management of Scots pine and Norway spruce stands in Finland. For. Policy Econ. 2007, 9, 789–798. [Google Scholar] [CrossRef]
- Pihlainen, S.; Tahvonen, O.; Niinimäki, S. The economics of timber and bioenergy production and carbon storage in Scots pine stands. Can. J. For. Res. 2014, 44, 1091–1102. [Google Scholar] [CrossRef]
- Boyce, J.K. Carbon pricing: Effectiveness and equity. Ecol. Econ. 2018, 50, 52–61. [Google Scholar] [CrossRef]
- Ricke, K.; Drouet, L.; Caldeira, K.; Tavoni, M. Country-level social costs of carbon. Nat. Clim. Chang. 2018, 8, 895–900. [Google Scholar] [CrossRef]
- Nordhaus, W.D.; Boyer, J. Warming the World: Economic Models of Global Warming; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Weitzman, M.L. A Review of the Stern Review on the economics of climate change. J. Econ. Lit. 2007, 45, 703–724. [Google Scholar] [CrossRef]
- Stern, N. The economics of climate change. Am. Econ. Rev. 2008, 98, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.R. Drivers of peak warming in a consumption-maximizing world. Nat. Clim. Chang. 2016, 6, 684–686. [Google Scholar] [CrossRef]
- Belfiori, M.E. Carbon pricing, carbon sequestration and social discounting. Eur. Econ. Rev. 2017, 96, 1–17. [Google Scholar] [CrossRef]
- Cao, T. Silvicultural Decisions Based on Simulation-Optimization Systems. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 18 May 2010. [Google Scholar]
- Tahvonen, O.; Pihlainen, S.; Niinimäki, S. On the economics of optimal timber production in boreal Scots pine stands. Can. J. For. Res. 2013, 43, 719–730. [Google Scholar] [CrossRef]
- Xue, H.; Mäkelä, A.; Valsta, L.; Vanclay, J.K.; Cao, T. Comparison of population-based algorithms for optimizing thinnings and rotation using a process-based growth model. Scand. J. For. Res. 2019, 34, 458–468. [Google Scholar] [CrossRef] [Green Version]
- Zobel, B.J.; Jett, J.B. Genetics of Wood Production; Springer: Berlin, Germany, 1995. [Google Scholar]
- Lamlom, S.H.; Savidge, R.A. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenergy 2003, 25, 381–388. [Google Scholar] [CrossRef]
- Antonova, G.F.; Varaksina, T.N.; Zheleznichenko, T.V.; Stasova, V.V. Lignin deposition during earlywood and latewood formation in Scots pine stems. Wood Sci. Technol. 2014, 48, 919–936. [Google Scholar] [CrossRef]
- Bouffier, L.; Raffin, A.; Rozenberg, P.; Meredieu, C.; Kremer, A. What are the consequences of growth selection on wood density in the French maritime pine breeding programme? Tree Genet. Genomes 2009, 5, 11–25. [Google Scholar] [CrossRef]
- Salmela, M.J.; Velmala, S.M.; Pennanen, T. Seedling traits from root to shoot exhibit genetic diversity and distinct responses to environmental heterogeneity within a tree population. Oikos 2020, 129, 544–558. [Google Scholar] [CrossRef]
- Juutinen, A.; Tolvanen, A.; Saarimaa, M.; Ojanen, P.; Sarkkola, S.; Ahtikoski, A.; Haikarainen, S.; Karhu, J.; Haara, A.; Nieminen, M.; et al. Cost-effective land-use options of drained peatlands–integrated biophysical-economic modeling approach. Ecol. Econ. 2020, 175, 106704. [Google Scholar] [CrossRef]
- Gustavsson, L.; Sathre, R. Energy and CO2 analysis of wood substitution in construction. Clim. Chang. 2011, 105, 129–153. [Google Scholar] [CrossRef]
- Gustavsson, L.; Haus, S.; Lundblad, M.; Lundström, A.; Ortiz, C.A.; Sathre, R.; le Truong, N.; Wikberg, P.E. Climate change effects of forestry and substitution of carbon-intensive materials and fossil fuels. Renew. Sustain. Energy Rev. 2017, 67, 612–624. [Google Scholar] [CrossRef]
- Simonsen, R. Optimal regeneration method—Planting vs. natural regeneration of Scots pine in northern Sweden. Silva Fenn. 2013, 47, 928. [Google Scholar] [CrossRef] [Green Version]

| Variable | Scenario | Region 1 Unimproved GG 10% GG 15% | Region 2 Unimproved GG 10% GG 15% | ||||
|---|---|---|---|---|---|---|---|
| Timing of the first thinning, yrs | TP | 46.3 (5.0) a) | 38.3 (5.0) | 36.3 (5.0) | 38.0 (1.8) | 41.3 (4.4) | 35.3 (1.9) |
| TP-CS | 49.0 (0.8) | 46.5 (0.6) | 42.3 (2.5) | 55.8 (5.0) | 52.0 (3.5) | 50.3 (1.5) | |
| Number of thinnings | TP | 3.8 (0.5) | 4.5 (0.6) | 2.0 (0.0) | 4.0 (0.0) | 4.3 (0.5) | 4.3 (0.5) |
| TP-CS | 2.0 (0.0) | 2.0 (0.0) | 3.3 (0.5) | 2.0 (0.0) | 2.5 (0.6) | 2.5 (0.5) | |
| Average removal in thinnings | TP | 78.8 (4.3) | 80.5 (3.9) | 85.1 (3.9) | 62.4 (4.3) | 72.7 (3.9) | 69.8 (2.9) |
| TP-CS | 83.1 (8.3) | 87.8 (3.7) | 92.4 (4.5) | 74.0 (1.4) | 80.8 (2.8) | 81.8 (2.8) | |
| Rotation period | TP | 93.8 (8.0) | 92.8 (2.6) | 88.5 (3.0) | 97.3 (5.7) | 94.0 (4.9) | 91.5 (2.1) |
| TP-CS | 81.1 (8.3) | 87.8 (3.7) | 92.4 (4.5) | 98.8 (8.1) | 99.5 (1.7) | 91.3 (3.8) | |
| MAI (m3 ha−1 yr−1) | TP | 5.4 (0.1) [62%] b) | 6.3 (0.1) [65%] | 6.9 (0.2) [65%] | 4.4 (0.3) [58%] | 5.2 (0.2) [60%] | 5.6 (0.3) [63%] |
| TP-CS | 5.6 (0.2) [63%] | 6.6 (0.1) [64%] | 7.0 (0.2) [67%] | 4.7 (0.6 [61%] | 5.3 (0.2 [66%] | 5.7 (0.2) [64%] | |
| Carbon benefit c) | TP | 0 d) | 0 | 0 | 0 | 0 | 0 |
| TP-CS | 33% | 29% | 27% | 42% | 34% | 32% | |
| Discount Rate | Instant Carbon Price Applied a) | Region 1 | Region 2 |
|---|---|---|---|
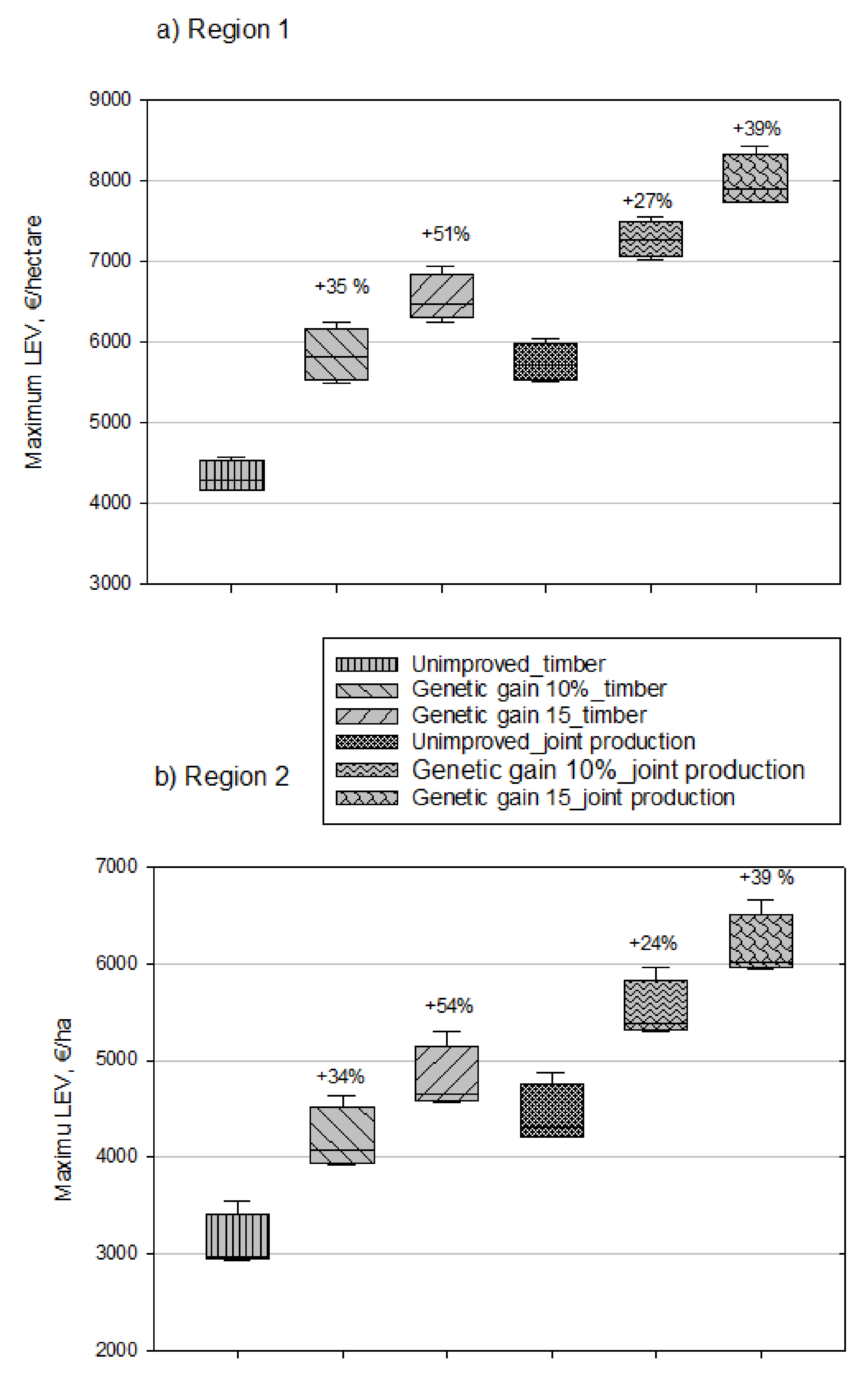
| 2% | 1 | Unimproved-TP: 4 334 (191) b) Genetic gain 10%-TP: 5 846 (332) Genetic gain 15%-TP: 6 540 (293) Unimproved-TP-CS: 5 753 (238) Genetic gain 10%-TP-CS: 7 280 (223) Genetic gain 15%-TP-CS: 8 000 (321) | Unimproved-TP: 3 109 (295) Genetic gain 10%-TP: 4 179 (325) Genetic gain 15%-TP: 4 796 (341) Unimproved-TP-CS: 4 426 (306) Genetic gain 10%-TP-CS: 5 507 (308) Genetic gain 15%-TP-CS: 6 158 (340) |
| 2 | Unimproved-TP-CS: 7 680 (232) c) Genetic gain 10%-TP-CS: 9 425 (261) Genetic gain 15%-TP-CS: 10 160 (303) | Unimproved-TP-CS: 6 099 (430) Genetic gain 10%-TP-CS: 7 229 (438) Genetic gain 15%-TP-CS: 8 028 (381) | |
| 4% | 1 | Unimproved-TP: 477 (78) d) Genetic gain 10%-TP: 932 (19) Geneticgain15%-TP:1164(41) Unimproved-TP-CS: 2 100 (45) Genetic gain 10%-TP-CS: 2 694 (51) Genetic gain 15%-TP-CS: 2 942 (69) | Unimproved-TP: 56 (21) Genetic gain 10%-TP: 430 (35) Genetic gain 15%-TP: 628 (39) Unimproved-TP-CS: 1 611 (69) Genetic gain 10%-TP-CS: 1 995 (42) Genetic gain 15%-TP-CS: 2 217 (35) |
| 2 | Unimproved-TP-CS: 4 231 (59) d) Genetic gain 10%-TP-CS: 5 035 (97) Genetic gain 15%-TP-CS: 5 374 (99) | Unimproved-TP-CS: 3 530 (138) Genetic gain 10%-TP-CS: 4 068 (84) Genetic gain 15%-TP-CS: 4 401 (98) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahtikoski, A.; Ahtikoski, R.; Haapanen, M.; Hynynen, J.; Kärkkäinen, K. Economic Performance of Genetically Improved Reforestation Material in Joint Production of Timber and Carbon Sequestration: A Case Study from Finland. Forests 2020, 11, 847. https://doi.org/10.3390/f11080847
Ahtikoski A, Ahtikoski R, Haapanen M, Hynynen J, Kärkkäinen K. Economic Performance of Genetically Improved Reforestation Material in Joint Production of Timber and Carbon Sequestration: A Case Study from Finland. Forests. 2020; 11(8):847. https://doi.org/10.3390/f11080847
Chicago/Turabian StyleAhtikoski, Anssi, Roope Ahtikoski, Matti Haapanen, Jari Hynynen, and Katri Kärkkäinen. 2020. "Economic Performance of Genetically Improved Reforestation Material in Joint Production of Timber and Carbon Sequestration: A Case Study from Finland" Forests 11, no. 8: 847. https://doi.org/10.3390/f11080847
APA StyleAhtikoski, A., Ahtikoski, R., Haapanen, M., Hynynen, J., & Kärkkäinen, K. (2020). Economic Performance of Genetically Improved Reforestation Material in Joint Production of Timber and Carbon Sequestration: A Case Study from Finland. Forests, 11(8), 847. https://doi.org/10.3390/f11080847






