Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion
Abstract
1. Introduction
2. Materials and Methods
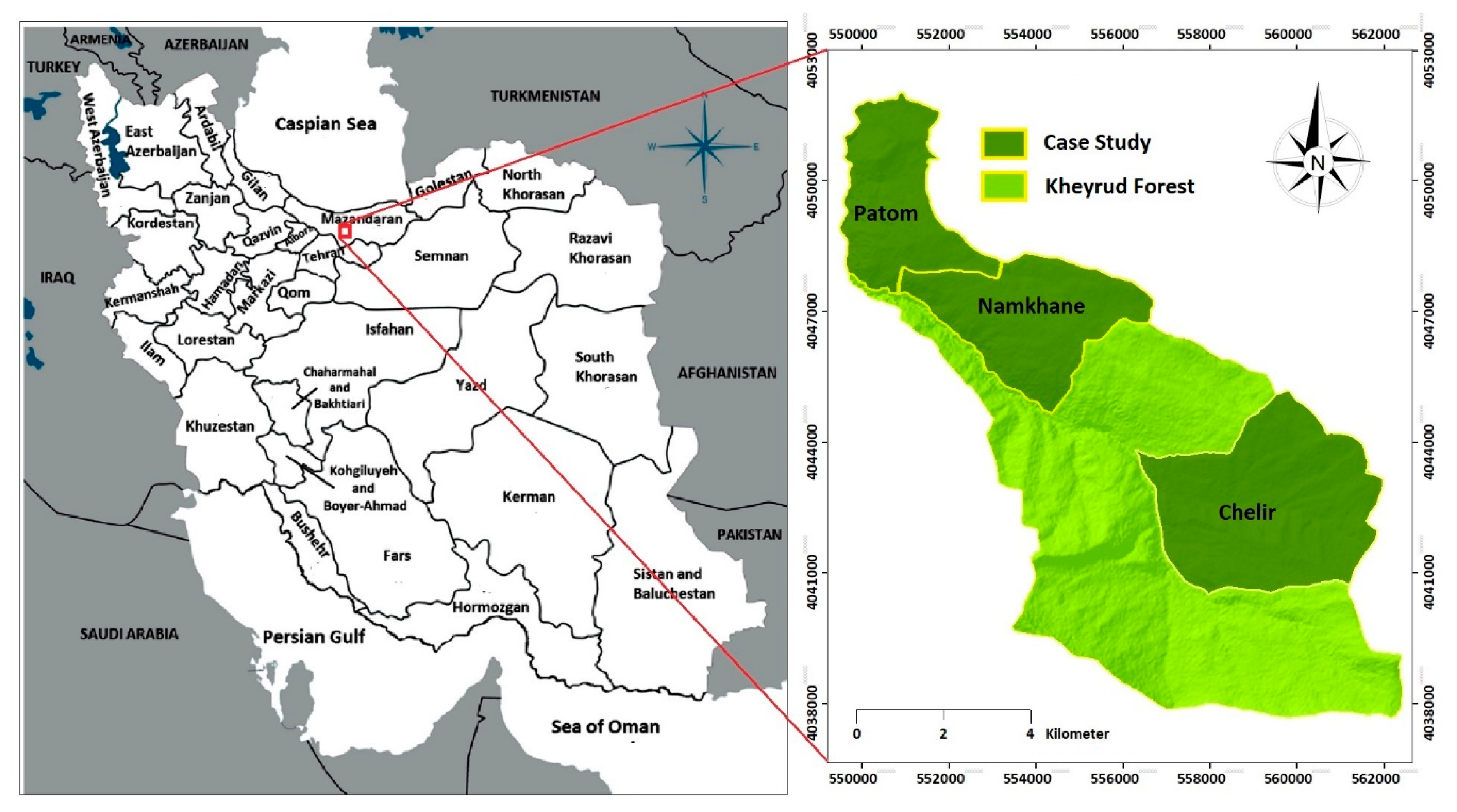
2.1. Study Site and Species
2.2. Sampling Design
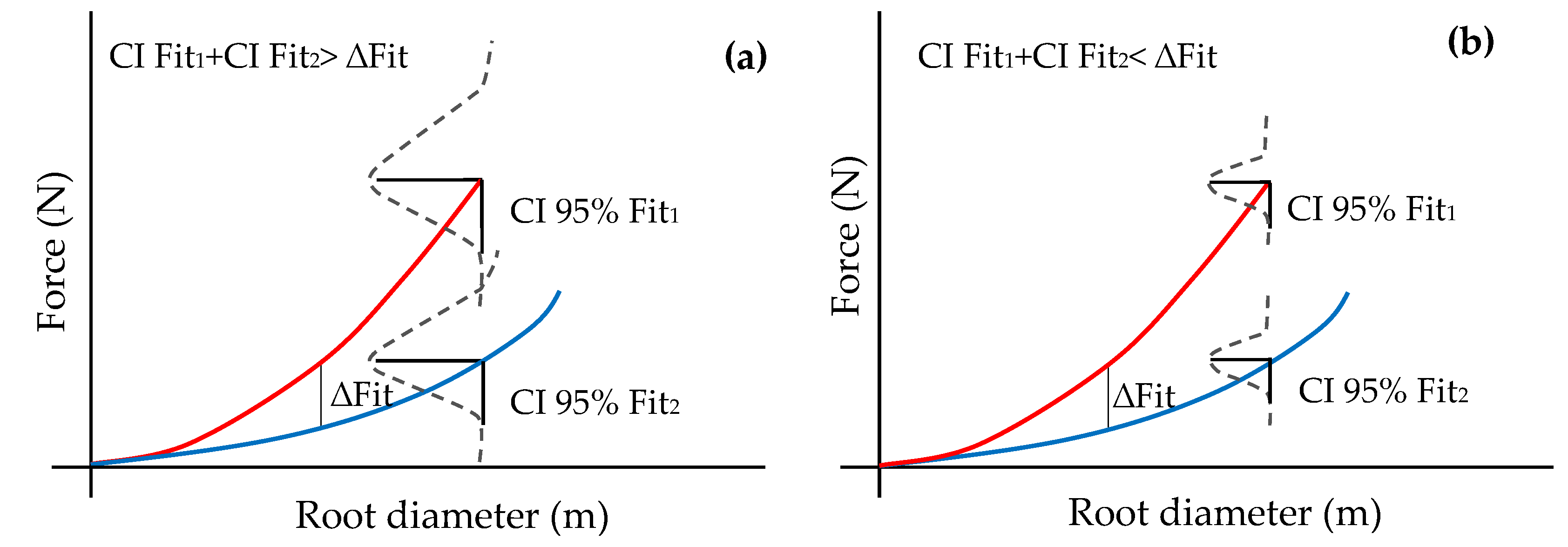
2.3. Statistical Analysis
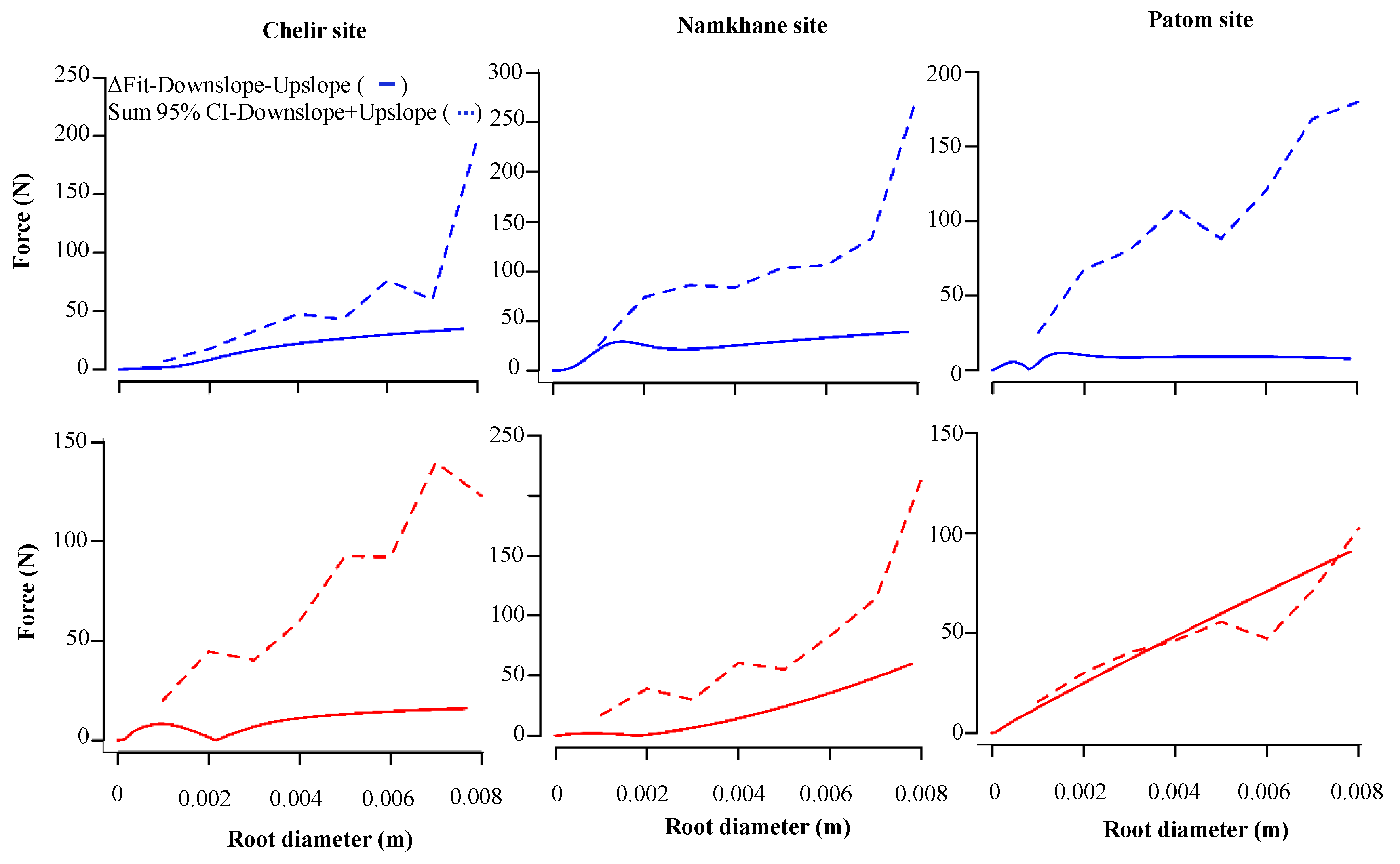
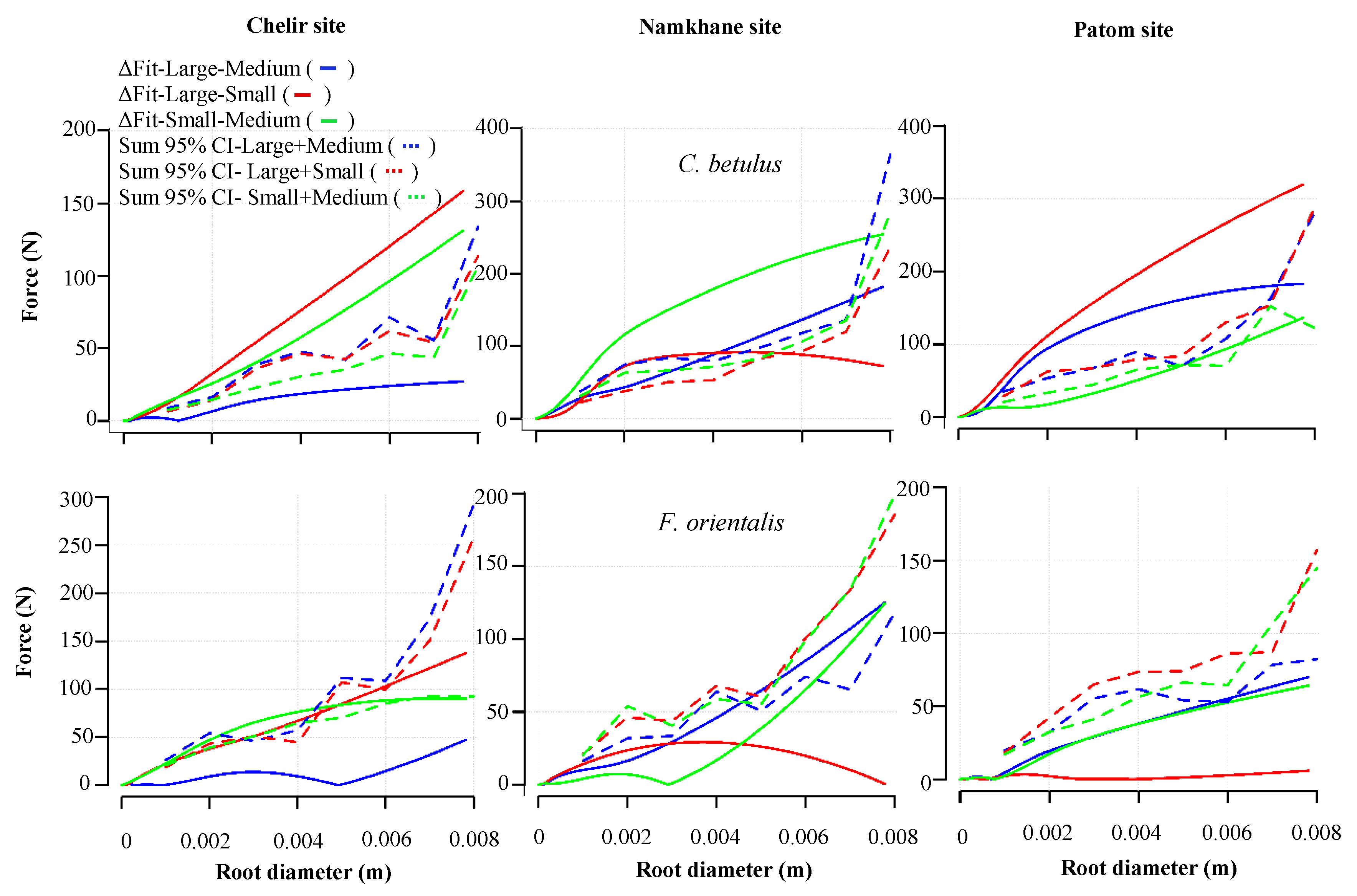
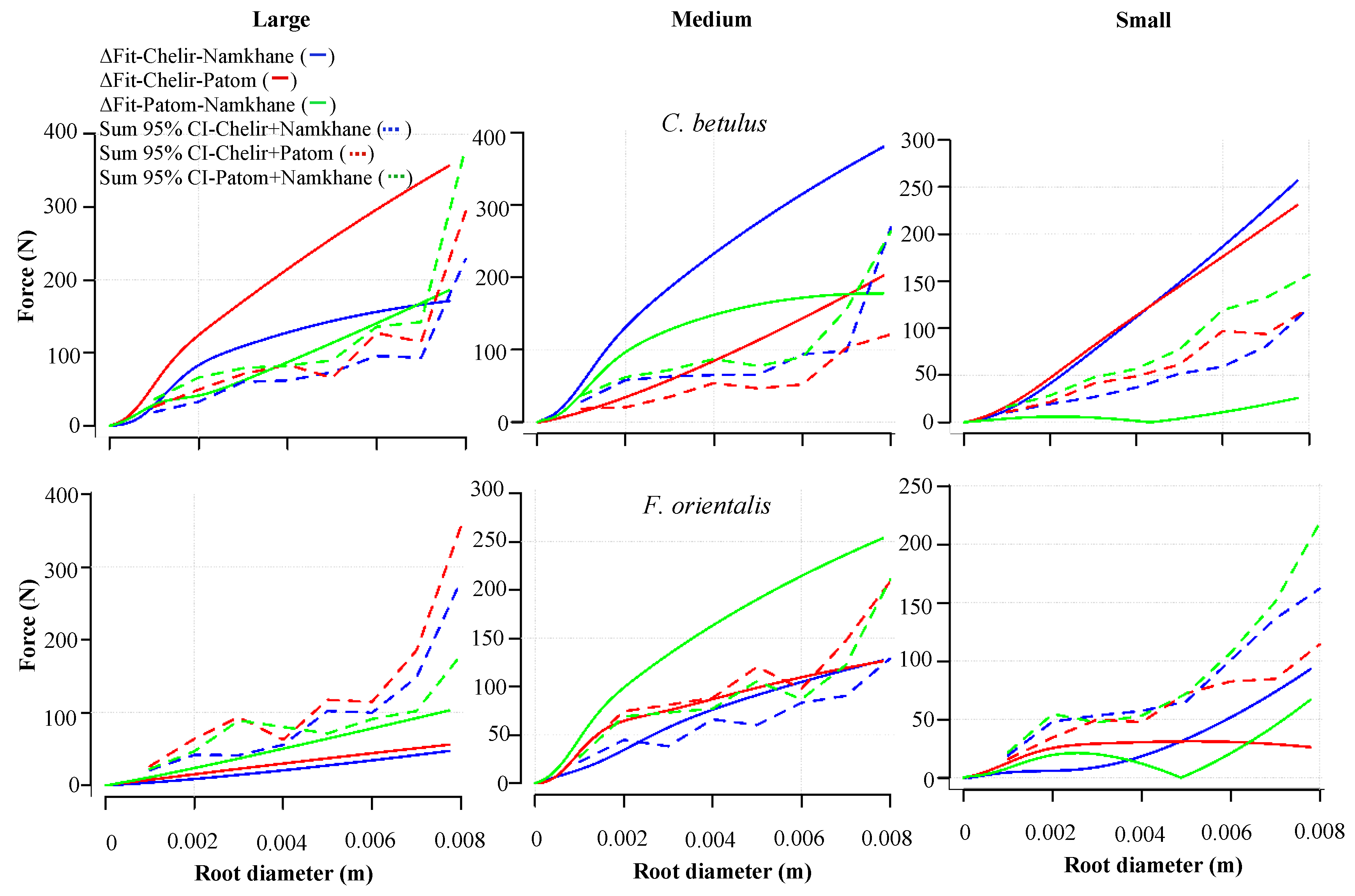
3. Results
3.1. ANCOVA
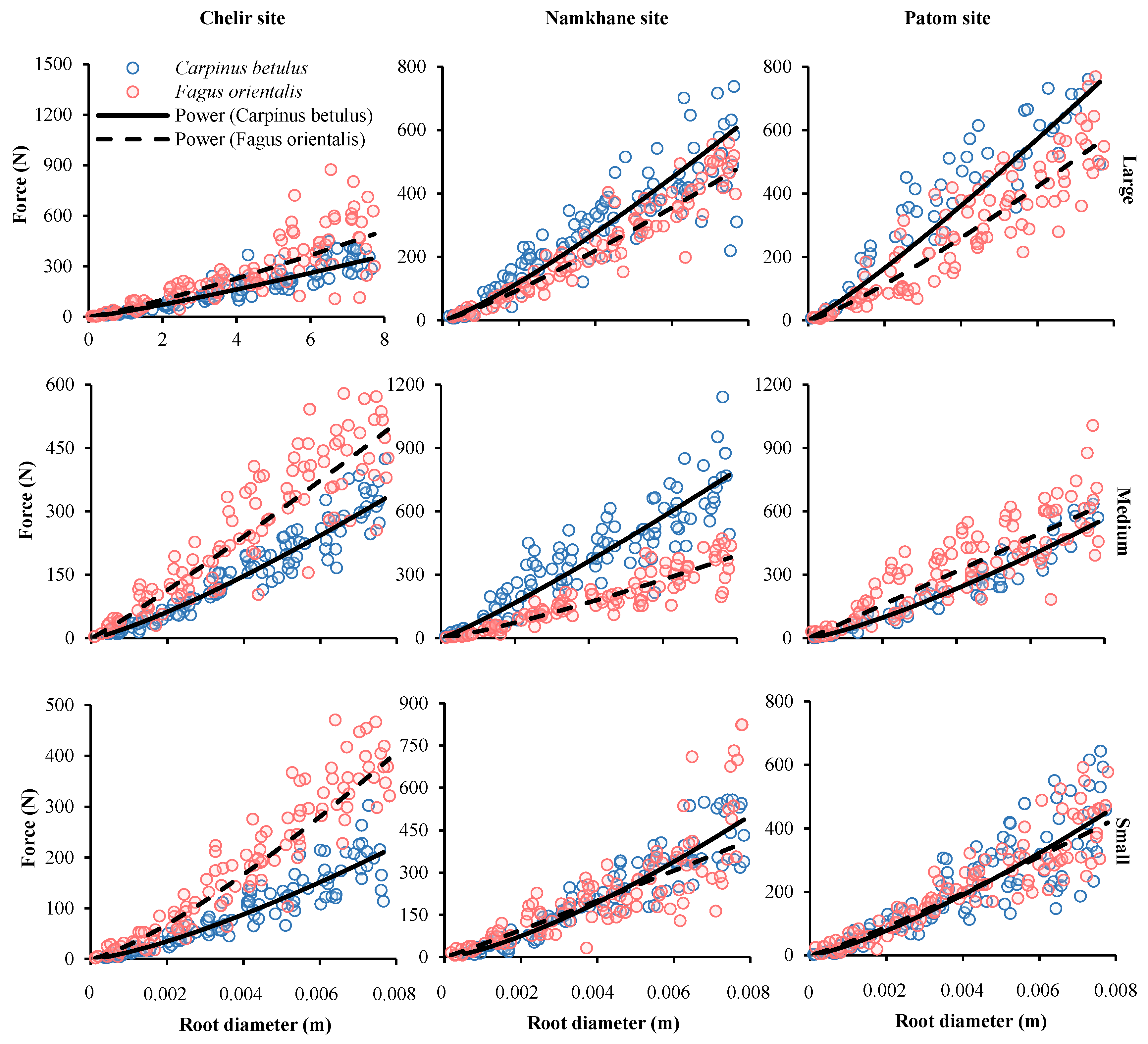
3.2. Species
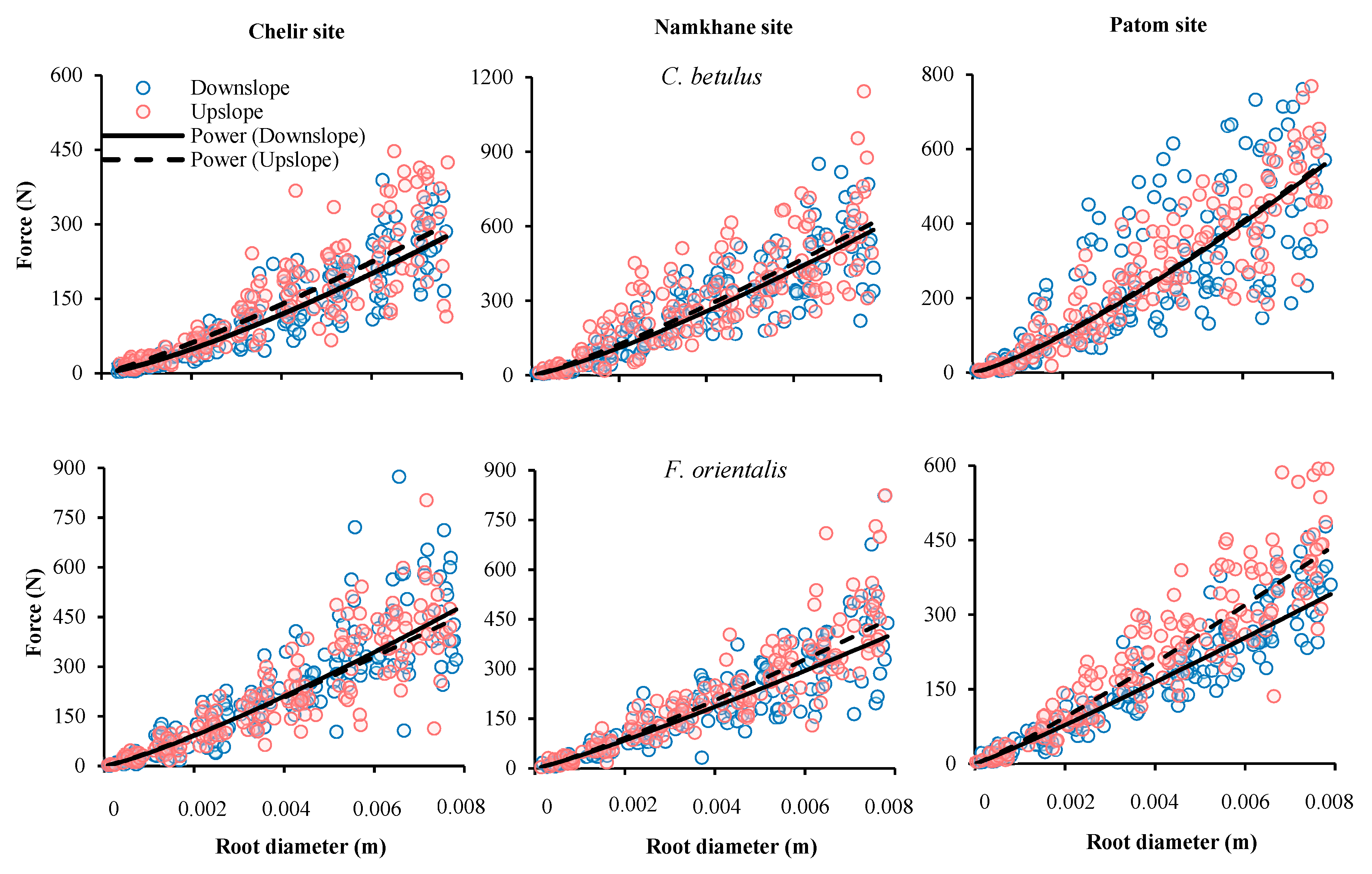
3.3. Slope Position
3.4. DBH
3.5. Study Sites
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mickovski, S.B.; Gonzalez-Ollauri, A.; Tardio, G. Novel approaches to quantification of the vegetation effects on soil strength. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–22 September 2017. [Google Scholar]
- Schwarz, M.; Phillips, C.; Marden, M.; McIvor, I.R.; Douglas, G.B.; Watson, A. Modelling of root reinforcement and erosion control by Veronese poplar on pastoral hill country in New Zealand. N. Z. J. For. Sci. 2016, 46, 4. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth-Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Stokes, A.; Atger, C.; Bengough, A.G.; Fourcaud, T.; Sidle, R.C. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant Soil 2009, 324, 1–30. [Google Scholar] [CrossRef]
- Schwarz, M.; Rist, A.; Cohen, D.; Giadrossich, F.; Egorov, P.; Buttner, D.; Stolz, M.; Thormann, J.J. Root reinforcement of soils under compression. J. Geophys. Res. Earth Surf. 2015, 120, 2103–2120. [Google Scholar] [CrossRef]
- Vergani, C.; Giadrossich, F.; Buckley, P.; Conedera, M.; Pividori, M.; Salbitano, F.; Rauch, H.S.; Lovreglio, R.; Schwarz, M. Root reinforcement dynamics of European coppice woodlands and their effect on shallow landslides: A review. Earth-Sci. Rev. 2017, 167, 88–102. [Google Scholar] [CrossRef]
- Dazio, E.; Conedera, M.; Schwarz, M. Impact of different chestnut coppice managements on root reinforcement and shallow landslide susceptibility. For. Ecol. Manag. 2018, 417, 63–76. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root failure weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Moresi, F.V.; Maesano, M.; Matteucci, G.; Romagnoli, M.; Sidle, R.C.; Scarascia Mugnozza, G. Root biomechanical traits in a montane Mediterranean forest watershed: Variations with species diversity and soil depth. Forests 2019, 10, 341. [Google Scholar] [CrossRef]
- Tsige, D.; Senadheera, S.; Talema, A. Stability analysis of plant-root-reinforced shallow slopes along mountainous road corridors based on numerical modeling. Geosciences 2020, 10, 19. [Google Scholar] [CrossRef]
- Cohen, D.; Schwarz, M. Tree-root control of shallow landslides. Earth Surf. Dyn. 2017, 5, 451–477. [Google Scholar] [CrossRef]
- Roering, J.; Schmidt, K.M.; Stock, J.D.; Dietrich, W.E.; Montgomery, D.R. Shallow landsliding, root reinforcement, and the spatial distribution of tress in the Oregon Coast range. Can. Geotech. J. 2003, 40, 237–253. [Google Scholar] [CrossRef]
- Loades, K.; Bengough, A.; Bransby, M.; Hallett, P. Planting density influence on fibrous root reinforcement of soils. Ecol. Eng. 2010, 36, 276–284. [Google Scholar] [CrossRef]
- Mao, Z.; Wang, Y.; McCormack, M.L.; Rowe, N.; Deng, X.; Yang, X.; Xia, S.; Nespoulous, J.; Sidle, R.C.; Guo, D.; et al. Mechanical traits of fine roots as a function of topology and anatomy. Ann. Bot 2018, 122, 1103–1116. [Google Scholar] [CrossRef]
- Genet, M.; Stokes, A.; Fourcaud, T.; Norris, J.E. The influence of plant diversity on slope stability in a moist evergreen deciduous forest. Ecol. Eng. 2010, 36, 265–275. [Google Scholar] [CrossRef]
- Abdi, E.; Majnounian, B.; Genet, M.; Rahimi, H. Quantifying the effects of root reinforcement of Persian ironwood (Parrotia persica) on slope stability; a case study: Hillslope of Hyrcanian forests, Northern Iran. Ecol. Eng. 2010, 36, 1409–1416. [Google Scholar] [CrossRef]
- Bassanelli, C.; Bischetti, G.B.; Chiaradia, E.A.; Rossi, L.; Vergani, C. The contribution of chestnut coppice forests on slope stability in abandoned territory: A case study. JAE 2013, 44, 68–73. [Google Scholar] [CrossRef][Green Version]
- Styczen, M.E.; Morgan, R.P.C. Engineering Properties of Vegetation; Taylor & Francis: London, UK, 1995. [Google Scholar]
- O’Loughlin, C.L.; Watson, A. Root-wood strength deterioration in radiata pine after clearfelling. N. Z. J. For. Sci. 1979, 9, 284–293. [Google Scholar]
- Hales, T.; Cole-Hawthorne, C.; Lovell, L.; Evans, S.L. Assessing the accuracy of simple field based root strength measurements. Plant Soil 2013, 372, 553–565. [Google Scholar] [CrossRef]
- Zhang, C.B.; Chen, L.H.; Jiang, J. Why fine tree roots are stronger than thicker roots: The role of cellulose and lignin in relation to slope stability. Geomorphology 2014, 206, 196–202. [Google Scholar] [CrossRef]
- Genet, M.; Stokes, A.; Salin, F.; Mickovski, S.B.; Fourcaud, T.; Dumail, J.F.; Van Beek, R. The influence of cellulose content on tensile strength in tree roots. Plant Soil 2005, 278, 1–9. [Google Scholar] [CrossRef]
- Hales, T.C.; Miniat, C.F. Soil moisture causes dynamic adjustments to root reinforcement that reduce slope stability. Earth Surf. Process. Landforms. 2017, 42, 803–817. [Google Scholar] [CrossRef]
- Dobson, M. Tree root system. Arboric 1995, 130, 1–6. [Google Scholar]
- Yarahmadi, J.; Rostaei, S.H.; Sharifikia, M.; Rostaei, M. Identifying and monitoring slope instability by using Differential SAR Interferometry, case study: Garmichay watershed, Miyane. JQGR 2015, 3, 44–59. [Google Scholar]
- Khajavi, E.; Arabkhedri, M.; Mahdian, M.H.; Shadfar, S. Investigation of Water Erosion and Soil Loss Values with using the Measured Data from Cs-137 Method and Experimental Plots in Iran. JWMR 2015, 6, 137–151. [Google Scholar]
- Karam, A. Quantitive Modelling and Landslide Risk Zonation in Faulted Zageros, Case Study: Sarkhon Basin in Char-Mahal-e-Bakhteyari. Ph.D. Thesis, Tarbiat Modares University, Noor, Iran, 2001. [Google Scholar]
- Sakals, M.E.; Sidle, R.C. A spatial and temporal model of root cohesion in forest soils. Can. J. For. Res. 2004, 34, 950–958. [Google Scholar] [CrossRef]
- Burylo, M.; Hudek, C.; Rey, F. Soil reinforcement by the roots of six dominant species on eroded mountainous marly slopes (Southern Alps, France). Catena 2011, 84, 70–78. [Google Scholar] [CrossRef]
- Sagheb-Talebi, K.; Sajedi, T.; Pourhashemi, M. Forests of Iran: A Treasure from the Past, a Hope for the Future; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Marvie-Mohadjer, M.R. Silviculture, 5th ed.; University of Tehran Press: Tehran, Iran, 2019; p. 418. [Google Scholar]
- Deljouei, A.; Abdi, E.; Marcantonio, M.; Majnounian, B.; Amici, V.; Sohrabi, H. The impact of forest roads on understory plant diversity in temperate hornbeam-beech forests of Northern Iran. Environ. Monit. Assess. 2017, 189, 392. [Google Scholar] [CrossRef]
- Deljouei, A.; Sadeghi, S.M.M.; Abdi, E.; Bernhardt-Römermann, M.; Pascoe, E.L.; Marcantonio, M. The impact of road disturbance on vegetation and soil properties in a beech stand, Hyrcanian forest. Eur. J. For. Res. 2018, 137, 759–770. [Google Scholar] [CrossRef]
- Soil Survey Staff. Soil Characterization and Profile Description Data; Soil Survey Laboratory, Natural Resources Conservation Service, USDA: Lincoln, NE, USA, 1995.
- Azaryan, M.; Marvie-Mohadjer, M.R.; Etemaad, V.; Shirvany, A.; Sadeghi, S.M.M. Morphological characteristics of old trees in Hyrcanian forest (Case study: Pattom and Namkhaneh districts, Kheyrud). JFWP 2015, 68, 47–59. [Google Scholar]
- Deljouei, A. Spatial Dynamics of Soil Reinforcement Due to Presence of Roots in Hyrcanian Forest (Case Study: Kheyroud Forest). Ph.D. Thesis, University of Tehran, Karaj, Iran, 2019. [Google Scholar]
- ASTM. ASTM D4318-00. In Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils, Annual Book of ASTM Standards; American Society for Testing and Materials: West Conshohocken, PA, USA, 2003; Volune 04.08, pp. 582–595. [Google Scholar]
- Anonymous. Technical Memo No. 3-357. In The Unified Soil Classification System; United States Army Corps of Engineers: Vicksburg, MS, USA, 1957.
- Sagheb-Talebi, K.; Eslami, A. Nature-based silviculture—How can we achieve the equilibrium state in uneven-aged oriental beech stands? In Proceedings of the 8th International Symposium, Hokkaido, Japan, 8–13 September 2008. [Google Scholar]
- Vergani, C.; Chiaradia, E.; Bischetti, G. Variability in the tensile resistance of roots in alpine forest tree species. Ecol. Eng. 2012, 46, 43–56. [Google Scholar] [CrossRef]
- De Baets, S.; Torri, D.; Poesen, J.; Meersmans, J. Modelling increased soil cohesion due to roots with EUROSEM. Earth Surf. Process. Landforms. 2008, 33, 1948–1963. [Google Scholar] [CrossRef]
- Chiaradia, E.A.; Vergani, C.; Bischetti, G.B. Evaluation of the effects of three European forest types on slope stability by field and probabilistic analyses and their implications for forest management. For. Ecol. Manag. 2016, 370, 114–129. [Google Scholar] [CrossRef]
- Vergani, C.; Schwarz, M.; Soldati, M.; Corda, A.; Giadrossich, F.; Chiaradia, E.A.; Morando, P.; Bassanelli, C. Root reinforcement dynamics in subalpine spruce forests following timber harvest: A case study in Canton Schwyz, Switzerland. Catena 2016, 143, 257–288. [Google Scholar] [CrossRef]
- Gilardelli, F.; Vergani, C.; Gentili, R.; Bonis, A.; Pierre, C.; Sandra, C.; Chiaradia, E.A. Root characteristics of herbaceous species for topsoil stabilization restoration in projects. Land Degrad. Dev. 2017, 28, 2074–2085. [Google Scholar]
- Abdi, E. Effect of oriental beech root reinforcement on slope stability (Hyrcanian Forest, Iran). J. For. Sci. 2014, 60, 166–173. [Google Scholar] [CrossRef]
- Nilaweera, N.; Nutalaya, P. Role of tree roots in slope stabilisation. Bull. Eng. Geol. Environ. 1999, 57, 337–342. [Google Scholar] [CrossRef]
- Yuan, Z.Y.; Chen, H.Y.H. Fine root biomass, production, turnover rates, and nutrient contents in boreal forest ecosystems in relation to species, climate, fertility, and stand age: Literature review and meta-analyses. Crit. Rev. Plant Sci. 2010, 29, 204–221. [Google Scholar] [CrossRef]
- Sidle, R.C.; Ochiai, H. Landslides: Processes, Prediction and Land Use; American Geographical Union: Washington, DC, USA, 2006. [Google Scholar]
- Forbes, K.; Broadhead, J. Forest and landslides. In The Role of Trees and Forests in the Prevention of Landslides and Rehabilitation of Landslide-Affected Areas in Asia; RAP Publication: Bangkok, Thailand, 2013. [Google Scholar]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. 2010, 115, F4. [Google Scholar] [CrossRef]
- Abdi, E. Root tensile force and resistance of several tree and shrub species of Hyrcanian forest, Iran. Croat. J. For. Eng. 2018, 39, 255–270. [Google Scholar]
- Comino, E.; Marengo, P.; Rolli, V. Root reinforcement effect of different grass species: A comparison between experimental and models results. Soil Tillage Res. 2010, 110, 60–68. [Google Scholar] [CrossRef]
- Lee, J.T.; Chu, M.Y.; Lin, Y.S.; Kung, K.N.; Lin, W.C.; Lee, M.J. Root traits and biomechanical properties of three tropical pioneer tree species for forest restoration in landslide areas. Forests 2020, 11, 179. [Google Scholar] [CrossRef]
- Wu, T.H. No 5, Dpt. of Civil Engineering. In Investigation on landslides on Prince of Wales Island, Alaska Geotech Rpt; Ohio State University: Columbus, OH, USA, 1976. [Google Scholar]
- Schwarz, M.; Cohen, D.; Or, D. Spatial characterization of root reinforcement at stand scale: Theory and case study. Geomorphology 2012, 171, 190–200. [Google Scholar] [CrossRef]
- Abdi, E.; Deljouei, A. Seasonal and spatial variability of root reinforcement in three pioneer species of the Hyrcanian forest. Austrian J. For. Sci. 2019, 136, 175–198. [Google Scholar]
- Boldrin, D.; Leung, A.K.; Bengough, A.G. Root biomechanical properties during establishment of woody perennials. Ecol. Eng. 2017, 109, 196–206. [Google Scholar] [CrossRef]
- Abdi, E.; Saleh, H.R.; Majnounian, B.; Deljouei, A. Soil fixation and erosion control by Haloxylon persicum roots in arid lands, Iran. J. Arid. Land. 2019, 11, 86–96. [Google Scholar] [CrossRef]
- Alidadi, F. Decay Dynamic of Beech and Hornbeam Dead Trees in Mixed Beech (Fagus orientalis Lipsky) Stands. Master’s Thesis, University of Tehran, Karaj, Iran, 2014. [Google Scholar]
- Abdi, E. An Investigation of the Effect of Tree Roots in Slope Stability in Order to Use in Practical Forest Road Construction and Bioengineering. Ph.D. Thesis, University of Tehran, Karaj, Iran, 2009. [Google Scholar]
- Bischetti, G.B.; Chiaradia, E.A.; Epis, T.; Morlotti, E. Root cohesion of forest species in the Italian Alps. Plant Soil 2009, 324, 71–89. [Google Scholar] [CrossRef]
- Stokes, A. Biomechanics of tree root anchorage. In Plant Roots: The Hidden Half, 3rd ed.; Waisel, Y., Eshel, A., Kafkafi, U., Eds.; CRC Press: Boca Raton, FL, USA, 2002; pp. 175–186. [Google Scholar]
- Khuder, H.; Danjon, F.; Stokes, A.; Fourcaud, T. Growth response and root architecture of black locust seedlings growing on slopes and subjected to mechanical perturbation. In Proceedings of the 5th plant biomechanics conference, Stockholm, Sweden, 28 August–1 September 2006. [Google Scholar]
- Genet, M.; Li, M.; Luo, T.; Fourcaud, T.; Clément-Vidal, A.; Stokes, A. Linking carbon supply to root cell-wall chemistry and mechanics at high altitudes in Abies Georgei. Ann. Bot. 2011, 107, 311–320. [Google Scholar] [CrossRef]
- Genet, M.; Stokes, A.; Fourcaud, T.; Cai, X.; Lu, Y. Soil fixation by tree roots: Changes in root reinforcement parameters with age in Cryptomeria Japonica D. Don. In Plantations. Disaster Mitigation of Debris Flows, Slope Failures and Landslides; Universal Academy Press, Inc.: Tokyo, Japan, 2006; pp. 535–542. [Google Scholar]
- Montagnoli, A.; Terzaghi, M.; Chiatante, D.; Scippa, G.S.; Lasserre, B.; Dumroese, R.K. Ongoing modifications to root system architecture of Pinus ponderosa growing on a sloped site revealed by tree-ring analysis. Dendrochronologia 2019, 58, 125650. [Google Scholar] [CrossRef]
- Marler, T.E.; Discekici, H.M. Root development of ‘Red Lady’ papaya plants grown on a hillside. Plant Soil 1997, 195, 37–42. [Google Scholar] [CrossRef]
- Di Iorio, A.; Lasserre, B.; Scippa, G.S.; Chiatante, D. Root system architecture of Quercus pubescens trees growing on different sloping conditions. Ann. Bot. 2005, 95, 351–361. [Google Scholar] [CrossRef]
- Ganatsas, P.; Spanos, I. Root system asymmetry of Mediterranean pines. Plant Soil 2005, 278, 75–83. [Google Scholar] [CrossRef]
- Dumroese, R.K.; Terzaghi, M.; Chiatante, D.; Scippa, G.S.; Lasserre, B.; Montagnoli, A. Functional traits of Pinus ponderosa coarse-roots in response to slope conditions. Front. Plant Sci. 2019, 10, 947. [Google Scholar] [CrossRef]
- Hales, T.C.; Ford, C.R.; Hwang, T.; Vose, J.M.; Band, L.E. Topographic and ecologic controls on root reinforcement. J. Geophys. Res. Earth Surf. 2009, 114, F03013. [Google Scholar] [CrossRef]
- Ba, M. Etude des Proprietes Biomecaniques et de La Capacite de Vie Symbiotique de Racines D’arbres D’acacia Senegal Willd et de Prosopis juliflora DC. Ph.D. Thesis, University Bordeaux, Bordeaux, France, 2008. [Google Scholar]
- Goodman, A.M.; Ennos, A.R. The effects of soil bulk density on the morphology and anchor age mechanics of the root systems of sunflower and maize. Ann. Bot. 1999, 83, 293–302. [Google Scholar] [CrossRef]
- Jourgholami, M.; Khoramizadeh, A.; Zenner, E.K. Effects of soil compaction on seedling morphology, growth, and architecture of chestnut-leaved oak (Quercus castaneifolia). iForest Biogeosci. For. 2016, 10, 145–153. [Google Scholar] [CrossRef]
- Hathaway, R.L.; Penny, D. Root strength in some Populus and Salix clones. N. Z. J. Bot. 1975, 13, 333–344. [Google Scholar] [CrossRef]
- Genet, M.; Kokutse, N.; Stokes, A.; Fourcaud, T.; Cai, X.; Ji, J.; Mickovski, S. Root reinforcement in plantations of Cryptomeria japonica D. Don: Effect of tree age and stand structure on slope stability. For. Ecol. Manag. 2008, 256, 1517–1526. [Google Scholar] [CrossRef]




| Soil Properties | Soil Depth (cm) | Study Site | ||
|---|---|---|---|---|
| Chelir | Namkhane | Patom | ||
| Dry density (g cm−3) | 30 | 1.13 (± 0.02) | 1.09 (± 0.02) | 1.16 (± 0.03) |
| Nitrogen (%) | 0–10 | 22.44 (± 3.02) | 24.89 (± 3.02) | 21.19 (± 2.25) |
| 10–20 | 13.94 (± 1.13) | 14.10 (± 0.80) | 9.19 (± 0.52) | |
| Phosphorus (ppm) | 0–10 | 20.98 (± 3.01) | 25.93 (± 3.13) | 23.57 (± 2.11) |
| 10–20 | 22.00 (± 2.59) | 34.45 (± 1.06) | 28.52(± 2.38) | |
| Potassium (ppm) | 0–10 | 1989.2 (± 197.7) | 1253.6 (± 131.6) | 1068.1 (± 91.6) |
| 10-20 | 1228.0 (± 150.5) | 1458.3 (± 110.5) | 866.7 (± 147.3) | |
| Carbon (%) | 0–10 | 2.84 (± 0.3) | 3.12 (± 0.31) | 2.50 (± 0.17) |
| 10–20 | 1.20 (± 0.10) | 1.48 (± 0.13) | 0.92 (± 0.06) | |
| Organic matter (%) | 0–10 | 4.90 (± 0.52) | 5.38 (± 0.59) | 4.31 (± 0.41) |
| 10–20 | 2.08 (± 0.19) | 2.56 (± 0.25) | 1.59 (± 0.14) | |
| pH | 0–10 | 5.54 (± 0.67) | 5.25 (± 0.54) | 5.42 (± 0.49) |
| 10–20 | 5.28 (± 0.57) | 5.08 (± 0.36) | 5.19 (± 0.40) | |
| EC (ds m−1) | 0–10 | 0.45 (± 0.02) | 0.45 (± 0.02) | 0.38 (± 0.01) |
| 10–20 | 0.30 (± 0.01) | 0.30 (± 0.01) | 0.32 (± 0.01) | |
| Soil liquid limit 1 | 30 | 85.70 (± 6.85) | 88.52 (± 7.44) | 65 (± 6.21) |
| Soil plastic limit 1 | 30 | 37.70 (± 3.71) | 38.32 (± 4.89) | 26.42 (± 3.05) |
| Soil plasticity index 1 | 30 | 48.00 (± 4.99) | 50.20 (± 4.56) | 38.58 (± 3.80) |
| Soil texture 2 | Silt loam | Silt loam | Silt loam | |
| Unified soil classification | - | CH | CH | CH |
| Site | DBH Classes 1 | Carpinus betulus | Fagus orientalis | ||
|---|---|---|---|---|---|
| Upslope | Downslope | Upslope | Downslope | ||
| Patom | Small | 58 (56) | 57 (56) | 62 (56) | 64 (56) |
| Medium | 59 (56) | 59 (56) | 61 (56) | 62 (56) | |
| Large | 60 (56) | 61 (56) | 68 (56) | 70 (56) | |
| Namkhane | Small | 57 (56) | 57 (56) | 60 (56) | 59 (56) |
| Medium | 58 (56) | 60 (56) | 61 (56) | 62 (56) | |
| Large | 59 (56) | 59 (56) | 64 (56) | 63 (56) | |
| Chelir | Small | 58 (56) | 59 (56) | 58 (56) | 57 (56) |
| Medium | 59 (56) | 60 (56) | 61 (56) | 59 (56) | |
| Large | 62 (56) | 61 (56) | 63 (56) | 62 (56) | |
| Site | Source | df | Sum Square | Mean Square | F Value | P Value | η2 |
|---|---|---|---|---|---|---|---|
| Chelir | Species (S) | 1 | 7.63 | 7.63 | 388.68 | 0.000 * | 0.049 |
| Slope position (SP) | 1 | 0.43 | 0.43 | 22.15 | 0.000 * | 0.003 | |
| DBH 1 | 1 | 6.13 | 6.13 | 312.01 | 0.000 * | 0.039 | |
| Root diameter 1 | 1 | 140.37 | 140.37 | 7150.01 | 0.000 * | 0.906 | |
| S × SP | 1 | 0.29 | 0.29 | 14.95 | 0.000 * | 0.002 | |
| Namkhane | Species (S) | 1 | 2.67 | 2.67 | 99.10 | 0.000 * | 0.019 |
| Slope position (SP) | 1 | 0.40 | 0.40 | 14.83 | 0.000 * | 0.003 | |
| DBH 1 | 1 | 0.90 | 0.90 | 33.46 | 0.000 * | 0.007 | |
| Root diameter 1 | 1 | 131.95 | 131.95 | 4891.88 | 0.000 * | 0.971 | |
| S × SP | 1 | 0.00 | 0.00 | 0.02 | 0.90 | 0 | |
| Patom | Species (S) | 1 | 1.44 | 1.44 | 47.86 | 0.000 * | 0.009 |
| Slope position (SP) | 1 | 0.33 | 0.33 | 10.83 | 0.001 * | 0.002 | |
| DBH 1 | 1 | 2.44 | 2.44 | 81.41 | 0.000 * | 0.016 | |
| Root diameter 1 | 1 | 146.82 | 146.82 | 4891.64 | 0.000 * | 0.970 | |
| S × SP | 1 | 0.26 | 0.26 | 8.60 | 0.003 * | 0.002 |
| Site | Species | DBH 1 | F0 | α | P Value | SE |
|---|---|---|---|---|---|---|
| Chelir | Carpinus betulus | Large | 32.44 | 1.16 | 0.000 | 1.235 × 104 |
| Medium | 26.54 | 1.24 | 0.000 | 1.625 × 104 | ||
| Small | 13.75 | 1.34 | 0.000 | 2.307 × 104 | ||
| Fagus orientalis | Large | 44.92 | 1.17 | 0.000 | 7.444 × 104 | |
| Medium | 53.84 | 1.08 | 0.000 | 2.224 × 104 | ||
| Small | 28.01 | 1.29 | 0.000 | 7.143 × 104 | ||
| Namkhane | Carpinus betulus | Large | 51.87 | 1.21 | 0.000 | 3.191 × 104 |
| Medium | 76.75 | 1.12 | 0.004 | 5.326 × 104 | ||
| Small | 28.98 | 1.37 | 0.000 | 1.278 × 105 | ||
| Fagus orientalis | Large | 42.88 | 1.18 | 0.000 | 5.439 × 104 | |
| Medium | 31.51 | 1.21 | 0.000 | 3.827 × 104 | ||
| Small | 46.42 | 1.05 | 0.000 | 5.166 × 104 | ||
| Patom | Carpinus betulus | Large | 75.22 | 1.33 | 0.000 | 2.250 × 104 |
| Medium | 40.21 | 1.27 | 0.000 | 2.190 × 104 | ||
| Small | 24.25 | 1.41 | 0.000 | 5.236 × 104 | ||
| Fagus orientalis | Large | 40.66 | 1.12 | 0.000 | 2.528 × 104 | |
| Medium | 30.94 | 1.19 | 0.000 | 1.087 × 104 | ||
| Small | 51.37 | 0.96 | 0.000 | 1.903 × 104 |
| Site | Species | Slope Position | F0 | α | P Value | SE |
|---|---|---|---|---|---|---|
| Chelir | Carpinus betulus | Down | 19.66 | 1.29 | 0.000 | 1.436 × 103 |
| Up | 26.88 | 1.18 | 0.000 | 1.246 × 104 | ||
| Fagus orientalis | Down | 39.72 | 1.20 | 0.000 | 6.109 × 104 | |
| Up | 42.06 | 1.15 | 0.000 | 3.540 × 104 | ||
| Namkhane | Carpinus betulus | Down | 47.01 | 1.23 | 0.000 | 3.198 × 104 |
| Up | 54.84 | 1.17 | 0.000 | 4.205 × 104 | ||
| Fagus orientalis | Down | 38.59 | 1.13 | 0.000 | 5.875 × 104 | |
| Up | 41.07 | 1.16 | 0.000 | 4.001 × 104 | ||
| Patom | Carpinus betulus | Down | 42.08 | 1.26 | 0.000 | 2.556 × 104 |
| Up | 43.63 | 1.24 | 0.000 | 3.198 × 104 | ||
| Fagus orientalis | Down | 36.94 | 1.08 | 0.000 | 2.065 × 104 | |
| Up | 43.11 | 1.12 | 0.000 | 2.188 × 104 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deljouei, A.; Abdi, E.; Schwarz, M.; Majnounian, B.; Sohrabi, H.; Dumroese, R.K. Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion. Forests 2020, 11, 345. https://doi.org/10.3390/f11030345
Deljouei A, Abdi E, Schwarz M, Majnounian B, Sohrabi H, Dumroese RK. Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion. Forests. 2020; 11(3):345. https://doi.org/10.3390/f11030345
Chicago/Turabian StyleDeljouei, Azade, Ehsan Abdi, Massimiliano Schwarz, Baris Majnounian, Hormoz Sohrabi, and R. Kasten Dumroese. 2020. "Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion" Forests 11, no. 3: 345. https://doi.org/10.3390/f11030345
APA StyleDeljouei, A., Abdi, E., Schwarz, M., Majnounian, B., Sohrabi, H., & Dumroese, R. K. (2020). Mechanical Characteristics of the Fine Roots of Two Broadleaved Tree Species from the Temperate Caspian Hyrcanian Ecoregion. Forests, 11(3), 345. https://doi.org/10.3390/f11030345








