Tensile Properties of Natural and Synthetic Rattan Strips Used as Furniture Woven Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
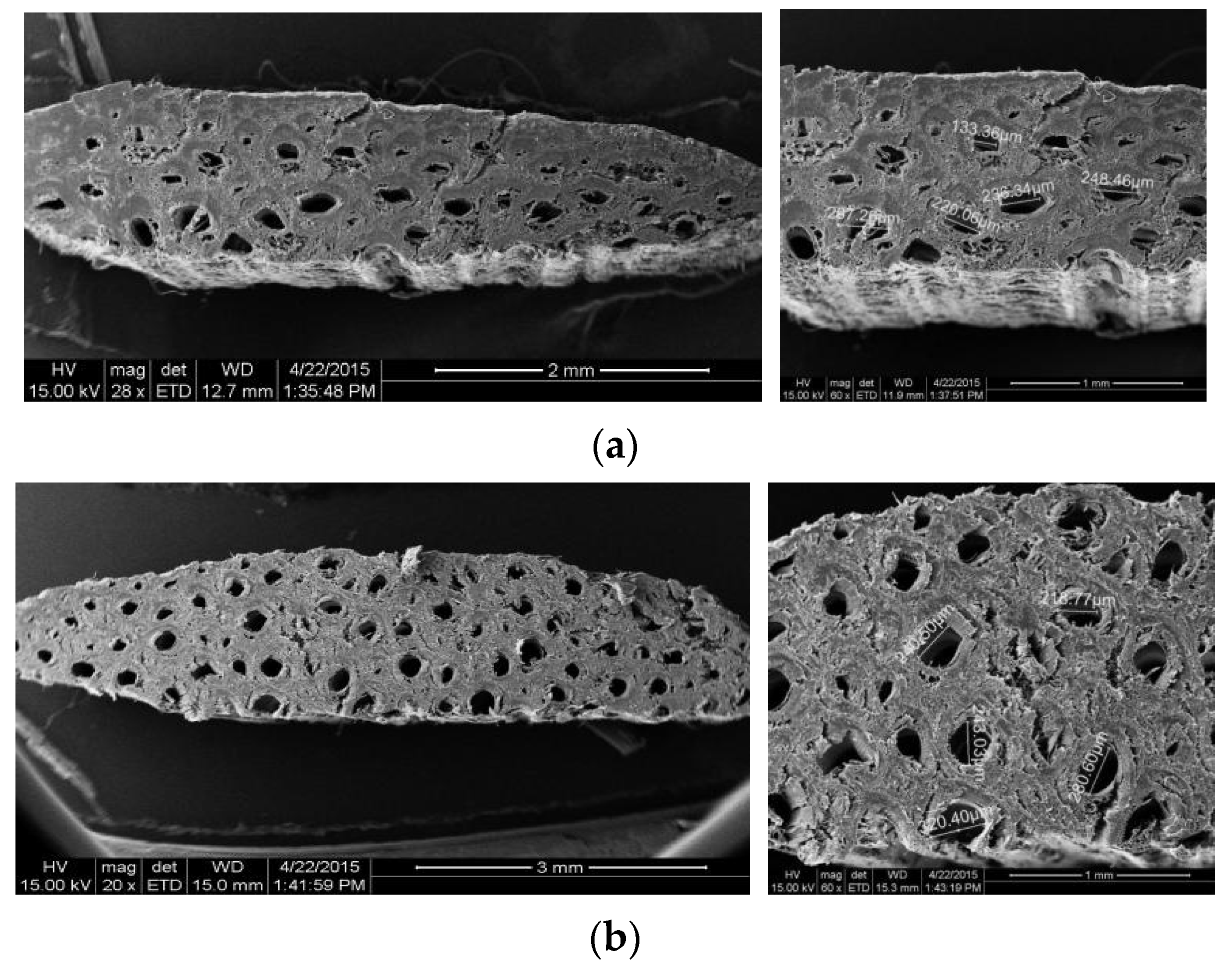
2.2. Cross-Sectional Area Calculation
2.3. Experimental Design
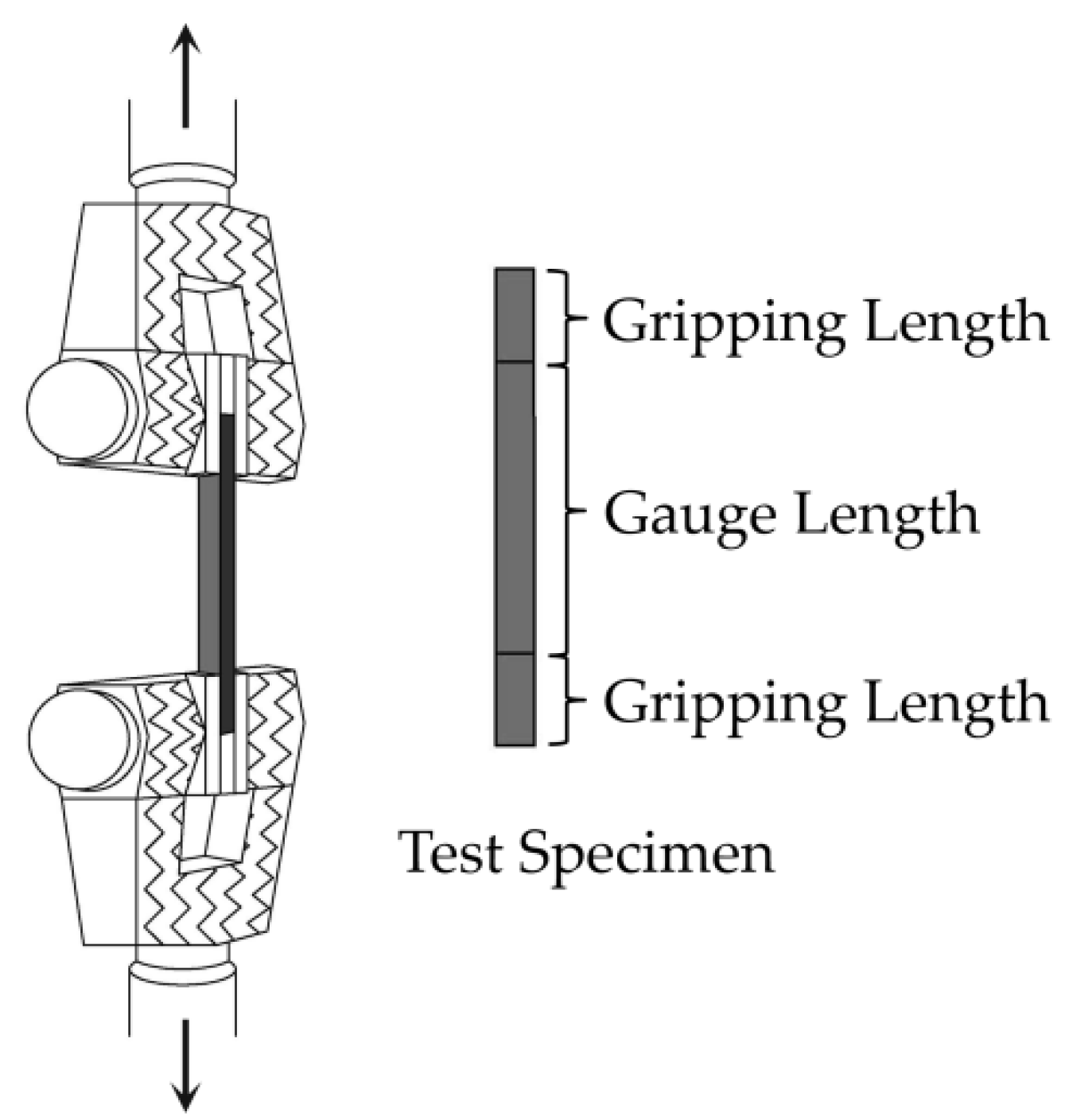
2.4. Experimental Preparation and Testing
2.5. Statistical Analyses
3. Results and Discussions
3.1. Rattan Type Effects
3.2. Factors on Bast Strip Properties
3.3. Unit Loading Speed Effect on Synthetic Rattan Strip Properties
4. Conclusions
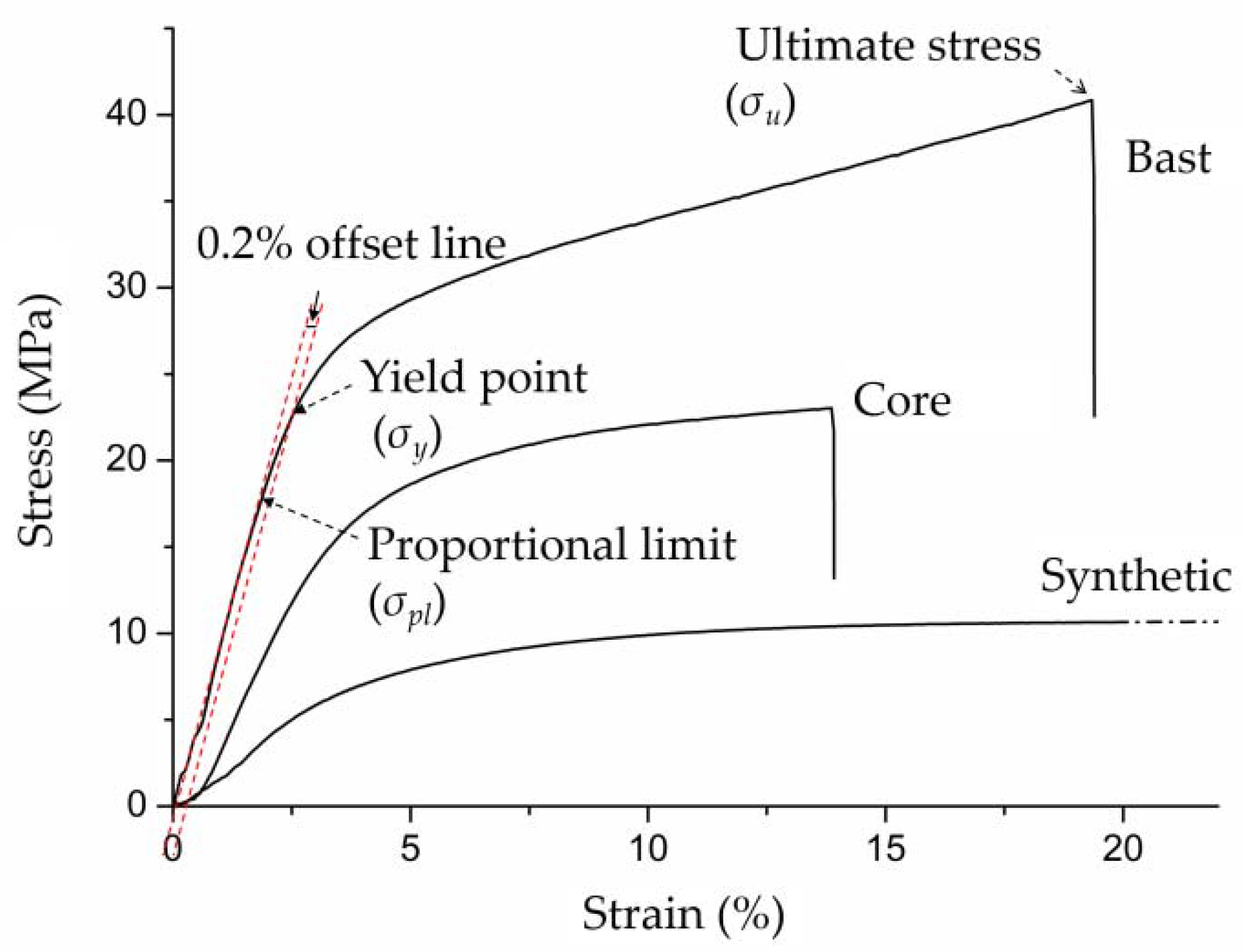
- NRSs, when subjected to tensile loading, behaved like SRSs in terms of their stress-strain curves showing excessive plastic deformation. Bast and synthetic strips had significantly larger plastic deformations than core ones. Bast rattan strips had the highest ultimate tensile strength and MOE values among the three materials evaluated in this study, followed by core strips and SRSs. Bast strips are more suitable for the weaving surface required a higher strength. Core strips with better elasticity can be good for hand knitting with easy operation. NRSs with the best elasticity can be used as a good substitute for NRSs.
- Major tensile properties of NRSs such as ultimate tensile strength, MOE, and failure strain can be significantly influenced by its gauge length adapted in its evaluation test. Unit loading speeds evaluated in this study, in general, had no significant effects on major tensile properties of NRSs tested under two gauge lengths of 100 mm and 140 mm. The exception case was when the bast strip of 140 mm gauge length was tested at 0.4 mm/min/mm. For structural strength assessments of natural rattan furniture, the variability of NRSs’ mechanical properties in the longitudinal direction should be considered.
- Unit loading speeds evaluated in this study tend to affect the ultimate strengths of SRSs used in this study significantly, but less significantly to strengths at the proportional limit and yield point. For structural assessments of synthetic rattan furniture, the loading speed should be taken into account.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gu, Y.T.; Wu, Z.H.; Zhang, Z.L. Load–deflection behavior of rattan chair seats. Wood Fiber Sci. 2016, 48, 1–12. [Google Scholar]
- Gu, Y.T.; Wu, Z.H.; Zhang, Z.L. Tensile and Bending Moment Resistances of T-Shaped Joints in Rattan Chairs. Wood Fiber Sci. 2013, 45, 429–441. [Google Scholar]
- Gu, Y.T.; Wu, Z.H.; Zhang, Z.L. Comparison on the axial tensile properties of five Calamus simplicfoilius. rattan strips used in rattan furniture. China For. Sci. Technol. 2015, 29, 105–108. [Google Scholar]
- Desmond, P.C. The Rattan Plant. Manual on the Production of Rattan Furniture; United National Industrial Development Organization: New York, NY, USA, 1983; pp. 5–6. [Google Scholar]
- Jiang, Z.H. The Rattan Plant. Bamboo and Rattan in the World; Liaoning Science and Technology Publishing House: Shenyang, China, 2002; pp. 567–571. [Google Scholar]
- Hu, W.G.; Liu, N.; Guan, H.Y. Optimal design of a furniture frame by reducing the volume of wood. Drewno 2019, 62, 85–97. [Google Scholar]
- Hu, W.G.; Liu, N. Numerical and Optimal Study on Bending Moment Capacity and Stiffness of Mortise-and-Tenon Joint for Wood Products. Forests 2020, 11, 501. [Google Scholar] [CrossRef]
- Yudodibroto, H. Anatomy Strength properties and the utilization of some Indonesian rattans. In Proceedings of the the Rattan Seminar, Kuala Lumpur, Malaysia, 2–4 October 1985; pp. 117–122. [Google Scholar]
- Bhat, K.M.; Thulasidas, P.K.; Mohamed, C.P. Strength properties of ten south Indian canes. Trop. For. Sci. J. 1992, 5, 26–34. [Google Scholar]
- Cai, Z.M. Testing of axial tensile strength of rattan canes. Sci. Silvae Sin. 1994, 30, 93–95. [Google Scholar]
- Lv, W.H.; Liu, X.E.; Wang, Y.H. The test methods of axial tensile strength of rattan canes. Wood Process. Mach. 2010, 21, 20–23. [Google Scholar]
- Luo, Z.F.; Zhang, X.F.; Lu, B.Y.; Pan, B.; Ruan, Z.Y. Mechanical Properties and Test Methods of Rattan. Furnit. Des. Room Dec. 2012, 7, 108–110. [Google Scholar]
- Liu, X.E.; Wang, R.; Tian, G.; Yang, Y.H.; Jiang, Z.H. Tensile properties of single rattan fibers. Wood Fiber Sci. 2014, 46, 1–8. [Google Scholar]
- Chen, Z.; Zhang, J.; Chen, H.H.; Su, M.Y. Analysis of Design Elements of Plastic Rattan Furniture. Furnit. Des. Room Dec. 2012, 2, 18–19. [Google Scholar]
- CNS. Method of Testing in Tensile Strength Parallel to Grain of Wood. GB/T 1938–2009; China National Standard: Beijing, China, 2009. [Google Scholar]
- CNS. Testing Methods of Physical and Mechanical Properties of Bamboos. GB/T 15780–1995; China National Standard: Beijing, China, 1995. [Google Scholar]
- ASTM. Standard Test Method for Tensile Properties of Thin Plastic Sheeting. ASTM D882–2012; American Society for Testing and Materials: West Consholocken, PA, USA, 2012. [Google Scholar]
- Liu, H.W. Stretch, compress and shear. In Mechanics of Materials I, 6th ed.; Higher Education Press: Beijing, China, 2017; pp. 13–27. [Google Scholar]
- Bian, H.Y.; Chen, L.D.; Dong, M.L.; Wang, L.Y.; Wang, R.B.; Zhou, X.L.; Wu, C.; Wang, X.; Ji, X.X.; Dai, H.Q. Natural lignocellulosic nanofibril film with excellent ultraviolet blocking performance and robust environment resistance. Int. J. Biol. Macromol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.P.; Huang, D.S.; Chen, S.S.; Zhang, P.D. Distribution of vascular bundles of bamboo and its tensile mechanical performances. Build. Mater. J. 2012, 15, 105–108. [Google Scholar]





| Species | Origin | Material Type | Tensile Strength (MPa) | Reference |
|---|---|---|---|---|
| C. inops | Sulawesi, Indonesia | bast | 121.5 | Yudodibroto 1985 [8] |
| C. inops | Sulawesi, Indonesia | core | 85.6 | Yudodibroto 1985 [8] |
| C. symphysipus | Sulawesi, Indonesia | bast | 81.5 | Yudodibroto 1985 [8] |
| C. symphysipus | Sulawesi, Indonesia | core | 74.1 | Yudodibroto 1985 [8] |
| C. sp. | Sulawesi, Indonesia | bast | 83.1 | Yudodibroto 1985 [8] |
| C. sp. | Sulawesi, Indonesia | core | 75.7 | Yudodibroto 1985 [8] |
| C. simplicifolius Wei | Hainan, China | bast | 79.5 | Cai 1994 [10] |
| C. simplicifolius Wei | Hainan, China | core | 49.9 | Cai 1994 [10] |
| C. simplicifolius Wei | Guangdong, China | bast | 75.7 | Cai 1994 [10] |
| C. simplicifolius Wei | Guangdong, China | core | 43.5 | Cai 1994 [10] |
| C. simplicifolius Wei | Guangdong, China | bast | 41.97 | Lv et al. 2010 [11] |
| Rattan Type | Failure Mode | No. of Strips | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Splintering | Brash | Combination | MOE | σpl | σy | σu | |||||||||
| Location | |||||||||||||||
| At Grips | Within Gauge Length | At Grips | Within Gauge Length | At Grips | Within Gauge Length | ||||||||||
| Near Grips | Middle | Near Grips | Middle | Off-Center | Near Grips | Middle | Entire | ||||||||
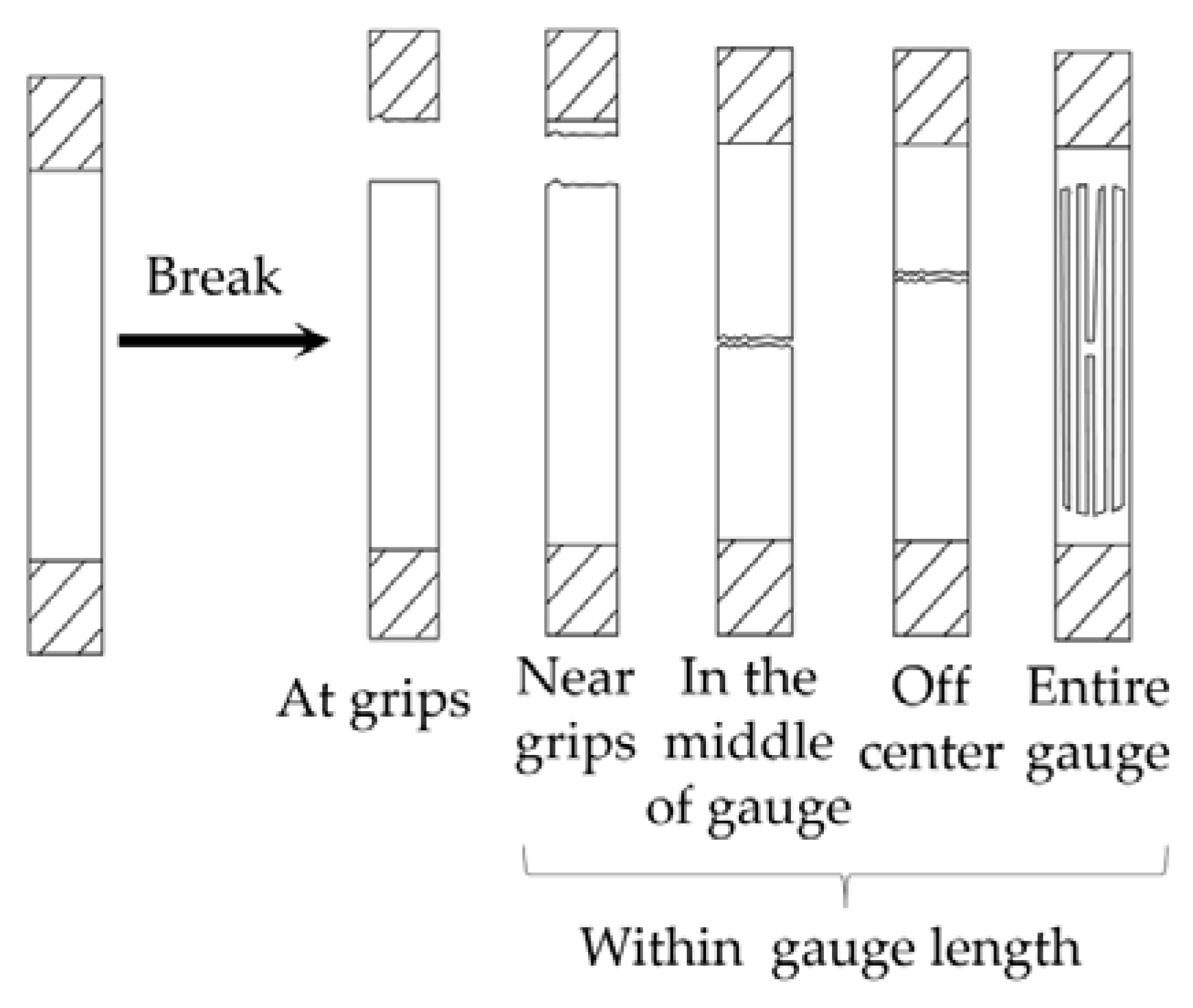
| Bast | 0 | 0 | 9 | 1 | 3 | 9 | 0 | 0 | 0 | 1 | 7 | 30 | 30 | 30 | 29 |
| Core | 0 | 0 | 2 | 2 | 2 | 11 | 7 | 0 | 2 | 3 | 1 | 30 | 30 | 30 | 28 |
| Rattan Type | Tensile Strength at | MOE | Strength Ratio | ||||
|---|---|---|---|---|---|---|---|
| Proportional Limit (σpl) | Yield Point (σy) | Ultimate Point (σu) | σy/σpl | σu/σy | σu/σpl | ||
| (MPa) | |||||||
| Bast | 17.57(16)(A) | 21.26(13)(A) | 35.00(18)(A) | 1004(13)A | 1.2 | 2.0 | 1.6 |
| Core | 16.22(19)(A) | 20.17(19)(A) | 30.13(17)(B) | 806(09)B | 1.2 | 1.9 | 1.5 |
| Synthetic | 4.84(17)(B) | 5.87(15)(B) | 10.29(05)(C) | 267(11)C | 1.2 | 1.8 | 2.1 |
| Rattan Type | Strain at | Strain Ratio | ||||
|---|---|---|---|---|---|---|
| Proportional Limit (εpl) | Yield Point (εy) | Ultimate Point (εu) | ||||
| (%) | εy/εpl | εu/εy | εu/εpl | |||
| Bast | 2.17(13)(A) | 3.00(17)(A) | 18.53(22)(A) | 1.5 | 6.2 | 8.5 |
| Core | 2.27(14)(A) | 2.92(10)(A) | 10.22(32)(B) | 1.3 | 3.5 | 4.5 |
| Synthetic | 2.71(20)(A) | 3.42(18)(A) | 20.03(0)(A) | 1.3 | 5.9 | 7.4 |
| Source | Ultimate Tensile Strength | MOE | Failure Strain | |||
|---|---|---|---|---|---|---|
| F Value | p Value | F Value | p Value | F Value | p Value | |
| Unit speed | 1.54 | 0.215 | 1.48 | 0.2295 | 5.76 | 0.0017 |
| Gauge length | 64.81 | <0.0001 | 50.09 | <0.0001 | 53.94 | <0.0001 |
| Unit speed × gauge length | 0.84 | 0.4776 | 3.18 | 0.0302 | 10.27 | <0.0001 |
| Gauge Length (mm) | Unit Loading Speed (mm/min/mm) | |||
|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | |
| Ultimate tensile strength (MPa) | ||||
| 100 | 44.19(13)(10)(A)(a) | 42.61(14)(9)(A)(a) | 41.89(14)(9)(A)(a) | 40.14(11)(10)(A)(a) |
| 140 | 32.63(12)(6)(B)(a) | 34.39(11)(7)(B)(a) | 29.43(9)(7)(B)(a) | 32.18(14)(6)(B)(a) |
| Strength ratio | 1.35 | 1.24 | 1.42 | 1.25 |
| Modulus (MPa) | ||||
| 100 | 1386(8)(10)(A)(a) | 1328(19)(9)(A)(a) | 1269(7)(10)(A)(a) | 1296(11)(10)(A)(a) |
| 140 | 1025(9)(8)(B)(b) | 1075(10)(9)(B)(b) | 1021(7)(8)(B)(b) | 1238(13)(6)(A)(a) |
| Modulus ratio | 1.35 | 1.24 | 1.24 | 1.05 |
| Failure strain (%) | ||||
| 100 | 9.7(33)(10)(A)(a) | 10.0(31)(9)(A)(a) | 15.0(27)(9)(A)(a) | 7.1(17)(10)(A)(a) |
| 140 | 6.3(33)(6)(B)(b) | 5.7(34)(7)(B)(b) | 4.1(28)(7)(B)(b) | 6.0(24)(6)(A)(a) |
| Strain ratio | 1.54 | 1.75 | 3.66 | 1.18 |
| Unit Loading Speed (mm/min/mm) | Tensile Strength at | MOE | Strength Ratio | ||||
|---|---|---|---|---|---|---|---|
| Proportional Limit (σpl) | Yield Point (σy) | Ultimate Point (σu) | σy/σpl | σu/σy | σu/σpl | ||
| (MPa) | |||||||
| 0.1 | 4.74(13)(B) | 5.76(14)(B) | 7.72(11)(C) | 199(11)(C) | 1.2 | 1.3 | 1.6 |
| 0.2 | 5.12(14)(AB) | 6.04(10)(AB) | 7.98(3)(C) | 227(5)(B) | 1.2 | 1.3 | 1.6 |
| 0.3 | 5.64(18)(AB) | 6.64(16)(AB) | 8.75(8)(B) | 258(5)(A) | 1.2 | 1.3 | 1.6 |
| 0.4 | 5.46(9)(AB) | 6.56(4)(AB) | 10.65(0)(A) | 263(8)(A) | 1.2 | 1.6 | 2.0 |
| 0.5 | 5.92(10)(A) | 6.95(9)(A) | 9.11(4)(B) | 262(4)(A) | 1.2 | 1.3 | 1.5 |
| LSD | 0.88 | 0.96 | 0.65 | 22 | |||
| Unit Loading Speed (mm/min/mm) | Strain at | Strain Ratio | ||||
|---|---|---|---|---|---|---|
| Proportional Limit (εpl) | Yield Point (εy) | Ultimate Point (εu) | εy/εpl | εu/εy | εu/εpl | |
| (%) | ||||||
| 0.1 | 2.81(12)(A) | 3.65(9)(A) | 20.00(0)(C) | 1.3 | 5.5 | 7 |
| 0.2 | 3.10(19)(A) | 3.65(9)(A) | 20.00(0)(C) | 1.2 | 5.5 | 6 |
| 0.3 | 3.26(12)(A) | 3.88(11)(A) | 20.01(0)(C) | 1.2 | 5.2 | 6 |
| 0.4 | 3.09(13)(A) | 3.87(10)(A) | 20.03(0)(B) | 1.3 | 5.2 | 6.5 |
| 0.5 | 2.71(12)(A) | 3.37(11)(A) | 20.05(0)(A) | 1.2 | 5.9 | 7.4 |
| LSD | 0.58 | 0.58 | 0.01 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Zhang, J. Tensile Properties of Natural and Synthetic Rattan Strips Used as Furniture Woven Materials. Forests 2020, 11, 1299. https://doi.org/10.3390/f11121299
Gu Y, Zhang J. Tensile Properties of Natural and Synthetic Rattan Strips Used as Furniture Woven Materials. Forests. 2020; 11(12):1299. https://doi.org/10.3390/f11121299
Chicago/Turabian StyleGu, Yanting, and Jilei Zhang. 2020. "Tensile Properties of Natural and Synthetic Rattan Strips Used as Furniture Woven Materials" Forests 11, no. 12: 1299. https://doi.org/10.3390/f11121299
APA StyleGu, Y., & Zhang, J. (2020). Tensile Properties of Natural and Synthetic Rattan Strips Used as Furniture Woven Materials. Forests, 11(12), 1299. https://doi.org/10.3390/f11121299




