Adaptive Model Building Framework for Production Planning in the Primary Wood Industry
Abstract
1. Introduction
2. Literature Review
2.1. Linear or Mixed-Integer Programming
2.2. Heuristic Approaches
2.3. Simulation
2.4. Uncertainties
2.5. Extended Models
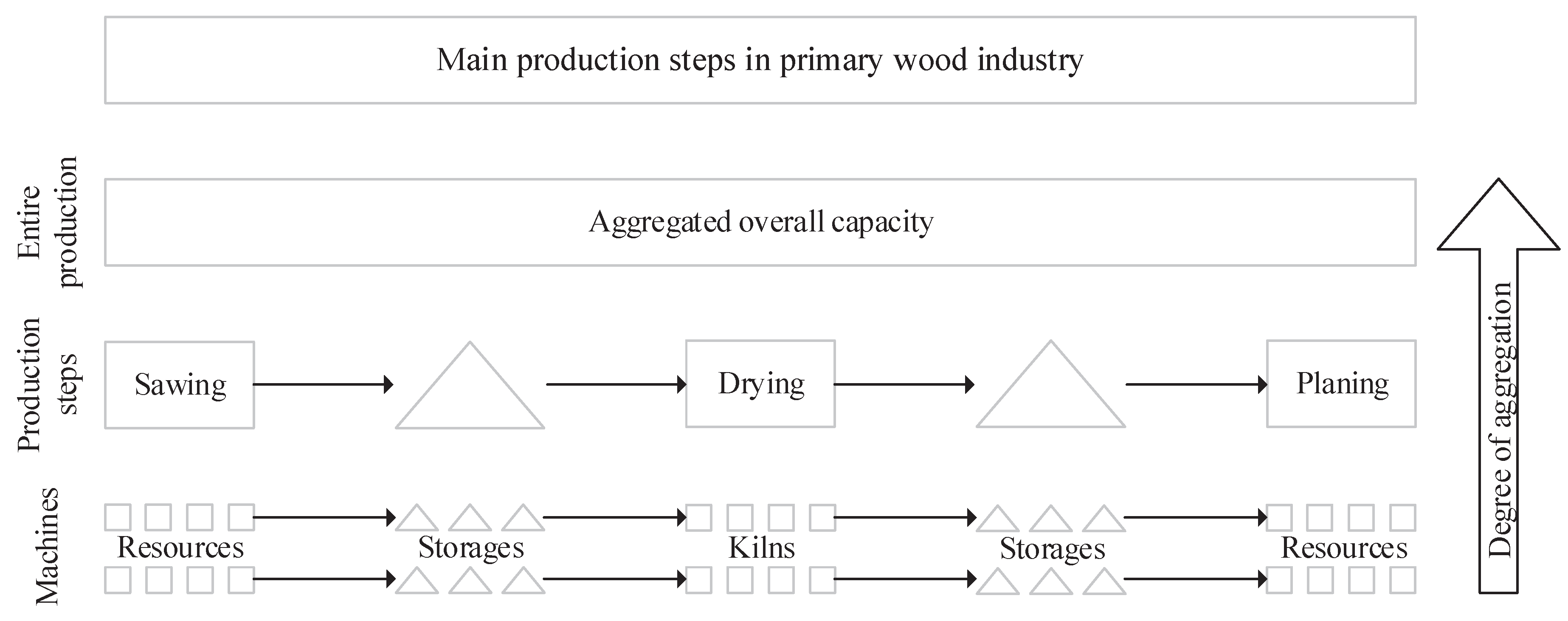
3. Material and Methods
3.1. Application Field
3.1.1. Case 1: Procurement and Sales Support
3.1.2. Case 2: Production Preview
3.1.3. Case 3: Operations Requirements
3.1.4. Case 4: Order Release, Loading and Scheduling
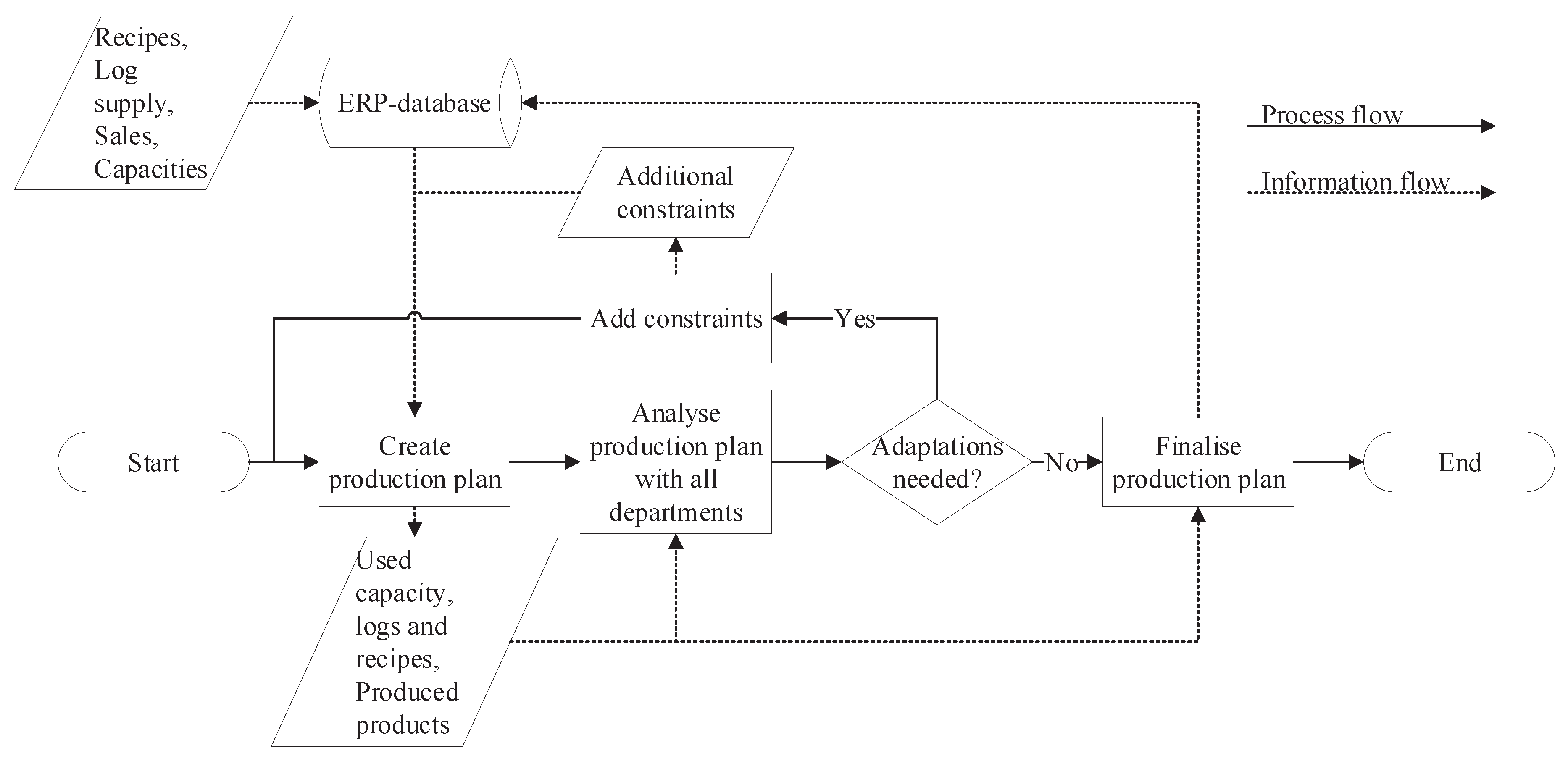
3.2. Planning Process
3.3. Modelling Approach
| Set of products | |
| Set of log types | |
| Set of periods | |
| Set of locations | |
| Set of production recipes | |
| Set of cutting recipes | |
| Set of drying recipes | |
| Set of planing recipes | |
| Set of sawing lines | |
| Set of kilns | |
| Set of planing lines | |
| Set of customers | |
| Raw material types (logs, green timber, dried timber, planed timber) | |
| Set of green products | |
| Set of dried products | |
| Set of planed products |
| Y | Yield of production with recipe in percentage |
| B | Assignment of raw material to recipe |
| N | Demand of product |
| R | Revenue of product |
| A | Available raw material |
| C | Costs |
| G | Duration of recipe per unit |
| M | Capacity for recipes |
| U | (Total) storage capacity |
| z | Volume of raw material processed with recipe |
| i | Stored volume |
| x | Sold volume |
| w | Backorder volume of product |
| f | Bought volume of product |
4. Industrial Application
5. Conclusions and Discussion
6. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huka, M.A.; Gronalt, M. Model development and comparison of different heuristics for production planning in large volume softwood sawmills. Eng. Optim. 2017, 49, 1829–1847. [Google Scholar] [CrossRef]
- Maness, T.C.; Norton, S.E. Multiple Period Combined Optimization Approach to Forest Production Planning. Scand. J. For. Res. 2002, 17, 460–471. [Google Scholar] [CrossRef]
- Pradenas, L.; Alvarez, C.; Ferland, J.A. A Solution for the Aggregate Production Planning Problem in a Multi-Plant, Multi-Period and Multi-Product Environment. Acta Math. Vietnam. 2009, 34, 11–17. [Google Scholar]
- Marier, P.; Bolduc, S.; Ben Ali, M.; Gaudreault, J. S&OP Network model for commodity lumber products. In Proceedings of the MOSIM 2014, 10ème Conférence Francophone de Modélisation, Optimisation et Simulation, Colloque Avec Actes et Comité de Lecture, Internationale, Nancy, France, 5–7 November 2014. [Google Scholar]
- Vergara, F.P.; Palma, C.D.; Sepúlveda, H. A Comparison of Optimization Models for Lumber Production Planning. Bosque 2015, 36, 239–246. [Google Scholar] [CrossRef]
- Alayet, C.; Lehoux, N.; Lebel, L. Logistics approaches assessment to better coordinate a forest products supply chain. J. For. Econ. 2018, 30, 13–24. [Google Scholar] [CrossRef]
- Broz, D.; Vanzetti, N.; Corsano, G.; Montagna, J.M. Goal programming application for the decision support in the daily production planning of sawmills. For. Policy Econ. 2019, 102, 29–40. [Google Scholar] [CrossRef]
- Kühle, S.; Teischinger, A.; Gronalt, M. Form-based postponement in the solid hardwood supply network. Cogent Bus. Manag. 2019, 6. [Google Scholar] [CrossRef]
- Ouhimmou, M.; D’Amours, S.; Beauregard, R.; Aït-Kadi, D.; Chauhan, S.S. Furniture supply chain tactical planning optimisation using a time decomposition approach. Eur. J. Oper. Res. 2008, 189, 952–970. [Google Scholar] [CrossRef]
- Maturana, S.; Pizani, E.; Vera, J.R. Scheduling Production for a Sawmill: A Comparison of a Mathematical Model Versus a Heuristic. Comput. Ind. Eng. 2010, 59, 667–674. [Google Scholar] [CrossRef]
- Gaudreault, J.; Frayret, J.M.; Rousseau, A.; D’Amours, S. Combined Planning and Scheduling in a Divergent Production System with Co-Production: A Case Study in the Lumber Industry. Comput. Oper. Res. 2011, 38, 1238–1250. [Google Scholar] [CrossRef]
- Bajgiran, O.S.; Zanjani, M.K.; Nourelfath, M. The Value of Integrated Tactical Planning Optimization in the Lumber Supply Chain. Int. J. Prod. Econ. 2016, 171, 22–33. [Google Scholar] [CrossRef]
- Vanzetti, N.; Broz, D.; Corsano, G.; Montagna, J.M. An optimisation approach for multiperiod production planning in a sawmill. For. Policy Econ. 2018, 97, 1–8. [Google Scholar] [CrossRef]
- Vanzetti, N.; Broz, D.; Corsano, G.; Montagna, J.M. A detailed mathematical programming model for the optimal daily planning of sawmills. Can. J. For. Res. 2019, 49, 1400–1411. [Google Scholar] [CrossRef]
- Mendoza, G.A.; Meimban, R.J.; Araman, P.A.; Luppold, W.G. Combined Log Inventory and Process Simulation Models for the Planning and Control of Sawmill Operations. In Proceedings of the 23rd CIRP International Seminar on Manufacturing Systems, Nancy, France, 6–7 June 1991; p. 8. [Google Scholar]
- Greigeritsch, T. Neue Methoden zur Planung und Optimierung der Schnittholzproduktion von Nadelholzsägewerken; [New Methods to Plan and Optimize the Zimber Production at Softwood Sawmills]; Gabler Research: Wiesbaden, Germany, 2009. [Google Scholar]
- Jerbi, W.; Gaudreault, J.; D’Amours, S.; Nourelfath, M.; Lemieux, S.; Marier, P.; Bouchard, M. Optimization/simulation-based framework for the evaluation of supply chain management policies in the forest product industry. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Korea, 14–17 October 2012; pp. 1742–1748. [Google Scholar] [CrossRef]
- Ben Ali, M.; Gaudreault, J.; D’Amours, S.; Carle, M.A. A Multi-Level Framework for Demand Fulfillment in a Make-to-Stock Environment-A Case Study in Canadian Softwood Lumber Industry. MOSIM 2014, 10ème Conférence Francophone de Modélisation, Optimisation et Simulation. 2014. Available online: https://hal.archives-ouvertes.fr/hal-01166600 (accessed on 25 November 2020).
- Vila, D.; Beauregard, R.; Martel, A. The Strategic Design of Forest Industry Supply Chains. INFOR Inf. Syst. Oper. Res. 2009, 47, 185–202. [Google Scholar] [CrossRef]
- Zanjani, M.K.; Aït-Kadi, D.; Nourelfath, M. Robust Production Planning in a Manufacturing Environment with Random Yield: A Case in Sawmill Production Planning. Eur. J. Oper. Res. 2010, 201, 882–891. [Google Scholar] [CrossRef]
- Zanjani, M.K.; Nourelfath, M.; Aït-Kadi, D. A multi-stage stochastic programming approach for production planning with uncertainty in the quality of raw materials and demand. Int. J. Prod. Res. 2010, 48, 4701–4723. [Google Scholar] [CrossRef]
- Zanjani, M.K.; Aït-Kadi, D.; Nourelfath, M. An accelerated scenario updating heuristic for stochastic production planning with set-up constraints in sawmills. Int. J. Prod. Res. 2013, 51, 993–1005. [Google Scholar] [CrossRef]
- Zanjani, M.K.; Aït-Kadi, D.; Nourelfath, M. A Stochastic Programming Approach for Sawmill Production Planning. Int. J. Math. Oper. Res. 2013, 5, 1–18. [Google Scholar] [CrossRef]
- Zanjani, M.K.; Nourelfath, M.; Aït-Kadi, D. A scenario decomposition approach for stochastic production planning in sawmills. J. Oper. Res. Soc. 2013, 64, 48–59. [Google Scholar] [CrossRef]
- Alvarez, P.P.; Vera, J.R. Application of robust optimisation to the sawmill planning problem. Ann. Oper. Res. 2014, 219, 457. [Google Scholar] [CrossRef]
- Varas, M.; Maturana, S.; Pascual, R.; Vargas, I.; Vera, J.R. Scheduling Production for a Sawmill: A Robust Optimization Approach. Int. J. Prod. Econ. 2014, 150, 37–51. [Google Scholar] [CrossRef]
- Lobos, A.; Vera, J.R. Intertemporal stochastic sawmill planning: Modeling and managerial insights. Comput. Ind. Eng. 2016, 95, 53–63. [Google Scholar] [CrossRef]
- D’Amours, S.; Rönnqvist, M.; Weintraub, A. Using operational research for supply chain planning in the forest products industry. INFOR Inf. Syst. Oper. Res. 2008, 46, 265–281. [Google Scholar] [CrossRef]
- Carlsson, D.; D’Amours, S.; Martel, A.; Rönnqvist, M. Supply chain planning models in the pulp and paper industry. INFOR Inf. Syst. Oper. Res. 2009, 47, 167–183. [Google Scholar] [CrossRef]
- Fleischmann, B.; Meyr, H.; Wagner, M. Advanced Planning. In Supply Chain Management and Advanced Planning, 2nd ed.; Stadtler, H., Kilger, C., Eds.; Springer: Berlin, Germany, 2002; Chapter 4; pp. 71–96. [Google Scholar] [CrossRef]
- Abasian, F.; Rönnqvist, M.; Marier, P.; Fjeld, D. The Transportation Game. INFORMS Trans. Educ. 2020. [Google Scholar] [CrossRef]
- Farrell, R.R.; Maness, T.C. A relational database approach to a linear programming-based decision support system for production planning in secondary wood product manufacturing. Decis. Support Syst. 2005, 40, 183–196. [Google Scholar] [CrossRef]
- Alem, D.J.; Morabito, R. Production planning in furniture settings via robust optimisation. Comput. Oper. Res. 2012, 39, 139–150. [Google Scholar] [CrossRef]
- Elghoneimy, E.; Gruver, W.A. Agent-Based Decision Support and Simulation for Wood Products Manufacturing. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 1656–1668. [Google Scholar] [CrossRef]

| Paper | Objective | Method | Application | Planning Horizon |
|---|---|---|---|---|
| Alayet et al. [6] | Minimise costs | Mixed-integer programming model with rolling planning horizon | Forest products supply chain, different inventory management policies | month [week] for a year |
| Alvarez and Vera [25] | Maximise economic benefit | Robust optimisation | Production planning sawmill (sawing, drying, outsourcing and reprocessing) | year [month] |
| Bajgiran et al. [12] | Maximise global net profit | Mixed-integer program, heuristic | Plan lumber supply chain (harvesting, procurement, production, distribution and sales activities) | year [month] |
| Ben Ali et al. [18] | Maximise net profit | Order promising model based on nested booking limits, simulation | Sales and operations planning, customer service level | 8 weeks [week] for a year |
| Broz et al. [7] | Weighted objective function of maximising profit, production, minimising raw material loss, inventory, unsatisfied demand | Mixed-integer linear program | Determine daily production plan satisfying several objectives | day [day] |
| Gaudreault et al. [11] | Minimise backorder | Mixed-integer program, constraint program, search procedure | Planning and scheduling drying and finishing | 60 days [day] |
| Greigeritsch [16] | Maximise contribution margin | Linear model, simulation | Sequence planning for sawmill production, material flow simulation, dry kiln occupancy | 14 weeks [1–2 weeks] |
| Huka and Gronalt [1] | Maximise contribution margin | Mixed-integer program, heuristics | Plan sawing, investigate loss of not following optimal plan, analyse inventory effects, different planning frequencies | 12 weeks [2 weeks] |
| Jerbi et al. [17] | Maximise profit | Aggregated optimisation, discrete-event simulation | Selection of supply chain management policies for lumber supply chain network, tactical and operational planning | year [week], week [day] |
| Kühle et al. [8] | Minimise costs | Linear programming model | Develop future production concept using form postponement | year [month] |
| Lobos and Vera [27] | Minimise costs | Two-stage stochastic programming | Determine log purchase and labour hiring under uncertainties in log supply | 50 months [month], 1 month [week] |
| Maness and Norton [2] | Maximise profit | Linear program | Production and sales planning for sawmills | quarter [month] |
| Marier et al. [4] | Maximise gross margin | Linear program | Production and sales planning for sawmills | year [week] |
| Maturana et al. [10] | Minimise costs | Mixed-integer program, heuristic | Production planning at sawmill with increasing uncertainty (rolling planning horizon, sub-periods in first period) | 6 weeks [week] |
| Mendoza et al. [15] | Maximise economic return | Combined linear inventory and simulation model | Determine optimal lumber production schedule | 10 h [hour] |
| Ouhimmou et al. [9] | Minimise costs | Mixed-integer program, heuristic | Furniture supply chain | year [week] |
| Pradenas et al. [3] | Maximise revenue | Linear model, simplex primal and dual, barrier method | Aggregated production planning for multiple sawmills and periods, determine levels of production, subcontracting and inventory | 2–8 periods |
| Vanzetti et al. [13] | Maximise net benefit | Mixed-integer linear program, heuristic to determine cutting patterns | Multi-period production planning with integrated cutting pattern generation | 5 days [day] |
| Vanzetti et al. [14] | Maximise profit | Mixed-integer linear program, heuristic to determine cutting patterns | Daily production planning with integrated primary cutting pattern generation | day [day] |
| Varas et al. [26] | Minimise cost (inventory, backorder) | Robust optimisation | Scheduling production for a sawmill with uncertainties in product demand and availability of raw materials | 6 weeks [week] |
| Vergara et al. [5] | Minimise cost, waste, number of logs, production time, maximise profit | Linear model | Production planning sawmill, compare objective functions | 3 days [hour] |
| Vila et al. [19] | Maximise expected corporate profits | Two-stage stochastic programming, sampling average approximation method | Design of forest industry supply chains, deploying production-distribution network | years [season] |
| Zanjani et al. [20] | Minimise costs (inventory, backorder, raw material) | Robust optimisation, stochastic programming | Sawmill production planning with random yields for robust customer service levels | month [day] |
| Zanjani et al. [21] | Minimise costs (inventory, backorder, raw material) | Multi-stage stochastic program, scenario tree | Production planning with uncertainty in the quality of raw materials and demand for a sawmill | month [day] |
| Zanjani et al. [22] | Minimise costs (inventory, backorder, raw material) | Stochastic mixed-integer model, accelerated scenario updating heuristic | Scheduling production for sawmills with randomness in yield and demand, | month [day] |
| Zanjani et al. [23] | Minimise costs (inventory and backorder) | Two-stage stochastic linear program | Randomness in yields modelled as scenarios with probability distributions | month [day] |
| Zanjani et al. [24] | Minimise costs (inventory, backorder, raw material) | Stochastic mixed-integer model, decomposition and cutting plane algorithms | Stochastic production planning in sawmills with randomness in yield and demand and set-up constraints | month [day] |
| Case | Insights | Adaptable Constraints | Actions/Decisions |
|---|---|---|---|
| 1 | Best supply | Min/Max quantity per log type | Purchase guidelines |
| Sales quantities | Min/Max quantity per product | Sales guidelines | |
| Unused logs | Capacity | Capacity planning | |
| By-products | |||
| Used capacity | |||
| 2 | Approximate production plan | Min/Max quantity per product | Sales guidelines |
| Aggregated dry kiln scheduling | New cutting patterns | Delivery promises | |
| Production quantities | |||
| Unused logs | |||
| Unsold by-products | |||
| Used capacity | |||
| 3 | Production plan | Min/Max quantity per product | Dry kiln scheduling |
| Used capacity | Stock quantities | External logistics | |
| Minimal production quantities | |||
| 4 | Production sequence scheduling | Capacities | Bottleneck analyses |
| Detailed dry kiln scheduling | Staff allocation |
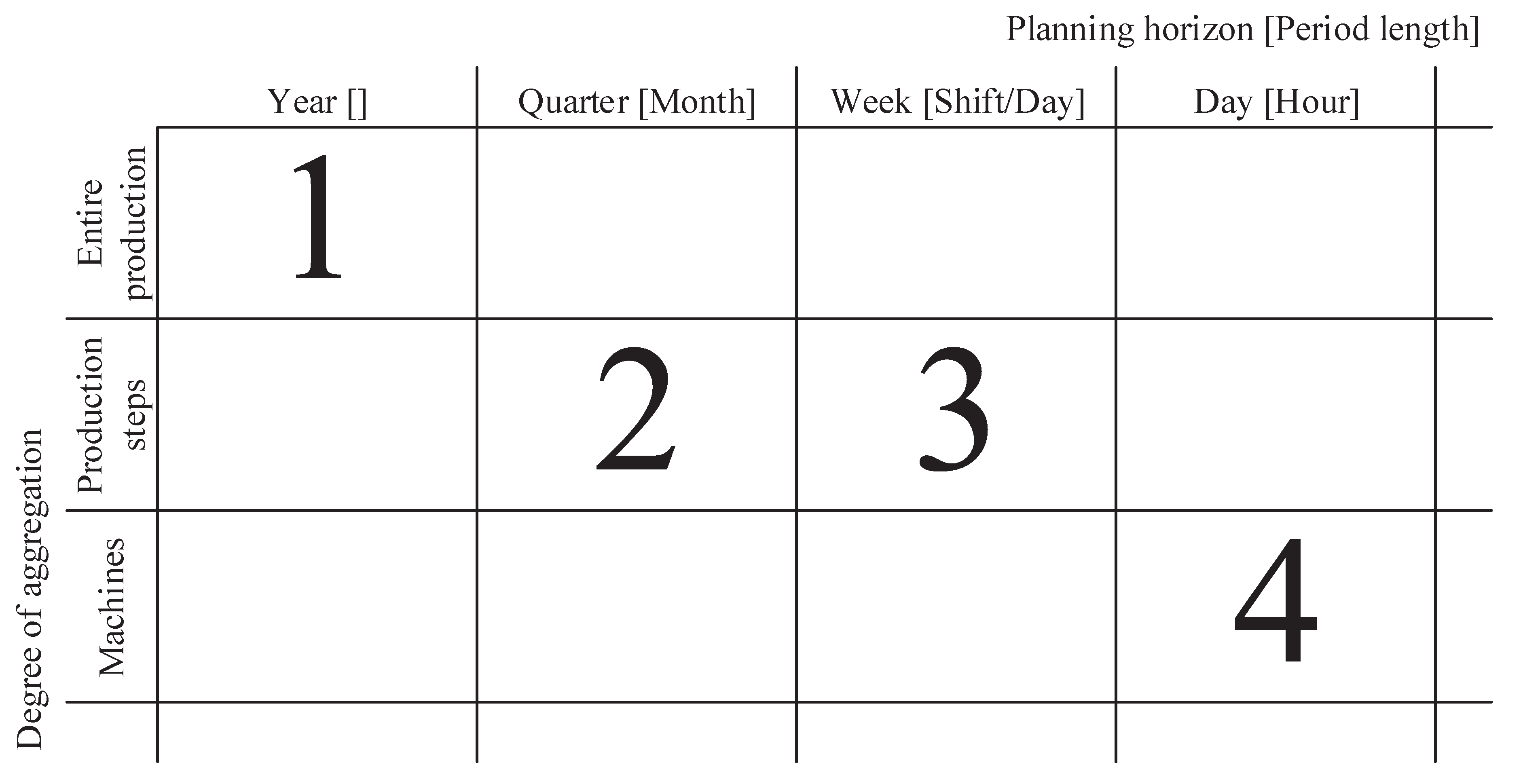
| Year | Quarter [Month] | Week [Shift/Day] | Day [Hour] | |
|---|---|---|---|---|
| Entire production | Vanzetti et al. [13] | Mendoza et al. [15] | ||
| Production steps | Alvarez and Vera [25] | Alayet et al. [6] | Maturana et al. [10] | Broz et al. [7] |
| Vila et al. [19] | Greigeritsch [16] | Varas et al. [26] | Vanzetti et al. [14] | |
| Huka and Gronalt [1] | Zanjani et al. [20,21,22,23,24] | Vergara et al. [5] | ||
| Maness and Norton [2] | ||||
| Pradenas et al. [3] | ||||
| Machines | Bajgiran et al. [12] | Ben Ali et al. [18] | Gaudreault et al. [11] | |
| Jerbi et al. [17] | Lobos and Vera [27] | Jerbi et al. [17] | ||
| Marier et al. [4] | ||||
| Ouhimmou et al. [9] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaltenbrunner, M.; Huka, M.A.; Gronalt, M. Adaptive Model Building Framework for Production Planning in the Primary Wood Industry. Forests 2020, 11, 1256. https://doi.org/10.3390/f11121256
Kaltenbrunner M, Huka MA, Gronalt M. Adaptive Model Building Framework for Production Planning in the Primary Wood Industry. Forests. 2020; 11(12):1256. https://doi.org/10.3390/f11121256
Chicago/Turabian StyleKaltenbrunner, Matthias, Maria Anna Huka, and Manfred Gronalt. 2020. "Adaptive Model Building Framework for Production Planning in the Primary Wood Industry" Forests 11, no. 12: 1256. https://doi.org/10.3390/f11121256
APA StyleKaltenbrunner, M., Huka, M. A., & Gronalt, M. (2020). Adaptive Model Building Framework for Production Planning in the Primary Wood Industry. Forests, 11(12), 1256. https://doi.org/10.3390/f11121256





