Wind and Snow Loading of Balsam Fir during a Canadian Winter: A Pioneer Study
Abstract
1. Introduction
- (1)
- The additional weight of the snow on the crown will increase the lever arm on the trunk, and trees will experience an increased turning moment at a particular wind speed with an increase of snow thickness in their crowns compared to when there is no snow in the crown.
- (2)
- The large negative temperatures will stiffen the trunk because of freezing, therefore trees will experience a globally lower turning moment at a particular wind speed in winter compared to during the summer because the crowns move less.
2. Materials and Methods
2.1. Stand and Climate
2.2. Sample Trees
2.3. Instrumentation
2.3.1. Anemometers and Wind Speed
2.3.2. Strain Gauges and Turning Moment
2.3.3. Hunting Camera and Snow
2.4. Statistical Analysis
2.4.1. Effect of Snow Thickness in the Crowns of Balsam Fir on the Overall Turning Moment
2.4.2. Seasonal Differences in Wind Loads in Balsam Fir Stands
Wind Profile
Model Selection
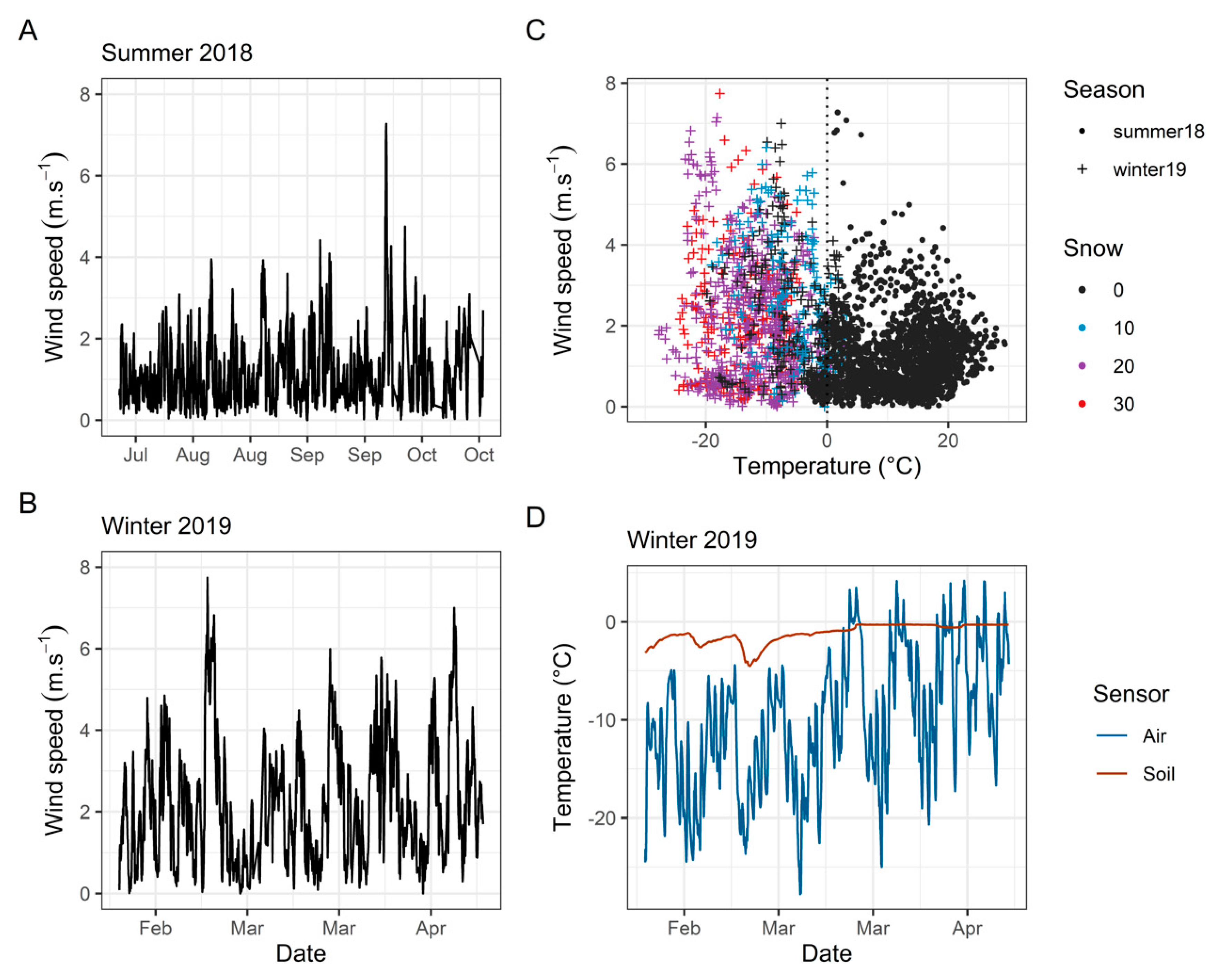
3. Results
3.1. Hypothesis 1: Effect of Snow Thickness in the Crowns of Balsam Fir on the Overall Turning Moment
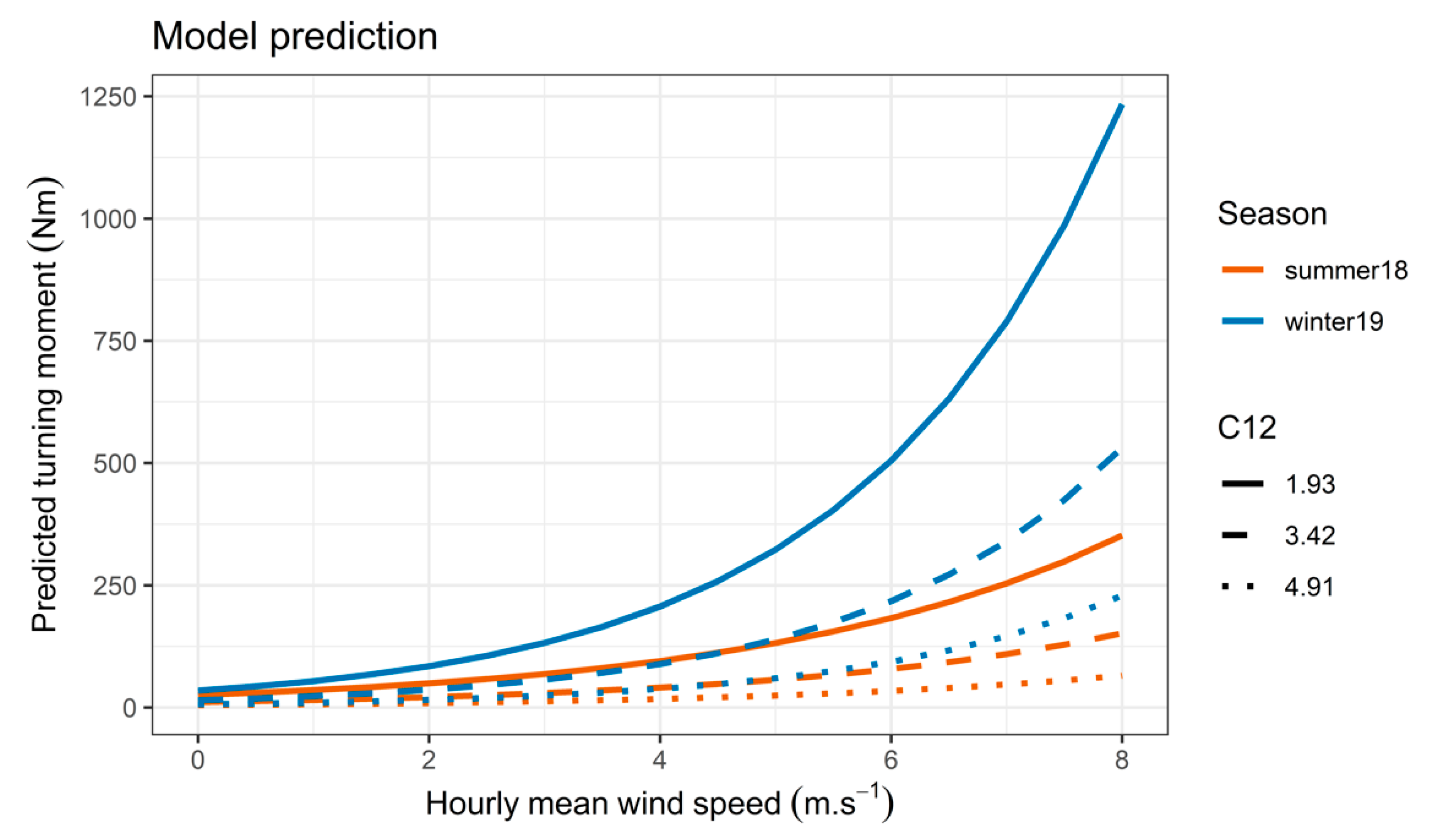
3.2. Hypothesis 2: Seasonal Differences in Wind Loads in Balsam Fir Stands
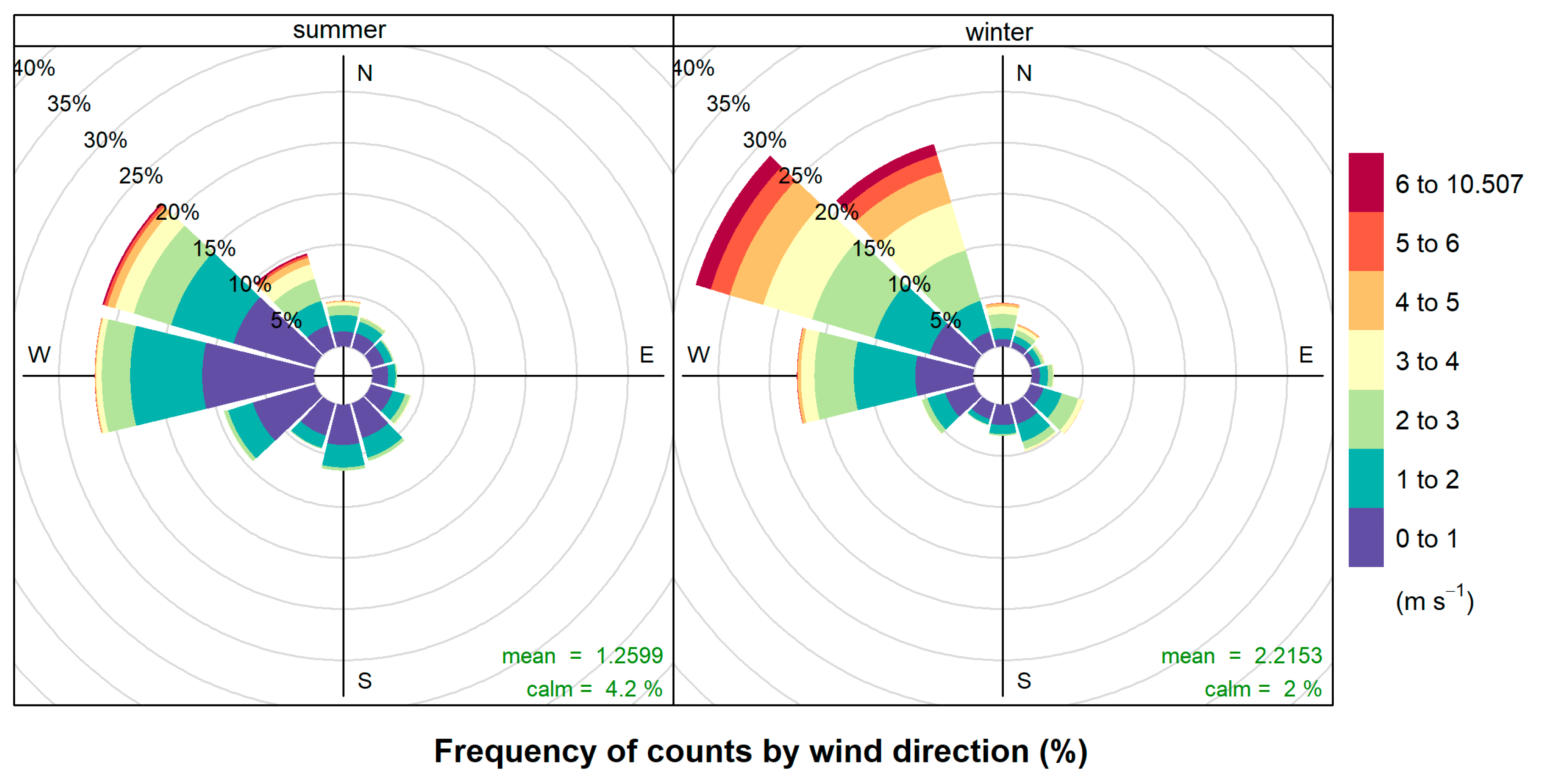
3.2.1. Wind Profile
3.2.2. Season Model Selection.
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Competition Indices
| Index Type | Index Formula | References/Definition |
|---|---|---|
| Distance-independent | [25] | |
| [27] | ||
| [27] | ||
| Distance-dependent (DBH) | [28] | |
| [26] | ||
| [26] | ||
| CIB |
References
- Meunier, S. Comparaison de la Résistance au Renversement du Sapin Baumier et de l’épinette Blanche sur site Mésique en Sapinière Boréale. Ph.D. Thesis, Université Laval, Québec, QC, Canada, 2002. [Google Scholar]
- Ruel, J.-C. Understanding windthrow: Silvicultural implications. For. Chron. 1995, 71, 434–445. [Google Scholar] [CrossRef]
- Achim, A.; Ruel, J.-C.; Gardiner, B.A.; Laflamme, G.; Meunier, S. Modelling the vulnerability of balsam fir forests to wind damage. For. Ecol. Manag. 2005, 204, 37–52. [Google Scholar] [CrossRef]
- Duperat, M.; Ruel, J.-C.; Gardiner, B. Testing an individual tree wind damage risk model in a naturally regenerated balsam fir stand: Potential impact of thinning on the level of risk. For. Int. J. For. Res. 2020, 10. [Google Scholar] [CrossRef]
- Gardiner, B.; Suárez, J.; Achim, A.; Hale, S.; Nicoll, B.F. A PC-based wind risk model for British Forests (User’s Guide). For. Comm. Edinb. 2004, 1, 23–36. [Google Scholar]
- Hale, S.; Nicoll, B.; Gardiner, B. Forest GALES—A Wind Risk Decision Sleupport Tool for Forest Management in Britain; User Manual; Version 2; Forestry Commission: Edinburgh, UK, 2015; p. 58. [Google Scholar]
- Anyomi, K.A.; Mitchell, S.J.; Ruel, J.-C. Windthrow modelling in old-growth and multi-layered boreal forests. Ecol. Model. 2016, 327, 105–114. [Google Scholar] [CrossRef]
- Ruel, J.-C.; Meunier, S.; Quine, C.P.; Suarez, J. Estimating windthrow risk in balsam fir stands with the Forest Gales model. For. Chron. 2000, 76, 329–337. [Google Scholar] [CrossRef]
- Lundqvist, L. Stem diameter growth of scots pine trees after increased mechanical load in the crown during dormancy and (or) growth. Ann. Bot. 1996, 77, 59–62. [Google Scholar] [CrossRef]
- Peltola, H.; Kellomäki, S.; Hassinen, A.; Granander, M. Mechanical stability of Scots pine, Norway spruce and birch: An analysis of tree-pulling experiments in Finland. For. Ecol. Manag. 2000, 135, 143–153. [Google Scholar] [CrossRef]
- Silins, U.; Lieffers, V.J.; Bach, L. The effect of temperature on mechanical properties of standing lodgepole pine trees. Trees 2000, 14, 424–428. [Google Scholar] [CrossRef]
- Nykänen, M.-L.; Peltola, H.; Quine, C.; Kellomäki, S.; Broadgate, M. Factors affecting snow damage of trees with particular reference to European conditions. Finn. Soc. For. Sci. Finn. For. Res. Inst. 1997, 2, 32–48. [Google Scholar] [CrossRef]
- Díaz-Yáñez, O.; Mola-Yudego, B.; González-Olabarria, J.R.; Pukkala, T. How does forest composition and structure affect the stability against wind and snow? For. Ecol. Manag. 2017, 401, 215–222. [Google Scholar] [CrossRef]
- Peltola, H.; Kellomäki, S.; Väisänen, H. A mechanistic model for assessing the risk of wind and snow damage to single trees and stands of Scots pine, Norway spruce, and birch. J. For. Res. 1999, 29, 15. [Google Scholar] [CrossRef]
- Valinger, E.; Fridman, J. Modelling probability of snow and wind damage in Scots pine stands using tree characteristics. For. Ecol. Manag. 1997, 97, 215–222. [Google Scholar] [CrossRef]
- Valinger, E.; Lundqvist, L.; Bondesson, L. Assessing the Risk of Snow and Wind Damage from Tree Physical Characteristics. Forestry 1993, 66, 249–260. [Google Scholar] [CrossRef]
- Valinger, E. Wind and snow damage in a thinning and fertilization experiment in Picea abies in southern Sweden. Forestry 1996, 69, 25–34. [Google Scholar] [CrossRef]
- Wallentin, C.; Nilsson, U. Storm and snow damage in a Norway spruce thinning experiment in southern Sweden. Forestry 2014, 87, 229–238. [Google Scholar] [CrossRef]
- R Core Team. R A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Wickham, H. Tidyverse: Easily Install and Load the “Tidyverse”. R Package Version 1.2.1. 2017. Available online: https://CRAN.R-project.org/package=tidyverse (accessed on 5 February 2019).
- Normales Climatiques Canadiennes. Available online: http://climat.meteo.gc.ca/climate_normals/ (accessed on 9 April 2019).
- Robitaille, A.; Saucier, J.P. Paysages Régionaux du Québec Méridional; Publication du Québec; Direction de la Gestion des Stocks Forestiers et Direction des relations Publiques, Ministère des Ressources Naturelles du Québec: Québec, QC, Canada, 1998. [Google Scholar]
- Hale, S.E.; Gardiner, B.A.; Wellpott, A.; Nicoll, B.C.; Achim, A. Wind loading of trees: Influence of tree size and competition. Eur. J. For. Res. 2012, 131, 203–217. [Google Scholar] [CrossRef]
- Seidl, R.; Rammer, W.; Blennow, K. Simulating wind disturbance impacts on forest landscapes: Tree-level heterogeneity matters. Environ. Model. Softw. 2014, 51, 1–11. [Google Scholar] [CrossRef]
- Biging, G.S.; Dobbertin, M. Evaluation of Competition Indices in Individual Tree Growth Models. For. Sci. 1995, 41, 360–377. [Google Scholar]
- Rouvinen, S.; Kuuluvainen, T. Structure and asymmetry of tree crowns in relation to local competition in a natural mature Scots pine forest. Can. J. For. Res. 1997, 2, 890–902. [Google Scholar] [CrossRef]
- Kiernan, D.H.; Bevilacqua, E.; Nyland, R.D. Individual-tree diameter growth model for sugar maple trees in uneven-aged northern hardwood stands under selection system. For. Ecol. Manag. 2008, 256, 1579–1586. [Google Scholar] [CrossRef]
- Hegyi, F. A simulation model for managing jack-pine stands. Growth Models Tree Stand Simul. 1974, 30, 74–90. [Google Scholar]
- Blackburn, G.R.A. The Growth and Mechanical Response of Trees to Wind Loading. Ph.D. Thesis, University of Manchester, Manchester, UK, 1997. [Google Scholar]
- Gardiner, B.A.; Stacey, G.R.; Belcher, R.E.; Wood, C.J. Field and wind tunnel assessments of the implications of respacing and thinning for tree stability. Forestry 1997, 70, 233–252. [Google Scholar] [CrossRef]
- Wellpott, A. The stability of Continuous Cover Forests. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2008. [Google Scholar]
- Butterworth, S. On the Theory of Filter Amplifiers. Exp. Wirel. 1930, 5, 536–541. [Google Scholar]
- Signal Developers. Signal: Signal Processing. 2014. Available online: https://CRAN.R-project.org/package=signal (accessed on 10 February 2019).
- Cook, N. The Designer’s Guide to Wind Loading of Building Structures; Butterworths: London, UK, 1985. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. Nlme: Linear and Nonlinear Mixed Effects Models. 2018. R package version 3.1-149. Available online: https://CRAN.R-project.org/package=nlme (accessed on 7 February 2019).
- Mazerolle, M. AICcmodavg: Model Selection and Multimodel Inference Based on (Q)AIC(c). 2019. R package version 2.3-1. Available online: https://cran.r-project.org/package=AICcmodavg (accessed on 10 November 2019).
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike information criterion statistics. Dordr. Neth. D. Reidel 1986, 81, 90–98. [Google Scholar]
- Carslaw, D.C.; Ropkins, K. openair—An R package for air quality data analysis. Environ. Model. Softw. 2012, 27, 52–61. [Google Scholar] [CrossRef]
- Keller, H.M. Snow Cover in Forest Stands; Proc. Davos IUFRO-Sem. Mountain Forests and Avalanches, 17–29, 1978.
- Saad, C.; Boulanger, Y.; Beaudet, M.; Gachon, P.; Ruel, J.-C.; Gauthier, S. Potential impact of climate change on the risk of windthrow in eastern Canada’s forests. Clim. Chang. 2017, 143, 487–501. [Google Scholar] [CrossRef]

| Tree | Morphological Criteria | Distance Independent | Distance Dependent | Competitors | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | DBH | H | DBH2H | CrownW | CrownD | BA | CIB | CBAL | Cdr | Cdrl | C11 | C12 | CHegyi | NCOM | NNCOM | NALL |
| a1 | 0.117 | 9.1 | 0.125 | 1.6 | 5.9 | 0.011 | 804.46 | 8.65 | 11.04 | 2.39 | 1.79 | 3.56 | 3.83 | 6 | 13 | 19 |
| a2 | 0.106 | 6.7 | 0.075 | 0.8 | 1.9 | 0.009 | 1337.38 | 11.80 | 8.32 | 5.46 | 1.01 | 3.62 | 2.83 | 7 | 6 | 13 |
| a3 | 0.110 | 9.2 | 0.111 | 1.5 | 5.7 | 0.01 | 1141.81 | 10.85 | 10.71 | 8.89 | 1.45 | 4.14 | 3.86 | 9 | 7 | 16 |
| a4 | 0.108 | 8.2 | 0.096 | 1.3 | 5.2 | 0.009 | 1249.22 | 11.44 | 7.34 | 2.76 | 1.32 | 3.20 | 3.00 | 7 | 4 | 11 |
| a5 | 0.175 | 12.5 | 0.383 | 1.8 | 9.0 | 0.024 | 43.61 | 1.05 | 7.30 | 0.00 | 1.03 | 1.76 | 2.55 | 5 | 1 | 6 |
| a6 | 0.131 | 9.3 | 0.160 | 1.6 | 5.1 | 0.013 | 417.79 | 5.63 | 4.92 | 3.15 | 0.98 | 2.04 | 2.07 | 4 | 6 | 10 |
| a7 | 0.110 | 9.0 | 0.109 | 1.1 | 5.4 | 0.01 | 1133.81 | 10.78 | 13.92 | 10.25 | 2.25 | 5.75 | 5.06 | 7 | 5 | 12 |
| a8 | 0.099 | 7.8 | 0.076 | 1.1 | 4.3 | 0.008 | 1832.37 | 14.11 | 16.51 | 12.57 | 2.04 | 6.39 | 5.39 | 6 | 6 | 12 |
| a9 | 0.115 | 8.7 | 0.115 | 1.5 | 5.3 | 0.01 | 873.12 | 9.07 | 8.38 | 1.11 | 0.79 | 2.34 | 2.52 | 7 | 6 | 13 |
| a11 | 0.171 | 8.9 | 0.260 | 1.7 | 5.8 | 0.023 | 53.99 | 1.24 | 4.73 | 0.00 | 0.62 | 1.13 | 1.65 | 8 | 3 | 11 |
| a12 | 0.103 | 7.4 | 0.079 | 1.4 | 4.4 | 0.008 | 1595.24 | 13.29 | 11.65 | 6.87 | 1.50 | 4.13 | 3.93 | 7 | 5 | 12 |
| a15 | 0.109 | 8.8 | 0.105 | 1.1 | 5.0 | 0.009 | 1202.72 | 11.22 | 8.09 | 4.59 | 1.08 | 3.00 | 2.89 | 9 | 7 | 16 |
| Step 1: Tree Variable Selection | ||||||
| log(Mmax) ~ ws + Snow + | K | AICc | ΔAICc | AICcWt | LL | Cum.Wt |
| CBAL | 8 | 10,116.09 | 0.00 | 0.18 | −5050.04 | 0.18 |
| DBH | 8 | 10,116.38 | 0.29 | 0.16 | −5050.18 | 0.34 |
| CIB | 8 | 10,116.74 | 0.64 | 0.13 | −5050.36 | 0.48 |
| CrownW | 8 | 10,116.85 | 0.76 | 0.12 | −5050.42 | 0.61 |
| BA | 8 | 10,116.89 | 0.80 | 0.12 | −5050.44 | 0.73 |
| DBH2 H | 8 | 10,117.77 | 1.68 | 0.08 | −5050.88 | 0.81 |
| C12 | 8 | 10,118.13 | 2.04 | 0.06 | −5051.06 | 0.88 |
| CrownS | 8 | 10,118.53 | 2.44 | 0.05 | −5051.26 | 0.93 |
| Cdr | 8 | 10,120.99 | 4.89 | 0.01 | −5052.48 | 0.95 |
| CHegyi | 8 | 10,121.14 | 5.05 | 0.01 | −5052.56 | 0.96 |
| H | 8 | 10,121.74 | 5.64 | 0.01 | −5052.86 | 0.98 |
| CrownD | 8 | 10,123.11 | 7.02 | 0.00 | −5053.55 | 0.98 |
| C11 | 8 | 10,123.23 | 7.13 | 0.00 | −5053.60 | 0.99 |
| - | 7 | 10,123.79 | 7.69 | 0.00 | −5054.89 | 0.99 |
| NCOM | 8 | 10,124.89 | 8.80 | 0.00 | −5054.44 | 0.99 |
| NALL | 8 | 10,125.62 | 9.53 | 0.00 | −5054.80 | 0.99 |
| NNCOM | 8 | 10,125.79 | 9.70 | 0.00 | −5054.89 | 1.00 |
| Step 3: Model selection | ||||||
| log(Mmax) ~ ws + | K | AICc | ΔAICc | AICcWt | LL | Cum.Wt |
| Snow + CBAL + ws:Snow + ws: CBAL + Snow: CBAL | 11 | 10,081.87 | 0.00 | 0.68 | −5029.93 | 0.68 |
| Snow + CBAL + ws:Snow + Snow: CBAL | 10 | 10,084.12 | 2.25 | 0.22 | −5032.05 | 0.90 |
| Snow + CBAL + ws:Snow + ws: CBAL | 10 | 10,086.19 | 4.32 | 0.08 | −5033.09 | 0.97 |
| Snow + CBAL + ws:Snow | 9 | 10,088.40 | 6.53 | 0.03 | −5035.19 | 1.00 |
| Snow + ws:Snow | 8 | 10,096.10 | 14.22 | 0.00 | −5040.04 | 1.00 |
| Snow + CBAL + ws: CBAL + snow: CBAL | 10 | 10,109.58 | 27.70 | 0.00 | −5044.78 | 1.00 |
| Snow + CBAL + Snow: CBAL | 9 | 10,111.83 | 29.95 | 0.00 | −5046.91 | 1.00 |
| Snow + CBAL + ws: CBAL | 9 | 10,113.88 | 32.01 | 0.00 | −5047.94 | 1.00 |
| Snow + CBAL | 8 | 10,116.09 | 34.22 | 0.00 | −5050.04 | 1.00 |
| Snow | 7 | 10,123.79 | 41.92 | 0.00 | −5054.89 | 1.00 |
| CBAL + ws: CBAL | 8 | 10,186.68 | 104.80 | 0.00 | −5085.33 | 1.00 |
| CBAL | 7 | 10,188.89 | 107.01 | 0.00 | −5087.44 | 1.00 |
| - | 6 | 10,196.58 | 114.71 | 0.00 | −5092.29 | 1.00 |
| Step 1: Tree Variable Selection | ||||||
| log(Mmax) ~ ws + Season + | K | AICc | ΔAICc | AICcWt | LL | Cum.Wt |
| C12 | 8 | 61,327.43 | 0.00 | 0.39 | −30,655.71 | 0.39 |
| CrownW | 8 | 61,329.18 | 1.75 | 0.16 | −30,656.59 | 0.55 |
| CBAL | 8 | 61,330.60 | 3.17 | 0.08 | −30,657.30 | 0.63 |
| DBH | 8 | 61,330.63 | 3.20 | 0.08 | −30,657.31 | 0.70 |
| Cdrl | 8 | 61,330.70 | 3.27 | 0.08 | −30,657.35 | 0.78 |
| CIB | 8 | 61,330.90 | 3.47 | 0.07 | −30,657.45 | 0.85 |
| BA | 8 | 61,331.12 | 3.69 | 0.06 | −30,657.56 | 0.91 |
| DBH2H | 8 | 61,332.65 | 5.22 | 0.03 | −30,568.32 | 0.94 |
| Chegyi | 8 | 61,333.06 | 5.63 | 0.02 | −30,658.53 | 0.96 |
| Cdr | 8 | 61,333.22 | 5.79 | 0.02 | −30,658.61 | 0.98 |
| C11 | 8 | 61,335.41 | 7.98 | 0.01 | −30,659.70 | 0.99 |
| CrownD | 8 | 61,336.04 | 8.61 | 0.01 | −30,660.02 | 0.99 |
| H | 8 | 61,336.78 | 9.35 | 0.00 | −30,660.39 | 1.00 |
| - | 7 | 61,340.32 | 12.89 | 0.00 | −30,663.16 | 1.00 |
| NNCOM | 8 | 61,341.79 | 14.36 | 0.00 | −30,662.89 | 1.00 |
| NALL | 8 | 61,341.82 | 14.39 | 0.00 | −30,662.91 | 1.00 |
| NCOM | 8 | 61,342.30 | 14.87 | 0.00 | −30,663.15 | 1.00 |
| Step 3: Model selection | ||||||
| log(Mmax) ~ ws + | K | AICc | ΔAICc | AICcWt | LL | Cum.Wt |
| Season +C12+ ws:Season | 9 | 61,163.61 | 0.00 | 0.54 | −30,572.80 | 0.54 |
| Season +C12 + ws:C12 + ws:Season | 10 | 61,163.96 | 0.35 | 0.45 | −30,571.98 | 1.00 |
| Season + C12 | 8 | 61,327.43 | 163.81 | 0.0 | −30,655.71 | 1.00 |
| Season +C12 + ws:C12 | 9 | 61,327.78 | 164.16 | 0.0 | −30,654.89 | 1.00 |
| Season | 7 | 61,340.32 | 176.70 | 0.0 | −30,663.16 | 1.00 |
| C12 | 7 | 65,576.69 | 4413.07 | 0.0 | −32,781.34 | 1.00 |
| - | 6 | 65,589.57 | 4425.95 | 0.0 | −32,788.79 | 1.00 |
| Log | CI Lower | Estimate | CI Upper | Std.Error | DF | t-Value |
|---|---|---|---|---|---|---|
| Intercept | 4.1587 | 4.3502 | 4.5417 | 0.0976 | 16,479 | 44.529 |
| ws | 0.5012 | 0.5179 | 0.5347 | 0.0085 | 16,479 | 60.624 |
| Snow | −0.0075 | −0.0026 | 0.0022 | 0.0025 | 16,479 | −1.043 |
| CBAL | −0.2027 | −0.1814 | −0.1600 | 0.0097 | 11 | −18.688 |
| Ws:Snow | −0.0008 | −0.0003 | 0.0001 | 0.0002 | 16,479 | −1.368 |
| Ws:CBAL | −0.0081 | −0.0066 | −0.0052 | 0.0007 | 16,479 | −9.139 |
| Snow:CBAL | −0.0003 | −0.0001 | 0.0005 | 0.0002 | 16,479 | 0.344 |
| Log | CI Lower | Estimate | CI Upper | Std.Error | DF | t-Value |
|---|---|---|---|---|---|---|
| Intercept | 3.2348 | 4.3401 | 5.4455 | 0.5639 | 35,997 | 7.694 |
| ws | 0.2789 | 0.3268 | 0.3747 | 0.0244 | 35,997 | 13.373 |
| Season | −0.2792 | 0.2947 | 0.8686 | 0.2928 | 35,997 | 1.006 |
| C12 | −0.8031 | −0.5656 | −0.3281 | 0.1065 | 10 | −5.306 |
| ws:Season | 0.0903 | 0.1199 | 0.1495 | 0.0151 | 35,997 | 7.929 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duperat, M.; Gardiner, B.; Ruel, J.-C. Wind and Snow Loading of Balsam Fir during a Canadian Winter: A Pioneer Study. Forests 2020, 11, 1089. https://doi.org/10.3390/f11101089
Duperat M, Gardiner B, Ruel J-C. Wind and Snow Loading of Balsam Fir during a Canadian Winter: A Pioneer Study. Forests. 2020; 11(10):1089. https://doi.org/10.3390/f11101089
Chicago/Turabian StyleDuperat, Marine, Barry Gardiner, and Jean-Claude Ruel. 2020. "Wind and Snow Loading of Balsam Fir during a Canadian Winter: A Pioneer Study" Forests 11, no. 10: 1089. https://doi.org/10.3390/f11101089
APA StyleDuperat, M., Gardiner, B., & Ruel, J.-C. (2020). Wind and Snow Loading of Balsam Fir during a Canadian Winter: A Pioneer Study. Forests, 11(10), 1089. https://doi.org/10.3390/f11101089





