1. Introduction
The use of airborne laser scanning (ALS) is increasing in forest inventories [
1]. ALS can be conducted from manned aircrafts or unmanned aerial vehicles. The use of these data in traditional forest management requires a segmentation step where the data are organized into spatially continuous areas that correspond to tree stands.
Tree stands are usually understood as homogeneous subareas of the forest. Tree height, stand density, tree species composition, site fertility, etc. should be more or less the same within a stand. This makes it possible to have “permanent” stands, as treatments and future development are similar for the whole stand.
The traditional way of delineating tree stands is visual (and manual) where stand borders are drawn on aerial photographs, using perhaps soil maps, canopy height models, etc. as additional information. Visual delineation is gradually being replaced by automated computer algorithms, which may use the same data sources as used in traditional delineation [
2]. Many methods were developed for numerical stand delineation [
3,
4,
5,
6,
7,
8]. These methods are often called segmentation methods, since the created areas do not necessarily correspond to traditional stand compartments. They might be too small for the implementation of forest management actions, which means that the segments must be further aggregated to obtain large enough continuous treatment blocks [
9,
10].
Many of the segmentation techniques developed for forestry are case- or task-specific [
5,
6,
7,
8]. As an alternative to task-specific methods, existing multi-purpose algorithms such as cellular automata and metaheuristics could also be used. The theoretical foundations of these methods might be stronger than that of case-specific methods, and there is much research from several fields on the multi-purpose algorithms.
Cellular automata (CA) are examples of multipurpose algorithms [
11,
12]. In forestry, CA were used to solve spatial forest planning problems [
13,
14,
15], in land-use planning [
16,
17], and to simulate the spread of forest pests [
18,
19] and diseases [
20]. Recently, they were also successfully used for stand delineation [
8,
10]. CA are self-organizing systems where the “state” of a cell depends on its neighborhood. The effect of other cells on a cell’s state decreases rapidly with distance [
16]. When CA are used for stand delineation, “cell state” corresponds to stand identification (ID) number. The purpose is to find such a stand number for each cell that cells belonging to the same stand form large enough continuous areas and their shape is “attractive”. The cells that constitute a stand should be similar in terms of stand and site variables.
Commercial companies often do the laser scanning, and they may also preprocess the data. For example, the company may use the scanning data to develop a canopy height model (CHM), i.e., the difference between canopy surface and the ground. The CHM often indicates the canopy height on a grid of small cells, for instance, in 1-m resolution.
The canopy height model may be the only ALS product that the forest manager uses. The CHM is a valuable aid in visual stand demarcation or in the assessment of tree height. However, the CHM contains little numerical information directly applicable to forest management planning. For example, canopy height is not equal to tree height since a single tree crown often covers many cells of the CHM. In a mature stand of 400 trees per ha, a tree occupies on average 25 cells. In such a forest, the maximum value of the CHM in a 5 × 5 window might be used as an estimate of the tree height. Even that value can underestimate tree height since the laser pulses do not hit all treetops.
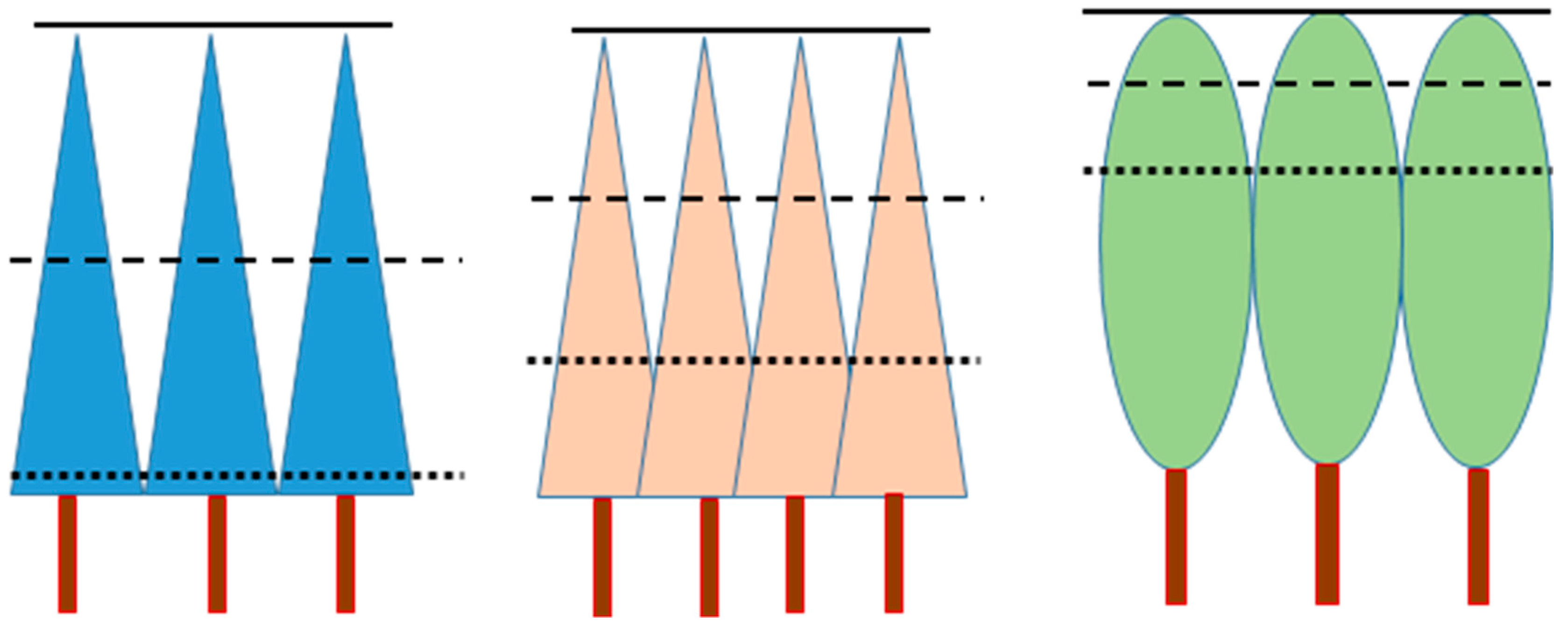
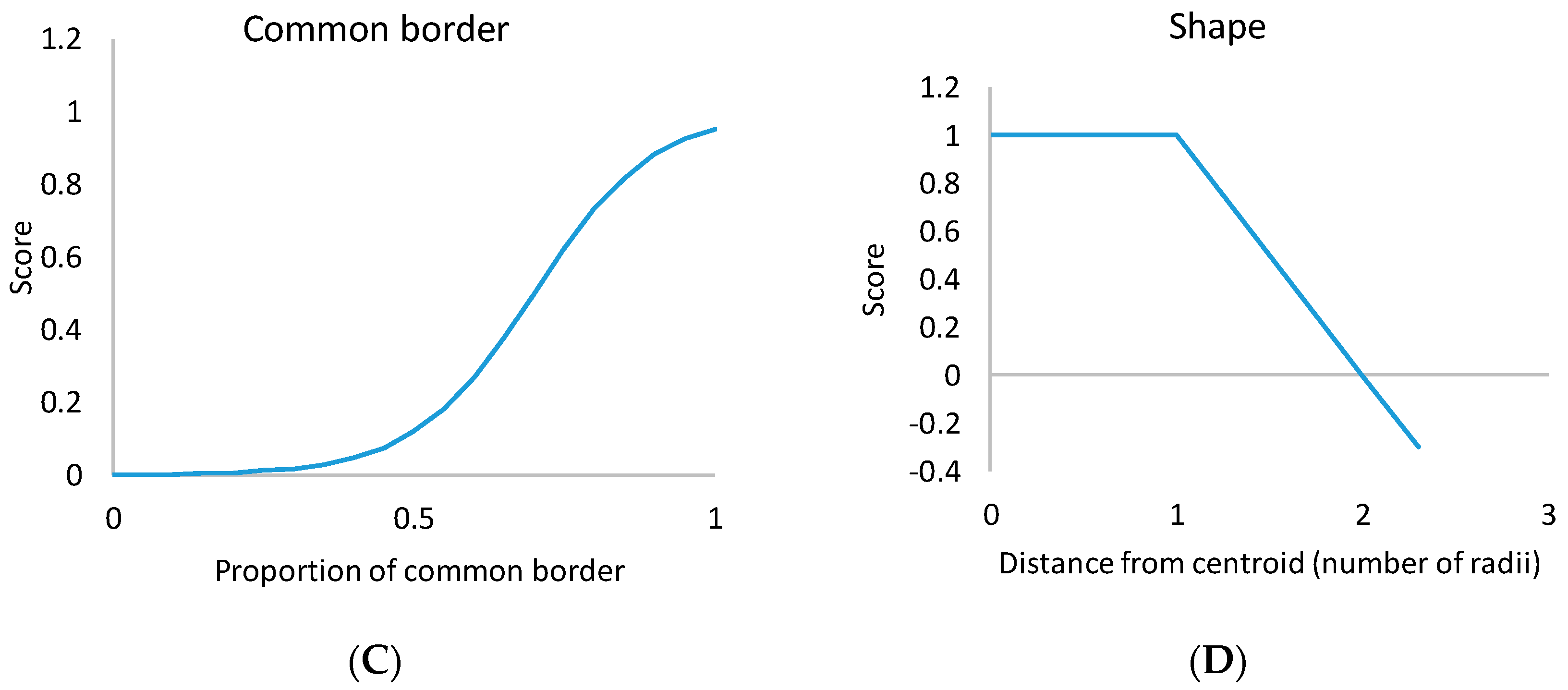
Due to the fact that the values of very small cells of a CHM do not measure stand height (not even tree height), there may be no reason to use the canopy height model directly for stand delineation. Instead, the values of the cells can be used to derive other variables like the maximum height within, for instance, a 5 m × 5 m window, which is an estimate of local tree height. The difference between maximum and minimum height is a measure of canopy depth. The difference between maximum and mean height, or between mean and minimum height, conveys information about crown shape and stand density (
Figure 1). Therefore, using the maximum, mean, and minimum height of the CHM within a certain window takes into account several features of the stand, and it may, therefore, lead to better stand delineation than using only one variable (e.g., the mean canopy height in a cell).
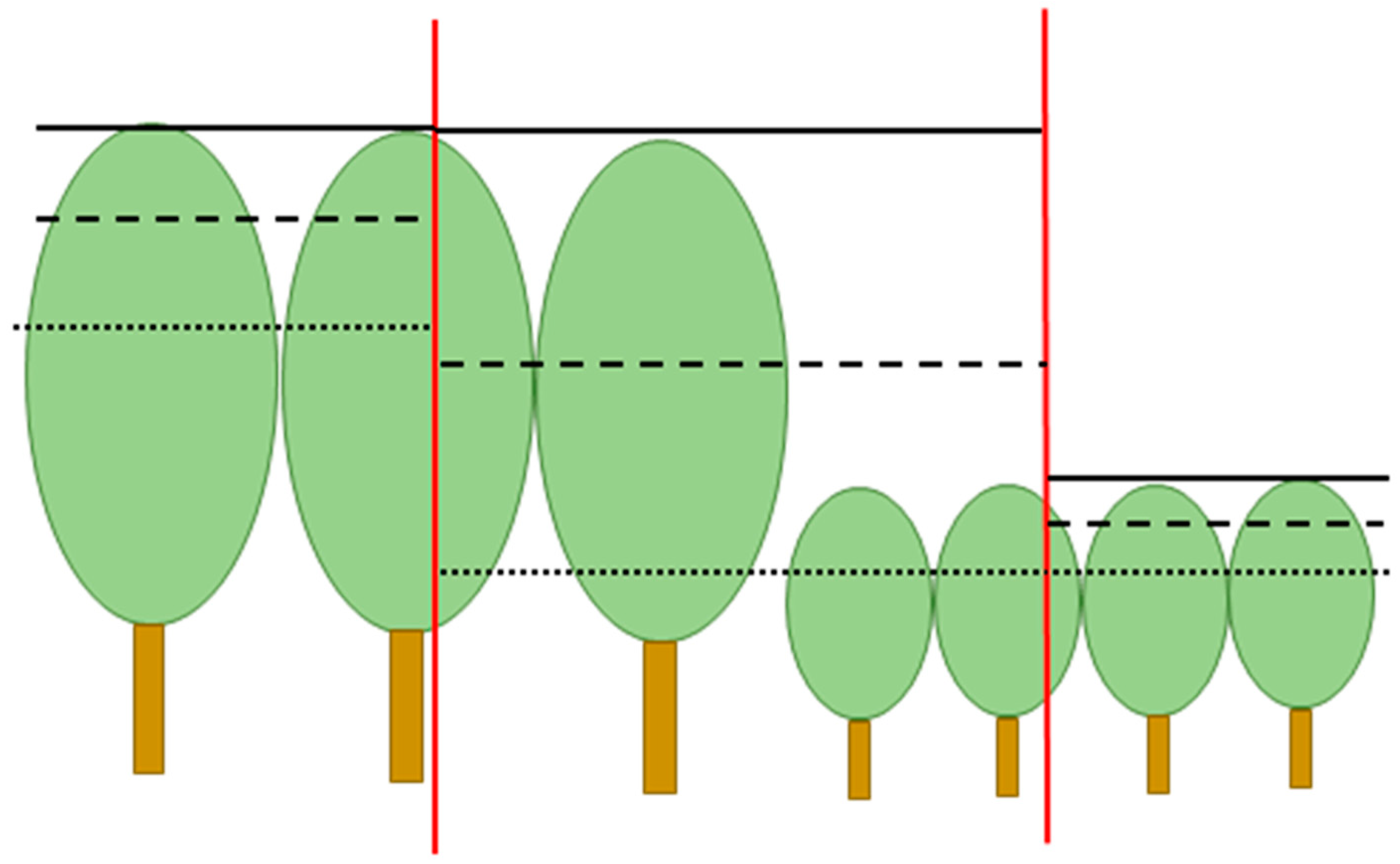
Replacing the values of the CHM by the mean, maximum, or minimum values of a window makes it possible to use a larger cell size, compared to the original CHM. Large cells allow faster calculations because the number of cells is reduced. Variables calculated for larger cells may also correlate better with stand variables. However, the use of large cells brings the mixed cell problem. A large cell might extend over more than one stand when located at the stand boundary. The mean canopy height of the enlarged cells is the average of two dissimilar stands. The maximum height of a stand of tall trees extends to adjacent stands, as does the minimum height of stands of short trees (
Figure 2).
There are typically three criteria in stand delineation: (1) stands should be homogeneous in terms of site and growing stock variables, (2) they should be large enough, and (3) stand shape should be acceptable (roundish, not too irregular). No overall measures and target levels exist for these criteria as the importance and the indicators of the criteria are subjective [
21]. However, homogeneity means that within-stand variation in stand variables should be small compared to between-stand variation. This can be measured with the
R2 statistic, which is the proportion of total variation explained by the stand delineation [
3,
8].
For the area of the stand, “the bigger the better” might not be true [
8]. A more common objective is to avoid small stands since they lead to too small and isolated harvest blocks and other treatment units. Another objective might be to have nearly equally sized stands and avoid very large stands. If stands are understood as indivisible treatment units, very large stands make it difficult to cut the same volume every year, for example. Regular stand shapes resembling squares, rectangles, circles, or hexagons are most probably favored by most forest managers.
The shape of the stand was not explicitly considered in previous research on the use of CA in stand delineation [
8,
10]. Earlier studies employed stand variables interpreted for grid cells as the basis of the delineation. In the current study, we investigate how well a canopy height model derived from ALS data is suited for automated stand delineation with self-organizing CA. The methods developed in earlier research are enhanced so that the shape of the stand is also explicitly included in the stand delineation process, in addition to stand area and homogeneity. The new variant of CA developed in this study is applied to a CHM of the Mengiagang forestry farm, located in the Heilogjiang province of China.
The objective of our study was to develop a CA for automated numerical stand delineation considering the homogeneity, area, and shape of the stands. Using the new algorithm, we analyzed the effect of increasing importance of stand area and stand shape on the outcome of the CA, compared to the case where all weight was on within-stand homogeneity. In addition, we analyzed the effect of enlarging the cell size on the delineation result.
Different stand delineations were compared in terms of R2. Minimum, mean, and maximum stand area, proportion of small stands, and two form indices were calculated for the delineations. They were also assessed visually with the help of stand maps. It was assumed that one hectare is a sufficient stand size, and smaller stand sizes were penalized. Circular stand shape was assumed to be ideal. Small within-stand variation and large between-stand variation were pursued.
2. Materials and Methods
2.1. Case Study Forest
The study area was the Mengjiagang forest farm (46°32′ north (N), 129°10′ east (E)), located in Huanan County, Heilongjiang Province, China (
Figure 3). The major planted tree species in this farm include
Pinus koraiensis (henceforth referred to as Korean pine),
Picea asperata,
Pinus sylvestris (Mongolian pine), and
Larix gmelinii (larch). The total area of the forest is 15,503 hectares, of which 4438 hectares are natural forests, accounting for 32.8% of the forest area.
2.2. Canopy Height Model
The airborne laser scanning was conducted between 31 May and 15 June in 2017. The flight altitude was 1000 m, with a pulse frequency of 300 kHz and a scanning angle of 30° in both directions from vertical. The average number of echoes per square meter was about four. The Institute of Forest Resource Information Techniques of the Chinese Academy of Forestry conducted the laser scanning. It also developed the canopy height model in October 2017. A digital elevation model (DEM) was generated from the ground echoes, and a digital surface model (DSM) was generated from the canopy echoes. The canopy height model (CHM) was obtained as the difference between the DSM and DEM [
22]. The resolution of the canopy height model was 1 m.
2.3. Data Preprocessing
A 2 km × 2 km subarea (2000 by 2000 cells) of the CHM of the Mengjiagang forest farm was selected for the analyses of this study. The main criteria for choosing the sub-area were that most of it had to be forest, there was variation in tree species and canopy height, and the area included both instant and gradual changes in canopy height (clear and unclear stand borders).
As the first step of data processing, the CHM was checked for outliers. A few cells were found where canopy height was negative, and these values were replaced by the mean canopy height of a window of 5 × 5 cells. There were no illogically high values. The maximum canopy height was 31.17 m.
Then, every third, fifth, seventh, etc. row and column were selected (until 13), and the maximum, mean, and minimum canopy heights were calculated from a window of 3 × 3, 5 × 5, 7 × 7, etc. cells (
Figure 4). When the window size (and the cell size of the output layer) was 3 × 3, the first row and column number was two, with the 5 × 5 window, it was three, etc.
A species raster was created from an existing forest map [
23], where different species of the forest were coded as follows: 1 = Korean pine, 2 = Mongolian pine, 3 = larch, 4 = other species. The species layer was split into four 0–1 layers, the first indicating whether (1) or not (0) the species was Korean pine, the second indicating Mongolian pine, the third larch, and the fourth other species. If the values of all species layers were zero, the cell was not forest. The splitting was done because the species codes do not represent an interval scale, making it impossible to use Euclidean distance as a numerical measure of the similarity of tree species.
As a result of preprocessing, seven variables were available for each cell: maximum, mean, and minimum canopy height, as well as the presence of Korean pine, Mongolian pine, larch, or another tree species. These seven growing stock variables were used in stand delineation. All layers were standardized to mean zero and standard deviation one to remove the effect of different units (mean was first subtracted from the original value, and the result was divided by standard deviation).
2.4. Cellular Automaton
The purpose of the cellular automaton was to find the optimal or best stand number (ID number of the stand) for each cell of a grid. All cells were evaluated systematically, and the most suitable stand number was given to the cell. A cell always took the stand number of one of its adjacent cells. The number of adjacent cells was eight, since corner cells to the northeast, southeast, southwest, and northwest were also considered adjacent.
The most suitable stand number was selected for every cell of the grid for several iterations, until the stand borders no longer changed (or changed only little). The process was started from an initial stand delineation, which in this study consisted of 1-ha square-shaped stands. All cells that were within the 1-ha square were given the same stand number. A cell that has no adjacent cells with the same stand number disappears during the process since the cell gets the stand number from one of its adjacent cells. The stands may become divided into two or more disconnected parts during the CA run. More detailed descriptions of the use of CA for stand delineation can be found from Pukkala [
8,
10].
The function that was used to select the stand number for a cell was as follows:
where
Pij is the priority, or score, if cell
i is joined to stand
j,
Dij is the Euclidean distance of stand attributes between cell
i and stand
j,
Aj is the area of stand
j,
Bij is the proportion of common border between cell
i and stand
j (of the total border length of cell
i),
Sij is the effect of joining cell
i to stand
j on the shape of stand
j,
pk is sub-priority function for criterion
k (
Figure 5), and
vk is the weight of criterion
k. The sum of the weights was equal to one. The score was calculated for each stand adjacent to cell
i, and the number of the stand having the highest score was given to cell
i. When calculating the border length, we assumed that the side borders of a cell (border with cells to east, west, south, and north) have a length equal to one and corner cells have a length equal to 0.3.
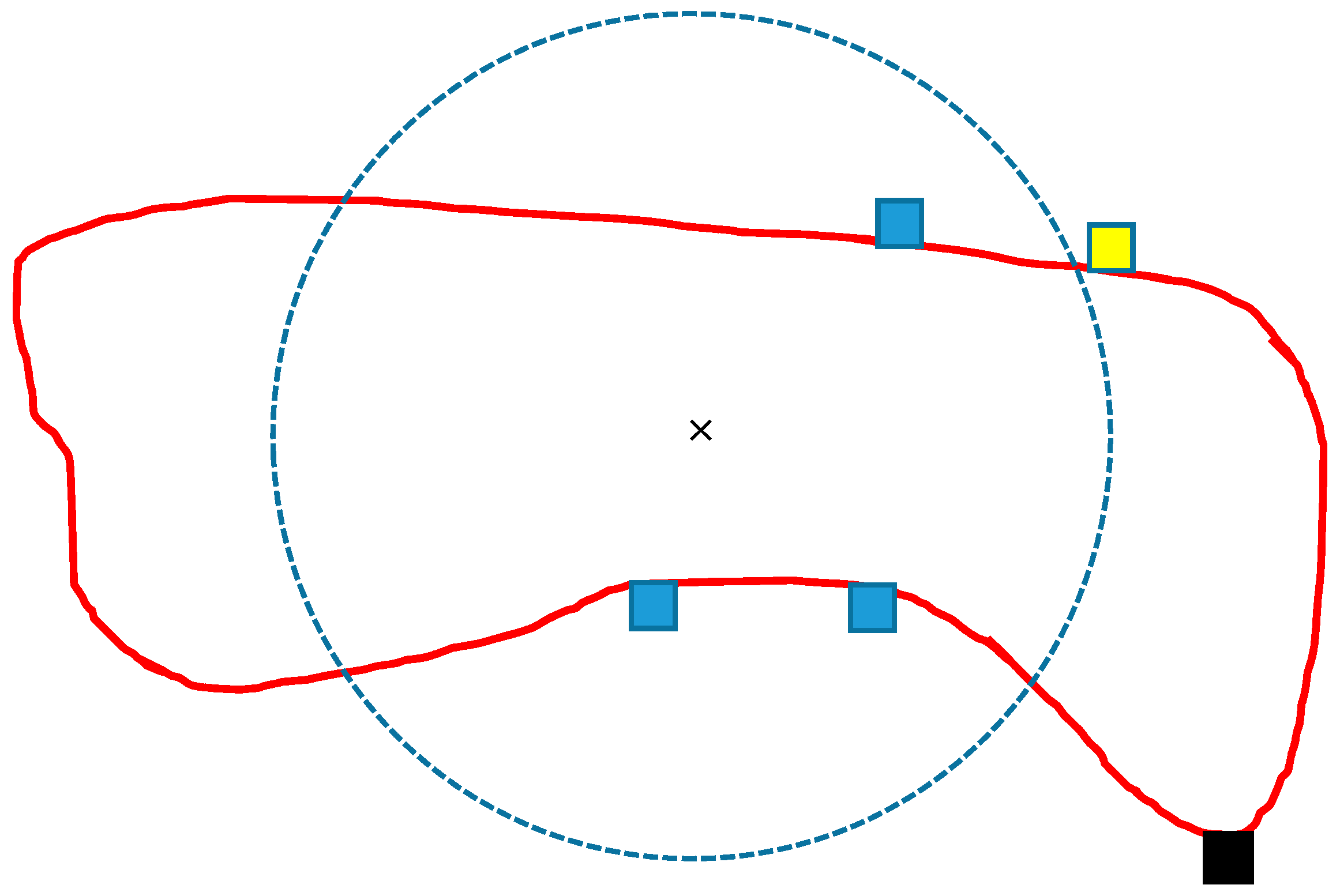
The idea of calculating the shape measure
Sij was that cells within a radius of a circle centred on the centroid of stand
j and having the same area as stand
j are not penalized because these cells do not deteriorate the stand’s shape, compared to the ideal circular shape (
Figure 6). If a cell is further from the centroid than the radius of a circular shape, the stand is penalized, and the further the cell is from the stand centroid.
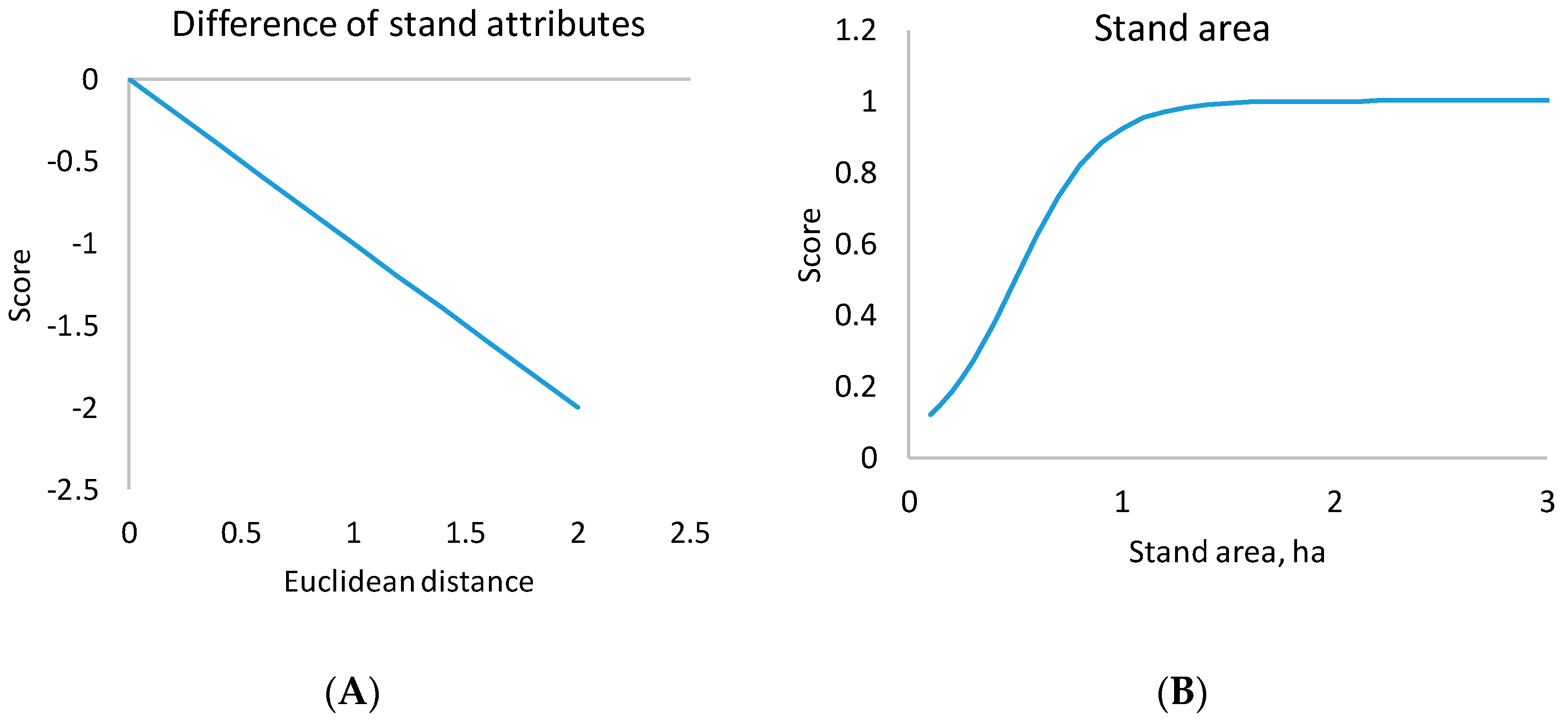
The proportion of common border between cell
i and stand
j (
Bij), as well as the area of stand
j (
Aj), had a nonlinear effect on the score (
Figure 5). The sigmoid type of relationship between stand area and score led to the avoidance of small stands, but stand area ceased to increase the score after about 1.5 ha. This means that very large stands were not considered better than 1.5-ha stands. A sigmoid relationship between common border (
Bij) and score led to avoiding stands that were composed of narrow strips of cells [
8]. The common border criterion affected stand shape at the local cell level, whereas the stand shape criterion took into account the overall shape of the whole stand.
The sigmoid-type relationships were described with logistic functions.
The values of the parameters were
a1 = −5,
a2 = 0.5,
b1 = −10, and
b2 = 0.7. They resulted in the relationships shown in
Figure 5. The distance of stand attributes between cell
i and stand
j was a weighted Euclidean distance.
where
xik is the value of standardized stand attribute
k in cell
i,
xjk is the average value of the same attribute in stand
j, and
wk is the weight of attribute
k. Index
k refers to the used stand attributes as follows (the weight used in this study is in parentheses): 1 = maximum canopy height (0.4); 2 = mean canopy height (0.3); 3 = minimum canopy height (0.2); 4 = Korean pine (0.025); 5 = Mongolian pine (0.025); 6 = larch (0.025); 7 = other species (0.025).
2.5. Stand Delineation Cases
This article concentrated on analyzing the effect of stand shape
(Sij) and stand area (
Aj) criteria on the stand delineation result (
Table 1). Firstly, a reference delineation was produced where the only criterion was the similarity of stand variables within a stand (in Equation (1),
v1 was 1, and all the other weights were zero).
Then, the effects of stand shape (
Sij in Equation (1)) and stand area (
Aj) criteria were analyzed by varying their weights. When the weight of stand area or shape was increased, the weight of the similarity of stand variables (
Dij) was decreased by the same amount such that the sum of criterion weights was always 1.
Table 1 is a summary of the analyzed CA runs.
The last part of the analyses examined the effect of the size of the window from which the maximum, mean, and minimum canopy heights were calculated (cell size was equal to window size). The species layer was resampled to the same cell size by using the mode filter (the most common tree species within the window was selected). The analyzed cell sizes were 1 × 1, 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, and 13 × 13 square meters (the cell size of the original CHM was 1 × 1 m). The number of iterations was 20 in all CA runs since it was found that the delineation almost stabilized during 20 iterations.
The results of different CA runs were compared in terms of the degree of explained variance of the stand attributes (
R2).
R2 was calculated as
where SSE is the variation not explained by the delineation, and SST is the total variation of the attribute within the grid. SST and SSE were calculated as follows:
where
N is the number of stands,
nj is the number of cells in stand
j,
is the value of the variable in cell
i belonging to stand
j,
is the overall mean of the variable, and
is the mean value of the variable among the cells that belonged to stand
j.
In addition, the proportion of stands smaller than 0.1 ha and two variables that described the form of the stands were calculated for every delineation.
Stand perimeter is the total length of the outer border of the stand without any smoothing, and square perimeter is the perimeter of a square having the same area as the stand. The latter form index was called form heterogeneity in Baatz and Schäpe [
21]. A small value of both indices implies “good” stand shape. The form indicators were calculated as unweighted averages of the stand values.
4. Discussion
Our study corroborated earlier findings that cellular automaton is an easy and flexible method capable of producing good stand delineation results [
8,
10]. Several criteria can be taken into account, depending on the preferences of the forest manager and the purpose of the delineation. As a difference to the previous studies, which used stand variables interpreted for rather large cells (16 m × 16 m), we used a high-resolution canopy height model developed from laser scanning data.
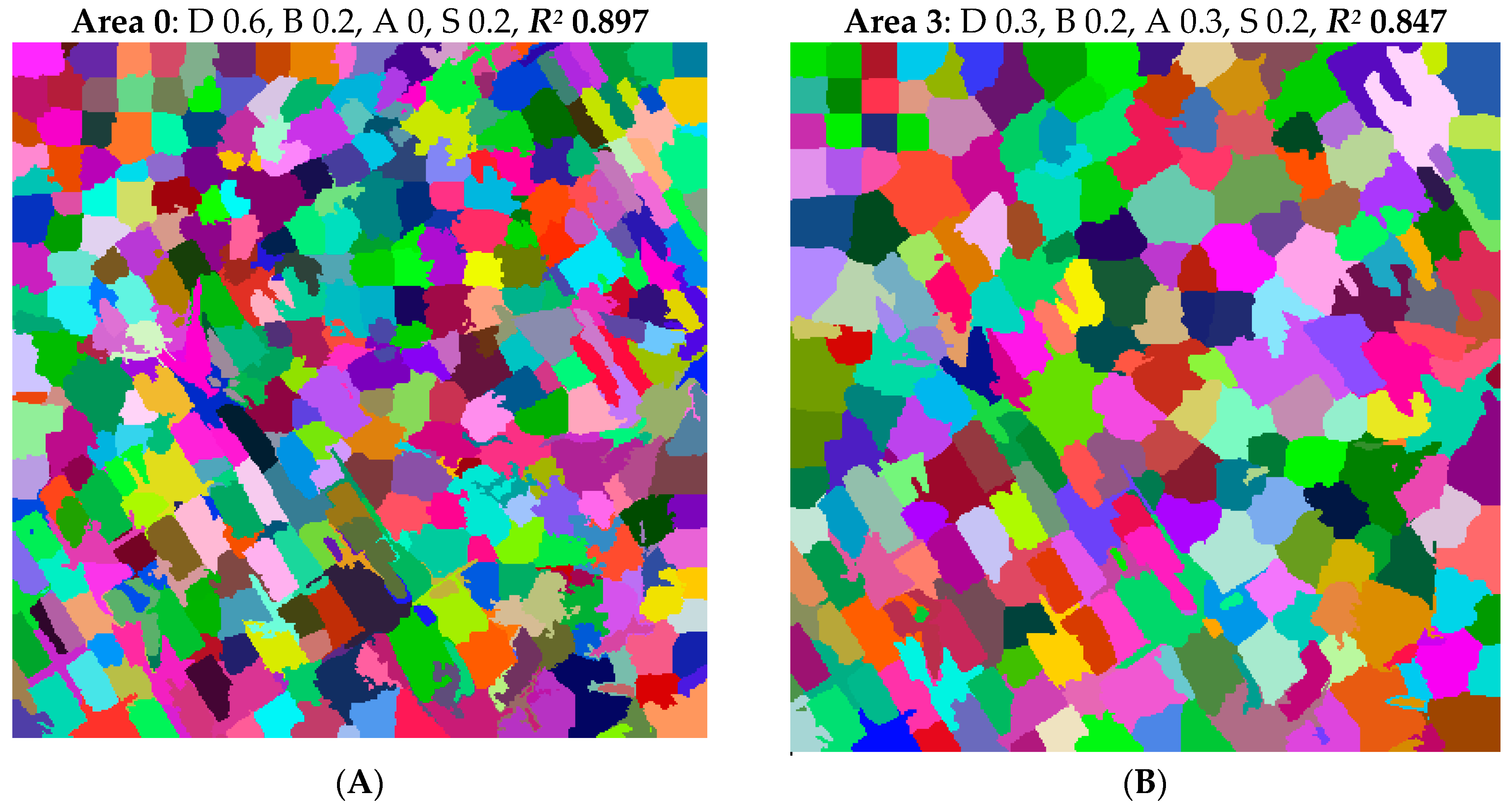
If there are several adjacent initial stands in a large homogeneous forest, the CA does not move the stand boundaries easily. This can be seen from
Figure 7D, where there are several square-shaped stands in the northwestern corner. These squares are almost the same as the initial stands. This result is partly due to the shape of the sub-priority function for stand area, which assumed that 1-ha stand size was ideal, and additional area no longer increased the stand’s area score. Linearizing the sub-priority function for stand area, using low weights for stand area and a common border, and letting the CA run longer would mitigate this problem.
Figure 12 shows that the CA fine-tuned for a certain area works equally well in areas other than the one which was used for fine-tuning. If required, the stand delineation produced by the CA can be finalized manually. Another option is to use the delineation as the starting point for another CA run, which uses different values for some parameters. For example, the somewhat rugged boundaries in some of the maps of
Figure 12 could be rectified by changing the shape of the sub-priority function to common and increasing its weight and running the CA for a few iterations. Geographic information system (GIS) software packages also include tools for smoothing rugged stand borders.
The spatial resolution of the CHM was 1 m. The small original cell size allowed us to compare different cell sizes in stand delineation. Since larger cells contained several initial cells, it was possible to calculate variables that described the range of variation in canopy height within short distance. We partitioned the single variable of the original canopy height model into three variables that conveyed more information about stand features than the canopy height alone. The variables used in this study were maximum, mean, and minimum canopy heights within the cell. It would be possible to calculate many more variables, such as standard deviation, skewness, and percentiles, but most probably the contribution of the additional variables to the delineation result would remain small.
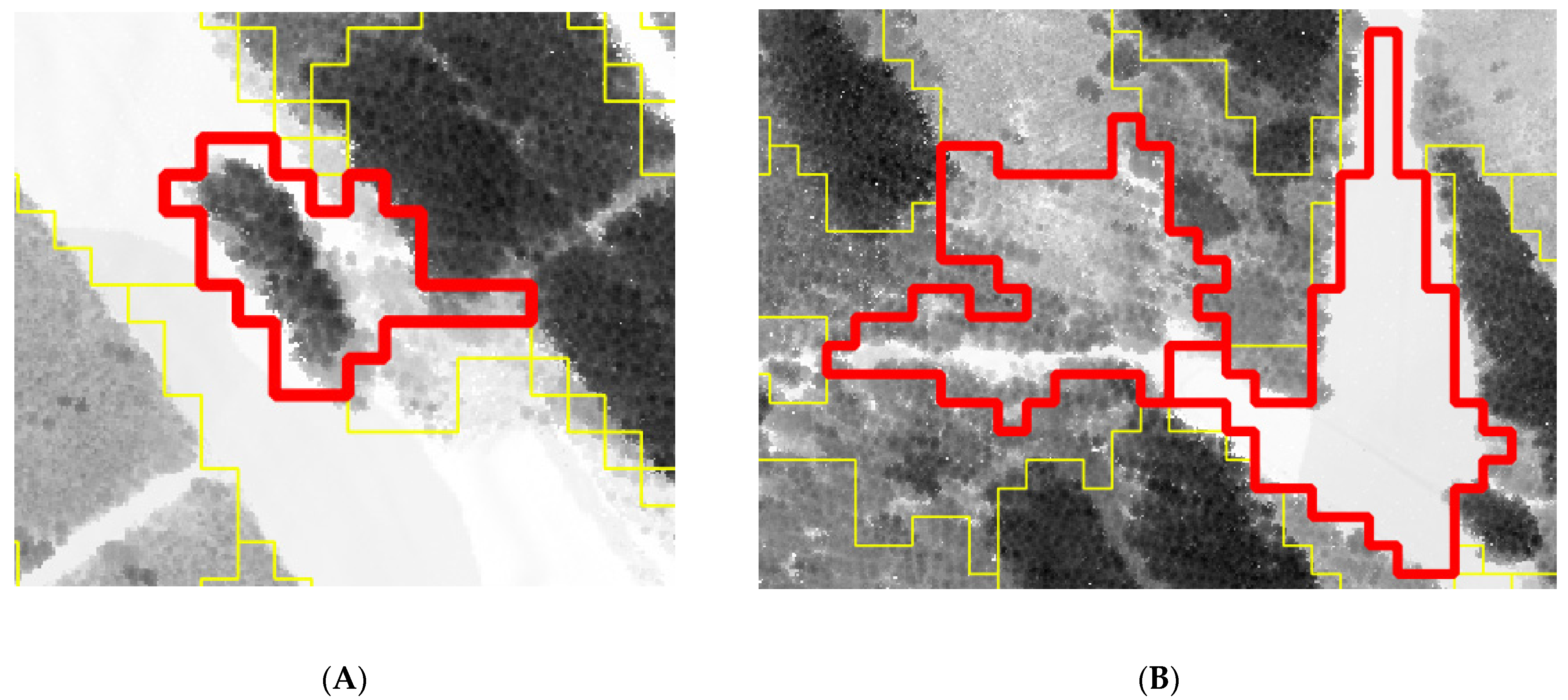
It was assumed that large cell size leads to the mixed cell problem, where narrow artefact stands are delineated at stand borders [
9]. However, the results showed that the mixed stand problem was not serious, most probably because the shape parameter prevented the creation of long and narrow stands. However, the other assumed consequence of large cell size, namely, the enlargement of stands of tall trees to adjacent stands (see
Figure 2), was apparent when cell size was large (
Figure 11). This result was partly due to the fact that the maximum canopy height had a larger weight in delineation than the mean and minimum height. High weight of minimum canopy height might have reversed the effect on enlarging cell size.
Tree species information was also used for stand delineation since it was assumed that tree species data are always available in plantation forests. However, the weight of the species layers was always low since we wanted to analyze the effect of other variables. The degree of explained variance for the four tree species layers was 0.8–0.9. Lack of perfect separation of stands with different species was most probably mainly due to the fact that the boundaries of the species map were straighter than the true stand borders, and they were not always exactly in the correct place.
The study developed a new way to consider stand shape on cellular automaton. The developed method worked as expected, and it had a clear improving influence on stand delineation when round-shaped stands with low perimeter/area ratio were targeted. Other shape indices for measuring stand shape were suggested in previous studies [
21], such as border length divided by the square root of the number of cells (Equation (5)). However, some of the earlier indices measure the smoothness of the border more than stand shape. The shape criterion employed in our CA does not use border length at all but measures deviations from circular shape. In most cases, small irregularities in stand border can be smoothed out, which reduces the length of stand border but has no effect on the overall shape of the stand.
The results of our study showed that both stand area and stand shape should be used as criteria when CA are used for stand delineation since, otherwise, the delineation may not be acceptable. Small weights are sufficient since additional improvements in stand shape and area would result in increased within-stand variation in stand attributes.
Increasing cell size greatly reduces the number of cells. The use of large cells makes it possible to divide large canopy height models into stands in short computing time. The use of very small cells was found to be even harmful since small cells may result in very long and complicated stand borders. However, as discussed above, too large cells bring problems too. On the basis of our study, it may be concluded that the optimal cell size is 5–10 m when canopy height models are used for stand delineation.
The results of this study can be generalized to other regions since canopy height models derived from ALS data are not very different in different regions and countries. However, separating stands with different species compositions requires more attention when the stands are not planted monocultures. Combined use of maximum, mean, and minimum canopy height most probably helps to separate stands with different species compositions. Additional information can be obtained from other remote sensing material (for instance, aerial photographs). High-density laser scanning data can be used to calculate alpha shape metrics, which also help in species identification [
24]. There are also other potential methods, based on statistical analysis and machine learning, which could be tested in species identification from laser data.