Bark Features for Identifying Resonance Spruce Standing Timber
Abstract
1. Introduction
2. Materials and Methods
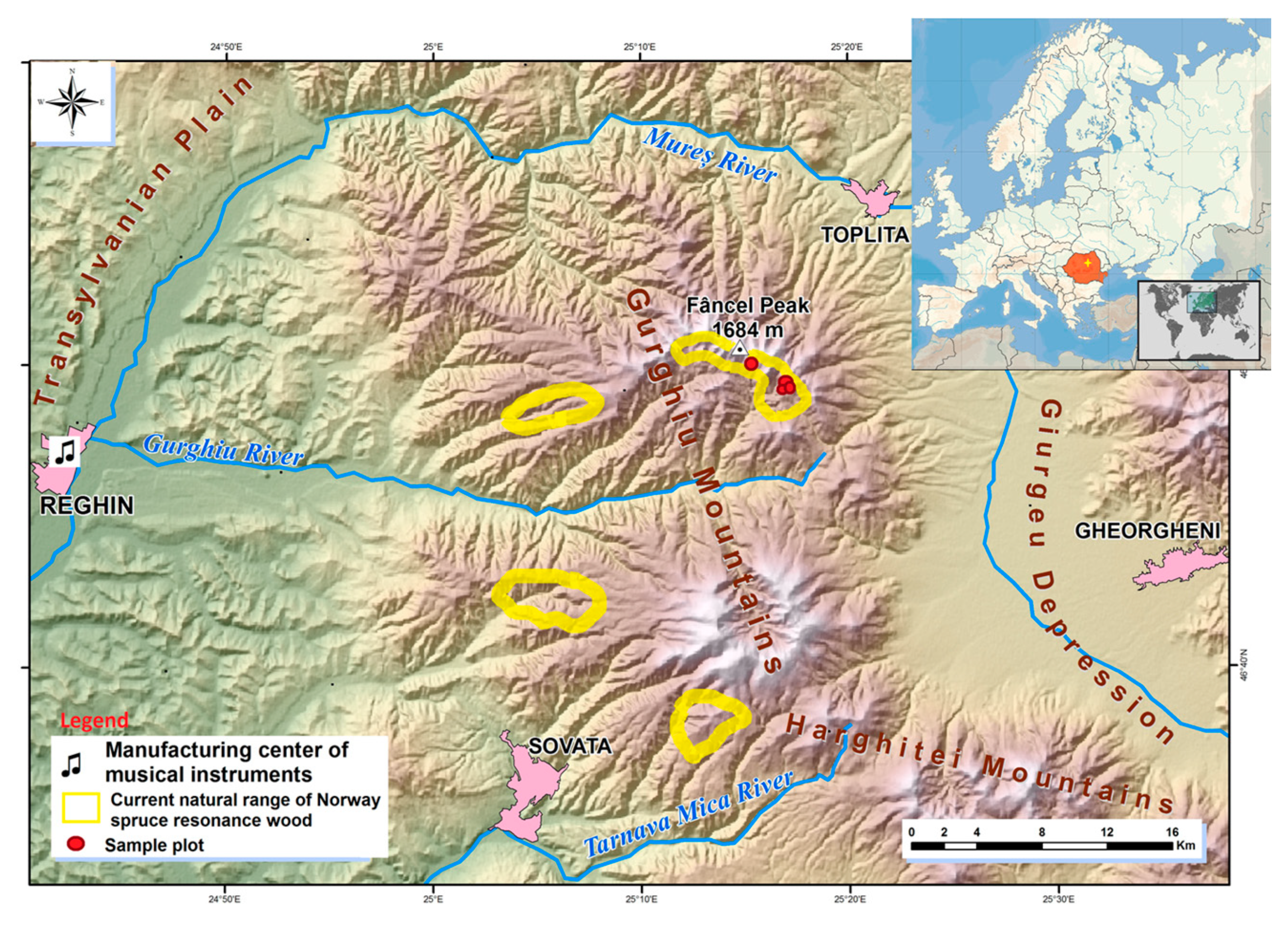
2.1. Sampled Area
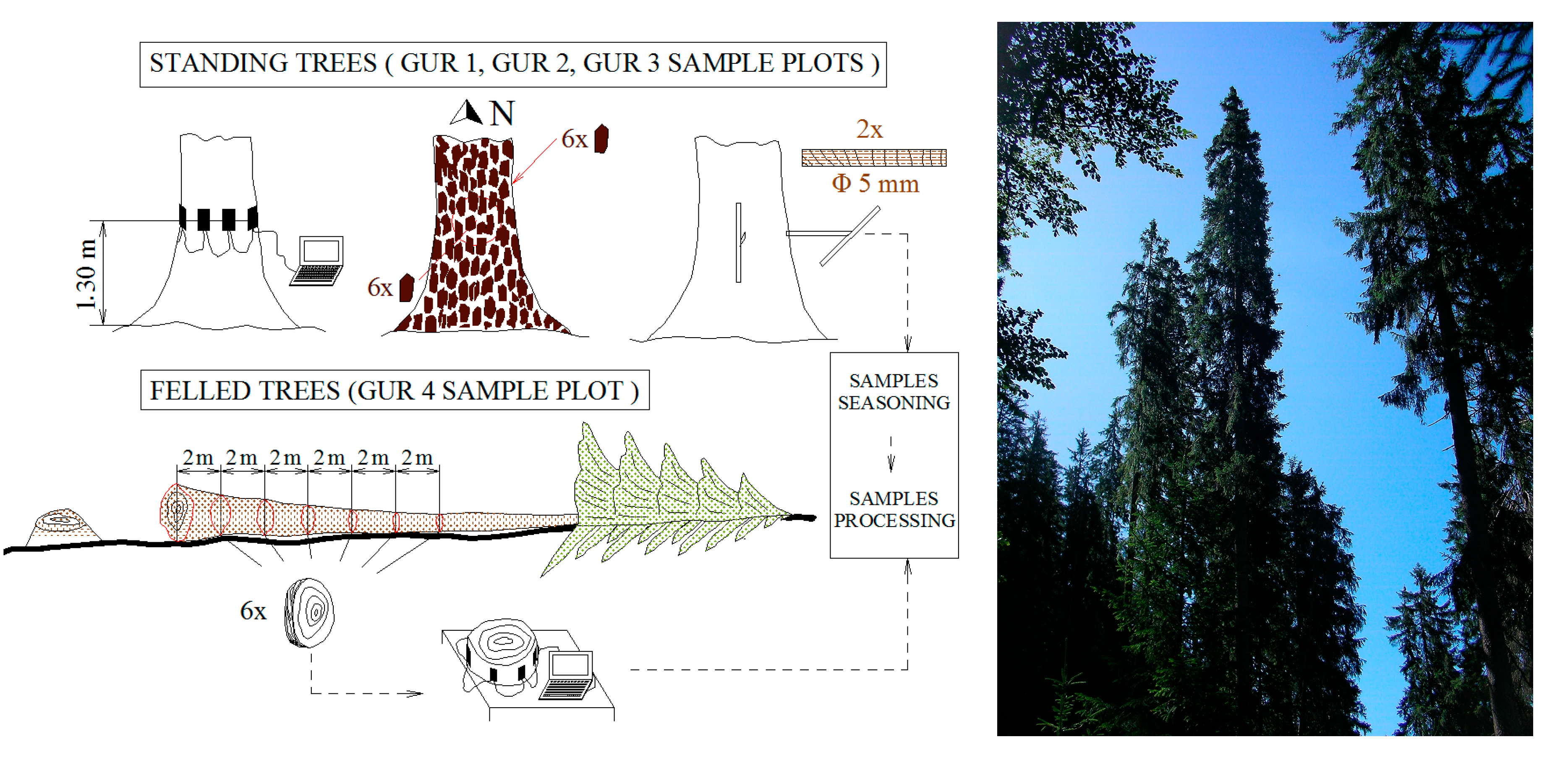
2.2. Sampling Design
2.3. Processing the Material
2.3.1. Bark Measurements
2.3.2. Wood Structural Data Acquisition
2.3.3. Acoustic Measurements
2.4. Data Processing
3. Results
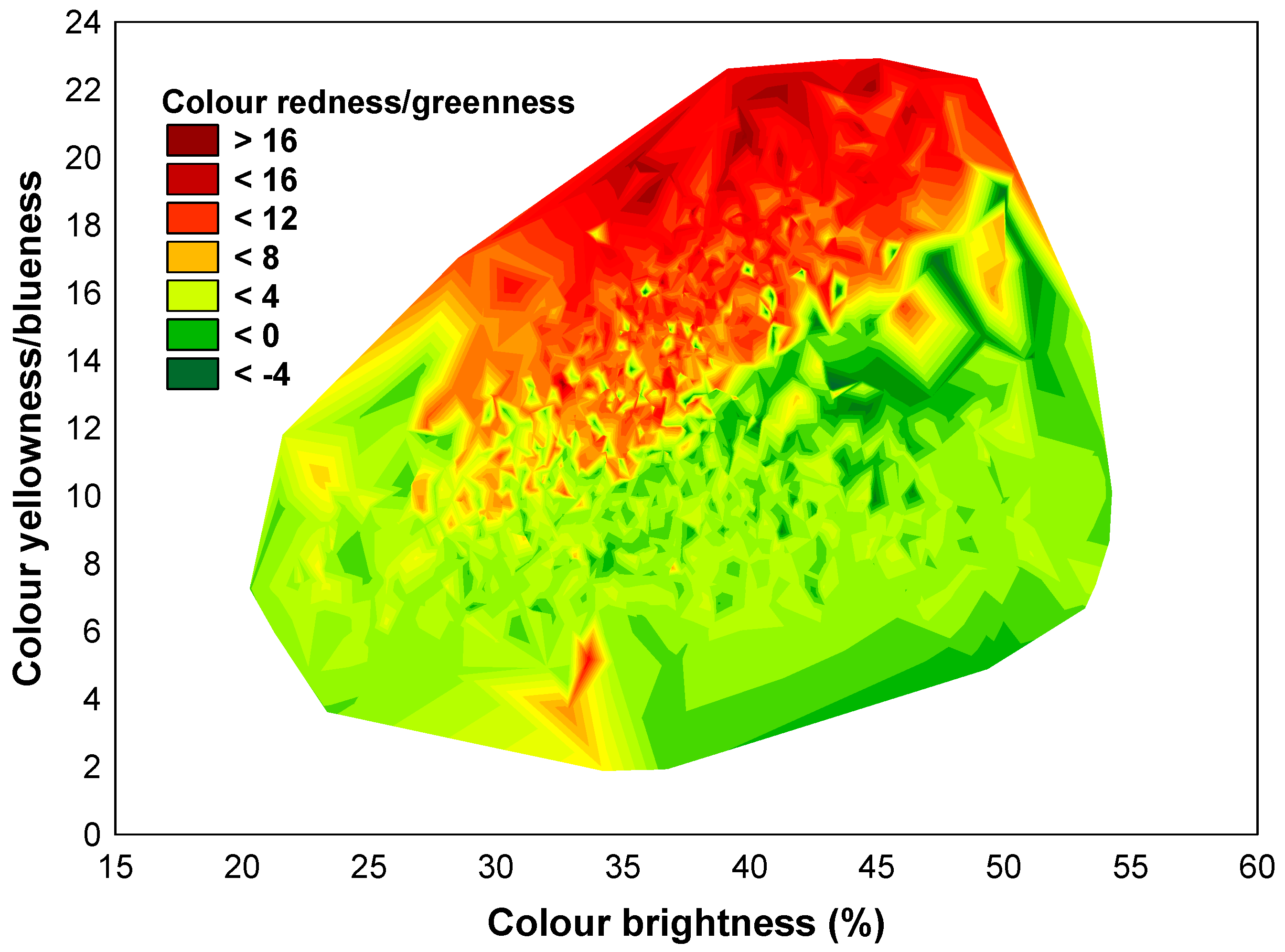
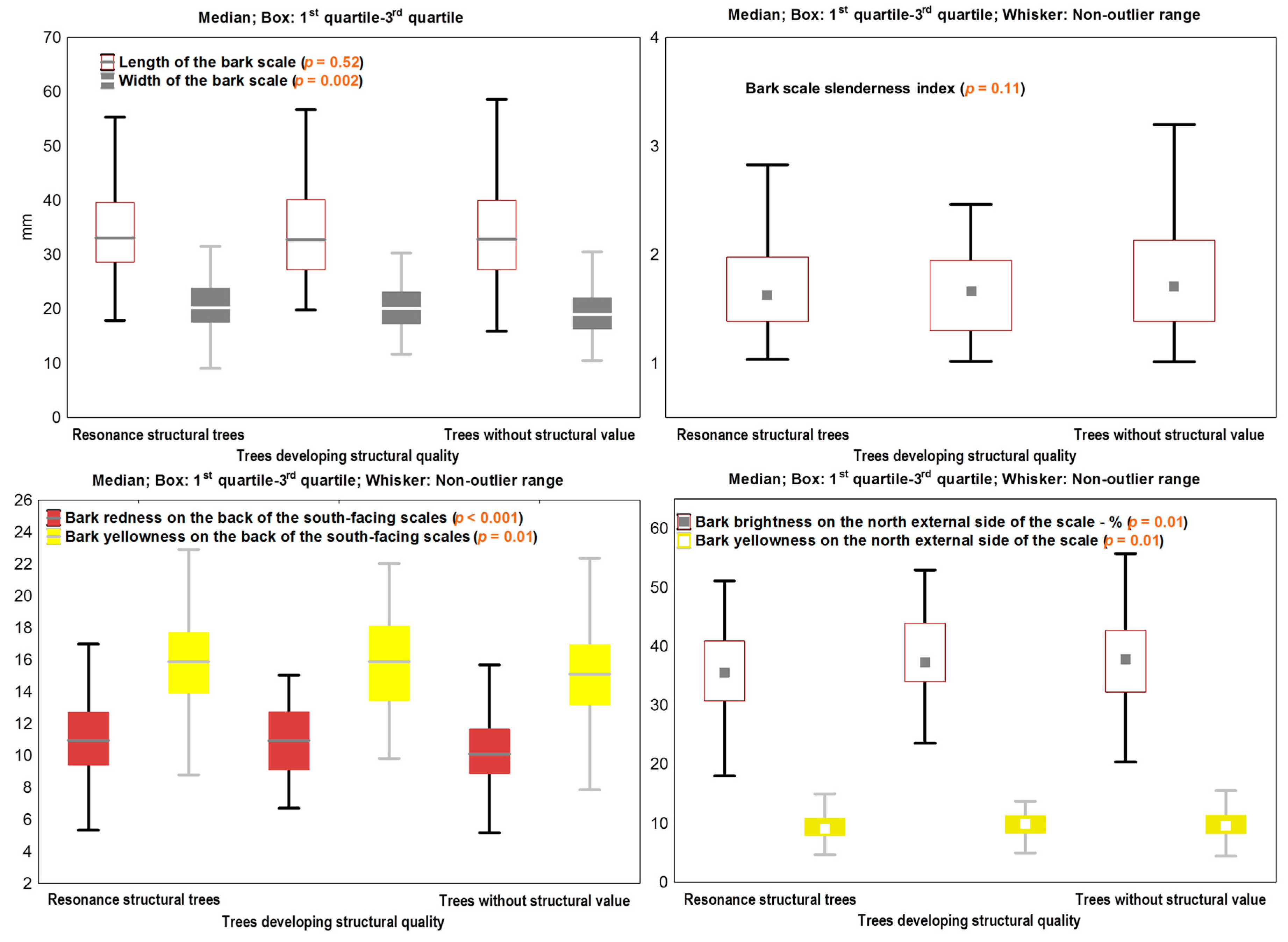
3.1. The Variability of the Bark Features
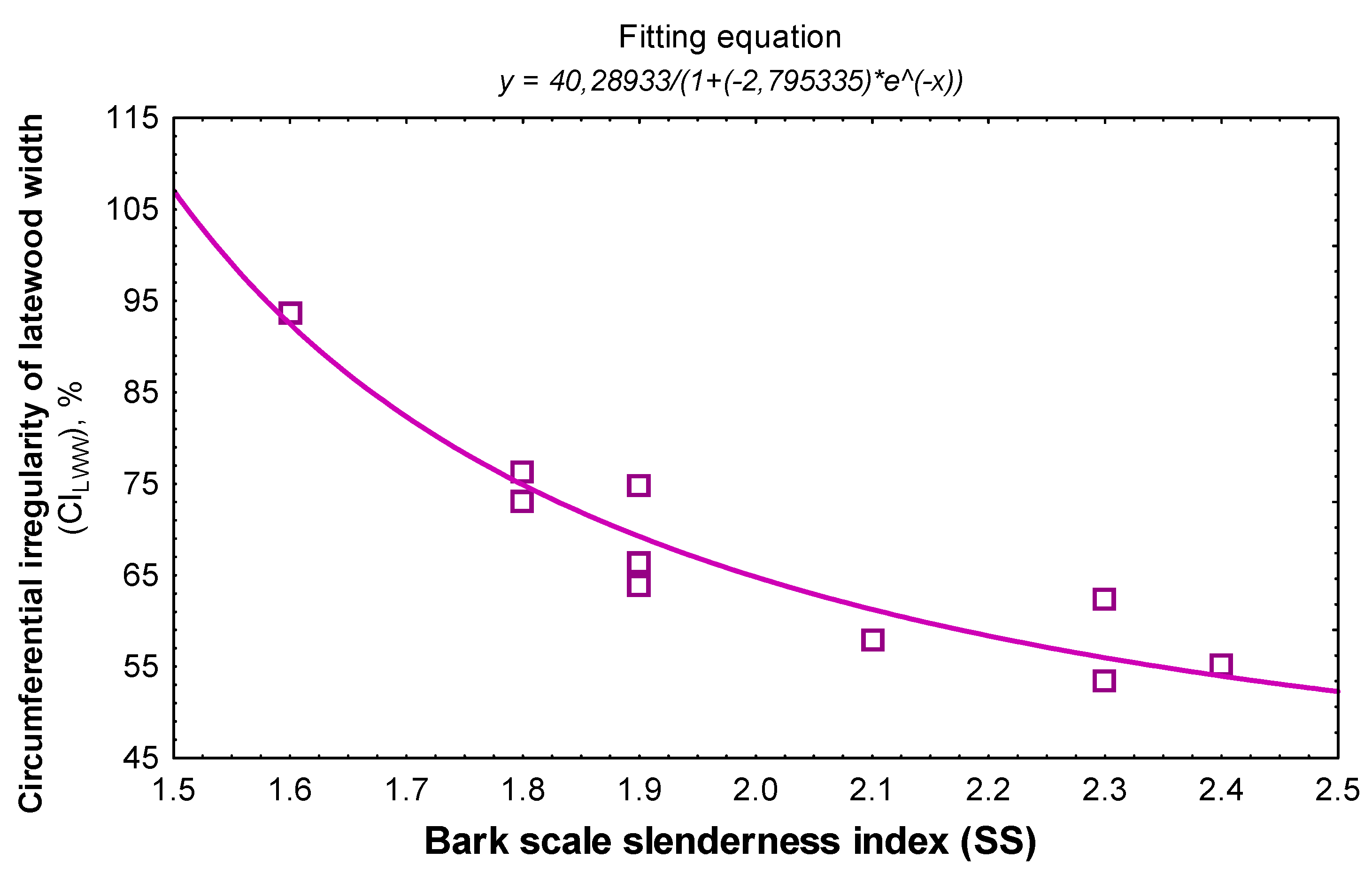
3.2. Linking Bark Features to the Wood Structure
3.3. Acoustic Screening of Bark Markers
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Şofletea, N.; Curtu, L. Dendrology; Pentru Viaţă Publishing House: Braşov, Romania, 2007; pp. 40–53. [Google Scholar]
- Surmiński, J. Wood properties and uses. In Biology and Ecology of Norway Spruce; Tjoelker, M.G., Boratyński, A., Bugała, W., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 333–342. [Google Scholar]
- Ege, K. The Piano Soundboard—Modal Studies in the Low- and Mid-Frequency Ranges. Ph.D. Thesis, École Polytechique, Palaiseau, France, 2009. [Google Scholar]
- Albu, C.T. Research on the Characteristics of Resonance Spruce Wood from Gurghiu River Basin in Conjunction with the Requirements of the Musical Instruments Industry. Ph.D. Thesis, Transilvania University of Braşov, Brașov, Romania, 2010. [Google Scholar]
- Ștefănescu, P. A Norway spruce forest site in Gurghiu Mountains containing resonance wood, located in the range of Sovata Forest District. Rev. Pădurilor 1961, 76, 85–92. [Google Scholar]
- Ștefănescu, P. Contributions to the knowledge of resonance Norway spruce from Gurghiu Mountains. Rev. Pădurilor 1964, 79, 511–517. [Google Scholar]
- Domont, P. Spruce Resonance Wood: A Jewel of Mountain Forests. Available online: https://www.waldwissen.net/waldwirtschaft/holz/verarbeitung/wsl_klangholz/index_FR (accessed on 10 July 2019).
- Fedyukov, V.I.; Saldaeva, E.Y.; Chernova, M.S.; Chernov, V.Y. Biomorphology of Spruce Trees as a Diagnostic Attribute for Non-Destructive Selection of Resonant Wood in a Forest. South-East Eur. For. 2018, 9, 147–153. [Google Scholar] [CrossRef]
- Grapini, V.; Constantinescu, N. Resonance Spruce; Forest Research Institute: Bucharest, Romania, 1968; p. 19. [Google Scholar]
- Zugliani, G.; Dotta, L. Resonance wood. Technical features and ecological conditions. Sherwood 2009, 154, 7–13. [Google Scholar]
- Krzysik, F. Problems of resonance wood sorting and use. Holzindustrie 1968, 1, 3–7. [Google Scholar]
- Hutchins, C.M. Wood for violins. Catgut Acoust. Soc. Newsl. 1978, 29, 14–18. [Google Scholar]
- Rocaboy, F.; Bucur, V. About the physical properties of wood of twentieth century violins. J. Acoust. Soc. Am. 1990, 1, 21–28. [Google Scholar]
- Bucur, V. Acoustics of Wood, 2nd ed.; Springer: Berlin, Germany, 2006; pp. 173–196. [Google Scholar]
- Zugliani, G.; Dotta, L. Resonance wood. Management, selection and manufacture in the state forest of Paneveggio. Sherwood 2009, 155, 14–18. [Google Scholar]
- Buksnowitz, C.; Teischinger, A.; Müller, U.; Pahler, A.; Evans, R. Resonance wood [Picea abies (L.) Karst.]: Evaluation and prediction of violin makers’ quality-grading. J. Acoust. Soc. Am. 2007, 121, 2384–2395. [Google Scholar] [CrossRef]
- Darnton, M. Violin Making. Available online: http://darntonviolins.com (accessed on 12 May 2009).
- Pașcovici, N. Spruce as resonance and keyboard wood. I Resonance spruce in forests. Rev. Pădurilor 1930, 46, 85–99. [Google Scholar]
- Nocetti, M.; Romagnoli, M. Seasonal cambial activity of spruce (Picea abies Karst.) with indented rings in the Paneveggio Forest (Trento, Italy). Acta Biol. Crac. Ser. Bot. 2008, 50, 27–34. [Google Scholar]
- Bonamini, G.; Uziellli, L. A simple non-destructive method to recognize resonance spruce. Monti e Boschi 1998, 6, 50–53. [Google Scholar]
- Domont, P. Development of Resonance Wood in Switzerland, Rep. no. 5.162. 2000. Available online: http://www.waldwissen.net/waldwirtschaft/holz/verarbeitung/wsl_klangholz/wsl_klangholz_rapport_final.pdf (accessed on 29 February 2016).
- Popescu, G.A. Conifers in the Hills of the Eastern and Curvature Subcarpathians; Ceres Publishing House: Bucharest, Romania, 1984; pp. 122–126, 192–200. [Google Scholar]
- Arco Molina, J.G.; Hadad, M.A.; Domínguez, D.P. Tree age and bark thickness as traits linked to frost ring probability on Araucaria araucana trees in northern Patagonia. Dendrochronologia 2016, 37, 116–125. [Google Scholar] [CrossRef]
- Otegbeye, G.O.; Kellison, R.C. Genetics of wood and bark characteristics of Eucalyptus viminalis. Silvae Genet. 1980, 29, 27–31. [Google Scholar]
- Bdeir, R.; Muchero, W.; Yordanov, Y.; Tuskan, G.A.; Busov, V.; Gailing, O. Quantitative trait locus mapping of Populus bark features and stem diameter. BMC Plant Biol. 2017, 17, 224. [Google Scholar] [CrossRef] [PubMed]
- Kalbande, R.B. Digital visual bark: An image based tool for plant diversity research, diversity in bark supports in tree identification. Int. J. Life Sci. Pharma Res. 2014, 4, 17–24. [Google Scholar]
- Boudra, S.; Yahiaoui, I.; Behloul, A. A Comparison of Multi-scale Local Binary Pattern Variants for Bark Image Retrieval. In Advanced Concepts for Intelligent Vision Systems; Battiato, S., Blanc-Talon, J., Gallo, G., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer: Cham, Switzerland, 2015; Volume 9386, pp. 764–775. [Google Scholar]
- Nicolai, V. The bark of trees: Thermal properties, microclima and fauna. Oecologia 1986, 69, 148–160. [Google Scholar] [CrossRef]
- Rossel, J.A.; Castorena, M.; Laws, C.A.; Westoby, M. Bark ecology of twigs vs. main stems: Functional traits across eighty-five species angiosperms. Oecologia 2015, 178, 1033–1043. [Google Scholar] [CrossRef]
- Wang, X.H.; Ma, X.H.; Jin, G.Q.; Chen, L.Y.; Zhou, Z.C. Variation pattern of individual types and wood characters in natural stands of Schima superba. Sci. Silvae Sin. 2011, 47, 133–139. [Google Scholar]
- Mihai, D. Research on Fir Variability in Romania with a View to Expand Valuable Specimens to Plantations. Ph.D. Thesis, University of Brașov, Braşov, Romania, 1978. [Google Scholar]
- Ogata, A.; Itai, A.; Nishiyama, M.; Ikeda, H.; Kanahama, K. Analyses of early rough bark phenotype found in seedlings of a cross between the European pear ‘Bartlett’ and the Chinese pear ‘Yali’. Sci. Hortic. 2012, 148, 1–8. [Google Scholar] [CrossRef]
- Carlisle, A. A guide to the named variants of Scots pine (Pinus silvestris, Linnaeus). Forestry 1958, 31, 203–224. [Google Scholar] [CrossRef]
- Schelleng, J.C. Wood for violins. Catgut Acoust. Soc. Newsl. 1982, 37, 8–19. [Google Scholar]
- Ono, T.; Norimoto, M. On physical criteria for the selection of wood for soundboards of musical instruments. Rheol. Acta 1984, 23, 652–656. [Google Scholar] [CrossRef]
- Meyer, H.G. A practical approach to the choice of tone wood for the instruments of the violin family. Catgut Acoust. Soc. J. 1995, 2, 9–13. [Google Scholar]
- Brémaud, I. What Do We Know on “Resonance Wood” Properties? Selective Review and Ongoing Research; Societé Française d’Acoustique: Nantes, France, 2012; pp. 2760–2764. [Google Scholar]
- Wegst, U.G.K. Wood for sound. Am. J. Bot. 2006, 93, 1439–1448. [Google Scholar] [CrossRef] [PubMed]
- Brémaud, I. Acoustical properties of wood in string instruments soundboards and tuned idiophones: Biological and cultural diversity. J. Acoust. Soc. Am. 2012, 131, 807–818. [Google Scholar] [CrossRef]
- Woodhouse, J. The acoustics of the violin: A review. Rep. Prog. Phys. 2014, 77, 115901. [Google Scholar] [CrossRef]
- Mania, P.; Fabisiak, E.; Skrodzka, E. Investigation of modal behaviour of resonance spruce wood samples (Picea abies L.). Arch. Acoust. 2017, 42, 23–28. [Google Scholar] [CrossRef][Green Version]
- Haines, D.W. On musical instruments wood. Catgut Acoust. Soc. Newsl. 1979, 31, 23–32. [Google Scholar]
- Bucur, V. Towards an objective assessment of violin wood properties. Rev. For. Fr. 1983, 32, 130–137. [Google Scholar] [CrossRef]
- Ouis, D. Vibrational and acoustical experiments on logs of spruce. Wood Sci. Technol. 1999, 33, 151–184. [Google Scholar] [CrossRef]
- Gilbert, E.A.; Smiley, E.T. Picus Sonic tomography for the quantification of decay in white oak (Quercus Alba) and Hickory (Carya spp.). J. Arboric. 2004, 30, 277–281. [Google Scholar]
- Rinn, F. Central Defects in Sonic Tomography. 2015. Available online: http://download.rinntech.com/RINN_CentralDefectsInSonicTreeTomography_WesternArborist_Spring_2015.pdf (accessed on 20 June 2019).
- Gilbert, G.S.; Ballesteros, J.O.; Barrios-Rodriguez, C.A.; Bonadies, E.F.; Cedeno-Sanchez, M.L.; Fossatti-Caballero, N.J.; Trejos-Rodriguez, M.M.; Perez-Suniga, J.M.; Holub-Young, K.S.; Henn, L.A.W.; et al. Use of Sonic Tomography to Detect and Quantify Wood Decay in Living Trees. Appl. Plant Sci. 2016, 4, 1600060. [Google Scholar] [CrossRef] [PubMed]
- Lindström, H.; Harris, P.; Nakada, R. Methods for measuring stiffness of young trees. Holz Als Roh- Werkstoff 2002, 60, 165–174. [Google Scholar] [CrossRef]
- Wang, X.; Carter, P.; Ross, R.J.; Brashaw, B.K. Acoustic assessment of wood quality of raw forest materials—A path to increased profitability. For. Prod. J. 2007, 57, 6–14. [Google Scholar]
- Caniato, M.; Favretto, S.; Bettarello, F.; Schmid, C. Acoustic characterization of resonance wood. Acta Acust. United Acust. 2018, 104, 1030–1040. [Google Scholar] [CrossRef]
- Brémaud, I.; Ruelle, J.; Thibaut, A.; Thibaut, B. Changes in viscoelastic vibrational properties between compression and normal wood: Role of microfibril angle and of lignin. Holzforschung 2013, 67, 75–85. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. World Reference Base for Soils Resources; World Soil Research Report No. 84; FAO: Rome, Italy, 1998. [Google Scholar]
- Bouvarel, P. Variability of Norway spruce (Picea excelsa Link.) in the French Jura Mountains. Distribution and characters of different types. Rev. For. Fr. 1954, 6, 85–98. [Google Scholar] [CrossRef]
- Ohaus Corporation. MB45 Moisture Analyzer. Instruction Manual; Ohaus Co.: Parsippany, NJ, USA, 2001; p. 71. [Google Scholar]
- Hunt, R.W.G. Measuring Colour, 3rd ed.; Fountain Press: Kingston-upon-Thames, UK, 1998; p. 153. [Google Scholar]
- Konica-Minolta. Chroma Meter CR-400/410. Instruction Manual; Konica-Minolta Sensing Inc.: Osaka, Japan, 2007; p. 156. [Google Scholar]
- Dirckx, O.; Triboulot-Trouy, M.C.; Merlin, A.; Deglise, X. Changes of wood colour of Abies grandis exposed to solar radiation. Ann. For. Sci. 1992, 49, 425–447. [Google Scholar] [CrossRef]
- WinDENDRO. WinDENDROTM2006 for Tree-Ring Analysis. Manual of Exploitation; Régent Instruments Inc.: Québec City, QC, Canada, 2007; p. 133. [Google Scholar]
- Dinulică, F.; Albu, C.T.; Borz, S.A.; Vasilescu, M.M.; Petritan, I.C. Specific structural indexes for resonance Norway spruce wood used for violin manufacturing. Bioresources 2015, 10, 7525–7543. [Google Scholar] [CrossRef]
- Rinn, F. ARBOTOM®: 3-D Tree Impulse Tomograph. User Manual; Rinntech: Heidelberg, Germany, 2012; p. 57. [Google Scholar]
- Shen, J. Relationships between longitudinal and radial Picea genera sound vibration parameters. Front. For. Chin. 2006, 4, 431–437. [Google Scholar] [CrossRef]
- Keylwerth, R. A contribution to qualitative increment analysis. Eur. J. Wood Wood Prod. 1954, 12, 77–83. [Google Scholar] [CrossRef]
- Keith, C.T. Resin content of red pine wood and its effect on specific gravity determinations. For. Chron. 1969, 45, 338–343. [Google Scholar] [CrossRef]
- Zaițev, E.V. The acoustic properties of cedar wood. Деревooбрабатывающая прoмышленнoсть 1969, 7, 18–19. [Google Scholar]
- Brémaud, I. Diversity of Woods Used or Usable in Musical Instruments Making. Ph.D. Thesis, Montpellier II University, Montpellier, France, 2006. [Google Scholar]
- Polge, H. The quality of wood of the principal exotic conifers used in French plantations. Ann. Eaux For. 1963, 20, 403–469. [Google Scholar]
- Williamson, G.B.; Wiemann, M.C. Measuring wood specific gravity… Correctly. Am. J. Bot. 2010, 97, 519–524. [Google Scholar] [CrossRef]
- Smith, D.M. Maximum Moisture Content Method for Determining Specific Gravity of Small Wood Samples; Rep. no. 2014. USDA; Forest Service: Madison, WI, USA, 1954; p. 9. Available online: http://hdl.handle.net/1957/2445 (accessed on 10 February 2019).
- StatSoft Inc. STATISTICA (Data Analysis Software System), version 8.0; StatSoft Inc.: Tulsa, OK, USA, 2007. [Google Scholar]
- Zar, J.H. Biostatistical Analysis, 5th ed.; Pearson Prentice-Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Beldeanu, E.C. Forest Products and Wood Science; Transilvania University Publishing House: Brașov, Romania, 1999. [Google Scholar]
- Kuprevicius, A.; Auty, D.; Achim, A.; Caspersen, J.P. Quantifying the influence of live crown ratio on the mechanical properties of clear wood. Forestry 2013, 86, 361–369. [Google Scholar] [CrossRef]
- Lundström, T.; Heiz, U.; Stoffel, M.; Stöckli, V. Fresh-wood bending: Linking the mechanical and growth properties of a Norway spruce stem. Tree Physiol. 2007, 27, 1229–1241. [Google Scholar] [CrossRef]
- Norimoto, M.; Ono, T.; Watanabe, Y. Selection of wood used for piano soundboards. J. Soc. Rheol. Jpn. 1984, 9, 115–119. [Google Scholar] [CrossRef][Green Version]
- Gyllenstrand, N.; Clapham, D.; Källman, T.; Lagercrantz, U. A Norway spruce FLOWERING LOCUS T Homolog is implicated in control of growth rhytm in conifers. Plant Physiol. 2007, 144, 248–257. [Google Scholar] [CrossRef]
- Lagercrantz, U. At the end of the day: A common molecular mechanism for photoperiod responses in plants? J. Exp. Bot. 2009, 60, 2501–2515. [Google Scholar] [CrossRef] [PubMed]
- Karlgren, A.; Gyllenstrand, N.; Clapham, D.; Lagercrantz, U. FLOWERING LOCUS T/TERMINAL FLOWER1-LIKE genes affect growth rhytm and bud set in Norway spruce. Plant Physiol. 2013, 163, 792–803. [Google Scholar] [CrossRef] [PubMed]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamic of Conifer Tree Rings. Images of Past and Future Environments; Springer: Berlin/Heidelberg, Germany, 2006; p. 354. [Google Scholar]
- Stănescu, V.; Șofletea, N.; Popescu, O. Phetotypical circumstances concerning the Norway spruce genome. Rev. Silvic. Cineg. 1997, 2, 3–5. [Google Scholar]
- Stănescu, V.; Şofletea, N. Ecological genetic study in mountain spruce forests. Rev. Pădurilor 1990, 105, 114–119. [Google Scholar]
- Przybylski, T. Morphology. In Biology and Ecology of Norway Spruce; Tjoelker, M.G., Boratyński, A., Bugała, W., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 9–14. [Google Scholar]
- Godet, J.D. Guide of Barks of European Trees. Identify and Compare the Species; Delachaux et Niestlé: Paris, France, 2012; pp. 36–37. [Google Scholar]
- Niţu, C.; Răiescu, V.; Creangă, I. Research Concerning the Behaviour of Norway Spruce Provenances Tested in Different Site Conditions; Forest Research and Management Institute: Bucharest, Romania, 1984; p. 36. [Google Scholar]
- Geambașu, N. Research on the Management of Norway Spruce Resonance and Keyboard Stands; Tehnică Silvică Publishing House: Bucharest, Romania, 1995; pp. 64–77. [Google Scholar]
- Pașcovici, N. The spruce as resonance and keyboard wood. II The forest site conditions for the resonance spruce. Rev. Pădurilor 1930, 46, 279–305. [Google Scholar]
- Bolea, V.V.; Popescu, N.E.; Surdu, A.; Mandai, M. Ecological significances of nutrition biodiversity in Norway spruce. 1 Chemical composition of needles in relation to soil, branching, bark colour and health condition of the tree. Rev. Silvic. Cineg. 1996, 1, 9–17. [Google Scholar]
- Hejnowicz, A. Anatomy, embryology, and karyology. Bud structure and shoot development. In Biology and Ecology of Norway Spruce; Tjoelker, M.G., Boratyński, A., Bugała, W., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 49–342. [Google Scholar]
- Józefaciukowa, W.; Ubysz-Borucka, L. Variation in habit forms of Scots pine (Pinus silvestris L.) on the area of Poland. Silvae Genet. 1972, 21, 9–17. [Google Scholar]
- Yin, Y.; Jiang, X.; Wang, L.; Bian, M. Predicting wood quality of green logs by resonance vibration and stress wave in plantation-grown Populus × euramericana. For. Prod. J. 2011, 61, 136–142. [Google Scholar] [CrossRef]
- Ghelmeziu, N.; Beldie, I.P. On the characteristics of resonance spruce wood. Bull. Transilvania Univ. Brașov 1970, 12, 315–326. [Google Scholar]
- Spycher, M.; Schwarze, F.W.M.R.; Steiger, R. Assesment of resonance wood quality by comparing its physical and histological properties. Wood Sci. Technol. 2008, 42, 325–342. [Google Scholar] [CrossRef]
- Brancheriau, L.; Baillères, H.; Détienne, P.; Gril, J.; Kronland, R.; Metzger, B. Classifying xylophone bar materials by perceptual, signal processing and wood anatomy analysis. Ann. For. Sci. 2006, 63, 73–81. [Google Scholar] [CrossRef]
- Budeanu, M. Testing the Genetic Value of Some Norway Spruce Seed Sources in Multisite Comparative Trials. Ph.D. Thesis, Transilvania University of Braşov, Brașov, Romania, 2012. [Google Scholar]
- Baar, J.; Tippner, J.; Gryc, V. The influence of wood density on longitudinal wave velocity determined by the ultrasound method in comparison to the resonance longitudinal method. Eur. J. Wood Prod. 2012, 70, 767–769. [Google Scholar] [CrossRef]
- Vorobicov, A.M.; Evdokimova, N.I.; Okolykhina, L.V. The influence of density and moisture on the velocity of ultrasonic oscillations transmission through pine wood. Lesnoy Zhurnal 1968, 135, 106–109. [Google Scholar]
- Macareva, T.A. Factors affecting the constant acoustic of resonance wood. Деревooбрабатывающая прoмышленнoсть 1968, 10, 14–15. [Google Scholar]
- Bucur, V.; Lanceleur, P.; Roge, B. Acoustic properties of wood in tridimensional representation of slowness surfaces. Ultrasonics 2002, 40, 537–541. [Google Scholar] [CrossRef]
- Lachenbruch, B.; Jonson, G.R.; Downes, G.M.; Evans, R. Relationship of density, microfibril angle and sound velocity with stiffness and strength in mature wood of Douglas-fir. Can. J. For. Res. 2010, 40, 55–64. [Google Scholar] [CrossRef]
- Dinulică, F.; Albu, C.T.; Zdrob, G.S. What and how much do we know about the determinism of resonance Norway spruce? Rev. Pădurilor 2015, 130, 23–40. [Google Scholar]

| Features | Sample Plot | |||
|---|---|---|---|---|
| GUR1 | GUR2 | GUR3 | GUR4 | |
| Altitude (m asl) | 1380 | 1300 | 1215 | 1580 |
| Facing | NE | NW | W | NE |
| Slope (°) | 33 | 31 | 24 | 17 |
| Soil type * | Cmeu | CMdy | PZrs | BOis |
| Species composition ** | 100%NS | 80%NS 20%BC | 80%NS 10%BC 10%SF | 100%NS |
| Number of sampled trees | 44 | 61 | 30 | 10 |
| Diameter at breast height (cm) *** | 25...52...81 | 22.5...42...81 | 33...58...101 | 42...53...62 |
| Tree height (m) *** | 23...33...39.5 | 20...29...40.3 | 21...37...49.5 | 28...30...35 |
| Tree age (years at breast height) *** | 144...181...298 | 152...182...278 | 122...242...418 | 95...168...238 |
| Number of measured samples (cores a/discs b) | 66 a | 104 a | 58 a | 65 b |
| Quality Grade (SQC) | Structural Requirements to the Resonance Wood Zone * |
|---|---|
| 1. Wood of high structural quality | Ring width = 0.8 to 2.5 mm (average ≥ 1.2 mm). |
| Average latewood proportion ≤ 20%. | |
| Average difference in width between consecutive rings ≤ 0.5 mm. | |
| Ring width regularity index ≤ 0.7. | |
| Width of resonance wood ≥ 130 mm. | |
| 2. Wood of average structural quality | Ring width = 0.8 to 2.5 mm. |
| Average latewood proportion ≤ 35%. | |
| Average difference in width between consecutive rings ≤ 0.6 mm. | |
| Width of resonance wood ≥ 130 mm. | |
| 3. Wood of low structural quality | Ring width ≤ 3.0 mm (average ≥ 0.5 mm). |
| Average latewood proportion ≤ 39%. | |
| Average difference in width between consecutive rings ≤ 1.0 mm. | |
| Width of resonance wood ≥ 130 mm. | |
| 4. Wood from young resonance trees | The wood meets the requirements imposed on SQC2—with the exception of the resonance zone width—which is insufficient for a violin flitch (130 mm), but exceeds 50 mm. |
| Diameter at breast height ≤ 38 cm. | |
| 5. Wood from thick trees, with insufficient width of the resonance wood | Diameter at breast height > 38 cm, tree age > 150 years; |
| 50 ≤ width of resonance wood < 130 mm. | |
| 6. Wood with no structural-acoustic qualities | Width of resonance wood < 50 mm or; |
| average ring width ≤ 0.5 mm. |
| Source of Variation | LS | WS | SS | L * | a * | b * | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | p | H | p | H | p | H | p | H | p | H | p | |
| Sample plot | 13.81 | 0.008 | 12.00 | 0.017 | 33.63 | <0.001 | 38.86 | <0.001 | 6.80 | 0.15 | 6.96 | 0.14 |
| Tree × plot | 11.00 | 0.25 | 9.88 | 0.36 | 10.82 | 0.29 | 14.75 | 0.10 | 3.12 | 0.96 | 16.49 | 0.05 |
| Tree | 23.08 | 0.006 | 15.52 | 0.08 | 16.04 | 0.007 | 30.03 | 0.0004 | 4.34 | 0.89 | 14.29 | 0.11 |
| Cardinal point | 3.02 | 0.08 | 7.22 | 0.007 | 0.29 | 0.59 | 1.93 | 0.17 | 1233.21 | <0.001 | 938.3 | <0.001 |
| Scale | 6.00 | 0.74 | 6.00 | 0.74 | 6.00 | 0.74 | 9.00 | 0.44 | 10.00 | 0.35 | 9.00 | 0.44 |
| Scale × sample plot | 132.23 | <0.001 | 45.72 | <0.001 | 18.31 | <0.001 | 0.814 | 0.67 | 1.85 | 0.40 | 0.03 | 0.98 |
| Predictor | Dependent Variable | Spearman Rank Order Simple Correlation/p | Multiple Correlation with TA or DBH/p | Partial Correlation with TA or DBH/p | ||
|---|---|---|---|---|---|---|
| TA/p • | DBH/p • | TA | DBH | |||
| Scale slenderness index | CITRW | −0.698/0.02 | 0.857/0.015 | 0.683/0.45 | −0.855 | −0.665 |
| CILWW | −0.914/<0.0001 | 0.903/0.25 | 0.879/0.98 | −0.903 | −0.879 | |
| CILWP | −0.729/0.02 | 0.921/0.03 | 0.837/0.503 | −0.875 | −0.834 | |
| SQC | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | - | 3.19/1.48 | 3.17/1.86 | 1.15/4.32 | 4.48/1.00 | 7.52/2.51 |
| 2 | - | 1.13/1.56 | 2.14/5.79 | 2.63/1.42 | 5.59/3.78 | |
| 3 | - | 2.03/5.56 | 1.63/0.94 | 4.73/3.05 | ||
| 4 | - | 3.40/4.79 | 6.49/2.75 | |||
| 5 | - | 3.13/2.46 | ||||
| 6 | - |
| Feature | Mean/Confidence | Coefficient of Variation (%) | Source of Variation | ||
|---|---|---|---|---|---|
| p from ANOVA F Test * | |||||
| Stand | Tree | SQC | |||
| Transverse velocity in standing trees ** (m·s−1) | 1132.99/1123.68–1142.31 | 14.52 | <0.001 | <0.001 | <0.001 |
| Transverse velocity in discs *** (m·s−1) | 1334.12/1251.82–1416.41 | 28.25 | - | 0.66 | 0.005 |
| Basic density (g·cm−3) | 0.366/0.358–0.373 | 11.08 | 0.54 | <0.001 | 0.69 |
| Transverse radiation ratio in standing trees (10−3·m4/kg·s) | 3047.17/2773.37–3320.98 | 20.78 | 0.99 | <0.001 | <0.001 |
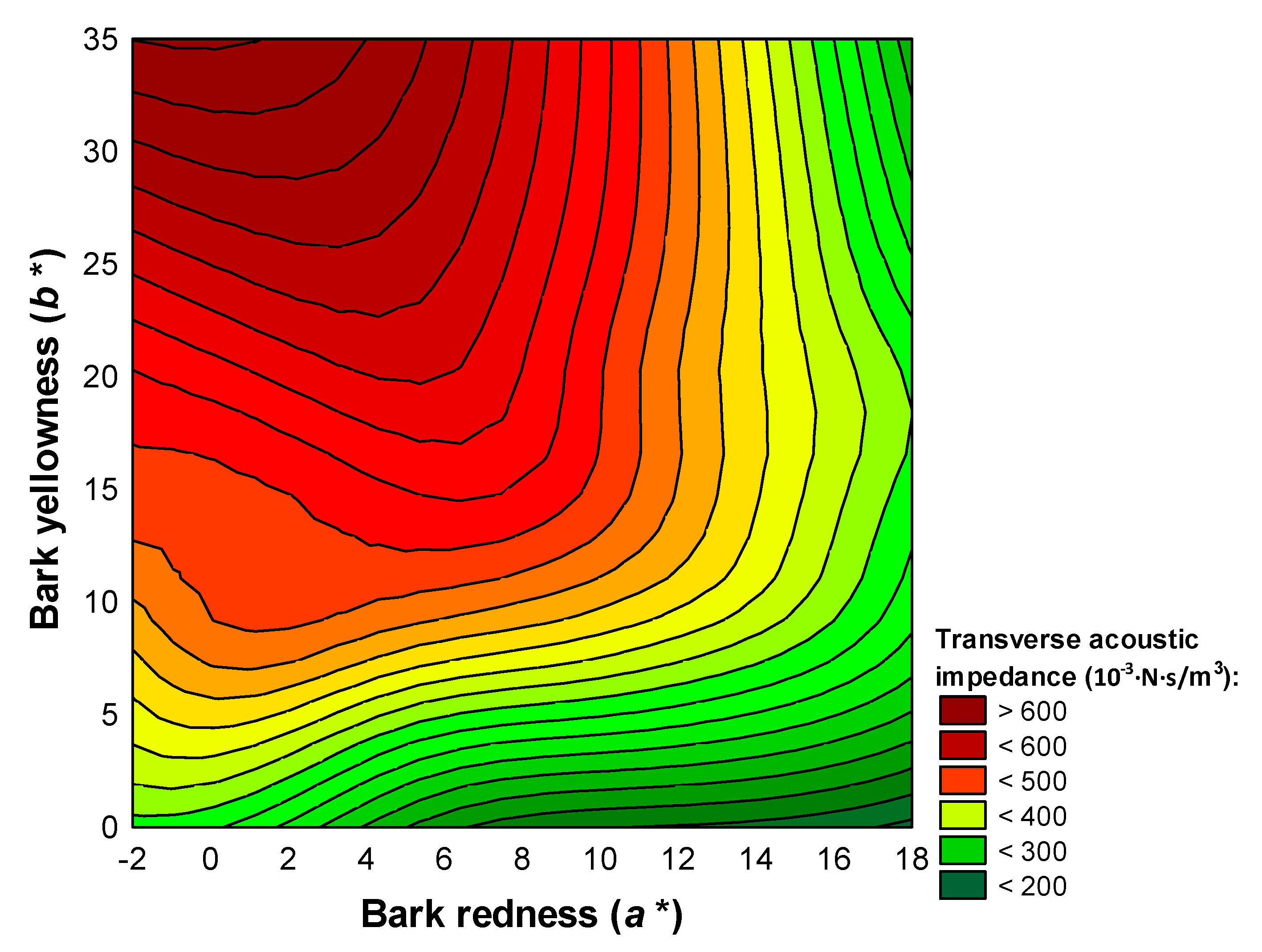
| Transverse acoustic impedance in standing trees (103·N·s/m3) | 437.85/406.05–469.65 | 16.80 | <0.001 | 0.75 | |
| Dependent Variable | Predictor (s) | Statistical Model | Adjusted R2 | F | p |
|---|---|---|---|---|---|
| Transverse sound velocity | Bark redness on the back of the north-facing scales (), bark redness on the outside of the south-facing scales () | y = 847.54 + 30.14 × − 57.88 × | 0.416 | 5.68 | <0.001 |
| Specific acoustic resistance of wood | Bark yellowness on the outside of the south-facing scales (), bark redness on the outside of the south-facing scales () | y = 279.85 + 25.18 × 36.57 × | 0.472 | 5.91 | 0.002 |
| Radiation ratio | Bark yellowness on the outside of the south-facing scales ( | y = 3953.14 − 130.24 × | 0.284 | 5.37 | 0.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dinulică, F.; Albu, C.-T.; Vasilescu, M.M.; Stanciu, M.D. Bark Features for Identifying Resonance Spruce Standing Timber. Forests 2019, 10, 799. https://doi.org/10.3390/f10090799
Dinulică F, Albu C-T, Vasilescu MM, Stanciu MD. Bark Features for Identifying Resonance Spruce Standing Timber. Forests. 2019; 10(9):799. https://doi.org/10.3390/f10090799
Chicago/Turabian StyleDinulică, Florin, Cristian-Teofil Albu, Maria Magdalena Vasilescu, and Mariana Domnica Stanciu. 2019. "Bark Features for Identifying Resonance Spruce Standing Timber" Forests 10, no. 9: 799. https://doi.org/10.3390/f10090799
APA StyleDinulică, F., Albu, C.-T., Vasilescu, M. M., & Stanciu, M. D. (2019). Bark Features for Identifying Resonance Spruce Standing Timber. Forests, 10(9), 799. https://doi.org/10.3390/f10090799






