Author Contributions
Conceptualization, L.G.B.; methodology, L.G.B. and J.R.B.; software, L.G.B. and S.M.; validation, L.G.B., S.M. and J.R.B.; writing of first manuscript draft, L.G.B.; review and editing of manuscript versions, L.B, J.R.B., S.M.; visualization, L.G.B. and J.R.B.; funding acquisition, J.R.B.
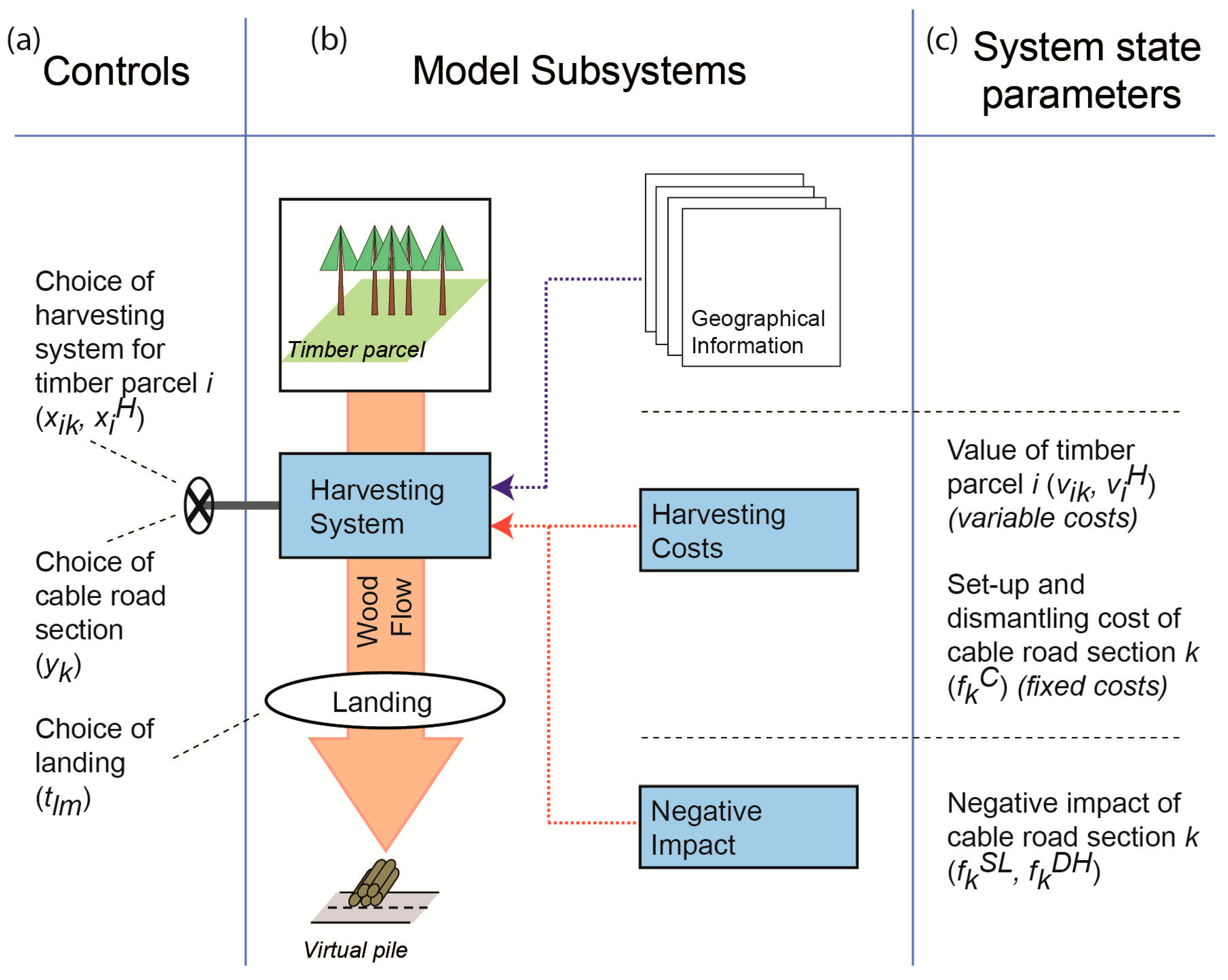
Figure 1.
Conceptual model with controls, i.e., decision variables (a), model subsystems (b), and system state parameters (c).
Figure 1.
Conceptual model with controls, i.e., decision variables (a), model subsystems (b), and system state parameters (c).
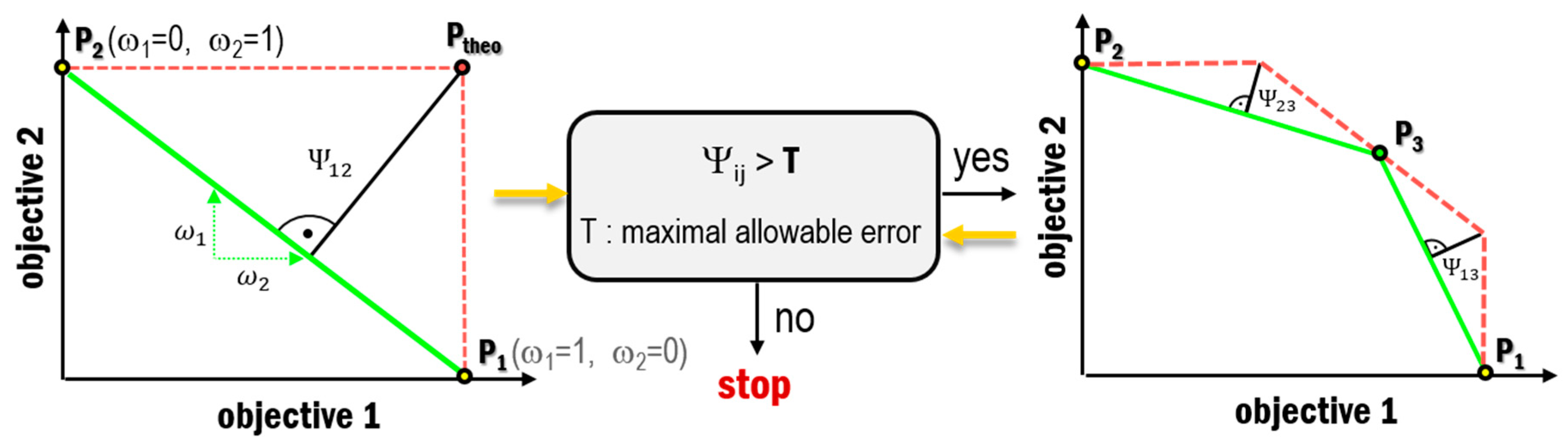
Figure 2.
The NISE approach, where solutions are iteratively added to the Pareto set until a maximum allowable error is no longer violated. The weight combinations for new solutions result from the slopes when the points of the current pareto set are connected.
Figure 2.
The NISE approach, where solutions are iteratively added to the Pareto set until a maximum allowable error is no longer violated. The weight combinations for new solutions result from the slopes when the points of the current pareto set are connected.
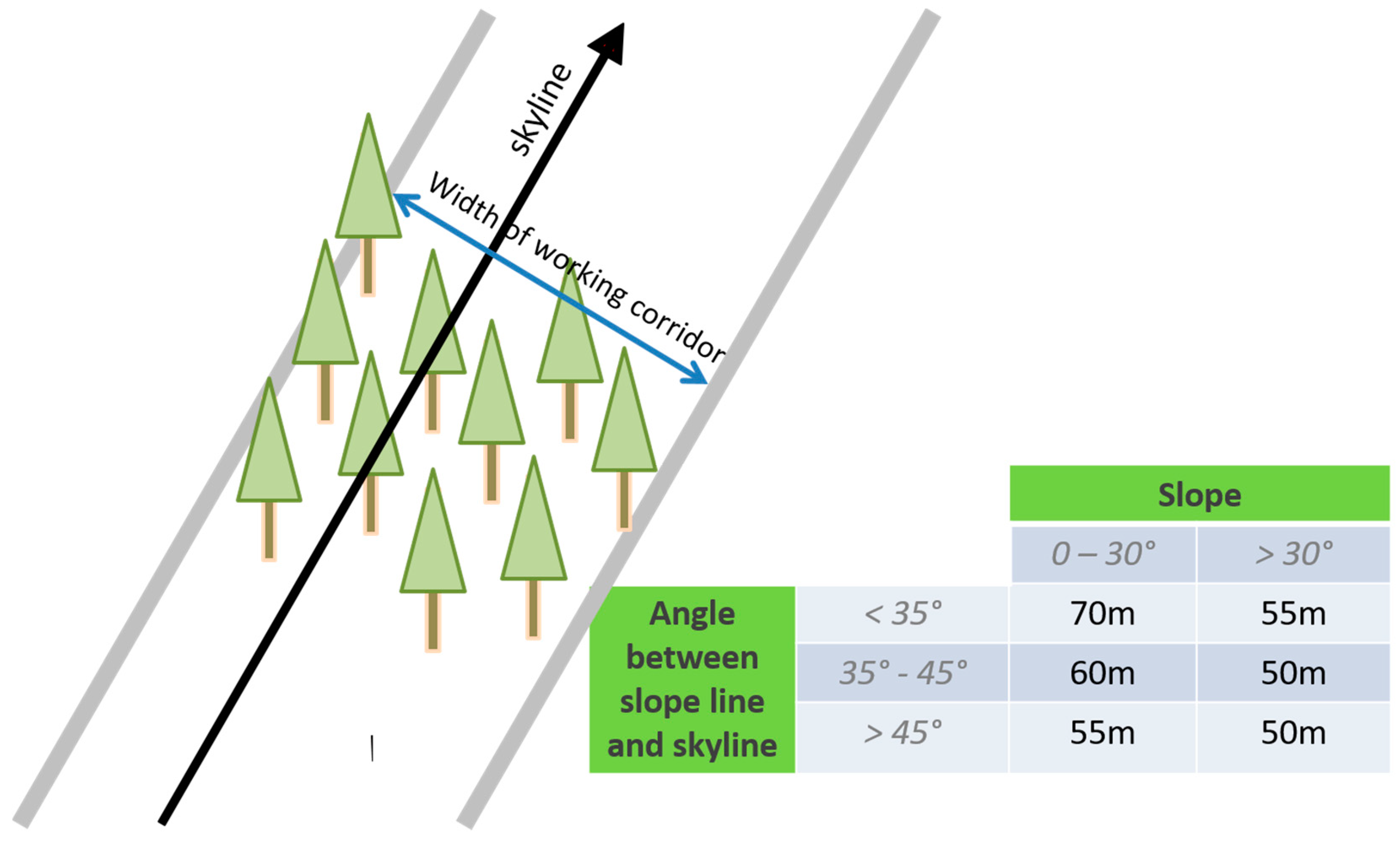
Figure 3.
Width of the working corridor within a CR, depending on the slope and the angle between slope line and skyline.
Figure 3.
Width of the working corridor within a CR, depending on the slope and the angle between slope line and skyline.
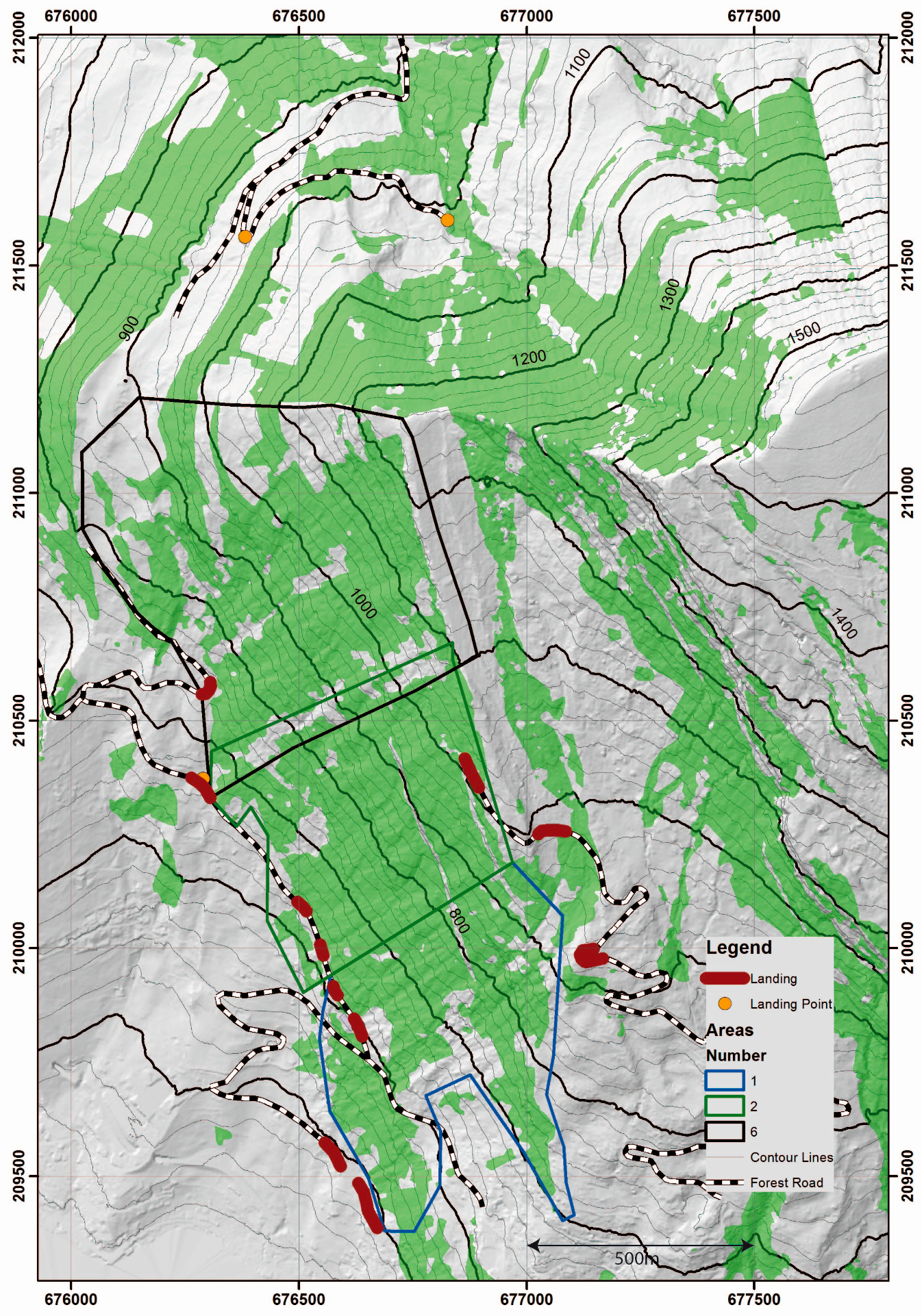
Figure 4.
Rigi test areas. Here only sub-area numbers 1, 2 and 6 are displayed. Sub-areas 7, 8 and 9 are not displayed. Area 7 is composed of sub-areas of areas 6 and 2, area 8 covers areas 1 and 2, and area 9 covers the whole project area. Note that the landings and the forest road at the bottom right have a limited bearing capacity, leading to additional trans-shipment costs of 15 CHF/m3 (hillshade map © swisstopo (JA100118)).
Figure 4.
Rigi test areas. Here only sub-area numbers 1, 2 and 6 are displayed. Sub-areas 7, 8 and 9 are not displayed. Area 7 is composed of sub-areas of areas 6 and 2, area 8 covers areas 1 and 2, and area 9 covers the whole project area. Note that the landings and the forest road at the bottom right have a limited bearing capacity, leading to additional trans-shipment costs of 15 CHF/m3 (hillshade map © swisstopo (JA100118)).
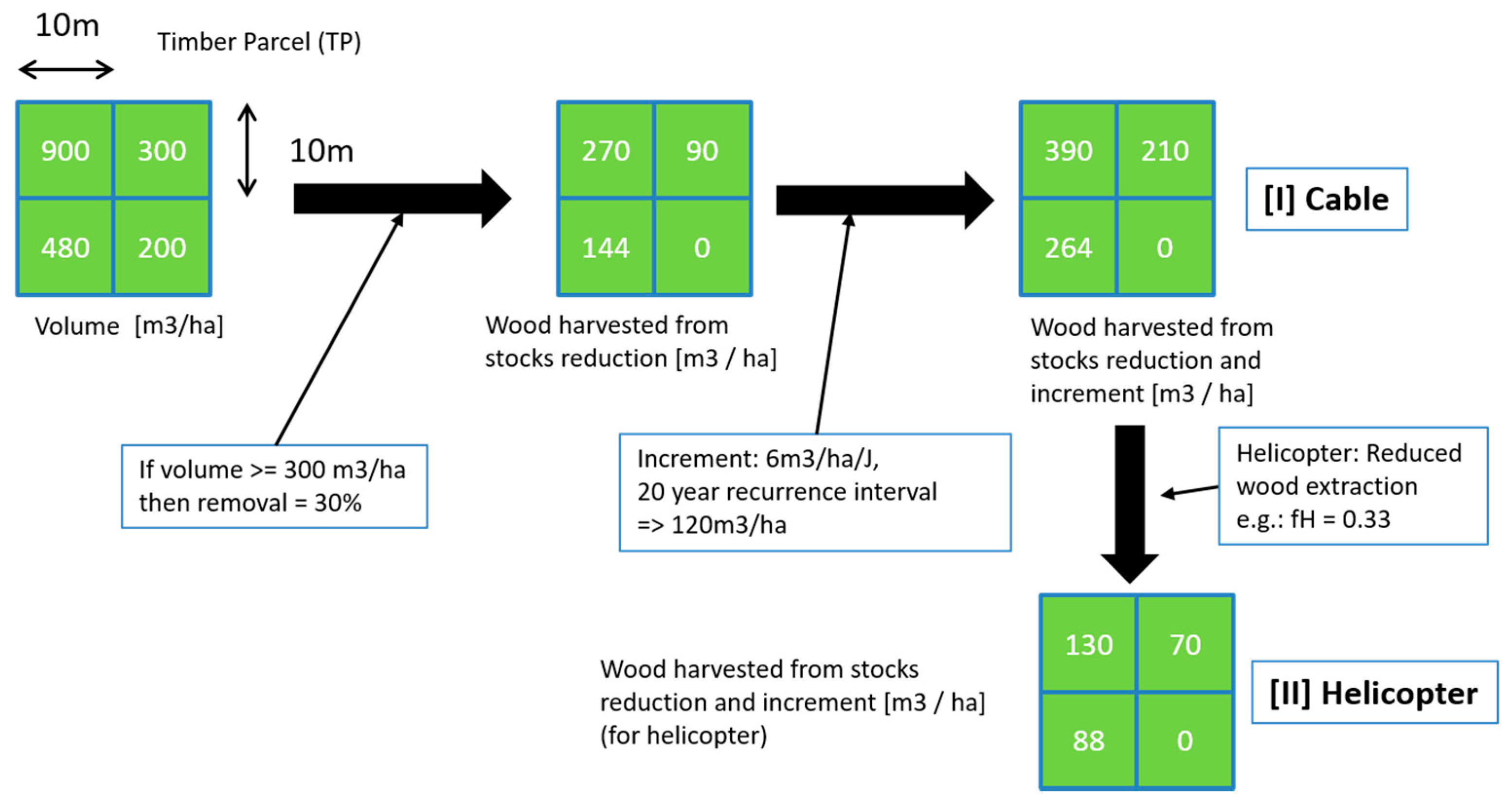
Figure 5.
Estimation of the amount of wood to harvest for some exemplary chosen numbers for the volume map.
Figure 5.
Estimation of the amount of wood to harvest for some exemplary chosen numbers for the volume map.
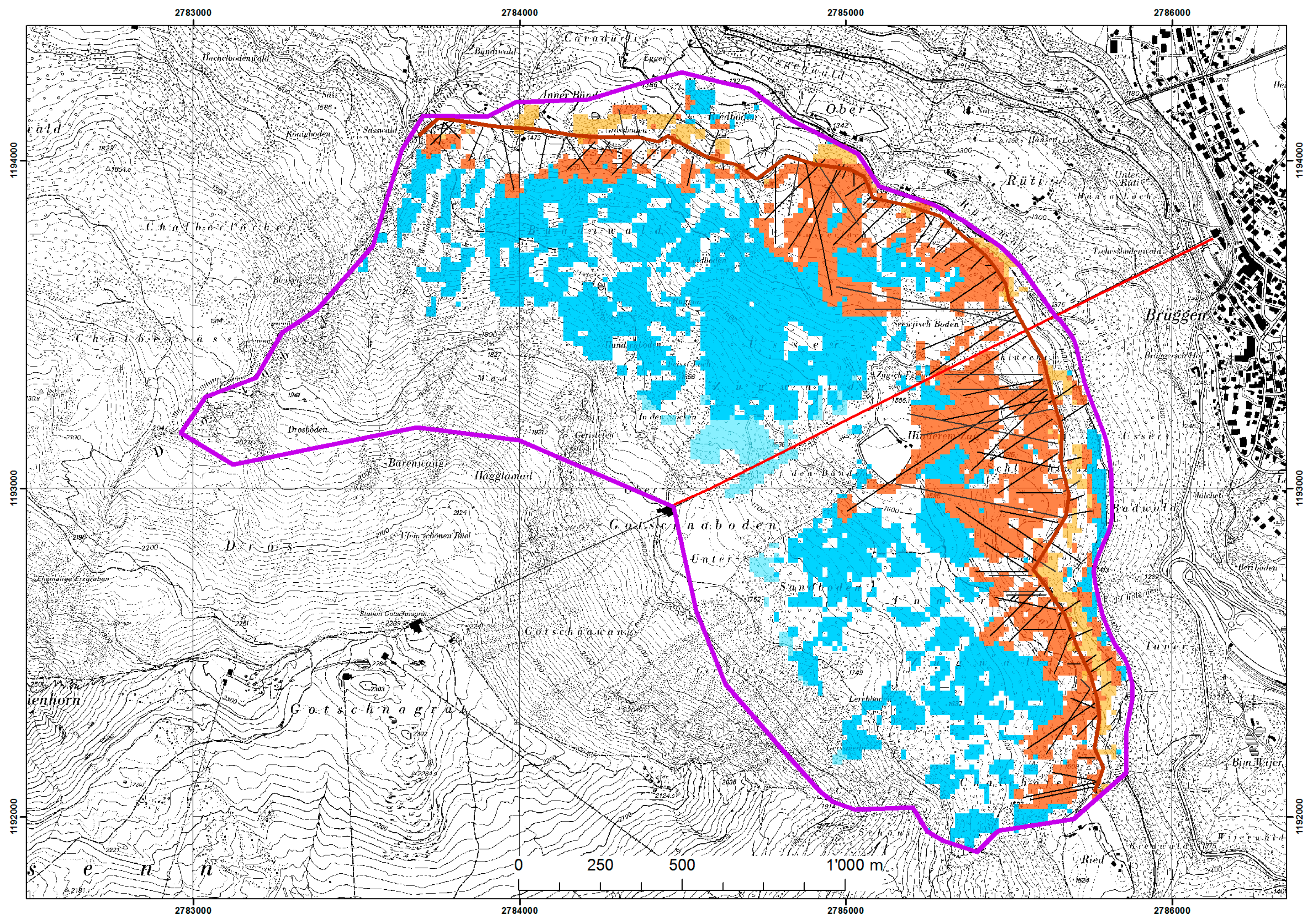
Figure 6.
Sub-areas (numbered) in the Gotschna area subject to computation (topographic map © swisstopo (JA100118)).
Figure 6.
Sub-areas (numbered) in the Gotschna area subject to computation (topographic map © swisstopo (JA100118)).
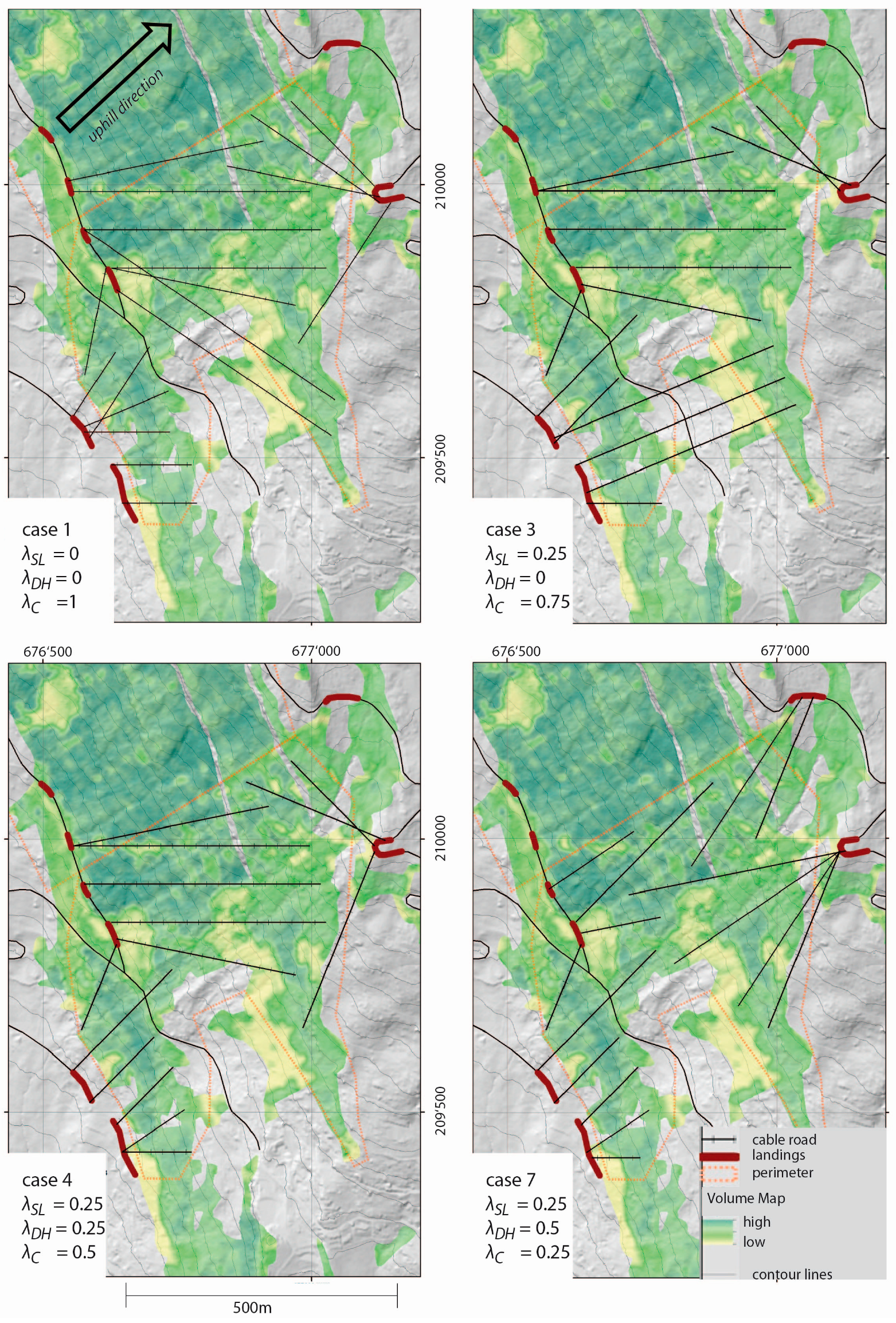
Figure 7.
CR and harvesting layouts of weighting cases 1, 3, 4, and 7 (with
fH = 0.7) for area 01. The corresponding properties of those layouts can be found in
Table 6.
Figure 7.
CR and harvesting layouts of weighting cases 1, 3, 4, and 7 (with
fH = 0.7) for area 01. The corresponding properties of those layouts can be found in
Table 6.
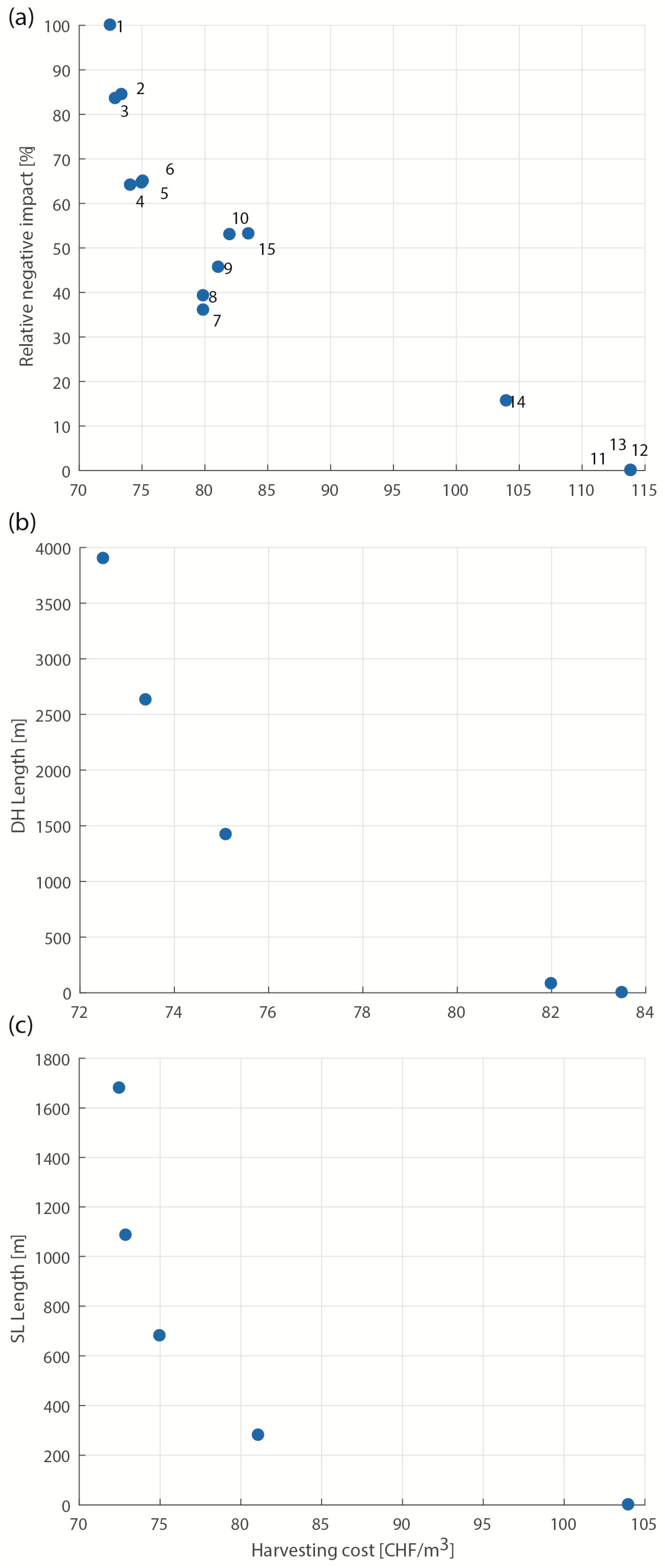
Figure 8.
Pareto-optimal solutions for Rigi, Area 01, for (a) harvesting costs and relative negative impact (RNI), with case numbers displayed; (b) downhill logging length and harvesting costs (only cases with λSL = 0); and (c) slope line length and harvesting costs (only cases with λDH = 0).
Figure 8.
Pareto-optimal solutions for Rigi, Area 01, for (a) harvesting costs and relative negative impact (RNI), with case numbers displayed; (b) downhill logging length and harvesting costs (only cases with λSL = 0); and (c) slope line length and harvesting costs (only cases with λDH = 0).
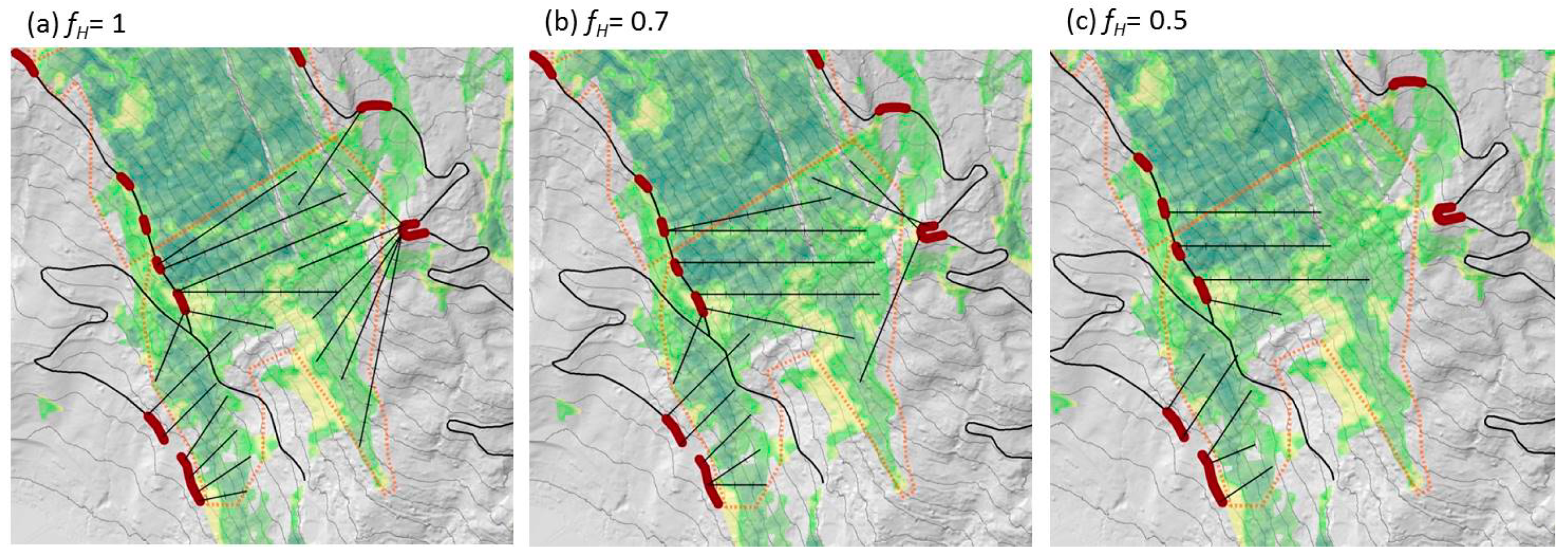
Figure 9.
Harvesting layout for area 1 (Rigi) for different
fH values (a: = 1, b: = 0.7, c: = 0.5) (helicopter wood extraction factor) (weighting:
λSL = 0.25,
λDH = 0.25,
λC = 0.50). The darker green areas have a larger volume per TP. The corresponding properties of those layouts can be found in
Table 6.
Figure 9.
Harvesting layout for area 1 (Rigi) for different
fH values (a: = 1, b: = 0.7, c: = 0.5) (helicopter wood extraction factor) (weighting:
λSL = 0.25,
λDH = 0.25,
λC = 0.50). The darker green areas have a larger volume per TP. The corresponding properties of those layouts can be found in
Table 6.
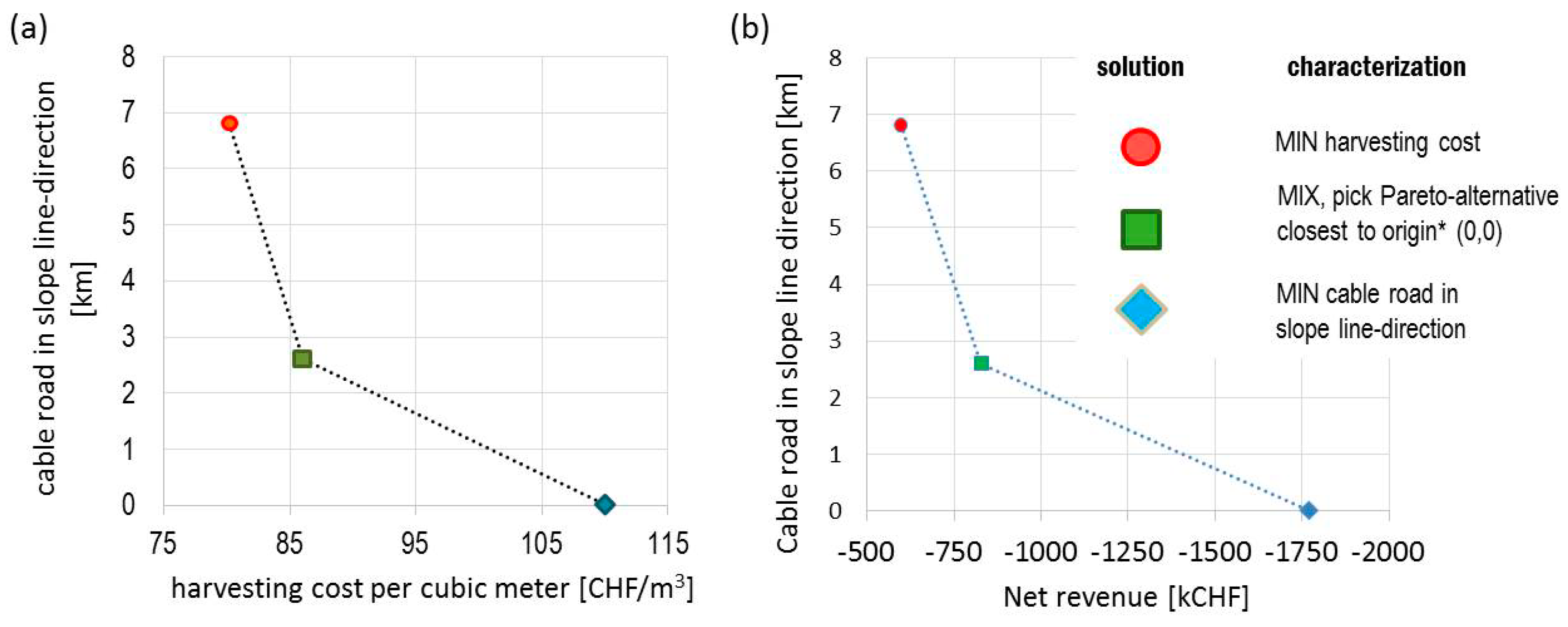
Figure 10.
Aggregated results of the Pareto set consisting of the variants minimum harvesting costs (MIN-EK) (circle), minimum CR length in unfavorable direction (MIN-UR) (diamond) and MIX (square). In (a) the variants are characterized according to the negative net revenue and the length of CR in an unfavorable direction relative to the slope line. In (b) the variants are characterized according to the average harvest costs per cubic meter. (* objective weights applied to sub-units differ ➲ define merging rule).
Figure 10.
Aggregated results of the Pareto set consisting of the variants minimum harvesting costs (MIN-EK) (circle), minimum CR length in unfavorable direction (MIN-UR) (diamond) and MIX (square). In (a) the variants are characterized according to the negative net revenue and the length of CR in an unfavorable direction relative to the slope line. In (b) the variants are characterized according to the average harvest costs per cubic meter. (* objective weights applied to sub-units differ ➲ define merging rule).
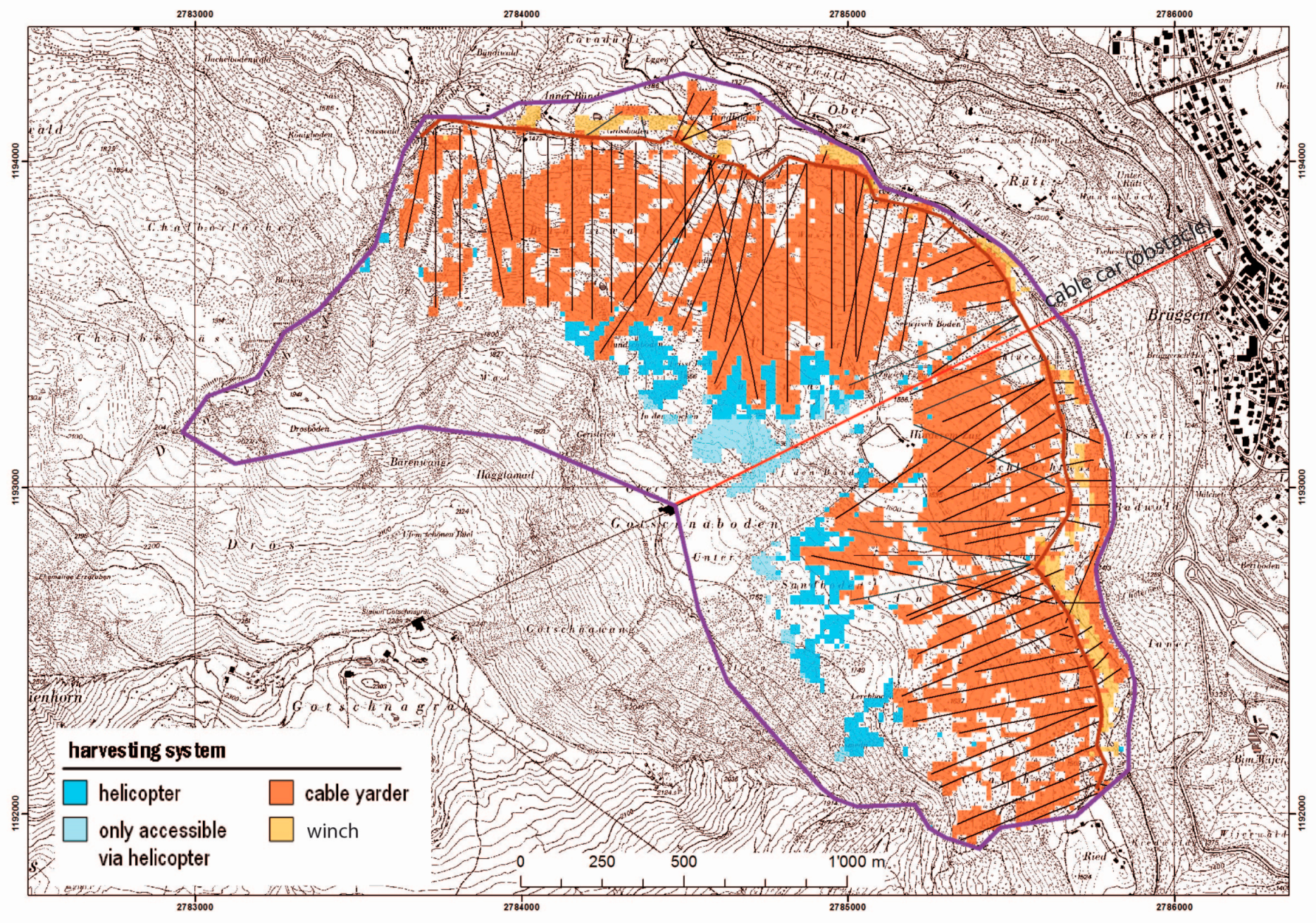
Figure 11.
Harvesting and CR layout for MIN-EK (minimize harvesting cost) (topographic map © swisstopo (JA100118)).
Figure 11.
Harvesting and CR layout for MIN-EK (minimize harvesting cost) (topographic map © swisstopo (JA100118)).
Figure 12.
Harvesting and CR layout for MIX (multiobjective solution) (topographic map © swisstopo (JA100118)).
Figure 12.
Harvesting and CR layout for MIX (multiobjective solution) (topographic map © swisstopo (JA100118)).
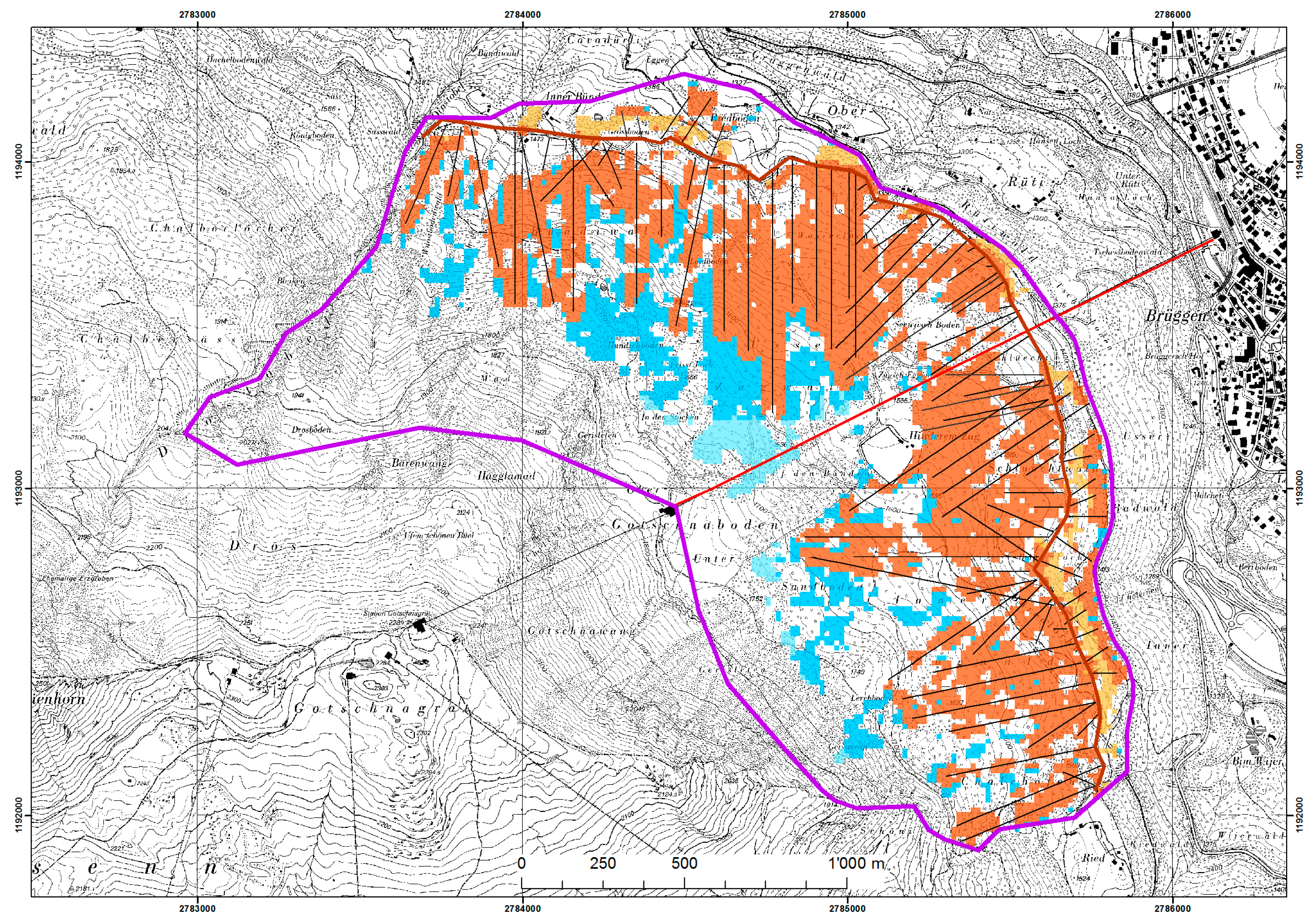
Figure 13.
Harvesting and CR layout for MIN-UR (minimize length in unfavorable CR direction) (topographic map © swisstopo (JA100118)).
Figure 13.
Harvesting and CR layout for MIN-UR (minimize length in unfavorable CR direction) (topographic map © swisstopo (JA100118)).
Table 1.
Critical aisle properties for avalanches. The first column indicates that aisles steeper than 30° and longer than 60 m can cause avalanches.
Table 1.
Critical aisle properties for avalanches. The first column indicates that aisles steeper than 30° and longer than 60 m can cause avalanches.
| Slope | Length of Aisle in Slope Line |
|---|
| >30° | >60 m |
| >35° | >50 m |
| >40° | >40 m |
| >45° | >30 m |
Table 2.
Penalty value for the angle of deviation of the cable roads (CR) direction from the slope line. (L: length of the CR within the corresponding angle of deviation).
Table 2.
Penalty value for the angle of deviation of the cable roads (CR) direction from the slope line. (L: length of the CR within the corresponding angle of deviation).
| Angle (α) of Deviation of the Yarding Direction from Slope Line | Penalty Values |
|---|
| Rigi | Gotschna |
|---|
| 0–10° | L × 0.5 | L |
| 10–25° | 0 | L |
| 25–35° | 0 | 0 |
| 35–45° | L × 0.5 | L |
| 45–90° | L × 2 | L |
Table 3.
Parameters of the harvesting techniques. (MSK: short distance yarder, KSK: long distance yarder).
Table 3.
Parameters of the harvesting techniques. (MSK: short distance yarder, KSK: long distance yarder).
| Harvesting Technique | Parameter | Unit | Values (Gotschna) | Values (Rigi) |
|---|
| Cable yarder | Minimum length (diagonal distance) (all) | m | 100 | 100 |
| | Maximum length (diagonal distance) (MSK/KSK) | m | 600/800 | 1000/-- |
| | average diagonal distance (used for calibration) | m | 500 | 600 |
| | Width of working corridor | m | 60 | dependent on slope |
| | Minimum ground clearance (load path) | m | 8 | 6 |
| | Design payload (carriage and load) | kN | 25 | 25 |
| | Range of values for favorable deviation from slope line | ° | 25–35 | 10–35 |
| | Installation cost (MSK/KSK) (used for calibration) | CHF | 200/800 | 200/800 |
| | Harvesting cost: felling, processing and yarding (MSK/KSK) (used for calibration) | CHF/m3 | 72/87 | 100/-- |
| Winch | Maximum skidding distance uphill | m | 60 | 60 |
| | Maximum skidding distance downhill | m | 0 | 50 |
| | Harvesting cost: felling, processing and skidding | CHF/m3 | 45 | 45 |
| Helicopter | Harvesting cost: felling, processing and logging | CHF/m3 | 135 | 150 |
| All | Average revenue for wood | CHF/m3 | 65 | 55 |
Table 4.
Size and properties of the variables of the test areas. The variables have the following meaning: xic: number of combinations to harvest a timber parcel (TP) (clustered with number of clusters = 3) yk: number of CR sections, tlm: number of landings, xiH: number of TPs.
Table 4.
Size and properties of the variables of the test areas. The variables have the following meaning: xic: number of combinations to harvest a timber parcel (TP) (clustered with number of clusters = 3) yk: number of CR sections, tlm: number of landings, xiH: number of TPs.
| | | Number of Variables & Variable Type | Size (ha) |
|---|
| | | xic (nc = 3) | yk | tlm | xiH | |
|---|
| | Area | cont. | integer | cont. | cont. | |
| Rigi | 1 | 6430 | 4871 | 83 | 2722 | 28 |
| 2 | 7664 | 4449 | 83 | 2924 | 30 |
| 6 | 10,027 | 2594 | 48 | 4415 | 45 |
| 7 | 9993 | 4719 | 61 | 3945 | 40 |
| 8 | 12,028 | 7428 | 92 | 4770 | 48 |
| 9 | 21,922 | 9531 | 92 | 9053 | 91 |
| Gotschna | 1 | 10,781 | 6923 | 373 | 1561 | 35 |
| 2 | 9350 | 5716 | 465 | 1497 | 34 |
| 3 | 15,763 | 14,552 | 220 | 3066 | 69 |
| 4 | 16,021 | 14,849 | 266 | 3009 | 68 |
| 5 | 13,201 | 8967 | 222 | 1515 | 34 |
| 6 | 11,185 | 14,807 | 138 | 2670 | 60 |
| 7 | 20,935 | 14,125 | 234 | 2569 | 58 |
Table 5.
Key values for different objective weighting alternatives (Rigi, Sub-area 1).
Table 5.
Key values for different objective weighting alternatives (Rigi, Sub-area 1).
| | Weight | | | | |
|---|
| Case | Cost | Slope Line | Downhill Logging | Net Revenue (CHF) | Harvesting Cost (CHF/m3) | Slope Line Penalty Value (m) | Length DH Logging (m) |
|---|
| 1 | 1.00 | 0 | 0 | −39,043 | 72.5 | 1680 | 3900 |
| 2 | 0.75 | 0 | 0.25 | −41,681 | 73.4 | 1780 | 2630 |
| 3 | 0.75 | 0.25 | 0 | −40,104 | 72.9 | 1085 | 3840 |
| 4 | 0.50 | 0.25 | 0.25 | −43,776 | 74.1 | 890 | 2840 |
| 5 | 0.50 | 0.50 | 0 | −46,697 | 75.0 | 680 | 3260 |
| 6 | 0.50 | 0 | 0.50 | −46,892 | 75.1 | 1700 | 1420 |
| 7 | 0.25 | 0.25 | 0.50 | −62,059 | 79.9 | 520 | 1560 |
| 8 | 0.25 | 0.50 | 0.25 | −62,048 | 79.9 | 375 | 2050 |
| 9 | 0.25 | 0.75 | 0 | −65,860 | 81.1 | 280 | 2670 |
| 10 | 0.25 | 0 | 0.75 | −68,674 | 82.0 | 1975 | 80 |
| 11 | 0.02 | 0.24 | 0.73 | −168,011 | 113.9 | 0 | 0 |
| 12 | 0.02 | 0.49 | 0.49 | −168,011 | 113.9 | 0 | 0 |
| 13 | 0.02 | 0.73 | 0.24 | −168,011 | 113.9 | 0 | 0 |
| 14 | 0.02 | 0.98 | 0.00 | −137,051 | 104.0 | 0 | 1090 |
| 15 | 0.02 | 0.00 | 0.98 | −73,055 | 83.5 | 2025 | 0 |
Table 6.
CR and harvesting layouts properties of weighting cases 1, 3, 4, and 7. The corresponding visualizations can be found in
Figure 7 and
Figure 9. A. (H, W): Alternative helicopter or winch.
Table 6.
CR and harvesting layouts properties of weighting cases 1, 3, 4, and 7. The corresponding visualizations can be found in
Figure 7 and
Figure 9. A. (H, W): Alternative helicopter or winch.
| Case Number | fH | No. of TPs Harvested by | Total Length of CRs (m) | Volume Harvested by (m3) |
|---|
| A. (H, W) | Yarder | A. (H, W) | Yarder | Total |
|---|
| 1 | 0.7 | 1055 | 1675 | 5310 | 189 | 2845 | 3034 |
| 3 | 0.7 | 1117 | 1613 | 4510 | 257 | 2748 | 3005 |
| 4 | 1 | 1117 | 1613 | 5070 | 379 | 2736 | 3115 |
| 0.7 | 1209 | 1521 | 3860 | 353 | 2611 | 2964 |
| 0.5 | 1837 | 893 | 1900 | 763 | 1590 | 2352 |
| 7 | 0.7 | 1291 | 1439 | 3850 | 452 | 2469 | 2921 |
Table 7.
Computation time for solving the optimization problem with GUROBI [seconds] (n.s.: not solved within 2 days, n.c.: not calculated). Area numbers with an “a” (e.g. 1a, 2a) indicate that the harvesting volume for helicopter logging is less than for cable logging per parcel (fH = 1/3, basis: fH = 1/2).
Table 7.
Computation time for solving the optimization problem with GUROBI [seconds] (n.s.: not solved within 2 days, n.c.: not calculated). Area numbers with an “a” (e.g. 1a, 2a) indicate that the harvesting volume for helicopter logging is less than for cable logging per parcel (fH = 1/3, basis: fH = 1/2).
| Weight | Area Number [Rigi] & Number of TPs | |
|---|
| Cost | Slope Line | Downhill | 1 | 1a | 2 | 2a | 6 | 6a | 7 | 7a | 8 | 8a | 9 | 9a |
|---|
| 2722 | 2722 | 2924 | 2924 | 4415 | 4415 | 3945 | 3945 | 4770 | 4770 | 9053 | 9053 |
|---|
| 1.00 | 0 | 0 | 126 | 12.9 | 7606 | 87.3 | 92.2 | 4.6 | n.s. | 4263 | n.s. | 7108 | n.s. | n.s. |
| 0.75 | 0 | 0.25 | 466 | 8.7 | 16 359 | 216 | 79.0 | 2.8 | n.c. | 4441 | n.c. | 9535 | n.c. | n.c. |
| 0.75 | 0.25 | 0 | 187 | 5.5 | 1429 | 49.6 | 17.0 | 8.0 | n.c. | 743 | n.c. | 5603 | n.c. | n.c. |
| 0.50 | 0.25 | 0.25 | 60.8 | 1.1 | 2136 | 13.0 | 17.1 | 1.8 | n.c. | 54.3 | n.c. | 1989 | n.c. | n.c. |
| 0.50 | 0.50 | 0 | 21.9 | 0.6 | 120 | 6.8 | 5.3 | 0.5 | n.c. | 7.0 | n.c. | 401 | n.c. | n.c. |
| 0.50 | 0 | 0.50 | 107 | 1.2 | 48 751 | 126 | 56.8 | 1.5 | n.c. | 579 | n.c. | 7993 | n.c. | n.c. |
| 0.25 | 0.25 | 0.50 | 49.6 | 0.2 | 909 | 1.4 | 5.5 | 0.4 | n.c. | 0.4 | n.c. | 3.6 | n.c. | n.c. |
| 0.25 | 0.50 | 0.25 | 11.7 | 0.4 | 75.1 | 0.9 | 1.5 | 0.2 | n.c. | 0.4 | n.c. | 1.8 | n.c. | n.c. |
| 0.25 | 0.75 | 0 | 1.4 | 0.9 | 4.2 | 1.2 | 0.8 | 1.0 | n.c. | 0.4 | n.c. | 4.4 | n.c. | n.c. |
| 0.25 | 0 | 0.75 | 6.2 | 0.6 | 141 | 1.0 | 2.4 | 0.4 | n.c. | 0.3 | n.c. | 0.6 | n.c. | n.c. |
| 0.01 | 0.25 | 0.74 | 0.4 | 0.2 | 0.5 | 0.3 | 0.2 | 0.4 | n.c. | 0.2 | n.c. | 0.3 | n.c. | n.c. |
| 0.01 | 0.50 | 0.50 | 0.8 | 0.2 | 0.2 | 0.6 | 0.2 | 0.2 | n.c. | 0.2 | n.c. | 0.3 | n.c. | n.c. |
| 0.01 | 0.74 | 0.25 | 0.3 | 0.2 | 0.3 | 0.2 | 0.2 | 0.2 | n.c. | 0.2 | n.c. | 0.3 | n.c. | n.c. |
| 0.01 | 0.99 | 0 | 0.3 | 0.2 | 0.7 | 0.9 | 0.2 | 0.2 | n.c. | 0.3 | n.c. | 0.4 | n.c. | n.c. |
| 0.01 | 0 | 0.99 | 1.4 | 0.3 | 6.9 | 0.2 | 0.2 | 0.2 | n.c. | 0.3 | n.c. | 0.4 | n.c. | n.c. |
Table 8.
Characteristic values of the CR layouts calculated with different weights λC and λSL. “L unfavorable” quantifies the CR length in the unfavorable direction.
Table 8.
Characteristic values of the CR layouts calculated with different weights λC and λSL. “L unfavorable” quantifies the CR length in the unfavorable direction.
| Variant | MIN-EK | MIN-UR | MIX |
|---|
| Net revenue (kCHF) | −596 | −1790 | −828 |
| L unfavorable (km) | 6.815 | 0.015 | 2.605 |
| λC | 1 | 0 | 0.21 |
| λSL | 0 | 1 | 0.79 |
| Share cable Yarder (%) | 88.2 | 33.8 | 75.6 |
| Share helicopter (%) | 11.2 | 65.2 | 23.7 |
| Share winch (%) | 0.6 | 1 | 0.7 |
Table 9.
CR and harvesting layouts properties of tested areas in Gotschna. The corresponding visualizations can be found in
Figure 11,
Figure 12 and
Figure 13.
Table 9.
CR and harvesting layouts properties of tested areas in Gotschna. The corresponding visualizations can be found in
Figure 11,
Figure 12 and
Figure 13.
| | No. of TPs harvested by | Volume Harvested by (m3) |
|---|
| Case | Alternative | Yarder | Alternative | Yarder | Total |
|---|
| MIX | 10,481 | 5406 | 9235 | 32,476 | 41,711 |
| MIN-EK | 9623 | 6264 | 4218 | 37,493 | 41,711 |
| MIN-UR | 13,175 | 2712 | 25,199 | 16,512 | 41,711 |
Table 10.
Properties and computation times (minutes) for the sub-areas in the Gotschna area.
Table 10.
Properties and computation times (minutes) for the sub-areas in the Gotschna area.
| Sub-Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| No. of TPs | 1561 | 1497 | 3066 | 3009 | 1515 | 2670 | 2569 |
| No. of potential CRs | 10,781 | 9350 | 15,763 | 16,021 | 13,201 | 11,185 | 20,935 |
| No. of NISE | 8 | 10 | 5 | 5 | 5 | 5 | 4 |
| comp. time (min) | 5 | 2 | 77 | 230 | 49 | 10 | 19 |