Wood–Moisture Relationships Studied with Molecular Simulations: Methodological Guidelines
Abstract
1. Introduction and Context
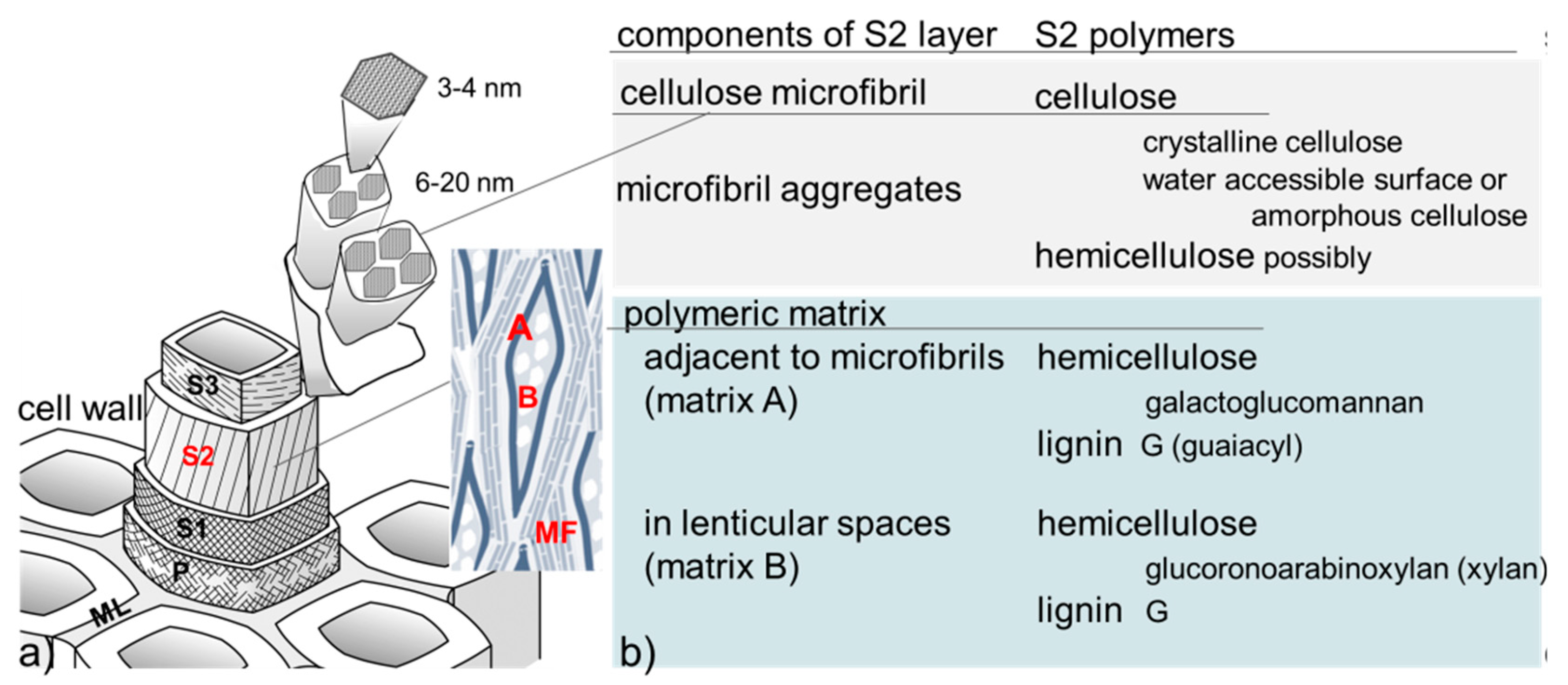
1.1. Summary of Wood Structure, Components, and Behavior
1.2. Using Molecular Simulations for Modeling of Molecular Level Wood–Moisture Interactions
2. Introduction to Molecular Simulation
2.1. Some Basic Notions
2.1.1. Chemical Potential
2.1.2. Intermolecular Potentials
2.1.3. Statistical Ensemble
2.2. Grand Canonical Monte Carlo (GCMC) Simulation
2.3. Molecular Dynamics Simulation
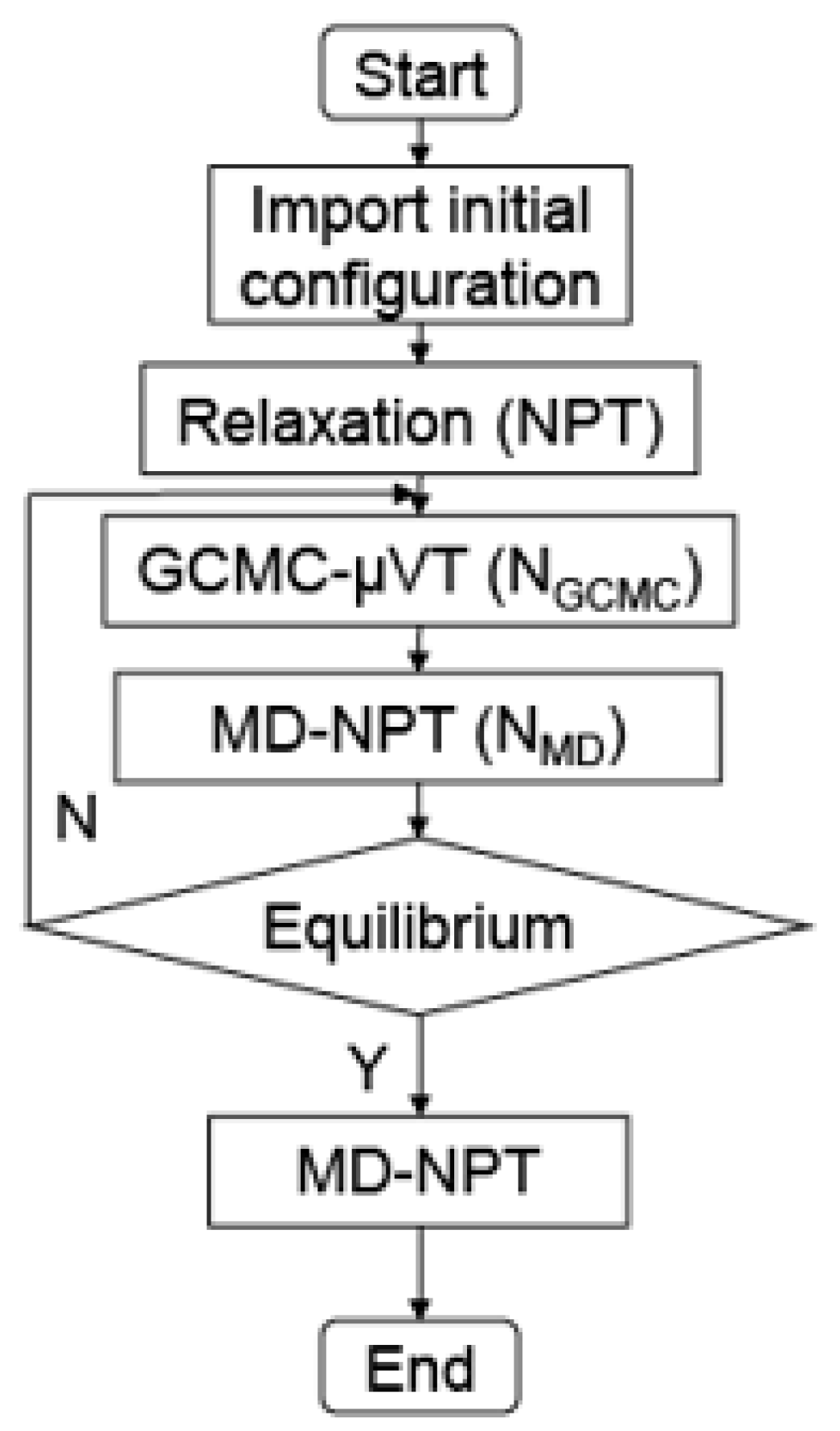
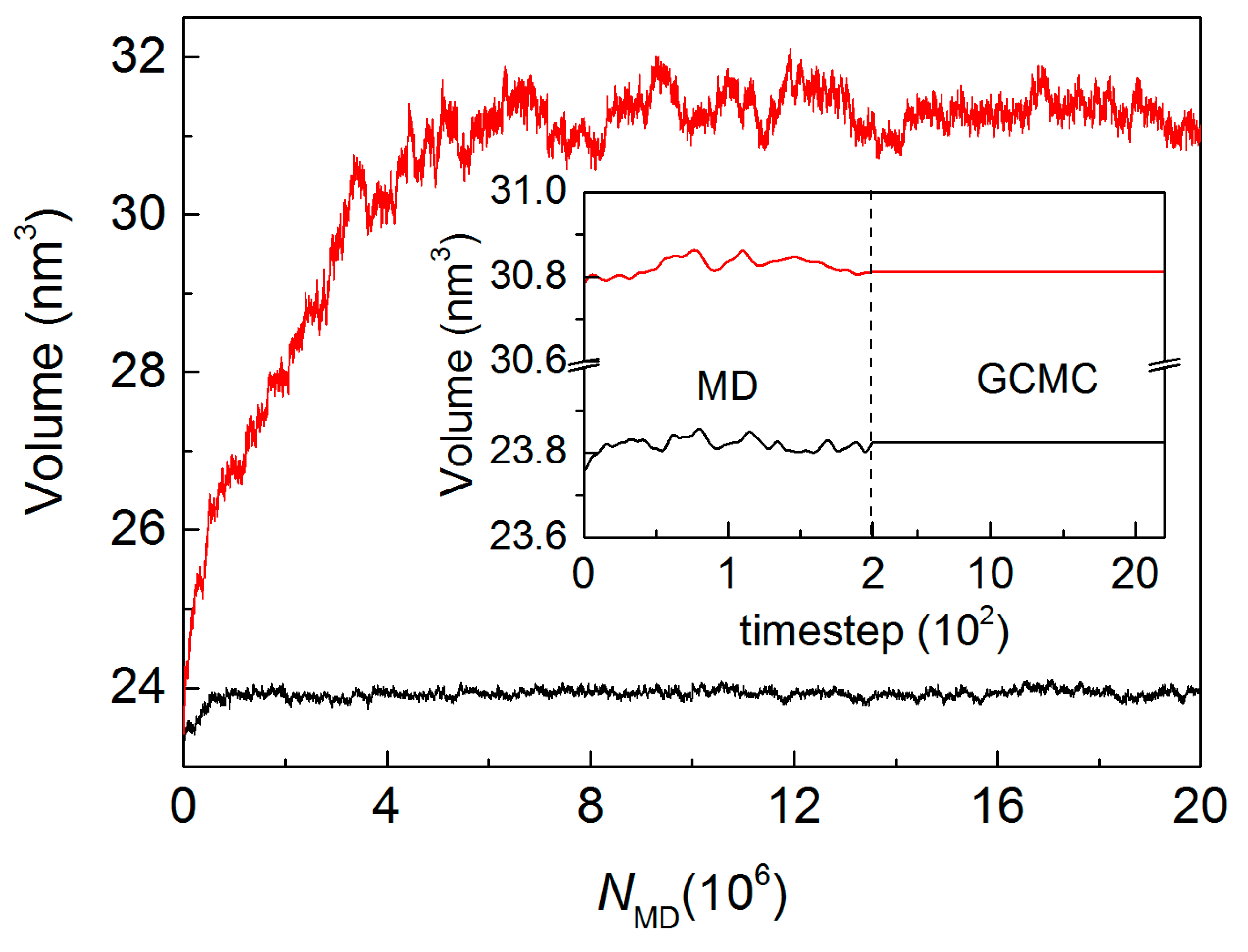
2.4. Hybrid GCMC/MD Simulation
2.5. Force Fields
2.5.1. GROMOS
2.5.2. Polymer Consistent Force Field (PCFF)
2.5.3. CHARMM
2.6. Solvers
3. Single Systems and Sorption
3.1. Building a Molecule
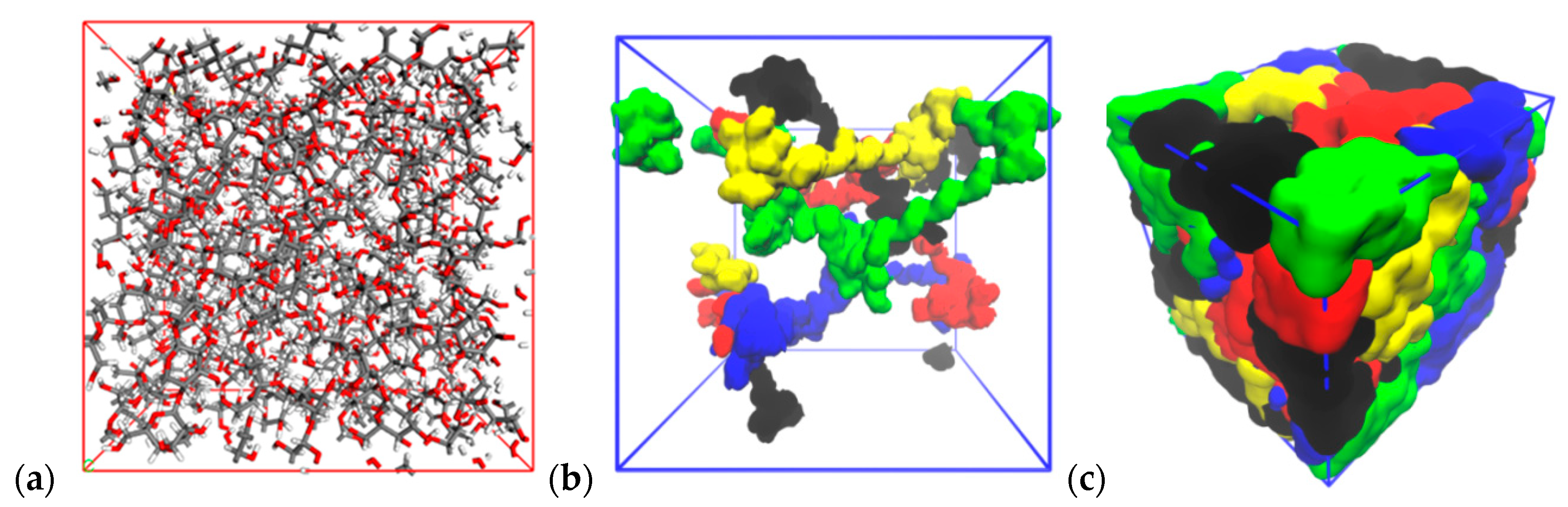
3.2. Building an Amorphous System
3.3. Water Molecules
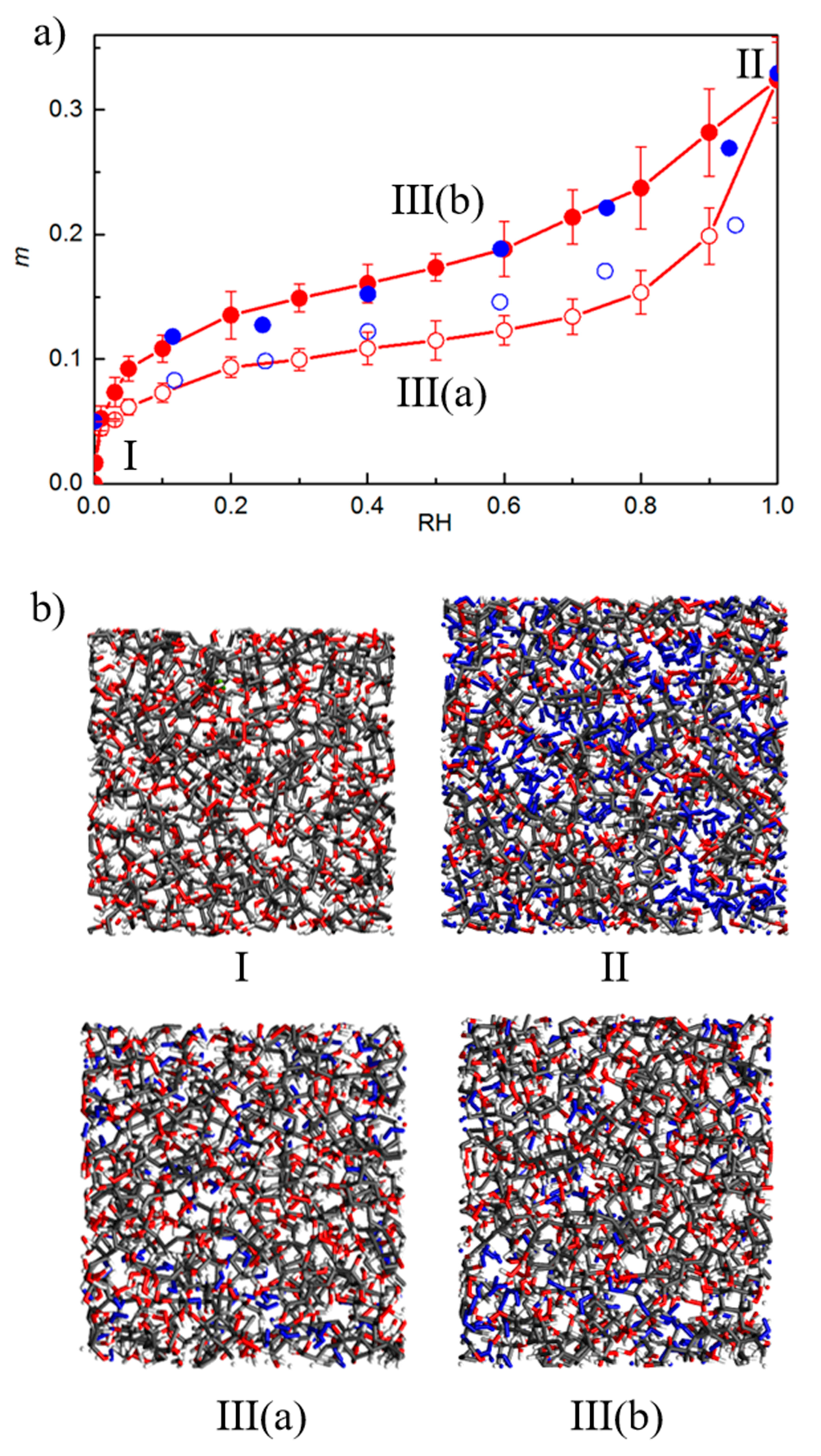
3.4. Varying the Moisture Content
4. Probing the Systems Towards Characterization
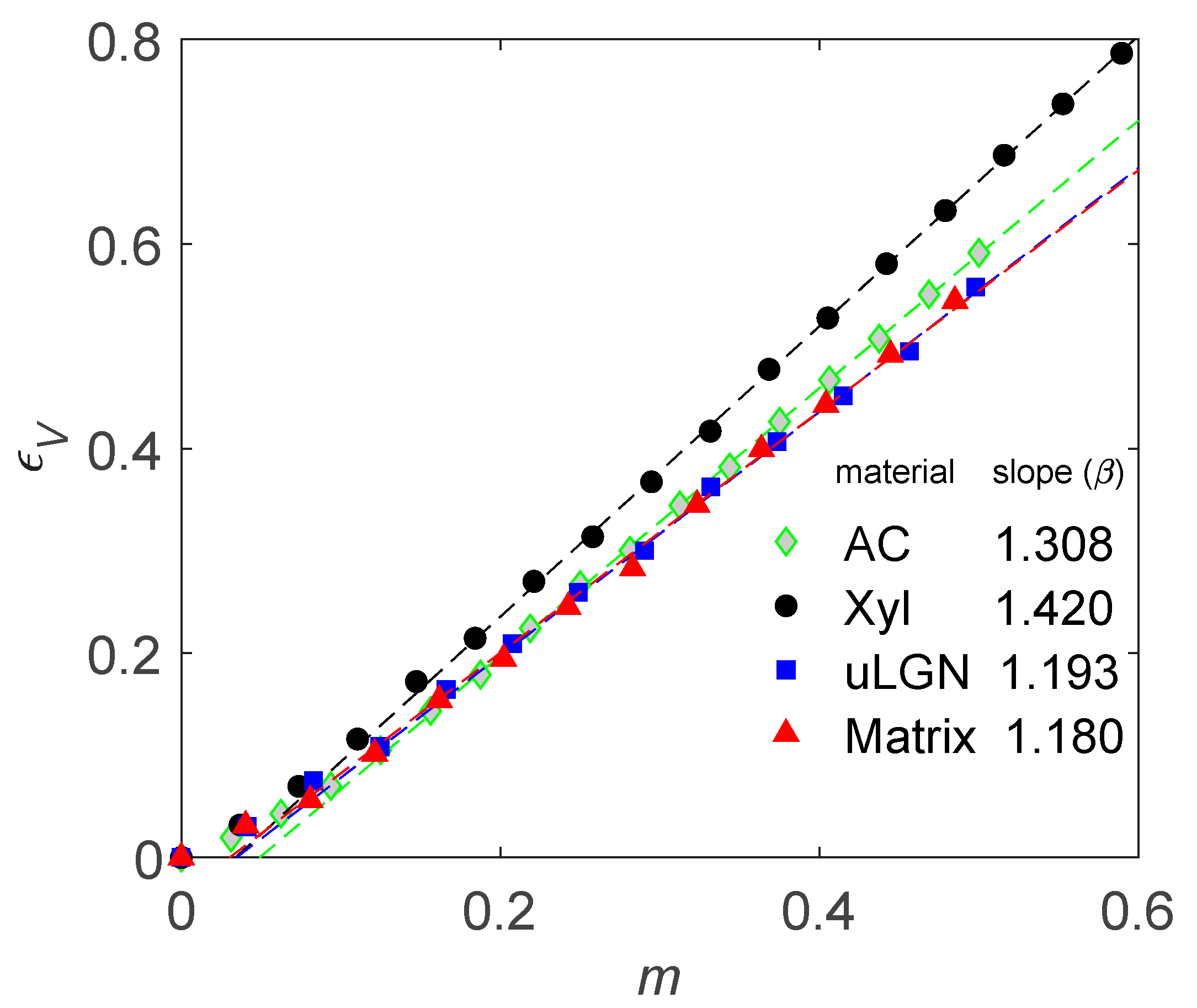
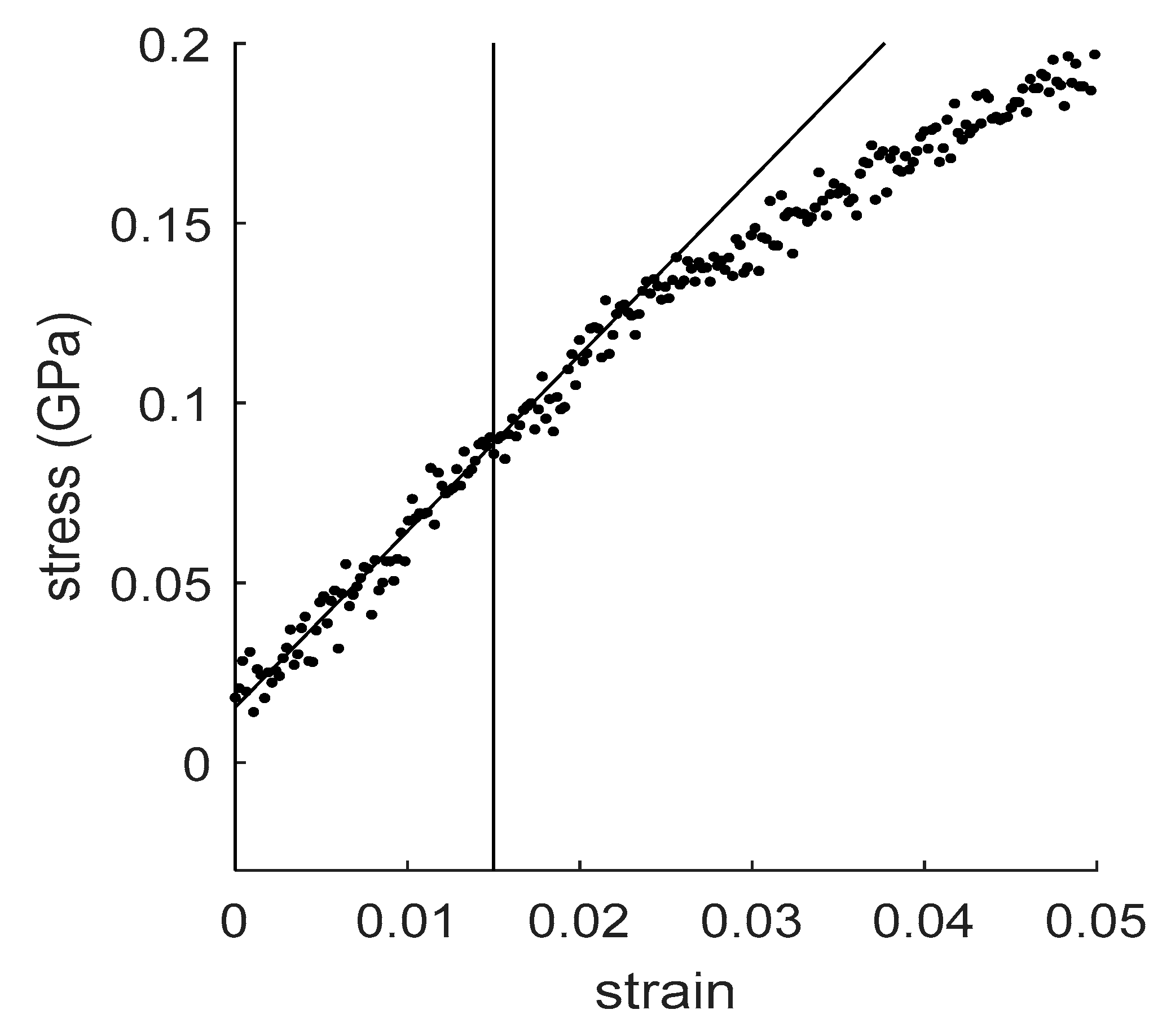
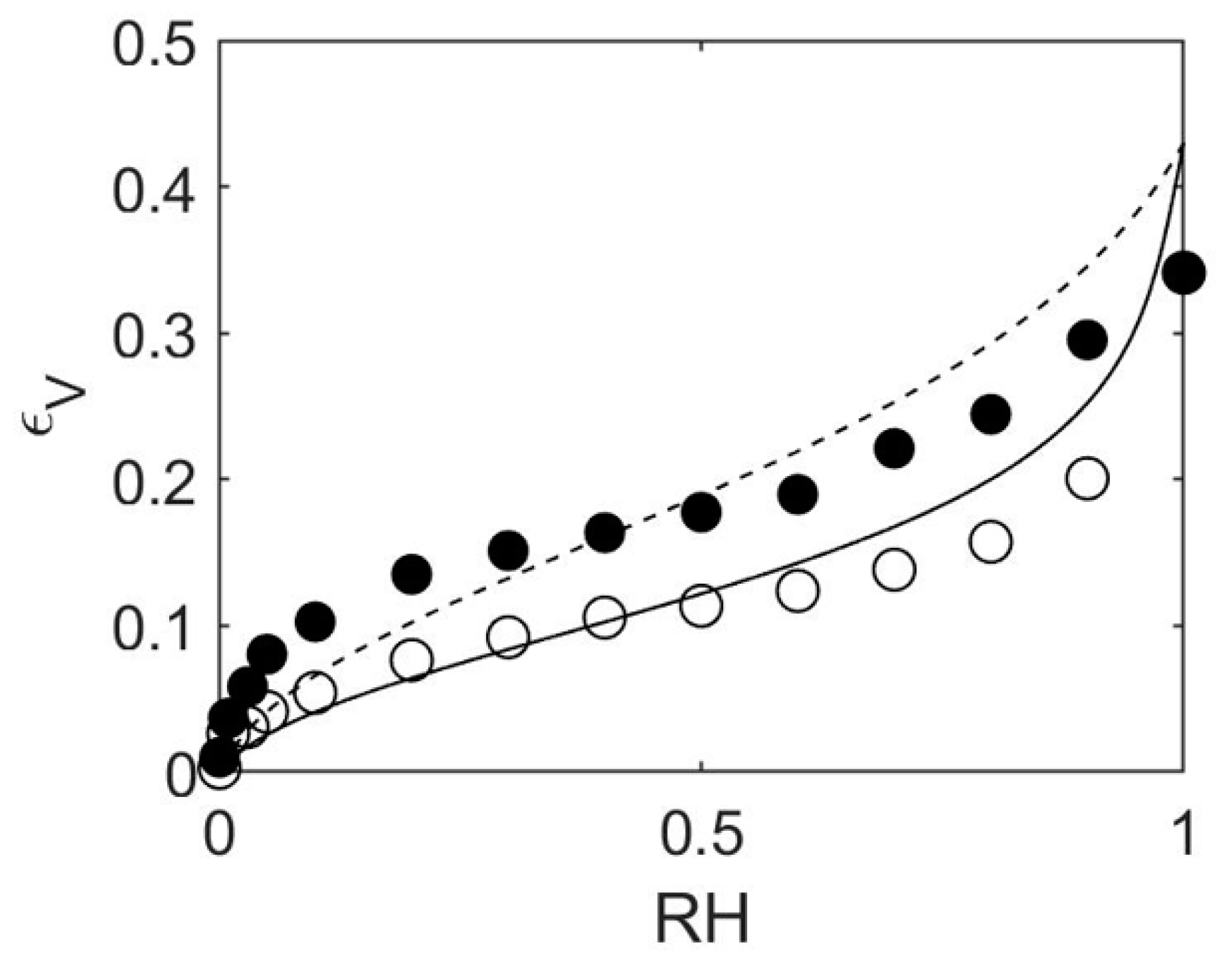
4.1. How to Determine Hygromechanical Properties: Swelling, Elastic Moduli
4.2. MD/GCMC Adsorption and Desorption
5. Upscaling
6. Conclusions and Perspectives
6.1. Highlights of Current Molecular Simulations Research in the Group
6.2. Reflections for Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boutelje, J.B. The relationship of structure to transverse anisotropy in wood with reference to shrinkage and elasticity. Holzforsch. Int. J. Biol. Chem. Phys. Technol. Wood 1962, 16, 33–46. [Google Scholar] [CrossRef]
- Watanabe, U.; Norimoto, M.; Morooka, T. Cell wall thickness and tangential Young’s modulus in coniferous early wood. J. Wood Sci. 2000, 46, 109–114. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Lanvermann, C.; Niemz, P.; Carmeliet, J.; Derome, D. Multiscale analysis of free swelling of Norway spruce. Compos. Part A Appl. Sci. Manuf. 2013, 54, 70–78. [Google Scholar] [CrossRef]
- Xu, P.; Donaldson, L.A.; Gergely, Z.R.; Staehelin, L.A. Dual-axis electron tomography: A new approach for investigating the spatial organization of wood cellulose microfibrils. Wood Sci. Technol. 2007, 41, 101–116. [Google Scholar] [CrossRef]
- Salmén, L.; Burgert, I. Cell wall features with regard to mechanical performance. A review COST Action E35 2004–2008: Wood machining—Micromechanics and fracture. Holzforschung 2009, 63, 121–129. [Google Scholar] [CrossRef]
- Ding, S.Y.; Liu, Y.S.; Zeng, Y.; Himmel, M.E.; Baker, J.O.; Bayer, E.A. How does plant cell wall nanoscale architecture correlate with enzymatic digestibility? Science 2012, 338, 1055–1060. [Google Scholar] [CrossRef] [PubMed]
- Derome, D.; Rafsanjani, A.; Patera, A.; Guyer, R.; Carmeliet, J. Hygromorphic behaviour of cellular material: Hysteretic swelling and shrinkage of wood probed by phase contrast X-ray tomography. Philos. Mag. 2012, 92, 3680–3698. [Google Scholar] [CrossRef]
- Beck-Candanedo, S.; Roman, M.; Gray, D.G. Effect of reaction conditions on the properties and behavior of wood cellulose nanocrystal suspensions. Biomacromolecules 2005, 6, 1048–1054. [Google Scholar] [CrossRef]
- Agarwal, U.P.; Ralph, S.A.; Reiner, R.S.; Baez, C. Probing crystallinity of never-dried wood cellulose with Raman spectroscopy. Cellulose 2016, 23, 125–144. [Google Scholar] [CrossRef]
- Fernandes, A.N.; Thomas, L.H.; Altaner, C.M.; Callow, P.; Forsyth, V.T.; Apperley, D.C.; Kennedy, C.J.; Jarvis, M.C. Nanostructure of cellulose microfibrils in spruce wood. Proc. Natl. Acad. Sci. USA 2011, 108, 1195–1203. [Google Scholar] [CrossRef]
- Salmén, L. Micromechanical understanding of the cell-wall structure. Comptes Rendus Biol. 2004, 327, 873–880. [Google Scholar] [CrossRef]
- Dinwoodie, J.M. Timber: Its Nature and Behaviour; Routledge: London, UK, 2000. [Google Scholar]
- Fahlén, J.; Salmén, L. Pore and matrix distribution in the fiber wall revealed by atomic force microscopy and image analysis. Biomacromolecules 2005, 6, 433–438. [Google Scholar] [CrossRef] [PubMed]
- Höfte, H.; Gonneau, M.; Vernhettes, S. Biosynthesis of cellulose. In Comprehensive Glycoscience; Elsevier: Amsterdam, The Netherlands, 2007; pp. 737–763. [Google Scholar]
- Eichhorn, S.J. Cellulose nanowhiskers: Promising materials for advanced applications. Soft Matter 2011, 7, 303–315. [Google Scholar] [CrossRef]
- Cosgrove, D.J. Re-constructing our models of cellulose and primary cell wall assembly. Curr. Opin. Plant Biol. 2014, 22, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, U.P.; Ralph, S.A.; Baez, C.; Reiner, R.S.; Verrill, S.P. Effect of sample moisture content on XRD-estimated cellulose crystallinity index and crystallite size. Cellulose 2017, 24, 1971–1984. [Google Scholar] [CrossRef]
- Terashima, N.; Kitano, K.; Kojima, M.; Yoshida, M.; Yamamoto, H.; Westermark, U. Nanostructural assembly of cellulose, hemicellulose, and lignin in the middle layer of secondary wall of ginkgo tracheid. J. Wood Sci. 2009, 55, 409–416. [Google Scholar] [CrossRef]
- Lawoko, M.; Henriksson, G.; Gellerstedt, G. Characterisation of lignin-carbohydrate complexes (LCCs) of spruce wood (Picea abies L.) isolated with two methods. Holzforschung 2006, 60, 156–161. [Google Scholar] [CrossRef]
- Balakshin, M.; Capanema, E.; Gracz, H.; Chang, H.; Jameel, H. Quantification of lignin–carbohydrate linkages with high-resolution NMR spectroscopy. Planta 2011, 233, 1097–1110. [Google Scholar] [CrossRef]
- Burgert, I.; Keplinger, T. Plant micro-and nanomechanics: Experimental techniques for plant cell-wall analysis. J. Exp. Bot. 2013, 64, 4635–4649. [Google Scholar] [CrossRef]
- Eder, M.; Arnould, O.; Dunlop, J.W.C.; Hornatowska, J.; Salmén, L. Experimental micromechanical characterisation of wood cell walls. Wood Sci. Technol. 2013, 47, 163–182. [Google Scholar] [CrossRef]
- Mohr, S.; Eixarch, M.; Amsler, M.; Mantsinen, M.J.; Genovese, L. Linear scaling DFT calculations for large tungsten systems using an optimized local basis. Nucl. Mater. Energy 2018, 15, 64–70. [Google Scholar] [CrossRef]
- Erba, A.; Baima, J.; Bush, I.; Orlando, R.; Dovesi, R. Large-Scale Condensed Matter DFT Simulations: Performance and Capabilities of the CRYSTAL Code. J. Chem. Theory Comput. 2017, 13, 5019–5027. [Google Scholar] [CrossRef] [PubMed]
- Reddy, T.; Shorthouse, D.; Parton, D.L.; Jefferys, E.; Fowler, P.W.; Chavent, M.; Baaden, M.; Sansom, M.S.P. Nothing to sneeze at: A dynamic and integrative computational model of an influenza A virion. Structure 2015, 23, 584–597. [Google Scholar] [CrossRef] [PubMed]
- Nishiyama, Y.; Langan, P.; Chanzy, H. Crystal Structure and Hydrogen-Bonding System in Cellulose Iβ from Synchrotron X-ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. [Google Scholar] [CrossRef] [PubMed]
- Kulasinski, K.; Keten, S.; Churakov, S.V.; Derome, D.; Carmeliet, J. A comparative molecular dynamics study of crystalline, paracrystalline and amorphous states of cellulose. Cellulose 2014, 21, 1103–1116. [Google Scholar] [CrossRef]
- Teleman, O.; Jönsson, B.; Engström, S. A molecular dynamics simulation of a water model with intramolecular degrees of freedom. Mol. Phys. 1987, 60, 193–203. [Google Scholar] [CrossRef]
- Kulasinski, K.; Guyer, R.; Keten, S.; Derome, D.; Carmeliet, J. Impact of moisture adsorption on structure and physical properties of amorphous biopolymers. Macromolecules 2015, 48, 2793–2800. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Lins, R.D.; Hünenberger, P.H. A new GROMOS force field for hexopyranose-based carbohydrates. J. Comput. Chem. 2005, 26, 1400–1412. [Google Scholar] [CrossRef]
- Xia, W.; Song, J.; Jeong, C.; Hsu, D.D.; Phelan, F.R.; Douglas, J.F.; Keten, S. Energy-renormalization for achieving temperature transferable coarse-graining of polymer dynamics. Macromolecules 2017, 50, 8787–8796. [Google Scholar] [CrossRef]
- Noid, W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 09B201_1. [Google Scholar] [CrossRef]
- Sinko, R.; Keten, S. Traction-separation laws and stick-slip shear phenomenon of interfaces between cellulose nanocrystals. J. Mech. Phys. Solids 2015, 78, 526–539. [Google Scholar] [CrossRef]
- Wu, X.; Moon, R.J.; Martini, A. Tensile strength of Iβ crystalline cellulose predicted by molecular dynamics simulation. Cellulose 2014, 21, 2233–2245. [Google Scholar] [CrossRef]
- Charlier, L.; Mazeau, K. Molecular modeling of the structural and dynamical properties of secondary plant cell walls: Influence of lignin chemistry. J. Phys. Chem. B 2012, 116, 4163–4174. [Google Scholar] [CrossRef]
- Deng, Q.; Li, S.; Chen, Y. Mechanical properties and failure mechanism of wood cell wall layers. Comput. Mater. Sci. 2012, 62, 221–226. [Google Scholar] [CrossRef]
- Maurer, R.J.; Sax, A.F.; Ribitsch, V. Molecular simulation of surface reorganization and wetting in crystalline cellulose I and II. Cellulose 2013, 20, 25–42. [Google Scholar] [CrossRef]
- Petridis, L.; O’Neill, H.M.; Johnsen, M.; Fan, B.; Schulz, R.; Mamontov, E.; Maranas, J.; Langan, P.; Smith, J.C. Hydration control of the mechanical and dynamical properties of cellulose. Biomacromolecules 2014, 15, 4152–4159. [Google Scholar] [CrossRef]
- Petridis, L.; Smith, J.C. Conformations of low-molecular-weight lignin polymers in water. ChemSusChem 2016, 9, 289–295. [Google Scholar] [CrossRef]
- Youssefian, S.; Jakes, J.E.; Rahbar, N. Variation of nanostructures, molecular interactions, and anisotropic elastic moduli of lignocellulosic cell walls with moisture. Sci. Rep. 2017, 7, 2054. [Google Scholar] [CrossRef]
- Rismiller, S.C.; Groves, M.M.; Meng, M.; Dong, Y.; Lin, J. Water assisted liquefaction of lignocellulose biomass by ReaxFF based molecular dynamic simulations. Fuel 2018, 215, 835–843. [Google Scholar] [CrossRef]
- Monti, S.; Srifa, P.; Kumaniaev, I.; Samec, J.S.M. ReaxFF Simulations of Lignin Fragmentation on a Palladium-Based Heterogeneous Catalyst in Methanol–Water Solution. J. Phys. Chem. Lett. 2018, 9, 5233–5239. [Google Scholar] [CrossRef] [PubMed]
- Vural, D.; Gainaru, C.; O’Neill, H.; Pu, Y.; Smith, M.D.; Parks, J.M.; Pingali, S.V.; Mamontov, E.; Davison, B.H.; Sokolov, A.P.; et al. Impact of hydration and temperature history on the structure and dynamics of lignin. Green Chem. 2018, 20, 1602–1611. [Google Scholar] [CrossRef]
- Manna, B.; Ghosh, A. Dissolution of cellulose in ionic liquid and water mixtures as revealed by molecular dynamics simulations. J. Biomol. Struct. Dyn. 2019, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Derome, D.; Carmeliet, J. Nanoscale Stick-Slip Behavior of Crystalline Polymer Surface. 2019; in preparation. [Google Scholar]
- Zhang, C.; Coasne, B.; Guyer, R.; Derome, D.; Carmeliet, J. Evolution of hygromechanical behavior of a softwood xylan with first and second layer completion of adsorption. 2019; in preparation. [Google Scholar]
- Kulasinski, K.; Guyer, R.A. Quantification of Nanopore Networks: Application to Amorphous Polymers. J. Phys. Chem. C 2016, 120, 28144–28151. [Google Scholar] [CrossRef]
- Kulasinski, K.; Keten, S.; Churakov, S.V.; Guyer, R.; Carmeliet, J.; Derome, D. Molecular Mechanism of Moisture-Induced Transition in Amorphous Cellulose. ACS Macro Lett. 2014, 3, 1037–1040. [Google Scholar] [CrossRef]
- Kulasinski, K.; Guyer, R.; Derome, D.; Carmeliet, J. Water Diffusion in Amorphous Hydrophilic Systems: A Stop and Go Process. Langmuir 2015, 31, 10843–10849. [Google Scholar] [CrossRef] [PubMed]
- Kulasinski, K.; Derome, D.; Carmeliet, J. Impact of hydration on the micromechanical properties of the polymer composite structure of wood investigated with atomistic simulations. J. Mech. Phys. Solids 2017, 103, 221–235. [Google Scholar] [CrossRef]
- Kulasinski, K.; Guyer, R.; Derome, D.; Carmeliet, J. Water Adsorption in Wood Microfibril-Hemicellulose System: Role of the Crystalline–Amorphous Interface. Biomacromolecules 2015, 16, 2972–2978. [Google Scholar] [CrossRef]
- Kulasinski, K.; Guyer, R.; Derome, D.; Carmeliet, J. Poroelastic model for adsorption-induced deformation of biopolymers obtained from molecular simulations. Phys. Rev. E 2015, 92, 022605. [Google Scholar] [CrossRef]
- Chen, M.; Coasne, B.; Guyer, R.; Derome, D.; Carmeliet, J. Role of hydrogen bonding in hysteresis observed in sorption-induced swelling of soft nanoporous polymers. Nat. Commun. 2018, 9, 3507. [Google Scholar] [CrossRef]
- Zhang, C.; Keten, S.; Coasne, B.; Guyer, R.; Derome, D.; Carmeliet, J. Atomistic characterization of the hygro-thermo-mechanical behavior of uncondensed lignin. 2019; in preparation. [Google Scholar]
- Cloutier, A.; Fortin, Y. A model of moisture movement in wood based on water potential and the determination of the effective water conductivity. Wood Sci. Technol. 1993, 27, 95–114. [Google Scholar] [CrossRef]
- Khanna, R.; Sahajwalla, V. Atomistic Simulations of Properties and Phenomena at High Temperatures. In Treatise on Process Metallurgy; Elsevier: Amsterdam, The Netherlands, 2014; pp. 287–393. [Google Scholar]
- McDonald, I.R. NpT-ensemble Monte Carlo calculations for binary liquid mixtures. Mol. Phys. 1972, 23, 41–58. [Google Scholar] [CrossRef]
- Jelfs, K.E.; Cooper, A.I. Molecular simulations to understand and to design porous organic molecules. Curr. Opin. Solid State Mater. Sci. 2013, 17, 19–30. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B.; Ratner, M.A. Understanding Molecular Simulation: From Algorithms to Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 2001; ISBN 978-0-12-267351-1. [Google Scholar]
- Pitera, J.W.; van Gunsteren, W.F. One-Step Perturbation Methods for Solvation Free Energies of Polar Solutes. J. Phys. Chem. B 2001, 105, 11264–11274. [Google Scholar] [CrossRef]
- Zhang, Y.; Pitkänen, L.; Douglade, J.; Tenkanen, M.; Remond, C.; Joly, C. Wheat bran arabinoxylans: Chemical structure and film properties of three isolated fractions. Carbohydr. Polym. 2011, 86, 852–859. [Google Scholar] [CrossRef]
- Ghoufi, A.; Maurin, G. Hybrid monte carlo simulations combined with a phase mixture model to predict the structural transitions of a porous metal—Organic framework material upon adsorption of guest molecules. J. Phys. Chem. C 2010, 114, 6496–6502. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab initio CFF93 all-atom force field for polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Yu, H.; Amann, M.; Hansson, T.; Köhler, J.; Wich, G.; van Gunsteren, W.F. Effect of methylation on the stability and solvation free energy of amylose and cellulose fragments: A molecular dynamics study. Carbohydr. Res. 2004, 339, 1697–1709. [Google Scholar] [CrossRef]
- Bergenstråhle, M.; Berglund, L.A.; Mazeau, K. Thermal response in crystalline Iβ cellulose: A molecular dynamics study. J. Phys. Chem. B 2007, 111, 9138–9145. [Google Scholar] [CrossRef]
- Chen, P.; Nishiyama, Y.; Putaux, J.L.; Mazeau, K. Diversity of potential hydrogen bonds in cellulose I revealed by molecular dynamics simulation. Cellulose 2014, 21, 897–908. [Google Scholar] [CrossRef]
- Tanaka, F.; Iwata, T. Estimation of the Elastic Modulus of Cellulose Crystal by Molecular Mechanics Simulation. Cellulose 2006, 13, 509–517. [Google Scholar] [CrossRef]
- Nishino, T.; Takano, K.; Nakamae, K. Elastic modulus of the crystalline regions of cellulose polymorphs. J. Polym. Sci. Part B Polym. Phys. 1995, 33, 1647–1651. [Google Scholar] [CrossRef]
- Da Silva Perez, D.; Ruggiero, R.; Morais, L.C.; Machado, A.E.H.; Mazeau, K. Theoretical and experimental studies on the adsorption of aromatic compounds onto cellulose. Langmuir 2004, 20, 3151–3158. [Google Scholar] [CrossRef]
- Xu, B.; Chen, Z. Formaldehyde diffusion within crystalline and amorphous cellulose at different temperatures and electric fields: A molecular dynamics study. Indoor Built Environ. 2019, 28, 175–185. [Google Scholar] [CrossRef]
- Fritsch, D.; Koepernik, K.; Richter, M.; Eschrig, H. Transition Metal Dimers as Potential Molecular Magnets. J. Comput. Chem. 2008, 1145, 2210–2219. [Google Scholar] [CrossRef]
- Piggot, T.J.; Piñeiro, Á.; Khalid, S. Molecular dynamics simulations of phosphatidylcholine membranes: A comparative force field study. J. Chem. Theory Comput. 2012, 8, 4593–4609. [Google Scholar] [CrossRef]
- Baker, C.M. Polarizable force fields for molecular dynamics simulations of biomolecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 241–254. [Google Scholar] [CrossRef]
- Reiling, S.; Brickmann, J. Theoretical investigations on the structure and physical properties of cellulose. Macromol. Theory Simul. 1995, 4, 725–743. [Google Scholar] [CrossRef]
- Matthews, J.F.; Beckham, G.T.; Bergenstråhle-Wohlert, M.; Brady, J.W.; Himmel, M.E.; Crowley, M.F. Comparison of cellulose Iβ simulations with three carbohydrate force fields. J. Chem. Theory Comput. 2012, 8, 735–748. [Google Scholar] [CrossRef]
- Matthews, J.F.; Skopec, C.E.; Mason, P.E.; Zuccato, P.; Torget, R.W.; Sugiyama, J.; Himmel, M.E.; Brady, J.W. Computer simulation studies of microcrystalline cellulose Iβ. Carbohydr. Res. 2006, 341, 138–152. [Google Scholar] [CrossRef]
- Zhao, Z.; Crespi, V.H.; Kubicki, J.D.; Cosgrove, D.J.; Zhong, L. Molecular dynamics simulation study of xyloglucan adsorption on cellulose surfaces: Effects of surface hydrophobicity and side-chain variation. Cellulose 2014, 21, 1025–1039. [Google Scholar] [CrossRef]
- Miyamoto, H.; Rein, D.M.; Ueda, K.; Yamane, C.; Cohen, Y. Molecular dynamics simulation of cellulose-coated oil-in-water emulsions. Cellulose 2017, 24, 2699–2711. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham III, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.A.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Gao, Y.; Iqbal, S.; Zhang, P.; Qiu, M. Performance and power analysis of high-density multi-GPGPU architectures: A preliminary case study. In Proceedings of the 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, New York, NY, USA, 24–26 August 2015; IEEE: Piscataway, NJ, USA; pp. 66–71. [Google Scholar]
- Loeffler Hannes, H.; Winn Martyn, D. Large Biomolecular Simulation on HPC Platforms III. AMBER, CHARMM, GROMACS, Large Biomolecular Simulation on HPC Platforms; Technical Report; STFC Daresbury Laboratory: Warrington, UK, 2012; pp. 1–26. [Google Scholar]
- Comparison of Software for Molecular Mechanics Modeling. Available online: https://en.wikipedia.org/wiki/Comparison_of_software_for_molecular_mechanics_modeling (accessed on 17 June 2019).
- Truhlar, D.G. Valence bond theory for chemical dynamics. J. Comput. Chem. 2007, 28, 73–86. [Google Scholar] [CrossRef]
- Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An automated force field topology builder (ATB) and repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef]
- Busse-Wicher, M.; Li, A.; Silveira, R.L.; Pereira, C.S.; Tryfona, T.; Gomes, T.C.F.; Skaf, M.S.; Dupree, P. Evolution of xylan substitution patterns in gymnosperms and angiosperms: Implications for xylan interaction with cellulose. Plant Physiol. 2016, 171, 2418–2431. [Google Scholar] [CrossRef]
- Beaugrand, J.; Chambat, G.; Wong, V.W.K.; Goubet, F.; Rémond, C.; Paës, G.; Benamrouche, S.; Debeire, P.; O’Donohue, M.; Chabbert, B. Impact and efficiency of GH10 and GH11 thermostable endoxylanases on wheat bran and alkali-extractable arabinoxylans. Carbohydr. Res. 2004, 339, 2529–2540. [Google Scholar] [CrossRef]
- Boukari, I.; Putaux, J.L.; Cathala, B.; Barakat, A.; Saake, B.; Rémond, C.; O’Donohue, M.; Chabbert, B. In vitro model assemblies to study the impact of lignin-carbohydrate interactions on the enzymatic conversion of xylan. Biomacromolecules 2009, 10, 2489–2498. [Google Scholar] [CrossRef]
- Chantreau, M.; Portelette, A.; Dauwe, R.; Kiyoto, S.; Crônier, D.; Morreel, K.; Arribat, S.; Neutelings, G.; Chabi, M.; Boerjan, W. Ectopic lignification in the flax lignified bast fiber1 mutant stem is associated with tissue-specific modifications in gene expression and cell wall composition. Plant Cell 2014, 26, 4462–4482. [Google Scholar] [CrossRef]
- Jin, K.; Qin, Z.; Buehler, M.J. Molecular deformation mechanisms of the wood cell wall material. J. Mech. Behav. Biomed. Mater. 2015, 42, 198–206. [Google Scholar] [CrossRef]
- Petridis, L.; Smith, J.C. A molecular mechanics force field for lignin. J. Comput. Chem. 2009, 30, 457–467. [Google Scholar] [CrossRef]
- Petridis, L.; Pingali, S.V.; Urban, V.; Heller, W.T.; O’Neill, H.M.; Foston, M.; Ragauskas, A.; Smith, J.C. Self-similar multiscale structure of lignin revealed by neutron scattering and molecular dynamics simulation. Phys. Rev. E 2011, 83, 61911. [Google Scholar] [CrossRef]
- Petridis, L.; Schulz, R.; Smith, J.C. Simulation analysis of the temperature dependence of lignin structure and dynamics. J. Am. Chem. Soc. 2011, 133, 20277–20287. [Google Scholar] [CrossRef]
- Sangha, A.K.; Petridis, L.; Smith, J.C.; Ziebell, A.; Parks, J.M. Molecular simulation as a tool for studying lignin. Environ. Prog. Sustain. Energy 2012, 31, 47–54. [Google Scholar] [CrossRef]
- Gomes, T.C.F.; Skaf, M.S. Cellulose-Builder: A toolkit for building crystalline structures of cellulose. J. Comput. Chem. 2012, 33, 1338–1346. [Google Scholar] [CrossRef]
- Vorholz, J.; Harismiadis, V.I.; Rumpf, B.; Panagiotopoulos, A.Z.; Maurer, G. Vapor+liquid equilibrium of water, carbon dioxide, and the binary system, water+carbon dioxide, from molecular simulation. Fluid Phase Equilib. 2000, 170, 203–234. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Derome, D.; Kulasinski, K.; Zhang, C.; Chen, M.; Carmeliet, J. Using Modeling to Understand the Hygromechanical and Hysteretic Behavior of the S2 Cell Wall Layer of Wood. In Plant Biomechanics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 247–269. [Google Scholar]
- Griebel, M.; Hamaekers, J. Molecular dynamics simulations of the elastic moduli of polymer-carbon nanotube composites. Comput. Methods Appl. Mech. Eng. 2004, 193, 1773–1788. [Google Scholar] [CrossRef]
- Mihranyan, A.; Llagostera, A.P.; Karmhag, R.; Strømme, M.; Ek, R. Moisture sorption by cellulose powders of varying crystallinity. Int. J. Pharm. 2004, 269, 433–442. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004; ISBN 047009270X. [Google Scholar]
- Vandamme, M. Coupling between adsorption and mechanics (and vice versa). Curr. Opin. Chem. Eng. 2019, 24, 12–18. [Google Scholar] [CrossRef]
- Brochard, L.; Vandamme, M.; Pellenq, R.J.M. Poromechanics of microporous media. J. Mech. Phys. Solids 2012, 60, 606–622. [Google Scholar] [CrossRef]
- Carmeliet, J.; Derome, D.; Dressler, M.; Guyer, R.A. Nonlinear Poro-Elastic Model for Unsaturated Porous Solids. J. Appl. Mech. 2013, 80, 020909. [Google Scholar] [CrossRef]
- Patera, A.; Derome, D.; Griffa, M.; Carmeliet, J. Hysteresis in swelling and in sorption of wood tissue. J. Struct. Biol. 2013, 182, 226–234. [Google Scholar] [CrossRef]
- Patera, A.; Derluyn, H.; Derome, D.; Carmeliet, J. Influence of sorption hysteresis on moisture transport in wood. Wood Sci. Technol. 2016, 50, 259–283. [Google Scholar] [CrossRef]
- Derluyn, H.; Derome, D.; Carmeliet, J.; Stora, E.; Barbarulo, R. Hysteretic moisture behavior of concrete: Modeling and analysis. Cem. Concr. Res. 2012, 42, 1379–1388. [Google Scholar] [CrossRef]
- Guyer, R.A.; Kim, H.A.; Derome, D.; Carmeliet, J.; Tencate, J. Hysteresis in modeling of poroelastic systems: Quasistatic equilibrium. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 061408. [Google Scholar] [CrossRef]
- Chen, M.; Coasne, B.; Derome, D.; Carmeliet, J. Coupling of Sorption and Deformation in Soft Nanoporous Polymers: Molecular Simulation and Poromechanics. J. Mech. Phys. Solids 2019. submitted. [Google Scholar]
- Brochard, L.; Vandamme, M.; Pellenq, R.J.M.; Fen-Chong, T. Adsorption-induced deformation of microporous materials: Coal swelling induced by CO 2-CH 4 competitive adsorption. Langmuir 2012, 28, 2659–2670. [Google Scholar] [CrossRef]
- Hocker, E.; Almkvist, G.; Sahlstedt, M. The Vasa experience with polyethylene glycol: A conservator’s perspective. J. Cult. Herit. 2012, 13, S175–S182. [Google Scholar] [CrossRef]
- Schofield, E.J.; Sarangi, R.; Mehta, A.; Jones, A.M.; Mosselmans, F.J.W.; Chadwick, A. V Nanoparticle de-acidification of the Mary Rose. Mater. Today 2011, 14, 354–358. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Zhang, C.; Shomali, A.; Coasne, B.; Carmeliet, J.; Derome, D. Wood–Moisture Relationships Studied with Molecular Simulations: Methodological Guidelines. Forests 2019, 10, 628. https://doi.org/10.3390/f10080628
Chen M, Zhang C, Shomali A, Coasne B, Carmeliet J, Derome D. Wood–Moisture Relationships Studied with Molecular Simulations: Methodological Guidelines. Forests. 2019; 10(8):628. https://doi.org/10.3390/f10080628
Chicago/Turabian StyleChen, Mingyang, Chi Zhang, Ali Shomali, Benoit Coasne, Jan Carmeliet, and Dominique Derome. 2019. "Wood–Moisture Relationships Studied with Molecular Simulations: Methodological Guidelines" Forests 10, no. 8: 628. https://doi.org/10.3390/f10080628
APA StyleChen, M., Zhang, C., Shomali, A., Coasne, B., Carmeliet, J., & Derome, D. (2019). Wood–Moisture Relationships Studied with Molecular Simulations: Methodological Guidelines. Forests, 10(8), 628. https://doi.org/10.3390/f10080628




