1. Introduction
A key challenge faced by Earth system scientists is to provide evidence that help to understand and quantify the trade-offs between the anthropic exploitation of natural resources as well as the resilience and capacity of these ecosystems for providing goods and services for human development [
1]. Natural forests are amongst the most exploited ecosystems, given the value of their derived products for human development (e.g., timber production) and their potential replacement for agricultural purposes. In addition to economic goods, these ecosystems provide vital ecosystem services, such as water quality regulation, water flow regulation, preservation of habitats and biodiversity, and regulation of carbon cycle [
1,
2].
From a global perspective and due to the trees’ carbon uptake capacity, forests play a leading role in limiting the carbon dioxide accumulation in the atmosphere and its impacts on climate. Indeed, an increase of 9.5 million km
2 in forests by 2050 (relative to 2010) is amongst the mitigation strategies to limit global warming to 1.5 °C [
3]. In theory, this global consensus should be favorable for the protection and recovery of natural forests. However, the climate change mitigation plans in some countries include also the plantation of fast-growing commercial trees within their pledged areas [
4]. While these forest plantations may support local economies and profits for the forest industry, they release the stored CO
2 back into the atmosphere after harvesting (rotation times varying around 12 to 22 years, depending on the tree species) [
4]. Further, the (different) impacts of forest plantations and natural forests on the hydrological cycle is still an ongoing field of research. This is an important factor to consider given the water supply risks associated with global warming [
5].
The role of forests on the hydrological cycle has attracted considerable attention from scientists and the general public over the last two centuries [
6]. Over the last decades, an increased number of studies examining the trade-offs among water and wood production have focused on South America, which hosts some of the most diverse forest ecosystems while containing mostly developing countries (whose economies rely on the exploitation of these resources) [
7,
8,
9,
10]. There are, however, important limitations in understanding the interaction between forest, water and development in the region. Firstly, the insights gained from a long-history of northern hemisphere studies cannot be transferred to South America, since natural forests in the latter are diverse and the industrial forest plantations (fast-growing non-native species) are managed on very short rotations [
7] (18 to 22 years for
Pinus spp. and 12 to 18 for
Eucalyptus spp.). While an increase of tree cover is, in general, associated with decreased water provision in the northern hemisphere [
1,
6], case studies in South America have shown that these conclusions might be too lax when we differentiate natural forests from industrial forest plantations within the total tree-covered area. It has been shown that the replacement of native forests by other types of land cover, such as industrial forest plantations (monocultures of
Eucalyptus and
Pinus spp. mainly used for timber harvesting), cropland and grassland, reduces water provision and water quality [
8,
10,
11]. On the other hand, increased areas of forest plantations have been associated with reduced streamflow, especially during the dry season [
8,
10,
12,
13,
14,
15,
16,
17,
18,
19]. These results may be partly explained by the high evapotranspiration rates of exotic forest plantations, which may exceed 90% of precipitation [
15,
20,
21,
22,
23].
The land-use-induced land cover change (LULCC) in Chile has been characterized by the expansion of forest plantations in detriment of native forests, shrublands and grasslands, from 250,000 ha in 1974 to nearly 3 million ha in 2016 [
24]. This expansion was triggered by an increased international demand for pulp and other forest commodities in the 1970s, to which Chile responded by promoting favorable economic conditions for investments in timber industry. In fact, a decree-law (DL701, [
25]) was implemented in the second year of the military dictatorship (1973 to 1990), establishing subsidies for forest plantations. These subsidies were maintained until 2014 [
24,
26].
As mentioned above, there have been some scientific advances towards the quantification of the inter-relation between natural vegetation, forest plantation and water supply. However, a critical challenge remains in transferring this knowledge into public policy and decision making that can effectively lead to achieving a sustainable development.
In this work we do not directly address the challenge of transferring scientific insights into policy and decision making (a task that is probably better achieved outside a scientific publication), however, we develop our analyses thinking of this final goal. Specifically, we aim at providing robust—and easy to interpret—scientific evidence about the impacts of forest plantation expansion on water supply. We address this from a large-sample perspective, moving from the classical paired-catchment framework (that requires data from long-term experimental basins with before-after and control-impact designs, which are scarce, and generally involves small catchments [
27]) or a physically-based modelling approach (which requires high resolution quality data), towards a comparative approach, which relies on extracting insights from the diversity of catchment characteristics (including hydrologic, climatic, topographic and geomorphologic characteristics). This space-for-time approach complements the insights from placed-based experiments by seeking conclusions and dominant patterns from analyses based on less detailed data over a large number of watersheds [
6,
28] (note that catchment, basin and watersheds are used indistinctively within the manuscript). Furthermore, we focus on large catchments (>200,000 ha), which have been poorly documented in the context of LULCC and their impacts on water provision.
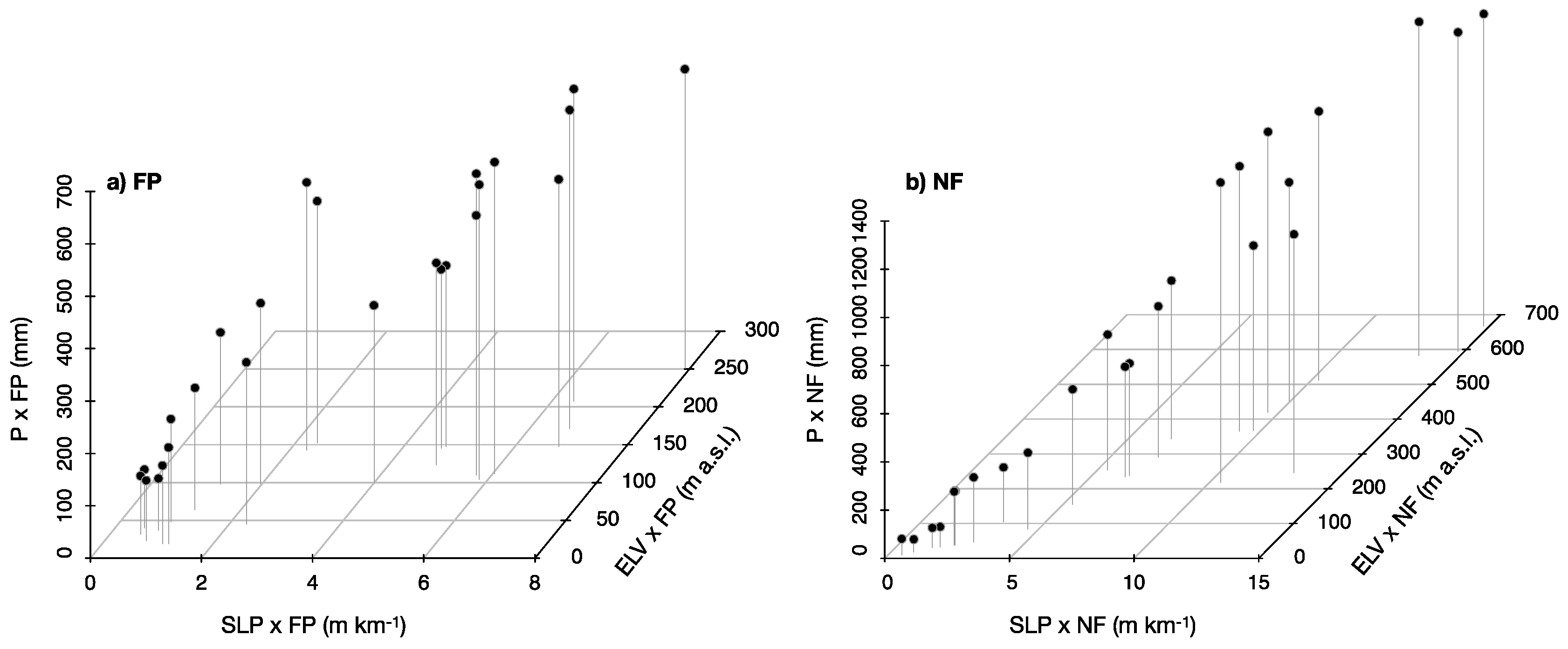
We focus our analysis in south-central Chile (35° S–41° S), the region that concentrates most of the country’s population and land use activities (agriculture and forestry). This region also holds natural forest ecosystems (Valdivian Ecoregion) that have been declared by the Global 200 initiative as a worldwide biodiversity hotspot with highest conservation priority [
29]. We analyze the water balance from 25 catchments covered by different combinations of natural vegetation (native forest, NF; grassland, GRA; and shrubland, SHR) and forest plantation (FP), by fitting a linear regression model to quantify the contribution to annual runoff from the portions of the catchments covered by each land cover class. The fitted model is then used to evaluate variations in water supply as a response to synthetic land cover transitions, where NF, GRA and SHR covers within the catchments are replaced by patches of FP. Additionally, we quantify the impacts on water supply due to the afforestation of 100,000 ha with different combinations of NF and FP, which is one of the mitigation strategies pledged in the Chilean NDC (Nationally Determined Contributions defined for the ratification of the Paris Agreement [
30]) to be accomplished by 2030 [
30]. We provide tools to quantify the impacts of natural vegetation and forest plantation on water resources, which can be used in the discussion of public policies and decision-making involving forests and land cover changes.
2. Data and Study Area
Time series of daily streamflow and daily precipitation were obtained from the CAMELS-CL (catchment attributes and meteorology for large sample studies—Chile) dataset [
31], which can be downloaded from the CAMELS-CL explorer (
http://camels.cr2.cl). This dataset provides catchment boundaries and catchment-averaged hydro-meteorological time series for 516 basins across Chile for the period 1979 to 2016, and 70 catchment attributes characterizing the topography, geology, climate, hydrology, land cover, and human intervention within the basins. Missing monthly streamflow records for a given station were filled by correlation with neighbor stations. The filling was done when the stations had a minimum of 30 coincident years, and a coefficient of determination above 0.8 between the monthly streamflow time series (similar procedure than in [
32]).
The study period to analyze annual runoff is defined from April 2000 to March 2015 (hydrological years—April to March—are considered in the analysis). This period is chosen due to land cover information [
33], which relies on Landsat imagery from 2014. Since the catchment dataset provided by [
31] does not include land cover information at different times, we assume that the 2014 land cover classification is constant within the study period, and restrict the analysis up to 15 years prior the land cover information date. This decision considers that the typical rotation times of forest plantations are 12 to 22 years, while aiming at leveraging the trade-off between record length (necessary for statistical analysis) with a realistic land cover characterization for the study period (based on two years of information).
From the 516 CAMELS-CL catchments, we selected those that fulfilled the following criteria: having more than 20% of their areas covered by forests (forest plantation or native forest); having less than 5% of the catchment covered by cropland (to avoid agriculture effects on streamflow); each of the land cover classes included as predictors in the statistical analysis should cover at least 5% of the catchment (to ensure a representative sample); and having no presence of large dams (as reported in [
31]) within the catchment (information provided by [
31]). A subset of 25 catchments fulfilled these criteria and were analyzed in this study.
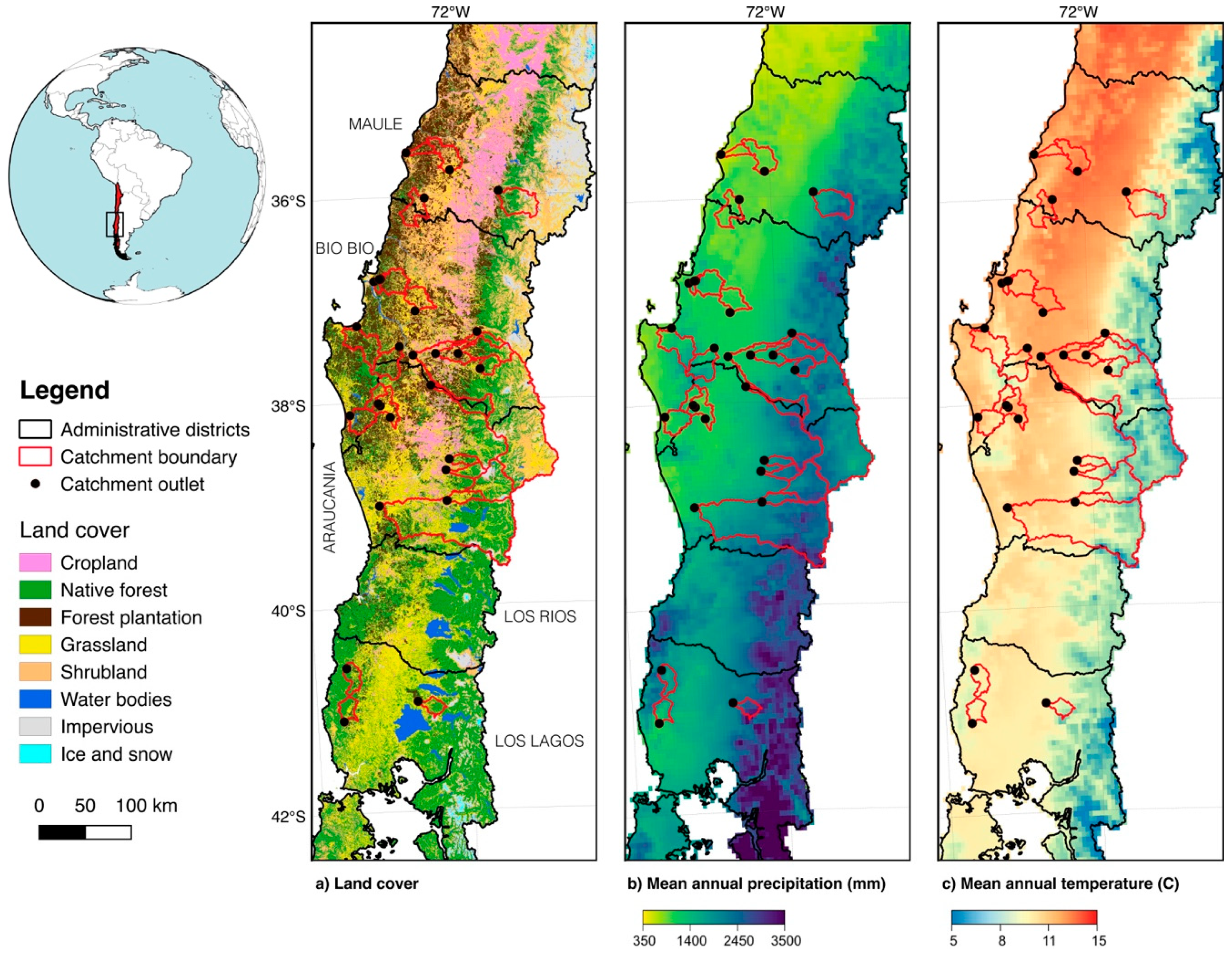
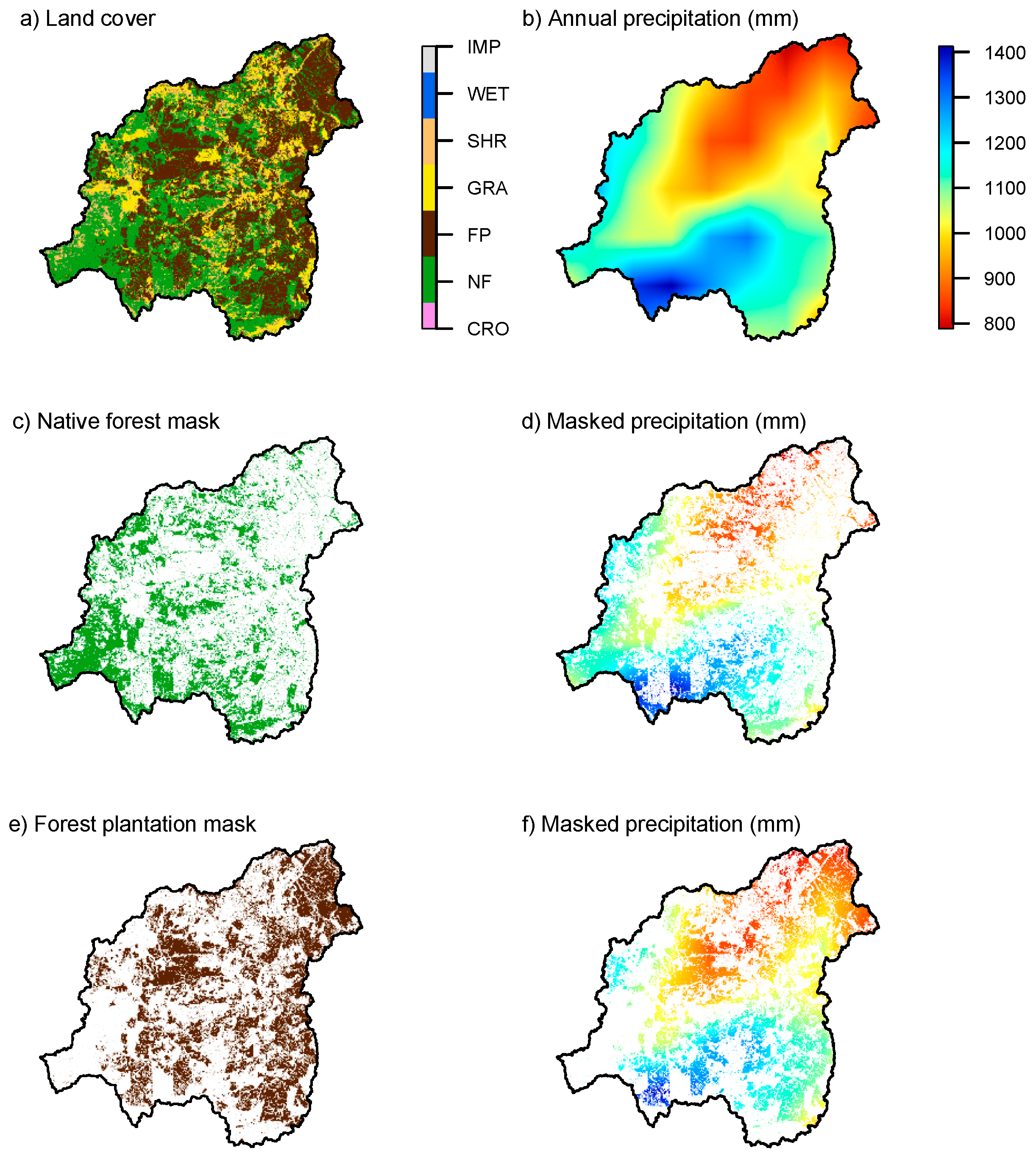
Figure 1 shows the selected catchments, which cover five administrative districts over the study region (35° S–41° S). The study basins feature diverse land cover classes (panel a, obtained from the land cover map provided by [
33]) and climatic conditions (panels b and c). The watersheds areas range from 211 km
2 to 11,137 km
2, with mean elevations ranging from 137 m a.s.l. to 1264 m a.s.l. and mean slopes ranging from 74 m km
−1 to 239 m km
−1. Although there is a greater presence of forest plantations towards the coastal region north of 39°S (
Figure 1a), several CAMELS-CL catchments within this region were not selected given the high percentage of cropland within those basins.
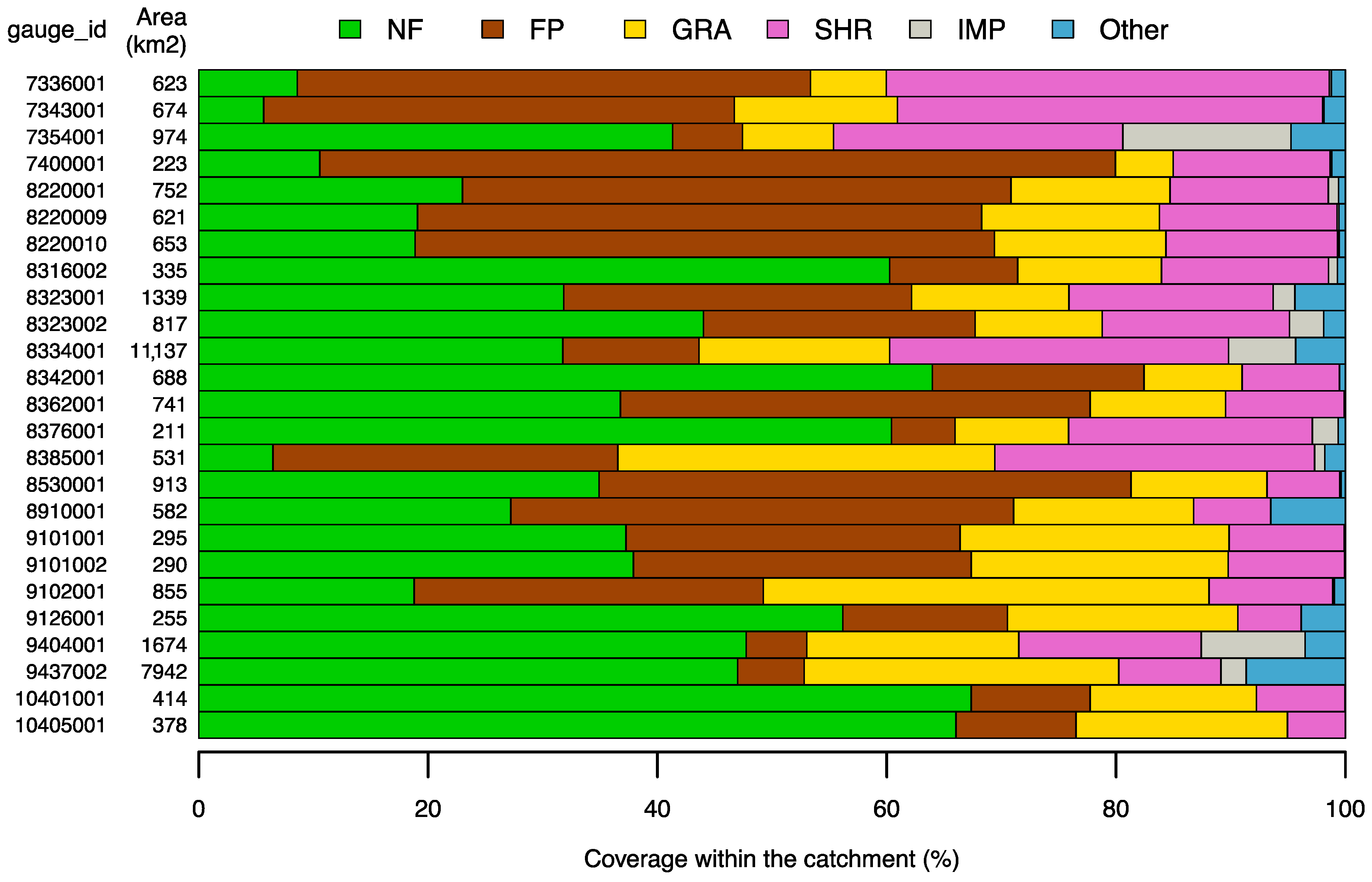
To visualize the land cover composition of the study catchments,
Figure 2 shows the percentages of the basin area covered by the main land cover classes of the study region. It can be seen that the selected catchments feature a mosaic of land cover types, with greater presence of shrubland and forest plantation in the north, and larger areas of native forest towards the south.
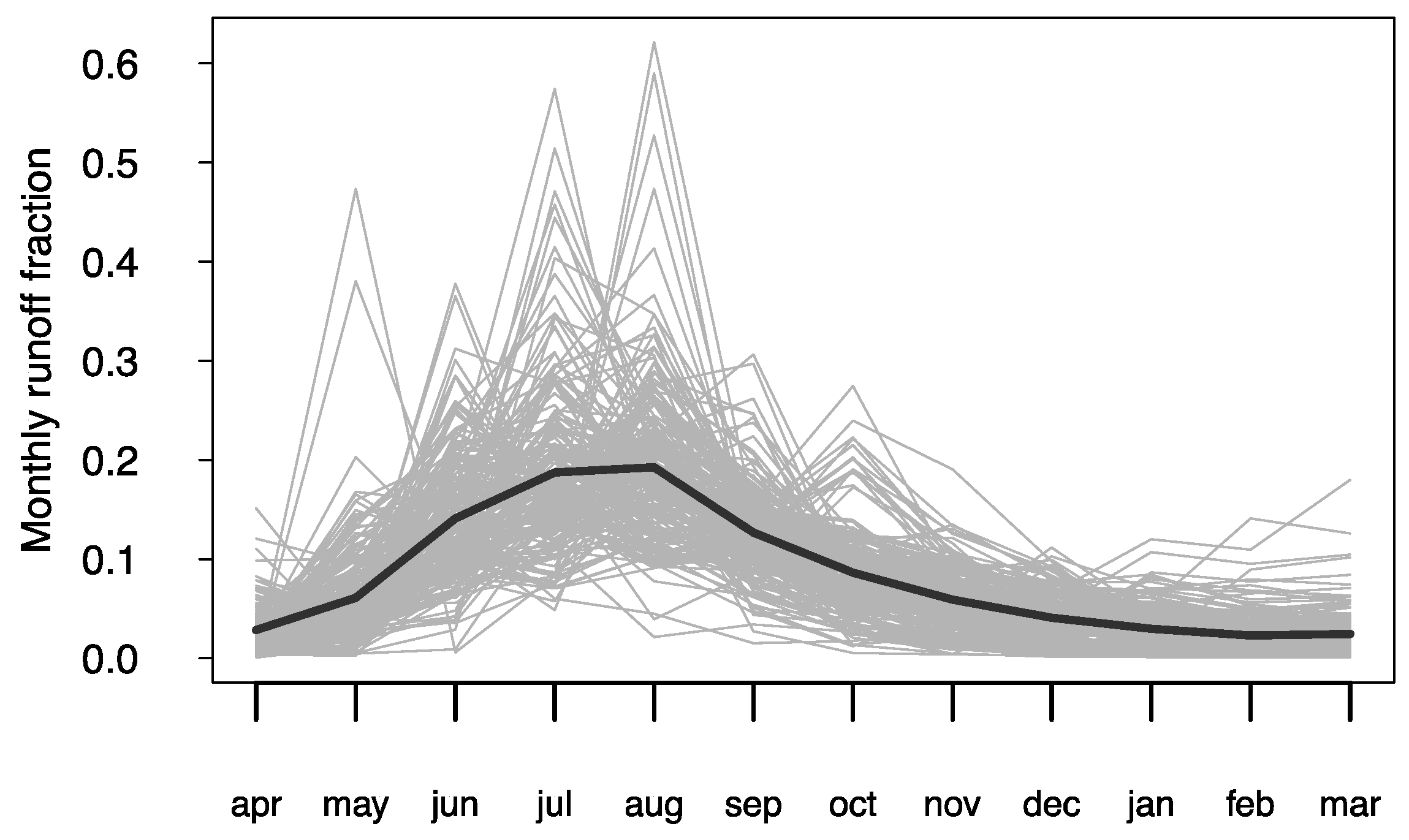
The mean hydrologic behavior of the study catchments is illustrated in
Figure 3, where the mean monthly streamflow (expressed as a fraction to the annual streamflow) is plotted for each basin. The streamflow seasonality indicates a prevailing pluvial regime governing the hydrologic response in most catchments. This suggests that snow accumulation and melting processes in high-elevation catchments (20% of the basins have mean elevations above 1000 m a.s.l.) do not dominate their main hydrologic response. The selected catchments are therefore comparable in terms of the governing hydrologic regime.
5. Discussion
5.1. Overall Approach
The results of this study rely on the outputs from a linear regression model. Such a model (as any statistical model) gauges correlations between predictors and the response variable that, in many cases, do not account for causality. Future work should explore the use of models based on hydrological processes.
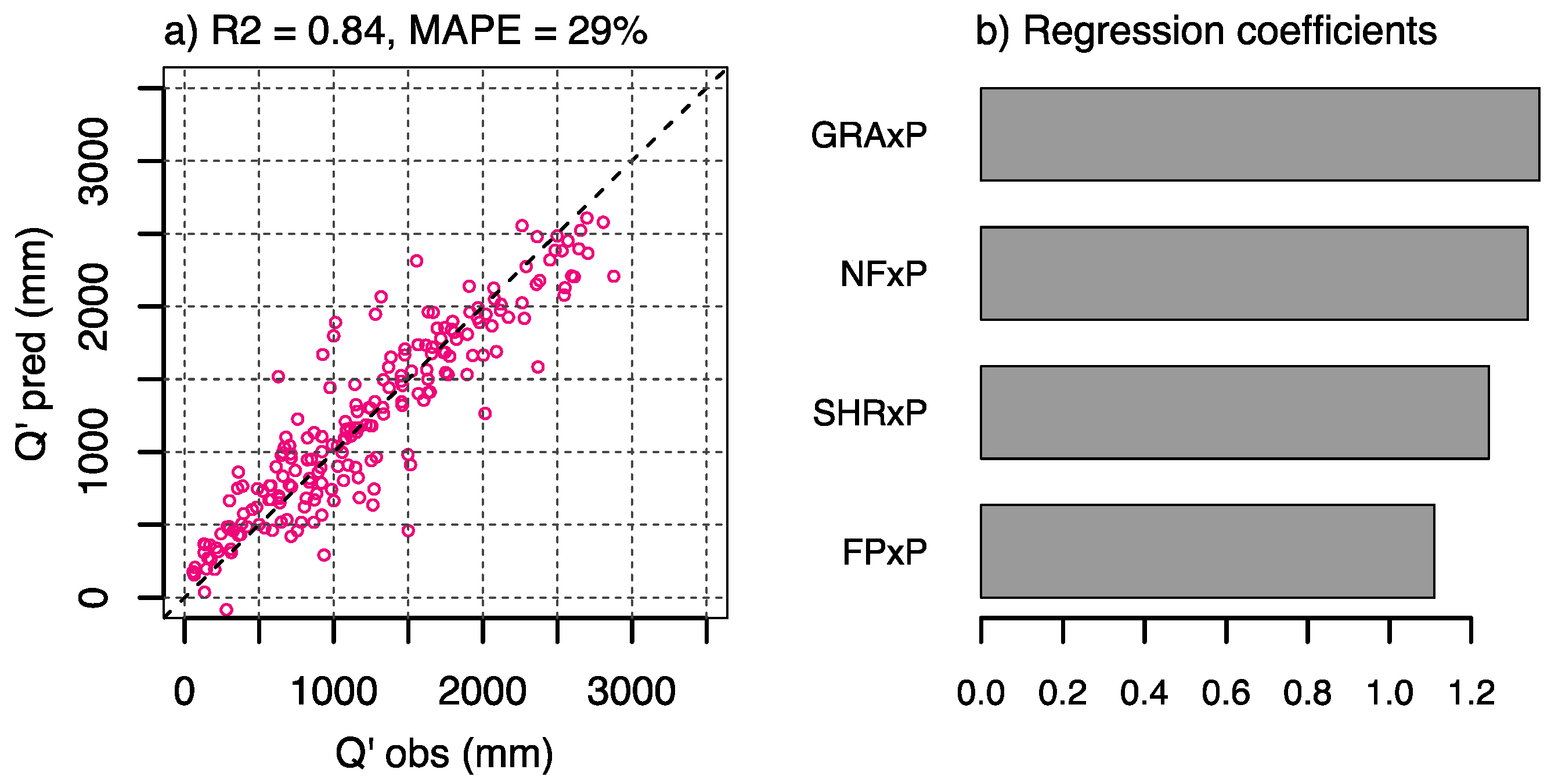
The physical basis of the empirical model proposed in this work is rooted on the annual water balance within a catchment and on the contribution of different land cover fractions to the total generated runoff. Despite this simplified representation of the water balance, the model provides a good representation of the annual runoff generated within forested catchments (
Section 4.1), and the water consumption (or runoff generation) derived for the different land cover classes do have a physical plausible explanation.
Given the annual precipitation received by each land cover patch within the watershed, GRA appears as the land cover with the highest runoff generation, followed by NF, SHR and finally FP (see regression coefficients in
Figure 8b). It should be noted that the model is not forced to intercept zero, therefore the regression coefficients should not be directly interpreted as the classical annual runoff coefficients (also known as runoff ratios [
31]) for each land cover class. The higher runoff generation indicated for GRA is consistent with its lower evapotranspiration rates compared with the other classes [
15,
36]. The higher water consumption in FP compared to NF is also consistent with higher evapotranspiration rates and lower soil water storage documented for FP compared with NF [
15,
20,
21,
22,
23]. The interpretation of SHR regression coefficients might be subject to pixel classification errors (as discussed in
Section 5.2).
While the model represents the overall catchment response (based on the total fractions of FP, NF, GRA and SHR within the catchments), local runoff generation mechanisms may change depending on the location of these land cover types within the basin, besides the effect of internal precipitation variation. In fact, water consumption of a same land cover class may change depending on its topographic position, since topography modulates water availability within the soil (lowlands may feature higher water availability than sharp sloped areas). On the other hand, land covers located in lowlands are subject to higher atmospheric demand due to highest air temperature and less humidity condition, leading to higher potential evapotranspiration and vapor pressure deficits, therefore more actual evapotranspiration is expected in those areas. That process can more intensively affect soil water depletion and hence summer flows.
Further, soil characteristics are affected by the land cover, particularly in watersheds where forest industrial activity is intensive. The extensive clear-cut strategy and the use of machinery for forest harvesting can cause soil compaction and the reduction of macropores, which reduces soil water holding capacity [
37]. Soil compaction and lower soil water storage associated with FP (compared to NF) may induce lower infiltration (less water contributing to baseflow), and therefore higher surface runoff. If storm events were analyzed, this effect should appear in the results. At the annual scale used here, the higher surface runoff from FP at specific events probably gets compensated by higher losses by evaporation from the surface, lower baseflow during no recharge periods or the summer season, and higher water consumption (higher evapotranspiration).
A way to account for these effects could be to formulate model predictors for different elevation or precipitation bands within the catchments (at the expense of decreasing model parsimony). Further, future work could also incorporate predictors accounting for soil spatial information for each land cover class.
Another important limitation of the empirical approach followed in this study is that the CAMELS-CL dataset does not provide a historical pathway of land cover within the catchments assessed here (we used a fixed national land cover map of 2014). To the best of our knowledge, such information is not available from other sources either (it should be noted that we require a land cover classification scheme coherent with [
33], which differentiates NF from FP).
As explained in
Section 2, to deal with the missing temporal land cover information, we assumed that the 2014 land cover provides an adequate representation of the previous 15 years, and thus we computed water balances for the period 2000–2015. This assumption should be valid for NF pixels, unless they correspond to stands younger than 15 years. In such cases, the pixel is probably classified as “mixed forest”, and therefore added to the FP class (details of this land cover aggregation is provided in [
31]). In the case of FP pixels, the assumption relies on having adult FP stands (rotation cuts are usually performed at 12 to 22 years). For young FP trees, there is a chance that these were classified as SHR (see discussion in
Section 5.2). This point relates to another issue with the land cover data: the land cover map does not provide the age of forests. These limitations restrict our understanding of the relationship between land cover (particularly, NF and FP) and streamflow generation processes. In fact, there is evidence on the different water consumption among stands of different ages [
38], and therefore, we could expect that streamflow generation mechanisms change with time in these forested basins.
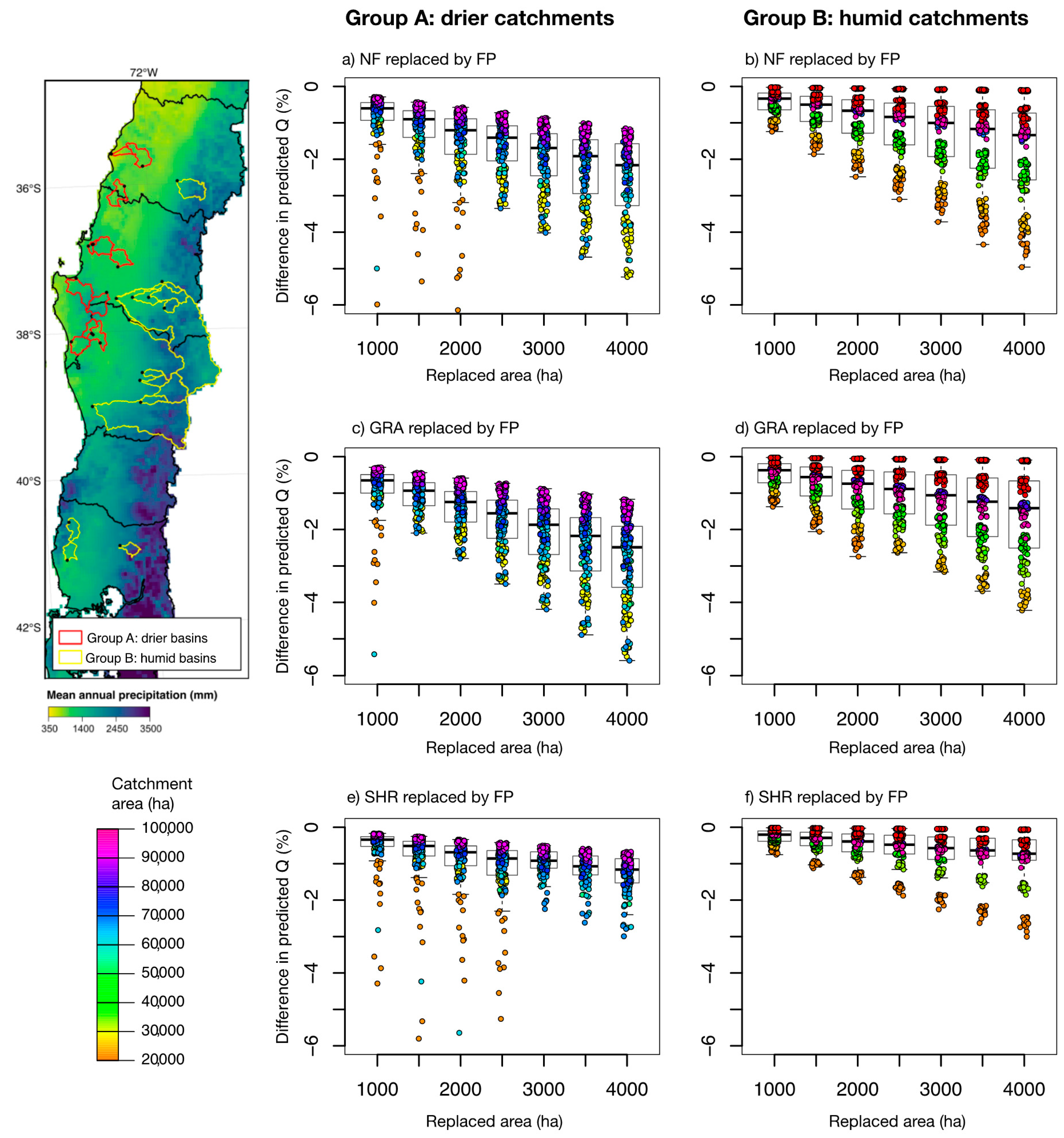
5.2. Impacts of the Expansion of Forest Plantation on Water Supply
The LULCC experiment indicates that for all catchment types, the expansion of FP has a higher impact when NF and GRA are replaced. This can be explained by the higher water consumption of FP compared to NF and GRA. The difference between FP and GRA is expected given the lower evapotranspiration rates associated to GRA [
15]. The higher losses in FP compared to NF suggested by these results would support previous place-based findings reporting higher evapotranspiration rates and lower soil water storage capacity in FP [
36].
When SHR is replaced by FP, the change in water supply is not as strong as when NF or GRA are replaced. Despite higher evapotranspiration rates documented for FP as compared to SHR [
15,
36],
Figure 9g and
Figure 8h suggest small differences in water consumptions from these two classes. We argue that this effect can be in part attributed to the potential presence of FP within SHR pixels. This mix may occur since young (less than five years) FP trees observed in Landsat images may be classified as SHR pixels. Furthermore, those SHR pixels might have been adult FP harvested in the previous five years. This limitation does not allow to clearly disentangle the effects of FP and SHR. To overcome this, we could use a time series of land cover within the catchment.
Figure 9 indicates that there is a strong dependency of LULCC results on the size of the catchment. For a given area of replaced land cover, the decrease in water supply is higher for smaller catchments. This is consistent with the higher percentage of the area that such an FP increment represents. Additionally, there is more dispersion of points within a same catchment (different basins can be distinguished by the color bar) for smaller catchment areas. The dispersion within a same catchment is due to the different annual precipitation each point represents. To visualize this effect, the color bar used in
Figure 9 can be computed based on the annual precipitation, instead of on the catchment area. These results (not shown here) indicate that drier years induce larger decreases in water supply.
In summary, the changes in annual runoff depend on several factors, in particular, the size of the catchment, the type of catchment (drier or humid), and the annual precipitation. This should be considered when interpreting the results presented here, as well as the results from any LULCC experiment. Indeed, the complex interdependency between runoff, land cover and precipitation, makes the results from different studies difficult to compare.
5.3. Impacts of NDC Mitigation Strategy on Water Supply
Regarding the NDC experiment, we should stress that it provides hypothetical scenarios, where the estimated changes in water supply are subject to limitations inherent to the study framework. Model predictions have uncertainties coming from the simplified representation of the water balance, the estimated parameters, and errors in the observed data. In addition, the model is fitted by using information from 25 catchments, which are not representative of the complete southern region of the country (
Section 2 summarizes the catchment selection criteria), and do not necessarily coincide with the characteristics of the landscape to be used in the real NDC afforestation plan. Furthermore, the rates of annual runoff change for increments of FP and NF were computed as the mean change for all catchments (
Table 1 and
Table 2), which is a practical generalization, although it does not account for the higher sensitivity reported for small catchments.
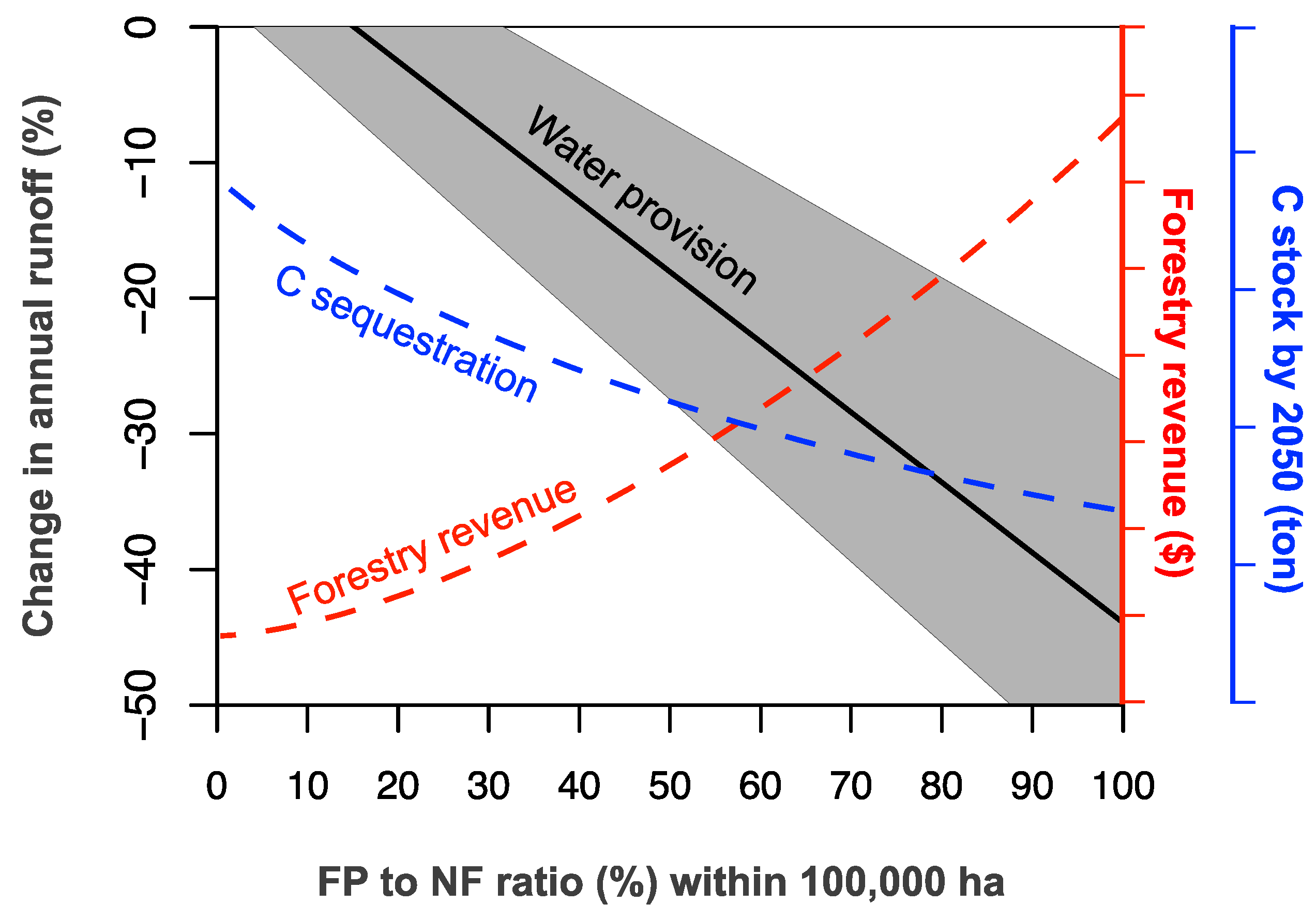
Acknowledging these limitations, the scheme in
Figure 10 provides valuable information that might be used for incorporating a water perspective in the decision of what proportion of typical exotic species (pines and eucalypts) versus native forests to use in order to meet the NDC pledged area. At present, this national commitment declares that the afforestation will be mainly with native species, but its actual proportion has not been defined.
In addition, other data could be added to the scheme as a way of incorporating other aspects into the discussion. These aspects may include water demand, national economic growth, promoting development in poor areas, biodiversity conservation, as well as the amount of stocked carbon. To visualize a couple of these aspects, we added hypothetical lines in
Figure 10, one related to potential forest industry revenues based on the planted area (and subsequent harvesting) of FP, and a second one related to the total amount of carbon sequestration at year 2050. The decrease in carbon stock with higher FP (higher FP to NF ratio) suggested in
Figure 10 is based on the fact that the carbon stored within FP trees will be released back into the atmosphere at harvesting times (given the typical rotation times, harvesting is likely to occur before 2015), while NF trees continue growing and storing carbon [
4]. These schematic lines are provided only with the purpose of visualizing the potential value of this exercise when the mitigation strategy is evaluated and discussed from different perspectives.
6. Conclusions
The work presented here corresponds to the first large sample study (25 basins) analyzing the impacts of vegetation cover on water supply, focusing on large catchments (>200,000 ha) in Chile. We proposed an empirical model to represent the annual water balance within a catchment based on the contribution of different land cover fractions to the total generated runoff. We highlighted the main limitations of the approach and recommended strategies to overcome them. These included the use of historical and future land use and land cover pathways, and moving towards a model based on hydrological processes.
The evidence provided here is consistent with previous finding focusing on small experimental watersheds. We showed that annual runoff consistently decreases with increments of FP (at the expense of natural vegetation land covers including NF, GRA and SHR). We highlighted that the magnitude of the change depends on several factors (e.g., initial land cover partition within the basin, the replaced land cover class and the annual precipitation), but most importantly, that it depends on the catchment area. In general, water supply in smaller catchments (areas below 50,000 ha) is more sensitive to land cover changes, and the decrease in annual runoff is further exacerbated during dry years.
In line with current global challenges to dampen global warming, we quantified the impacts on water supply due to different combinations of NF and FP to fulfill the afforestation area pledged in the Chilean NDC (100,000 ha). At present, this national commitment declares that the afforestation will be mainly with native species, but its actual proportion has not been defined. If the FP to NF ratio is set as 0.5, we predict a 18% average decrease (ranging from 7% to 27% decreases for the 75th and 25th percentiles, respectively) in mean annual runoff generated at catchments in central-south Chile. This decrease of water availability would be aggravated if the afforestation is performed within small catchments. In addition, such decreases in water supply would be exacerbated within dry periods, such as the megadrought experienced in the region over the last decade [
32,
39]. According to climate projections, such dry conditions constitute a probable scenario for the following decades over the region [
40]. Therefore, we argue that water availability—under a changing climate—must be incorporated in the discussion of the NDC afforestation strategy, along with other aspects such as carbon stock and economic growth (as proposed in
Figure 10).
Overall, the evidence presented here highlight the vulnerability of water supply under LULCC scenarios, especially within the context of climate change. Our results can be used to incorporate a water perspective into public policy and decision making that can effectively lead to achieving a sustainable development. Such development should leverage economic benefits from forests management, the long-term sustainability of the natural systems, and the fulfillment of climate change mitigation goals.