1. Introduction
Slope stability and soil erosion are significant environmental and societal issues worldwide, particularly in the Mediterranean region [
1,
2]. The importance of these geomorphic processes is growing in relation to the intensification of precipitation, as well as in response to the increasing occurrence of extreme rain events in recent years [
3], which are predicted to increase even more in the future [
4]. In addition to rainfall, earthquakes, storm surges, shallow groundwater-level changes, and streambank erosion can all induce instability in hillslopes, triggering hydrogeomorphic hazards, such as mass movements of rock, debris, and soil [
5]. Moreover, factors such as poor land management, forest degradation and conversion, forest fires, road construction, urban sprawl, and climate change can all affect slope stability [
6]. In this context, forest conservation and appropriate forest management play significant roles in preventing and mitigating hydrogeomorphic hazards induced or exacerbated by human activities. In fact, the presence of plant roots enhances soil properties (e.g., organic matter content, soil structure, pore size distribution) and significantly increases the shear strength of soils [
7,
8,
9,
10]. Analyzing landslide inventories clearly shows an increase in landslide frequency and an accelerated displacement of existing landslides after forest harvesting and vegetation removal [
11,
12]. These studies attribute enhanced landslide occurrence to the reduction in root reinforcement following the removal of forest vegetation. Forest cover has also been suggested to ameliorate slope stability via rainfall interception [
13], although other studies have shown that this influence is very limited [
14]. Indeed, forests improve the infiltration capacity of the soil, thus reducing the potential for surface erosion [
6].
The anchorage of roots into stable substrate and the consequent improvement of slope stability is related to increased soil shear strength [
7,
15], which also depends on specific properties of the root systems, such as root density and distribution [
16] and root tensile strength. The role of vegetation in slope stability has been clearly established [
9], whereby root reinforcement mechanisms are particularly dominant in forest soils [
17]. In fact, on steep soil slopes, techniques such as restoring woody vegetation cover are applied to prevent shallow failures [
18]. Plant roots increase the strength of the soil–root mass by enhancing the confining pressure and the resistance to sliding [
19]. Root tensile strength together with root distribution and root area ratio (RAR) are important factors for determining soil reinforcement and contributing to the safety factor of hillslopes [
20]. RAR provides a measure of root density within the soil and is defined as the fraction of the soil cross-sectional area occupied by roots [
21]. RAR is strongly influenced by local soil and climate characteristics, land management, and associated vegetation. RAR decreases with depth and distance from the tree trunk [
22]. Another essential parameter that influences slope stability is root cohesion, which varies according to the species and is highly dependent on root morphology [
23]. Zhang et al. [
24] showed that root cohesion is produced by the transfer of shear stress in the soil due to tensile resistance in the roots.
Many studies have evaluated mechanical properties of plant roots and their role in soil stability [
17,
25,
26,
27], but there is a lack of such information in Mediterranean environments and vegetation. Furthermore, assessing root cohesion values for different tree and shrub species could improve our understanding of how vegetation affects slope stability and how best to apply phytotechnology for landscape restoration. One aspect which has been rarely taken into account in such investigations is the moisture content in the roots for different species and site characteristics, and its possible effect on mechanical properties [
24]. The basic assumption is derived from wood technology studies [
28], which report a remarkable effect of moisture content on mechanical properties (including tensile strength) in the wood hygroscopic range from 0 to 30%, where 30% is roughly assumed to be the wood fiber saturation point (FSP) and values above this usually do not influence mechanical properties [
28]. The fiber saturation point represents the moisture content at which the maximum water content bonds to cell walls by means of hydrogen bonds and the assumed value of 30% only significantly changes in very degraded wood, such as waterlogged wood [
29]. Root biomechanical traits are greatly affected by species and site conditions [
30], while they represent relevant properties to be considered for modeling slope stability and landslide initiation. This study aims to investigate the role that important montane Mediterranean forest trees and shrubs play in soil stability and erosion control in largely forested regions of Southern Italy, such as the Sila National Park. In this context, soil erosion and slope stability are critical issues due to geomorphology, ecosystem management, forest fires, and rainfall regimes with irregular but intense events. The purpose of this study was to validate the following objectives:
Soil–root reinforcement in mountains and hillslopes is highly dependent on forest species biodiversity, particularly in the Mediterranean region;
Root properties, such as tensile strength and root cohesion, are important biomechanical traits that could be efficiently utilized in nature-based solutions to improve soil stability in the region;
Root moisture conditions affect root tensile strength.
3. Results
3.1. Tensile Strength
Fresh water content (FWC) in roots ranged from 73% in
Quercus cerris L. to 164% in
Pinus nigra subsp.
laricio (Poir.) Maire, but variability was large (
Table 3). This high variability was particularly evident for
Quercus cerris L. (coefficient of variation 89%) and
Crataegus monogyna Jacq. (coefficient of variation 80%). Maximum water content (MWC) ranged from 132% in alder up to 252% in hawthorn and variability for all species was also very high (
Table 3).
Kruskal–Wallis H tests indicated no statistically significant differences in tensile strength of the roots related to their water content (both FWC and MWC) for all species and roots classes (
Castanea sativa Mill. χ
2(1) = 0.337,
p = 0.561;
Alnus glutinosa (L.) Gaertn χ
2(1) = 0.198,
p = 0.655;
Quercus cerris L. χ
2(1) = 0.016,
p = 0.898;
Pinus nigra subsp.
laricio (Poir.) Maire χ
2(1) = 3.347, p = 0.067;
Ilex aquifolium L. χ
2(1) = 1.471,
p = 0.225;
Crataegus monogyna Jacq χ
2(1) = 1.928,
p = 0.164;
Cytisus scoparius L. χ
2(1) = 0.007,
p = 0.932;
Spartium junceum L. χ
2(1) = 0.355,
p = 0.551), hence, all samples of the same species (FWC and MWC) were grouped together for the purpose of this study. Tensile strength (T
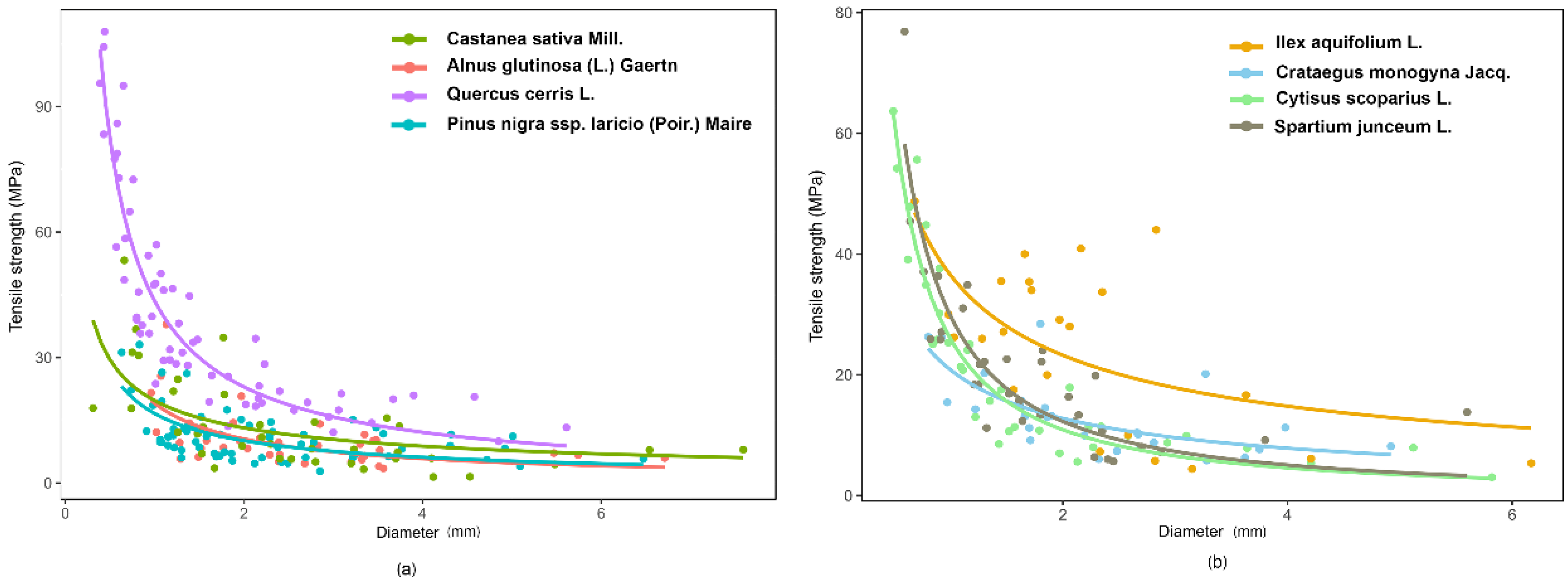
r) decreased with increasing diameter (D), according to a power law curve (
Figure 4). The parameters of the root strength–diameter power law relationship are reported in
Table 4. In total, 346 root trials were performed. Diameter of the tested roots varied between 0.31 and 7.59 mm, while the minimum and maximum tensile strength values were 1.44 and 107.91 MPa, respectively (
Table 4). Power law functions for different species had
R2 values ranging from 0.27 (
Pinus nigra subsp.
laricio (Poir.) Maire) to 0.84 (
Cytisus scoparius L.), but for all species, the relationships were highly significant (
p < 0.001;
Table 5).
ANCOVA analysis indicated significant differences in root tensile strength among species (F
(7,730) = 33.96,
p-value < 0.001) (root diameter as covariate). Indeed, analysing T
r(D) log-transformed values, we found that the angular coefficients were different among the species, resulting in non-parallel curves (
Figure 4).
The ANCOVA analysis confirms that the tensile strength depends on diameter and that the slope of the regression between Tr and D is species-specific. The LSD test divided the tested species into four significantly different groups based on tensile strength: 1—Quercus cerris L.; 2—Ilex aquifolium L. and Cytisus scoparius L.; 3—Spartium junceum L.; 4—Crataegus monogyna Jacq., Castanea sativa Mill., Pinus nigra subsp. laricio (Poir.) Maire, and Alnus glutinosa (L.) Gaertn. Quercus cerris L. had the largest values of Tr and therefore greater root resistance. Moreover, considering plant type (trees versus shrubs) the two series are parallel (ANCOVA, F(1,342) = 0.11, p-value = 0.73) and significantly different (ANCOVA, F(1,342) = 2.72, p-value < 0.1). The LSD post hoc test highlighted that shrubs have a significantly higher root tensile strength than trees and, therefore, the shrubs have a higher resistance to tension stress.
Young modulus could add interesting information to predicting root reinforcement [
50]. Nevertheless, the stress strain curves of many samples show a shape quite tortuous, as in agreement with Commandeur and Pyles [
50] too. Indeed, in order to measure the Young modulus, several traits of stress strain curve must be selected, applying for each trait a different model to determine the root’s real behavior. This part of the research needs a focused investigation. The results of the modulus of elasticity, processed by testing machine “ProLine”-Zwick Roell” for each species, were:
Castanea sativa Mill. 63.3 MPa ± 1.49,
Alnus glutinosa (L.) Gaertn 256.4 MPa ± 0.49,
Quercus cerris L. 77.2 MPa ± 1.61,
Pinus nigra subsp.
laricio (Poir.) Maire 118.2 MPa ± 0.186,
Ilex aquifolium L. 250.2 MPa ± 0.261,
Crataegus monogyna Jacq. 136.2 ± 0.206,
Cytisus scoparius L. 143.5 ± 0.625, and
Spartium junceum L. 177.2 MPa ± 0.486. The measured values are comparable with Commandeur and Pyles [
50] and Wu et al. [
51].
3.2. Root Area Ratio—RAR
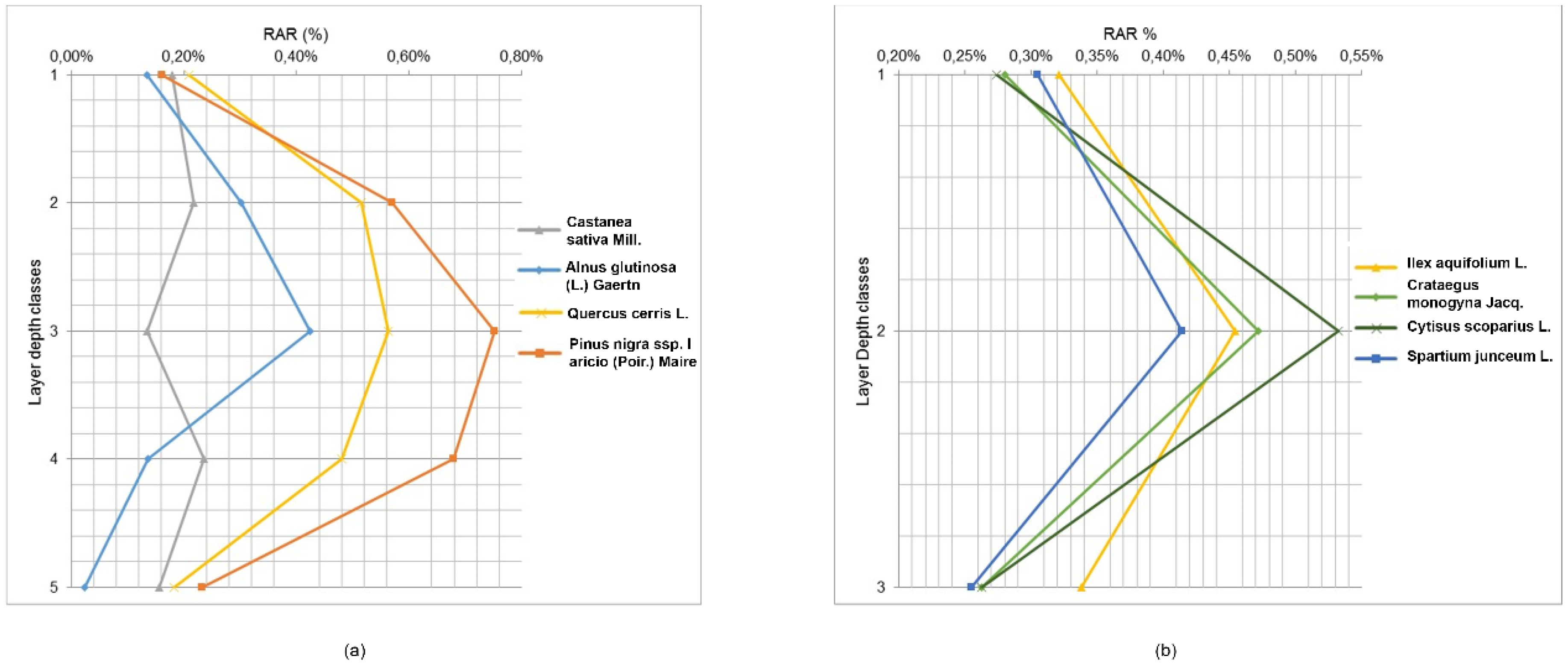
In the trenches, tree roots were measured at depth increments of 10 cm and divided into 3 depth classes for shrubs and 5 depth classes for trees. The percentage of roots varied according to soil depth and species (
Figure 5 and
Table 6).
For trees, RAR values in the first layer (0–10 cm depth) ranged from 0.13% (Alnus glutinosa (L.) Gaertn) to 0.21% (Quercus cerris L.); in the second layer (10–20 cm), these values range from 0.22% (Castanea sativa Mill.) to 0.57% (Pinus nigra subsp. laricio (Poir.) Maire); in the third layer (20–30 cm), the values range from 0.13% (Castanea sativa Mill.) to 0.75% (Pinus nigra subsp. laricio (Poir.) Maire); in the fourth layer (30–40 cm), these range from 0.14% (Alnus glutinosa (L.) Gaertn) to 0.68% (Pinus nigra subsp. laricio (Poir.) Maire); and in the deepest layer (40–50 cm), the values range from 0.02% (Alnus glutinosa (L.) Gaertn) to 0.23% (Pinus nigra subsp. laricio (Poir.) Maire). Shrub species revealed similar trends, although roots did not extend as deep as tree roots. In this context, RAR values in the first layer (0–10 cm depth) ranged from 0.27% (Cytisus scoparius L.) to 0.32% (Ilex aquifolium L.); in the second layer (10–20 cm), these values varied from 0.41% (Spartium junceum L.) to 0.53% (Cytisus scoparius L.); and in the deepest layer (20–30 cm), the values ranged from 0.25% (Spartium junceum L.) to 0.34% (Ilex aquifolium L.). The variability of root density with depth among different species was also quite large; root systems of trees were concentrated in the 20–30 cm layer, while shrub roots were concentrated in the 10–20 cm layer.
For tree species, results of the ANCOVA showed that RAR is significantly different among species F(4,35) = 4.26, p-value < 0.0065 (depth as covariate). The post hoc LSD test showed that Pinus nigra subsp. laricio (Poir.) Maire and Quercus cerris L. had significantly higher RAR values than the other tree species. This result is confirmed by the ANOVA test, in fact, the main effect of species was significant, F(3,20) = 17.31, p value < 0.0001, as was the main effect of layer depth classes, F(4,20) = 14.06, p-value < 0.0001. Furthermore, the interaction of these two factors was significant, F(12,20) = 2.59, p-value = 0.029. The post hoc LSD test showed that the RAR values in the 10–20 cm, 20–30 cm, and 30–40 cm depth classes were significantly different with respect to the other classes (0–10 cm and 40–50 cm). For shrubs, results of the ANCOVA confirmed that the RAR is not significantly different among species F(4,19) = 0.075, p-value = 0.99 (depth as covariate). This result is confirmed by the ANOVA test, in which the main effect of species was not significant, F(3,12) = 0.09, p value = 0.96, nor was the main effect of layer depth classes, F(2,12) = 3.08, p-value = 0.08. The interaction of these two factors was also not significant, F(6,12) = 0.11, p-value = 0.99. The ANCOVA for tree and shrub categories in the first three depth classes showed that the RAR is not significantly different among categories (F(2,45) = 2.34, p-value = 0.10).
3.3. Root Cohesion
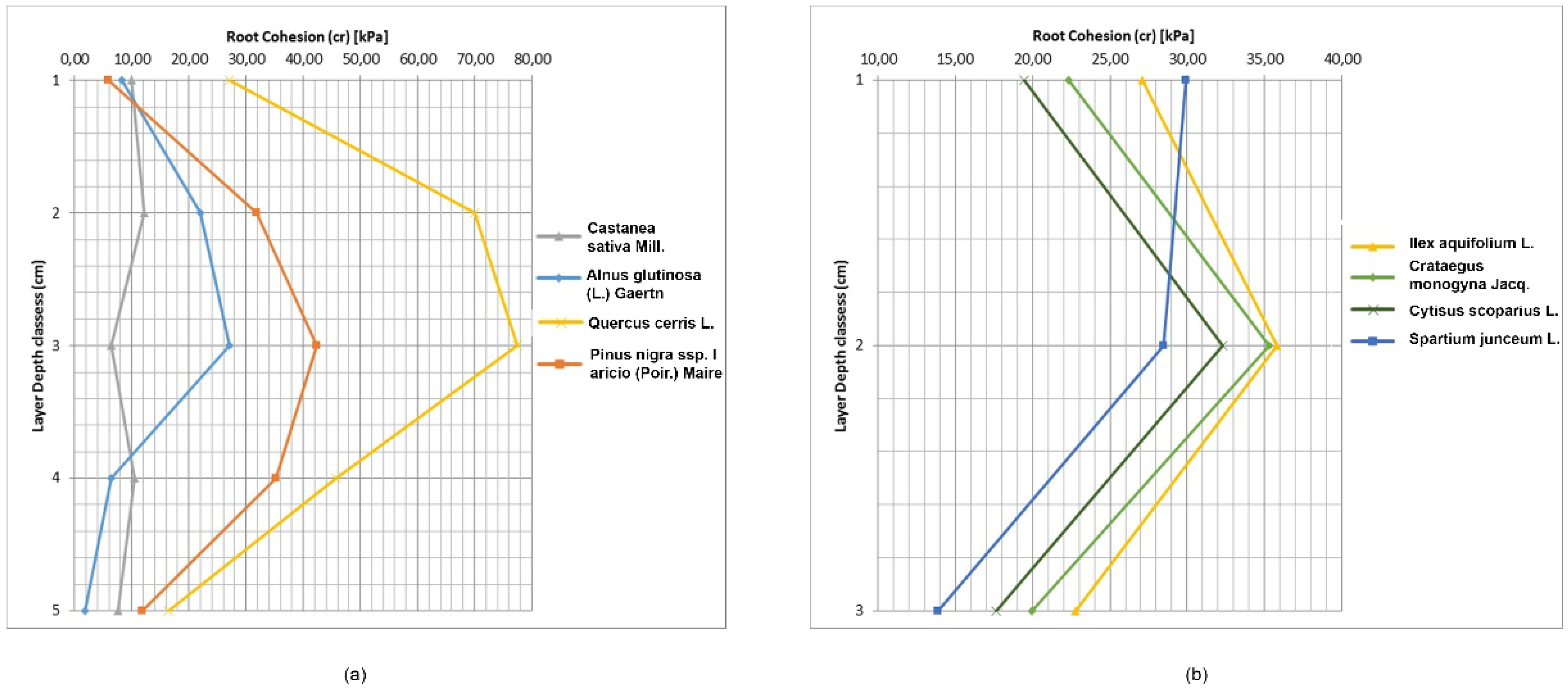
Equation (5) for estimating soil reinforcement by roots was applied and the results were highly variable for both species and depth. Values of c
r ranged from 1.90 kPa for
Alnus glutinosa (L.) Gaertn to 77.53 kPa for
Quercus cerris L., while for shrubs, the highest c
r was for
Ilex aquifolium L. (35.80 kPa) and the lowest for
Spartium junceum L. (13.86 kPa) (
Table 7 and
Figure 6). Root cohesion in the 10–20 cm depth was highest in all species. For trees, the second and third depth layer had elevated c
r values. Below this depth, c
r declined similarly to other studies [
9,
30,
41,
43,
52,
53]
4. Discussion
The analysis of the root systems of important montane Mediterranean tree and shrub species indicates significant differences in their strength characteristics. A total of 346 undamaged roots with diameters smaller than 1 cm and a constant root length of 20 cm were tested for tensile strength. In general, the root tensile strength (T
r) decreased with increasing root diameter (D). The generally accepted form of the relationship between T
r and D is a simple power function [
7,
9]. Many studies have confirmed the validity of this relationship [
41,
45], while the influence of root diameter on tensile properties has been studied from the perspective of chemical components [
23]. ANCOVA tests showed that species are the most important factor determining root tensile strength, as also shown by previous studies [
41]. Furthermore, root diameter acts together with species characteristics to affect root tensile strength. Differences in tensile strengths between trees and shrubs were not statistically significant. Tensile strength values of
Quercus cerris L. roots were the highest among the species tested;
Alnus glutinosa (L.) Gaertn and
Pinus nigra subsp.
laricio (Poir.) Maire had the lowest tensile strength values, while other species showed an intermediate behavior. The tensile strength values of
Pinus nigra subsp.
laricio (Poir.) Maire are comparable with the other Pinus species [
24,
54]. Generally, roots of deciduous trees have higher tensile strengths than conifers [
54] and this is confirmed in our study, except for
Alnus glutinosa (L.) Gaertn, which could be explained by its wood density being similar to the density of pine trees. The values of tensile strength obtained in all the hardwoods and shrubs fall within ranges reported by other studies [
24,
27,
41,
55], especially with regard to
Quercus cerris L. [
26]. However, in many studies, most of the species showed large variability in tensile strength [
56]. This variability can arise from different conditions in the growing environment [
26], including soil moisture content and physical characteristics, and other factors, such as the methods used for preserving roots prior to measurements, the time elapsed before testing, and differences in machines used to conduct tensile strength tests [
41].
The comparison between tensile strength measured in fresh roots (FWC), as collected in the field, and water-saturated roots (MWC) requires more discussion. Apparently, by choosing the wettest conditions, the test should represent the minimum strength value of a particular root and, more likely, the strength of the root in conditions of root failure during landslide initiation caused by soil water saturation [
54]. The role of moisture content in roots is controversial because an increase in moisture has been shown to induce a decrease in mechanical strength [
54,
57]. Yang et al. [
54] showed that the quadratic equation was the most applicable model for explaining the relationship between root moisture content and tensile strength. A comparable result was obtained by [
58], who also took into account decreasing root diameter due to water content loss [
58,
59] and, consequently, root strength. However, in our study, the variation of water content in the roots, from ambient soil moisture conditions to maximum water content, did not significantly affect tensile strength performance. This can be related to the fact that moisture content values were generally higher than the wood fiber saturation point (about 30%), above which the physical–mechanical properties usually did not change significantly [
56]. In any case, in relation to the high variability of soil moisture content, soil properties, climate conditions, root structure (especially diameter [
54]), species (hardwood or conifers), and tree physiological status [
57] (vegetative season or dormant period), fresh root water content needs to be further investigated, as it would be preferable to make experiments on the real fiber saturation point at different conditions.
Our findings confirm the trend of decreasing RAR with soil depth that has been associated with reduced availability of nutrients, decrease in soil aeration, and the presence of more compact layers [
60]. RAR patterns were investigated separately for trees and shrubs and assessed to depths of 0.50 m and 0.30 m, respectively. Our method only considered roots typically smaller than those of second- and third-order roots. Furthermore, the effects of different root system structures for various species were not considered. For example, we found that
Pinus nigra subsp.
laricio (Poir.) Maire,
Quercus cerris L., and
Alnus glutinosa (L.) Gaertn have a similar RAR distribution trend with very deep taproots and well-developed radical structures, whereas
Castanea sativa Mill. had the highest RAR value in the second and fourth depth class layer and roots expanded more laterally than in depth [
61]. For woody shrubs, RAR values were very similar for all four species, while the largest number of roots were present in the 10 to 20 cm soil depth interval. Significantly, because of our mountainous site, more lateral roots were located below the upper 10 cm soil depth; plants growing on relatively flat sites typically have more abundant lateral roots in the upper 10 cm of soil compared to hillslopes [
62]. RAR trends for shrub and tree profiles in our study can be compared with previous results [
63]. Lombardi et al. [
62] found that the number of fine roots of
Spartium junceum L. was highest in the upper 10 cm and decreased with soil depth. In our study, RAR values were generally higher compared to the values obtained in other Mediterranean and alpine sites [
27,
41], except for values of chestnut, which are comparable with the results obtained by Bischetti et al. [
41].
The model reported by Wu et al. [
10] was used to calculate root cohesion. The choice of the coefficients k′ and k″, as reported in Equations (5) and (6), play a crucial role in estimating root cohesion. Many authors have demonstrated that k″ can assume values much smaller than 1.0, dramatically affecting the value of root reinforcement [
45,
48]. Hammond et al. [
49] proposed a k″ factor of 0.56 for forest vegetation. Moreover, the value of root cohesion varies as a function of the RAR distribution patterns, although some discrepancies can be associated with the dependency on root tensile strength and root diameter distribution. Usually, estimated root cohesion values are significantly higher in the upper soil layers (10–40 cm) and decline with soil depth. Furthermore, our results show that the investigated plant species have comparable reinforcement to previously studied tree and shrub species [
22,
60]. Maximum root cohesion occurred from 10 to 20 cm depth in all species examined in our study. The type of vegetation affects the value of root cohesion as well as the land use. Schmidt et al. [
30] noted lower root cohesion values in intensively managed clear-cut forests compared to natural forests. The root cohesion values obtained in the Bonis basin were very similar to those found by Schmidt et al. [
30] for unharvested natural forests and those reported by Greenway [
22] (average root cohesion up to 40 kPa for trees).
5. Conclusions
Our findings contribute to knowledge about the root tensile strength, RAR, and the cohesion model of some typical trees and wood shrubs in the Mediterranean region. The results could significantly increase knowledge to improve natural hazard prevention and mitigation in Mediterranean forest environments. The results related to tensile strength, RAR, and cohesion are not all comparable with values obtained in previous studies, indicating the significant role of site features, such as soil type and management history of forest stands. While
Quercus cerris L. maintained the strongest role in soil reinforcement, pioneer shrub species like
Spartium junceum L., with root tensile strengths comparable or even higher than some tree species, have important stabilizing roles. Shrubs can increase soil shear strength considerably without having the more complex effects attributed to wind stress or static surcharge of the trees. Furthermore, retaining woody shrubs with high root strength via forest cable logging operations could benefit soil stability, compared to harvesting operations that damage the understory layer [
64]. Increases in soil shear strength are mostly attributed to roots (1 < D < 10 mm) that often exert their maximum tensile strength during soil displacement [
43]. Our results confirmed the very important role of small roots, which increase soil shear strength by anchoring the soil mantle and by forming a binding network within the soil profile. The role played by
Pinus nigra subsp.
laricio (Poir.) Maire, which has been used extensively in reforestation throughout Europe and in other continents, was quite important. Although the tensile strength of
Pinus nigra subsp.
laricio (Poir.) Maire is modest, root cohesion is quite high, as displayed by maximum values of RAR. Thus,
Pinus nigra subsp.
laricio (Poir.) Maire can significantly contribute to soil slope stabilization and, providing that appropriate forest management practices are used, could also allow for recolonization by other late-successional trees and woody shrubs, further stabilizing the soil, considering that diverse tree root types greatly contribute to slope stability [
65]. Knowledge of the behavior of root systems can be helpful for designing and using bioengineering techniques [
16,
56,
66] and can be useful for mapping slope stability in wooded areas, particularly in Mediterranean environments. Moreover, the results of our experimental data can be used in slope stability models, opening up new research scenarios, especially by including root cohesion in models of mountain stability [
6,
67]. Root properties such as tensile strength and root morphology are important biomechanical traits that could be efficiently utilized in nature-based solutions to improve soil stability in the region. In this context, forest management in sustainable ways could play a key role in improving slope stability [
68] and enhance the ecosystem services associated with forests [
69]. Therefore, managing forests against mass wasting hazards is one of the most important ecosystem services provided in mountain regions [
68,
70].