Recent Deforestation Pattern Changes (2000–2017) in the Central Carpathians: A Gray-Level Co-Occurrence Matrix and Fractal Analysis Approach
Abstract
:1. Introduction
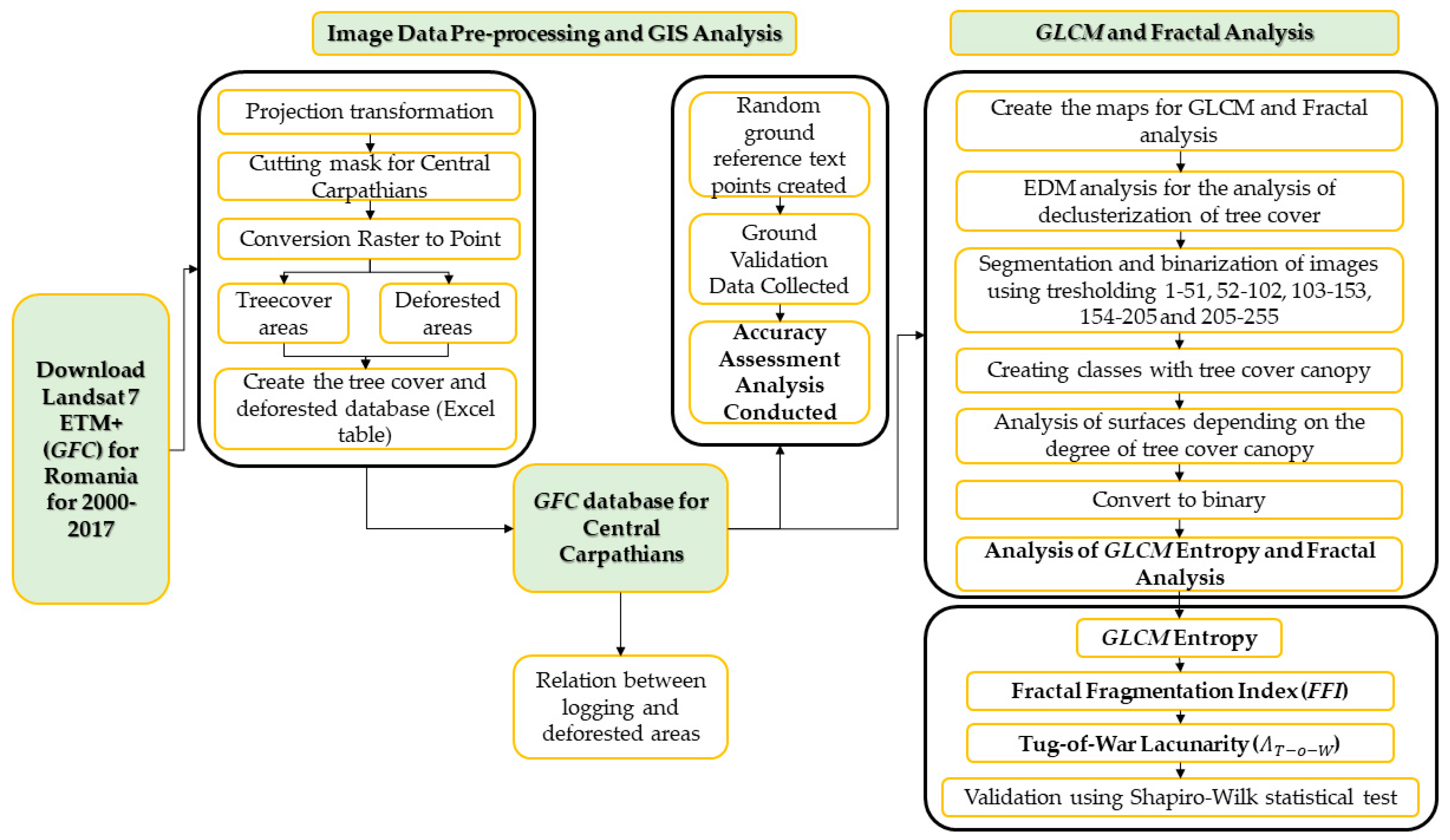
2. Materials and Methods
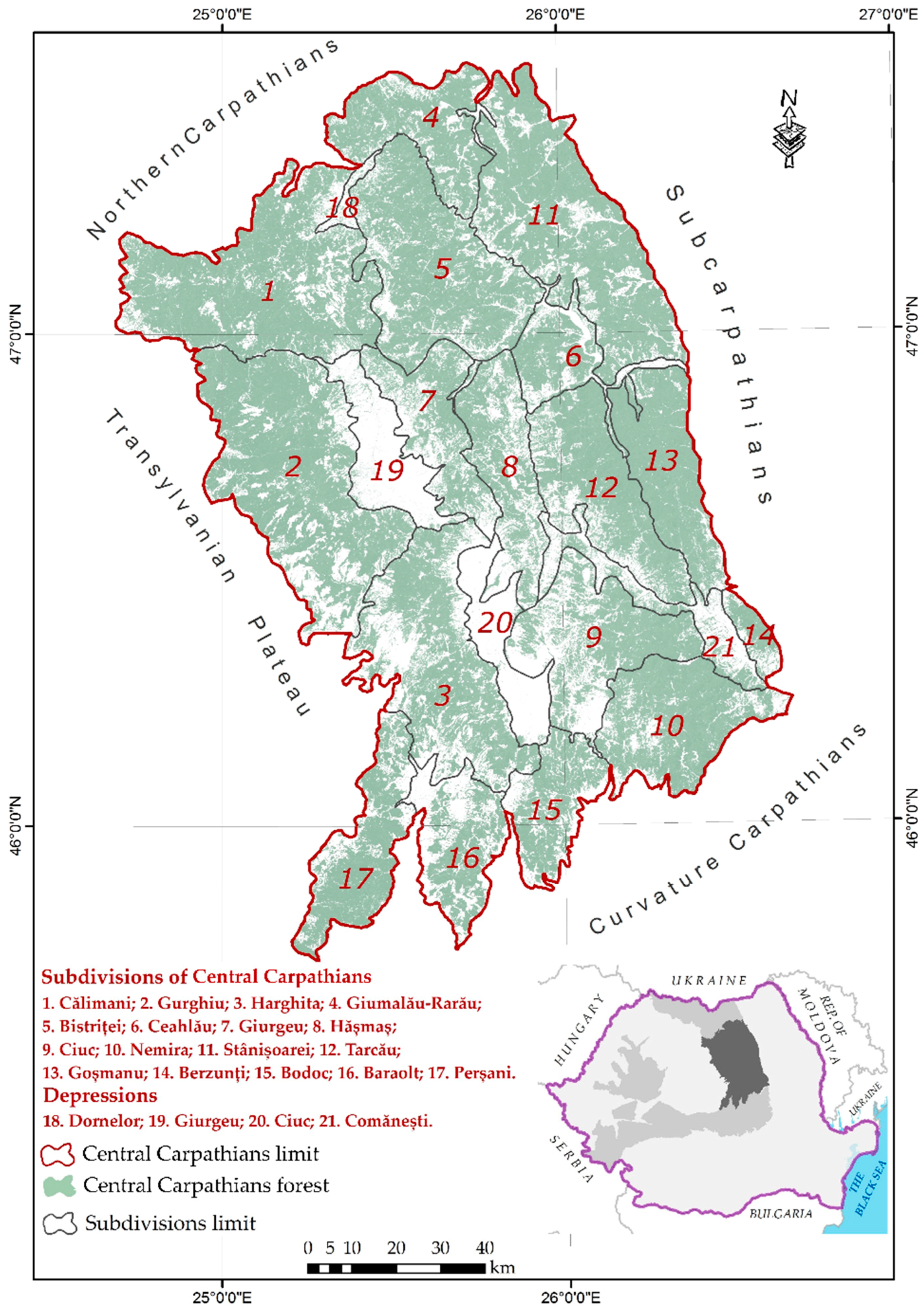
2.1. Study Area
2.2. Forest Imagery and Pre-Processing
2.3. Classification Accuracy Assessment
2.4. Preprocessing of GFC for GLCM and Fractal Analysis
2.5. GLCM and Fractal Analysis
2.6. Validation of GLCM and Fractal Analysis Indices
3. Results
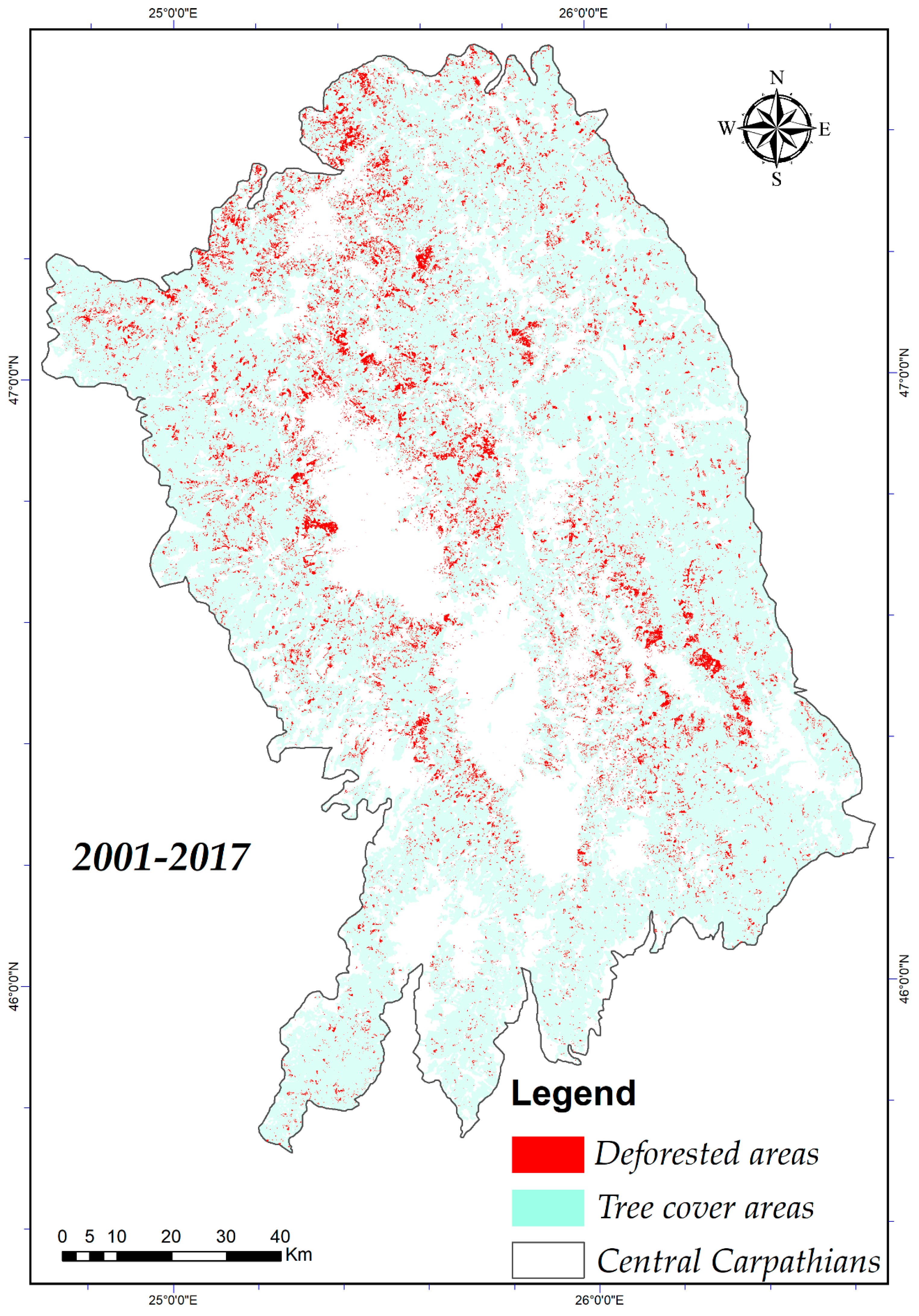
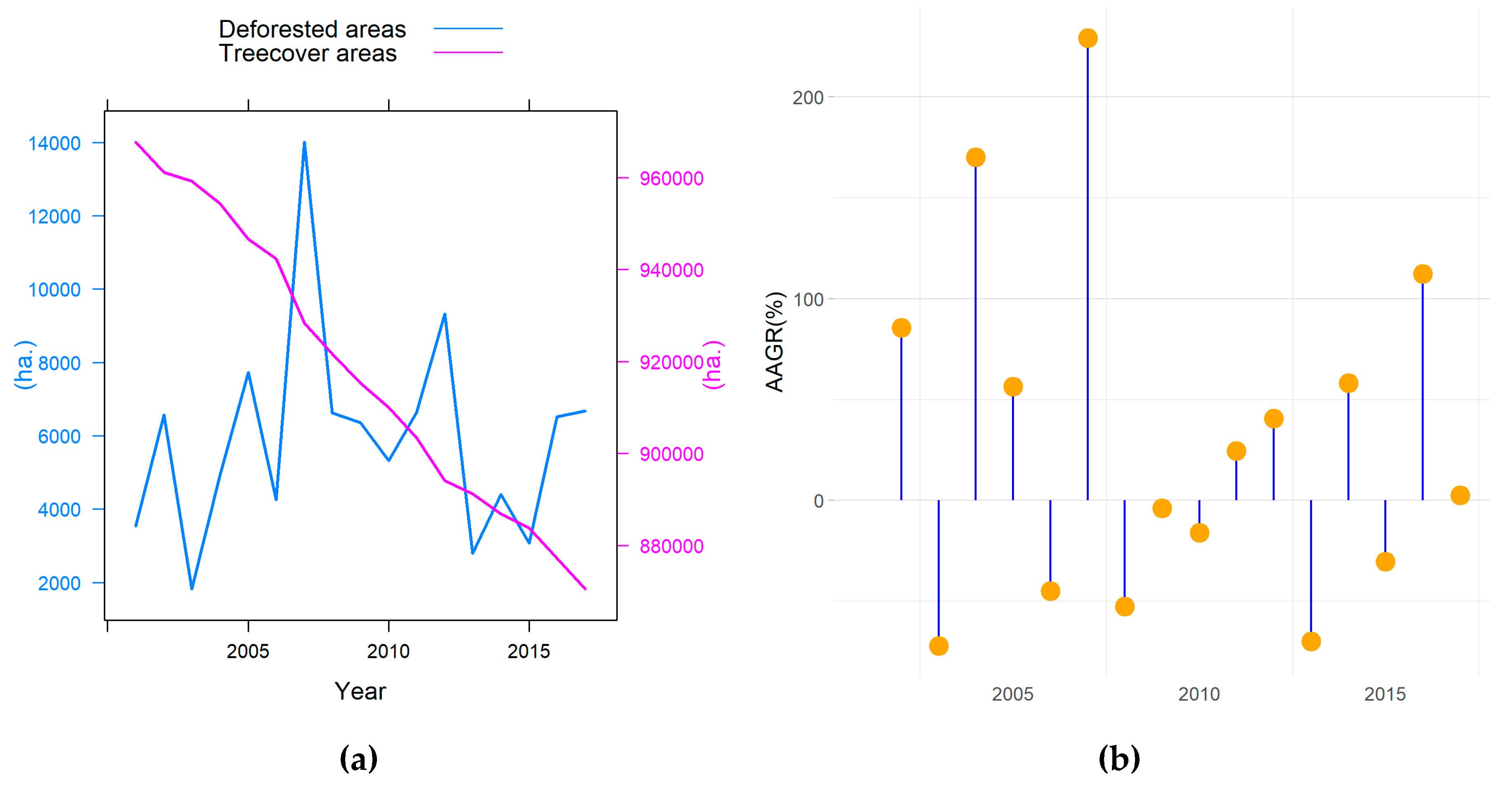
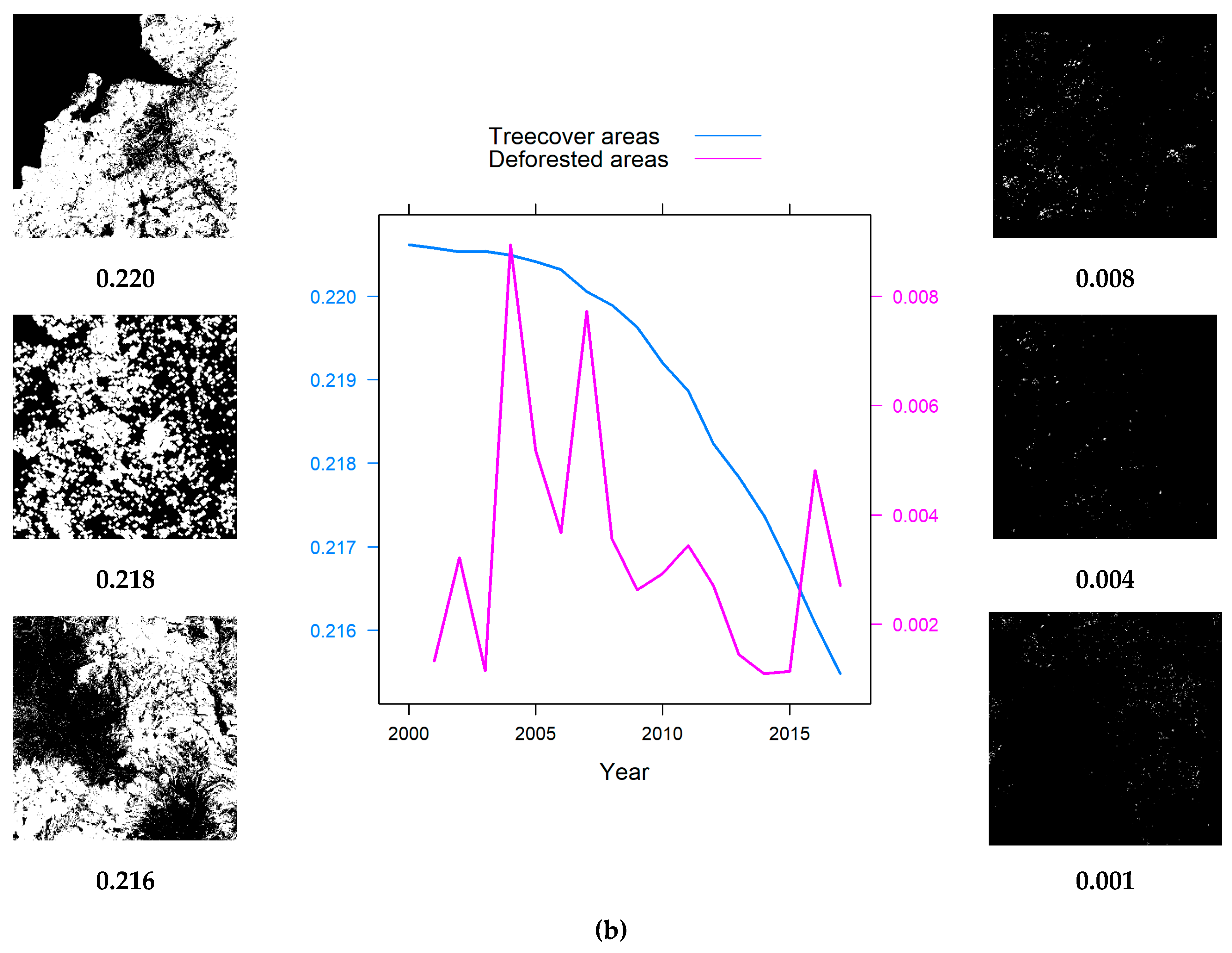
3.1. The Analysis of Deforested Areas from Central Carpathians
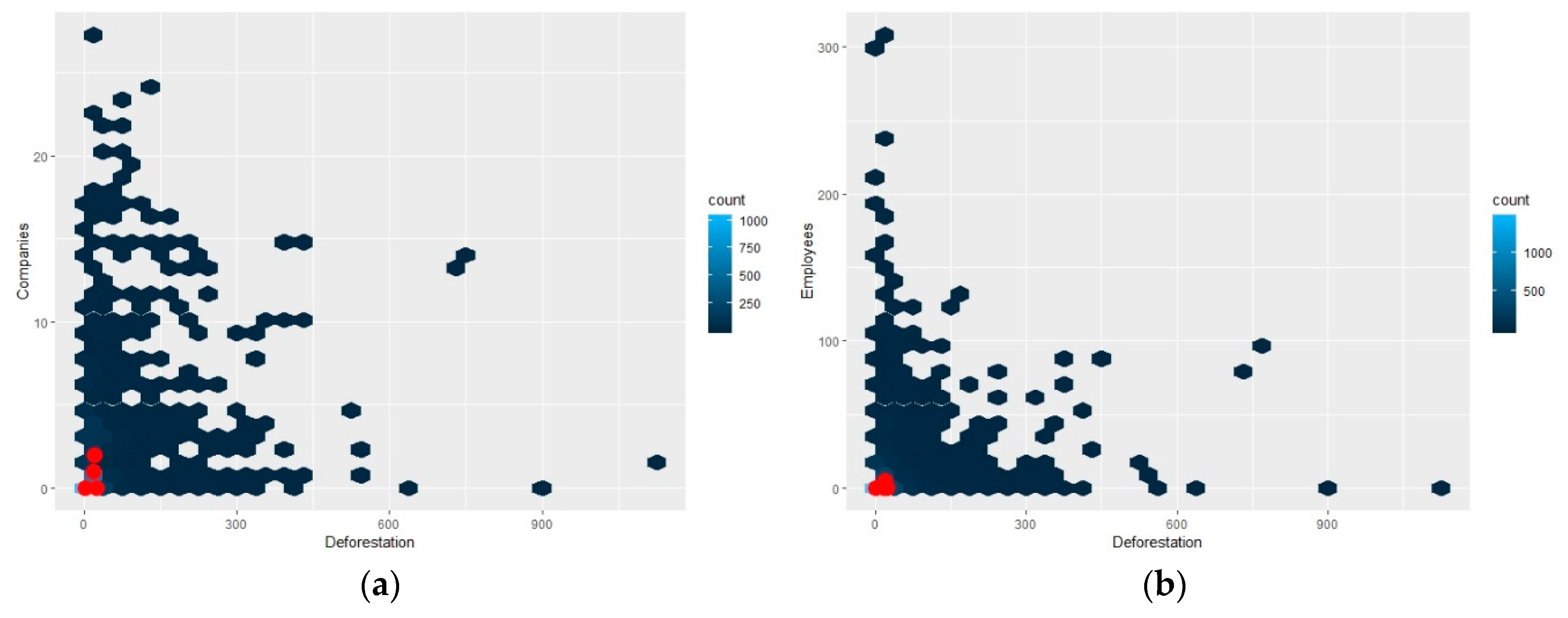
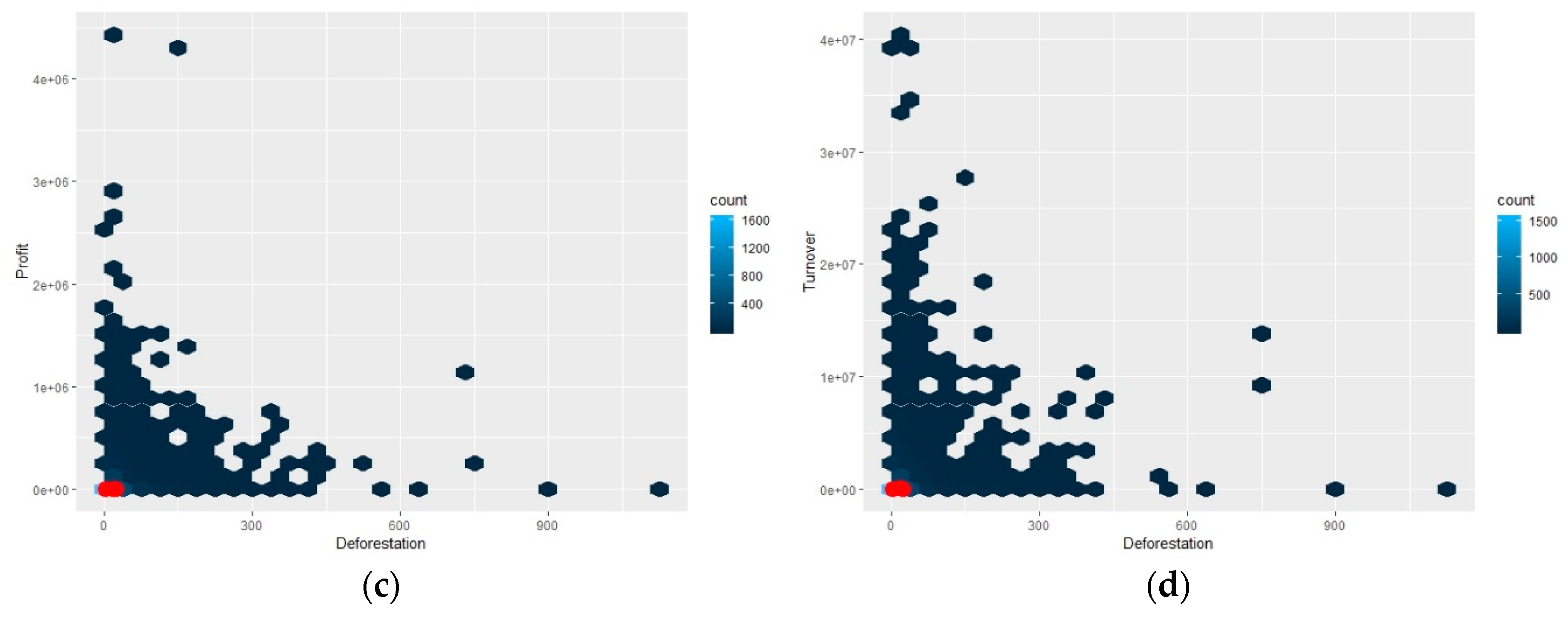
3.2. Correlation between Deforested Areas and Logging Activities
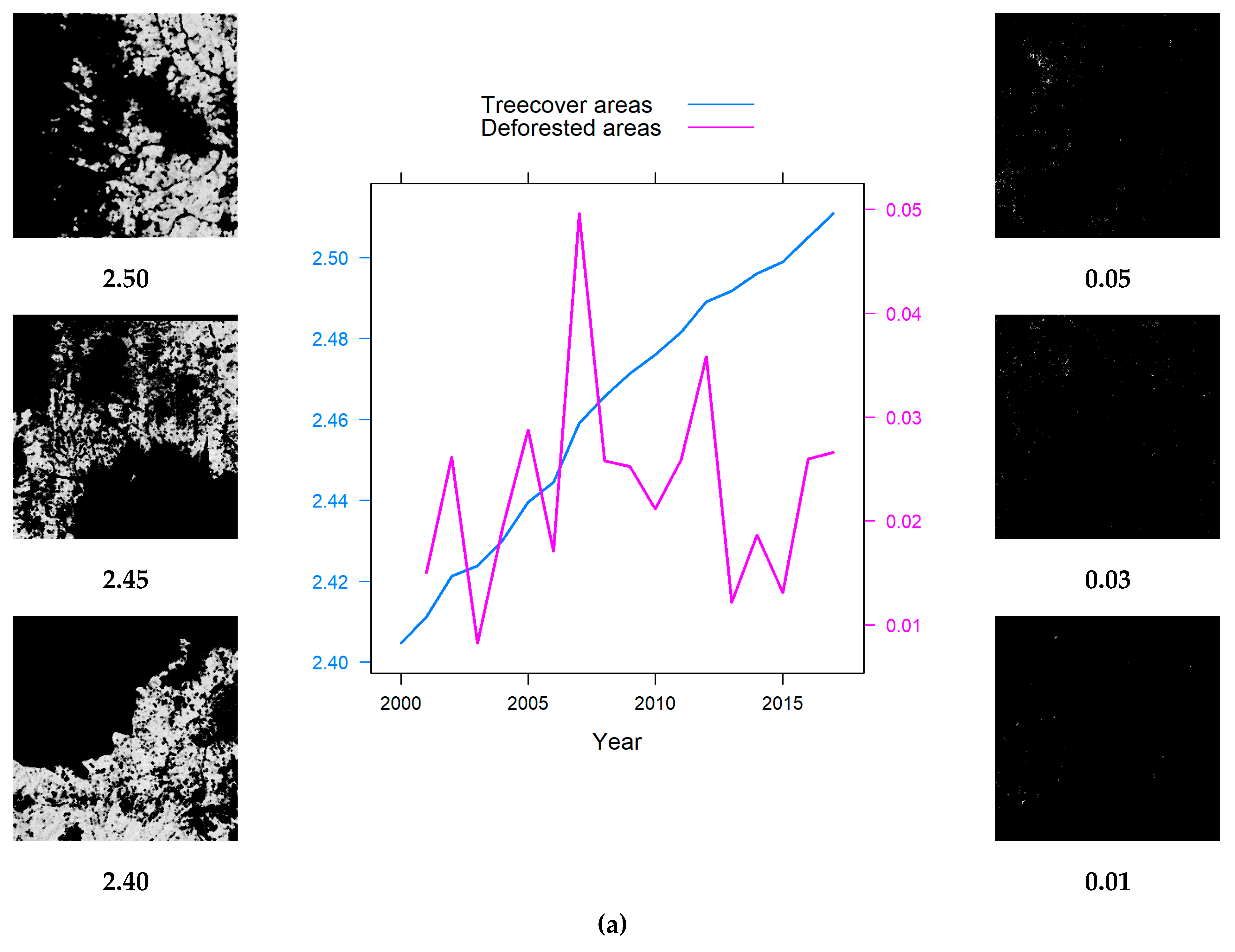
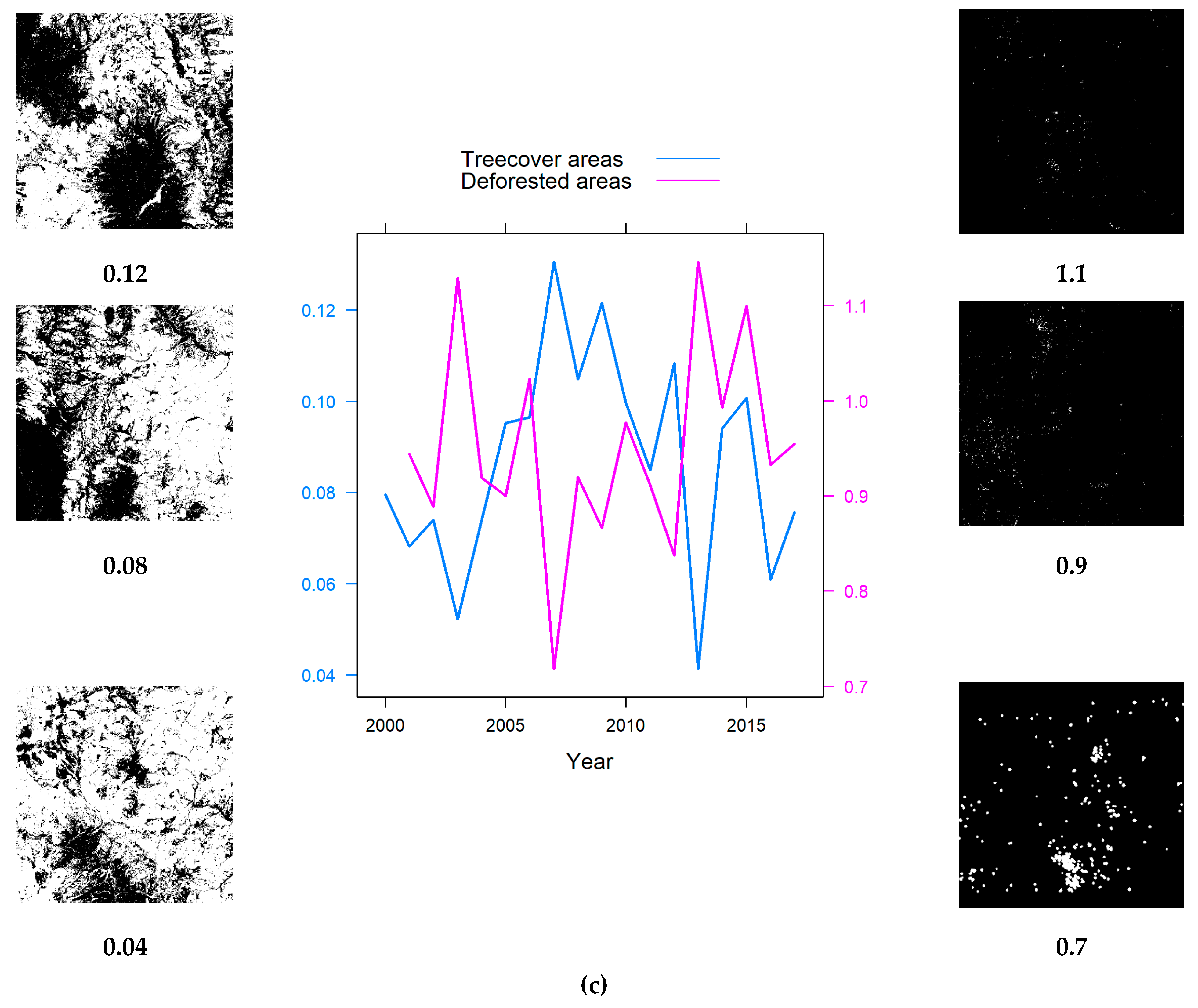
3.3. The Analysis of GLCM Entropy
3.4. The Analysed Fractal Indices
4. Discussion
4.1. Deforestation changes in Central Carpathians
4.2. Use of GLCM and Fractal Analysis for Quantification the Deforestation Changes
- Fractal methods may provide valuable complementary information to currently available methodologies in the field of forestry research;
- A continuous decrease of tree cover areas has occurred during the period of analysis, however with considerable inter-annual variability;
- Results indicate that, as the loss areas increased, forest fragmentation and heterogeneity also increased. The process of homogenization and compaction of cumulative loss has also been confirmed;
- Differences between the fractal and GLCM indices arise from the type of image analyzed and from the information extracted. For the Entropy, the images are grey-scale 8-bits, and we obtain the clutter of spatial pixel distribution in grayscale within patches of tree cover and loss. Thus, the analysis is at the level of forest cover as the forest looks dense. For and FFI, the images are binary, and we extract information about how these patches are spatially distributed, regardless of how the forest looks or how loss has occurred within these patches, resulting in anti-parallel developments.
4.3. Prospects About Sustainable Forest Management
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grebner, D.L.; Bettinger, P.; Siry, J.P. A Brief History of Forestry and Natural Resource Management. In Introduction to Forestry and Natural Resources; Academic Press: Waltham, MA, USA, 2013; pp. 1–20. [Google Scholar]
- Hossain, S.M.Y.; Robak, E.W. A Forest Management Process to Incorporate Multiple Objectives: A Framework for Systematic Public Input. Forests 2010, 1, 99–113. [Google Scholar] [CrossRef]
- Nordlund, A.; Westin, K. Forest Values and Forest Management Attitudes among Private Forest Owners in Sweden. Forests 2011, 2, 30–50. [Google Scholar] [CrossRef]
- Beaudoin, G.; Rafanoharana, S.; Boissiere, M.; Wijaya, A.; Wardhana, W. Completing the Picture: Importance of Considering Participatory Mapping for REDD plus Measurement, Reporting and Verification (MRV). PLoS ONE 2016, 11, e0166592. [Google Scholar] [CrossRef]
- Borrelli, P.; Panagos, P.; Marker, M.; Modugno, S.; Schütt, B. Assessment of the impacts of clear-cutting on soil loss by water erosion in Italian forests: First comprehensive monitoring and modelling approach. Catena 2017, 149, 770–781. [Google Scholar] [CrossRef]
- Pazur, R.; Bolliger, J. Land changes in Slovakia: Past processes and future directions. Appl. Geogr. 2017, 85, 163–175. [Google Scholar] [CrossRef]
- Bayer, A.D.; Lindeskog, M.; Pugh, T.A.M.; Anthoni, P.M.; Fuchs, R.; Arneth, A. Uncertainties in the land-use flux resulting from land-use change reconstructions and gross land transitions. Earth Syst. Dyn. 2017, 8, 91–111. [Google Scholar] [CrossRef]
- Knorn, J.; Kuemmerle, T.; Radeloff, V.C.; Szabo, A.; Mîndrescu, M.; Keeton, W.S.; Abrudan, I.; Griffiths, P.; Gancz, V.; Hostert, P. Forest restitution and protected area effectiveness in post-socialist Romania. Biol. Conserv. 2012, 146, 204–212. [Google Scholar] [CrossRef]
- Bouriaud, L.; Nichiforel, L.; Weiss, G.; Bajraktari, A.; Curovic, M.; Dobsinska, Z.; Glavonjic, P.; Jarsky, V.; Sarvasova, Z.; Teder, M.; et al. Governance of private forests in Eastern and Central Europe: An analysis of forest harvesting and management rights. Ann. For. Res. 2013, 56, 199–215. [Google Scholar]
- Crăciunescu, A.; Stanciu, S.; Moatăr, M. The Implementation of European Forest Legislation for a Sustainable Development. Res. J. Agric. Sci. 2014, 46, 158–165. [Google Scholar]
- Cojoc, G.M.; Romanescu, G.; Tirnovan, A. Exceptional floods on a developed river: Case study for the Bistrița River from the Eastern Carpathians (Romania). Nat. Hazards 2015, 77, 1421–1451. [Google Scholar] [CrossRef]
- Stoffel, M.; Wyzga, B.; Marston, R.A. Floods in mountain environments: A synthesis. Geomorphology 2016, 272, 1–9. [Google Scholar] [CrossRef]
- Simons, P. After Skiing, The Deluge—Deforestation Increases Avalanches and Landslides in The Alps. New Sci. 1988, 117, 49–52. [Google Scholar]
- Comănescu, L.; Nedelea, A. Public perception of the hazards affecting geomorphological heritage-case study: The central area of Bucegi Mts. (Southern Carpathians, Romania). Environ. Earth Sci. 2015, 73, 8487–8497. [Google Scholar] [CrossRef]
- Malek, Z.; Boerboom, L.; Glade, T. Future Forest Cover Change Scenarios with Implications for Landslide Risk: An Example from Buzău Subcarpathians, Romania. Environ. Manag. 2015, 56, 1228–1243. [Google Scholar] [CrossRef]
- De la Paix, M.J.; Lanhai, L.; Xi, C.; Ahmed, S.; Varenyam, A. Soil Degradation and Altered Flood Risk as a Consequence of Deforestation. Land Degrad. Dev. 2013, 24, 478–485. [Google Scholar] [CrossRef]
- Fahrig, L. Effects of habitat fragmentation on biodiversity. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 487–515. [Google Scholar] [CrossRef]
- Gamfeldt, L.; Snall, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Froberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher levels of multiple ecosystem services are found in forests with more tree species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef]
- Karstensen, J.; Peters, G.P.; Andrew, R.M. Attribution of CO2 emissions from Brazilian deforestation to consumers between 1990 and 2010. Environ. Res. Lett. 2013, 8, 2. [Google Scholar] [CrossRef]
- Kaplan, J.O.; Krumhardt, K.M.; Gaillard, M.J.; Sugita, S.; Trondman, A.K.; Fyfe, R.; Marquer, L.; Mazier, F.; Nielsen, A.B. Constraining the Deforestation History of Europe: Evaluation of Historical Land Use Scenarios with Pollen-Based Land Cover Reconstructions. Land 2017, 6, 4. [Google Scholar] [CrossRef]
- Krasovskii, A.; Khaharov, N.; Ohersteiner, M. CO2-intensive power generation and REDD-based emission offsets with a benefit-sharing mechanism. Energy Syst. 2017, 8, 857–883. [Google Scholar] [CrossRef]
- Chakravarty, S.; Ghosh, S.K.; Suresh, C.P.; Dey, A.N.; Shukla, G. Deforestation: Causes, Effects and Control Strategies. Global Perspectives on Sustainable Forest Management 2012. Available online: http://cdn.intechopen.com/pdfs/36125/InTechDeforestation_causes_effects_and_control_strategies.pdf (accessed on 24 February 2019).
- Food and Agriculture Organization of the United Nations—Deforestation. Available online: http://www.fao.org/3/j9345e/j9345e07.htm (accessed on 24 February 2019).
- Spiecker, H. Silvicultural management in maintaining biodiversity and resistance of forests in Europe-temperate zone. J. Environ. Manag. 2003, 67, 55–65. [Google Scholar] [CrossRef]
- Vitasse, Y.; Francois, C.; Delpierre, N.; Dufrene, E.; Kremer, A.; Chuine, I.; Delzon, S. Assessing the effects of climate change on the phenology of European temperate trees. Agric. For. Meteorol. 2011, 151, 969–980. [Google Scholar] [CrossRef]
- Domingo, F.; Puigdefabregas, J.; Moro, M.J.; Bellot, J. Role of Vegetation Cover in the Biogeochemical Balances of Small Afforested Catchment in Southeastern Spain. J. Hydrol. 1994, 159, 275–289. [Google Scholar] [CrossRef]
- Robinson, M.; Cognard-Plancq, A.L.; Cosandey, C.; David, J.; Durand, P.; Fuhrer, H.W.; Hall, R.; Hendriques, M.O.; Marc, V.; McCarthy, R.; et al. Studies of the impact of forests on peak flows and baseflows: A European perspective. For. Ecol. Manag. 2003, 186, 85–97. [Google Scholar] [CrossRef]
- Lim, S.S.; Innes, J.L.; Sheppard, S.R.J. Awareness of Aesthetic and Other Forest Values: The Role of Forestry Knowledge and Education. Soc. Nat. Resour. 2015, 28, 1308–1322. [Google Scholar] [CrossRef]
- Lim, S.S.; Innes, J.L. Forest aesthetic indicators in sustainable forest management standards. Can. J. For. Res. 2017, 47, 536–544. [Google Scholar] [CrossRef]
- Veen, P.; Fanta, J.; Raev, I.; Biris, I.A.; de Smidt, J.; Maes, B. Virgin forests in Romania and Bulgaria: Results of two national inventory projects and their implications for protection. Biodivers. Conserv. 2010, 19, 1805–1819. [Google Scholar] [CrossRef]
- Hurdu, B.I.; Pușcaș, M. Centres of endemism, spatial barriers and biogeography of the South-Eastern Carpathians inferred from multivariate analysis of endemic plant species distribution. Acta Biol. Ser. Bot. 2013, 55, 24. [Google Scholar]
- Price, M.F.; Gratzer, G.; Duguma, L.A.; Kohler, T.; Maselli, D.; Romeo, R. Mountain Forests in a Changing World—Realizing Values, Addressing Challenges; FAO/MPS and SDC: Rome, Italy, 2011; pp. 1–86. [Google Scholar]
- Mraz, P.; Ronikier, M. Biogeography of the Carpathians: Evolutionary and spatial facets of biodiversity. Biol. J. Linn. Soc. 2016, 119, 528–559. [Google Scholar] [CrossRef]
- Abrudan, I.V.; Marinescu, V.; Ionescu, O.; Ioras, F.; Horodnic, S.A.; Sestras, R. Developments in the Romanian Forestry and its linkages with other sectors. Not. Cluj-Napoca 2009, 37, 14–21. [Google Scholar]
- Banski, J. Changes in agricultural land ownership in Poland in the period of the market economy. Agric. Econ. Zemed. 2011, 57, 93–101. [Google Scholar]
- Sarvasova, Z.; Zivojinovic, I.; Weiss, G.; Dobsinska, Z.; Dragoi, M.; Gal, J.; Jarsky, V.; Mizaraite, D.; Pollumae, P.; Salka, J.; et al. Forest Owners Associations in the Central and Eastern European Region. Small-Scale For. 2015, 14, 217–232. [Google Scholar] [CrossRef]
- Kuemmerle, T.; Hostert, P.; Radeloff, V.C.; Perzanowski, K.; Kruhlov, I. Post-socialist forest disturbance in the Carpathian border region of Poland, Slovakia, and Ukraine. Ecol. Indic. 2007, 17, 1279–1295. [Google Scholar] [CrossRef]
- Griffiths, P.; Kuemmerle, T.; Baumann, M.; Radeloff, V.C.; Abrudan, I.V.; Lieskovsky, J.; Munteanu, C.; Ostapowicz, K.; Hostert, P. Forest disturbances, forest recovery, and changes in forest types across the Carpathian ecoregion from 1985 to 2010 based on Landsat image composites. Remote Sens. Environ. 2014, 151, 72–88. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Z.J.; Zhen, Q.; Southworth, J.; Perz, S. Fractally deforested landscape: Pattern and process in a tri-national Amazon frontier. Appl. Geogr. 2014, 52, 204–211. [Google Scholar] [CrossRef]
- Andronache, I.; Ahammer, H.; Jelinek, H.F.; Peptenatu, D.; Ciobotaru, A.-M.; Drăghici, C.-C.; Pintilii, R.D.; Simion, A.G.; Teodorescu, C. Fractal analysis for studying the evolution of forests. Chaossolitons Fractals 2016, 91, 310–318. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. Available online: http://earthenginepartners.appspot.com/science-2013-global-forest (accessed on 21 January 2016). [CrossRef] [PubMed]
- Andronache, I.; Fensholt, R.; Ahammer, H.; Ciobotaru, A.-M.; Pintilii, R.-D.; Peptenatu, D.; Drăghici, C.-C.; Diaconu, D.C.; Radulovic, M.; Pulighe, G.; et al. Assessment of Textural Differentiations in Forest Resources in Romania Using Fractal Analysis. Forests 2017, 8, 54. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Texture parameters for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Ahammer, H.; Andronache, I. IQM Plugin FFI. 2016. Available online: https://sourceforge.net/projects/iqm-plugin-ffi/ (accessed on 6 January 2017).
- Reiss, M.A.; Lemmerer, B.; Hanslmeier, A.; Ahammer, H. Tug-of-war lacunarity—A novel approach for estimating lacunarity. Chaos 2016, 26, 113102. [Google Scholar] [CrossRef] [PubMed]
- Kainz, P.; Mayrhofer-Reinhartshuber, M.; Ahammer, H. IQM: An Extensible and Portable Open Source Application for Image and Signal Analysis in Java. PLoS ONE 2015, 10, e0116329. [Google Scholar] [CrossRef]
- Russel, D.; Hanson, J.; Ott, E. Dimension of strange attractors. Phys. Rev. Lett. 1980, 45, 1175–1178. [Google Scholar] [CrossRef]
- Karperien, A.; Ahammer, H.; Jelinek, H.F. Quantitating the subtleties of microglial morphology with fractal analysis. Front. Cell. Neurosci. 2013, 7. [Google Scholar] [CrossRef]
- Plotnick, R.E.; Gardner, R.H.; Oneill, R.V. Lacunarity Indexes as Measures of Landscape Texture. Landsc. Ecol. 1993, 8, 201–211. [Google Scholar] [CrossRef]
- Taylor, R.P.; Martin, T.P.; Montgomery, R.D.; Smith, J.H.; Micolich, A.P.; Boydston, C.; Scannell, B.C.; Fairbanks, M.S.; Spehar, B. Seeing shapes in seemingly random spatial patterns: Fractal analysis of Rorschach inkblots. PLoS ONE 2017, 12. [Google Scholar] [CrossRef]
- Romanian Government Official Monitor. Law no. 247/2005 on the Reform of Property and Justice, as Well as Some Accompanying Measures (Legea nr. 247 din 2005 Privind Reforma în Domeniile Proprietăţii şi Justiţiei, Precum şi unele Măsuri Adiacente). Available online: http://legislatie.just.ro/Public/DetaliiDocument/63447 (accessed on 24 February 2019).
- Munteanu, C.; Kuemmerle, T.; Keuler, N.S.; Muller, D.; Balazs, P.; Dobosz, M.; Griffiths, P.; Halada, L.; Kaim, D.; Kiraly, G.; et al. Legacies of 19th century land use shape contemporary forest cover. Glob. Environ. Chang. Hum. Policy Dimens. 2015, 34, 83–94. [Google Scholar] [CrossRef]
- Knorn, J.; Kuemmerle, T.; Radeloff, V.C.; Keeton, W.S.; Gancz, V.; Biris, I.A.; Svoboda, M.; Griffiths, P.; Hagatis, A.; Hostert, P. Continued loss of temperate old-growth forests in the Romanian Carpathians despite an increasing protected area network. Environ. Conserv. 2013, 40, 182–193. [Google Scholar] [CrossRef]
- Singh, M.; Evans, D.; Friess, D.A.; Tan, B.S.; Nin, C.S. Mapping Above-Ground Biomass in a Tropical Forest in Cambodia Using Canopy Textures Derived from Google Earth. Remote Sens. 2015, 7, 5057–5076. [Google Scholar] [CrossRef]
- Weissgerber, F.; Colin-Koeniguer, E.; Nicolas, N.; Nicolas, J.M. A Temporal Estimation of Entropy and Its Comparison With Spatial Estimations on PolSAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3809–3820. [Google Scholar] [CrossRef]
- Garcia-Gigorro, S.; Saura, S. Forest Fragmentation Estimated from Remotely Sensed Data: Is Comparison Across Scales Possible? For. Sci. 2005, 51, 51–63. [Google Scholar]
- Garcia, D.; Quevedo, M.; Obeso, J.R.; Abajo, A. Fragmentation patterns and protection of montane forest in the Cantabrian range (NW Spain). For. Ecol. Manag. 2005, 208, 29–43. [Google Scholar] [CrossRef]
- Pintilii, R.-D.; Andronache, I.; Diaconu, D.C.; Dobrea, R.C.; Zeleňáková, M.; Fensholt, R.; Peptenatu, D.; Drăghici, C.-C.; Ciobotaru, A.-M. Using Fractal Analysis in Modeling the Dynamics of Forest Areas and Economic Impact Assessment: Maramureș County, Romania, as a Case Study. Forests 2017, 8, 25. [Google Scholar] [CrossRef]
- Frankhauser, P. The fractal approach. A new tool for the spatial analysis of urban agglomerations. Population 1998, 10, 205–240. [Google Scholar]
- Tannier, C.; Pumain, D. Fractals in urban geography: A theoretical outline and an empirical example. Cybergeo Eur. J. Geogr. 2005, 307, 10–4000. [Google Scholar] [CrossRef]
- Chen, Y.G.; Feng, J. Spatial analysis of cities using Renyi entropy and fractal parameters. Chaos Solitons Fractals 2017, 105, 279–287. [Google Scholar] [CrossRef]
- Petrișor, A.I.; Andronache, I.; Petrișor, L.E.; Ciobotaru, A.M.; Peptenatu, D. Assessing the fragmentation of the green infrastructure in Romanian cities using fractal models and numerical taxonomy. Procedia Environ. Sci. 2016, 32, 110–123. [Google Scholar] [CrossRef]
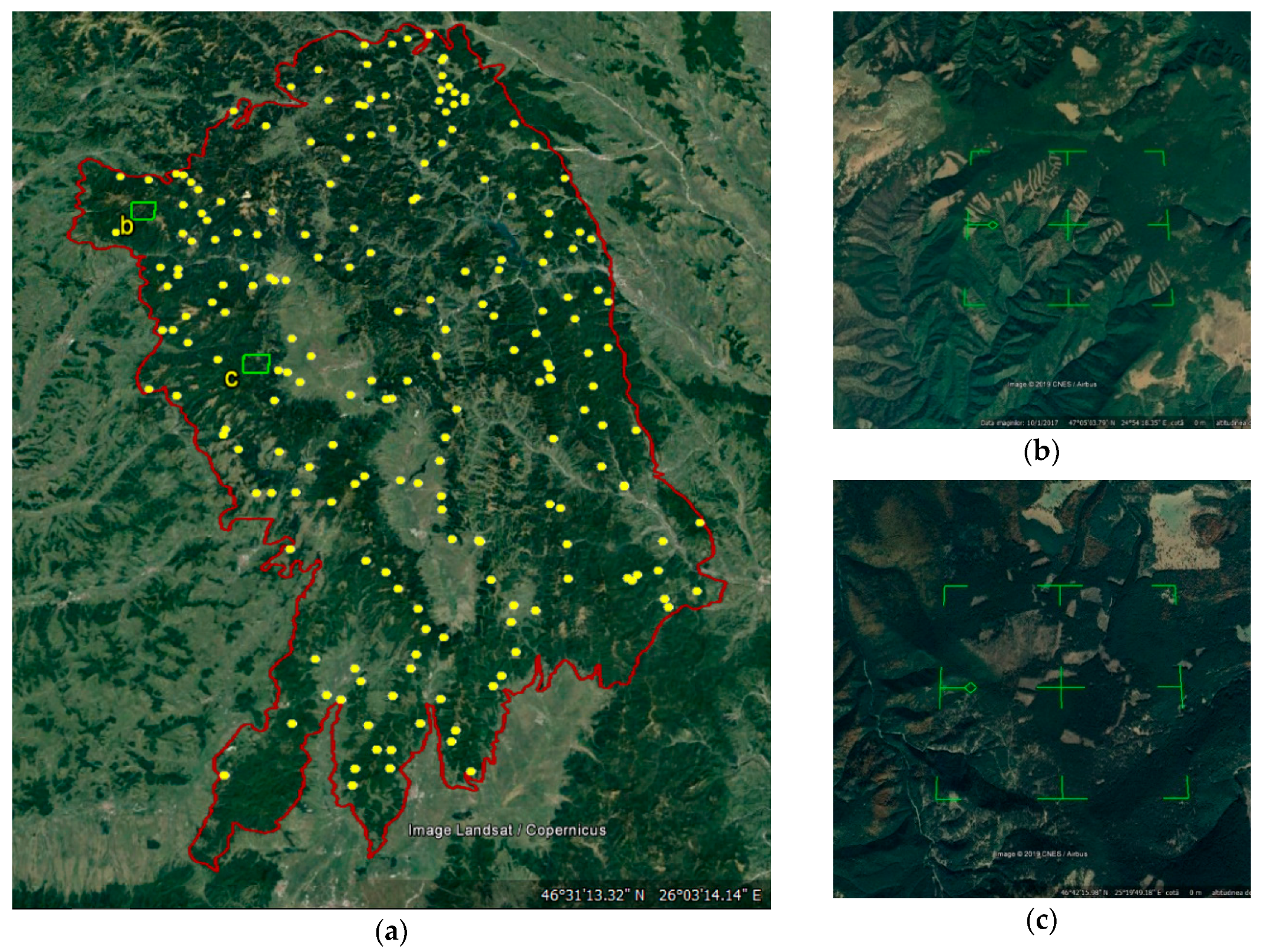
| No. | Satellite Images | Spatial Resolution | Longitude | Latitude | Paths | Rows | Data Source |
|---|---|---|---|---|---|---|---|
| 1. | LANDSAT 7 ETM+ | 30 m | 50°00′ N | 20°18′ E | 188 | 25 | GFC |
| 2. | LANDSAT 7 ETM+ | 30 m | 50°00′ N | 30°18′ E | 181 | 25 | GFC |
| 3. | LANDSAT 7 ETM+ | 30 m | 39°60′ N | 20°18′ E | 185 | 32 | GFC |
| 4. | LANDSAT 7 ETM+ | 30 m | 39°60′ N | 30°18′ E | 179 | 32 | GFC |
| Classified data | Reference Data (Ground Reference Test Points) | |||||
| Classified data | Deforested | Non-deforested | Row total | User’s Accuracy (%) | Commission errors (%) | |
| Deforested | 3 | 3 | 6 | 50 | 50 | |
| Non-deforested | 2 | 192 | 194 | |||
| Column total | 5 | 195 | 200 | 97.5 | 2.5 | |
| Producer’s Accuracy (%) | 60 | 98.46 | ||||
| Omission errors (%) | 40 | 1.54 | ||||
| Overall accuracy = 97% | ||||||
| Cohen’s Kappa Coefficient = 53% | ||||||
| Indices of GFC | Indices of GLCM Analysis | Indices of Fractal Analysis | ||||||
|---|---|---|---|---|---|---|---|---|
| Tree Cover Areas | Deforested Areas | Entropy_T | Entropy_Def | FFI_T | FFI_Def | ΛT−o−W_T | ΛT−o−W_Def | |
| W | 0.7708 | 0.89494 | 0.93885 | 0.9178 | 0.84919 | 0.85661 | 0.98681 | 0.95226 |
| p | 0.0006047 | 0.05592 | 0.2769 | 0.1356 | 0.008224 | 0.01355 | 0.9934 | 0.4932 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciobotaru, A.-M.; Andronache, I.; Ahammer, H.; Jelinek, H.F.; Radulovic, M.; Pintilii, R.-D.; Peptenatu, D.; Drăghici, C.-C.; Simion, A.-G.; Papuc, R.-M.; et al. Recent Deforestation Pattern Changes (2000–2017) in the Central Carpathians: A Gray-Level Co-Occurrence Matrix and Fractal Analysis Approach. Forests 2019, 10, 308. https://doi.org/10.3390/f10040308
Ciobotaru A-M, Andronache I, Ahammer H, Jelinek HF, Radulovic M, Pintilii R-D, Peptenatu D, Drăghici C-C, Simion A-G, Papuc R-M, et al. Recent Deforestation Pattern Changes (2000–2017) in the Central Carpathians: A Gray-Level Co-Occurrence Matrix and Fractal Analysis Approach. Forests. 2019; 10(4):308. https://doi.org/10.3390/f10040308
Chicago/Turabian StyleCiobotaru, Ana-Maria, Ion Andronache, Helmut Ahammer, Herbert F. Jelinek, Marko Radulovic, Radu-Daniel Pintilii, Daniel Peptenatu, Cristian-Constantin Drăghici, Adrian-Gabriel Simion, Răzvan-Mihail Papuc, and et al. 2019. "Recent Deforestation Pattern Changes (2000–2017) in the Central Carpathians: A Gray-Level Co-Occurrence Matrix and Fractal Analysis Approach" Forests 10, no. 4: 308. https://doi.org/10.3390/f10040308
APA StyleCiobotaru, A.-M., Andronache, I., Ahammer, H., Jelinek, H. F., Radulovic, M., Pintilii, R.-D., Peptenatu, D., Drăghici, C.-C., Simion, A.-G., Papuc, R.-M., Marin, M., Radu, R.-A., Grecu, A., Gruia, A. K., Loghin, I.-V., & Fensholt, R. (2019). Recent Deforestation Pattern Changes (2000–2017) in the Central Carpathians: A Gray-Level Co-Occurrence Matrix and Fractal Analysis Approach. Forests, 10(4), 308. https://doi.org/10.3390/f10040308









