Abstract
Forest development models have been used to predict future harvesting potentials and forest management reference levels under the Kyoto guidelines. This contribution aims at presenting the individual-tree simulator MASSIMO (MAnagement Scenario SImulation Model) and demonstrating its scope of applications with simulations of two possible forest management reference levels (base or business as usual) in an example application. MASSIMO is a suitable tool to predict timber harvesting potentials and forest management reference levels to assess future carbon budgets of Swiss forests. While the current version of MASSIMO accurately accounts for legacy effects and management scenarios, effects of climate and nitrogen deposition on growth, mortality, and regeneration are not yet included. In addition to including climate sensitivity, the software may be further improved by including effects of species mixture on tree growth and assessing ecosystem service provision based on indicators.
1. Introduction
International commitments, such as the Paris agreement [1], require country-specific estimates of current and future carbon budgets, harvesting potentials, and forest management reference levels. The European Union proposed to establish those reference levels “transparently and in consideration of the business-as-usual procedures” compared to the period 1990–2009 [2]. Reliable estimates of the present state and the future development of forests shall be nationally representative for forest types, management interventions, and harvesting amounts. Many European countries therefore develop their own systems to simulate current management practices [3], based on national forest inventories (NFI) and forest development models.
Forest development models have been used to predict the state and changes of forest systems for a long time. Among the first were yield tables that were developed to predict the yield of pure even-aged stands on the basis of long-term observations from experimental forest plots [4,5]. As yield tables represent growth of whole stands under fixed site conditions (i.e., site quality expressed as dominant tree height at a reference age), they can neither be transferred in time nor space. An alternative approach offer ‘process-based’ models [5]. These models incorporate empirically- and/or theoretically-derived relationships on ecological and eco-physiological processes, such as competition, photosynthesis, respiration, carbon allocation, and consequently growth of tree cohorts, individual trees or tree compartments. These relationships are considered fundamental and therefore assumed to be valid also under changing environmental conditions. However, process-based models are often difficult to parameterize, especially for applications over large spatial extents or at fine spatial resolutions. This led to the development of forest gap models and forest landscape models, which describe processes at a higher level of aggregation (i.e., tree growth vs. photosynthesis) with process-based and/or semi-empirical models based on ecological theory [6,7,8]. Especially over short time-scales (e.g., <30 years), these model types are less accurate in terms of timber harvest and growing stock estimates compared to pure empirical stand or sample-plot simulators at tree level. Consequently, their use for countrywide, spatially representative forest management scenario analyses is rather limited.
With their NFI, most countries in Europe perform representative, regularly updated, long-term forest monitoring [9] that are used to parameterize and initialize empirical individual-tree growth models (e.g., [3,10]). Those models are representative over larger areas and allow to accurately project short- to mid-term forest resource development from the landscapes to national scale [3]. Another advantage of this kind of forest development models is that they accurately represent the current forest state, since they are initialized with NFI sample plot data and, therefore, also account for the legacy of past management. For example, forests in Switzerland are characterized by a high diversity of biotic and abiotic site, stand and management conditions on a small spatial scale. The empirical MAnagement Scenario SImulation MOdel MASSIMO [11] has been developed to account for this diversity. MASSIMO is a distance-independent individual-tree simulator that represents demographic processes (regeneration, growth and mortality) with empirical models that have been parameterized with data from the Swiss NFI. Tree regeneration, growth and mortality are simulated on the regular grid of sample plots of the Swiss NFI, which allows for statistically representative simulations of forest development. MASSIMO has been used at the national scale to predict timber harvesting potentials [12], to assess the potentials for carbon sequestration of Swiss forests while respecting the full timber supply chain [13,14], and for the Forest Management Reference Level (FMRL) under the Kyoto protocol [1,2]. Further, MASSIMO has been used to evaluate various timber mobilization scenarios in a mountainous landscape [15] and to value timber mobilization strategies and habitat tree retention in low-elevation Swiss forests [16].
An early version of MASSIMO had been presented in a simplified manner [11] and it was compared to other models [17], however, MASSIMO has never been described and critically assessed as a whole. This corresponds also to a few of the models mentioned in Barreiro et al. [3]. Due to its relevance for several projects and because we are willing to further develop MASSIMO, we aim in this contribution to describe how MASSIMO in its current state is initialized and structured, to introduce the NFI-based (sub-) models for growth, mortality, harvesting, and regeneration, and to illustrate how management scenarios can be defined. Thereby we present the important assumptions and formulations that are typical for a data-driven, single-tree management scenario simulator, and thus may be applicable for similar models. Specifically, we present an example application that includes simulating two possible FMRLs (base scenario and business as usual) for timber harvesting and carbon sequestration. Growing stock in Swiss forests has been increasing since the first NFI in 1983/85 [12], however, there are large regional differences. Thus, a base scenario maintaining a constant growing stock over the whole of Switzerland may increase harvesting in some areas of Switzerland, and reduce in other regions. We addressed the following questions: how do growing stock and harvesting potential develop under the base and business as usual management scenarios? What regional shifts of harvesting amounts must be expected when the current timber demand is harvested in the long-term? Finally, we will discuss the strengths and weaknesses of the MASSIMO model and point out potential for future improvement.
2. Materials and Methods
2.1. Initialization with NFI Data
MASSIMO was developed to run on the common grid of sample plots within the productive forest (no shrubs) of two consecutive Swiss NFIs. Input data for MASSIMO are provided from the NFI data storage and analysis system NAFIDAS [18]. In the current version of MASSIMO, the initialized grid encompasses measures of the second (NFI2: 1993–1995) and the third NFI (NFI3: 2004–2006) resulting in a common grid of 5086 sample plots in the productive forests. These sample plots are grouped into 14 economic regions that are biogeographically assembled into five production regions. Sample plots consist of two concentric circles of 200 m2 and 500 m2, respectively, with specific calliper thresholds of 12 cm on the inner and 36 cm on the outer circle. Upon extrapolation of measured and derived quantities to hectare values, trees are weighted according to sample plot size accounting for sampling in inner or outer circles and for partially sampled plots at forest edges [19]. Sampling on the common productive forest led to a record of 59,229 trees with Norway spruce (Picea abies, 44.2%), European beech (Fagus sylvatica, 18.1%) silver fir (Abies alba, 14.8), and larch (Larix decidua and L. kaempferi, 5.5%) being the most frequent tree species [20].
2.2. Structure of MASSIMO
MASSIMO is an empirical, stochastic and dynamic individual-tree simulator: Empirical, since NFI-data were used to statistically derive models on growth, storm damage, harvesting, mortality and regeneration [11,21,22,23]; stochastic, as leavers (trees leaving the pool of survivor trees due to harvesting or mortality) are drawn randomly according to a removal probability that depends on diameter at breast height (dbh), competition indices and stand characteristics; and dynamic, because the simulator tracks changes in the state of individual trees and sample plots over time.
After loading tree- and plot-level data from the NFI data base the program reads the files containing specific settings for simulation scenarios (e.g., harvest restrictions, regulation of species mixture, harvesting targets etc.; see Section 2.8). Input tables are checked for null values and, when necessary, imputed with strata-specific average values as a default (Figure 1). MASSIMO simulations are replicated to account for the stochasticity in the regeneration, harvesting, mortality, and wind throw modules. Previous simulations have shown that 20 replications are sufficient for output values to converge (i.e., the mean of the replicates remains stable). Results of the iterations are averaged and standard errors are calculated as a measure of variation.
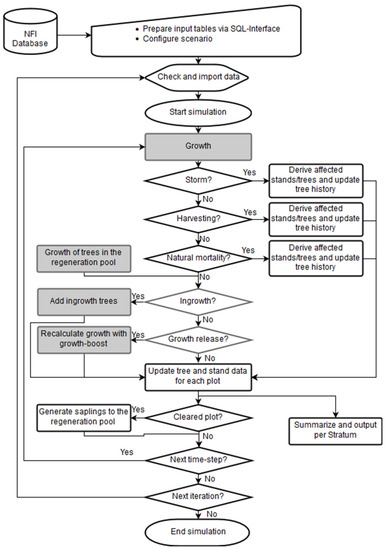
Figure 1.
Flowchart of the individual-tree simulator MASSIMO (MAnagement Scenario SImulation Model). Note: the grey shaded fields complement the growth sub-model; tree history is used as a tree-level state variable.
These replications are implemented as an outer iteration loop. An inner time-step loop typically runs through up to 10 time-steps of 10 years. Within the loops, the MASSIMO program calls sub-models for (i) growth, (ii) storm (iii) harvesting, (iv) mortality, and (v) regeneration. In order to vary simulated management strategies (i.e., scenarios) the harvesting sub-model is controlled by an iterative scenario approximation routine that adjusts thinning and shelterwood felling based on user defined harvesting or growing stock targets (not shown in Figure 1, cf. Section 2.8 Creating scenarios). MASSIMO has been implemented in SAS® (Cary, NC, USA) and is currently transferred to Java SE 8 (© Oracle, Redwood Shores, CA, USA).
For each event happening to a tree, its state, i.e., history will be changed (Table 1, Figure 1). MASSIMO differentiates between six tree states with three of them pointing to survivors (i.e., trees that will be living at the beginning of the next time-step) and the other pointing to leavers (i.e., trees that leave the pool of living trees during the simulated time-step). The history variable is used to record all changes (e.g., growth, harvesting, mortality) between two consecutive time-steps.

Table 1.
Tree history in MASSIMO.
2.3. Growth
2.3.1. Single Tree Increment
To simulate tree growth, a species-specific model for individual-tree basal area increment (bai) over 10-year periods is applied. The diameter at breast height (dbh) at the beginning of the time step and the estimated bai are used to derive the dbh at the beginning of the next time step. The increment model has been evaluated and presented beforehand [21,22], when the “growth boost” (release effect after thinning) was introduced into MASSIMO [11]. After completion of the third Swiss NFI [20], it was recalibrated and further stratified to the main tree species, production regions, forest structure (even- vs. uneven-aged forest) and the storey (under- vs. overstorey) a tree belongs to. The increment model follows the formulation by Teck and Hilt [24] and has the form:
where are the explanatory variables (B1: basal area per ha (BAPH), B2: basal area of trees larger than the subject tree (BAL), B3: site index “Total Mean Increment” TMI [25], B4: elevation, B5: stand age (in case of even-aged forests) or dominant diameter (in case of uneven-aged forests), B6: growth boost (binary)), are the model coefficients, is a normally distributed random variable accounting for stochastic effects with being estimated from the residual distribution (cf. Supplementary S1).
The increment model is applied to (i) estimate the growth of survivors (i.e., trees that had not been felled in the previous time step nor died) and leavers (that are growing for half a time step), (ii) to estimate the growth boost as a release effect after thinning or mortality, and (iii) to simulate ingrowth of trees.
2.3.2. Single Tree Volume
According to Swiss NFI, tree volume is estimated for all trees with dbh ≥ 12 cm. The volume is derived from dbh using tariff models (cf. [21]). These models have been refitted with data of NFI3 [20]. The volume V is calculated as:
where are the explanatory variables (B3: site index “Total Mean Increment” (TMI), B4: dominant diameter, B5: bifurcation (binary), B6: elevation, B7: overstorey (binary)), are the model coefficients, is a normally distributed random variable accounting for stochastic effects with being estimated from the residual distribution (cf. Supplementary S2, Table S4).
2.4. Storm Damage
In Switzerland the country-level return interval for severe storm events was estimated to 15 years [26], with a mean affected area of approximately 20,000 km2 that typically is restricted to Northern Switzerland and the Alps [23]. Hence, the default return interval in MASSIMO is set to 15 years and the extent of simulated storm tracks are rectangles of 200 by 100 km that are tilted by 30° and, thus, account for the prevailing west-southwestern wind direction (Figure 2). The location (easting and northing) of the storm tracks is determined by randomly selecting from nine possible southwestern corners. This results in storms being most frequently simulated in the Bernese Pre-Alps, which corresponds to storm hazard maps based on historic data [26]. The proportion of sample plots that experience damages and the severity of damage (% of killed trees) are based on observations of the three most severe past storm events (a series of storms in February 1967, Vivian in 1990 and Lothar in 1999). These storm events are distinguished with three relative storm severity levels (0.1, 0.6, 1) that are simulated with equal probability of occurrence. To simulate possible storm scenarios, e.g., under climate change, the return interval can be varied.
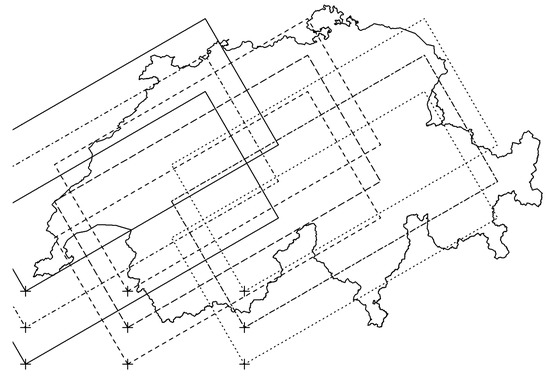
Figure 2.
Nine possible 200 by 100 km storm tracks that are simulated in MASSIMO. The storm tracks are selected by randomly picking one out of nine lower left corners.
For sample plots within the storm track two damage probabilities are calculated using sigmoidal functions. The first is the probability for partial damage Ppd (20% of the trees killed) depends on the relative storm severity level, dominant diameter, forest structure (even vs. uneven aged forests) and conifer proportion and is given by:
where s is the storm severity in (with three relative levels 0.1, 0.6, and 1) with:
and:
where is the natural logarithm of plot-level dominant diameter (mean diameter of the 100 thickest trees per ha), and iα, iβ, idd, and iM are coefficients specific to forest structure (even-aged vs. uneven-aged) and conifer proportion M in two classes (M: >90% conifer basal area vs. ≤ 90% conifer basal area) (Supplementary S3, Table S5). Although the coefficients differ for both stand type and conifer proportion, the realization (Supplementary S3, Figure S1) indicates little difference between plots that have over or under 90% conifers. The proportion for stand replacing damage Psrd (all trees killed) depends on Ppd and the same covariates and is given by:
2.5. Harvesting
2.5.1. Thinning
Thinning in even-aged high forest is executed as soon as stand basal area (BA) surpasses a default value of 1.1 times the BA observed directly before the last thinning (hereafter BA_lower). When initializing MASSIMO, it is known for each plot whether it has been managed in between the last two inventories (i.e., between NFI2 and NFI3) or not. In case it has not been managed in the meantime, the basal area observed at NFI2 is treated as ba_lower. Otherwise, when a plot was managed, ba_lower is given by the basal area observed from NFI3. The ratio of current BA to BA_lower (delta thinning: Δthin) can iteratively be adapted to approximate scenario-specific harvesting targets (Section 2.8). By default, thinning removes 30% (pthin = 30%) of the BA of the sample plot, whereby the dbh-dependent selection probability for an individual tree to be cut down was estimated from NFI data using Weibull-fits (c.f. [11]). To this end, the selection probabilities were estimated as the ratio of the dbh-distribution of trees before thinning to the dbh-distribution of the logged trees (removals) multiplied by the given thinning proportion pthin, i.e., the removed BA percentage. In uneven-aged forests Δthin is set to the fixed value of 1.05 and pthin to 25% and both cannot be adapted to approximate scenario-specific harvesting targets, because these values maintain a stable stand structure in uneven-aged forests (i.e., only small fluctuations in diameter-distribution and growing stock), which is a predefined objective in MASSIMO (c.f. [27]).
2.5.2. Shelterwood Cutting
In MASSIMO, sample plots located in even-aged forests are managed with a shelterwood system (which. predominant type of felling in even-aged forest of Switzerland) with a fixed rotation period depending on conifer proportion and site index (Table 2) and regeneration is initiated via shelterwood cutting. Although the processes thinning and shelterwood cutting are executed independently, the first intervention of a shelterwood cutting (typically named as seed cutting) is assumed to be performed via thinning routine. Thereafter, the first intervention in the shelterwood routine (i.e., the second cutting) harvests 80% of the remaining overstorey trees (corresponds to approx. 56% of the shelter at the beginning of felling). The remaining shelter will then be removed in the next time-step, if the sample plot is located in the colline, sub-montane, or montane elevation belt. Otherwise, i.e., if the sample plot is located in the upper montane or subalpine elevation belt, the shelter will be removed by two cuttings in the subsequent time-steps.

Table 2.
Rotation period in the shelterwood system.
In order to first harvest the oldest stands, sample plots of a stratum (i.e., the same rotation period and economic region) are ranked according to an estimated stand age (c.f. [21]). Shelterwood cuttings are then conducted sequentially on the sampling plots until the default number of treated plots corresponds to the predefined rotation period (e.g., under a given time-step of 10 years and a rotation period of 90 years in lowland-conifer forests 100/(90/10) = 11.11% of the sample plots experience a shelterwood cutting). To iteratively approximate simulated harvests to predefined targets (Section 2.8), the rotation period and, thus, the number of treated sample plots can be adjusted with the modifying factor delta shelterwood felling Δfell. Additionally, shelterwood cuttings take place on sample plots in uneven-aged high forests with a probability of 0.05, as this is in agreement with observations between NFI1 and NFI2.
2.5.3. Management in Protection Forests
In Switzerland, protection forests i.e., forest with protective function against gravitational hazards, are managed according to national guidelines [28,29]. In MASSIMO, no shelterwood cutting is simulated in protection forests, but regeneration is initiated by means of thinning.
2.5.4. Forest Reserves
MASSIMO allows to simulate growth and mortality of trees in managed as well as unmanaged stands. To do so, each sample plot was assigned to ‘forest available for wood supply’ (FAWS) or ‘forest not available for wood supply’ (FNAWS) [30]. If the simulation setup specifies to simulate forest reserves, on sample plots being assigned to FNAWS no harvesting is simulated. Note that criteria for natural forest reserves are customizable to shrink or enlarge areas without harvesting.
2.6. Mortality
The probability for mortality has been estimated from NFI observations and differentiated between background mortality and density-dependent mortality. While the decadal probability of a tree suffering from background mortality is fixed ( = 0.03), the probability of density-dependent mortality increases with increasing basal area, decreasing conifer proportion and increasing stand age and is stratified in four levels (lowest: 0; highest: 0.0582), resulting in a proportion of natural mortality ranging from 0.03 to 0.0882. depends on the mortality factor (values in (1, 1.5, 2, 3) accounting for age and density dependent mortality and :
with being defaulted to 1 on young growth plots with low stand basal area BA (<60 m2ha−1) but will be increased to 3 in old grown forests to (i.e., stand age >150 years, on the Plateau, >200 years in Jura, pre-Alps or Alps, and >250 years in the Alps). Further, is increased when the BA exceeds some thresholds depending from stand type and conifer proportion (Table 3). For example, if a spruce stand with the stand type ‘pole timber’ has a BA > 85 is set to 1.5.

Table 3.
Thresholds of stand basal area BA that lead to increased levels of the mortality factor fm depending from stand type and species mixture.
2.7. Regeneration and Ingrowth
The regeneration sub-model accounts for two processes: First, regeneration under shelter, and second, regeneration in response to improved light conditions following shelterwood cutting and storm events. Both processes lead to an accumulation of trees in the regeneration pool that consists of young trees with dbh < 12 cm. Growth of trees in the regeneration pool is assumed to follow the same tree species-specific growth models as trees beyond the caliper threshold of 12 cm dbh. Trees growing beyond this threshold are termed ingrowth. Regeneration under shelter is assumed to be independent of management and is intended to represent regeneration from seeds available on the sample plot. For the first time step, counts of young trees by species are available from NFI observations in regeneration subplots located in the same elevation zone and production region as the affected plot. To feed the regeneration pool in subsequent time steps, however, MASSIMO needs routines to stochastically simulate regeneration. To this end, for each new ingrowth tree a region-dependent number of new young trees of the same species are added to the regeneration pool (Table 4). Trees in the regeneration pool have a region-specific survival probability both per decade and when they surpass the caliper threshold.

Table 4.
Decadal survival rates and replication numbers of new young trees by production regions.
To simulate regeneration following shelterwood cutting or a stand replacing storm, new young trees are randomly drawn from an observed regeneration subplot that is located in the same elevation zone and production region as the affected sample plot. Thereby, only sample plots in early development phases (i.e., young growth and thicket stage) are considered for random draws and tree data (count of trees and their species) from the randomly selected regeneration subplot are added to the regeneration pool of the affected sample plot with their dbh being set to 1 cm. Thus, by default, the species composition of the simulated regeneration reflects the measurements of the last inventory. However, MASSIMO allows to influence the proportion of conifers in the regeneration data by the simulation of tending interventions. If the scenario settings (c.f. Section 2.8) specify tending interventions to control the conifer proportion of a sample plot undergoing a storm- or harvest-induced regeneration, the maximal conifer proportion and the species mixture of conifers can be adjusted. Target values for conifer proportions are based on silvicultural recommendations in protection forests and are specific to phyto-sociological communities [28,29]. To this end, the observed conifer proportion is either enhanced or lowered, respectively, if its proportion is lower or higher than recommended (c.f. Supplementary S4, Table S6).
2.8. Creating Scenarios
2.8.1. Simulation Setup
The setup of a simulation consists of three steps. First: definition of the input data for the model initialization (see Section 2.1), second: general configuration of the simulation and specific settings for a scenario (Table 5) and third: predefining growing stock or harvesting targets (see below). The scenario settings listed in Table 4 allow for the simulation of a relatively broad range of scenarios as, for example, recent assessments of timber harvesting potentials for Switzerland [12]. However, highly specific applications such as thinning of coppice forests [31] or habitat tree retention [16] require introducing specific intervention routines into the program code of the harvesting sub-model. Typically, MASSIMO is run with time-steps of 10 years and for each simulation, and 20 iterations (i.e., replicates) are simulated.

Table 5.
Configuration and setting possibilities in MASSIMO. (d) refers to the default.
Additional to density-dependent and background mortality (Section 2.6), mortality rates can be adjusted to fit estimates for ‘Switzerland’s Second Initial Report under the Kyoto Protocol’ [32]. To this end, the user specifies mortality rates (mort) as proportions of the harvestings that are allocated to the mortality pool. This additional dead wood can be interpreted as harvesting losses. Using the default setting of mort = 15% of the harvestings approximates a total mortality of 16.34% which is given by Switzerland’s Second Initial Report under the Kyoto Protocol. We refer to salvage logging, if storm-damaged trees are harvested, which is the typical treatment in Switzerland.
2.8.2. Iterative Scenario Adaption Routine
In addition to general scenario settings and configuration, MASSIMO allows to specify growing stock or harvesting targets for each economic region and each time step. While running in the iterative scenario adaption routine, the results of a first simulation routine are compared to the target values of growing stock or harvesting amounts, respectively. Thereafter, the parameters delta thinning Δthin and delta felling Δfell are iteratively adjusted to minimize the difference between the simulation and the target values (for details cf. Supplementary S5). A decrease in Δthin leads to an increase in the number of sample plots that experience thinning, while a decrease in Δfell reduces the number of felled plots. Thus, to balance between thinning and felling interventions, values of Δthin and Δfell are adjusted simultaneously in opposite directions, when adapting to predefined targets. Eventually, the adaption routine leads to changes in the realized rotation period and in the return interval of thinning, while thinning intensities i.e., basal area thinning proportions, remain constant. To keep management interventions within a silviculturally-plausible range, Δthin cannot be adjusted to values below 0.9, which sets an upper limit to the thinning frequency, i.e., stand basal area in the focal decade must be at least 90% of the basal area at the previous intervention. The approximation routine is limited to even-aged forests outside the perimeter of forest reserves. For protection forests, only the thinning parameter Δthin can be adjusted because in these forests no shelterwood cutting is simulated. Uneven-aged forests are not controlled by the adaption routine as thinning in these forests follows predefined rules to maintain forest structure. While these exceptions are needed to simulate plausible management in protection forests, forest reserves and uneven-aged forests, they limit the degree to which Δthin and Δfell can be adjusted, especially in strata with a high proportion of such stands. Thus, in extreme scenarios, i.e., scenarios with a large increase or decrease of harvesting, predefined targets may not be reached because the adaption only influences the even-aged part of the sample plots in an economic region. Typically, the approximation of Δthin and Δfell is iterated five times for each time-step.
3. Model Application
3.1. Base and Business as Usual Scenarios
As an example application we simulated two harvesting scenarios starting from NFI3 (2004–2006) and with the number of time-steps being 10 and the length of time-steps being 10 years. For both scenarios the first time-step (i.e., decade 2007–2016) was used to meet observed growing stocks from NFI4 (2009–2013) using the growing stock adaption routine. For the next nine time-steps growing stock was stabilized at this level in a base scenario. As an alternative, the business as usual (BAU) scenario aimed at stabilizing harvesting amounts. Both scenarios followed the default settings as given in Table 4. The scenarios were run until year 2106, replicated 20 times and the adaption routine was iterated five times.
3.2. Simulation Results
At national level as well as for all production regions (not shown here), both the base scenario and the business as usual (BAU) met the predefined targets. As anticipated, the growing stock remained constant when applying the base scenario, while national harvesting amounts where kept at the NFI4-level in the BAU scenario (Figure 3). As the time-step of the MASSIMO simulation is longer than the interval between NFI3 and NFI4 (10 years versus 3 to 9 years), the harvesting amount of the first simulation step was adjusted to meet growing stock of NFI4 data. In the BAU scenario, this adjustment led to a high harvesting amount in the first compared to the subsequent decades. Independent of the scenario the conifer-proportion remained stable. In the BAU scenario, growing stock increased remarkably at the national level. However, on the Plateau growing stock decreased strongly following the observed trends since NFI2. For both scenarios gross growth including ingrowth (GGI) of conifers increased until the end of the century, while we simulated a slightly reduced GGI for broadleaves. Considering all species, GGI remained nearly stable in the base scenario with a weak tendency to increase at the end of the century, while it increased considerably under BAU. In general, mortality increased with increasing growing stock and, thus, this effect was more pronounced for conifers than for broadleaves and stronger in the BAU scenario than in the base scenario.
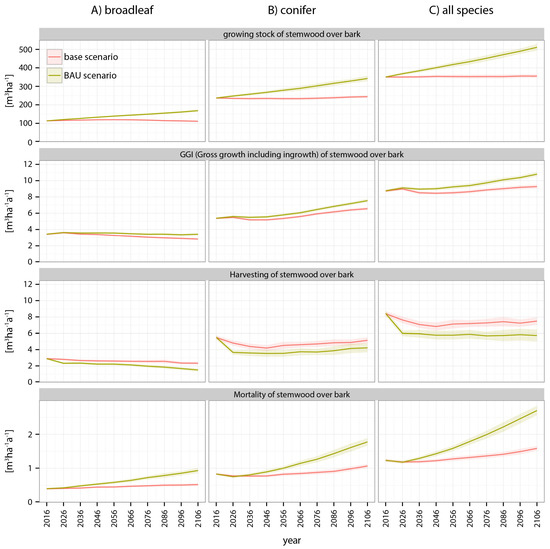
Figure 3.
Development of growing stock, GGI, harvesting and mortality at national level under a base and a business as usual (BAU) scenario. (A) shows broadleaves, (B) shows conifers and (C) shows all species together. The shaded areas represent the standard error of the mean.
To maintain a constant growing stock in the base scenario, harvesting of merchantable wood fluctuated close to 7.7 million m3/year (Figure 4). Regarding production regions, harvesting amounts fluctuated more on the Plateau, in the pre-Alps and in the Alps than in Jura Mountains and in the Southern Alps. The BAU scenario was defined with an average harvesting amount of 6.3 million m3/year. Under the base scenario 1.4 million m3/year more could be harvested when maintaining a constant growing stock. The BAU scenario could not be realized for more than 30 years on the Plateau. In this region, the harvesting amounts recorded between NFI2 and NFI3 exceed the observed increment by far. Continuing this harvesting amounts for more than 30 years in the simulations resulted in a strong decrease of growing stock and consequently a decreasing increment. From 2026 onwards, harvesting increased in regions having a substantial proportion of uneven-aged forests (pre-Alps and Alps) and protection forests (pre-Alps, Alps, and Southern Alps). This resulted from the fixed thinning routine in uneven-aged and protection forests that is not adjusted by the approximation routine. As a consequence, simulated harvesting in those regions slightly exceeded previously defined amounts.
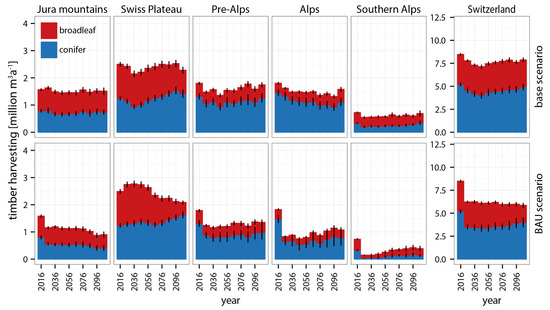
Figure 4.
Harvesting of merchantable wood (stem and branch volume with minimal diameter > 7 cm without bark) for production regions of Switzerland under the base and business as usual (BAU) scenarios. Error bars represent the standard error of the mean.
3.3. Discussion of Simulation Results
In our case study, the effect of two different forest management scenarios, a base scenario and a business as usual (BAU) on growing stock and harvesting amounts was investigated. In the BAU scenario, the current harvesting amount is kept constant for all regions at approximately 6.3 million m3/year. For Switzerland in total and all regions except the Plateau, this means an increase in growing stock as those harvesting amounts are lower than the average annual increments. However, on the Plateau with its easily accessible and economically affordable timber stocks, current harvesting amounts are already larger than the increment. The BAU scenario, therefore, results in a strong decrease of growing stock in the next 30 years on the Plateau reflecting the trend observed since the second NFI (1993–1995) [33]. Continuing this harvesting amount results in simulations with very low growing stocks and strongly reduced increments. On the other hand, growing stocks in the mountainous regions continually increase under a BAU scenario. In the long term, the BAU scenario may therefore lead to increased susceptibility of (protective) forests in mountainous regions to disturbances such as wind throw and bark beetles [34,35]. Moreover, total harvesting amounts in Switzerland might decrease due to the simulated decrease of harvesting amounts on the Plateau. This might have further consequences on the downstream wood supply chain such as an increase of the proportion of imported round wood and semi-finished wood products [36]. Therefore, a more balanced distribution of overall harvesting amounts to all regions including mountainous regions seems to be necessary, yet at the expense of increased harvesting costs [12,15].
In the base scenario, growing stock is assumed to be stabilized in each economic region over the simulation period. To achieve this goal, harvesting amounts in all regions except increase sustainably under the base scenario, except for the Plateau, where current harvesting amounts exceed the increment already. Thus, applying the base scenario leads to a general increase of the national harvesting amount, which is in line with the Swiss Confederation’s Forest Policy 2020 [36] that aims for a sustainable level of timber harvesting. However, due to the simulated decrease of mid-term harvesting amounts on the Plateau, such an increase in harvesting amounts must be realized either in steeper mountainous regions with higher harvesting cost or alternatively substituted by imports. Increased harvesting costs in steeper, less accessible forests might ask for structural changes in the planning and execution of management intervention towards larger-scale collaborations (e.g., [12,37,38]).
To conclude, the base scenario is more balanced than BAU with respect to the long-term availability of timber and sustains growing stock, forest structure and timber industries. This is an important point to be reflected when defining a forest reference level for Switzerland for post-2020 GHG accounting (cf. [39]) compatible with the approach presented in EU Regulation 2018/841 [40].
4. Discussion
4.1. Strengths and Weaknesses of MASSIMO
MASSIMO runs on the regular grid of the Swiss NFI encompassing all forest types and biogeographic regions of Switzerland and, thus, predictions are statistically representative. Consequently, MASSIMO is well suited for applications that predict large-scale development of forest states, harvesting amounts and forest management reference levels at the regional (e.g., [15,16]) to national scale (e.g., [12,13]). However, environmental, economic or social changes are not considered, as MASSIMO is based on a pure empirical approach. Further, interpretation at the scale of individual sample plots is restricted due to their relatively small size (500 m2). Results are typically aggregated at the scale of NFI production regions, economic regions or large cantons, for which at least 30 NFI sample plots are available. Nevertheless, in order to simulate plausible thinning and felling, harvesting is simulated at the plot-level. As thinning is dependent on growth, the time interval between consecutive thinnings may vary. Thus, flexible intervals between two thinnings are a big advantage over fixed thinning cycles for two reasons: first, they allow to define management scenarios at a large scale and to approximate given growing stock and harvesting targets. Second, anticipating future developments toward climate-sensitive sub-models for growth, mortality and regeneration, flexible management intervals allow to adapt thinning and shelterwood cutting to future conditions, i.e., to changing growth rates due to altered species mixture or climate change.
Mortality is composed of a background rate for natural mortality and an additional rate for density-dependent mortality that increases with increasing development stage, stand age, and basal area and differs for conifer- and broadleaf-dominated forests. However, tree species, various mixtures and climate variables are not considered as explanatory variables. In addition, tree size and previous growth are not included in the mortality prediction, although both have been shown to be related to individual-tree mortality [41,42]. While thinning routines in MASSIMO will compensate for potentially underestimated mortality rates, mortality may still be underestimated in low- and no-management scenarios (i.e., plots treated as forest reserves) [15].
The growth of trees in the regeneration pool (<12 cm in dbh) is assumed to follow the same growth model as used for trees larger than 12 cm dbh. Since NFI does not have repeated measurements of trees on the regeneration sub-plots, it remains unclear whether this assumption is biased or not. While simulated ingrowth rates match with observations at national level, regional predictions only stay in a plausible range when adjusting survival rates at caliper threshold [16]. Nevertheless, species composition in MASSIMO simulations tends to shift towards spruce-dominated forests that do not correlate with newest observations [33].
Projected temperature increases, and more frequent heavy storm and drought events will result in increasing probabilities of disturbance events. While increasing storm damages can be simulated in Massimo, disturbances by bark beetles are not included in the disturbance regime. Bark beetles often occur after storm damages [43,44,45] and their population growth strongly depends on temperature [46,47,48]. Thus, including bark beetle disturbances into MASSIMO may improve long-term projections. However, the small sample plot areas and their gridded spatial arrangement poses challenges to simulating disturbance interactions and spatially auto-correlated processes, such as spreading bark beetle infestations, but also wildfire and seed dispersal of both native and invasive tree species.
Individual tree growth in MASSIMO was implemented as nonlinear models for several tree species and ecological gradients according to the formulation of Teck and Hilt [24]. When evaluated with independent data, these models proved to perform reasonably well [22]. Tree volume is predicted from the simulated dbh by using tariff models. The models for bai and volume both incorporate a wide range of explanatory variables specifying individual-tree characteristics, site conditions, stand conditions, and management. In addition, MASSIMO includes some uncertainty of the bai and volume predictions by taking into account the residual standard error (SE) of the models. This is done by adding an error component that results from randomly drawing from the normal distribution N(0, SE2) to the point estimate in every replication. The fact that the resulting variance of the predictions among the replications is involved in MASSIMO simulations explicitly takes into account the prediction uncertainty of the empirical models for bai and volume.
4.2. Future Development
Although MASSIMO integrates various potential influences on forest development such as management, site, and stand effects, it has so far been based on the assumption of constant environmental conditions. With the effects of climate change on forest development becoming increasingly apparent already today (e.g., [49,50,51]), this assumption cannot be supported anymore and limits the validity of long-term projections with MASSIMO. Plans to overcome this limitation by including empirical models that represent climatic effects on tree growth and regeneration into MASSIMO have already been initialized [52,53,54], which is in line with developments in other empirical forest growth simulators [55,56]. However, additionally including climate-sensitivity into mortality will be inevitable to allow for analyses of scenarios assuming changing climatic conditions.
In recent years, the relationship between tree species diversity and productivity has gained increasing attention. Several studies have indicated—under certain conditions—increased productivity in mixed compared to mono-specific stands, likely as a consequence of niche partitioning, facilitation and/or stress reduction among different tree species (e.g., [57,58]). Furthermore, mixed forests are expected to provide a higher flexibility if exposed to changing environmental conditions, particularly if well adapted tree species are represented in the mixture [59]. Thus, beneficial effects of mixed forests may be of high economic and ecological interest, also regarding the estimation of harvesting potentials and carbon sequestration. Although the current version of MASSIMO does not yet consider species mixture effects, empirical results based on the Swiss NFI [57,60], may provide a strong basis for a future inclusion of such effects into MASSIMO.
The individual tree as the smallest simulation entity in MASSIMO, allows broadening the set of indicators on forest ecosystem service provision beyond harvested timber amounts and carbon sequestration and storage [61]. The economic feasibility of timber harvesting can be examined by quantifying the costs of simulated harvesting interventions by coupling the harvesting productivity model HeProMo [62] to MASSIMO [12]. Stem counts, conifer proportions, and estimates of basal area derived from MASSIMO outputs can be used together with topographic variables to assess the influence of management strategies on the efficacy of forests to protect against rockfall and avalanches [63,64]. Stand structural indicators such as Shannon-index of dbh classes and density of large trees as well as indicators of tree species diversity, such as the Shannon index, number of tree species, or conifer proportion can be used as proxies for various aspects of biodiversity. Stand-structural and -compositional characteristics associated with high quality for recreation become increasingly available, especially at the local scale [65], such that MASSIMO could potentially be used to assess management policy impacts on forest recreational values. However, the applications of such indicators requires an accurate simulation of forest dynamics such that limitations in MASSIMO also limit the interpretation of indicators. Since the current version of MASSIMO does not account for effects of management on the species composition in the regeneration, for example, the investigation of management effects on tree species diversity makes little sense.
5. Conclusions
To conclude, developments in growth, regeneration and mortality sub-models not only broaden the range of environmental conditions under which MASSIMO can be applied, but also the range of indicators that can be used to characterize forest ecosystem service provision. As such, MASSIMO is a powerful tool for analyses of trade-offs and synergies among ecosystem services under regional to national forest management scenarios and yields great potential for further applications also under climate change.
Supplementary Materials
The following are available online at http://www.mdpi.com/1999-4907/10/2/94/s1, Stadelmann_etal_2019_forests_supplementary_materials.
Author Contributions
G.S. conceived and performed the example application and wrote the manuscript. C.T., B.R., and E.T. contributed to improve the manuscript. G.S., C.T., B.R., M.D, A.H., and E.R. prepared the technical software documentation (internal document) on the basis of which this manuscript has been written.
Acknowledgments
We would like to thank Edgar Kaufmann, who developed the earlier versions of MASSIMO. We further thank the Swiss NFI team for their efforts in fieldwork and data management. Finally, we acknowledge two anonymous reviewers who provided useful suggestions that helped improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- UNFCCC. Adoption of the Paris Agreement (No. FCCC/CP/2015/l.9/rev.1); UNFCCC: Paris, France, 2015. [Google Scholar]
- Krug, J.H.A. Accounting of ghg emissions and removals from forest management: A long road from Kyoto to Paris. Carbon Balance Manag. 2018, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, S.; Schelhaas, M.-J.; Kändler, G.; Antón-Fernández, C.; Colin, A.; Bontemps, J.-D.; Alberdi, I.; Condés, S.; Dumitru, M.; Ferezliev, A.; et al. Overview of methods and tools for evaluating future woody biomass availability in European countries. Ann. For. Sci. 2016, 73, 823–837. [Google Scholar] [CrossRef]
- Pretzsch, H.; Grote, R.; Reineking, B.; Rotzer, T.; Seifert, S. Models for forest ecosystem management: A european perspective. Ann. Bot. 2008, 101, 1065–1087. [Google Scholar] [CrossRef] [PubMed]
- Peng, C. Growth and yield models for uneven-aged stands: Past, present and future. For. Ecol. Manag. 2000, 132, 259–279. [Google Scholar] [CrossRef]
- Bugmann, H. A review of forest gap models. Clim. Chang. 2001, 51, 259–305. [Google Scholar] [CrossRef]
- Schumacher, S.; Bugmann, H.; Mladenoff, D.J. Improving the formulation of tree growth and succession in a spatially explicit landscape model. Ecol. Model. 2004, 180, 175–194. [Google Scholar] [CrossRef]
- Seidl, R.; Rammer, W.; Scheller, R.M.; Spies, T.A. An individual-based process model to simulate landscape-scale forest ecosystem dynamics. Ecol. Model. 2012, 231, 87–100. [Google Scholar] [CrossRef]
- Vidal, C.; Alberdi, I.; Hernández, L.; Redmond, J. National Forest Inventories. Assessment of Wood Availability and Use; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Pilli, R.; Grassi, G.; Kurz, W.A.; Fiorese, G.; Cescatti, A. The European forest sector: Past and future carbon budget and fluxes under different management scenarios. Biogeosciences 2017, 14, 2387–2405. [Google Scholar] [CrossRef]
- Kaufmann, E. Prognosis and management scenarios. In Swiss National Forest Inventory: Methods and Models of the Second Assessment; Brassel, P., Lischke, H., Eds.; Swiss Federal Research Institute WSL: Birmensdorf, Switzerland, 2001; pp. 197–206. [Google Scholar]
- Stadelmann, G.; Herold, A.; Didion, M.; Vidondo, B.; Gómez, A.; Thürig, E. Timber-harvesting potential of Swiss forests: Simulation of management scenarios | [Holzerntepotenzial im Schweizer Wald: Simulation von Bewirtschaftungsszenarien]. Schweiz. Z. Forstwes. 2016, 167, 152–161. [Google Scholar] [CrossRef]
- Werner, F.; Taverna, R.; Hofer, P.; Thürig, E.; Kaufmann, E. National and global greenhouse gas dynamics of different forest management and wood use scenarios: A model-based assessment. Environ. Sci. Policy 2010, 13, 72–85. [Google Scholar] [CrossRef]
- Thürig, E.; Kaufmann, E. Waldbewirtschaftung zur Senkenerhöhung? Mögliche Konfliktfelder und Synergien | increasing carbon sinks by forest management? Conflicts and synergies. Schweiz. Z. Forstwes. 2008, 159, 281–287. [Google Scholar] [CrossRef]
- Temperli, C.; Stadelmann, G.; Thürig, E.; Brang, P. Silvicultural strategies for increased timber harvesting in a central european mountain landscape. Eur. J. For. Res. 2017, 136, 493–509. [Google Scholar] [CrossRef]
- Temperli, C.; Stadelmann, G.; Thürig, E.; Brang, P. Timber mobilization and habitat tree retention in low-elevation mixed forests in Switzerland: An inventory-based scenario analysis of opportunities and constraints. Eur. J. For. Res. 2017, 136, 711–725. [Google Scholar] [CrossRef]
- Schmid, S.; Thürig, E.; Kaufmann, E.; Lischke, H.; Bugmann, H. Effect of forest management on future carbon pools and fluxes: A model comparison. For. Ecol. Manag. 2006, 237, 65–82. [Google Scholar] [CrossRef]
- Traub, B.; Meile, R.; Speich, S.; Rösler, E. The data storage and analysis system of the Swiss national forest inventory. Comput. Electron. Agric. 2017, 132, 97–107. [Google Scholar] [CrossRef]
- Stierlin, H.R.; Zinggeler, J. Terrestrial inventory. In Swiss National Forest Inventory: Methods and Models of the Second Assessment; Brassel, P., Lischke, H., Eds.; Swiss Federal Research Institute WSL: Birmensdorf, Switzerland, 2001; pp. 65–87. [Google Scholar]
- Brändli, U.-B. Schweizerisches Landesforstinventar. Ergebnisse der dritten Erhebung 2004–2006; Birmensdorf, Eidgenössische Forschungsanstalt für Wald, Schnee und Landschaft WSL; Bundesamt für Umwelt BAFU: Bern, Switzerland, 2010; p. 312. [Google Scholar]
- Kaufmann, E. Estimation of standing timber, growth and cut. In Swiss National forest Inventory: Methods and Models of the Second Assessment; Brassel, P., Lischke, H., Eds.; Swiss Federal Research Institute WSL: Birmensdorf, Switzerland, 2001; pp. 162–196. [Google Scholar]
- Thürig, E.; Kaufmann, E.; Frisullo, R.; Bugmann, H. Evaluation of the growth function of an empirical forest scenario model. For. Ecol. Manag. 2005, 204, 53–68. [Google Scholar] [CrossRef]
- Thürig, E.; Palosuo, T.; Bucher, J.; Kaufmann, E. The impact of windthrow on carbon sequestration in switzerland: A model-based assessment. For. Ecol. Manag. 2005, 210, 337–350. [Google Scholar] [CrossRef]
- Teck, R.; Hilt, D. Individual-Tree Diameter Growth Model for the Northeastern United States; US Department of Agriculture, Forest Service, Northeastern Forest Experiment Station: Radnor, PA, USA, 1991.
- Keller, W. Einfacher ertragskundlicher Bonitätsschlüssel für Waldbestände in der Schweiz. Mitteilungen der eidgenössischen Forschungsanstalt für Wald, Schnee und Landschaft; Swiss Federal Institute WSL: Birmensdorf, Switzerland, 1978; Volume 54. [Google Scholar]
- Pfister, C. Wetternachhersage. 500 Jahre Klimavariationen und Naturkatastrophen (1496–1995); Verlag P. Haupt: Bern, Switzerland, 1999. [Google Scholar]
- Leibundgut, H. Femelschlag und Plenterung. Beitrag zur Festlegung waldbaulicher Begriffe. Schweiz. Z. Forstwes. 1946, 97, 306–317. [Google Scholar]
- Frehner, M.; Wasser, B.; Schwitter, R. Nachhaltigkeit und Erfolgskontrolle im Schutzwald; Wegleitung für Pflegemassnahmen in Wäldern mit Schutzfunktion; Bundesamt für Umwelt, Wald und Landschaft: Bern, Switzerland, 2005; p. 564. [Google Scholar]
- Frehner, M.; Wasser, B.; Schwitter, R. Sustainability and Success Monitoring in Protection Forests. Guidelines for Silvicultural Interventions in Forests with Protective Functions; Federal Office for the Environment (FOEN): Bern, Switzerland, 2007. [Google Scholar]
- Alberdi, I.; Michalak, R.; Fischer, C.; Gasparini, P.; Brändli, U.-B.; Tomter, S.M.; Kuliesis, A.; Snorrason, A.; Redmond, J.; Hernández, L.; et al. Towards harmonized assessment of european forest availability for wood supply in europe. For. Policy Econ. 2016, 70, 20–29. [Google Scholar] [CrossRef]
- Stadelmann, G.; Temperli, C.; Conedera, M.; Gómez, A.; Brang, P. Timber mobilization possibilities for the chestnut belt of Ticino | [Möglichkeiten zur Holzmobilisierung im Tessiner Kastaniengürtel]. Schweiz. Z. Forstwes. 2015, 166, 291–298. [Google Scholar] [CrossRef]
- FOEN. Switzerland’s Second Initial Report under the Kyoto Protocol; Report to Facilitate the Calculation of the assigned Amount Pursuant to Article 3, Paragraphs 7bis, 8 and 8bis, of the Kyoto Protocol for the Second Commitment Period 2013–2020; FOEN, Climate Division: Bern, Switzerland, 2016; p. 20. Available online: https://www.Bafu.Admin.Ch/bafu/en/home/topics/climate/state/data/climate-reporting/initial-reports.Html (accessed on 16 November 2018).
- Abegg, M.B.; Brändli, U.-B.; Cioldi, F.; Fischer, C.; Herold-Bonardi, A.; Huber, M.; Keller, M.; Meile, R.; Rösler, E.; Speich, S.; et al. Fourth National Forest Inventory—Result Tables and Maps on the Internet for the NFI 2009–2013 (NFI4B). [published online 06.11.2014]. Available online: http://www.Lfi.Ch/resultate/ (accessed on 11 December 2018).
- Bebi, P.; Seidl, R.; Motta, R.; Fuhr, M.; Firm, D.; Krumm, F.; Conedera, M.; Ginzler, C.; Wohlgemuth, T.; Kulakowski, D. Changes of forest cover and disturbance regimes in the mountain forests of the alps. For. Ecol. Manag. 2017, 388, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Brůna, J.; Wild, J.; Svoboda, M.; Heurich, M.; Müllerová, J. Impacts and underlying factors of landscape-scale, historical disturbance of mountain forest identified using archival documents. For. Ecol. Manag. 2013, 305, 294–306. [Google Scholar] [CrossRef]
- BAFU. Waldpolitik 2020. Visionen, Ziele und Massnahmen für eine nachhaltige Bewirtschaftung des Schweizer Waldes; Bundesamt für Umwelt: Bern, Switzerland, 2013; p. 66. [Google Scholar]
- Holm, S.; Thees, O.; Lemm, R.; Olschewski, R.; Hilty, L.M. An agent-based model of wood markets: Scenario analysis. For. Policy Econ. 2018, 95, 26–36. [Google Scholar] [CrossRef]
- Olschewski, R.; Schaller, M.; Dittgen, A.; Lemm, R.; Kimmich, C.; Markovic, J.; Thees, O. Marktverhalten öffentlicher Forstbetriebe in Graubünden und im Aargau. Schweiz. Z. Forstwes. 2015, 166, 282–290. [Google Scholar] [CrossRef]
- Grassi, G.; Pilli, R.; House, J.; Federici, S.; Kurz, W.A. Science-based approach for credible accounting of mitigation in managed forests. Carbon Balance Manag. 2018, 13, 8. [Google Scholar] [CrossRef] [PubMed]
- Forsell, N.; Korosuo, A.; Federici, S.; Gusti, M.; Rincón-Cristóbal, J.-J.; Rüter, S.; Sánchez-Jiménez, B.; Dore, C.; Brajterman, O.; Gardiner, J. Guidance on Developing and Reporting Forest Reference Levels in Accordance with Regulation (EU) 2018/841. Available online: Https://ec.Europa.Eu/clima/policies/forests/lulucf_en (accessed on 11 December 2018).
- Hülsmann, L.; Bugmann, H.; Cailleret, M.; Brang, P. How to kill a tree: Empirical mortality models for 18 species and their performance in a dynamic forest model. Ecol. Appl. 2018, 28, 522–540. [Google Scholar]
- Cailleret, M.; Jansen, S.; Robert, E.M.R.; Desoto, L.; Aakala, T.; Antos, J.A.; Beikircher, B.; Bigler, C.; Bugmann, H.; Caccianiga, M.; et al. A synthesis of radial growth patterns preceding tree mortality. Glob. Chang. Biol. 2017, 23, 1675–1690. [Google Scholar] [CrossRef]
- Stadelmann, G.; Bugmann, H.; Wermelinger, B.; Bigler, C. Spatial interactions between storm damage and subsequent infestations by the European spruce bark beetle. For. Ecol. Manag. 2014, 318, 167–174. [Google Scholar] [CrossRef]
- Stadelmann, G.; Bugmann, H.; Meier, F.; Wermelinger, B.; Bigler, C. Effects of salvage logging and sanitation felling on bark beetle (Ips typographus L.) infestations. For. Ecol. Manag. 2013, 305, 273–281. [Google Scholar] [CrossRef]
- Temperli, C.; Bugmann, H.; Elkin, C. Cross-scale interactions among bark beetles, climate change, and wind disturbances: A landscape modeling approach. Ecol. Monogr. 2013, 83, 383–402. [Google Scholar] [CrossRef]
- Stadelmann, G.; Bugmann, H.; Wermelinger, B.; Meier, F.; Bigler, C. A predictive framework to assess spatio-temporal variability of infestations by the European spruce bark beetle. Ecography 2013, 36, 1208–1217. [Google Scholar] [CrossRef]
- Wermelinger, B.; Seifert, M. Temperature-dependent reproduction of the spruce bark beetle Ips typographus, and analysis of the potential population growth. Ecol. Entomol. 1999, 24, 103–110. [Google Scholar] [CrossRef]
- Jakoby, O.; Stadelmann, G.; Lischke, H.; Wermelinger, B. Borkenkäfer und Befallsdisposition der Fichte im Klimawandel. In Wald im Klimawandel. Grundlagen für Adaptionsstrategien; Pluess, A.R., Augustin, S., Brang, P., Eds.; Bundesamt für Umwelt BAFU; Eidg. Forschungsanstalt WSL: Birmensdorf, Switzerland, 2016; pp. 247–265. [Google Scholar]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395. [Google Scholar] [CrossRef] [PubMed]
- Schelhaas, M.-J.; Nabuurs, G.-J.; Hengeveld, G.; Reyer, C.; Hanewinkel, M.; Zimmermann, N.E.; Cullmann, D. Alternative forest management strategies to account for climate change-induced productivity and species suitability changes in Europe. Reg. Environ. Chang. 2015, 15, 1581–1594. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Bathgate, S.; Blennow, K.; Borges, J.G.; Bugmann, H.; Delzon, S.; Faias, S.P.; Garcia-Gonzalo, J.; Gardiner, B.; Gonzalez-Olabarria, J.R.; et al. Are forest disturbances amplifying or canceling out climate change-induced productivity changes in European forests? Environ. Res. Lett. 2017, 12, 034027. [Google Scholar]
- Rohner, B.; Waldner, P.; Lischke, H.; Ferretti, M.; Thürig, E. Predicting individual-tree growth of central European tree species as a function of site, stand, management, nutrient, and climate effects. Eur. J. For. Res. 2017, 137, 29–44. [Google Scholar] [CrossRef]
- Rohner, B.; Weber, P.; Thürig, E. Bridging tree rings and forest inventories: How climate effects on spruce and beech growth aggregate over time. For. Ecol. Manag. 2016, 360, 159–169. [Google Scholar] [CrossRef]
- Zell, J.; Rohner, B.; Thürig, E.; Stadelmann, G. Modeling ingrowth for empirical forest prediction systems. For. Ecol. Manag. 2019, 433, 771–779. [Google Scholar] [CrossRef]
- Kindermann, G. A climate sensitive refining of the basal area increment model in PrognAus | [Eine klimasensitive Weiterentwicklung des Kreisflächenzuwachsmodells aus PrognAus]. Aust. J. For. Sci. 2010, 147–178. [Google Scholar]
- Matala, J.; Ojansuu, R.; Peltola, H.; Sievänen, R.; Kellomäki, S. Introducing effects of temperature and co2 elevation on tree growth into a statistical growth and yield model. Ecol. Model. 2005, 181, 173–190. [Google Scholar] [CrossRef]
- Mina, M.; Huber, M.O.; Forrester, D.I.; Thürig, E.; Rohner, B. Multiple factors modulate tree growth complementarity in central european mixed forests. J. Ecol. 2018, 106, 1106–1119. [Google Scholar] [CrossRef]
- Morin, X.; Fahse, L.; Scherer-Lorenzen, M.; Bugmann, H. Tree species richness promotes productivity in temperate forests through strong complementarity between species. Ecol. Lett. 2011, 14, 1211–1219. [Google Scholar] [CrossRef] [PubMed]
- Bolte, A.; Ammer, C.; Löf, M.; Madsen, P.; Nabuurs, G.-J.; Schall, P.; Spathelf, P.; Rock, J. Adaptive forest management in central Europe: Climate change impacts, strategies and integrative concept. Scand. J. For. Res. 2009, 24, 473–482. [Google Scholar] [CrossRef]
- Mina, M.; Río, M.; Huber, M.O.; Thürig, E.; Rohner, B. The symmetry of competitive interactions in mixed Norway spruce, silver fir and European beech forests. J. Veg. Sci. 2018, 29, 775–787. [Google Scholar] [CrossRef]
- Blattert, C.; Lemm, R.; Thees, O.; Lexer, M.J.; Hanewinkel, M. Management of ecosystem services in mountain forests: Review of indicators and value functions for model based multi-criteria decision analysis. Ecol. Indic. 2017, 79, 391–409. [Google Scholar] [CrossRef]
- Frutig, F.; Thees, O.; Lemm, R.; Kostadinov, F. Holzernteproduktivitätsmodelle HeProMo—Konzeption, Realisierung, Nutzung und Weiterentwicklung Eidg; Forschungsanstalt für Wald, Schnee und Landschaft, WSL: Birmensdorf, Switzerland, 2009; pp. 441–466. [Google Scholar]
- Dorren, L.; Berger, F.; Frehner, M.; Huber, M.; Kühne, K.; Métral, R.; Sandri, A.; Schwitter, R.; Thormann, J.-J.; Wasser, B. The new NaiS target profile for rockfall | [Das neue NaiS-Anforderungsprofil Steinschlag]. Schweiz. Z. Forstwes. 2015, 166, 16–23. [Google Scholar] [CrossRef]
- Berger, F.; Dorren, L.K.A. Principles of the tool rockfor.Net for quantifying the rockfall hazard below a protection forest. Schweiz. Z. Forstwes. 2007, 158, 157–165. [Google Scholar] [CrossRef]
- Hegetschweiler, K.T.; Plum, C.; Fischer, C.; Brändli, U.-B.; Ginzler, C.; Hunziker, M. Towards a comprehensive social and natural scientific forest-recreation monitoring instrument—A prototypical approach. Landsc. Urban Plan 2017, 167, 84–97. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).