4.1. Change Trend of Hydro-Meteorological Variables
The trends of precipitation, temperature, pan evaporation, wind speed, solar radiation, and runoff depth over the period of 1960–2012 for the Qingliu River basin have been analyzed by using the simple linear regression method and the Mann–Kendall test method.
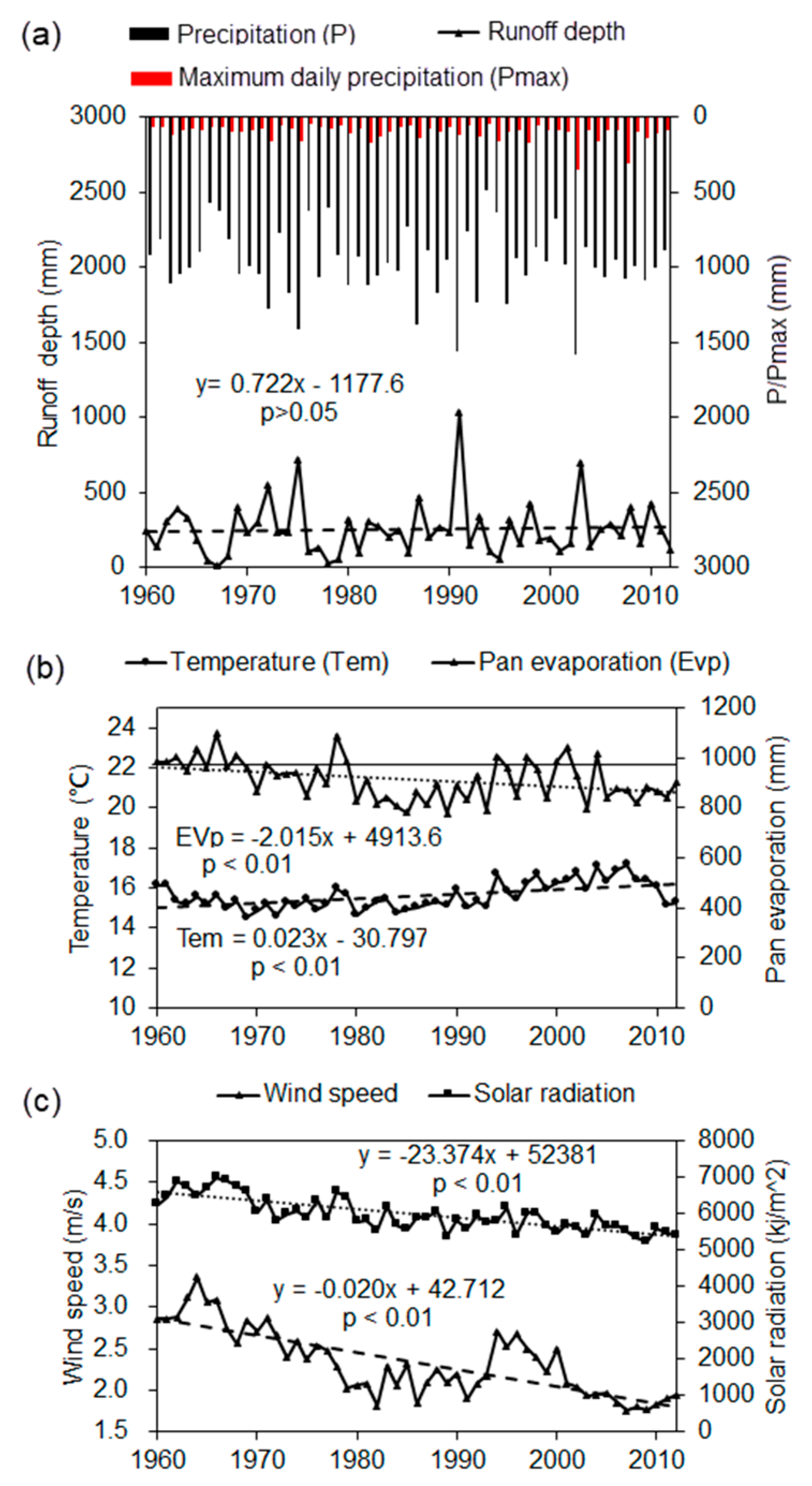
Figure 2 illustrates the inter-annual change of these hydro-meteorological variables, and
Table 2 shows the statistical information of the trend analysis on the annual and seasonal scales.
The results indicate that the mean annual runoff increased insignificantly, while the winter runoff increased significantly with a magnitude of 0.37 mm/year (
Figure 2a). The mean annual temperature shows an upward trend during 1960–2012 with a rate of 0.02 °C/year (
p < 0.01,
Figure 2b). All of the seasonal temperatures increased significantly (
p < 0.01) except for the summer temperature. In contrast, the average annual pan evaporation declined significantly with a magnitude of 2.01 mm/year (
p < 0.01,
Figure 2b). It infers that there exists an evaporation paradox, which has been widely observed across China [
40,
41]. The phenomenon of the evaporation paradox can be attributed to the significant decrease of solar radiation and wind speed (
Figure 2c) in the study area. The findings are consistent with the results published by Han et al. [
41,
42].
The mean annual precipitation exhibited a weak increase trend (1.68 mm/year,
p > 0.05) during 1960–2012, which was associated with insignificant decrease in spring and autumn, and a significant increase in winter (1.19 mm/year,
p < 0.01) (
Table 2). Correspondingly, it can be noted that the number of rainy days has decreased in the spring (
p < 0.05) and autumn (
p < 0.05), and increased in winter (
p < 0.01). The annual maximum daily precipitation indicated an increasing trend (
p = 0.018) over the study period. Similar trends can also be identified in the summer maximum daily precipitation and winter maximum daily precipitation. The number of days with daily precipitation over 25 mm increased significantly in winter. The results imply that: (1) the winter became wetter and warmer, while the spring and autumn became drier and warmer; (2) the maximum daily precipitation intensity on the annual, summer, and winter scales all tended to be higher; and (3) precipitation in winter became more intensive.
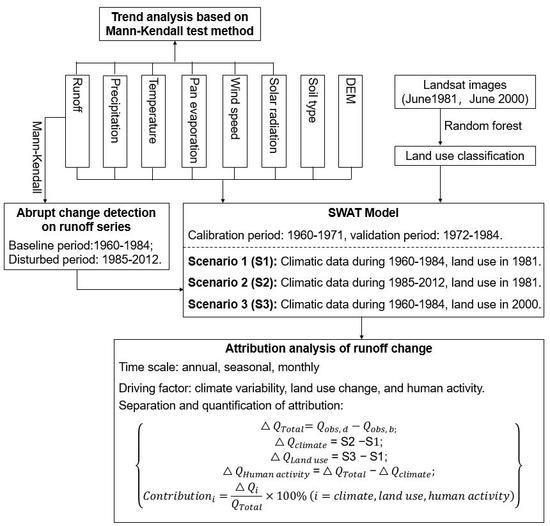
4.2. Abrupt Change Detection of Runoff Series
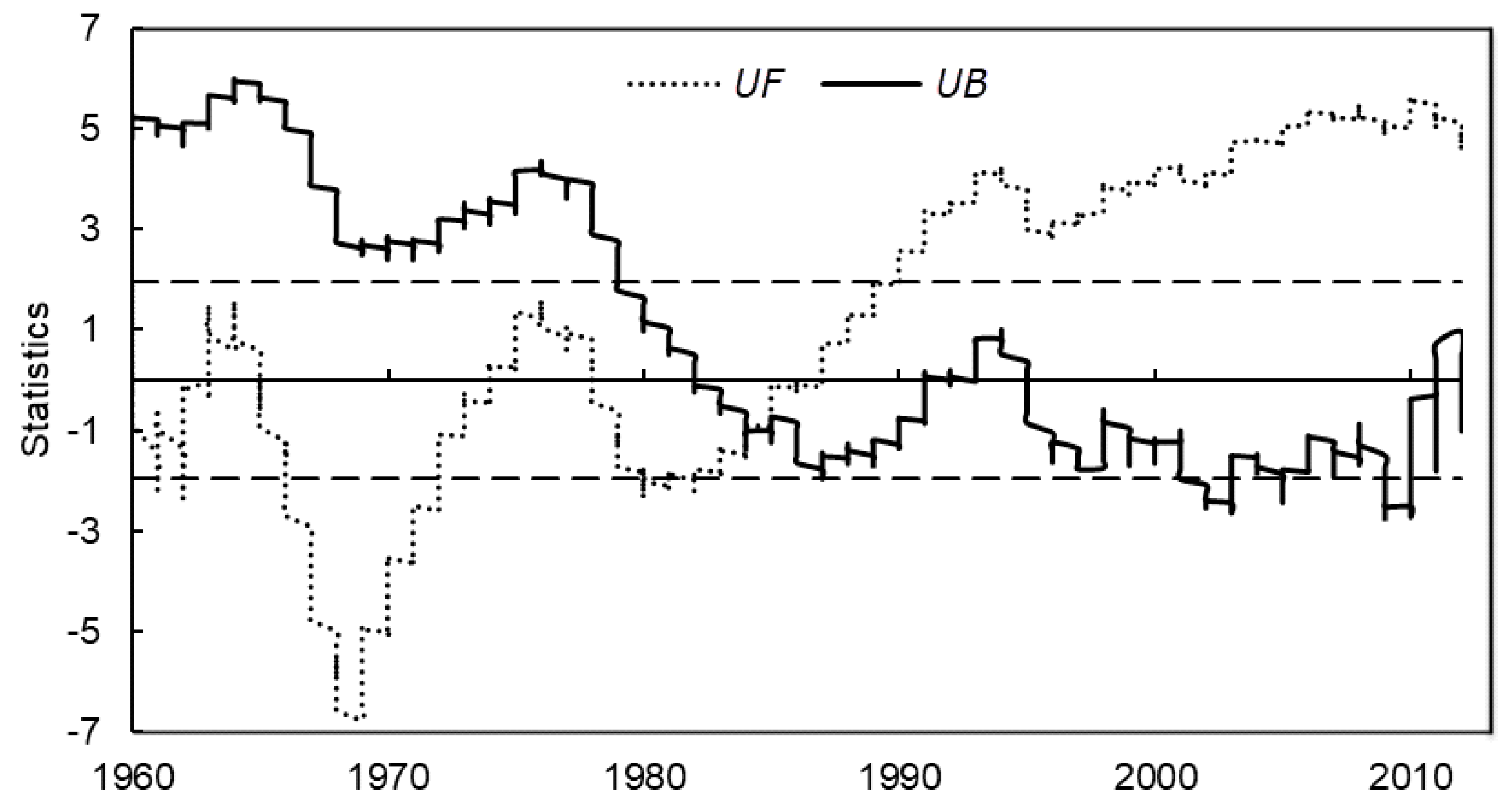
Based on the Mann–Kendall method, an abrupt change of runoff in the Qingliu River basin was detected in 1984 (as shown in
Figure 3). The
UF value for each year indicates the trend from the starting year (1960) to that specific year. In addition,
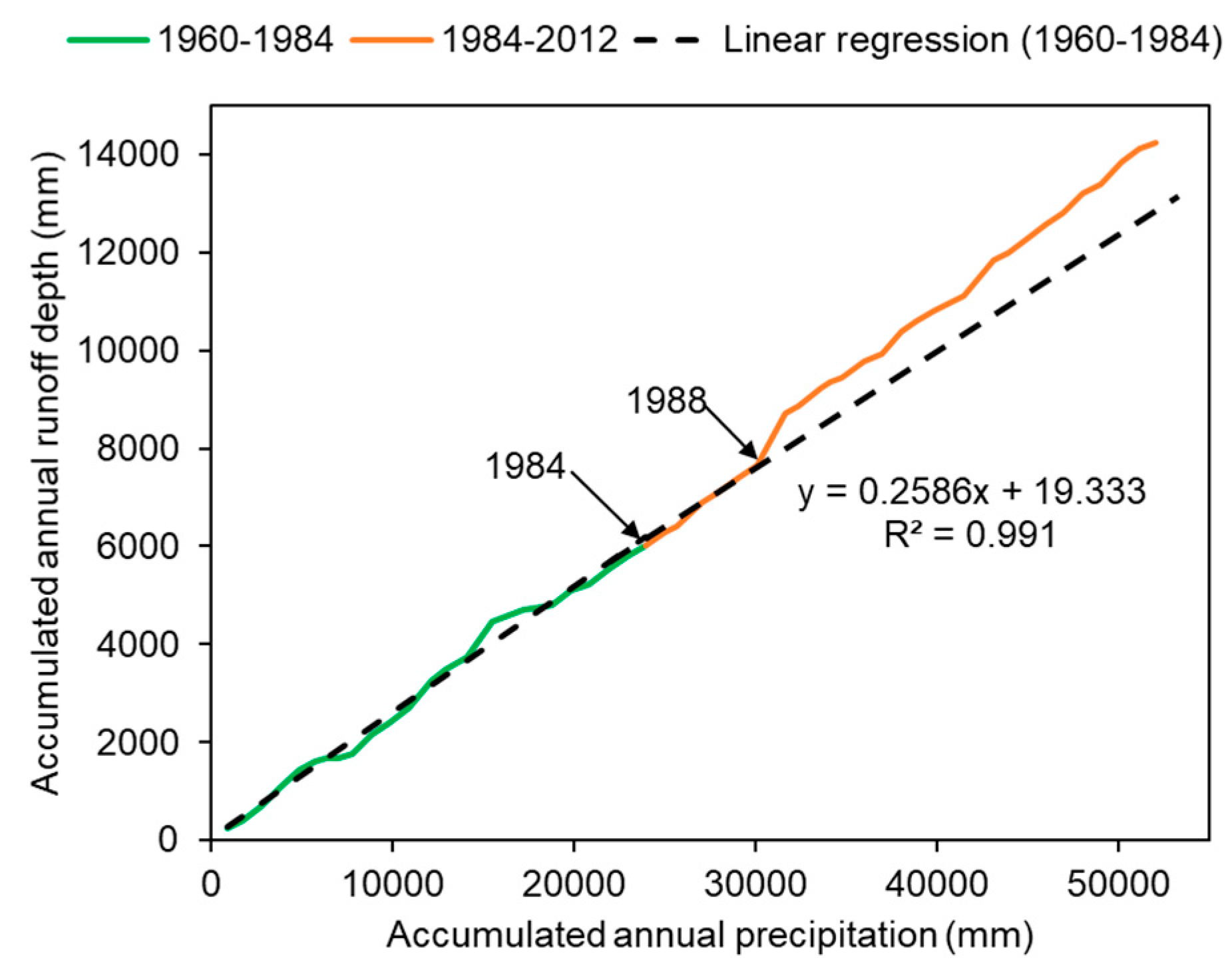
Figure 4 presents the double-mass curve of the accumulated runoff depth and precipitation. It can be observed that since 1988, the curve started to deviate from the original regression line, which implies that human activities had more intensive impacts on runoff.
Furthermore, since 1984, the population has increased rapidly, with a mean annual growth rate of 13.36% during 1984–2000. Due to the reform of the economic system during 1978–1984, agriculture and partial industry have developed dramatically since 1984 [
43]. Compared with the GDP in 1978 being 4.2 times that in 1949, the GDP in 1986 doubled from 1980, indicating a more rapid development [
43]. With the growths of the population, agriculture, and industry, transportation and urbanization have developed, and water withdrawals have increased accordingly [
43]. The Chengxi reservoir provided irrigation for an area of 70 km
2 during 1960–1980, and was mainly used for domestic and industrial water supply since the mid-1980s.
According to the results of the Mann–Kendall method and the double-mass curve as well as the socio-economic development, we selected 1984 as the abrupt change point of the runoff series, and divided the study period into the baseline period (1960–1984) and the disturbed period (1985–2012).
To investigate the variations of hydro-meteorological data before and after the abrupt change point, comparisons were made on the mean annual level and inner-annual level, respectively (illustrated in
Table 3 and
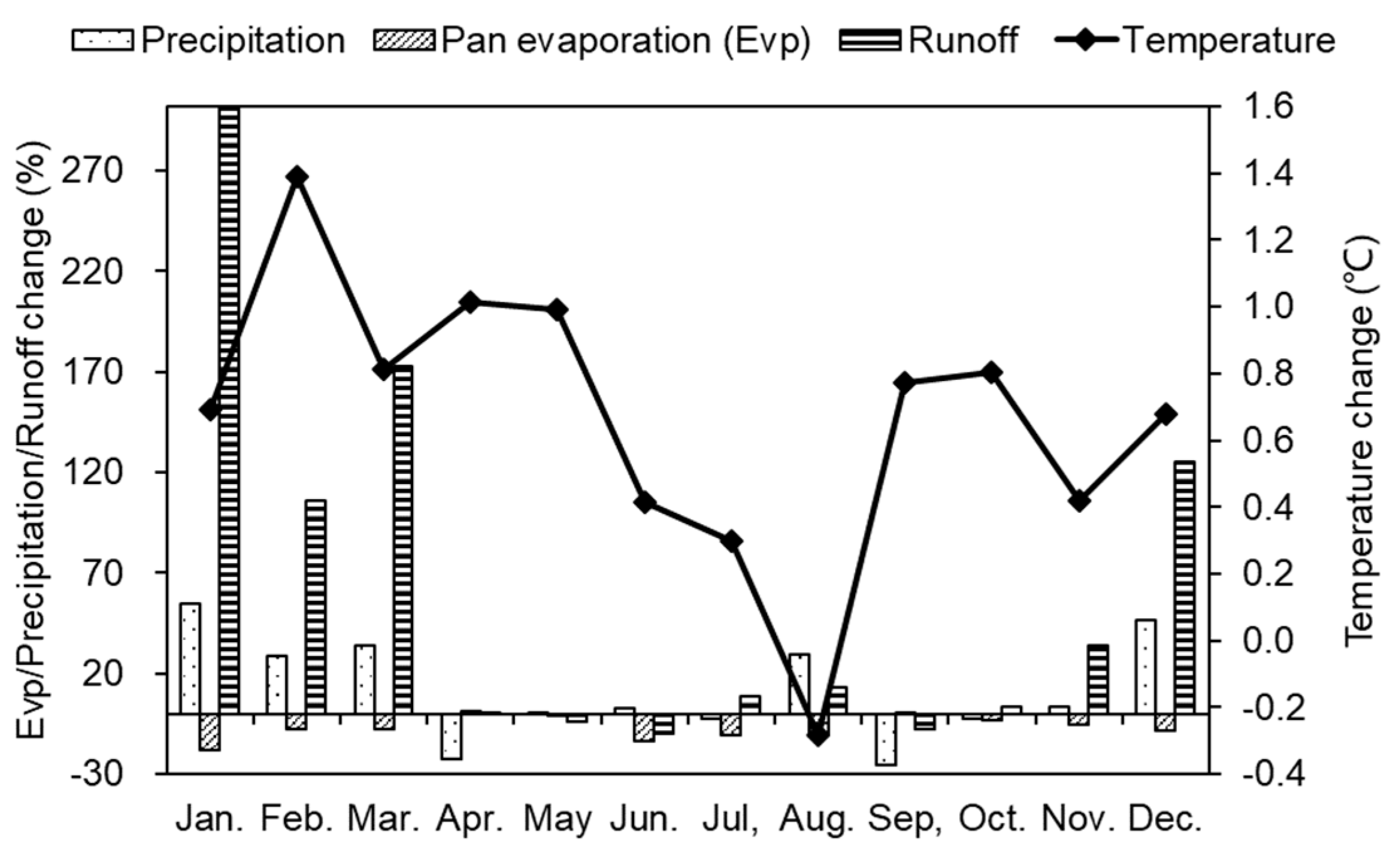
Figure 5, correspondingly).
Table 3 indicates that during 1985–2012, the temperature rose by 0.67 °C, while precipitation, pan evaporation, and runoff changed by 4.65%, −6.67%, and 16.05% relative to 1960–1984, respectively. However, the variations were uneven over the year (
Figure 5).
In general, the variations in winter and early spring were much higher than those between April and November. The larger the change magnitudes of precipitation and pan evaporation, the large change in the runoff. Runoff increases were often associated with an increase of precipitation and decline of pan evaporation. Specifically, the temperature rose in all the months except for August, ranging from −0.28 °C to 1.39 °C, with the highest rise occurring in February. The mean precipitation increased by 12.27%, with the largest increase (54.61%) in January and the largest reduction (−25.67%) in September. Pan evaporation declined in all months except for April, May, and September, with the highest decrease (−17.89%) occurring in January. As an integrated result, runoff increased in most months (especially for January, February, March, and December), ranging from 0.69% to 301.20%. Runoff increased the most in January, which is consistent with the change features of precipitation and pan evaporation. The largest decrease (−9.73%) of runoff occurred in June. The variations in April, May, and June imply that there should be some other factors affecting runoff.
4.3. Land-Use Change for the Qingliu River Basin
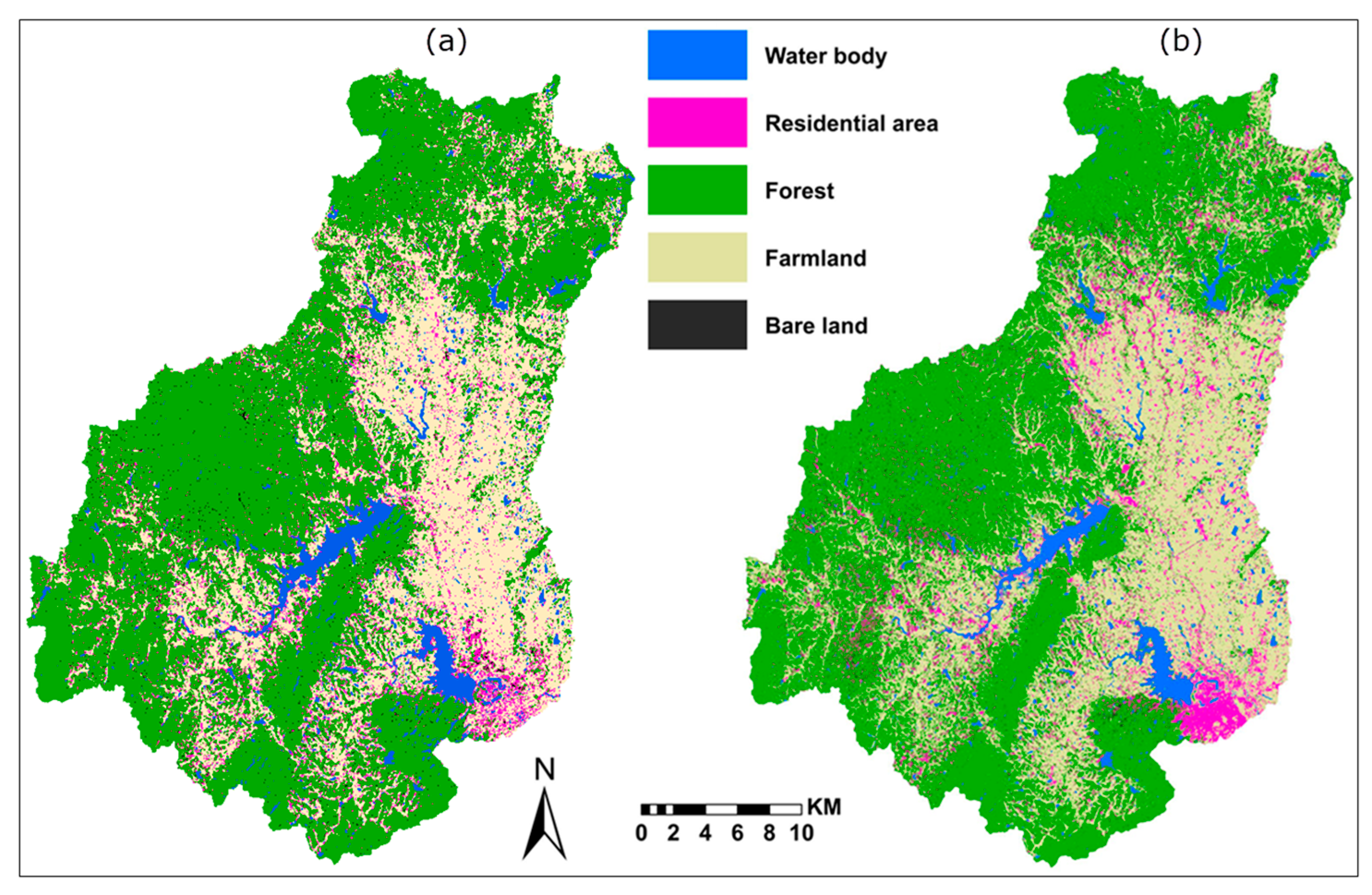
Based on the Landsat imagery and random forest classifier, land use was classified into five categories, namely forest, farmland, residential area, water body, and barren land.
Figure 6 shows the land-use classification results for 1981 and 2000, respectively. It can be observed that the forest dominates land use in the study area, and the residential area has expanded between 1981 and 2000.
Table 4 displays the transmission matrix for land-use changes from 1981 to 2000. The results indicate that in total, 10.35% of the study area (110.79 km
2) experienced land-use changes, which mainly refer to transmission among the forest, farmland, and residential area. Specifically, the residential area expanded from 52.40 km
2 in 1981 to 73.64 km
2 in 2000, increasing by 40.53% relative to 1981. However, the total increase of residential area (21.24 km
2) only accounts for 1.99% of the whole research area. The forest decreased by 57.44 km
2, while the farmland increased by 41.59 km
2, accounting for 5.37% and 3.89% of the study region, respectively.
4.4. SWAT Model Calibration and Validation for Monthly Runoff Simulation
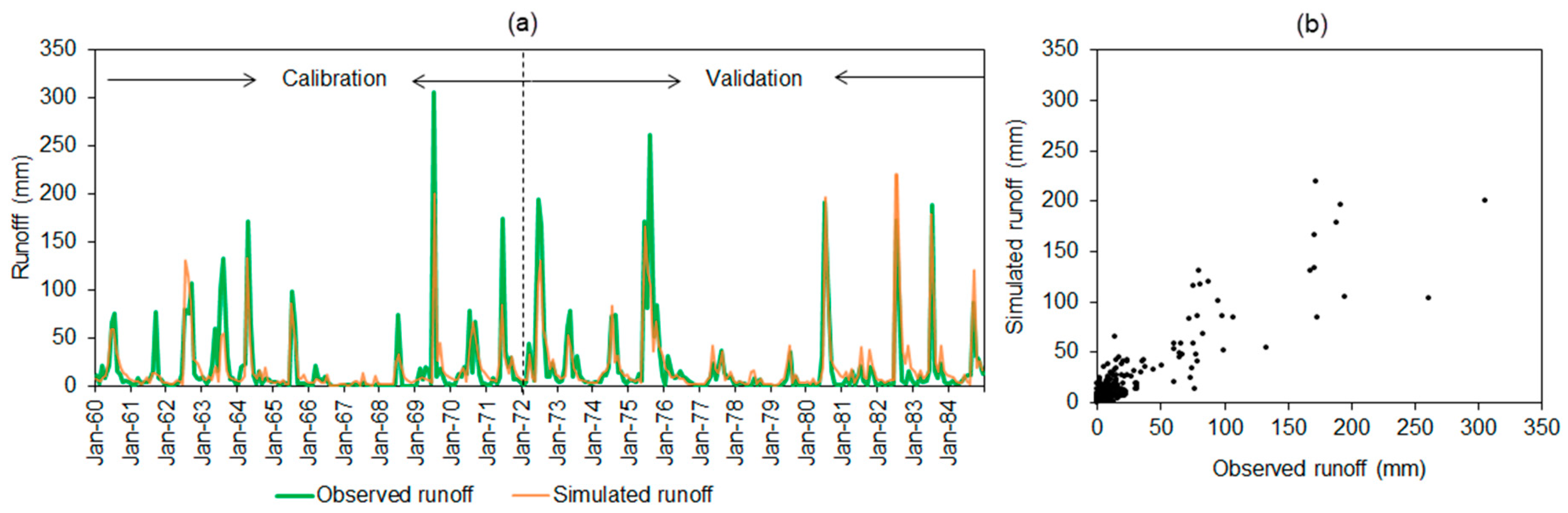
Taking the detected abrupt change in 1984 as a break point, the whole study period was divided into the baseline period (1960–1984) and the disturbed period (1985–2012). The SWAT model was calibrated and validated over the baseline period. Specifically, data during 1960–1971 were used for model calibration, while data during 1972–1984 were applied for model validation.
Figure 7 illustrates the simulated and observed monthly runoff between 1960 and 1984. The performance evaluation of the SWAT model is listed in
Table 5. It indicates that on the monthly scale, the Nash–Shutcliffe efficiency (NSE) were 0.76 and 0.81 for the calibration and validation periods, respectively. The relative error values imply that the monthly runoff was underestimated in the calibration period, and overestimated in the validation period.
Over the validated period (1972–1984), in contrast to performance of the monthly runoff simulation, the SWAT model performed better on the annual runoff simulation (NSE = 0.83) and runoff simulation in the wet season (NSE = 0.87). The relative error of runoff simulation in the dry season (11.57%) was higher than that in wet season (−3.30%), which might be because the Qingliu River almost dried up in dry seasons between 1976 and 1980, but the SWAT model overestimated the runoff.
4.5. Attribution Analysis of Runoff Change for the Qingliu River Basin
Based on the runoff observations and runoff simulations derived from the SWAT model under three scenarios (S1, S2, and S3), the contributions of individual factors (climate variability, land-use change, and human activity) to runoff change in the Qingliu River were quantified at multiple scales (annual, seasonal, and monthly) over three periods (1985–2012, 1985–2000, and 2001–2012). Specially, the attribution to land-use change was only analyzed on the annual and seasonal scales over the whole disturbed period (1985–2012). One reason is that the computation of land use-induced runoff change (i.e., the discrepancies between runoff simulations under Scenario 3 and Scenario 1) requires the comparison period having the same length as the baseline period. Furthermore, land-use change is mostly characterized by annual and seasonal scale changes instead of at a monthly scale.
Table 6 presents the attribution analysis results for the Qingliu River on the annual scale. It indicates that annual runoff during 1985–2012 increased by 38.05 mm in total relative to 1960–1984. Climate variability, land-use change, and human activity contribute 95.36%, 4.64%, and 12.26% to the total change of runoff, respectively. The results imply that climate variability dominates runoff variation in the Qingliu River on the annual scale. Land-use changes (mainly for deforestation and urbanization) resulted in a runoff increase, which may be derived from the reduction of evaporation and interception, and the increase of impermeable area. Compared with land-use change, human activity showed a smaller contribution to runoff change. It infers that some other human activities caused runoff decrease such as water withdraw by irrigation due to the increase of farmland from 1981 to 2000 (41.59 km
2).
It is worth noting that runoff change and its attribution vary over different periods. For instance, the total increase of runoff during 1985–2000 (42.81 mm) was larger than that during 2001–2012 (31.70 mm). Over the periods of 1985–2000 and 2001–2012, climate variability and human activity accounted for 58.64% and 41.36%, and 161.49% and −61.49% of runoff change, respectively. The results imply that human activity after 2000 has become more intensive, and runoff subsequently decreased. It may partially due to more water withdrawals for different sectors to support the socio-economic development.
Here, considering the property of precipitation distribution, we divided the whole year into the wet season (from May to September) and the dry season (from January to April, and from October to December).
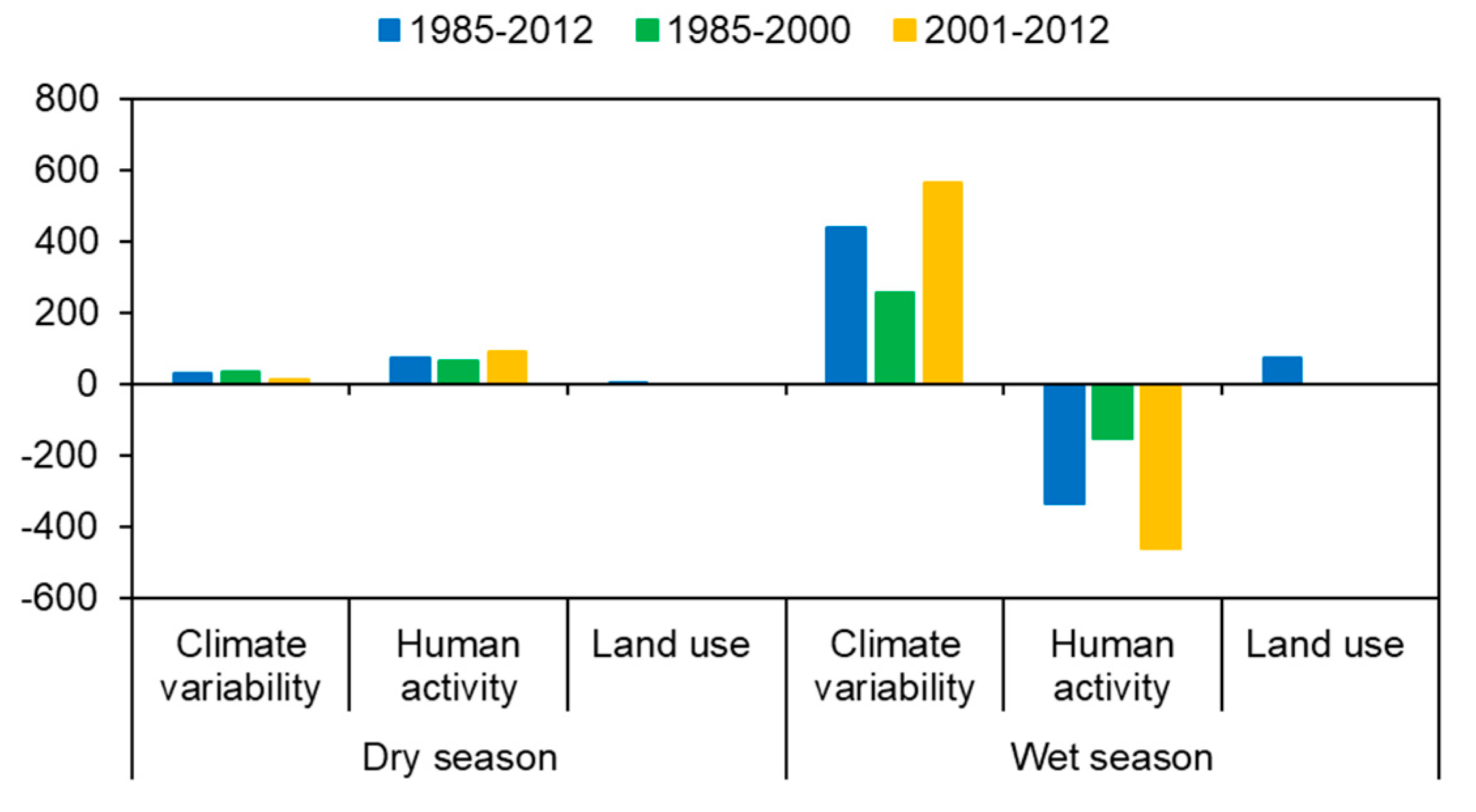
Table 7 displays the results of attribution for runoff change in the Qingliu River on a seasonal scale during 1985–2012. The results indicate the total change of runoff in the wet season over the whole disturbed period increased by 6.26 mm relative to the baseline period. However, the runoff increased by 27.42 mm, which was induced by climate variability, and declined by 21.15 mm, which was induced by human activity, respectively. The finding implies that in the wet season, climate variability and human activity both have a major impact on the runoff, and their influences counteract with each other. In contrast, the total change of runoff in the dry season was 31.78 mm, accounting for 61.12% of that in the baseline period. The contributions of climate variability, land-use change, and human activity account for 27.89%, 0.18%, and 72.11% of runoff change in the dry season, respectively. It indicates that human activity is the primary contributor to runoff increase in the dry season, which might be because of the operations of reservoirs in the basin. However, due to the relative error of runoff simulation (−3.30% for the wet season, 11.57% for the dry season), uncertainties are associated with the attribution analysis results on the seasonal scale especially for the dry season.
Furthermore,
Figure 8 shows the contributions of different drivers to runoff change in the dry season and the wet season over three periods (1985–2012, 1985–2000, and 2001–2012). Similar to 1985–2012, during the two sub-periods, human activity dominated runoff change in the dry season, while climate variability dominated runoff change in the wet season. In the dry season, both climate variability and human activity increased runoff. The impact of climate variability on runoff during 1985–2000 (10.36%) became weaker than that during 2001–2012 (35.80%), while the impact of human activity exhibited an opposite trend. Regarding the wet season, climate variability increased runoff, while human activity decreased runoff, and their effects became stronger during 2001–2012 compared with the period of 1985–2000. The impact of land use on runoff in the wet season was much higher than that in the dry season.
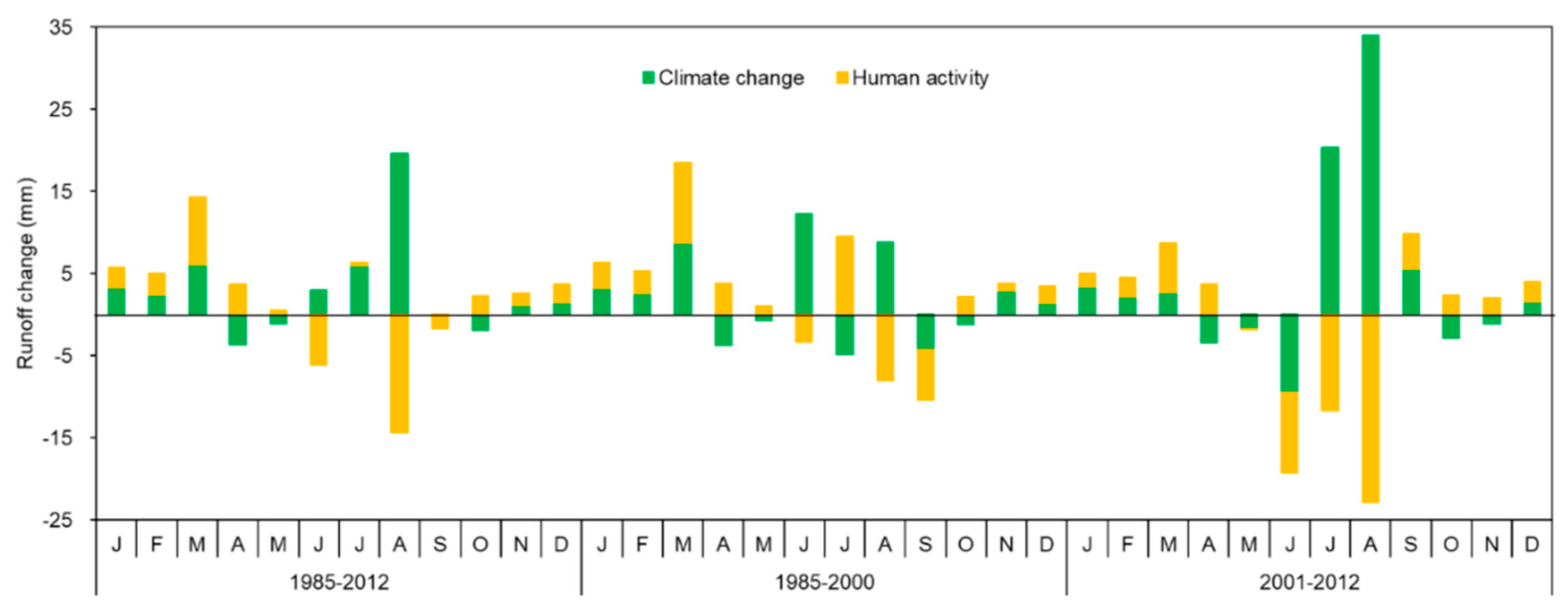
Runoff change and its attribution in individual months for the Qingliu River are illustrated in
Figure 9. The results show that the impacts of driving factors (i.e., climate variability and human activity) differ across different months and over different periods. During 1985–2012, the largest total change (14.30 mm) appeared in March. The highest changes caused by climate variability and human activity both occurred in August, where runoff increased by 19.64 mm due to climate variability and decreased by 14.37 mm due to human activity. Human activity dominated runoff change in all months except January, May, July, and August, most of which belong to the wet season.
In contrast, during 1985–2000, the largest total change was 18.50 mm in March. Climate variability caused the largest increase in runoff in June (12.29 mm), while human activity mostly increased runoff in March. Over the period of 2001–2012, the largest changes induced by climate and human activity appeared in August as well, but with greater magnitudes. Compared with 1985–2000, human activity had a more intensive impact on runoff decline during 2001–2012.
In combination with
Table 8, it can be noted that the largest total change of runoff and the largest runoff change induced by climate are highly related with the magnitude of precipitation change. For all three periods, the largest increase of runoff induced by human activity occurred in March, and the largest decrease of runoff induced by human activity occurred in August. The reason behind it might be related to reservoir operations, which also reflects the roles that human beings play in water resources management.
Comparing the findings on three different scales, people may find that attribution on finer (seasonal and monthly) scales would reveal more detailed information for runoff attribution analysis, which might be weakened or offset on a coarser (annual) scale. Investigating runoff change and its causes over different time periods can also benefit attribution analysis. It can deliver how the dominant drivers change along with time. Therefore, attributing runoff change to different driving forces on multiple scales over different periods would provide more detailed support for decision and policy makers on adaptive water resources management, sustainable utilization, and planning.
A previous study on runoff attribution in humid and semi-humid regions in southern China indicated that climate change dominated runoff change and contributed to runoff increase [
21]. In this study, findings on the annual scale are consistent with the results in the previous work. Zhai et al. [
3] reported that in the 2000s, climate variability contributed to runoff decrease, and human activity contributed more to runoff change than in the 1990s, and dominated runoff change in the Xixian basin and Changle basin. In this study, human activity during 2001–2012 exerted more impact on runoff change compared with that during 1985–2000, which is consistent with the findings in the literature published by Zhai et al. [
3]. However, differently, we found that climate variability caused an increase in runoff and dominated runoff change in all periods.
4.6. Discussion on Uncertainty and Future Work
The attribution analysis in this study is based on comparison between the observed runoff and the simulated runoff derived from the SWAT model. Although the hydrological model performed well, there exist some differences between the simulations and the observations. Specifically, the relative errors of runoff simulations on annual and monthly scales (6.56%) were relatively lower than those in the dry season (11.57%) and higher than those in the wet season (−3.30%). Correspondingly, uncertainties are associated in the attribution results of runoff change and differ from different temporal scales. Briefly, attribution results of runoff variation in the wet season and on monthly and annual scales have lower uncertainty than those in the dry season. However, the conclusions drawn regarding the contributions trends of different driving factors (climate variability, land-use change, and human activity) to runoff change are sound.
In this study, the impact of land-use change on run variation was quantified separately from that of human activity. However, other human activities such as reservoir operations and water withdrawals were not analyzed separately due to the lack of detailed data. Nevertheless, different kinds of human activities may exert different impacts on runoff. Therefore, separation of the impacts of different kinds of human activities on runoff variation can be further investigated in the future.
It has been well-documented that climate variability and human activities are two main contributors to runoff changes. In this study, similar to many previous studies, the authors have assumed that the impacts of climate variability and human activities are independent. In reality, climate and human activities interact with each other, and it is difficult to separate their impacts on runoff. Therefore, more detailed assessments could be made on how to integrate the relationships among different driving factors into an attribution analysis of runoff change in future work.
Based on the Mann–Kendall test method, double-mass curve, and the facts of socio-economic development, the study period was divided into the baseline period and the disturbed period (which was further divided into two sub-periods), and the authors assumed that there was no human intervention in the baseline period. However, human activity existed over the whole period and exerted different magnitudes of impacts on runoff over different periods. Therefore, more dynamic attribution that considers changing attribution should be recommended in the future.