Comparisons of Estimated Circuity Factor of Forest Roads with Different Vertical Heights in Mountainous Areas, Republic of Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Computation of Circuity Factors
2.3. Factors Affecting the Forest Road Circuity
2.4. Statistics
3. Results
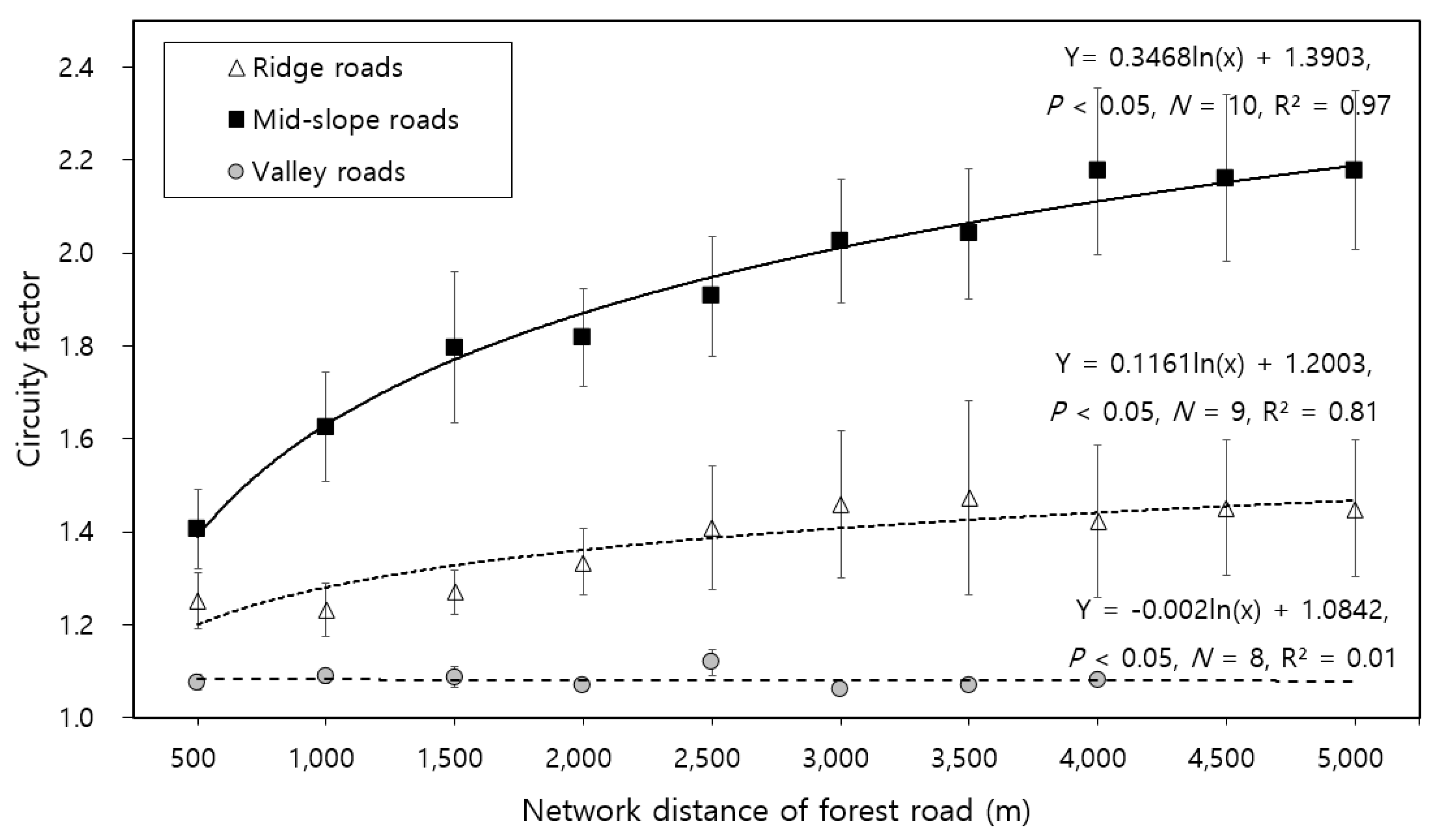
3.1. Circuity Factors Vary with Cumulative Network Distance at the Vertical Position of Forest Roads
3.2. Circuity Factors in 500-m Interval Sections per Vertical Position of Forest Roads
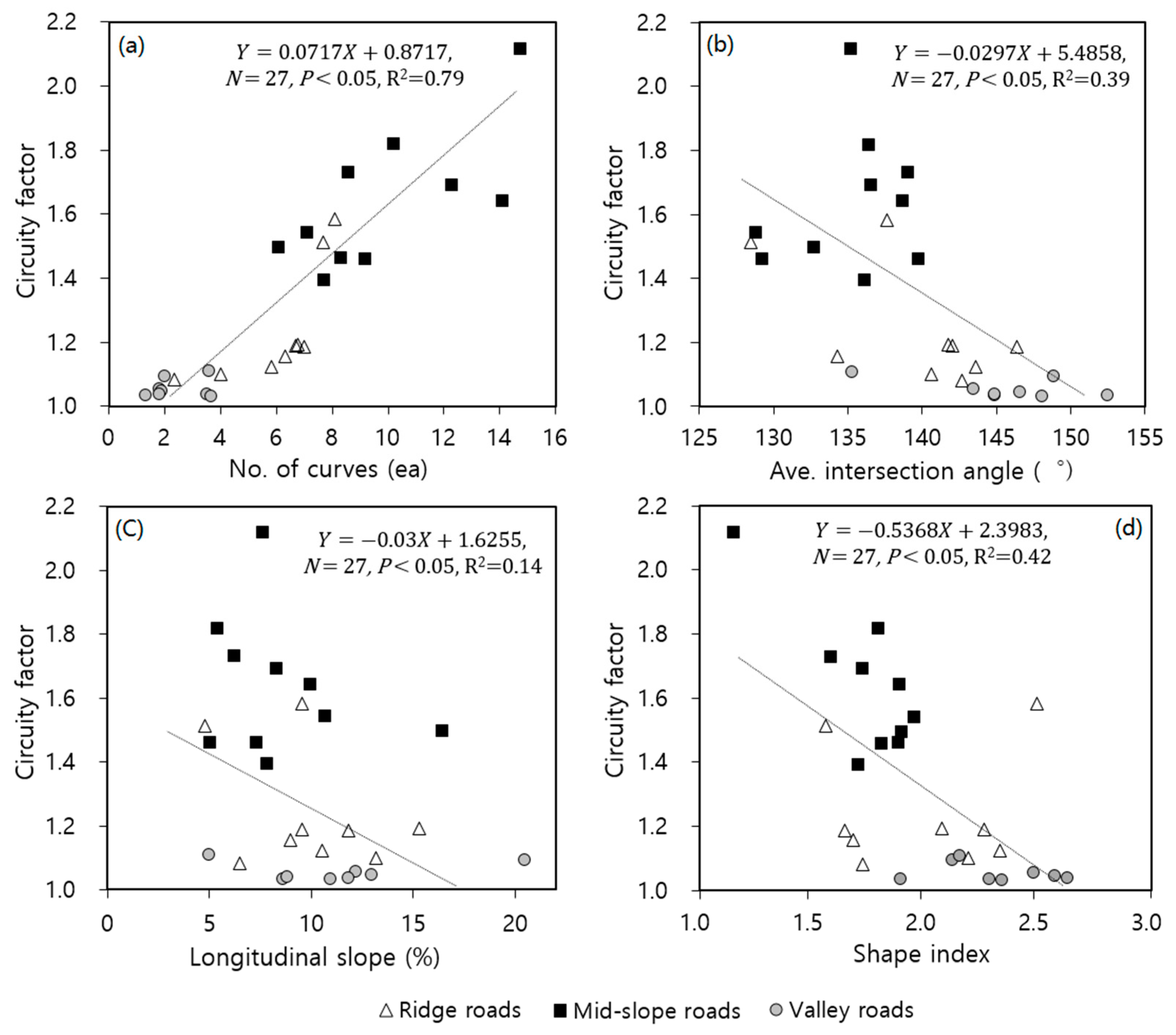
3.3. Correlation between Circuity and Each Influential Factor
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, T.; Shin, Y.; Lee, J.; Suh, K. Calculation of regional circuity factors using road network distance in South Korea. J. Korean Plan. Assoc. 2013, 48, 319–329. (In Korean) [Google Scholar]
- Wolf, J.; Schoenfelder, S.; Samaga, U.; Oliveira, M.; Axhausen, K. Eighty weeks of global positioning system traces: Approaches to enriching trip information. Transp. Res. Rec. J. Transp. Res. Board 2004, 1870, 46–54. [Google Scholar] [CrossRef]
- Ballow, R.; Handoko, R.; Noriaki, S. Selected country circuity factors for road travel distance estimation. Transp. Res. Part A 2002, 36, 843–848. [Google Scholar] [CrossRef]
- Levinson, D.; El-Geneidy, A. The Minimum Circuity Frontier and the Journey to Work. Reg. Sci. Urban Ecol. 2009, 39, 732–738. [Google Scholar] [CrossRef]
- Jeon, J.; Park, M.; Yoon, S.; Seo, K.; Kim, E. Calculation of road circuity factors considering public facilities and road condition in rural area. J. Korean Soc. Rural Plan. 2017, 23, 55–65. [Google Scholar] [CrossRef]
- Giacomin, D.; Levinson, D. Road network circuity in metropolitan areas. Environ. Plan. 2015, 42, 1040–1053. [Google Scholar] [CrossRef]
- Giacomin, D.; James, L.; Levinson, D. Trends in Metropolitan Network Circuity. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.259.6416&rep=rep1&type=pdf (accessed on 21 October 2018).
- O’Sullivan, S.; Morrall, J. Walking distances to and from light-rail transit stations. Transp. Res. Rec. J. Transp. Res. Board 1996, 1538, 19–26. [Google Scholar] [CrossRef]
- Lee, J.; Kim, N. A method to evaluate distance efficiency of Seoul metropolitan subway by estimating subway detour factor. J. Korean Soc. Transp. 2015, 33, 304–314. [Google Scholar] [CrossRef]
- Parthasarathi, P.; Hochmair, H.; Levinson, D.M. The Influence of Network Structure on Travel Distance. Available online: http://dx.doi.org/10.2139/ssrn.1736326 (accessed on 21 October 2018).
- Sakai, H. Forest Operational Road; Zenrinkyou: Tokyo, Japan, 2004; p. 281. ISBN 4-88138-133-4. (In Japanese) [Google Scholar]
- Love, R.F.; Morris, G. Mathematical models of road travel distances. Manag. Sci. 1979, 25, 130–139. [Google Scholar] [CrossRef]
- El-Geneidy, A.; Levinson, D. Network circuity and the location of home and work. In Proceedings of the University Transportation Study Group Conference, Harrowgate, UK, 3–5 January 2007. [Google Scholar]
- Newell, G. Traffic Flow on Transportation Networks; MIT Press: Cambridge, MA, USA, 1980; ISBN 0-262-14032-2. [Google Scholar]
- Nakazawa, M.; Oka, M.; Tanaka, Y.; Yoshida, C.; Kondo, K. A study on roundabout rate on road network in mountinous area. JIFES 2008, 22, 261–264. (In Japanese) [Google Scholar] [CrossRef]
- Kweon, H.; Kim, M.; Lee, J.; Seo, J.; Rhee, H. Comparison of horizontal accuracy, shape similarity and cost of three different road mapping techniques. Forests 2019, 10, 452. [Google Scholar] [CrossRef]
- Sugihara, H.; Iwakawa, O. A study on the roundabout rate of road. J. Jpn. For. Soc. 1960, 42, 269–275. (In Japanese) [Google Scholar]
- Hujiwara, N. Average slope of mountainous terrain around forest roads and route circuity. J. Jpn. For. Soc. 1969, 17, 138–141. (In Japanese) [Google Scholar] [CrossRef]
- Cha, D.; Ji, B.; Cho, G. The calculation of elongation coefficients of forest roads. Res. Bull. Inst. For. Sci. Kangwon Natl. Univ. 1994, 10, 49–54. (In Korean) [Google Scholar]
- Cha, D.S.; Cho, G.H. The analysis of relationships between road alignment and terrain conditions for national forest road. J. Korean For. Soc. 1995, 84, 517–524. (In Korean) [Google Scholar]
- KFRI (Korea Forest Research Institute). The Manual of Forest Site and Soil Map; KFRI: Seoul, Korea, 2011; p. 143. ISBN 9788981768065. (In Korean) [Google Scholar]
- Korea Forest Service (KFS). Available online: http://www.law.go.kr/DRF/MDRFLawService.do?OC=foalaw&ID=10317 (accessed on 6 August 2018).
- Tveite, H.; Langaas, S. An accuracy assessment method for geographical line data sets based on buffering. Int. J. Geogr. Inform. Sci. 1999, 13, 27–47. [Google Scholar] [CrossRef]
- Kim, M.; Ahn, D. Landscape ecological analysis of urban parks –analysis of index of patch shape and the dispersion of patches. J. Korean Inst. Landsc. Archit. 1996, 23, 12–19. (In Korean) [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). Watershed Management Field Manual. Available online: http://www.fao.org/docrep/006/T0099E/T0099E00.HTM (accessed on 1 April 2018).
- Visser, R.; Spinelli, R.; Magagnotti, N. Landing characteristics for harvesting operations in New Zealand. Int. J. For. Eng. 2011, 22, 23–27. [Google Scholar] [CrossRef]
- Hwang, J. A Study on Timber Transportation Costs Reduction by Improving Forest Road Structures. Ph.D. Thesis, Kangwon National University, Chuncheon-si, Korea, 2016. [Google Scholar]

| Road No. | Administrative District | Road Length (m) 1 | Elevation (m) | Longitudinal Slope (%) 4 | Vertical Location | |
|---|---|---|---|---|---|---|
| B.P. 2 | E.P. 3 | |||||
| 1 | Donghae, Kangwon | 5000 | 223 | 261 | 8.98 | Ridge |
| 2 | Chuncheon, Kangwon | 4779 | 537 | 624 | 15.29 | |
| 3 | Heongseong, Kangwon | 3229 | 992 | 1129 | 6.47 | |
| 4 | Milyang, Kyeongnam | 4417 | 721 | 1077 | 10.98 | |
| 5 | Yeongyang, Kyeongbuk | 5000 | 255 | 462 | 9.56 | |
| 6 | Uiseong, Kyeongbuk | 3384 | 171 | 271 | 4.31 | |
| 7 | Bukgu, Ulsan | 5000 | 128 | 218 | 9.54 | |
| 8 | Bukgu, Ulsan | 5000 | 286 | 389 | 10.54 | |
| 9 | Boryeng, Chungnam | 2512 | 202 | 498 | 11.84 | |
| 10 | Heongseong, Kangwon | 5000 | 720 | 853 | 9.96 | Mid-slope |
| 11 | Pyeongchang, Kangwon | 5000 | 323 | 638 | 16.44 | |
| 12 | Bonghwa, Kyeongbuk | 2444 | 405 | 523 | 7.65 | |
| 13 | Yeongdeok, Kyeongbuk | 5000 | 798 | 813 | 8.30 | |
| 14 | Yeongyang, Kyeongbuk | 3742 | 459 | 455 | 6.23 | |
| 15 | Yeongyang, Kyeongbuk | 5000 | 378 | 420 | 9.16 | |
| 16 | Gongju, Chungnam | 5000 | 291 | 399 | 5.06 | |
| 17 | Nonsan, Chungnam | 3835 | 58 | 159 | 7.83 | |
| 18 | Dangjin, Chungnam | 5000 | 78 | 142 | 7.32 | |
| 19 | Cheonan, Chungnam | 5000 | 203 | 360 | 10.70 | |
| 20 | Inje, Kangwon | 4273 | 635 | 963 | 12.98 | Valley |
| 21 | Heongseong, Kangwon | 2511 | 392 | 685 | 12.20 | |
| 22 | Bonghwa, Kyeongbuk | 4593 | 167 | 325 | 8.42 | |
| 23 | Munkyeong, Kyeongbuk | 1861 | 436 | 654 | 20.47 | |
| 24 | Yeongyang, Kyeongbuk | 2247 | 586 | 750 | 11.80 | |
| 25 | Yeongyang, Kyeongbuk | 1826 | 501 | 746 | 8.60 | |
| 26 | Geumsan, Chungnam | 1743 | 350 | 433 | 10.93 | |
| 27 | Chungju, Chungbuk | 2556 | 323 | 480 | 8.84 | |
| Total | - | 104,952 | - | |||
| Vertical Location | Road No. | 500-m Section Average Circuity Factor | Mean | SD 1 | F | p |
|---|---|---|---|---|---|---|
| Ridge road (n = 74) | 1 | 1.16 (n = 10) | 1.24 a | 0.328 | 3.041 | <0.01 |
| 2 | 1.18 (n = 9) | |||||
| 3 | 1.08 (n = 6) | |||||
| 4 | 1.14 (n = 8) | |||||
| 5 | 1.58 (n = 10) | |||||
| 6 | 1.36 (n = 6) | |||||
| 7 | 1.19 (n = 10) | |||||
| 8 | 1.12 (n = 10) | |||||
| 9 | 1.19 (n = 5) | |||||
| Mid-slope road (n = 88) | 10 | 1.64 (n = 10) | 1.61 b | 0.482 | ||
| 11 | 1.50 (n = 10) | |||||
| 12 | 2.12 (n = 4) | |||||
| 13 | 1.69 (n = 10) | |||||
| 14 | 1.82 (n = 7) | |||||
| 15 | 1.54 (n = 10) | |||||
| 16 | 1.46 (n = 10) | |||||
| 17 | 1.39 (n = 7) | |||||
| 18 | 1.46 (n = 10) | |||||
| 19 | 1.73 (n = 10) | |||||
| Valley road (n = 40) | 20 | 1.05 (n = 8) | 1.06 c | 0.057 | ||
| 21 | 1.05 (n = 5) | |||||
| 22 | 1.09 (n = 9) | |||||
| 23 | 1.13 (n = 3) | |||||
| 24 | 1.04 (n = 4) | |||||
| 25 | 1.03 (n = 3) | |||||
| 26 | 1.03 (n = 3) | |||||
| 27 | 1.04 (n = 5) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kweon, H. Comparisons of Estimated Circuity Factor of Forest Roads with Different Vertical Heights in Mountainous Areas, Republic of Korea. Forests 2019, 10, 1147. https://doi.org/10.3390/f10121147
Kweon H. Comparisons of Estimated Circuity Factor of Forest Roads with Different Vertical Heights in Mountainous Areas, Republic of Korea. Forests. 2019; 10(12):1147. https://doi.org/10.3390/f10121147
Chicago/Turabian StyleKweon, Hyeongkeun. 2019. "Comparisons of Estimated Circuity Factor of Forest Roads with Different Vertical Heights in Mountainous Areas, Republic of Korea" Forests 10, no. 12: 1147. https://doi.org/10.3390/f10121147
APA StyleKweon, H. (2019). Comparisons of Estimated Circuity Factor of Forest Roads with Different Vertical Heights in Mountainous Areas, Republic of Korea. Forests, 10(12), 1147. https://doi.org/10.3390/f10121147





