1. Introduction
Norway spruce is the most important economically usable tree species in the Czech Republic and one of the most widespread tree species in Central Europe. Consequently, exact determination of the volume of individual trees and whole stands, and its inclusion in the marketable timber assortments, is important in development of forest management plans, as well as for planning the future of the forest sector and the timber industry [
1]. In addition to economic importance, the determination of timber volume of individual stems and, subsequently, growing stock in large areas, is very important for estimates of the amount and development of forest above ground biomass as well as carbon dioxide sequestered in it—the most significant of greenhouse gases contributing to global warming.
The stem taper model is considered to be the most effective and universal method of determining the volume of a tree [
1,
2]. The development of new, more accurate stem taper models and the determination of the stem volume is important for more accurate, flexible and user-friendly determination of the diameter or volume of any part of the stem, taking the development of the requirements of the timber-processing industry into account. In this context, it is important to note that the stem taper curve equation does not only characterize the shape of the stem. It can also be used to estimate the total volume of the stem, the merchantable volume of the stem, the volume of the stem segment which is bounded by two different heights of the stem, and the volume of the stem segment which is bounded by two different stem diameters. In addition, it can be used to determine the diameter of the stem at any height or, conversely, to determine the height at which the stem achieves a specified diameter [
3,
4].
According to [
5] the general shape of the stem taper curve (STC) is given by the equation:
where
di is stem diameter at height
hi,
d is diameter at breast height,
h is tree height, and
hi is measuring point height.
Assuming a circular cross-section of the stem, the volume of any stem segment (between height
h1 and height
h2) is determined through integration:
where
is volume of the stem segment height between height
h1 and height
h2,
k is
π/4 multiplied by the constant dependent on units of
di and
gi (the circular surface area of the stem at a height of
hi).
Stem taper curve models can be divided into three groups:
Models for the entire stem—describing the entire stem by a single equation. Due to the complicated shape of the stem, these are usually comprehensive and mathematically complex equations with multiple parameters e.g., [
6,
7,
8].
Segmented STC models—consist of sub-models that describe specific parts of a stem; those parts connect to each other in the inflection points between segments (e.g., [
9,
10,
11]). In this group of models, the most frequently used are [
12] and [
13].
Models with variable parameters—continuous functions for the description of the shape of the entire stem, with model parameters varying for each part of the stem (capturing neiloid, paraboloid and conical shapes). This type of model was introduced in the study of [
14] and elaborated by other authors (e.g., [
15]), as well as through an adjusted equation according to [
3], which is currently one of the most widely used models.
It can be stated that, currently, models included in groups (2) and (3) are mostly preferred.
Publications mostly highlight (e.g., [
16] or [
17]) that the suitability of models is highly dependent on a specific tree species and region. A large number of models were parameterized for different tree species and territories in North America and Europe (notably Spain, e.g., [
18,
19,
20,
21,
22]); recently, the territory of Turkey and the Middle East was included [
2,
4,
17].
Since the STC is usually defined for larger areas, spatial heterogeneity is an important problem to be addressed, with mixed regression models being the most widely used e.g., [
21,
23,
24,
25,
26,
27,
28]. There are also reports that discuss the issue of what parameters influence the calculation of the volume of a specific part of the stem in more detail, i.e., what parameters are advisable to model as mixed parameters e.g., [
29] discusses the model of [
3], suggesting that the bottom segment is influenced by parameter
b2 and parameter
b3, the middle part is affected by
b4,
b6 and
b8, and the top segment is controlled by
b5. Another problem that often appears in the relationship between the stem taper curve—and hence the stem volume—and the other tree quantities measured (the relationship varies between individual locations and also between areas with different growth circumstances) involves nested data. Since such data are of a hierarchical structure, the condition of independence between measurements is not satisfied as one of the basic assumptions for using ordinary least squares (OLS) [
30].
The mixed effects model [
31] is a very effective tool for analysing hierarchical data (thus eliminating the problem of dependence between data). Each mixed model has two parts—fixed effects that are identical for the entire population and random effects which relate to each of the hierarchical levels [
32]. Fixed effects describe the influence of individual covariates or treatment effects on the entire population as in the OLS regression [
33]. Random effects, on the other hand, explain the randomness and heterogeneity in the data caused by known and unknown [
34]. Mixed effects models explain a substantial part of random variability of the population model and use local data to derive one general flexible model for a given area [
35].
The aim of this study is to develop and test a procedure for an accurate prediction of merchantable wood volume of standing Norway spruce stems. From the very beginning of this study, only the approach based on mixed effects STC models has been considered. The major research question was whether one or two upper diameter measurements taken by Meopta telescope can lead to a practically significant improvement of volume prediction. The upper diameter measurements are used to calibrate the STC to take account of plot and sample tree-level specific factors.
Meopta telescopes have been in use by the Czech NFI since 2011. To date, however, the available upper diameter measurements have not been used for the merchantable volume estimation within the Czech NFI. Instead, the merchantable volume of standing sample trees has always been derived based on diameter at breast height and total tree height only, i.e., by two-way nationally specific volume tables or equations. However, according to some NFI stakeholders, this method allegedly introduces a considerable bias into the NFI estimates. Although the study is motivated by the application within the Czech NFI, it is believed that the presented findings have a broad application potential in common forest mensuration practice.
2. Materials and Methods
2.1. Dataset
The data was collected as part of a dedicated survey focused on stem shape analysis of selected tree species in the Czech Republic. This survey included measurements of dendrometric quantities on standing sample trees and, subsequently, on the same trees when felled. The survey was carried out by the Forest Management Institute Brandýs nad Labem in forests throughout the Czech Republic in 2008–2011. A total of 9399 measurements of diameter at different heights (above tree base) on the stem were available as part of the dataset of 716 sample trees of Norway spruce (Picea abies (L.) H. Karst.). The sample trees were measured at 169 locations with 3 to 5 trees per location surveyed.
Before the felling, tree diameter at breast height (DBH) was measured (by caliper) along with the overall tree height; stem diameter was also measured by a remote method at heights of 5 and 7 m using a modified telescope manufactured by the Meopta company. This telescope was developed especially for use by the Czech NFI and it was modified from a telescope with variable zoom (1.5−5 × 20) from the product series Meopta Artemis 3000. After felling, the diameter at stump was measured along with the stump height and the distance from the first cut up to the point where the tree diameter was 7 cm. Measurements also included identifying the diameter at heights of 5 and 7 m, which was done at the same points and in the same direction (as marked by colour on the tree), as was done by remote method. The felled stem was also visually split into segments of two metres where diameters was measured (by caliper) at the beginning, in the middle and at the end of each segment. Measurements of all diameters (except optical measurement and contact measurement done at the same places as optical measurement) were carried out (by caliper) twice perpendicular to each other, and the average diameter at the given measuring point was calculated from the measured diameters and recorded in the database. All measured diameters at different heights on the stem were also converted to cross-sectional area of the stem. For each tree, the age was also determined by counting tree-rings on the stump after felling. Optical measurements of upper diameters are available for part of the dataset only (measured in 2008). Thus, both measurement methods, i.e., optical as well as contact (after felling), were only available for the 2008 subset involving 126 sample trees at 45 locations. These data were used further as a validation dataset. The remaining portion of the data (parametrisation dataset, 590 sample trees at 124 locations) was used for a re-parametrisation of the best STC model identified. All the implementation details of this survey can be found in the field instructions [
36].
2.2. STC Modelling Procedure
The merchantable timber volume identified through numeric integration of the natural cubic spline that interpolated diameters measured by caliper (cross-directional measurements along the virtually segmented stem) after felling was considered as the reference merchantable volume. The integration took place from the butt end (actual stump height) to the height at which the diameter of the stem (including the bark) reached 7 cm (merchantable wood threshold). We consider the use of spline to be more appropriate than a linear interpolation because the spline better reflects the shape of the different parts of the stem. Compared to the determination of volume using, e.g., the Smalian formula, the use of the spline reduces overestimation of the volume in the stem base (neiloid shape), which, according to our recent results of calculating the volume of timber, outweighs the adverse effects (underestimation) in the top part of the stem. Volume predictions obtained through each of the prediction methods were compared to this reference volume. All references to merchantable or any other volume refer to the volume including bark (over-bark volume). Basic statistical characteristics of measured quantities are indicated in
Table 1.
The Kozak 02 model was selected for STC modelling [
3]:
where
di is stem diameter at a height of
hi, d is diameter at breast height,
h is tree height,
hi is measuring point height,
b1,
b2, ...,
b9,
p are parameters of the model.
Models of the STC were fitted as nonlinear least squares models (NLS) in addition to nonlinear mixed effects models (NLME—detailed information is described below in the
Section 2.3) using the full dataset of 716 sample trees. In this phase of model development, the aim was to identify significant model parameters, to select the best combination of random parameters of the NLME model, and to test and compensate for presence of heteroscedasticity and autocorrelation of prediction errors. Every single step of this model development was evaluated by Akaike´s information criterion (AIC) [
37], likelihood ratio test, and graphic analysis by assessing the distribution of residuals. The best models (both NLS and NLME) of dependent variables
di and
gi (instead of
di,
gi was substituted into equation (3)) were selected by this approach. This means that four final models were selected—NLS for
di, NLS for
gi, NLME for
di, and NLME for
gi. The best model among these was selected and used for the next analyses. It was chosen based on the minimum mean relative deviation of volume predictions (obtained by numerical integration of the respective model) from the reference volume.
We selected the NLME model with response variable
gi as the best model. For this model it was found that the parameter
b4 correlates with the total height of the sample tree. The model (Equation (3)) was therefore extended as follows:
where
b4 is the basic Kozak model 02 parameter (Equation (3)),
h is tree height, and
a1,
a2 are parameters of the model.
After the best model structure was determined based on the full dataset, the model was re-parametrised using the parametrization dataset only. Only in this step were the final values of model parameters determined. Finally, the re-parametrized model was used for calibrated prediction (involving calibration process) of merchantable volume of stems of the validation dataset. The calibrated predictions of stem merchantable volume were carried out with the options described later in this section.
Section 3 lists only the outputs for the best NLME STC model, which is based on fitting the cross-sectional areas (
gi) of the stem.
All statistical analyses were carried out using the R software application [
38], with
α = 0.05 being the level of significance. The package nlme [
39] was used for fitting the NLME model.
2.3. Mixed Effects Models
The stem profile data have a hierarchical structure with regard to the method of their sourcing (several diameter measurements within a single sample tree, several sample trees at each location) and great spatial variability. Under such circumstances it is appropriate to use mixed effects models [
40].
A nonlinear mixed effects (NLME) model can be written in the form of a matrix as follows [
41]:
where
yijk is an
n-dimensional vector of the
n observations for the tree diameter at height
i taken from the
jth tree and
kth sample plot;
f is a nonlinear function;
θijk is an
r-dimensional vector of model parameters;
Xijk is an
n ×
r predictor matrix for the
jth tree and
kth sample plot;
εijk is an
n-dimensional vector of residuals;
Rijk is a variance-covariance matrix for error terms;
β is a
p-dimensional vector of fixed parameters;
uijk is a
q-dimensional vector of random parameters, which have multivariate normal distribution with mean 0 and variance-covariance matrix
D;
Aijk is an
r ×
p design matrix of explanatory variables associated with fixed effects of the model; and
Bijk is an
r ×
q design matrix for random effects specific to each tree on the sample plot.
The significance of various combinations of fixed and random effects was tested by the likelihood ratio test during the respective model development. For each of the mixed effects model options, three parameters were used each time with random effects; the specific effect choice took place so that each one of these parameters regulates the shape of a stem segment, i.e., the bottom, the middle and the upper portion. Parameters influencing each of those segments were taken from [
29]. As a result, a large number of various combinations of models with random parameters was produced. As mentioned above, AIC, likelihood ratio test and graphic analysis of residuals were used to select the best NLME model.
In most of the fitted models, heteroscedasticity of errors (residuals) was found. Its influence was restricted using the commonly used variance (weight) function. The power function was applied [
40] where the value of DBH in centimetres/100 was preferred to be used as the covariate of
X after testing several options:
where
Xjk is DBH of the
jth tree in the
kth plot and
γ1 is a parameter.
To compensate for the effects of autocorrelation, the autoregression model of the 1st order (corCAR1) was used with the measuring point height being a continuous covariate.
2.4. Calibration Strategy of NLME Model
As stated above, calibration of the NLME model was carried out for sample stems and localities in the validation dataset. The calibration of the stem taper curve model as such was done according to the procedure used in [
42]. As part of the model calibration, two methods of taking additional measurements of the tree diameter at a particular height on the stem (the upper stem diameters) were tested.
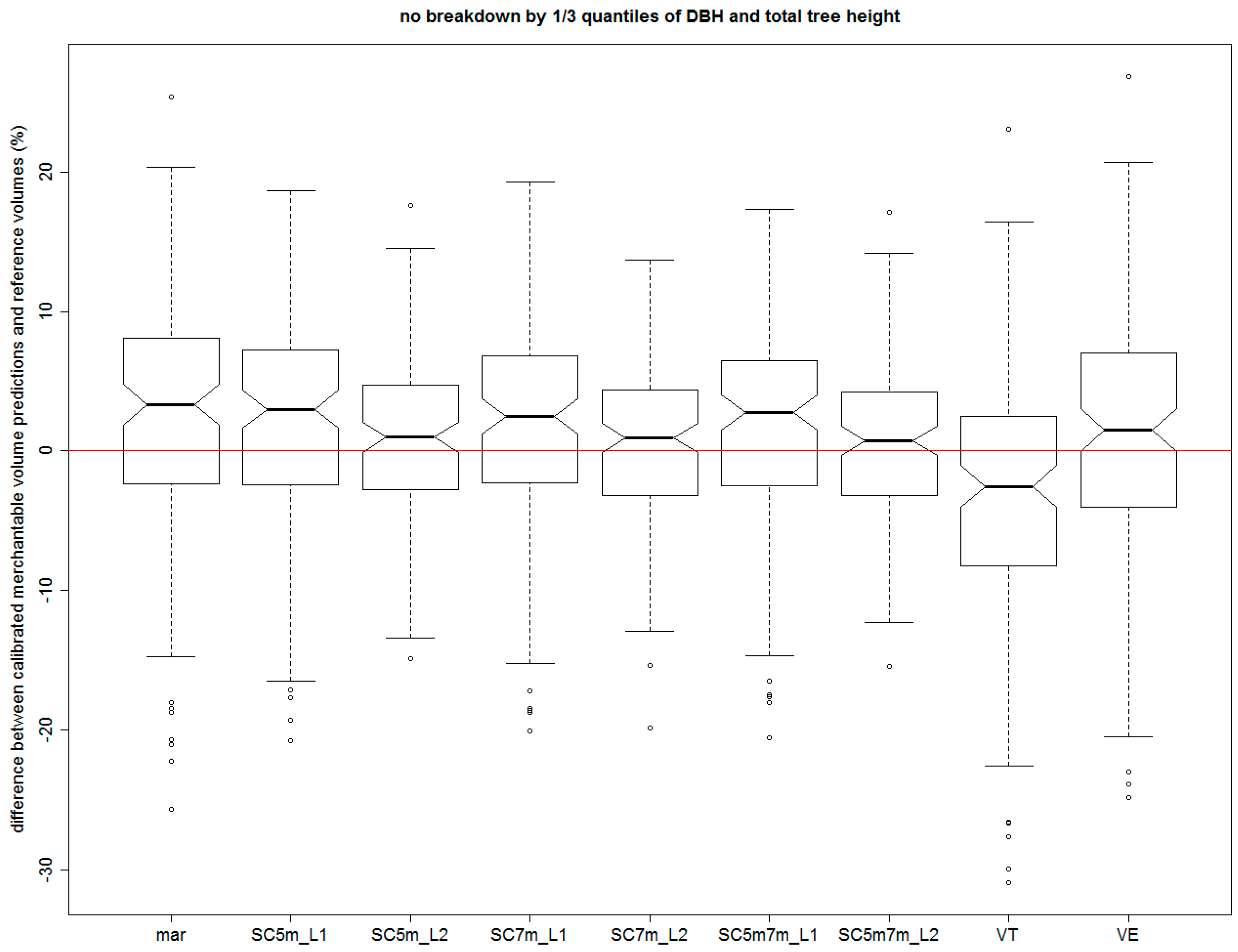
The first method used remote upper diameter measurements through an optical device, the Meopta telescope. In all of the measuring points studied on the stem, the diameter was always measured from exactly the same position. As a result, all the measuring points of one stem shared a single measurement direction that was marked by spraying on the still standing sample tree. In the text which follows, the term “calibration type” refers to one of the three options: (i) calibration using the diameter measured at a height of 5 m only; (ii) calibration using the diameter measured at a height of 7 m only; or (iii) calibration using the diameters measured at both of these heights. The calibration was carried out at two levels—L1 and L2 corresponding to the hierarchical structure of the NLME model. In terms of the L1 level, the STC model accounts for specific condition of a particular location. Therefore, predictions at the L1 level include random effects of localities, but no sample tree specific random effects. L1 predictions can even be obtained for trees without any upper diameter measurement, provided there is another sample tree within the same locality, on which upper diameter measurement was measured. The L2 level predictions include random effects of locality as well as random effects of sample trees (within locality). More formally, one could write L1/L2 instead just L2, but for sake of simplicity the most detailed hierarchical level of mixed model is marked by L2 in this paper. L2 predictions can only be obtained for sample trees on which upper diameter was actually measured.
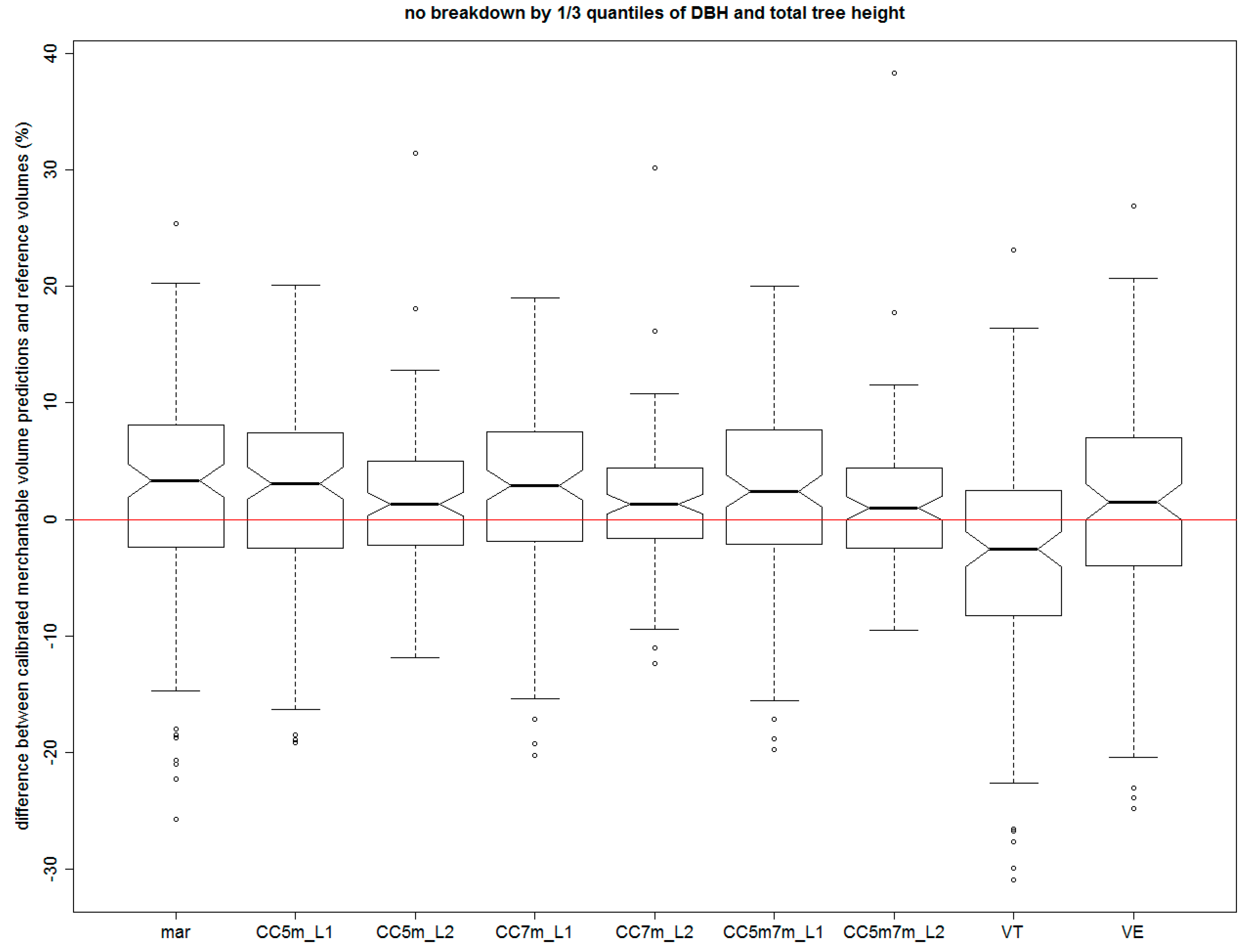
The second calibration method was based on the contact measurement when diameters were measured at identical measuring points, i.e., at the same heights and direction as with the optical measurement. This measurement was done after felling the sample tree. Calibration was done, once again, using three types, i.e., using the diameter at (i) 5 m; (ii) 7 m; or (iii) both of these heights. For this method, two modifications were developed. In the first, the diameter was measured only once at each measuring point (in the same direction as with the remote measurement method). In the second case, the diameter was measured twice using two mutually perpendicular caliper positions at each of the measuring points. Consequently, the arithmetic mean was calculated from the two perpendicular measurements. This cross-directional contact measurement was carried out in order to determine whether or not the mean upper diameter obtained from the two measurements leads to a better calibration and a better prediction compared with the single-directional contact diameter measurement. Cross-directional measurements, however, were not carried out exactly at the point of optical measurements. Rather, they had to be obtained from independently obtained stem profiles (after felling) through selecting a measuring point that was closest to the location of that optical measurement. Due to the length of segments of stem profiles on the felled sample trees being two metres maximum, the distance of the position of the cross-directional contact measurement point from that of the optical measurement point never exceeded one metre. In this option, too, calibration was carried out at the L1 and L2 hierarchical levels.
Calibration measurements were carried out following nine different approaches; taking the hierarchical levels L1 and L2 of the mixed effects model into account, this led to 18 different calibration procedures that were tested in our analysis.
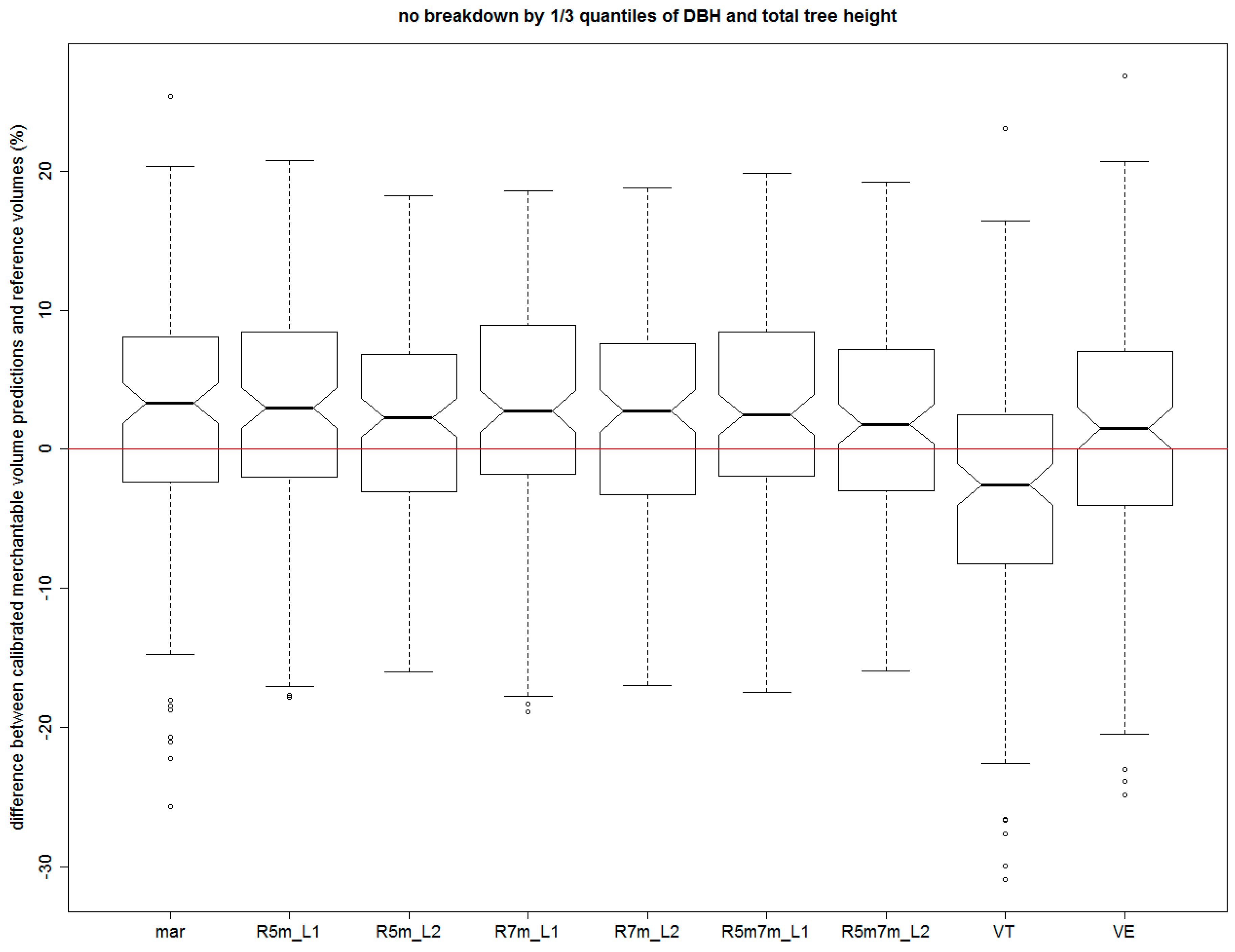
2.5. Analysis of Volume Estimation Errors
The merchantable volume of the stems for which the calibration of the NLME model was performed was determined using the numeric integration of STC. The same method was applied to derive the merchantable volume of stems when using marginal (uncalibrated) NLME model (i.e., all random effects set to zero corresponding to a situation with no upper diameter measurements). The volume determined by integrating the natural cubic spline (from the stump height to the diameter of 7 cm including bark) was used as a reference volume, to which all predictions were compared (see
Section 2.2). Merchantable volume of stems was also derived on the basis of the two standard procedures used in forestry practice of the Czech Republic. These involved Czech–Slovak volume equations (VE) [
43] and volume tables (VT) [
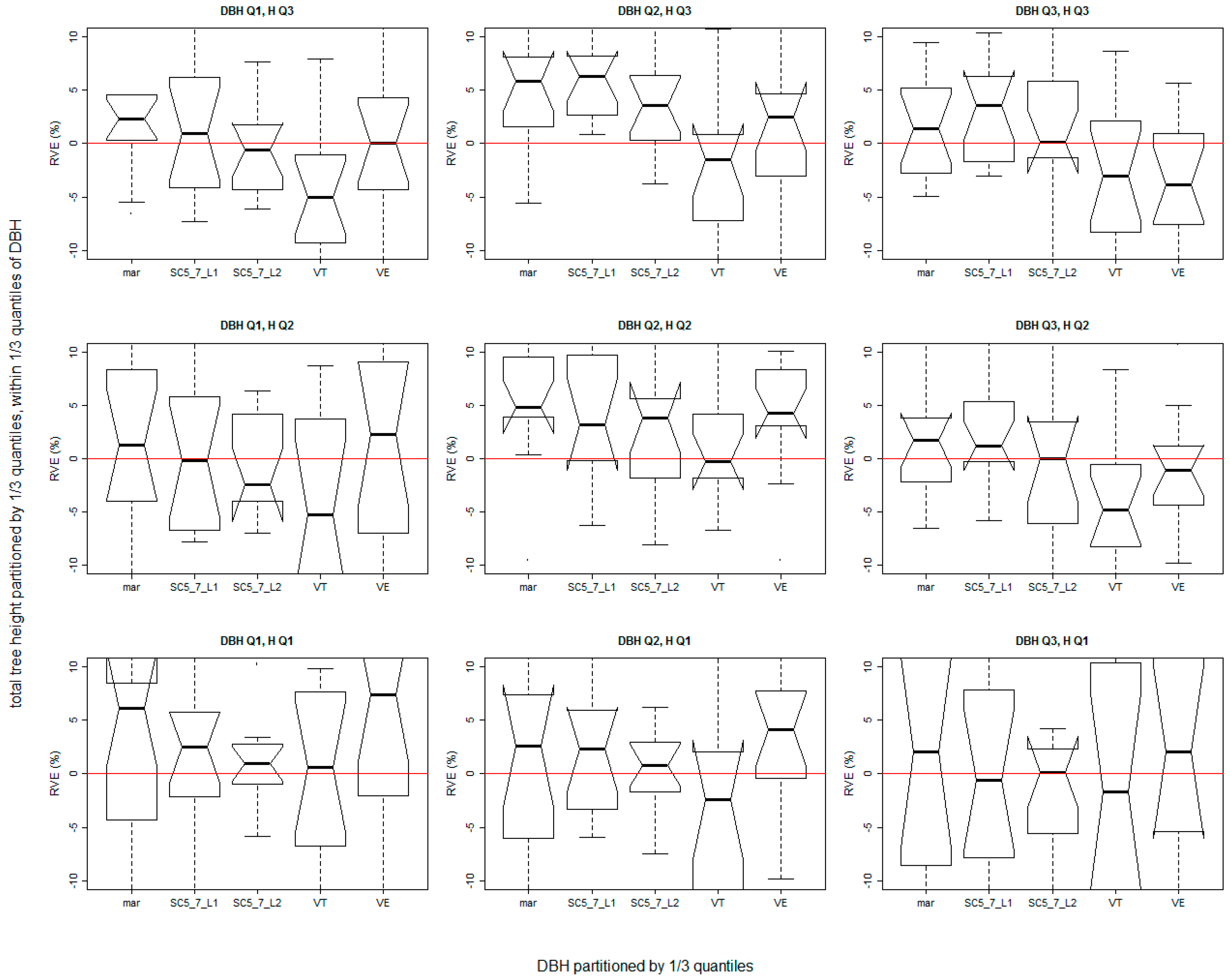
44]. Overall, 22 different merchantable volume predictions were determined for each of the stems belonging to the validation dataset: 18 predictions according to the calibrated NLME models, one according to the marginal NLME model, one according to VE, one according to VT, and finally the reference merchantable volume. The quality of the fitted models was evaluated by means of relative deviations from the reference volume, in terms of their mean and variance. The distribution of the deviations was visualised using boxplots. The box displays the interquartile range, and the middle of the box represents the median with its confidence interval (notches of the box). The whiskers show the minimum and maximum value in the case of the absence of outliers. Dots show outliers, if they are in the dataset. To verify the dependence of relative errors of merchantable volume predictions on the diameter at breast height and the total tree height, a graphical analysis of deviations was supplemented by an analysis of covariance (ANCOVA). In the framework of ANCOVA, the relative error of merchantable volume predictions was entered as the dependent variable; the approach of merchantable volume prediction (calibrated NLME model, marginal NLME model, VE, and VT) was used as a qualitative explanatory variable; and DBH in conjunction with the total tree height were used as a metric, explanatory variables (covariates used independently of each other in two separate ANCOVAs). If ANCOVA results showed rejection of null hypothesis supposing no difference, the differences between pairs of calibration approaches were assessed by Tukey’s multiple comparison test.
The match of the volumes predicted against the reference volume was assessed by regression-based equivalence testing [
45]. Unlike conventional statistical tests (H
0: µ
d = 0), the equivalence test formulates the null hypothesis as H
0: µ
d ≠ 0, where µ
d is a mean value of differences of observed (reference) values and predictions. On the basis of the above, it can be concluded that:
If the null hypothesis is rejected, then the match of the reference values and predicted is significant and the probability of error of this statement does not exceed α;
If the null hypothesis is not rejected, then there is no sufficiently strong statistical evidence of a match between the reference values and those predicted.
This method [
45] fits a regression line between predictions (centred by subtraction of their mean) and observed values. If predictions match the observations, the regression estimate of the absolute term should be close to zero and the estimate of slope should be close to one. Consequently, two one-sided t-tests (TOST) are performed―one for the intercept (testing the potential difference between prediction and observation means, i.e., testing the presence of bias) and the other for slope (testing proportionality, i.e., whether a unit increase of observations is properly reflected by a unit increase of predictions). For each of the two TOSTs, a region of equivalence is established by the analyst, or it might be prescribed by a standard or legal regulation. The equivalence regions reflect how much deviation from zero (test of bias) or one (test of proportionality) one would tolerate as a practically negligible difference from a perfect match between predictions and observations.
An R package termed equivalence [
46] was used to perform these tests. The package makes it possible to reverse the equivalence test and to obtain the smallest region of equivalence that still leads to rejection of the null hypothesis of dissimilarity. Selected approaches of merchantable volume prediction were assessed and mutually compared, namely, on the bases of their respective smallest regions of equivalence.
4. Discussion
To model the STC for Norway spruce in the situation of the Czech Republic, we used the Kozak 02 variable-exponent taper function [
3]. The reason for choosing this was that the function had been evaluated as the most appropriate for STC modelling by a large number of previous studies, from the time the function was published, i.e., 2004. For example, Rojo et al. [
19], having analysed 31 various taper functions for modelling the STC, for maritime pine in the territory of north-west Spain, selected this particular function as the best for the purpose. The same function was identified as the most accurate for estimating stem diameter for
Cupressus lusitanica in Ethiopia [
47]. It was also determined to be the most appropriate for modelling the stem taper model for lodgepole pine for the territory of Alberta, Canada [
23], while recommended for stem taper models of multiple species in the region of Acadia, North America [
16,
48]. In Iceland, it was evaluated as the best for modelling STC of lodgepole pine and Siberian larch [
49]. In modelling the stem taper of
Betula pubescens in north-west Spain, the function received recommendations [
25]; it also became the option of choice for
Quercus glauca in South Korea [
50]. It was recommended for modelling stem taper of several tropical species in the area of the Philippines [
51], as well as for estimating stem diameter of
Tectona grandis in mid-western Brazil [
52]. The range of species for which the Kozak function has been recommended, as well as the number of regions for which it has been used, both make it possible to deduce that the taper function is a species-specific function. It means that the accuracy of the resultant model (when determining stem diameter) is dependent on the tree species [
15]. In addition to the tree species, significant factors for the shape of the stem may also include, for instance, the stand density, the technique to recover the stand, the soil type, or the geo-climatic characteristics [
16].
The main disadvantage of variable-form equations—which include the equation of Kozak 02 [
3] —is that any direct analytical integration is not possible in determining the total volume of the stem or parts thereof [
18]. Stem volume needs to be established using the numerical integration of the stem taper curve [
14].
If prediction of the volume is the primary aim of the stem taper curve modelling, it is more appropriate to use the cross-sectional area of the stem than the diameter as the variable to be predicted [
53,
54,
55]. The reason for this is the transformation of the probability distribution of diameter errors (assuming a zero mean value and a normal, i.e., symmetrical, distribution of errors) by power of two (to calculate the cross-sectional area), i.e., by a convex function. The result of this transformation is a non-symmetrical (right-skewed) distribution of cross-section area prediction errors with mean values higher than zero (see Jensen’s inequality). As the taper curve integration is carried out along the stem length, the transformation-based overestimation of the cross-sectional area leads to overestimation of stem volume.
At this point it should be noted that even determining the actual volume by measuring the diameter at regular intervals of the stem length (segment by segment), leads to an overestimation of volume, due to transformation of the presumably symmetrical distribution of diameter measurement errors into the right skewed distribution of cross-section area errors. It can be shown easily that a systematic overestimation of cross-section area corresponding by a few millimetres of diameter will cause an overestimation of timber volume in the order of percent units. In addition, this overestimation increases with increasing size of the stem.
Cross-sectional areas were also selected as more appropriate for modelling, when compared with tree diameter, in previous studies, e.g., [
56] or [
57].
Predicting merchantable volume of standing stems achieved the best results when using one contact measurement of diameter at a height of 7 m. Although some options of cross-directional contact measurements appeared to be applicable (e.g., cross-directional contact measurements carried out at 5 and 7 m), they cannot be recommended due to the four-fold increase in time taken and the resulting higher costs. Conformity with our results regarding the number of contact measurements can be found in several different publications. For example, single contact measurement (however at height of 5.3 m) was identified as the most appropriate method, e.g., in the study of [
23]. Equally, [
25] used only calibrations in their studies that were based on a single upper diameter measurement. Their choice, thus our results, can be confirmed by the fact that [
58] also compared the use of one or two calibration contact measurements in their study, and found that the accuracy of the results was comparable, such that it is simply enough to use one additional contact measurement of the diameter at a given height.
Our results also suggest that the use of optical measurement of upper diameters for sake of calibration is, purely from the aspect of the accuracy achieved, less appropriate, because the resulting merchantable volume predictions are affected by somewhat larger systematic errors; or, more accurately, errors in relation to the reference volume. On the basis of equivalence testing, predicting merchantable volume of Norway spruce using STC calibration by means of optical measurements of the upper diameter at 5 and 7 m simultaneously can be recommended if volume prediction errors in the range from 3.2% to 3.7% are acceptable. This accuracy bound could potentially be decreased if a larger validation set of sample trees was used for equivalence testing. With the given number of validation stems (126), there is not enough evidence supporting smaller equivalence regions.
The position of the calibration measurement is deemed to be a very important parameter which influences the quality of volume prediction. The determination of the number and the position of calibration measurements is always a compromise between the requirement to achieve the highest accuracy of prediction as possible, and time and financial demands of the measurement itself as well as the accuracy thereof; generally, diameters measured at lower heights are more precise and easier to measure compared with those measured at higher stem positions. Arias-Rodil et al. [
21] recommend a single measurement for STC calibration; more measurements would be unprofitable in terms of measurement time/cost demand. They do not recommend calibration measurements near the foot or peak of the stem, since models calibrated this way are normally worse than the OLS model; instead, measurements are recommended to be taken between 40% and 60% of height. This is in accordance with the recommendation of [
59] who proposed calibration measurement at 60% height for loblolly pine in the southern U.S. states, and for radiata pine in New Zealand. Arias-Rodil et al. [
22] recommend 50% to calibrate the measurement for radiata pine in Spain. Measurements taken at 50% of height are also recommended as an initial situation for calibration [
26,
27]. Gómez-García et al. [
25] used Kozak’s function to predict the stem taper of
Betula pubescens in north-west Spain. In terms of the height of the calibration measurement, they examined the values in the range of 2–8 m, and found that the quality of prediction is connected with which parameters possess the random component, in addition to the fixed component; they studied a total of 55 options for expansion of one or two parameters. From that aspect, they distinguished two groups of models, from which one group was represented by the best model with random effects for the parameters of
a1 and
b0, and was significantly better for lower calibration heights, i.e., up to 5 m. For higher calibration heights, the quality of prediction was similar to the second group represented by a model with random effects for the parameters of
b0 and
b6; this model was evaluated as the best for a calibration height of 8 m. Gómez-García et al. [
25] recommended accordingly—for ease and accuracy of measurements—using rather lower calibration heights where both groups of models are comparable in terms of quality. They also recall that, in many cases, attempts were made to include other variables in the calibration process; this mostly involved variables associated with the dimensions of the crown, age, and other tree/stand characteristics, e.g., [
60,
61,
62]. A widely accepted conclusion is that the inclusion of these variables improves the quality of calibration by only very little, and is not viable considering the efforts made to obtain the variables, e.g., the parameter of
d/h contained in the Kozak 02 model [
3] has a close relationship with the size of the crown and characteristics of the stand [
60,
63], so it is not necessary to make the calibration process more complicated by adding more variables. If comparing recommended heights of calibration measurements, as indicated in the studies mentioned above, it is possible to conclude that the calibration heights of 5 and 7 m that we used match these recommendations.
5. Conclusions
With regard to the prediction of the merchantable volume of stem, the best STC model identified (within the Kozak 02 specification) fitted gi instead of di.
Prediction of merchantable wood volume of Norway spruce by integration of STC Kozak 02 [
3], after calibration by means of optical upper diameter measurement (on standing stems), tends to underestimate the reference volume. Underestimations of reference volume ranging from 2.12% to 2.29% for given height and number of calibration measurements were observed. The determined smallest equivalence regions were 3.7% for bias (or 0.053 m
3 in absolute terms) and 3.2% concerning proportionality (simultaneous use of two upper diameter measurements at the heights of 5 and 7 m). Prediction of merchantable wood volume using this method can be recommended provided these error levels are acceptable. Specifically, in case of the Czech Republic, this merchantable volume prediction approach led to better results than the two national alternatives, the VE [
43] and VT [
44].
The calibration option of NLME of the STC model based on single-directional contact measurement (using a caliper on a felled stem), reduced the mean of relative errors or volume predictions to the range of 0.6% to 1.3% (underestimation of the reference volume). The lowest errors could be obtained for calibration using upper diameter at the height of 7 m. The obtained smallest regions of equivalence for this prediction method were 2.4% (bias, in absolute terms 0.035 m3) and 2.0% (proportionality).
Using calibration based on cross-directional contact measurements (by a caliper on a felled stem) did not lead to a significant reduction of differences between the predicted stem merchantable volume and the reference volume. In this study, the mean values of relative differences between predicted and reference volumes ranged from 1.1% to 1.4% (underestimation of the reference volume). The smallest regions of equivalence obtained for cross-directional upper diameter measurements (both measurement heights, L2) were 2.8% (bias, 0.04 m3 in absolute terms) and 3.5% (proportionality).
According to our results, calibrated predictions of merchantable volume of Norway spruce, based on contact upper diameter measurements (by a caliper, after felling), are more accurate than the optical calibration (by Meopta telescope, measurements on standing trees). However, the difference in the smallest equivalence regions between the best contact measurement calibration (upper diameter at 7 m height, L2 level) and the best optical approach (calibration by upper diameter measurements at 5 and 7 m, L2 level) was about 1.3% (bias) and 1.2% (proportionality). In our view, such small differences do not pose a sufficient argument for a clear preference of contact measurements or exclusion of optical measurements of upper diameters. It has to be emphasised that the results of contact measurements (by a caliper) were obtained after the respective sample trees were felled. Therefore, such accuracy can hardly be expected unless sample trees are felled which is not permissible in case of the non-destructive Czech National Forest Inventory. The value of results obtained for mechanical upper diameter measurements consists in showing the theoretically best accuracy of the merchantable volume prediction by the Kozak 02 function when applied to Norway spruce in Czech conditions.
Moreover, we cannot ignore the fact that measurement devices are not commonly available (at least on the European market), that would allow contact measurements of upper diameter on standing trees (e.g., at 7 m) with an accuracy comparable to that of a mechanical caliper (with double arm, on a felled tree). Optical measurements of upper diameter on standing trees are feasible under normal circumstances and it can be assumed that these methods will be gradually perfected.